Как найти вершины треугольника зная уравнения сторон

Найти вершины треугольника зная уравнения сторон

Стороны треугольника заданы уравнениями:

Найти координаты вершин треугольника.

Координаты вершины A найдем, решая систему, составленную из уравнений сторон AB и AC:

Систему двух линейных уравнений с двумя неизвестными решаем способами, известными из элементарной алгебры, и получаем

Вершина A имеет координаты

Координаты вершины B найдем, решая систему из уравнений сторон AB и BC:

получаем .

Координаты вершины C получим, решая систему из уравнений сторон BC и AC:

Вершина C имеет координаты .

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

Уравнения сторон треугольника

Как составить уравнение сторон треугольника по координатам его вершин?

Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.

Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)

Составить уравнения сторон треугольника.

1) Составим уравнение прямой AB, проходящей через 2 точки A и B.

Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:

Таким образом, уравнение стороны AB

2) Прямая BC проходит через точки B(7;-4) и C(3;7):

Отсюда уравнение стороны BC —

3) Прямая AC проходит через точки A(-5;1) и C(3;7):

[spoiler title=”источники:”]

http://www.matburo.ru/ex_ag.php?p1=agtr

[/spoiler]

Найти координаты вершин треугольника,
если стороны заданы уравнениями:

x – 2y + 3 = 0;
2x – y – 3 = 0;
x + y – 3 = 0;

Дано: АВ: х-2у+3=0, АС: 2х-у-3=0, ВС: х+у-3=0

Найти: А,В и С.

Решение.

Найдем вершины треугольника АВС, как
точки пересечения сторон треугольника.

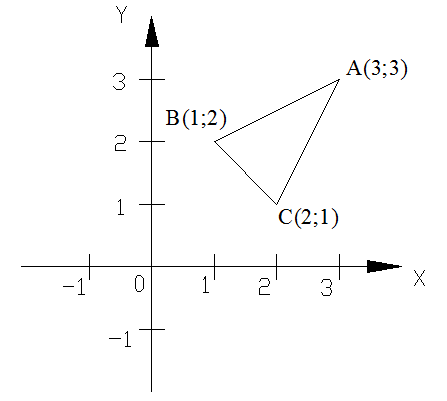
т.А:

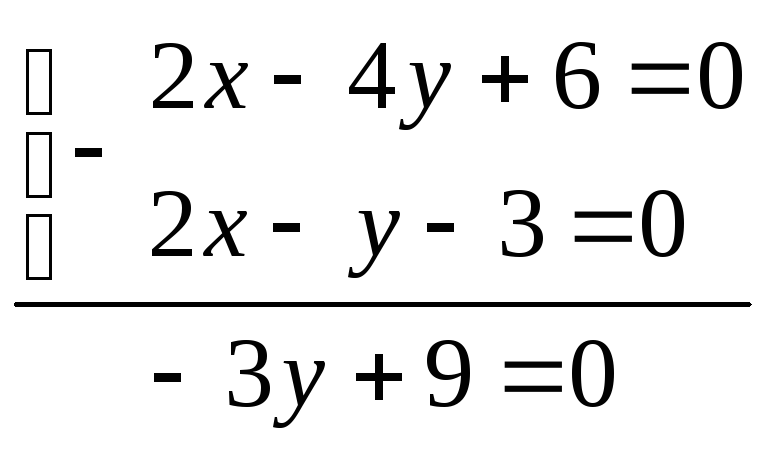
3у=-9 у=3,
x-2*3+3=0, у=3, х=3

имеем: A(3;3)

т. В:

.

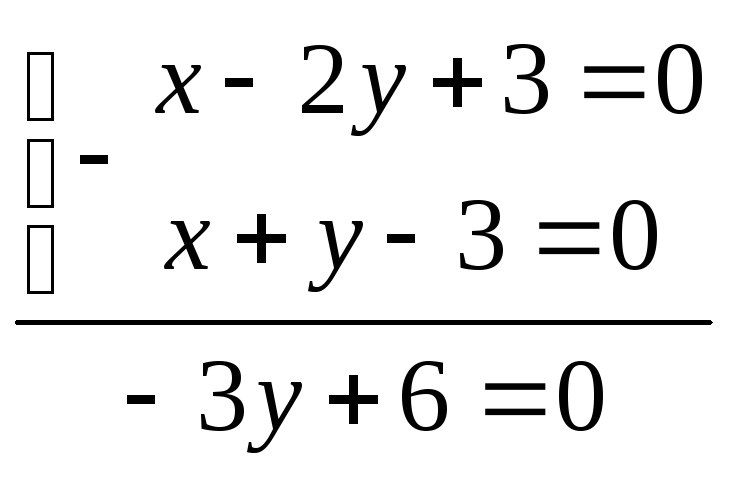х-2*2+3=0,
у=2, х=1

имеем: т. B(1;2)

т.С :

.

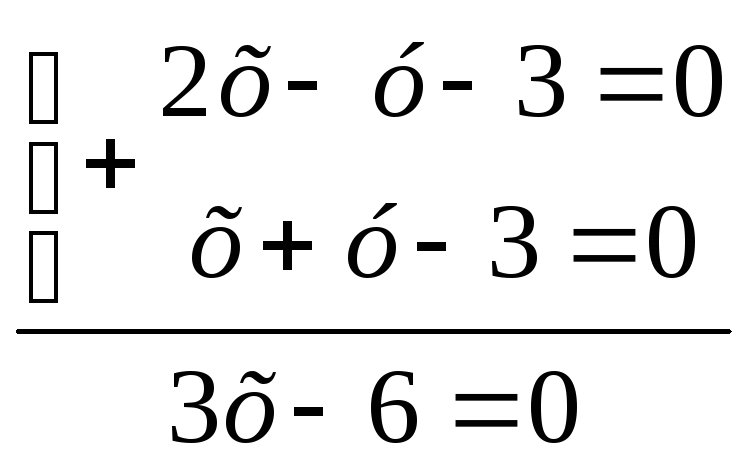3х=6 х=2, 2+y-3=0,
х=3, y=1

имеем: т. C(2;1)

Ответ: координаты вершин треугольника:
А (3;3); В(1;2); С(2;1).

Задача №2

Даны вершины треугольника:;2);

;3);

;1).

Написать уравнение высоты, опущенной
из точки

Решение

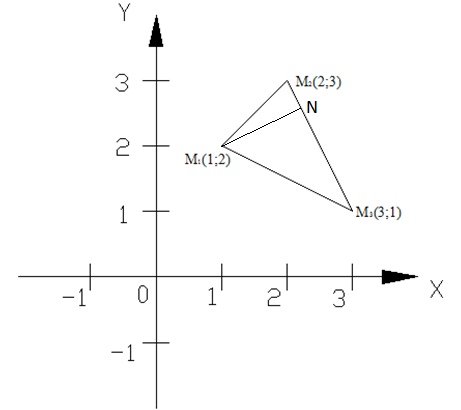
Дано:
(1;2);
(2;3);

(3;1)
– вершины треугольника

Решение: проведем из точки
высоту
к стороне

запишем уравнение стороны

_{откуда имеем}

-2х+4-у+2=0,

у+2х-6=0, у = -2х+6, т.е. угловой коэффициент
прямой k= -2. Тогда, угловой
коэффициент перпендикулярной прямой
(высоты
)
будет
.
Найдем уравнение высоты, как уравнение
прямой, проходящей через одну точку:
y-y₁
=k(x-x₁),
Где x₁ и y₁
– координаты точки .

y-2=
(x-1), откуда имеем 2y-x-3=0

.

откуда, преобразовав, получим

_2у-х-3=0

Ответ: уравнение высоты 2у-х-3=0

Задача №3.

Даны
вершины треугольника M₁M₂M₃:
М₁(-3;0), M₂(2;5),
M₃(3;2).

а)
Найти периметр треугольника, вершинами
которого служат середины сторон.

б)
Найти периметр треугольника, вершинами
которого служат основания высот,
проведенных из вершин M₁
M₂ M₃
к противоположным сторонам.

в)
Найти периметр треугольника, вершинами
которого служат основания биссектрис,
проведенных из вершин M₁
M₂ M₃
к противоположным сторонам.

Решение.

а)
Построение:

К, Е,
F – середины соответствующих
сторон М₁М₃, М₁М₂,
М₂М₃.

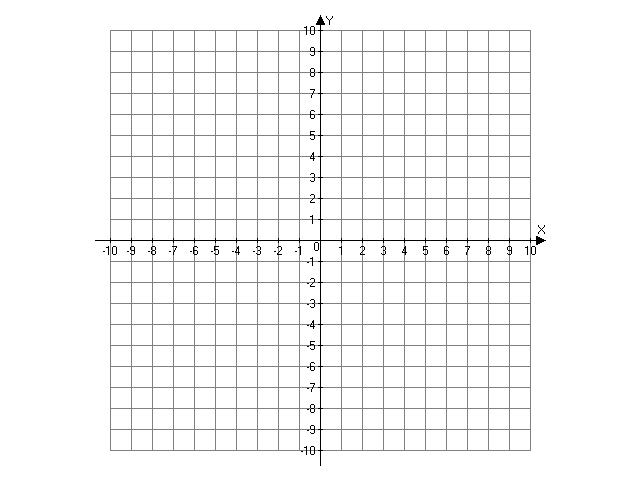
F

E

K

M₁

M₂

M₃

К –
середина М₁М₃, тогда координаты
середины стороны будут:

Тогда К(0;1).

Е –
середина М₁М₂, тогда координаты
середины стороны будут:

тогда Е(-0,5; 2,5).

F
– середина М₂М₃, тогда
координаты середины стороны будут:

.

тогда
F(2,5; 3,5).

KF=

Аналогично: EF=;
EK=.

Тогда периметр
треугольника будет:

б)

M₁

M₂

M₃=N=M

K

Где
М₁ ?

Покажем,
что треугольник прямоугольный и его
три высоты не могут составить замкнутую
фигуру.

Найдем
уравнение стороны М₁М₂:

откуда имеем

5x+15=5y;
y=x+3. Хорошо
видно, что угловой коэффициент этой
прямой k₁=1, а

т. к. высота М₃К перпендикулярна
стороне М₁М₂, то k₂

Используя уравнение прямой через точку:
у-y₁=k(x-x₁)
имеем

M₃K:

y-2=-1(x-3),
y-2=-x+3
откуда получаем y+x-5=0.

Уравнение
пучка прямых:

.

2y=8,

y=4,
то x=1, тогда М₃КМ₁М₂=К(1;4).

Найдем
уравнение стороны М₂М₃:

.

-3x+6=y-5,
y=-3x+11, откуда
видно что угловой коэффициент этой
прямой k₁=-3,

т. к. М₁N
перпендикуляреныМ₂М₃, k₂

тогда уравнение стороны М₂М₃
будет

,
3y-x-3=0

Уравнение
пучка прямых:

.

у=11-3x,
33-9x-x-3=0.
x=3 y=2, то
x=3,

тогда
М₁NМ₂М₃=N(3;2).

Найдем
уравнение стороны М₁М₃:

.

2x+6=6y,
3x-x-3=0,

y=x+1,
k₁=,
то k₂
т. к. М₂M перпендикулярна
М₁М₃, k₂=.
Найдем уравнение
стороны М₁N:

y-5=-3(x-2),
y-5=-3x+6,
y+3x-11=0.

Уравнение
пучка прямых:

.

y=2,
то x=3,

тогда М₂MМ₁М₃=N(3;2).

Имеем:

KN=;
КM=;
NM=0; т.е. мы доказали, что

ΔКNM не существует

_в)Построение:
М₁А, М₂В и М₃С –
биссектрисы углов при вершинах М₁М₂
М₃

A

C

B

M₃

M₂

M₁

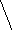
Найти
периметр треугольника АВС

1)

.

(у-х-3)=3у-х-3;

у-х-3=3у-х-3;

у(-3)+х(-+1)+(3-3)=0
– уравнение биссектрисы

2)

.

(у-х-3)=у+3х+11;

у-х-3=у+3х+11;

у(-1)+х(--3)+(-3+11)=0
– уравнение биссектрисы

3)

.

3у-х-3=у+3х-11;

2у-4х+8=0 – уравнение
биссектрисы

Найдем основания биссектрис, как точки
пересечения сторон треугольника и с
ответствующей биссектрисы :

1)
=-4_;

=-20+20;

₌

.

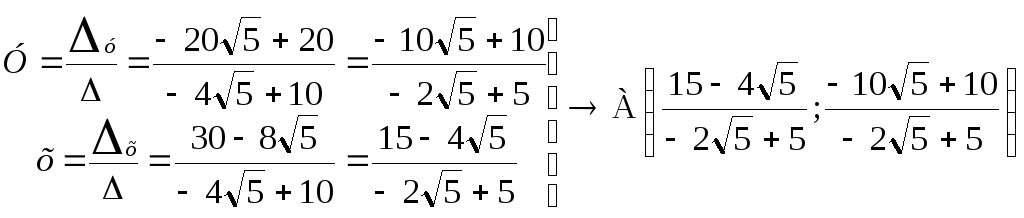2)

_;

;

.

.

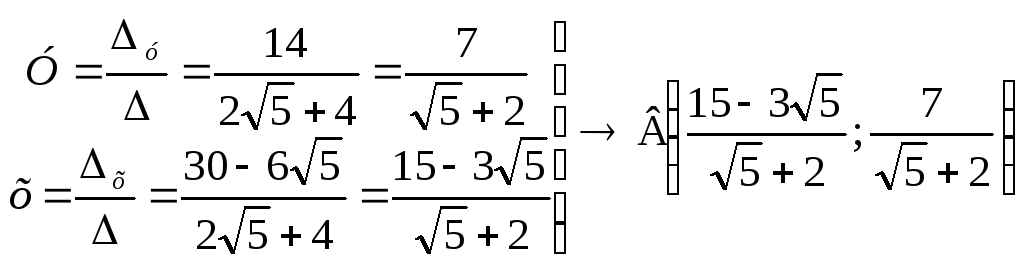3)

.

у =10,
х=7 Следовательно С(7,0)

Найдем

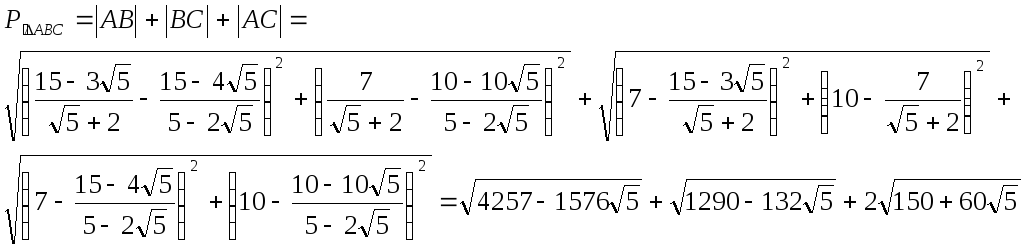
Задача №4

Даны вершины равнобедренного треугольника

а)Доказать, что середины сторон
равнобедренного треугольника являются
также вершинами равнобедренного
треугольника.

б) Доказать, что биссектриса, проведенная
из вершины при основании равны.

в) Медианы, проведенные из вершин при
основании равны.

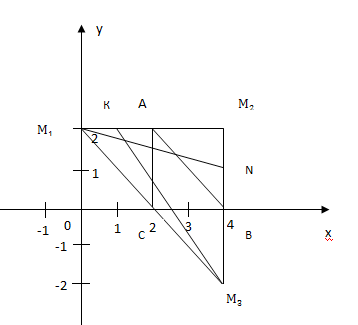
а)Дано: ΔАВС

Доказать, что середины сторон
равнобедренного треугольника являются
также вершинами равнобедренного
треугольника.

Доказательство.

Найдем середины сторон треугольника

1) Найдём середину отрезка A

А(2;
2)

2) Найдём середину отрезка B

В(4;0)

3) Найдём середину отрезка C(

С(2;0)

4)
АС=CB

треугольник
АВС – равнобедренный, что и
требовалось доказать

б)Дано:

Доказать, что биссектриса, проведенная
из вершины при основании равны.

Доказательство.

1)

Найдём каноническое уравнение 2-ух точек
M₃, M₁

4-x=y+2,

x+y-2=0

x-4=0

Найдём каноническое уравнение 2-ух точек

y+x-3=

у+(1-

_у=2,

y-2=0

.

Составим систему уравнения из

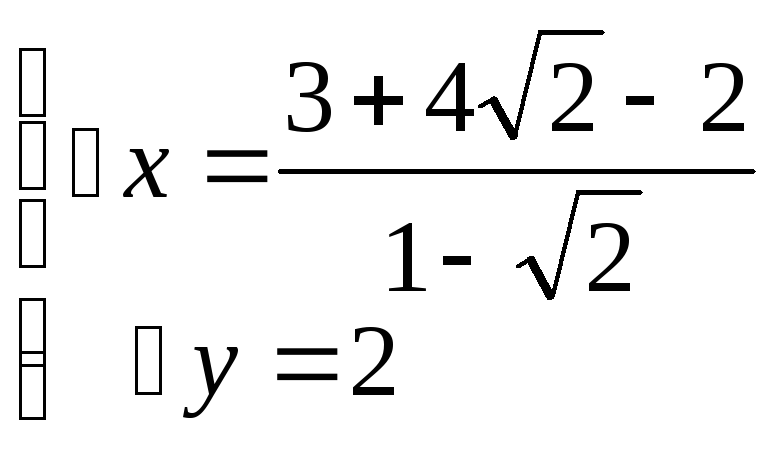
K

Найдем длину.

2) Найдём каноническое уравнение 2-ух
точек

у

Составим систему уравнения из

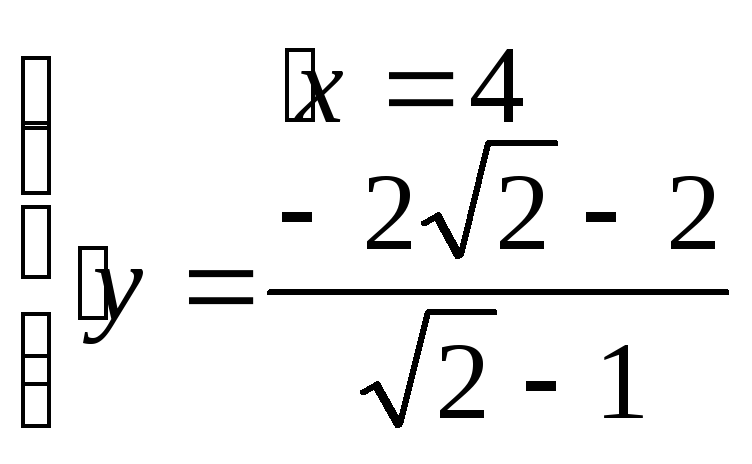
Найдем длину

что и требовалось доказать

в)Дано: ΔАВС и
оказать,
что медианы, проведенные из вершин при
основании равны.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Раз уж вы нашли косинус и синус угла в треугольнике – дальше вы можете просто повернуть на этот угол вектор одной из сторон и получить направление второй стороны, а дальше нужно лишь изменить длину вектора.

Но есть и решение в векторах, вообще без тригонометрии.

---

Рассмотрим задачу в общем виде: у нас заданы вершины A и B, нам надо найти третью вершину треугольника С зная прилежащие к ней стороны – AC=a и BC=b соответственно. Построим окружности нужных радиусов с центрами в точках A и B, и тогда точка C как раз будет на их пересечении:

Обозначим через rA, rB и rC радиус-векторы точек. Тогда получаем следующую систему уравнений:

(rC-rA)² = a²
(rC-rB)² = b²

Решив её относительно rC можно получить ответ. Для решения первым делом вычтем одно уравнение из другого, чтобы избавиться от квадрата rC:

(rC-rA)² - (rC-rB)² = a² - b²
(rC² - 2rCrA + rA²) - (rC² - 2rCrB + rB²) = a² - b²
2rC(rB-rA) + rA² - rB² = a² - b²
2rC(rB-rA) = a² - b² - (rA² - rB²)

У нас получилось, внезапно или не очень, уравнение прямой в одном из своих форм. Этой прямой по построению принадлежат точки C и C’ – значит, это уравнение прямой CC’. Кстати, разности rB – rA будет в дальнейшем встречаться часто, поэтому обозначим её как AB (потому что это и есть вектор стороны AB).

В принципе, на этом этапе можно перейти от векторного вида к координатному, выразить через это уравнение переменную y через x или наоборот, подставить в любое уравнение окружности и решить обыкновенное квадратное уравнение. Однако, любого кто так попытается сделать, ожидает засада под названием “сингулярность”: если прямая CC’ вертикальная, то при попытке выразить y через x в формуле будет деление на ноль, а если она горизонтальная – деление на ноль будет при попытке выразить x через y.

Можно было бы просто разобрать два случая, но есть вариант лучше. Для этого надо перейти к параметрическому виду уравнения прямой СС’. Напомню, что параметрический вид уравнения прямой выглядит вот так:

r = r0 + t u

Чтобы получить параметрическое уравнение прямой, нужно знать направляющий вектор и любую точку на этой прямой. Точки C и С’ мы узнать не можем (точнее можем, но если узнаем – задача будет уже решена), поэтому попытаемся найти точку пересечения прямых CC’ и AB.

Это сделать не так сложно как кажется, потому что у нас есть уравнение прямой CC’ и мы можем составить параметрическое уравнение прямой AB:

r = rA + tAB
2r·AB = a² - b² - (rA² - rB²)

Подставим первое уравнение во второе и решим его относительно переменной t:

2(rA + tAB)·AB = a² - b² - (rA² - rB²)

2rA·AB + 2t AB² = a² - b² - (rA² - rB²)

t = (a² - b² - rA² + rB² - 2rA·AB) / 2AB²

t = (a² - b² - rA² + rB² + 2rA² - 2rA·rB) / 2AB²

t = (a² - b² + rA² + rB² - 2rA·rB) / 2AB²

t = (a² - b² + (rA - rB)²) / 2AB²

t = (a² - b² + AB²) / 2AB²

Осталось подставить эту переменную обратно в параметрическое уравнение:

t = (a² - b² + AB²) / 2AB²
r0 = rA + tAB

Формула выглядит страшно, но не имеет сингулярностей пока A и B – разные точки. Даже в случае некорректных начальных данных у тут будет какое-то решение.

Кстати, для проверки корректности формулы можно подставить сюда вырожденные треугольники: при a=0, b=AB точка r0 окажется равна rA; а при a=AB, b=0 точка r0 окажется равна rB. Пока всё нормально.

И так, у нас есть точка r0, осталось найти направляющий вектор прямой CC’. Ну, это тоже просто: надо лишь взять вектор AB и повернуть его на прямой угол в любую сторону. Это делается тоже просто, если вектор AB был с координатами (xB – xA, yB – yA) – то повёрнутый будет с координатами (-yB + yA, xB – xA). Почему так – объясняется по ссылке, которую я уже приводил ранее. Обозначим его через AB^.

Ну, теперь у нас есть параметрическое уравнение прямой CC’ и уравнение одной из окружностей, осталось их пересечь и мы найдём точки C и C’.

rC = r0 + k AB^
(rC-rA)² = a²

И снова мы можем просто подставить одно уравнение в другое (вот почему я так люблю параметрические уравнения прямых в задачах на геометрию!):

(r0-rA + k AB^)² = a²

k² AB^² + 2k AB^ (r0-rA) + (r0-rA)² - a² = 0

Тут есть и дальнейшие упрощения: вектор r0–rA сонаправлен AB, а потому при умножении на AB^ будет чистый ноль, можно и не считать. Кстати, длина вектора AB^ равна длине вектора AB, что тоже позволяет чуть упростить формулу.

Суммируя всё что написано выше, получаем следующую систему уравнений:

t = (a² - b² + AB²) / 2AB²
k² AB² = a² - t² AB²
r0 = rA + t AB
rC = r0 + k AB^

Осталось решить примитивное квадратное уравнение:

t = (a² - b² + AB²) / 2AB²
k = ± sqrt(a² / AB² - t²)
rC = rA + t AB + k AB^

Дальше осталось перейти от векторов к координатам и решение готово.