Как найти вертикальное перемещение точки - Сайт, где вы сможете решить свои вопросы

Задача. Для балки определить перемещения в т. А, В, С, D, подобрать сечение из двух швеллеров из условия прочности, проверить жесткость, показать изогнутую ось балки. Материал — сталь Ст3, допускаемое перемещение .

Определим опорные реакции.

Наносим значение опорных реакций на расчетную схему

2. Строим эпюру моментов от заданной нагрузки – грузовую эпюру М_F.

Т.к. под равномерно распределенной нагрузкой линия параболическая кривая, то для её проведения потребуется дополнительная точка – поставим т.К в середине нагрузки.

Строим эпюру М_F от заданной нагрузки.

3. Подберем сечение из двух швеллеров:

Подбираем 2 швеллера №33 см³.

Проверим прочность подобранного сечения.

Прочность обеспечена.

4. Определим перемещения в заданных точках. Снимаем с балки всю нагрузку. Для определения линейных перемещений (прогибов) прикладываем единичную силу (F=1), а для определения угловых перемещений — единичный момент .

Точки А и В – это опоры, и по граничным условиям в шарнирных опорах прогиб невозможен, а угловое перемещение присутствует. В точках С и D будут и линейные (прогибы), и угловые (углы поворота) перемещения.

Определим угловое перемещение в т.А. Прикладываем в А единичный момент (рис. б). Строим эп , определяем в ней необходимые ординаты. (рис. в).

Ординаты эп.М_F – все положительные, эп. – тоже.

Перемещения будем определять методом Мора по формуле Симпсона.

Определим момент инерции I_х для сечения.

Модуль продольной упругости Е для Ст3 Е = 2·10⁵МПа = 2·10⁸кПа. Тогда:

Угол поворота φ_А получился положительным, это значит, что угол поворота сечения совпадает с направлением единичного момента.

Определим угол поворота φ_В. (рис.г,д )

Теперь определим перемещения в т. С (линейное и угловое). Прикладываем единичную силу (рис. е), определяем опорные реакции и строим эп. от единичной силы (рис.ж).

Рассмотрим рис. е.

Строим эп. :

Определим прогиб в т. С.

Для определения угла поворота в т. С приложим единичный момент (рис. з), определим опорные реакции и построим эпюру единичных моментов (рис. и).

(знак “— “ говорит о том, что реакция R_А направлена в обратную сторону. Показываем это на расчетной схеме – рис.з).

Строим эп. ,

Поскольку m=1 приложен в т. С пролета балки, то момент в т. С определим как от левых, так и от правых сил.

Определим прогиб в точке С.

(знак «-» говорит о том, что угол поворота направлен противоположно направлению единичного момента)

Аналогично определим линейное и угловое перемещения в т. D.

Определим у_D. (рис. к).

Строим эп. (рис.л) :

Определим φ_D (рис. м):

Строим эп. — (рис.н).

Определим угол поворота:

(угол поворота направлен в сторону, противоположную единичному моменту).

Теперь покажем изогнутую ось балки (упругую линию), которой стала прямолинейная ось под действием нагрузки. Для этого зарисуем первоначальное положение оси и в масштабе отложим вычисленные перемещения (рис.о).

Проверим жесткость балки , где f – максимальный прогиб.

Максимальный прогиб — жесткость не обеспечена.

Т.о. в данной задаче мы убедились в том, что не всегда сечения, подобранные из условия прочности (в данном случае – сечение из двух швеллеров) удовлетворяют условиям жесткости.

Задача. Определить горизонтальное перемещение свободного конца рамы по интегралу Мора

1. Составляем выражение изгибающего момента M_F от действующей нагрузки.

2. Снимаем с балки все нагрузки, и в точке, где необходимо определить перемещение, прикладываем единичную силу (если определяем линейное перемещение) либо единичный момент (если определяем угловое перемещение) по направлению искомого перемещения. В нашей задаче прикладываем горизонтальную единичную силу. Составляем выражение изгибающего момента.

Определяем моменты от единичной нагрузки F=1

По интегралу Мора вычисляем горизонтальное перемещение:

Перемещение имеет положительное значение. Это значит, что оно соответствует направлению единичной силы.

Интеграл Мора, формула Мора. В криволинейном брусе определить горизонтальное перемещение точки А. Жесткость в пределах всей длины бруса постоянна.

Ось бруса очерчена по параболе, уравнение которой:

Учитывая, что брус безраспорный и достаточно пологий (f/ι = 3/15 = 0,2), влиянием продольных и поперечных сил пренебрегаем. Поэтому для определения перемещения воспользуемся формулой:

Так как жесткость EJ постоянна, то:

Составим выражение M₁ для действительного состояния бруса (1-го состояния) (рис. а):

Снимаем с бруса все нагрузки и прикладываем в точке А горизонтальную единичную силу (2-е состояние) (рис. б). Составляем выражение для :

Вычисляем искомое перемещение в точке А:

Знак минус указывает на то, что перемещение точки А противоположно направлению единичной силы, т.е. это точка смещается по горизонтали влево.

Интеграл Мора, формула Мора.Определить угол поворота шарнирной опоры D для рамы с определенными опорными реакциями, Жесткости элементов указаны на расчетной схеме.

Составим выражение М₁, используя схему системы в 1-м состоянии. М₁ – функция внутреннего изгибающего момента на силовом участке для заданной балки или рамы от действия заданных нагрузок 1-го состояния.

Освобождаем раму от нагрузок, прикладываем единичный момент на опоре D, получаем систему второго состояния.

Составляем выражения – это функция внутреннего изгибающего момента на силовом участке для вспомогательной системы 2- го состояния, нагруженной единичным усилием:Находим искомое перемещение — угол поворота по формуле (интегралу) Мора:Значение угла поворота положительно, значит направление соответствует выбранному направлению единичного момента.

Интеграл Мора (формула Мора). Для рамы определить горизонтальное перемещение точки C. Жесткости элементов указаны на рисунке. Назовем заданную систему системой первого состояния. . Составляем для каждого элемента выражение М₁, пользуясь схемой 1-го состояния системы:

Снимаем с рамы все нагрузки и получим 2-е состояние рамы, приложив по направлению искомого перемещения горизонтальную единичную силу. Составляем выражение единичных моментов : . Вычисляем по формуле (интегралу) Мора искомое перемещение:

Тогда получим:

Знак минус указывает, что направление перемещения противоположно направлению единичной силы.

Для стальной балки подобрать размеры поперечного сечения, состоящего из двух двутавров, на основе условия прочности по нормальным напряжениям, построить эпюры линейных и угловых перемещений. Дано:

Расчет опорных реакций и значений грузовой эпюры (эпюры изгибающих моментов) приводить не будем, покажем без расчетов. Итак, грузовая эпюра моментов:

При этом на эпюре М у значений изгибающих моментов отсутствуют знаки, указываются волокна, испытывающие сжатие. Как видно из эпюры, в опасном сечении: М_С=М_max=86,7кНм.

Подберем сечение из двух двутавров. Из условия прочности:

Согласно сортаменту прокатной стали выбираем двутавр №27а, у которого I_x₁=5500см³, h=27см. Фактическое значение осевого момента сопротивления всего сечения W_x=2I_x₁/(h/2)=2·5500/(27/2)=815см^3.

Вычисляем линейные и угловые перемещения сечения балки методом О.Мора, применяя формулу Симпсона. Выбор количества сечений, необходимого для построения эпюр линейных и угловых перемещений в балке, зависит от числа участков и характера эпюры изгибающих моментов. В рассматриваемой балке к таким можно отнести сечения А, B, C, D (принадлежат границам силовых участков) и сечения 1, 2, 3 – в середине участков (определение перемещений в этих сечениях повышает точность построения эпюр).

Сечение А. Как известно, линейное перемещение сечения в шарнирной опоре y_A=0.

Для вычисления углового перемещения θ_а загружаем вспомогательную систему единичной парой сил -моментом, равным единицеУравнения равновесия

Решая уравнения равновесия, получим:

Определяем значения моментов в характерных сечениях

Участок АD:

В середине участка АВ значение изгибающего момента грузовой эпюры M_F равно f=73,3·1- 80·1²/2=33,3кНм

Определяем угловое перемещение сечения А по формуле Симпсона:

Угловое перемещение сечения А направлено против часовой стрелки (противоположно действию единичного момента).

Сечение В

Прикладываем в сечении В силу, равную единице, для определения линейного перемещения, и строим единичную эпюру моментов

Уравнения равновесия:

Из решения уравнений равновесия следует:

Определяем значения моментов в характерных сечениях:

Определяем линейное перемещение y_В.

Линейное перемещение y_В=3,65×10^-3м направлено вверх (противоположно действию единичной силы).

Для определения углового перемещения в сечении В прикладываем единичный момент и строим единичную эпюру моментов.

В результате «перемножения» единичной эпюры и грузовой эпюры получим угловое перемещение:

Угловое перемещение направлено против часовой стрелки.

Сечение С.

Линейное перемещение:

Линейное перемещение y_С=5,4 ×10^{-3 м} направлено вверх.

Угловое перемещение:

Угловое перемещение направлено по часовой стрелке.

Сечение D. Линейное перемещение в данном сечении равно нулю.

Угловое перемещение:

Угловое перемещение направлено по часовой стрелке.

Дополнительные сечения:

Сечение 1 (z=0,5ℓ)

Линейное перемещение y₁=1,34×10^-3м направлено вверх;

Угловое перемещение:

Угловое перемещение направлено против часовой стрелки.

Аналогично строим единичные эпюры для сечения 2 (z=1,5ℓ) и сечения 3 (z=2,5ℓ),находим перемещения.

Применяя правило знаков для линейных перемещений вверх — плюс, вниз — минус, а для угловых перемещений против часовой стрелки — плюс, по часовой стрелке – минус, строим эпюры линейных и угловых перемещений y и θ.

Для балки определить максимальный прогиб и максимальный угол поворота.

Ввиду симметрии нагрузки опорные реакции А=В=ql/2

Дифференциальное уравнение изогнутой оси балки:

Интегрируем данное уравнение дважды. После первого интегрирования получаем уравнение углов поворота:

(а)

После второго интегрирования получаем уравнение прогибов:

(б)

Необходимо определить значение постоянных интегрирования — С и Д. Определим их из граничных условий. В сечениях А и В балка имеет шарнирные опоры, значит прогибы в них равны нулю. Следовательно, имеем граничные условия:

1) z = 0, y = 0.

2) z = l, y = 0.

Используем первое граничное условие: z = 0, y = 0.

Тогда из (б) имеем:

Второе граничное условие при z =l дает:

, откуда:

Окончательно получаем.

Уравнение углов поворота:

Уравнение прогибов:

При угол поворота равен нулю, а прогиб будет максимальным:

Знак минус говорит о том, что при принятом положительном направлении оси вверх, прогиб будет направлен вниз.

Наибольшее значение угол поворота имеет на опорных сечениях, например, при

z = 0:

Знак минус говорит о том, что угол поворота при z = 0 направлен по часовой стрелке.

Для рамы требуется определить угол поворота сечения 1 и горизонтальное перемещение сечения 2.

Дано: L=8 м, F=2 кН, q=1 кН/м, h=6 м, моменты инерции I₁=I, I₂=2I

1. Определяем опорные реакции и строим грузовую эпюру:

а) Определяем опорные реакции:

Проверка сошлась. Вертикальные реакции определены верно. Для определения горизонтальных реакций нужно использовать свойство шарнира, а именно — записать уравнение моментов относительно шарнира от всех сил, расположенных с одной стороны рамы.

Проверка сошлась, значит, горизонтальные реакции определены верно.

б) Строим грузовую эпюру — эпюру от заданной нагрузки. Грузовую эпюру будем строить на растянутых волокнах.

Разбиваем раму на участки. На каждом участке намечаем сечения в начале и конце участка, а на участках с распределенной нагрузкой дополнительное сечение в середине. В каждом сечении определяем значение внутреннего изгибающего момента по правилу: изгибающий момент равен алгебраической сумме моментов всех внешних сил, расположенных с одной стороны от сечения, относительно центра этого сечения. Правило знаков для изгибающего момента: момент считается положительным, если он растягивает нижние волокна.

Строим грузовую эпюру.

2.Определяем угол поворота сечения (1)

а) Для того, чтобы определить угол поворота указанного сечения, нужно зарисовать исходную раму без внешней нагрузки и к заданному сечению приложить единичный момент.

Сначала определяем реакции:

Строим единичную эпюру моментов.

б) Определяем угол поворота по формуле Симпсона, подставив I₁=I, I₂=2I:

Знак « — » означает, что поворот сечения происходит против направления единичного момента, т.е. по часовой стрелке.

3. Определяем горизонтальное перемещение сечения (2).

а) Для того, чтобы определить горизонтальное перемещение в указанном сечении, нужно зарисовать исходную раму без внешней нагрузки и к заданному сечению приложить в горизонтальном направлении единичную силу.

Определяем реакции:

Строим единичную эпюру моментов

б) Определяем горизонтальное перемещение сечения (2) по формуле Симпсона:

Результат получился с «+», значит точка (2) перемещается по направлению единичной силы, т.е. вправо.

Для балки определить линейные и угловые перемещения в точках A, B, C, предварительно подобрав сечение двутавра из условия прочности.

Дано: a=2 м, b=4 м, с=3 м, F=20 кН, М=18 кНм, q=6 кН/м, σ_adm=160 МПа, Е=2 10⁵ МПа

1) Вычерчиваем схему балки, определяем опорные реакции. В жёсткой заделке возникает 3 реакции — вертикальная и горизонтальная, а так же опорный момент. Поскольку горизонтальных нагрузок нет – соответствующая реакция равна нулю. Для того, чтобы найти реакции в точке E, составим уравнения равновесия.

∑F_y= 0 q7-F+R_E=0

R_E=-q7+F=-67+20=-22кН (знак говорит о том, что реакция направлена в обратную сторону, показываем это на схеме)

Найдем опорный момент в жесткой заделке, для чего решим уравнение моментов относительно любой выбранной точки.

∑M_C: -M_E-R_E9-F6-q77/2-M=0

M_E=-18-229+649/2=-18-198+147=-69кНм (знак говорит о том, что реакция направлена в обратную сторону, показываем это на схеме)

Далее требуется выполнить проверку правильности определения реакций, составив уравнение равновесия относительно любой точки, к примеру, точки Е, ∑M_Е= 0.

2) Строим грузовую эпюру M^F– эпюру моментов от заданной нагрузки.

Для построения эпюр моментов найдем моменты в характерных точках. В точке В определяем моменты как от правых, так и от левых сил, поскольку в этой точке приложен момент.

Для построения эпюры момента на линии действия распределенной нагрузки (участки АВ и ВС) нам нужны дополнительные точки для построения кривой. Определим моменты в серединах этих участков. Это моменты в серединах участков АВ и ВС 15,34 кНм и 23,25кНм. Строим грузовую эпюру.

3) Для определения линейных и угловых перемещений в точке необходимо приложить в этой точке, в первом случае, единичную силу (F=1) и построить эпюру моментов, во втором случае, единичный момент (M=1) и построить эпюру моментов. Строим эпюры от единичных нагрузок для каждой точки – А, В и С.

4) Для нахождения перемещений мы используем формулу Симпсона.

где l_i– длина участка;

EI_i– жесткость балки на участке;

M_F – значения изгибающих моментов с грузовой эпюры, соответственно в начале, в середине и в конце участка;

– значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.

Если ординаты эпюр расположены с одной стороны от оси балки, то при перемножении учитывается знак «+», если с разных, то знак «-».

Если результат получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением соответствующего единичного силового фактора.

Рассмотрим применение формулы Симпсона на примере определения перемещений в точке А.

Определим прогиб, перемножив грузовую эпюру на эпюру от единичной силы.

Прогиб получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением единичной силы (направлено вверх).

Определим угол поворота, перемножив грузовую эпюру на эпюру от единичного момента.

Угол поворота получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением соответствующего единичного момента (направлен против часовой стрелки).

5) Для определения конкретных значений перемещений требуется подобрать сечение. Подберем сечение двутавра

где M_max – это максимальный момент на грузовой эпюре моментов

Подбираем по сортаменту двутавр №30 с W_x=472см³ и I_x= 7080см⁴

6) Определяем перемещения в точках, раскрывая жесткость сечения: E – модуль продольной упругости материала или модуль Юнга (2 10⁵МПа), J_x – осевой момент инерции сечения

Прогиб в точке А (вверх)

Угол поворота (против часовой стрелки)

Если требуется построить изогнутую ось балки, то балка вычерчивается без нагрузки, и в точках откладываются прогибы в соответствующие стороны — строится плавная кривая – изогнутая ось балки.

Определить прогиб и угол поворота в сечении В

Сначала построим грузовую эпюру от заданной нагрузки. Площадь грузовой эпюры имеет криволинейное очертание и равна:

Теперь снимем с балки нагрузку и приложим в точке, где необходимо определить перемещение единичную силу для определения прогиба и единичный момент для определения угла поворота. Строим эпюры от единичных нагрузок.

Центр тяжести грузовой эпюры находится на расстоянии одной четверти (см. эпюру)

Ординаты единичных эпюр напротив центра тяжести грузовой эпюры :

Теперь по формуле правила Верещагина определяем:

сначала прогиб

затем угол поворота:

В знаменателе формулы – жесткость сечения.

Источник

Лекция
13 (продолжение). Примеры
решения на вычисление перемещений
методом Мора-Верещагина и задачи для
самостоятельного решения

Определение
перемещений в балках

Пример
1.

Определить
перемещение точки К балки
(см. рис.) при помощи интеграла Мора.

Решение.

1) Составляем
уравнение изгибающего момента от внешней
силы M_F.

2)
Прикладываем в точке К единичную
силу F =
1.

3)
Записываем уравнение изгибающего
момента от единичной силы .

4)
Определяем перемещения

Пример
2.

Определить
перемещение точки К балки
по способу Верещагина.

Решение.

1) Строим
грузовую эпюру.

2)
Прикладываем в точке К единичную силу.

3)
Строим единичную эпюру.

4)
Определяем прогиб

; ;

Пример
3.

Определить
углы поворота на опорах А и В для
заданной балки (см. рис.).

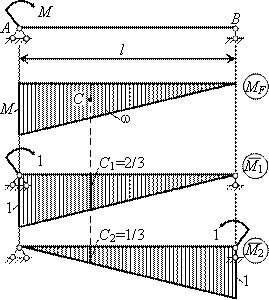
Решение.

Строим
эпюры от заданной нагрузки и от единичных
моментов, приложенных в сечениях А и В (см.
рис.). Искомые перемещения определяем
с помощью интегралов Мора

, которые вычисляем
по правилу Верещагина.

Находим
параметры эпюр

C₁ =
2/3, C₂ =
1/3,

а затем и углы поворота на
опорах А и В

Пример
4.

Определить
угол поворота сечения С для
заданной балки (см. рис.).

Решение.

Определяем
опорные реакции R_A=R_B,

, , R_A = R_B = qa.

Строим
эпюры изгибающего момента от заданной
нагрузки и от единичного момента,
приложенного в сечении С,
где ищется угол поворота. Интеграл Мора
вычисляем по правилу
Верещагина. Находим параметры эпюр

C₂ =
–C₁ =
-1/4,

а
по ним и искомое перемещение

Пример
5.

Определить прогиб в сечении С для
заданной балки (см. рис.).

Решение.

1.
Построение эпюр изгибающих моментов.

Эпюра M_F (рис.
б)

Опорные
реакции:

ВЕ: , ,

, R_B+ R_E = F, R_E =
0;

АВ: , R_А = R_В = F; , .

Вычисляем
моменты в характерных точках , M_B =
0, M_C = Fa и строим эпюру изгибающего
момента от заданной нагрузки.

Эпюра (рис.
в).

В
сечении С,
где ищется прогиб, прикладываем единичную
силу  и
строим от нее эпюру изгибающего момента,
вычисляя сначала опорные
реакции  ВЕ – ,   ,    =
2/3;   ,  ,    =
1/3,   а затем моменты в характерных
точках   ,   ,   .

2.
Определение искомого прогиба. Воспользуемся
правилом Верещагина и вычислим
предварительно параметры эпюр и :

Прогиб
сечения С

Пример
6.

Определить прогиб в сечении С для
заданной балки (см. рис.).

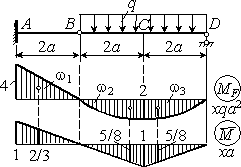
Решение.

Строим
эпюры изгибающих моментов от заданной
нагрузки и от единичной силы, приложенной
в точке С. Пользуясь
правилом Верещагина, вычисляем параметры
эпюр ,

и
находим искомый прогиб

Пример
7.

Определить
прогиб в сечении С для
заданной балки (см. рис.).

Решение.

1.
Построение эпюр изгибающих моментов.

Опорные
реакции:

, , R_A =
2qa,

, R_A+ R_D =
3qa, R_D = qa.

Строим
эпюры изгибающих моментов от заданной
нагрузки и от единичной силы, приложенной
в точке С.

2.
Определение перемещений. Для вычисления
интеграла Мора воспользуемся формулой
Симпсона, последовательно применяя ее
к каждому из трех участков, на которые
разбивается балка.

Участок АВ:

Участок ВС:

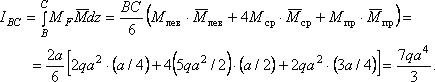
Участок СD:

Искомое
перемещение

Пример
8.

Определить
прогиб сечения А и
угол поворота сечения Е для
заданной балки (рис. а).

Решение.

1.
Построение эпюр изгибающих моментов.

Эпюра М_F (рис. в).
Определив опорные реакции

, , R_B =
19qa/8,

, R_D =
13qa/8,
строим эпюры поперечной силы Q и
изгибающего момента М_F от
заданной нагрузки.

Эпюра (рис.
д). В сечении А,
где ищется прогиб, прикладываем единичную
силу и строим от нее эпюру изгибающего
момента.

Эпюра (рис.
е). Эта эпюра строится от единичного
момента, приложенного в сечении Е,
где ищется угол поворота.

2.
Определение перемещений. Прогиб
сечения А находим,
пользуясь правилом Верещагина. Эпюру М_F на
участках ВС и CD разбиваем
на простые части (рис. г). Необходимые
вычисления представляем в виде таблицы.

Номер части	1	2	3	4	5	6	7
	–qa³/6	2qa³/3	–qa³/2	qa³/4	qa³/4	–qa³	–qa³/2
C_i	-3a/4	-3a/4	-5a/6	-2a/3	–a/3	–a/6	0
	qa⁴/8	–qa⁴/2	5qa⁴/12	–qa⁴/6	–qa⁴/12	qa⁴/6	0	–qa⁴/24

Получаем .

Знак
“минус” в результате означает, что
точка А перемещается
не вниз, как была направлена единичная
сила, а вверх.

Угол
поворота сечения Е находим
двумя способами: по правилу Верещагина
и по формуле Симпсона.

По
правилу Верещагина, перемножая
эпюры M_F и ,
по аналогии с предыдущим получим

Для
нахождения угла поворота по формуле
Симпсона вычислим предварительно
изгибающие моменты посредине участков:

Искомое
перемещение, увеличенное в EI_x раз,

Пример
9.

Определить,
при каком значении коэффициента k прогиб
сечения С будет
равен нулю. При найденном значении k построить
эпюру изгибающего момента и изобразить
примерный вид упругой линии балки (см.
рис.).

Решение.

Строим эпюры изгибающих
моментов от заданной нагрузки
и от единичной силы, приложенной в
сечении С,
где ищется прогиб.

По
условию задачи V_C =
0. С другой стороны, .
Интеграл на участке АВ вычисляем
по формуле Симпсона, а на участке ВС –
по правилу Верещагина.

Находим
предварительно

Перемещение
сечения С ,

Отсюда , .

При
найденном значении k определяем
значение опорной реакции в
точке А: , , ,
исходя из которого находим положение
точки экстремума на эпюре М согласно
условию .

По
значениям момента в характерных точках

, ,

строим
эпюру изгибающего момента (рис. г).

Пример
10.

Определить
вертикальное перемещение точки В консольной
балки, изображенной на рисунке.

Решение.

Строим
эпюру изгибающих моментов М от
действия внешней сосредоточенной
силы F: М_В =
0, М_А =
–F2l (эпюра
линейная).

По
условию задачи требуется определить
вертикальное перемещение у_В точки В консольной
балки, поэтому строим единичную эпюру от
действия вертикальной единичной
силы F_i =
1, приложенной в точке В.

Учитывая,
что консольная балка состоит из двух
участков с разной жесткостью на изгиб,
эпюры и М перемножаем
с помощью правила Верещагина по участкам
отдельно. Эпюры М ипервого
участка перемножаем по формуле ,
а эпюры второго участка – как площадь
эпюры М второго
участка Fl²/2
на ординату 2l/3
эпюры второго
участка под центром тяжести треугольной
эпюры М этого
же участка.

В
этом случае формула дает:

Пример
11.

Определить
вертикальное перемещение точки В однопролетной
балки, изображенной на рисунке. Балка
имеет постоянную по всей длине жесткость
на изгиб EI.

Решение.

Строим
эпюру изгибающих моментов М от
действия внешней распределенной
нагрузки: М_А =
0; M_D=
0;

Прикладываем
в точке В единичную
вертикальную силу F_i= 1
и строим эпюру (см.
рис.):

откуда R_a=
2/3;

откуда R_d =
1/3, поэтому M_a =
0; M_d =
0; .

Разделим
рассматриваемую балку на 3 участка.
Перемножение эпюр 1-го и 3-го участков
не вызывает трудностей, так как перемножаем
треугольные эпюры. Для того чтобы
применить правило Верещагина ко 2-му
участку, разобьем эпюру М 2-го
участка на две составляющие эпюры:
прямоугольную и параболическую с
площадью (см.
таблицу).

Центр
тяжести параболической части эпюры М лежит
посередине 2-го участка.

Таким
образом, формула при
использовании правила Верещагина дает:

Пример
12.

Определить
максимальный прогиб в двухопорной
балке, нагруженной равномерно
распределенной нагрузкой интенсивности q (см.
рис.).

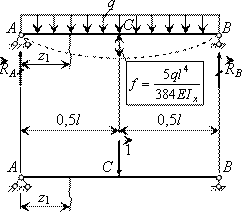
Решение.

Находим
изгибающие моменты:

–
от заданной нагрузки

–
от единичной силы, приложенной в точке С,
где ищется прогиб .

Вычисляем
искомый наибольший прогиб, который
возникает в среднем сечении балки

Пример
13.

Определить
прогиб в точке В балки,
показанной на рисунке.

Решение.

Строим
эпюры изгибающих моментов от заданной
нагрузки и единичной силы, приложенной
в точке В. Чтобы
перемножить эти эпюры, надо балку разбить
на три участка, так как единичная эпюра
ограничена тремя различными прямыми.

Операция
перемножения эпюр на втором и третьем
участках осуществляется просто.
Затруднения возникают при вычислении
площади и координат центра тяжести
основной эпюры на первом участке. В
таких случаях намного упрощает решение
задачи построение расслоенных эпюр.
При этом удобно одно из сечений принять
условно за неподвижное и строить эпюры
от каждой из нагрузок, приближаясь
справа и слева к этому сечению.
Целесообразно за неподвижное принимать
сечение в месте перелома на эпюре
единичных нагрузок.

Расслоенная
эпюра, в которой за неподвижное принято
сечение В,
представлена на рисунке. Вычислив
площади составных частей расслоенной
эпюры и соответствующие им ординаты
единичной эпюры, получаем

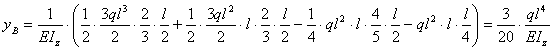Пример
14.

Определить
перемещения в точках 1 и 2 балки (рис. а).

Решение.

Приведем
эпюры М и Q для
балки при а=2
м; q=10
кН/м; С=1,5а; М=0,5qa²; Р=0,8qa; М₀=М; =200
МПа (рис. б и в).

Далее
определяем перемещения в точках 1 и 2 балки
(рис. а). Состояние балки под действием
заданной нагрузки обозначим q.

Определим
вертикальное перемещение  центра
сечения, где приложен сосредоточенный
момент. Для  этого рассмотрим балку
в состоянии  под
действием только сосредоточенной
силы  приложенной
в точке 1 перпендикулярно оси балки (по
направлению искомого перемещения )
(рис. г).

Вычислим
опорные реакции, составив три уравнения
равновесия

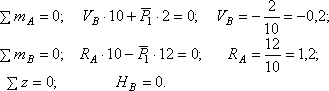
Проверка

Реакции
найдены верно.

Для
построения эпюры рассмотрим
три участка (рис. г).

1
участок

2
участок

3
участок

По
этим данным строим эпюру (рис.
д) со стороны растянутых волокон.

Определим по
формуле Мора с помощью правила Верещагина.
При этом криволинейную эпюру ,
на участке между опорами, можно представить
в виде сложения трех эпюр. Стрелка

Знак
«минус» означает, что точка 1 перемещается
вверх (в направлении противоположном ).

Определим
вертикальное перемещение  точки
2, где приложена сосредоточенная сила.
Для этого рассмотрим балку в состоянии  под
действием только сосредоточенной
силы  приложенной
в точке 2 перпендикулярно оси балки (по
направлению искомого перемещения )
(рис. е).

Эпюра строится
аналогично предыдущей.

Далее
по формуле Мора

Точка
2 перемещается вверх.

Определим
угол поворота сечения,
где приложен сосредоточенный момент.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

Пример решения задачи 2.2.
Пример решения задачи 2.3.
Пример решения задачи 3.1.
Пример решения задачи 3.2.

Метод Максвелла – Мора представляет собой универсальный способ для определения линейных и угловых перемещений в любых плоских и пространственных системах.

Напомним основные этапы использования метода Максвелла -Мора.

При отыскании линейного перемещения к системе, освобожденной от заданных нагрузок, в направлении искомого перемещения (в заданной точке) прикладывается безразмерная единичная сила. Аналогично, при определении углового перемещения в сечении, поворот которого требуется найти, прикладывается пара сил (в плоскости искомого поворота) с моментом, равным безразмерной единице.

Строятся эпюры внутренних силовых факторов от заданной нагрузки и единичных воздействий.

Искомое перемещение определяется из выражения:

правую часть, которого называют интегралами Мора, где: искомое перемещение (линейное или угловое). Первый индекс указывает номер искомого перемещения второй индекс указывает причины, вызывающие деформации отдельных элементов системы и как следствие , перемещение (индекс указывает, что перемещение определяется от заданной нагрузки);

аналитические выражения продольной, поперечной сил и изгибающего момента соответственно от единичного и заданного воздействия (единичные и грузовые эпюры внутренних усилий);

жесткости поперечных сечений стержня соответственно на растяжение, сдвиг, изгиб;

коэффициент отражает неравномерность распределения касательных напряжений по поперечному сечению. Этот коэффициент зависит от формы сечения, например, для прямоугольника для круга

Направление единичного воздействия выбирается произвольно. Полученный по формуле (2.1) положительный результат указывает на то, что направление искомого перемещения совпадает с принятым направлением единичного воздействия, либо противоположно принятому направлению, если получен отрицательный результат.

В формуле (2.1) каждый интеграл четко выражает вклад соответствующей деформации в искомое перемещение. Обычно учитываются лишь основные виды деформации. В конструкциях работающих на изгиб учитывается влияние изгибающих моментов, а поперечными силами пренебрегают.

В комбинированных системах, где часть стержней работает на растяжение-сжатие, а часть – на изгиб, учитываются обе эти деформации. В фермах, где каждый стержень работает на растяжение -сжатие в формуле (2.1) остается только первый интеграл.

В случаях, когда ось бруса прямолинейна и жесткость поперечного сечения в пределах отдельных участков постоянна, интегралы

Мора, входящие в выражение (2.1) целесообразно вычислять, используя правило Верещагина или формулу Симпсона.

Возможно вам будут полезны данные страницы:

Пример решения задачи 2.2.

Определить прогиб конца консольной балки (рис. 2.2,а), учитывая лишь деформации, изгиба, жесткость поперечного сечения балки постоянна.

Решение:

Эпюра изгибающих моментов от заданной нагрузки показана на рис.

Построим единичную эпюру, для этой цели, сняв с балки заданную нагрузку, приложим к концу консоли (точка рис. 2.2 в),

вертикально направленную единичную силу , направление

единичной силы выбирается произвольно , например направим ее вниз, т.е. предполагаем , что точка переместится вниз по отношению продольной оси балки .

При заданном загружении (рис. 2.2,в), балка имеет один участок Единичный изгибающий момент для произвольного сечения участка будет равен

Подставляя в полученное уравнение прямой координаты начала и конца участка, построим единичную эпюру изгибающих моментов (рис. 2.2, г ).

Для определения прогиба точки надо «перемножить» эпюры от заданной нагрузки и от единичной силы. Проделаем это. Балка имеет два участка, На участке интеграл Мора вычислим по способу Верещагина.

Перемещение положительно, так как обе сопрягаемые эпюры, лежат по одну сторону от базы ( продольной оси бруса ).

На участке грузовая эпюра нелинейная и заранее неизвестно, где находится ее центр тяжести, использовать правило Верещагина на этом участке затруднительно. Для вычисления интеграла Мора на участке воспользуемся формулой Симпсона. Применяя ее, найдем:

Прогиб сечения равняется сумме интегралов Мора на участках

Знак плюс прогиба указывает на то, что сечение переместится по направлению единичной силы, т.е. вниз.

Пример решения задачи 2.3.

Определить угол поворота сечения двухопорной балки с консолью (рис. 2.3,а), учитывая лишь деформации изгиба, жесткость, балки постоянна.

Решение:

Эпюра изгибающих моментов от заданной нагрузки построена ранее в примере, ее вид показан (рис. 2.3, б).

Построим единичную эпюру, для этой цели, сняв с балки заданую нагрузку, приложим в сечении единичный момент направление единичного момента выбираем произвольно, например по ходу часовой стрелки (рис. 2.3,в).

Балка имеет три участка. Сопряжение эпюр проведем по участкам. На первом участке (участок для вычисления угла поворота, используем формулу Симпсона, так как эпюра на участке интегрирования нелинейная:

На втором участке (участок обе эпюры изгибающих моментов линейны.

Поэтому интеграл Мора на этом участке можно вычислить по формуле трапеций. Применяя ее, найдем:

Полученные выражения отрицательны потому, что знаки ординат «перемножаемых» эпюр противоположны. На третьем участке (участок интеграл Мора вычислим способом Верещагина:

Получен отрицательный результат потому, что эпюры и лежат по разные сторону от базы ( продольной оси бруса ). Угол поворота сечения равняется сумме интегралов Мора на трех участках ( на участках