Как найти вертикальную асимптоту гиперболы - Сайт, где вы сможете решить свои вопросы

Заказать задачи по любым предметам можно здесь от 10 минут

Асимптоты графика функции

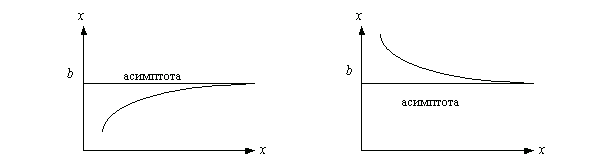
Часто задание на нахождение асимптот функции встречается в курсе математического анализа, в частности при решении задач на тему исследования функции. Для того, чтобы успешно ответить на вопрос: как найти асимптоты функции? необходимо уметь вычислять пределы, понимать что они собой представляют, знать основные методы решения пределов. Если всё это вы умеете на должном уровне, тогда найти асимптоты для вас не будет проблемой. Итак, что такое асимптота? Асимптота это линия, к которой бесконечно приближается ветвь графика функции. Чтобы было наглядно, посмотрите на изображения представленные ниже.

Обратите внимание, что соприкосновения между асимптотой и графиками нет, и не должно быть. Асимптота бесконечно приближается к графику функции. Давайте рассмотрим какие виды асимптоты функции бывают и как их находить, но о последнем будет рассказано далее.

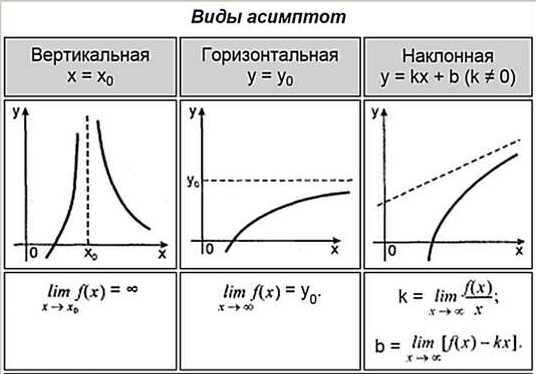
Из таблицы узнаем, что асимптоты у функции бывают трех видов: вертикальные, горизонтальные, наклонные. Каждую найти асимптоту функции нужно по своему. Для этого нужны лимиты. Сколько бывает асимптот всего у функции? Ответ: ни одной, одна, две, три… и бесконечно много. У каждой функции по разному.

Вертикальные асимптоты

Чтобы найти данный вид асимптот необходимо найти область определения заданной функции и отметить точки разрыва. В этих точках предел функции будет равен бесконечности, а это значит, что функция в этой точке бесконечно приближается к линии асимптоты.

Горизонтальные асимптоты

Необходимо устремить аргумент лимита функции к бесконечности. Если предел существует и равен числу, то горизонтальная асимптота будет найдена и равна $ y=y_0 $ как показано во втором столбце таблицы

Наклонные асимптоты

Наклонная асимптота представляется в виде $ y = kx+b $. Где $ k $ – это коэффициент наклона асимптоты. Сначала находится коэффициент $ k $, затем $ b $. Если какой либо из них равен $ infty $, тогда наклонной асимптоты нет. А если $ k = 0 $, то получаем горизонтальную асимптоту. Так что для экономии времени лучше сразу находить наклонную асимптоту, а горизонтальная проявится сама собой в случае её существования.

Примеры решений

Пример 1

Найти все асимптоты графика функции $$ f(x) = frac{5x}{3x+2} $$

Решение

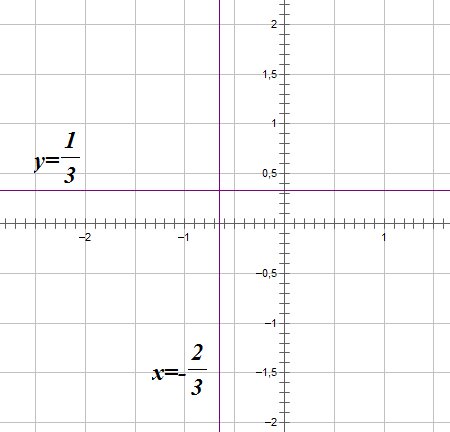
Для начала решения найдем вертикальные асимптоты, но прежде найдем область определения функции $ f(x) $. По определению знаменатель не должен быть равен нулю. Поэтому имеем, $ 3x+2 neq 0; 3x neq -2; x neq -frac{2}{3} $. Получили точку разрыва $ x = -frac{2}{3} $. Вычислим в ней предел функции и убедимся окончательно, что вертикальная асимптота это $ x = -frac{2}{3} $.

$$ limlimits_{{x rightarrow -frac{2}{3}}} frac{5x}{3x+2} = (-frac{10}{infty}) = -infty $$.

Теперь найдем горизонтальные асимптоты, но прежде рассчитаем коэффициенты $ k $ и $ b $.

$$ k = limlimits_{x rightarrow infty} frac{f(x)}{x} =limlimits_{x rightarrow infty} frac{5}{3x+2}=frac{5}{infty}=0 $$

Так как $ k = 0 $, то мы уже понимаем то, что наклонных асимптот нет, а есть горизонтальные. Найдем теперь коэффициент $ b $.

$$ b = limlimits_{x rightarrow infty} [f(x)-kx] = limlimits_{x rightarrow infty} frac{5x}{3x+2} = frac{infty}{infty} =frac{5}{3} $$

Подставляем найденные коэффициенты в формулу $ y = kx + b $, получаем, что $ y = frac{5}{3} $ – горизонтальная асимптота.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ y = frac{5}{3} $$

Пример 2

Найти все асимптоты графика функции $ f(x) = frac{1}{1-x} $

Решение

Найдем область определения данного примера, чтобы определить вертикальные асимптоты. $ 1-x neq 0; x neq 1; $. Точка разрыва $ x = 1 $, а это значит что это и есть вертикальная асимптота. Найдем для доказательства предположения предел в этой точке. $$ limlimits_{x rightarrow 1} frac{1}{1-x} = frac{1}{0} = infty $$

Приступим к поиску наклонных асимптот.

$$ k = limlimits_{x rightarrow infty}frac{f(x)}{x}=limlimits_{x rightarrow infty}frac{1}{x(1-x)} = frac{1}{infty}=0 $$

$$ b =limlimits_{x rightarrow infty}[f(x)-kx]=limlimits_{x rightarrow infty}frac{1}{1-x} = frac{1}{infty}=0 $$

Итого, $ y=0 $ – горизонтальная асимптота.

Ответ

$$ y=0 $$

Пример 3

Найти все асимптоты графика функции $ f(x) = frac{x^3}{3x^2+5} $

Решение

Замечаем, что знаменатель не обращается в ноль при любом значении икса. А это значит, что нет точек разрыва и следовательно нет вертикальных асимптот. Остается найти горизонтальные асимптоты.

$$ k = limlimits_{x rightarrow infty} frac{f(x)}{x} =limlimits_{x rightarrow infty}frac{x^2}{3x^2+5} =limlimits_{x rightarrow infty} frac{2x}{6x} = frac{1}{3} $$

Так как $ k $ конечное число, не равное $ 0 $ или бесконечности, то существует наклонная асимптота. Вычислим недостающее число $ b $.

$$ b =limlimits_{x rightarrow infty} [f(x)-kx] =limlimits_{x rightarrow infty} [frac{x^3}{3x^2+5}-frac{x}{3}] =limlimits_{x rightarrow infty} -frac{5x}{3(3x^2+5)}= $$ $$ = -frac{5}{3}limlimits_{x rightarrow infty} frac{x}{3x^2+5} =-frac{5}{3}limlimits_{x rightarrow infty} frac{1}{6x} =-frac{5}{3}frac{1}{infty} = 0 $$

$ y =frac{1}{3}x $ – наклонная асимптота к функции с углом наклона одна третья.

Ответ

$$ y =frac{1}{3}x $$

Пример 4

Найти асимптоты $ f(x) = xe^{-x} $

Решение

Нет точек разрыва, а это значит, нет вертикальных асимптот.

$$ k=limlimits_{x rightarrow infty} frac{1}{e^x} = frac{1}{infty} = 0 $$

$$ b=limlimits_{x rightarrow infty} frac{x}{e^x} =limlimits_{x rightarrow infty} frac{1}{e^x} = frac{1}{infty} = 0 $$

$ y = 0 $ – горизонтальная асимптота

Ответ

$$ y = 0 $$

Если в задачах даются элементарные функции, то заранее известно сколько и есть ли асимптоты. Например, у параболы, кубической параболы, синусоиды вообще нет никаких. У графиков функций таких как логарифмическая или экспоненциальная есть по одной. А у функций тангенса и котангенса бесчисленное множество асимптот, но арктангенс и арккатангенс имеет по две штуки.

Во всех приведенных примерах пределы вычислялись с помощью правило Лопиталя, которое очень ускоряет процесс вычисления и создает меньше ошибок.

Источник

Для гиперболы ${displaystyle y={frac {1}{x}}}$ асимптотами являются оси абсцисс и ординат. Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от неё

Асимпто́та, или аси́мптота^[1] (от др.-греч. ἀσύμπτωτος — несовпадающая, не касающаяся кривой с бесконечной ветвью) — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность^[2]. Термин впервые появился у Аполлония Пергского, хотя асимптоты гиперболы исследовал ещё Архимед^[3].

Затухающие колебания. ${displaystyle y=e^{-0.1x}sin(x)}$ . Кривая может бесконечное множество раз пересекать асимптоту

Пример асимптоты для кривой в пространстве. Спираль бесконечно приближается к прямой

Виды асимптот графиков[править | править код]

Вертикальная[править | править код]

Прямая вида x=a является вертикальной асимптотой при выполнении хотя бы одного из равенств:

${displaystyle lim _{xto a^{-}}f(x)=pm infty }$
${displaystyle lim _{xto a^{+}}f(x)=pm infty }$ .

Вертикальных асимптот может быть любое количество.

Прямая не может быть вертикальной асимптотой, если функция непрерывна в точке . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.

Горизонтальная и наклонная[править | править код]

На графике функции x+1/x, ось y (x = 0) и линия y=x являются асимптотами.

Наклонная асимптота — прямая вида y=kx+b , если выполняется хотя бы одно из равенств:

${displaystyle lim _{xto +infty }(f(x)-kx)=b}$
${displaystyle lim _{xto -infty }(f(x)-kx)=b}$ .

При этом, если выполняется первое условие, то говорят, что эта прямая является асимптотой при , а если второе, то асимптотой при ^[4].

Если k=0 , то асимптота также называется горизонтальной.

Замечание 1: Число наклонных асимптот у функции не может быть больше двух: одна при и одна при , но она может быть одна или их вовсе может не быть.

Замечание 2: Некоторые источники включают требование, чтобы кривая не пересекала эту прямую в окрестности бесконечности^[5].

Замечание 3: В некоторых случаях, таких как алгебраическая геометрия, асимптота определена, как прямая, которая является «касательной» к кривой на бесконечности^[5].

Функция y=arctgx с двумя горизонтальными асимптотами

Нахождение асимптот[править | править код]

Порядок нахождения асимптот[править | править код]

Нахождение точек разрыва, выбор точек, в которых есть вертикальная асимптота (прямой проверкой, что предел в этой точке есть бесконечность).
Проверка, не являются ли конечными пределы ${displaystyle lim _{xto +infty }f(x)=b}$ и ${displaystyle lim _{xto -infty }f(x)=b}$ . Если да, то существует горизонтальная асимптота при и соответственно.
Нахождение двух пределов $lim_{x to pm infty}frac{f(x)}{x}=k$
Нахождение двух пределов $lim_{x to pm infty}(f(x)-kx)=b$ , если хотя бы один из пределов в пункте 3 или 4 не существует (или равен ), то наклонной асимптоты при (или ) не существует.

Наклонная асимптота — выделение целой части[править | править код]

Также наклонную асимптоту можно найти, выделив целую часть. Например:

Дана функция ${displaystyle f(x)={frac {2x^{3}+5x^{2}+1}{x^{2}+1}}}$ .

Разделив нацело числитель на знаменатель, получим: ${displaystyle f(x)=2x+5+{frac {-2x-4}{x^{2}+1}}=2x+5+(-2)cdot {frac {x+2}{x^{2}+1}}}$ .

При , $frac{x+2}{x^2+1} to 0$ ,

и является искомым уравнением наклонной асимптоты, причем с обеих сторон.

Свойства[править | править код]

Среди конических сечений асимптоты имеют только гиперболы. Асимптоты гиперболы как конического сечения параллельны образующим конуса, лежащим в плоскости, проходящей через вершину конуса параллельно секущей плоскости^[6]. Максимальный угол между асимптотами гиперболы для данного конуса равен углу раствора конуса и достигается при секущей плоскости, параллельной оси конуса.

См. также[править | править код]

Асимптотическая кривая

Примечания[править | править код]

↑ Двойное ударение указано в Советском энциклопедическом словаре. В словарях XIX и первой половины XX века (например, в кн.: Словарь иностранных слов / Под ред. И. В. Лёхина и проф. Ф. Н. Петрова. — М.: Гос. изд-во иностр. и нац. словарей, 1955. — С. 77. — 856 с.) указывался единственный вариант ударения «асимпто́та».
↑ Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1. Архивная копия от 13 ноября 2013 на Wayback Machine
↑ Математический энциклопедический словарь Архивная копия от 1 августа 2013 на Wayback Machine — М.: Советская энциклопедия, 1988. — 847 с.
↑ Кудрявцев Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003. — Т. 1. — С. 374-375. — 704 с. — ISBN 5-7107-4119-1.
↑ ¹ ² «Asymptotes» by Louis A. Talman
↑ Taylor C. Geometrical Conics; Including Anharmonic Ratio and Projection, With Numerous Examples. — Cambridge: Macmillan, 1863. — С. 170.

Литература[править | править код]

Рашевский П. К. Курс дифференциальной геометрии, 4-е изд. М., 1956.
Графики функций: Справочник / Вирченко Н. А., Ляшко И. И., Швецов К. И. — Киев: Наук. думка, 1979, — 320 с.

Ссылки[править | править код]

Асимптота // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Асимптота / Э. Г. Позняк // Ангола — Барзас. — М. : Советская энциклопедия, 1970. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 2).

Источник

Асимптоты графика функции. График дробно-линейной функции

Асимптоты графика функции. График дробно-линейной функции.

В этой статье мы рассмотрим, что такое асимптота графика функции, и как ее находить.

Асимптота – это прямая, к которой бесконечно близко приближается график функции.

Асимптоты бывают горизонтальные, вертикальные и наклонные.

Если мы посмотрим на хорошо известный нам график функции y=1/x , то увидим, что график этой функции бесконечно близко приближается к прямой x=0 (ось ОY) – это вертикальная асимптота, и к прямой y=0 (ось ОХ) – это горизонтальная асимптота:

В общем случае горизонтальная асимптота – это прямая, параллельная оси OX. Уравнение горизонтальной асимптоты имеет вид y=b , где – число, к которому стремятся значения функции y=f(x) , когда стремится к infty .

То есть .

Вертикальная асимптота – это прямая, параллельная оси OY. Уравнение вертикальной асимптоты имеет вид x=a . Здесь – значение переменной , при котором функция y=f(x) не определена. Как правило, это ноль знаменателя. Если значение стремится к точке, в которой знаменатель равен нулю, то абсолютное значение дроби при этом неограниченно возрастает.

В некоторых случаях для построения графика функции бывает достаточно найти асимптоты графика.

Рассмотрим дробно-линейную функцию. В общем виде уравнение дробно-линейной функции имеет вид: .

График дробно-линейной функции – это гипербола. Как мы знаем, гипербола имеет две асимптоты: горизонтальную и вертикальную.

Заметим, что при x=-d/c знаменатель равен нулю, в этой точке функция не определена. Поэтому прямая x=-d/c – вертикальная асимптота.

Степень в числителе дроби равна степени в знаменателе. Поэтому при числитель и знаменатель растут с одинаковой скоростью, и

и уравнение горизонтальной асимптоты имеет вид y=a/c .

График дробно-линейной функции – это гипербола, симметричная относительно точки пересечения асимптот графика. Поэтому, чтобы построить график, нам остается только выяснить его расположение относительно этой точки.

Для этого достаточно найти точки пересечения графика с осями координат.

Точка пересечения с осью OX (y=o): x=-b/a .

Точка пересечения с осью OY (x=0): y=b/d .

Построим график функции . Это дробно-линейная функция и ее график – гипербола.

Найдем горизонтальную и вертикальную асимптоты.

Уравнение горизонтальной асимптоты: y=1/3 ;

уравнение вертикальной асимптоты (ноль знаменателя): x=-2/3

Найдем точки пересечения с осями координат:

С осью ОХ: x+1=0 ; x=-1

с осью OY(x=0): y=1/2 .

То есть график функции выглядит как-то так:

И, наконец, наклонная асимптота. Наклонная асимптота – это к прямая, к кторой стремится график функции на бесконечности.

Уравнение наклонной асимптоты имеет вид y=kx+b .

Коэффициенты и вычисляются следующим образом:

Найдем асимптоты графика функции $y={3-x^2}/{x+2}$

1. Начнем с области определения функции. Функция $y={3-x^2}/{x+2}$ не определена в точке x=-2 , следовательно прямая x=-2 является вертикальной асимптотой.

2. Степень числителя дроби ${3-x^2}/{x+2}$ на единицу больше степени знаменателя, поэтому предел этого отношения при отношения равен бесконечности. Следовательно, график функции $y={3-x^2}/{x+2}$ не имеет горизонтальной асимптоты.

3. Попробуем найти наклонную асимптоту.

$k=lim{x{right}{infty}}{{{3-x^2}/{(x+2)x}}}=-1$

(Предел функции равен отношению коэффициентов при максимальных степенях в числителе и знаменателе дроби).

$b=lim{x{right}{infty}}{({{3-x^2}/{x+2}}-(-1)x)}=$ $lim{x{right}{infty}}{{3-x^2+x^2+2x}/{x+2}}=$

Итак, уравнение наклонной асимптоты: y=-x+2

График функции $y={3-x^2}/{x+2}$ , построенный с помощью специальной программы, показывает, что асимптоты были найдены верно:

И.В. Фельдман, репетитор по математике.

Источник

Загрузить PDF

Асимптоты гиперболы – это прямые, проходящие через центр гиперболы. Гипербола приближается к асимптотам, но никогда не пересекает (и даже не касается) их. Найти уравнения асимптот можно двумя способами, которые помогут понять саму концепцию асимптот.

1
Запишите каноническое уравнение гиперболы. Рассмотрим простейший пример – гиперболу, центр которой расположен в начале координат. В этом случае каноническое уравнение гиперболы имеет вид: ^x²/_a² – ^y²/_b² = 1 (когда ветви гиперболы направлены вправо или влево) или ^y²/_b² – ^x²/_a² = 1 (когда ветви гиперболы направлены вверх или вниз).^[1] Имейте в виду, что в этом уравнении «х» и «у» – это переменные, а «а» и «b» – постоянные (то есть числа).
- Пример 1: ^x²/₉ – ^y²/₁₆ = 1
- Некоторые преподаватели и авторы учебников меняют местами постоянные «а» и «b».^[2] Поэтому изучите данное вам уравнение, чтобы понять, что к чему. Не стоит просто запоминать уравнение – в этом случае вы ничего не поймете, если переменные и/или постоянные будут обозначены другими символами.
2
Приравняйте каноническое уравнение к нулю (а не к единице). Новое уравнение описывает обе асимптоты, но чтобы получить уравнение каждой асимптоты, придется приложить некоторые усилия.^[3]
- Пример 1: ^x²/₉ – ^y²/₁₆ = 0
3
Разложите на множители новое уравнение. Разложите на множители левую часть уравнения. Вспомните, как раскладывать на множители квадратное уравнение, и читайте дальше.
- Конечное уравнение (то есть уравнение, разложенное на множители) будет иметь вид (__ ± __)(__ ± __) = 0.
- При перемножении первых членов (внутри каждой пары скобок) должен получиться член ^x²/₉, поэтому из этого члена извлеките квадратный корень, и результат запишите вместо первого пробела внутри каждой пары скобок:(^x/₃ ± __)(^x/₃ ± __) = 0
- Аналогично извлеките квадратный корень из члена ^y²/₁₆, и результат запишите вместо второго пробела внутри каждой пары скобок: (^x/₃ ± ^y/₄)(^x/₃ ± ^y/₄) = 0
- Вы нашли все члены уравнения, поэтому внутри одной пары скобок между членами напишите знак плюс, а внутри второй – знак минус, чтобы при перемножении соответствующие члены сокращались: (^x/₃ + ^y/₄)(^x/₃ – ^y/₄) = 0
4
Приравняйте каждый двучлен (то есть выражение внутри каждой пары скобок) к нулю и вычислите «y». Так вы найдете два уравнения, которые описывают каждую асимптоту.
- Пример 1: Так как (^x/₃ + ^y/₄)(^x/₃ – ^y/₄) = 0, то ^x/₃ + ^y/₄ = 0 и ^x/₃ – ^y/₄ = 0
- Перепишите уравнение следующим образом: ^x/₃ + ^y/₄ = 0 → ^y/₄ = – ^x/₃ → y = – ^4x/₃
- Перепишите уравнение следующим образом: ^x/₃ – ^y/₄ = 0 → – ^y/₄ = – ^x/₃ → y = ^4x/₃
5
Выполните описанные действия с гиперболой, уравнение которой отличается от канонического. В предыдущем шаге вы нашли уравнения асимптот гиперболы с центром в начале координат. Если центр гиперболы находится в точке с координатами (h,k), то она описывается следующим уравнением: ^{(x – h)²}/_a² – ^{(y – k)²}/_b² = 1 или ^{(y – k)²}/_b² – ^{(x – h)²}/_a² = 1. Это уравнение также можно разложить на множители. Но в этом случае не трогайте двучлены (x – h) и (y – k) до тех пор, пока не придете к последнему шагу.
- Пример 2: ^{(x – 3)²}/₄ – ^{(y + 1)²}/₂₅ = 1
- Приравняйте это уравнение к 0 и разложите его на множители:
- (^{(x – 3)}/₂ + ^{(y + 1)}/₅)(^{(x – 3)}/₂ – ^{(y + 1)}/₅) = 0
- Приравняйте каждый двучлен (то есть выражение внутри каждой пары скобок) к нулю и вычислите «y», чтобы найти уравнения асимптот:
- ^{(x – 3)}/₂ + ^{(y + 1)}/₅ = 0 → y = –⁵/₂x + ¹³/₂
- (^{(x – 3)}/₂ – ^{(y + 1)}/₅) = 0 → y = ⁵/₂x – ¹⁷/₂
Реклама

1
Обособьте член y² на левой стороне уравнения гиперболы. Применяйте этот метод в том случае, когда уравнение гиперболы дано в квадратичной форме. Даже если дано каноническое уравнение гиперболы, этот метод позволит лучше понять концепцию асимптот. Обособьте y² или (y – k)² на левой стороне уравнения.
- Пример 3: ^{(y + 2)²}/₁₆ – ^{(x + 3)²}/₄ = 1
- К обеим частям уравнения прибавьте «х», а затем умножьте обе части на 16:
- (y + 2)² = 16(1 + ^{(x + 3)²}/₄)
- Упростите полученное уравнение:
- (y + 2)² = 16 + 4(x + 3)²
2
Извлеките квадратный корень из каждой части уравнения. При этом не упрощайте правую часть уравнения, так как при извлечении квадратного корня получаются два результата – положительный и отрицательный (например, -2 * -2 = 4, поэтому √4 = 2 и √4 = -2). Чтобы привести оба результата, используйте символ ±.
- √((y + 2)²) = √(16 + 4(x + 3)²)
- (y+2) = ± √(16 + 4(x + 3)²)
3

Уясните понятие асимптоты. Сделайте это до того, как перейти к следующему шагу. Асимптота – это прямая, к которой приближается гипербола с ростом значений «х». Гипербола никогда не пересечет асимптоту, но с увеличением «х» гипербола приблизится к асимптоте на бесконечно малое расстояние.
4
Преобразуйте уравнение с учетом больших значений «х». Как правило, при работе с уравнениями асимптот учитываются только большие значения «х» (то есть такие значения, которые стремятся к бесконечности). Поэтому в уравнении можно пренебречь определенными константами, так как по сравнению с «х» их вклад невелик. Например, если переменная «х» равна нескольким миллиардам, то прибавление числа (константы) 3 окажет мизерное влияние на значение «х».
- В уравнении (y+2) = ± √(16 + 4(x + 3)²) при стремлении «x» к бесконечности постоянной 16 можно пренебречь.
- При больших значениях «х» (y+2) ≈ ± √(4(x + 3)²)
5
Вычислите «у», чтобы найти уравнения асимптот. Избавившись от констант, можно упростить подкоренное выражение. Помните, что в ответе нужно записать два уравнения – одно со знаком плюс, а второе со знаком минус.
- y + 2 = ±√(4(x+3)^2)
- y + 2 = ±2(x+3)
- y + 2 = 2x + 6 и y + 2 = -2x – 6
- y = 2x + 4 и y = -2x – 8
Реклама

Советы

Помните, что уравнение гиперболы и уравнения ее асимптот всегда включают постоянные (константы).
Равносторонняя гипербола – это гипербола, в уравнении которой а = b = с (константа).
Если дано уравнение равносторонней гиперболы, сначала преобразуйте его в каноническую форму, а затем найдите уравнения асимптот.

Предупреждения

Помните, что ответ не всегда записывается в канонической форме.

Об этой статье

Эту страницу просматривали 91 746 раз.

Была ли эта статья полезной?

Источник

Свойства гиперболы

1) Область определения и область значений

По аналитическому заданию функции видно, что х ≠-a, поскольку знаменатель дроби не может ровняться нулю. Таким образом получим:

D(f)=(-∞;-а) U (-a;+∞)

Область значений

Е(f)=(-∞;+∞)

2) Нули функции

Если b=0, то график функции не пересекает ось ОХ;

Если b≠0, то гипербола имеет одну точку пересечения с ОХ:*

x=-(k+ab)/b

3) Промежутки знакопостоянства

Рассмотрим только 2 простых случая, остальные случаи вы можете рассмотреть аналитически самостоятельно по алгоритму из раздела Свойства функций -> Знакопостоянство

Случай 1: a=0, b=0, k>0

f(x)>0, при x ∈ (0; +∞)

f(x)<0, при x ∈ (-∞;0)

Случай 1: a=0, b=0, k<0

f(x)<0, при x ∈ (0; +∞)

f(x)>0, при x ∈ (-∞;0)

4) Промежутки монотонности

Аналогично с промежутками знакопостоянства рассмотрим только 2 случая

Случай 1: a=0, b=0, k>0

Функция убывает при

x ∈ (-∞;0) U (0; +∞)

Функция возрастает при

x ∈ (-∞;0) U (0; +∞)

5) Четность и нечетность

Функция является нечетной при a=0, b=0, то есть если имеет вид y=k/x

Источник

Асимптоты графика функции

Вертикальные асимптоты

Горизонтальные асимптоты

Наклонные асимптоты

Примеры решений

Виды асимптот графиков[править | править код]

Вертикальная[править | править код]

Горизонтальная и наклонная[править | править код]

Нахождение асимптот[править | править код]

Порядок нахождения асимптот[править | править код]

Наклонная асимптота — выделение целой части[править | править код]

Свойства[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Асимптоты графика функции. График дробно-линейной функции

Советы

Предупреждения

Об этой статье

Была ли эта статья полезной?

Вам также может понравиться

Как найти канал двд

Как найти фазный провод в выключателе

Как найти железо для вагнера

Добавить комментарий Отменить ответ