
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
синоптика.pdf
Скачиваний:
885
Добавлен:
13.03.2016
Размер:
13.13 Mб
Скачать
|
9. Основные характеристики полей метеорологических величин |
99 |
плых и холодных океанических и морских течений, зимой у береговой линии температура воздуха по горизонтали часто меняется скачкообразно.
Однако уже на уровне 1.5 км (АТ850) поле температуры становится более сглаженным, отражая, однако, основные черты приземного термического поля. Поэтому при определении положения фронтальных зон у Земли привлекаются результаты анализа поля температуры на АТ850.
Важной характеристикой скалярного термического поля являются вертикальный и горизонтальный температурные градиенты.
Характеристикой изменения температуры по вертикали является вертикальный температурный градиент
∂T γ = − ∂z .
Обычно в тропосфере температура воздуха с высотой уменьшается. Тем не менее, в некоторых слоях тропосферы имеет место рост температуры γ <0 или постоянст-
во её с высотой γ =0.
Для оценки устойчивости атмосферы служат такие показатели как адиабатиче-
ский ( γ a ), влажноадиабатический ( γ вa ) градиенты температуры:
γa ≈ 0.98 o100м,
γвa ≈ 0.66 o100м .
Влажноадиабатический градиент температуры воздуха определяется как
γ вa = βγ a ,
где β – множитель, равный
|
β = |
P + a |
, |
a = 0.623 |
LE |
, |
b = 0.623 |
L dE |
|
. |
|||||||
|
P + b |
ART |
cp |
dT |
В изобарической системе из уравнения конденсационной (влажной) адиабаты:
|
dT |
= |
AR |
β |
dP |
, γ ва |
= − |
dT |
= −β |
ART 1 |
|
|
T |
cp |
P |
dP |
cp P |
||||||
|
Влажноадиабатический градиент γ вa |
зависит от температуры воздуха и давле- |
ния.
Н.А. Дашко Курс лекций по синоптической метеорологии

|
9. Основные характеристики полей метеорологических величин |
100 |
При Р=1000 гПа для значений температуры 40, 20, 0, -20, -40°С γ вa =0.32, 0.44, 0.66, 0.88, 0.98°/100 м, соответственно.
При Р=500 гПа для значений температуры 40, 20, 0, -20, -40°С γ вa =0.26, 0.34, 0.52, 0.78, 0.95°/100 м, соответственно.
При низких температурах воздуха γ вa приближается к сухоадиабатическому.
Таким образом, тёплая воздушная масса потенциально более неустойчива, чем холодная.
Если каком-либо слое атмосферы γ > γ a то данный слой находится в неустой-
чивом термодинамическом равновесии.
При γ < γ a в слое атмосферы наблюдается устойчивое равновесие. Особенно устойчивыми будут слои, где γ <0, следовательно, температура воздуха с высотой воз-
растает (инверсионный слой), либо не меняется – γ =0 (изотермия).
Слои инверсии и изотермии, а также слои с градиентами, близкими к нулю, называют задерживающими слоями атмосферы. Задерживающие слои оказывают мощное стабилизирующее влияние на все движения, ослабляя турбулентное перемешивание, конвективные потоки, препятствуя обмену воздухом между задерживающим слоем и слоями воздуха выше и ниже.
Изменение температуры по горизонтали характеризует горизонтальный градиент температуры. Горизонтальный термический градиент Горизонтальный градиент температуры примерно в 1000 и более раз меньше вертикального. Порядок величин горизонтального термического градиента – десятые доли градуса на 100 км. Для фронтальных зон характерны повышенные значения горизонтальных градиентов температуры, которые могут достигать здесь порядка 5-10°С/100км по нормали к изотермам.
9.11.2. Адиабатические изменения температуры воздуха
Рассмотрим изменение температуры воздуха фиксированной частицы, происходящее без обмена теплом между этой частицей и средой:
dTdt = 0 .
Такое изменение термодинамического состояния воздуха называется адиабатическим. При адиабатическом процессе внутренняя энергия и с нею температура воздуха меняются за счёт работы сжатия или расширения. При сжатии давление и внутрен-
Н.А. Дашко Курс лекций по синоптической метеорологии

|
9. Основные характеристики полей метеорологических величин |
101 |
няя энергия воздуха возрастают, и температура повышается. При расширении – давление и внутренняя энергия убывают, и температура падает.
Адиабатическое приближение дает хорошие результаты. Адиабатическими можно считать атмосферные процессы при условии, что продолжительность процесса и тем самым теплообмен со средой не велики, например, адиабатическое приближение можно принять при образовании конвективных облаков и др.
Преобразуем данное уравнение, используя основное уравнение статики атмо-
сферы.
|
∂T |
+ u |
∂T |
+ v |
∂T |
+ w |
∂T |
= 0 , – |
∂T |
= γ , |
|
∂t |
∂x |
∂y |
∂z |
∂z |
γ – вертикальный градиент температуры воздуха. Или, решая в Р-системе:
dTdt = ∂∂Tt + u ∂∂Tx + v ∂∂Ty + τ ∂∂Tp = 0 ,
Здесь τ – аналог вертикальной скорости (система X, Y, P).
|
∂Z |
1 ∂P |
∂P |
∂Z |
||||||||
|
w = |
∂t |
= − |
∂t , |
∂t |
= |
−ρg |
∂t |
, |
|||
|
ρg |
|||||||||||
|
τ = |
∂P |
= −wρg, w |
= − |
1 |
τ |
||||||
|
∂t |
ρg |
||||||||||
|
∂T |
1 ∂T |
1 |
RT |
||||||||
|
w ∂z |
= −τ |
∂z = −γ |
τ = −γ |
τ, |
|||||||
|
ρg |
ρg |
Pg |
тогда уравнение примет вид:
|
dT |
= |
∂T |
+ u |
∂T |
+ v |
∂T |
− γ |
RT τ |
= 0. |
(9.11.1) |
|
∂t |
∂x |
∂y |
||||||||
|
dt |
g P |
Но при вертикальном перемещении воздушных частиц даже при отсутствии притоков тепла температура воздушной частицы меняется за счёт адиабатического нагрева при сжатии, когда частица опускается (температура повышается), или при расширении, когда частица поднимается (температура понижается):
|
dT |
= ( |
dT |
)1 |
− ( |
dT |
)a , |
|
dt |
||||||
|
dt |
dt |
dT
где ( dt )a ≠ 0 – изменения Т при условии адиабатического процесса.
|
( |
∂T )a = 0, |
( |
∂T )a = 0 , |
( |
dT |
)a = w |
∂T |
= wγ a |
|
∂z |
||||||||
|
∂x |
∂y |
dt |
Н.А. Дашко Курс лекций по синоптической метеорологии

|
9. Основные характеристики полей метеорологических величин |
102 |
||||||||||||||||||
|
или в Р-системе: |
|||||||||||||||||||
|
( |
dT |
)a |
= τ( |
∂T)a |
= τ( ∂T)a |
dz |
= −γ a |
1 |
τ |
||||||||||
|
dp |
ρg |
||||||||||||||||||
|
dt |
∂p |
∂z |
|||||||||||||||||
|
( |
dT |
)a |
= − |
RT |
γ a |
τ |
, |
||||||||||||
|
dt |
g |
P |
|||||||||||||||||
|
Уравнение притока тепла примет вид: |
|||||||||||||||||||
|
dT |
= |
∂T + u |
∂T + v ∂T − (γ a − γ ) |
τ RT |
= 0 |
(9.11.2) |
|||||||||||||
|
p |
g |
||||||||||||||||||
|
dt |
∂t |
∂x |
∂y |
В общем случае в правой части должна быть учтена величина притока тепла от внешних источников (ε). Сюда входят приток (отток) тепла, связанный с турбулентным теплообменом между частицей воздуха и окружающими частицами, с лучистым теплообменом, при процессах конденсации (испарения) влаги внутри объёма, занятого фик-
сированной частицей воздуха. Но обычно в первом приближении считается ε=0.
9.11.3. Термический ветер
Связь между изменением давления у Земли и на высотах выражается как:
|
∂Pверх |
r |
r |
||||||||||||||||
|
∂P |
∂T |
|||||||||||||||||
|
нижн |
m |
(9.11.3) |
||||||||||||||||
|
∂n = k 1 |
∂n |
+ k 2 ∆Z |
∂n |
, |
||||||||||||||
|
где k |
1 |
= |
P2 |
, k |
2 |
= |
gρm |
. |
||||||||||
|
P |
T |
|||||||||||||||||
|
1 |
m |
|||||||||||||||||
|
Барический градиент на верхнем уровне |
∂Pверх |
, кроме всего прочего, зависит |
||||||||||||||||
|
∂n |
||||||||||||||||||
|
от дополнительного термического градиента k 2 |
∆Z |
∂Tm |
, пропорционального толщине |
|||||||||||||||
|
∂n |
рассматриваемого слоя ∆Z = (Z верх − Z нижн ) и величине горизонтального градиента
температуры данного слоя ∂∂Tnm , направленного параллельно барическому градиенту.
С увеличением высоты ρm и Tm уменьшаются, ∆Z растет. В результате дополнительный градиент возрастает.
Кроме того, первый член уравнения быстро убывает с высотой вместе с падением давления Рверх, следовательно, с высотой дополнительный градиент оказывает большее влияние на величину барического градиента на верхнем уровне.
Н.А. Дашко Курс лекций по синоптической метеорологии
|
9. Основные характеристики полей метеорологических величин |
103 |
В результате с возрастанием высоты барический градиент верхнего уровня стремится приблизиться по направлению к среднему термическому градиенту, а изобары – к средним изотермам.
Таким образом, в свободной атмосфере основную роль в изменении скорости и направления ветра играет не сила трения, а изменения барического градиента, происходящие под влиянием горизонтального градиента температуры
Но барический градиент определяет собой направление ветра. Если барический градиент с высотой приближается по направлению к термическому градиенту, следовательно, градиентный ветер с высотой будет приближаться к изотерме. Так же будет вести себя и действительный ветер, который в свободной атмосфере практически не отличается от градиентного.
Рассмотрим зависимость
|
H 500 |
= 6.74 lg |
P1 |
T = a |
1,2 |
T . |
|
1000 |
P2 |
m |
m |
||
Продифференцировав данное выражение по X и Y:
|
∂ |
H500 |
= |
∂ |
(H |
− H |
) = a |
∂ |
T |
||||||||||||||||||||||||||||||||||||||
|
p2 |
1,2 |
|||||||||||||||||||||||||||||||||||||||||||||
|
∂x |
1000 |
∂x |
p1 |
∂x |
m |
|||||||||||||||||||||||||||||||||||||||||
|
, |
||||||||||||||||||||||||||||||||||||||||||||||
|
∂ |
∂ |
∂ |
||||||||||||||||||||||||||||||||||||||||||||
|
H500 |
= |
(H |
− H |
) = a |
T |
|||||||||||||||||||||||||||||||||||||||||
|
1000 |
p2 |
p1 |
1,2 |
m |
||||||||||||||||||||||||||||||||||||||||||
|
∂y |
∂y |
∂y |
||||||||||||||||||||||||||||||||||||||||||||
|
получим: |
||||||||||||||||||||||||||||||||||||||||||||||
|
∂Hp |
2 |
− |
∂Hp |
1 |
= a |
∂ |
T |
(9.11.4) |
||||||||||||||||||||||||||||||||||||||
|
∂x |
∂x |
1,2 |
∂x |
m |
||||||||||||||||||||||||||||||||||||||||||
|
∂Hp2 |
∂Hp1 |
∂ |
||||||||||||||||||||||||||||||||||||||||||||
|
− |
= a1,2 |
Tm |
(9.11.5) |
|||||||||||||||||||||||||||||||||||||||||||
|
∂y |
∂y |
∂y |
||||||||||||||||||||||||||||||||||||||||||||
|
Умножим правую и левую части уравнения (9.11.4) на |
g |
, уравнения (9.11.5) – |
||||||||||||||||||||||||||||||||||||||||||||
|
l |
||||||||||||||||||||||||||||||||||||||||||||||
|
на (- |
g |
): |
||||||||||||||||||||||||||||||||||||||||||||
|
l |
||||||||||||||||||||||||||||||||||||||||||||||
|
g ∂Hp2 |
− |
g ∂Hp1 |
= a |
g ∂ |
T |
|||||||||||||||||||||||||||||||||||||||||
|
∂x |
l |
∂x |
1,2 l ∂x |
|||||||||||||||||||||||||||||||||||||||||||
|
l |
m |
, |
||||||||||||||||||||||||||||||||||||||||||||
|
∂Hp2 |
∂Hp1 |
|||||||||||||||||||||||||||||||||||||||||||||
|
− |
g |
+ |
g |
= −a |
1,2 |
g |
∂ |
T |
||||||||||||||||||||||||||||||||||||||
|
l |
∂y |
l ∂y |
l ∂y |
m |
||||||||||||||||||||||||||||||||||||||||||
Отсюда имеем:
Н.А. Дашко Курс лекций по синоптической метеорологии
|
9. Основные характеристики полей метеорологических величин |
104 |
|||||||||||||||||||||||||
|
g |
∂ |
(9.11.6) |
||||||||||||||||||||||||
|
vg1 |
− vg2 |
= a1,2 |
Tm |
|||||||||||||||||||||||
|
l ∂x |
||||||||||||||||||||||||||
|
. |
||||||||||||||||||||||||||
|
g ∂ |
||||||||||||||||||||||||||
|
u |
g1 |
− u |
= −a |
1,2 |
T |
(9.11.7) |
||||||||||||||||||||
|
g2 |
l ∂y |
m |
||||||||||||||||||||||||
|
Обозначив |
||||||||||||||||||||||||||
|
a |
g ∂ |
T |
= v |
− a |
g ∂ |
T |
= u |
, запишем |
||||||||||||||||||
|
T, |
1,2 l ∂y |
T |
||||||||||||||||||||||||
|
1,2 l ∂x |
m |
m |
||||||||||||||||||||||||
|
v |
g |
2 |
= v |
g1 |
+ v |
T |
||||||||||||||||||||
|
. |
||||||||||||||||||||||||||
|
= u |
+ u |
|||||||||||||||||||||||||
|
u |
g |
2 |
g1 |
T |
||||||||||||||||||||||
|
Для VT ( uT , vT ), где VT – вектор термического ветра, uT и vT – составляю- |
||||||||||||||||||||||||||
|
щие термического ветра: Vg2 |
= Vg1 + VT . |
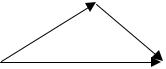
Под термическим ветром понимают приращение вектора геострофического вет-
ра при переходе с нижнего уровня атмосферы на верхний, т.е. VT = Vg2 − Vg1 , т.е. век-
торная разность геострофического ветра на двух уровнях (рис. 9.18):
V1 VT
V2
Рис. 9.18. Построение вектора термического ветра
Вектор термического ветра направлен по изотерме так, что в северном полушарии область более низких температур воздуха остается слева, область более высоких – справа, если смотреть по направлению ветра.
Таким образом, для VT горизонтальный градиент температуры слоя играет ту же роль, что и для Vg – барический градиент.
По взаимному расположению вектора скорости и вектора термического ветра (по взаимному расположению термического и барического градиента) судят о термической адвекции, т.е. об адвекции тепла или холода.
Адвекция холода имеет место, если воздушные течения направлены из области более низких температур, адвекция тепла – если они направлены из области более высоких температур. Направление течений показывают карты абсолютной топографии
Н.А. Дашко Курс лекций по синоптической метеорологии
|
9. Основные характеристики полей метеорологических величин |
105 |
(обычно используются карты АТ700 или АТ500). Распределение температуры в слое по-
казывают карты относительной топографии (обычно используется карта OT1000500 ).
При совмещении карты течений и карты распределения средней температуры слоя получают карту термобарического поля, по которой судят о термической адвекции.
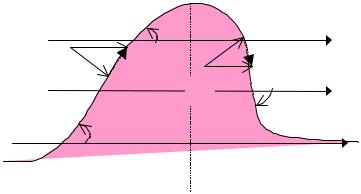
Рассмотрим карту термобарического поля (рис. 9.19).
|
Изогипса H500 |
||||
|
V2 |
V1 |
|||
|
VT |
VT |
|||
|
Холод |
V1 |
V2 |
Холод |
|
|
(ложбина холода) |
•A |
•B |
||
|
(ложбина холода) |
||||
|
Изогипса H500 |
Изотерма ОТ |
|||
|
Изотерма ОТ |
Тепло (гребень тепла) |
Рис. 9.19. Схема для определения адвекции температуры
Имеем поле изогипс на уровне Р2 (например, H500 ) и поле средней температуры
слоя (например, H5001000 ).
Движение по изогипсам АТ в северном полушарии происходит в направлении градиентного ветра так, что низкое давление остается слева, а высокое – справа. По на-
правлению изогипс H500 , можем задать вектор скорости геострофического ветра на этом уровне ( V2 ).
Вектор термического ветра VT направлен по изотерме H5001000 так, что область более низких температур остается слева, высоких – справа.
Согласно определению VT как векторной разности ветре при переходе с нижне-
го на верхний уровень, достроим вектор скорости геострофического ветра на нижнем уровне ( V1 ), в нашем примере – на уровне 1000 гПа,.
В область т. А происходит перенос из области с более низкими температурами воздуха (т.е. через некоторое время здесь можно ожидать понижения температуры) – адвекция холода.
Н.А. Дашко Курс лекций по синоптической метеорологии

|
9. Основные характеристики полей метеорологических величин |
106 |
Заметим, что:
При переходе от нижнего уровня к верхнему происходит левый поворот ветра
(поворот против часовой стрелки). Слева от т.А изотермы H5001000 отклоняются от изо-
гипс H500 влево.
В область т. В происходит перенос из области с более высокими температурами воздуха (т.е. через некоторое время здесь можно ожидать повышения температуры) – адвекция тепла.
При переходе от нижнего уровня к верхнему происходит правый поворот ветра
(поворот по часовой стрелке). Справа от т. А изотермы H5001000 отклоняются от изогипс
H500 вправо.
Таким образом, в северном полушарии:
•Области адвекции холода соответствует левый поворот ветра с высотой (против часовой стрелки), при этом изотермы H5001000 отклоняются от изогипс H500 влево
•Области адвекции тепла соответствует правый поворот ветра с высотой (по ча-
совой стрелке), при этом изотермы H5001000 отклоняются от изогипс H500 вправо.
Следовательно, во-первых, отклонение изотерм от изогипс показывает направление термической адвекции, во-вторых, имея данные о направлении ветра на различных высотах, можно судить о знаке адвекции температуры в различных слоях атмосферы.
•Если изотермы параллельны изогипсам, то изменений в ходе температуры воздуха не происходит (нулевая адвекция).
Поскольку вектор термического ветра равен
VT = 6.74 lg P1 g ∂Tm ,
P2 l ∂ν
где ν – нормаль к изотерме, то большей толщине слоя между уровнями P1 и P2 соот-
ветствует и большая величина VT при одном и том же значении ∂∂νTm .
Термический ветер наиболее часто вычисляют для H5001000 , где изогипсы эквива-
лентны изотермам слоя через 2°С. Направление VT на данной карте определяется по касательной к изогипсам (аналогично Vg на картах АТ). Скорость термического ветра можно рассчитывать по обычной градиентной линейке, поскольку
Н.А. Дашко Курс лекций по синоптической метеорологии
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вертикальный градиент температуры
Если восходящий воздух не насыщен (т. е. не достиг своей точки росы), то он будет охлаждаться приблизительно на 1° на каждые 100 м подъема. Изменение температуры воздуха с его поднятием называется вертикальным градиентом температуры восходящего потока. По мере того как поднимающийся воздух достигает своей точки росы, вертикальный градиент уменьшается до ~0,6° на 100 м. При конденсации водяного пара выделяется теплота. Это и уменьшает вертикальный градиент.
Следует иметь в виду, что указанные вертикальные градиенты температуры относятся только к таким поднимающимся или опускающимся потокам воздуха, которые не получают и не отдают тепла окружающему воздуху. В спокойном воздухе (т. е. не поднимающемся и не опускающемся) обычно температура также уменьшается с высотой. Однако вертикальный градиент в спокойном воздухе редко совпадает с вертикальным градиентом восходящего или нисходящего воздушного потока.
Влияние температуры воздуха на погоду и климат
Если бы Земля не вращалась, то циркуляция земной атмосферы происходила бы примерно так. Воздух сильнее всего нагревается вблизи экватора, то он начал бы здесь расширяться, сделался бы менее плотным и стал бы вытесняться вверх более холодным воздухом из полярных областей, устремившимся сюда для уравнивания давления. Поднимающийся вверх воздух стал бы продвигаться от экватора по направлению к полюсам, создавая постоянную область низкого давления у экватора. У полюсов воздух был бы холодным и плотным, так что здесь было бы высокое атмосферное давление.
Однако в действительности происходит иначе, по мере того как «растекающийся» — движущийся в верхних слоях — воздух удаляется от экватора к полюсам, он, вследствие вращения Земли с запада на восток, отклоняется к востоку, и, когда этот воздух достигает приблизительно 30-й параллели, он движется почти точно на восток. Таким образом, на этих широтах происходит накопление воздуха, в результате чего здесь образуются зоны высокого давления, которые окружают Землю к югу и к северу от экватора.
От каждой зоны высокого давления часть воздуха в нижних слоях атмосферы направляется к полюсу, порождая ветры, известные под названием «преобладающих западных ветров». Другая часть направляется к экватору, образуя северо-восточные и юго-восточные пассаты. Эти пассаты сталкиваются у экватора, в значительной степени взаимно уничтожаются и создают экваториальную штилевую зону.
Часть воздуха верхних слоев атмосферы на широте 30° вытесняется к полюсам, но не опускается к земной поверхности. В результате, когда этот воздух достигает полярных областей, он оказывается очень холодным и тяжелым (плотным). Здесь он оседает, образуя большие массы воздуха высокого давления. По мере накопления этого холодного воздуха в нижних слоях атмосферы он устремляется по направлению к экватору. На широте приблизительно 60° фронт этой массы полярного воздуха, так называемый полярный фронт, встречается со значительно более теплым и менее плотным воздухом западных ветров, опускается под него и заставляет его подниматься. Этот поднимающийся, относительно теплый, легкий воздух образует зоны низкого давления по обе стороны от экватора на широте около 60°. Однако время от времени большая масса полярного воздуха высокого давления прорывается к экватору. Передняя граница этой массы, обращенная к экватору, называется холодным фронтом. Эти центры высокого давления и холодные фронты играют огромную роль в формировании погоды и климата.
В общем, мы знаем, что температура уменьшается с высотой. Этот вариант известен под названием вертикальный температурный градиент, и это потому, что источник тепла, излучающий атмосферу, исходит от земли. Таким образом, чем дальше вы удаляетесь от источника, тем холоднее будет воздух.
Этот градиент может быть изменен несколькими процессами: внезапным падением или повышением температуры почвы или сильным ветром. Чтобы лучше понять это, в этом выпуске мы увидим, какова структура атмосферы и почему температура меняется при повышении.
Индекс
- 1 Структура атмосферы
- 2 Вертикальный температурный градиент
- 3 Что такое тепловая инверсия?
Структура атмосферы
Атмосфера состоит из 5 слоев: тропосфера, стратосфера, мезосфера, термосфера и экзосфера.
- Тропосфера: это то место, где мы находимся, высота около 12km. Здесь образуются облака, живут растения и животные, мы находим океан и пустыни и т. Д.
- Стратосфера: расположена между 12 и 50 км высоты, там мы увидим сверхзвуковые самолеты.
- Мезосфера: расположена между 50 и 80 км высоты. Здесь «плывут» радиоволны и приходят космические лучи.
- Термосфера: среди 80 и 690 км высоты помимо космических кораблей на околоземной орбите появится северное сияние.
- Экзосфера: и, наконец, от 690км на высоте мы найдем Спутник I.
Вертикальный температурный градиент
Как мы уже говорили, температура обычно снижается с высотой. В тропосфере он имеет приблизительное значение шесть градусов на километр. Это означает, что если, например, температура на уровне моря составляет 15 градусов, на высоте примерно пять километров она достигнет значения -15 градусов (снижение на 30 градусов).
Солнечные лучи не достигают всех частей земного шара одинаково, и они не достигают времен года. Таким образом, в умеренных зонах температурный градиент намного больше, чем в тропической зоне, 1ºC на каждые 155 м высотыиз-за меньшей инсоляции и меньшей толщины атмосферы. Также в этих же областях есть разные вариации, связанные с ориентацией рельефа и удаленностью от экватора, а также от полюсов.
В тропической зоне температура снижается на один градус на каждые 180 м высоты. примерно, поскольку атмосфера более плотная и находится очень близко к экватору. К этому, в дополнение к собственному вращательному движению планеты, создается теплый климат.
Но в некоторых регионах атмосферы происходит обратное, то есть температура увеличивается с высотой. В этом случае говорят, что вертикальный градиент температуры равен отрицательный. Например: если температура увеличивается на 21 градус для уклона 1 км, вертикальный градиент температуры считается равным -2ºC на км. Это может произойти даже в некоторых слоях тропосферы, вызывая так называемую температурную инверсию.
Температурные инверсии также происходят в верхней части стратосферы. Напротив, в мезосфере температура в среднем понижается при повышении, то есть вертикальный температурный градиент положительный.
В термосфере температура увеличивается с высотой и, следовательно, вертикальный градиент температуры снова становится отрицательным в этой области атмосферы.
Что такое тепловая инверсия?

Это явление возникает, когда земля быстро охлаждается радиацией, которая, в свою очередь, охлаждает соприкасающийся с ней воздух. И, в свою очередь, более холодный и тяжелый воздух в верхнем слое становится еще холоднее. Таким образом, скорость, с которой два слоя воздуха смешиваются, резко уменьшается.
Обычно это происходит особенно зимой, что приводит к стойким туманам и морозам. Хотя инверсия имеет тенденцию к разрыву через несколько часов, в неблагоприятных условиях может сохраняться несколько дней пока воздух, соприкасающийся с землей, не нагреется и не восстановит циркуляцию в тропосфере.
Яркий пример инвестиций можно увидеть в Известь, за счет тока Гумбольдта. Это океаническое течение охлаждает побережье, а верхние слои, которые более теплые, делают небо очень облачным, и в этом районе более прохладный и сухой климат, чем следовало бы, учитывая его широту.
Тем не менее, если нет изменений в воздушных массах, то есть если в атмосфере нет нестабильности или нет активных фронтов, температура будет увеличиваться по отношению к высоте, в некоторых местах больше, чем в других.
Знаете ли вы, что такое вертикальный температурный градиент и из чего он состоит? Это было вам полезно?
Содержание статьи соответствует нашим принципам редакционная этика. Чтобы сообщить об ошибке, нажмите здесь.
Вы можете быть заинтересованы
Лешан Татьяна Анатольевна,
учитель географии и экономики
МОУ «СШ № 16 г. Макеевки»
Решение географических задач
по теме «Атмосфера»
Задача 1. Какова
температура воздуха на высоте 3,5 км, если на уровне моря она = + 22оС?
Решение:
Вертикальный температурный градиент (Δt) – это величина, на которую изменяется
температура воздуха с высотой.
Δt =
6оС/1 км или 0,6оС/100 м высоты
1) 3,5 км × 6оС/ км = 21оС – разница температур
2) + 22оС – 21оС = + 1оС – температура
на высоте 3,5 км
Ответ: на высоте 3,5
км температура воздуха равна + 1оС.
Задача 2. Над
побережьем Азовского моря летит самолет на высоте 5 км. Температура за бортом
самолета равна (– 9оС). Какая температура в этот момент на берегу
моря?
Решение:
1) 5 км × 6оС/ км = 30оС – разница температур
2) 30оС + (-9оС) = + 21оС – температура
на берегу моря
Ответ: на берегу
Азовского моря температура воздуха равна + 21оС.
Задача 3. За бортом
самолета температура воздуха равна (- 32оС). На какой высоте летит
самолет, если температура над земной поверхностью равна (+ 16оС)?
Решение:
1) + 16оС – (- 32оС) = 48оС – разница
температур
2) 48оС : 6оС/ км = 8 км – высота самолета
Ответ: самолет летит на высоте 8 км.
Задача 4. Определите
вертикальный температурный градиент (Δt), если разница температур между высотами в
2200 м равна 11оС.
Решение:
Вертикальный температурный градиент можно определить с помощью пропорции:
11оС – 2200 м
Х – 100 м
Х = 11оС × 100 м : 2200 м = 0,5оС/100 м
Ответ: Δt = 0,5оС/100
м высоты.
Задача 5. Температура
воздуха, который быстро поднимается вверх со скоростью 5 см/с в течение 7,5
часов понизилась на 13,5оС. Определите, на сколько градусов понижалась
температура воздуха при поднятии его на каждые 100 м?
Решение:
1) Определим скорость подъема воздуха в час:
5 см/с × 3600 с = 18000 см/час = 180 м/час
2) Определим высоту, на которую поднялся воздух за 7,5 часов:
180 м/час × 7,5 часов = 1350 м
3) Δt = 13,5оС : 1350 м = 0,01оС /м =
1оС/100 м
Ответ: температура
воздуха понижалась на 1оС на каждые 100 м подъема.
Задача 6. 1 м2
поверхности нашей планеты от прямых лучей Солнца каждый день получает энергию,
которая приблизительно равна 1 кВт. Подсчитайте энергию, которую получает
пустыня Сахара за год, если ее площадь 7 млн. км2. Количество
солнечных дней в году – 300.
Решение:
1) За 1 день 1 м2 поверхности Земли получает 1 кВт энергии,
значит за 300 дней 1 м2 Сахары получит 300 кВт энергии.
300 кВт = 3 × 102 кВт
2) 1 км2 = 1 000 000 м2 = 1× 106
м2
3) Площадь Сахары 7 000 000 км2 = 7 × 106 км2
= 7× 1012 м2
4) 7× 1012 м2 × 3 × 102 кВт = 21 × 1014
кВт энергии – получит Сахара за год
Ответ: за год Сахара
получает 21 × 1014 кВт энергии.
Задача 7. На какой
высоте летит самолет, если за его бортом атмосферное давление равно 360 мм рт.
ст.?
Решение:
Вертикальный барический градиент (ΔР) – это величина, на которую изменяется атмосферное
давление с высотой.
ΔР = 1 мм рт. ст.
/ 10 м высоты
Барическая ступень (ΔС)
– это высота, на которую нужно подняться или опуститься, чтобы атмосферное
давление изменилось на 1 мм рт. ст.
1) Атмосферное давление на уровне моря = 760 мм рт. ст.
760 мм рт. ст. – 360 мм рт. ст. = 400 мм рт. ст. – разница атмосферного
давления
2) h = (P1 – P2):
ΔР
400 мм рт. ст. ×10 м : 1 мм рт. ст. = 4000 м – высота самолета
Ответ: самолет летит
на высоте 4000 м или 4 км.
Задача 8. Какова
относительная высота горы, если у ее подножия атмосферное давление равно 733 мм
рт. ст., а на вершине – 693 мм рт. ст.?
Решение:
1) 733 мм рт. ст. – 693 мм рт. ст. = 40 мм рт. ст. – разница атмосферного
давления
2) h = (P1 – P2):
ΔР
40 мм рт. ст. ×10 м : 1 мм рт. ст. = 400 м – относительная высота горы
Ответ: относительная
высота горы – 400 м.
Задача 9. Каково
атмосферное давление на вершине заводской трубы, если ее высота – 50 м, а
давление воздуха у основания трубы = 750 мм рт. ст.?
Решение:
1) Определим, на сколько мм рт. ст. изменится атмосферное давление при
подъеме на 50 м:
h × ΔР = 50 м × 1 мм рт. ст. :
10 м = 5 мм рт. ст.
2) Найдем атмосферное давление на вершине трубы:
750 мм рт. ст. – 5 мм рт. ст. = 745 мм рт. ст.
Ответ: атмосферное
давление на вершине заводской трубы = 745 мм рт. ст.
Задача 10. Каково
атмосферное давление на вершине Роман-Кош (Крым), если в городе Запорожье
(абсолютная высота 75 м) давление – 740 мм рт. ст.?
Решение:
1) Найдем разницу высот: 1545 м – 75 м = 1470 м
2) Определим, на сколько мм рт. ст. изменится атмосферное давление при
подъеме на 1470 м:
h × ΔР = 1470 м × 1 мм рт. ст.
: 10 м = 147 мм рт. ст.
3) Найдем атмосферное давление на горе Роман-Кош:
740 мм рт. ст. – 147 мм рт. ст. = 593 мм рт. ст.
Ответ: атмосферное
давление на вершине Роман-Кош = 593 мм рт. ст.
Задача 11. При
нормальных условиях атмосферное давление на вершине горы = 286 мм рт. ст., а у
ее подножия – 625 мм рт. ст. Определите абсолютную и относительную высоту горы.
Решение:
![]()
![]()

![]()
286 мм рт. ст. 1) 625 мм рт. ст. – 286 мм рт. ст. = 339 мм рт. ст.
–
разница давления между подножием и вершиной горы
h абс. h отн.
2) h
= (P1 – P2):
ΔР = 339 мм рт. ст. : 1 мм рт. ст. × 10 м =
![]()
625 мм рт. ст. 3390 м – относительная высота горы
3)
760 мм рт. ст. – 286 мм рт. ст. = 474 мм рт. ст. –
разница
давления между уровнем моря и вершиной горы
![]()
760 мм рт. ст. 4) h = (P1 – P2): ΔР = 474 мм рт. ст. : 1 мм рт. ст. × 10 м =
4740 м – абсолютная высота горы
Ответ: h абс. =
4740 м, h отн. = 3390 м.
Задача 12. Температура
воздуха = – 20оС. Абсолютная влажность воздуха = 0,65 г/м3.
Определите относительную влажность воздуха.
Решение:
Абсолютная влажность ( q )
– это количество влаги, которое находится в 1 м3 воздуха в данный
момент.
Относительная влажность (
r ) – это отношение абсолютной влажности ( q ) к максимально возможной
при данной температуре ( Q ), выраженное в процентах.
Абсолютная влажность воздуха, который
находится
в состоянии насыщения в зависимости от
температуры:
|
tо |
Q г/м3 |
tо |
Q г/м3 |
tо |
Q г/м3 |
tо |
Q г/м3 |
tо |
Q г/м3 |
tо |
Q г/м3 |
|
– 20 – 19 – 18 – 17 – 16 – 15 – 14 – 13 – 12 – 11 |
1,0 1,15 1,3 1,45 1,6 1,75 1,9 2,05 2,2 2,35 |
– 10 – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2 – 1 |
2,5 2,75 3,0 3,25 3,5 3,75 4,0 4,25 4,5 4,74 |
0 1 2 3 4 5 6 7 8 9 |
5,0 5,4 5,8 6,2 6,6 7,0 7,4 7,8 8,2 8,6 |
10 11 12 13 14 15 16 17 18 19 |
9,0 9,8 10,6 11,4 12,2 13,0 13,8 14,6 15,4 16,2 |
20 21 22 23 24 25 26 27 28 29 |
17,0 18,3 19,6 20,9 22,2 23,5 24,8 26,1 27,4 28,7 |
30 31 32 33 34 35 36 37 38 39 |
30,0 32,1 34,2 36,3 38,4 40,5 42,6 44,7 46,8 48,9 |
1) По таблице определяем, что при температуре (- 20о С) Q = 1
г/м3
2) r = q : Q × 100 % = 0,65 г/м3 : 1 г/м3
× 100 % = 65 % – относительная влажность воздуха
Ответ: при
температуре (- 20оС) относительная влажность воздуха равна 65 %.
Задача 13. Воздух имеет
температуру + 27оС и относительную влажность 33 %. Найти абсолютную
влажность этого воздуха.
Решение:
Используя формулу относительной влажности воздуха: r = q : Q × 100
%,
выведем формулу, по которой определим абсолютную влажность воздуха: q = Q × r :
100 %
По таблице определяем, что при температуре (+ 27о С) Q = 26,1
г/м3
q = 26,1 г/м3 × 33% : 100% = 26,1
г/м3 × 0,33 = 8,7 г/м3
Ответ: абсолютная
влажность воздуха равна 8,7 г/м3
Задача 14. Температура воздуха равна +17о С. Абсолютная влажность воздуха
– 9,5 г/м3. Определите дефицит влажности этого воздуха.
Решение:
Дефицит влажности
– это количество влаги, которой не хватает до полного
насыщения воздуха (= Q – q).
По таблице определяем, что при температуре (+ 17о С) Q = 14,6
г/м3
Найдем дефицит влажности:
14,6 г/м3 – 9,5 г/м3 = 5,1 г/м3
Ответ: чтобы
достигнуть состояния насыщения, в каждом м3 воздуха должно быть на 5,1 г влаги больше, чем
есть в данный момент.
Задача 15. Одна из воздушных масс имеет температуру 0оС и абсолютную
влажность 4,5 г/м3, вторая воздушная масса имеет температуру +15оС
и абсолютную влажность 9,6 г/м3. Определите, в какой из воздушных
масс и во сколько раз относительная влажность больше.
Решение:
1) По таблице определяем, что при температуре 0оС
Q = 5 г/м3, при температуре +15оС Q = 13
г/м3
2) Определим относительную влажность первой воздушной массы:
r = q : Q × 100 % = 4,5 г/м3 : 5 г/м3
× 100 % = 90 %
3) Определим относительную влажность второй воздушной массы:
r = q : Q × 100 % = 9,6 г/м3 : 13 г/м3
× 100 % = 74 %
4) 90 % : 74 % = в 1,2 раза – относительная влажность первой воздушной
массы больше.
Ответ: относительная
влажность первой воздушной массы больше в 1,2 раза.
Задача 16. Воздух,
который имеет относительную влажность 75 % и температуру + 22оС, в
течение ночи охладился до + 14оС. Образуется ли роса утром?
Решение:
Для того, чтобы водяной пар, который находится в воздухе, перешел в
жидкое состояние (конденсировался) или в твердое состояние, необходимо, чтобы
воздух, пройдя точку насыщения, стал перенасыщенным водяными парами. При этом в
приземном слое воздуха могут образовываться роса, туман, изморозь, иней или
облака, но при условии, что воздух поднимается.
Точка росы – это
температура, при которой влажный насыщенный воздух становится перенасыщенным.
1) По таблице определяем, что при температуре +22оС Q = 19,6
г/м3, при температуре +14оС Q = 12,2
г/м3.
2) Используя формулу относительной влажности воздуха: r = q : Q × 100
%,
выведем формулу, по которой определим абсолютную влажность воздуха:
q = Q × r : 100 % = 19,6 г/м3 × 75 % : 100 %
= 14,7 г/м3
3) 14,7 г/м3 – 12,2 г/м3 = 2,5 г/м3 –
столь влаги сможет конденсировать каждый м3 воздуха.
Ответ: утром образуется роса потому, что воздух, который
содержит 14,7 г/м3 влаги, будет перенасыщенным от того, что состояние
насыщения будет равно Q = 12,2 г/м3.
Задача 17. Температура
воздуха +15оС. Дефицит влаги равен 3,2 г/м3. Какова
относительная влажность воздуха?
Решение:
1) По таблице определяем, что при температуре +15оС Q = 13
г/м3
2) Найдем абсолютную влажность: q = 13 г/м3 – 3,2 г/м3 =
9,8 г/м3
3) Определим относительную влажность воздуха:
r = q : Q × 100 % = 9,8 г/м3 : 13 г/м3
× 100 % = 75,4 %
Ответ: относительная
влажность воздуха равна 75,4 %.
Задача 18. Воздух,
температура которого + 24оС и относительная влажность воздуха 52%,
поднялся на высоту 2 км. Образует ли этот воздух облака?
Решение:
1) 2 км × 6оС/ км = 12оС – разница температур
2) + 24оС – 12оС = +12оС – температура
воздуха на высоте 2 км
3) По таблице определяем, что при температуре +24оС Q = 22,2
г/м3, при температуре +12оС Q = 10,6
г/м3.
4) q = Q × r : 100 % = 22,2 г/м3 × 52 % : 100 %
= 11,5 г/м3 – абсолютная влажность воздуха
5) 11,5 г/м3 – 10,6 г/м3 = 0,9 г/м3 –
столь влаги сможет конденсировать каждый м3 воздуха.
Ответ: этот воздух
образует облака, потому что содержит 11,5 г/м3 влаги, а может
содержать при данной температуре только 10,6 г/м3.
Задача 19. В каждом м3
воздуха, температура которого + 20оС, содержится 9,7 г влаги. На
сколько градусов этот воздух должен охладиться, чтобы в нем начался процесс
конденсации?
Решение:
1) По таблице находим, что воздух, содержащий 9,7 г влаги, становится
насыщенным при температуре ниже, чем +11оС.
2) 20оС – 11оС = 9оС – на столько
градусов должен охладиться воздух, чтобы в нем начался процесс конденсации.
Ответ: воздух должен
охладиться на 9оС, чтобы в нем начался процесс конденсации.
Задача 20. О чем
говорит ситуация, когда дневной бриз на берегу океана сменяется на ночной в
полдень?
Решение:
Бриз – ветер прибрежной
зоны, дующий днем с моря на сушу, а ночью – с суши на море.
Резкое понижение давления над акваторией океана приводит к изменению
направления ветра. Направление бриза меняется на противоположное – с берега на
океан, что свидетельствует о приближении шторма. Чем быстрее падает давление, тем
сильнее ожидается ветер.
Ответ: изменение направления бриза в полдень говорит о
приближении шторма.
Задача 21. Определите,
на сколько мм рт. ст. нормальное атмосферное давление высшей точки равнинной
части Украины больше давления на вершине самой высокой горы Украины.
Решение:
1) Высшая точка равнинной части Украины – г. Берда (515 м).
Определим нормальное атмосферное давление для этой точки:
760 мм рт. ст. – h × ΔР = 760 мм рт. ст. – 515 м
× 1 мм рт. ст. : 10 м = 708,5 мм рт. ст.
2) Высшая точка Украины – г. Говерла (2061 м).
Определим нормальное атмосферное давление для этой точки:
760 мм рт. ст. – h × ΔР = 760 мм рт. ст. – 2061
м × 1 мм рт. ст. : 10 м = 553,9 мм рт. ст.
3) Найдем разницу атмосферного давления на двух вершинах:
708,5 мм рт. ст. – 553,9 мм рт. ст. = 154,6 мм рт. ст.
Ответ: нормальное атмосферное давление на г. Берда выше
давления на г. Говерла на 154,6 мм рт. ст.
Задача 22. Самолет
вылетел из аэропорта при нормальной погоде (t = 25оС,
Р = 765 мм рт. ст.). Достигнув намеченной высоты (5000 м), он частично
разгерметизировался. Давление в салоне стало падать на 2,5 мм рт. ст. за каждые
10 с. Сколько времени есть у пилотов, чтобы опустить самолет на высоту 1000 м
над уровнем моря?
Решение:
1) До разгерметизации давление в салоне самолета было такое же, как у
поверхности Земли – 765 мм рт. ст.
Определим разницу давления в салоне самолета и на высоте 1000 м:
765 мм рт. ст. – h × ΔР = 765 мм рт. ст. – 1000
м × 1 мм рт. ст. : 10 м = 765 мм рт. ст. – 100 мм рт. ст. = 665 мм рт. ст.
2) Давление в самолете падает на 2,5 мм рт. ст. за 10 с или на 15 мм рт.
ст. за 1 мин.
3) Определим время, которое есть у пилотов для спуска на нужную высоту:
665 мм рт. ст. : 15 мм рт. ст. / 1 мин. = 44,33 мин, или 44 мин 20 с.
Ответ: у пилотов есть 44 мин 20 с, чтобы опустить самолет на
высоту 1000 м над уровнем моря.
Задача 23. От мощного
ледяного поля в Антарктиде откололся айсберг. Определите атмосферное давление
на вершине айсберга, если над ледяным полем толщиной 1800 м давление равнялось
540 мм рт. ст.
Решение:

![]() 1800 м – Р = 540 мм рт. ст. 1)
1800 м – Р = 540 мм рт. ст. 1)
Плотность льда и воды не одинакова и соотносится как 900 :
1000, т. е. попав в воду 9/10 айсберга будет находиться под
водой, а 1/10 – над водой. Определим высоту айсберга над водой:
180 м – Р? 1800
м × 0,1 = 180 м
![]() 180 м
180 м  2) Найдем разницу высот между
2) Найдем разницу высот между
поверхностью ледяного поля и
![]()
0 м айсбергом: 1800 м – 180 м = 1620 м
3)
Найдем давление на поверхности айсберга:
540 мм рт. ст. + 1620 м × 1 мм рт. ст. : 10 м = 702 мм рт. ст.
Ответ:
атмосферное давление на вершине айсберга составляет
702 мм рт. ст.
![]()
Задача 24. Четыре
метеостанции в стране одновременно зафиксировали такие показатели атмосферного
давления: А (север) – 755 мм рт. ст., Б (юг) – 740 мм рт. ст., В (запад) – 748
мм рт. ст., Г (восток) – 758 мм рт. ст. Определите направление ветра в центре
этой страны.
Решение:
 755 мм рт.
755 мм рт.
ст. Ветер – движение воздуха из области
высокого в область
низкого давления.
 В
В
этом задании область высокого давления находится на
748 мм рт. ст. 758 мм рт. ст.
северо-востоке, а низкого – на юго-западе.
В
центре страны будет дуть северо-восточный ветер.
Ответ: в центре страны будет дуть северо-восточный
ветер.
740 мм рт. ст.
