Второй закон Ньютона это закон который был выведен в результате проведения опытов Ньютоном.
В результате чего были выведена новая формула второго закона ньютона а = F /m,
Что такое второй закон Ньютона, масса и вес тела
 Обобщая результаты опытов Галилея по падению тяжелых тел, астрономические законы Кеплера о движении планет, данные собственных исследований.
Обобщая результаты опытов Галилея по падению тяжелых тел, астрономические законы Кеплера о движении планет, данные собственных исследований.
Ньютон сформулировал второй закон динамики, количественно связывающий изменение движения тела с силами, вызывающими это изменение.
Чтобы исследовать зависимость между силой и ускорением количественно, рассмотрим некоторые опыты.
Ускорение от величины силы
I. Рассмотрим, как зависит ускорение одного и того же тела от величины силы, действующей на это тело. Предположим, что к тележке прикреплен динамометр, по показаниям которого измеряют силу.
Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле s = (at2) : 2 определим ускорение a.
Изменяя величину силы, проделаем опыт несколько раз. Результаты измерения покажут, что ускорение прямо пропорционально силе, действующей на тележку
a1 : a2 = F1 : F2
ИЛИ
а ~ F.
Отношение силы, действующей на тело, к ускорению есть величина постоянная, которую обозначим m. Это отношение назовем массой тела.
Зависимость ускорения от массы
II. Установим зависимость ускорения тела от его массы. Для этого будем действовать на тележку какой-нибудь постоянной силой, изменяя массу (помещая различные грузы на тележку).
Ускорения тележки будем определять так же, как и в первом опыте. Опыт покажет, что ускорение тележки обратно пропорционально массе, то есть
(a1/a2) = (m2/m1), или а ~ (1/m)
Обобщая результаты опытов, можно заметить, что ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе данного тела (второй закон ньютона формулировка).
Этот вывод называется вторым законом Ньютона. Математически этот закон можно записать так (формула второго закона ньютона):
а = F /m
где а — ускорение, m—масса тела, F — результирующая всех сил, приложенных к телу. В частном случае на тело может действовать и одна сила.
Результирующая сила F равна векторной сумме всех сил, приложенных к телу;
F = mа.
Следовательно, сила равна произведению массы на ускорение.
Второй закон динамики можно записать в иной более удобной форме. Учитывая, что ускорение
а = (υ2 — υ1) / (t2 — t1)
подставим это выражение в уравнение второго закона Ньютона. Получим
F = ma = (mυ2 — mυ1) / (t2 — t1) = (∆(mυ))/∆t
Что такое импульс
Импульсом, или количеством движения, называется вектор, равный произведению массы тела на его скорость (тυ).
Тогда основной закон динамики можно сформулировать следующим образом: сила равна изменению импульса в единицу времени (второй закон ньютона в импульсной форме)
F = (∆(mυ))/∆t
Это и есть наиболее общая формулировка второго закона Ньютона. Массу тела Ньютон определил как количество вещества, содержащегося в данной теле. Это определение несовершенно.
Из второго закона Ньютона вытекает следующее определение массы. Из равенства
a1/a2= m2/m1
видно, что чем больше масса тела, тем меньше ускорение получает тело, то есть тем труднее изменить скорость этого тела и наоборот.
Следовательно, чем больше масса тела, тем в большей степени это тело способно сохранять скорость неизменной, то есть больше инертности. Тогда можно сказать, что масса есть мера инертности тела.
Эйнштейн доказал, что масса тела остается постоянной только при определенных условиях. В зависимости от скорости движения тела его масса изменяется по такому закону:

где m — масса тела, движущегося со скоростью υ; m0 — масса этого же тела, находящегося в покое; с = 3 • 108м/с скорость света в вакууме.
Проанализируем данное уравнение:
- Если υ«с, то величиной —, как очень малой, можно пренебречь и m = m0, то есть при скоростях движения, много меньших скорости света, масса тела не зависит от скорости движения;
- Если υ ≈ с, то υ2/с2 ≈ 1, тогда т = m0/0— отсюда вытекает, что m → ∞.
По мере увеличения скорости тела для его дальнейшего ускорения нужно будет прикладывать все увеличивающиеся силы.
Но бесконечно больших сил, которые потребовались бы для сообщения телу скорости, равной скорости света, в природе не существует.
Таким образом, заставить рассматриваемое тело двигаться со скоростью света принципиально невозможно.
Со скоростями, близкими к скорости света, современная физика встречается: так разгоняются, например, элементарные частицы в ускорителях.
Масса тела с ростом скорости
Масса тела с ростом скорости увеличивается, но количество вещества остается неизменным, возрастает инертность. Поэтому массу нельзя путать с количеством вещества.
Покажем связь между силой тяжести, массой тела и ускорением свободного падения. Любое тело, поднятое над Землей и ничем не поддерживаемое, падает снова на Землю.
Это происходит вследствие того, что между телом и Землей существует притяжение (этот вопрос более подробно рассмотрим позже).
Сила, с которой тело притягивается к Земле, называется силой тяжести. Падение тел в безвоздушном пространстве под действием силы тяжести (при υ0 = 0) называется свободным падением.
Отметим, что для тел, покоящихся в поле сил тяготения, сила тяжести равна весу тела Р.
Весом тела называется сила, с которой тело давит на горизонтальную подставку, неподвижную относительно Земли, или действует на подвес.
Если Р— сила тяжести, m — масса, g — ускорение силы тяжести (в данной точке Земли оно для всех тел одинаковой среднее его значение равно 9,8м/с2), то применяя второй закон динамики, получим
P = mg.
Выразим с помощью этой формулы веса двух различных тел. Тогда:
P1 = m1g и Р2 = m2g. Разделив почленно эти два равенства, будем иметь
P1/P2 = m1/m2
Следовательно, веса тел в данной точке земной поверхности прямо пропорциональны их массам.
Задачи на второй закон ньютона
1. Какая сила F действует на автомобиль массой кгm=1000 кг, если он движется с ускорением мсa=1 м/с2.
Дано:
m = 1000 кг
a = 1 м/с2
Найти: F — ?
Решение:
Запишем второй закон Ньютона :
F = mа.
F = 1000 кг • 1 м/с2 = 1000 Н
Ответ: 1000 Н.
2. На мяч действует сила F = 70Н, масса мяча m = 0,2 кг, найти его ускорение a.
Дано:
m = 0,2 кг,
F = 70Н
Найти:
a — ?
Решение:
Запишем второй закон Ньютона :
F = mа.
Следовательно а = F / m.
а = 70Н : 0,2 кг = 350 м/с.
Ответ: а = 350 м/с.
Статья на тему Второй закон Ньютона
С древних времен люди замечали, что всякий брошенный вверх предмет неминуемо падает вниз, на землю. Это явление в современной физике описывается в рамках классической механики с привлечением понятия гравитационного притяжения нашей планетой всех окружающих тел. С силой гравитации тесно связан вес тела. В данной статье рассмотрим эту физическую величину и приведем формулы веса.
Что такое вес тела?
Прежде чем приводить формулу веса в физике, рассмотрим определение самой величины. Весом называют силу, с которой тело воздействует на опору либо растягивает подвес, к которому оно прикреплено. В этом принципиальное отличие веса тела от массы. Последняя является физической характеристикой инерционных свойств объектов. Масса – это неотъемлемое свойство тел, вес же – это величина переменная, поскольку она зависит от характеристик гравитационного поля, в котором находится рассматриваемое тело.
Примером действия веса является ситуация, когда мы становимся на весы. Хотя последние откалиброваны таким образом, что они показывают массу в килограммах, в действительности же измеряется именно вес, с которым наше тело давит на весы.

Другой пример – это взвешивание предметов с помощью ручных пружинных весов, которые называют кантером. Подвешенный к прибору предмет растягивает пружину до тех пор, пока сила ее упругости не уравновесит вес тела. Эти весы, как и предыдущие, откалиброваны на шкалу массы.
Формула веса тела в покое
В середине XVII века, наблюдая за поведением небесных тел (планет, естественных спутников, комет) и используя экспериментальные данные, Исаак Ньютон сформулировал закон всемирного тяготения. Благодаря этому закону появилась возможность численного расчета гравитационных сил, с которыми взаимодействуют тела в природе. Согласно этому закону, сила тяжести Ft на поверхности любой планеты может быть рассчитана по формуле:
Ft = m*g
Где m – масса тела, g – это линейное ускорение, которое планета сообщает всем телам, находящимся вблизи нее. Для Земли оно равно 9,81 м/с2. Сразу отметим, что величина g от массы не зависит, однако она зависит от расстояния до планеты, убывая, как его квадрат.
Когда любое тело массой m находится на поверхности, например стакан с водой стоит на столе, то на него действуют две силы:
- тяжести Ft;
- реакции опоры N.
Так как тело никуда не движется и покоится, то обе силы противоположны по направлению и равны по модулю, то есть:
- Ft = N
Согласно определению веса, формула для него принимает вид:
P = N = Ft = m*g
Именно с силой Ft стакан с водой давит на стол.
Свободное падение и вес тела
Проведем следующий мысленный эксперимент: предположим, что в деревянный ящик поместили камень некоторой массы m, затем бросили этот ящик с высоты. Какой вес будет иметь камень в процессе свободного падения?
Для ответа на этот вопрос следует записать основное уравнение динамики. В данном случае оно имеет вид:
m*a = Ft – N
Здесь a – ускорение, с которым падает ящик и камень. В случае свободного падения, это ускорение равно величине g. Тогда получаем:
m*g = m*g – N =>
N = 0
То есть сила реакции опоры равна нулю. Этот вывод уравнения движения говорит о том, что камень во время свободного падения давить на дно ящика не будет, то есть его вес будет равным нулю. Такая ситуация наблюдается на космических станциях, на которых центробежная сила и сила тяжести уравновешивают друг друга.

Для движения с произвольным ускорением вниз формула веса примет вид:
P = m*(a – g)
Решение задачи
Известно, что во время старта ракеты ее ускорение равно 40 м/с2. Необходимо определить вес космонавта, находящегося в ней, если его масса равна 70 кг.
Для начала запишем второй закон Ньютона для рассматриваемой задачи. Имеем:
m*a = N – m*g
Здесь сила тяжести направлена против ускорения, а реакция опоры – вдоль вектора ускорения. Из этого равенства получаем:
P = N = m*(g + a)

Подставляя данные, получаем, что вес космонавта во время старта ракеты будет равен 3486,7 Н. Если бы в процессе старта космонавт встал на весы, то они бы показали значение его массы 355,4 кг.
Вес тела. Калькулятор онлайн.
Калькулятор вычисления веса тела, вычислит вес тела, массу, ускорение свободного падения и даст подробное решение.
Калькулятор содержит:
Калькулятор вычисления веса тела, если известны масса тела и ускорение свободного падения.
Калькулятор вычисления массы тела, если известны вес тела и ускорение свободного падения.
Калькулятор вычисления ускорения свободного падения, если известны вес тела и его масса.
В данной таблице приведены значения ускорения свободного падения для планет Солнечной системы и их спутников.
Калькулятор вычисления веса тела, если известны масса тела и ускорение свободного падения.
Вес тела P, которое покоится в инерциальной системе отсчета равен произведению массы m этого тела и ускорения свободного падения g над поверхностью космического тела.
Ускорение свободного падения g на поверхности Земли равно 9.780327 м/с2
Единицей измерения силы – Ньютон (Н, N)
Масса m =
Ускорение свободного падения g =
Единица измерения веса P
Калькулятор вычисления массы тела, если известны вес тела и ускорение свободного падения.
Масса тела m равна отношению веса P к ускорению свободного падения g над поверхностью космического тела.
Ускорение свободного падения g на поверхности Земли равно 9.780327 м/с2
Единица массы – килограмм, но также можно использовать и другие единицы, например грамм, тонна, миллиграмм и т.д.
Вес P =
Ускорение свободного падения g =
Единица измерения массы m
Калькулятор вычисления ускорения свободного падения, если известны вес тела и его масса.
Ускорение свободного падения g равно отношению веса тела P к его массе m.
Ускорение свободного падения g на поверхности Земли равно 9.780327 м/с2
Ускорение свободного падения — это ускорение, которое тело приобретает под действием гравитационной силы около поверхности небесных тел в космическом пространстве.
Единица ускорения – метр в секунду в квадрате.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Вес тела — это сила, с которой тело, вследствие притяжения к Земле, действует на опору или подвес.
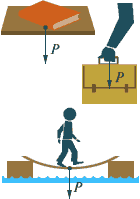
P=N = mg
В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес – это упругая сила, приложенная к опоре или подвесу (т.е. к связи).
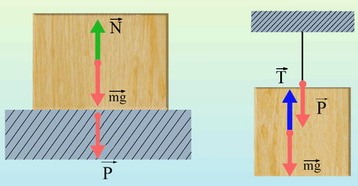
Вес тела в различных условиях движения.
1) опора покоится или движется равномерно
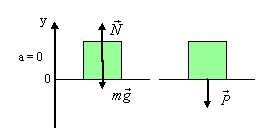
N=mg – сила реакции опоры
P=N значит P=mg Вес тела равен действующей на тело силе тяжести.
2) опора движется с ускорением a вверх.
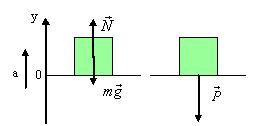
N–mg=ma – второй закон Ньютона
N=mg+ma
P=N=m·(g+a)
P>mg Вес тела, движущегося с ускорением направленным вверх больше силы тяжести.
Увеличение веса тела, вызванное его ускоренным движением, называется перегрузкой.
3) опора движется с ускорением а вниз.
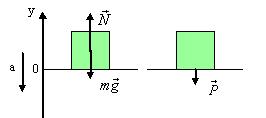
mg-N=ma – второй закон Ньютона
N=mg-ma
P=N=m·(g-a)
P<mg Вес тела, движущегося с ускорением вниз уменьшается.
Падение тел в вакууме без начальной скорости называется свободным падением. При свободном падении a=g из P=m·(g-a) следует, что P=0, т.е. вес отсутствует.
Если тела движутся только под действием силы тяжести, т.е. свободно падают, то они находятся в состоянии невесомости – состояние, при котором вес тела отсутствует (НО! масса у тела есть всегда).
Обозначения:
N – сила реакции опоры
P – вес тела
m – масса тела
g – ускорение свободного падения
a – ускорение, с которым движется тело
Загрузить PDF
Загрузить PDF
Вес — сила, с которой тело действует на опору (или другой вид крепления), возникающая в поле силы тяжести. Масса связана с энергией и импульсом тела и эквивалентна энергии его покоя. Масса не зависит от силы тяжести (точнее от ускорения свободного падения). Поэтому тело, на Земле имеющее массу 20 кг, на Луне будет иметь массу 20 кг, но совсем другой вес (потому что ускорение свободного падения на Луне в 6 раз меньше, чем на Земле).
-

1
Для вычисления веса используйте формулу
. Вес — это сила, с которой тело действует на опору, и его можно рассчитать, зная массу тела. В физике используется формула
.[1]
-

2
Определите массу тела. Так как ускорение свободного падения — это стандартная величина, то необходимо знать массу тела, чтобы найти его вес. Масса должна быть выражена в килограммах.
-

3
Узнайте величину ускорения свободного падения. На Земле, как уже было сказано выше, g = 9,8 м/с2. В других местах Вселенной эта величина меняется.[3]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
- Ускорение свободного падения на Солнце приблизительно равно 274,0 м/с2 (примерно в 28 раз больше, чем на Земле). Поэтому ваш вес на Солнце будет в 28 раз больше вашего земного веса (если, конечно, вы выживете на Солнце, что еще не факт!).[5]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
-

4
Подставьте значения в формулу
. Теперь, когда вы знаете массу
и ускорение свободного падения
, подставьте их значения в формулу
. Так вы найдете вес тела (измеряется в ньютонах, Н).
Реклама
-

1
Задача № 1. Найдите вес тела массой 100 кг на поверхности Земли.
-

2
Задача № 2. Найдите вес тела массой 40 кг на поверхности Луны.
-

3
Задача № 3. Найдите массу тела, которое на поверхности Земли весит 549 Н.
Реклама
-

1
Не путайте массу и вес. Самая распространенная ошибка — перепутать вес и массу (что немудрено, ведь в повседневной жизни мы обычно называем массу весом). Но в физике все не так. Запомните, масса — это постоянное свойство объекта, то, сколько в нем вещества (килограммов), где бы он ни находился. Вес — это сила, с которой объект всеми своими килограммами давит на поверхность, и эта сила на разных небесных телах будет различной.
- Масса измеряется в килограммах или граммах. Запомните, что в этих словах, как и в слове «масса», есть буква «м».
-

2
Используйте правильные единицы измерения. В задачах по физике вес или силу измеряют в ньютонах (Н), ускорение свободного падения — в метрах на секунду в квадрате (м/с2), а массу — в килограммах (кг). Если для какой-либо из этих величин вы возьмете не ту единицу измерения, воспользоваться формулой будет нельзя. Если масса в условиях задачи указана в граммах или тоннах, не забудьте перевести ее в килограммы.
Реклама
Приложение: вес, выраженный в кгс
- Ньютон — это единица измерения силы в международной системе единиц СИ. Нередко сила выражается в килограмм-силах, или кгс (в системе единиц МКГСС). Эта единица очень удобна для сравнения весов на Земле и в космосе.
- 1 кгс = 9,8166 Н.
- Разделите вес, выраженный в ньютонах, на 9,80665.
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне.
- Международная система единиц СИ — система единиц физических величин, которая является наиболее широко используемой системой единиц в мире.
Советы
- Самая трудная задача — уяснить разницу между весом и массой, так как в повседневной жизни слова «вес» и «масса» используются как синонимы. Вес — это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу.
- Ускорение свободного падения также может быть выражено в Н/кг. 1 Н/кг = 1 м/с2.
- Плечевые весы измеряют массу (в кг), в то время как весы, работа которых основана на сжатии или расширении пружины, измеряют вес (в кгс).
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне. На нейтронной звезде он будет весить еще больше, но он, вероятно, этого не заметит.
- Единица измерения «Ньютон» применяется намного чаще (чем удобная «кгс»), так как можно найти множество других величин, если сила измеряется в ньютонах.
Реклама
Предупреждения
- Выражение «атомный вес» не имеет ничего общего с весом атома, это масса. В современной науке оно заменено на выражение «атомная масса».
Реклама
Об этой статье
Эту страницу просматривали 113 467 раз.
