sdfrsd kyuggg
Профи
(549)
13 лет назад
Вот задача, которой мы и займёмся на этом уроке: Имеется 9 одинаковых монет. Но одна из них фальшивая. Она легче остальных. (восемь монет одинаковые на вес) Требуется при помощи 2 взвешиваний на чашечных весах без гирь выделить фальшивую монету. Что надо сделать? Для начала я дам Вам весы и девять монет (каждому ученику) Всем хватило? Хорошо. Теперь повторяйте мои действия. Сначала разделим монеты на три группы. В каждой-по три монете. Одну группу оставляем на столе, вторую кладём на одну сторону весов, третью на другую половину. Все положили? Хорошо. У меня чаши равны. Это значит, что фальшивка в группе, которая у меня на столе. Я вижу, у многих учеников та же ситуация. Теперь мы взвешиваем две монеты из третьей группы. Они тоже одинаковые на вес. Значит, третья фальшивая. Теперь я объясню для тех учеников, у которых при взвешивании двух групп монет весы показали неравенство. На той чаше, где веса меньше, лежит фальшивка. Теперь тоже взвесьте по две монеты.
Катя Булычёва
Знаток
(455)
13 лет назад
Делим монеты на две равные кучки. Из каждой кучки берем по 3 монеты, кладем на весы и взвешиваем. Если вес одинаковый то взвешиваем оставшиеся 1и 1 монеты и выявляем фальшивую (более легкую) . Если же одна группа из трех монет легче другой, значит там есть фальшивая монета. Оставляем более легкую группу из трех монет и кладем на весы 1и 1 и действуем по предыдущему алгоритму: если вес одинаков, значит фальшива третья, а если нет то та которая легче.
Genixy
Знаток
(279)
13 лет назад
Элементарно, тока что придумал. При условии что известно что фальшивка тяжелее, либо легче.
Кароче берешь на одну чашу весов ставишь 3 монеты и на другую чашу весов 3 монеты.
1 Если весы ровные, то оставшиеся 3 монеты взвешиваем иначе (ведь фальшивка там) . Взвешиваем по 2 из этих монет. Если весы ровные значит третья фальшивка. Если одна чаша перевешивает другую значит в ней фальшивка.
2 Если при первом взвешивании когда на чашах по 3 монеты.. . перевешивает какая то из чаш, значит там фальшивка, из той чаши опять взвешиваем 2 монеты а третью держим в руке. Весы покажут где фальшивка, – гна перевесившей чаше либо у вас в руке 🙂 типа того.
Zinxxx
Ученик
(176)
6 лет назад
1 Что мы делаем это : 3 монеты на одну чашу весов, 3 на другую, три в стороне. Так находм кучку из трёх монет, в которой есть фальшивая.
2 Что мы делаем это :Из этих трёх монет по одной на чаши весов, одну в стороне. Так находим фальшивую.
Как найти фальшивую монету двумя взвешиваниями – логическая задача
Загадки на логику
Перед нами логическая задача, чтобы решить которую нужно немного пораскинуть мозгами.
Итак условия задачи следующие:
На столе лежат 9 монет. Известно, что одна из монет фальшивая. Фальшивая монета весит меньше чем остальные. У нас имеются весы для взвешивания.
Вопрос:
Как при помощи двух взвешиваний найти фальшивую монету?
Внимание!
Ниже приведен правильный ответ!
Правильный ответ:
Вначале на каждую чашу весов нужно положить по три монеты.
Если после этого весы приходят в равновесие, значит среди этих монет нет фальшивой, берем две из трех оставшихся монет, кладем на разные чаши весов. Если фальшивая монета среди этих двух, то мы поймем на какой она чаше, эта чаша поднимется выше.
А если весы снова придут в равновесие, значит фальшивая монета осталась на столе.
Если же при первом взвешивании весы не пришли в состояние равновесия, значит фальшивая монета уже находится на весах, берем 2 монеты из тех трех, что оказались легче, кладем по 1 на каждую чашу, если одна чаша поднялась выше, значит фальшивая монета на ней, если чаши уравновесились, значит фальшивая – оставшаяся третья.
Похожие новости

Все загадки
Все загадки

Все загадки
Все загадки
Все загадки
Все загадки
Задача абсолютно стандартная. Разобрана в миллиарде книг. Мне кажется, даже каждый школьный учитель её рассказывает в какой-то момент своим ученикам. Тем не менее задача встречается на олимпиадах в разных классах едва ли не чаще остальных. И все равно находятся люди, которые не понимают что к чему. Даже среди взрослых.
Давайте разберем одну из таких задач. Имеется 12 монет. Одна из которых фальшивая. Она отличается от подлинных только по весу (но заранее не известно в меньшую или в большую сторону). Как на чашечных весах определить фальшивку за 3 взвешивания и понять легче она или тяжелее, чем остальные? Как вы понимаете количество монет и взвешиваний может быть разным. От этого суть не изменится.
В любом случае нам надо будет разбить монеты на кучки, чтобы взвешивать их группами. В данной задаче удобно разбить монеты на 3 кучки по 4 монеты в каждой.
В какой-то момент в одном из случаев вам может показаться, что для некоторых случаев трех взвешиваний мало и надо бы четвертое. Ну или не получится определить легче или тяжелее фальшивка. Если так, то вы ошибаетесь, надо думать снова. Трех взвешиваний достаточно в любом случае. И в любом случае получится узнать легче фальшивка или тяжелее.
Для наглядности пронумеруем монеты: {1,2, 3, 4}; {5, 6,7, 8}; {9,10, 11, 12} и приступим к решению.
Первое взвешивание
Сравниваем первые две кучки монет {1,2, 3, 4} и {5, 6,7, 8}. Если весы находятся в равновесии, значит фальшивка в третьей кучке. Переходим к пункту а) во втором взвешивании.
Если весы не в равновесии, то фальшивка в одной из этих двух кучек, а в третьей все монеты настоящие. Запоминаем, какая кучка перевесила [я для примера буду считать, что перевесила кучка {1,2,3,4}, но если нет, то решение будет симметричным] и переходим к пункту б) во втором взвешивании.
Второе и третье взвешивания
а) Фальшивка среди монет {9,10, 11, 12}. Взвешиваем {1, 2, 3} и {9,10, 11}. Если весы в равновесии, значит фальшивая монета под номером 12. третьим взвешиванием узнаем, легче она или тяжелее.
Если не равны, значит, фальшивка среди монет 9, 10, 11. При этом уже после второго взвешивания мы будем точно знать легче фальшивка или тяжелее. Третьим взвешиванием однозначно находим фальшивку: взвешиваем монеты 9 и 10. Если они равны, то фальшивка – 11. Если не равны, то фальшивка либо 9, либо 10 в зависимости от того, какая монета легче (оригинал или фальшивка), ведь эту информацию мы узнали после второго взвешивания.
б) Фальшивка в одной из первых двух кучек. Для того, чтобы понять в какой, взвесим {1, 2, 5} и {3, 4, 9} [опечатки нет, монета 9 заведомо настоящая]. Если весы в равновесии, значит, фальшивка среди 6, 7, 8, причем одна из них легче остальных [это потому что мы для ясности рассматриваем случай, когда первое взвешивание показало, что первая кучка тяжелее]. Третьим взвешиванием сравниваем монеты 6 и 7. Если они равны, то фальшивка – 8. Если нет, то фальшивка та, которая весит меньше.
Если весы после второго взвешивания оказались не в равновесии, возникает два случая
б.1) Если перевесила кучка {1, 2, 5}, то фальшивка среди монет 1 и 2. Третьим взвешиванием мы узнаем, какая из них тяжелее и это и есть фальшивка.
б.2) Если перевесила кучка {3, 4, 9}, то фальшивка среди монет 3, 4 и 5. Если фальшивка – 5, то она будет легче других. А если 3 или 4, то фальшивка тяжелее настоящих. Третьим взвешиванием сравниваем монеты 3 и 4. Если одна из них тяжелее, то это фальшивка. Если они равны, то фальшивка – 5 и она легче.
Всё. Как вам задачка? Как видите, рассмотрены все случаи и трех взвешиваний достаточно даже для того, чтобы определить не только фальшивку, но и её относительный вес.
Ещё интересно:
Разминка для мозга: сможете решить задачу про фальшивую монету? Проверьте!
25 августа 2020
Отдых
Есть 12 монет, среди них одна поддельная. Помогите математику обнаружить её всего за три взвешивания.
Анастасия Сукманова
Избранное
За критику налоговой системы император заточил в темницу величайшего математика страны. Но однажды пленнику представился шанс вновь обрести свободу. Один из 12 наместников императора уплатил налог фальшивой монетой, которая уже попала в казну. Император пообещал освободить математика, если тот сумеет найти подделку.
Перед пленником поставили стол, на котором были чашечные весы, карандаш и 12 одинаковых на вид монет. А потом сказали, что фальшивка отличается от остальных денег по весу в большую или меньшую сторону. Взвесить монеты разрешили лишь трижды. Как математику вычислить подделку?
Показать ответ
Скрыть ответ
Читайте также ✅
- Сложная задачка про голубоглазых пленников, которые застряли на острове
- Задача про пленников и колпаки, цвет которых нужно определить
- Задача про тайник Леонардо да Винчи, в который не так-то легко пробраться
Задача
Имеется 8 монет одинакового достоинства, одна из которых фальшивая. Фальшивая монета легче настоящей. Как с помощью всего лишь двух взвешиваний найти фальшивую монету? В вашем распоряжении аптекарские весы без гирь, которые показывают только легче-тяжелее.
Решение этой задачи состоит в том, что исходный набор монет надо разделить на три кучки, в двух из которых число монет обязательно должно быть равным.
Если мы взвесим на весах с двумя чашами две кучки с одинаковым числом монет одинакового достоинства и одна из них окажется легче, значит фальшивая монета в этой кучке, и уже её надо разделить на три части, в двух из которых число монет обязательно должно быть равным.
Если же у взвешенных двух кучек монет одинаковый вес, значит фальшивая монета в третьей кучке.
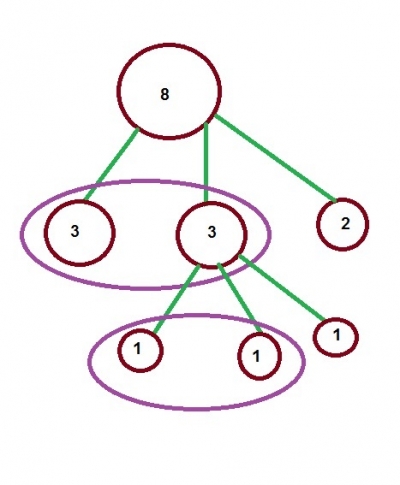
Покажем схему взвешивания для наших 8 монет:
Вначале у нас есть 8 монет. Мы делим их на кучки по 3, 3 и 2 монеты.
Взвешиваем две кучки по 3 монеты. Предположим, что одна из этих кучек оказалась легче. Значит, фальшивая монета в ней. Теперь делим эту кучку на три по 1 монете в каждой.
Теперь нам достаточно взвесить любые две монеты, чтобы определить, где фальшивая – она окажется или на весах, или это будет третья монета.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Задача
Имеется 10 монет одинакового достоинства, одна из которых фальшивая. Фальшивая монета легче настоящей. За какое минимально гарантированное количество взвешиваний можно найти фальшивую монету? В вашем распоряжении аптекарские весы без гирь, которые показывают только легче-тяжелее.
Это точно такая же задача, как и предыдущая, но в ней на 2 монеты больше, и взвешиваний будет на одно больше.
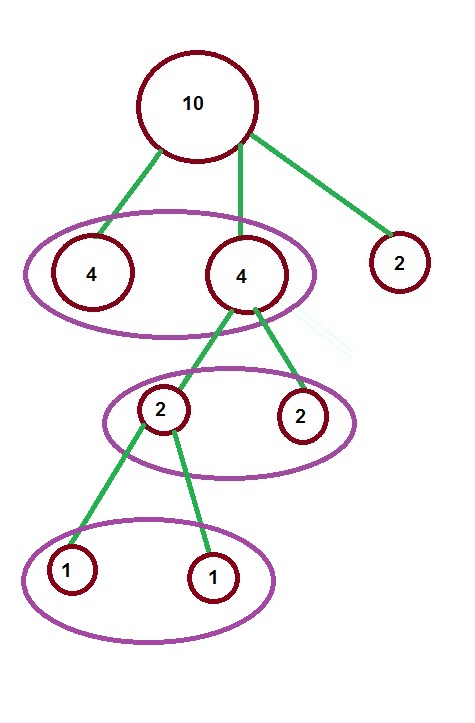
Вот схема взвешивания:
Как видим, на втором взвешивании у нас образовались кучки по две монеты, поэтому, когда мы определили, в какой из этих кучек находится фальшивая, то дальше смогли разделить её только на две “кучки” по 1 монете в каждой.
Дата публикации
17.04.2020

.jpg)