Динамометр (от греческого слова «динамис» — сила) — это прибор для измерения силы.
Существуют различные конструкции динамометров. Силу тяги тракторов, тягачей, буксиров и т. д. измеряют с помощью тяговых динамометров (рис. 35). Для измерения мышечной силы руки используют медицинский динамометр — силомер (рис. 36).
На рисунке 37 изображен учебный пружинный динамометр, рассчитанный на измерение сил до 4 Н. Он состоит из стальной пружины с указателем и крючком, прикрепленном к пластмассовому (в старых конструкциях к деревянному) основанию, на которое нанесена шкала (буква «N» на шкале динамометра — это международное обозначение ньютона).
Действие пружинного динамометра основано на уравновешивании измеряемой силы силой упругости пружины.
Градуирование пружины динамометра (т. е. создание шкалы с делениями) можно осуществить следующим образом. К основанию динамометра (под пружиной) прикрепляют полоску белой бумаги. Затем отмечают положение указателя при нерастянутой пружине — это нулевое деление (рис. 38, а). После этого к крючку подвешивают груз массой 102 г. На этот груз действует сила тяжести 1 Н. Под действием этого груза пружина растягивается и указатель перемещается вниз. В положении равновесия сила тяжести, действующая на груз, уравновешивается противоположно направленной силой упругости. Следовательно, растяжение пружины при этом будет соответствовать силе упругости, также равной 1 Н. Поэтому новое положение указателя отмечают на бумаге цифрой 1 (рис. 38, б).
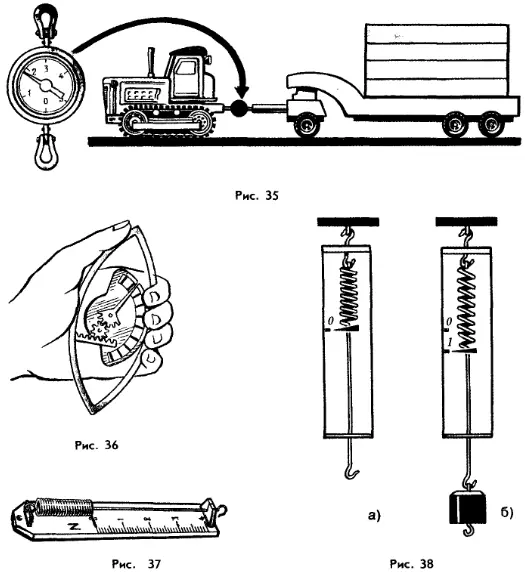
Затем к первому грузу подвешивают еще один такой же, увеличивая тем самым общую массу до 204 г, а силу тяжести — до 2 Н. Соответствующее положение указателя отмечают цифрой 2. После этого прикрепляют третий, а затем четвертый груз, каждый раз отмечая положение указателя соответствующей цифрой.
Для того чтобы можно было измерять десятые доли ньютона, каждое из расстояний между отметками 0 и 1, 1 и 2, 2 и 3, 3 и 4 делят на десять равных частей. Такое построение шкалы возможно благодаря закону Гука, из которого следует, что сила упругости пружины увеличивается во столько же раз, во сколько раз увеличивается ее удлинение.
Динамометр можно применять и для измерения веса тела. Весом тела называют силу, с которой оно давит на горизонтальную опору или растягивает вертикальный подвес.
Р — вес тела.
Если к вертикально расположенному пружинному динамометру прикрепить груз, то после того, как груз растянет пружину и остановится, на крючок динамометра будут действовать две силы: сила упругости пружины Fупр и вес груза Р. Эти силы будут противоположны по направлению, но равны по величине. Поэтому динамометр позволяет измерить не только силу упругости (и равную ей силу тяжести груза), но и вес тела Р.
Вес покоящегося, а также равномерно и прямолинейно движущегося (относительно Земли) тела равен действующей на него силе тяжести:
P = mg.
Несмотря на совпадение формул, между силой тяжести и весом тела есть существенное различие. Сила тяжести приложена к телу, на которое действует Земля, а вес тела приложен к подвесу или опоре, на которую это тело давит. Если обе эти силы изобразить в виде стрелок, указывающих их направление (а направлены эти силы вертикально вниз), то это будет выглядеть так, как показано на рисунке 39.
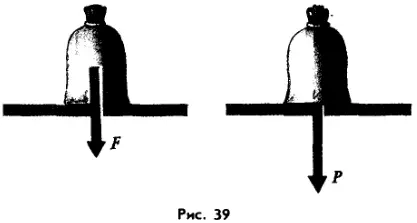
Вес тела не следует путать с его массой. Масса тела измеряется в килограммах, а вес тела (как и любая другая сила) — в ньютонах. Вес тела имеет направление, а масса никакого направления не имеет.
1. Что такое динамометр? 2. На чем основано действие пружинного динамометра? 3. Что называют весом тела? 4. По какой формуле находится вес покоящегося тела? 5. Чем отличается вес тела от силы тяжести и массы тела?
Пo рисунку 76 определите, с какой силой растягивается каждая пружина под действием подвешенного к ней груза (масса одного груза 102 г).
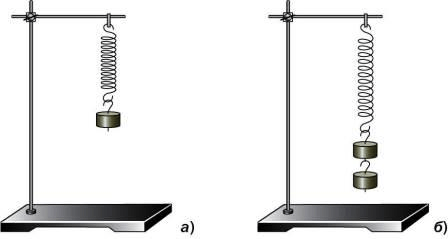
рис. 76

reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. §30. Упражнение 11. Номер №3
Решение
![]() Получай решения и ответы с помощью нашего бота
Получай решения и ответы с помощью нашего бота
Дано:
m
1
=102 г.
Найти:
F
1
− ?
F
2
− ?
Решение:
P=gm;
g = 9,8 Н/кг:
1 г = 0,001 кг;
F
1
=
9
,
8
∗
102
∗
0
,
001
≈
1
Н;
F
2
=
9
,
8
∗
2
∗
102
∗
0
,
001
≈
2
Н.
Ответ: 1 Н; 2 Н.
Сила тяжести. Вес
- Движение тел вблизи поверхности Земли
- Сила тяжести
- Вес тела
- Невесомость
- Задачи
- Лабораторная работа №7. Градуирование шкалы динамометра и измерение силы тяжести
п.1. Движение тел вблизи поверхности Земли
Вблизи поверхности Земли все тела, предоставленные самим себе, падают вниз, независимо от направления начальной скорости.
Такое движение тел называют свободным падением.
п.2. Сила тяжести
Многочисленные эксперименты показали, что в свободном падении все тела вблизи поверхности Земли падают с одинаковым ускорением (overrightarrow{g}), которое направлено вниз, к центру Земли.
В системе отсчета, связанной с Землей, на любое тело массой (m) действует сила тяжести $$ overrightarrow{F_{text{тяж}}}=m overrightarrow{g} $$
 |
Сила тяжести прямо пропорциональна массе тела. Точка приложения силы тяжести – центр масс тела. Сила тяжести всегда направлена вертикально вниз, к центру Земли. |
 |
Измерения показывают, что на средних географических широтах ускорение свободного падения (gapprox 9,81 text{м/с}^2). Т.е., скорость при падении увеличивается на (9,81 text{м/с}) каждую следующую секунду.
В общем случае, ускорение свободного падения зависит от широты рассматриваемого места, высоты над уровнем моря, времени суток и ещё нескольких более «тонких» факторов. В школьных задачах, если другое не оговорено, для вычислений используют приблизительное значение (gapprox 10 text{м/с}^2). |
п.3. Вес тела
Если подвесить тело или положить его на опору, сила тяжести, действующая на тело, будет уравновешена силой, которую называют силой реакции подвеса или силой реакции опоры.
Т.к. силы уравновешивают друг друга, выполняется соотношение $$ moverrightarrow{g}=-overrightarrow{N} $$ где (moverrightarrow{g}) – сила тяжести, (overrightarrow{N}) – реакция подвеса или опоры.
По третьему закону Ньютона, если подвес или опора действуют на тело с силой (overrightarrow{N}), то и тело действует на подвес или опору с силой (overrightarrow{P}=-overrightarrow{N})
Вес тела – это сила, с которой тело действует на подвес или опору.
Получаем, что (overrightarrow{P}=moverrightarrow{g}), вес и сила тяжести равны по величине и направлению, но приложены к разным точкам: сила тяжести – к центру масс тела, вес – к подвесу или опоре.
По своей природе реакции подвеса или опоры являются силами упругости: под действием веса тела подвес или опора деформируются, и силы упругости стремятся восстановить их форму и размеры.
Равенство (overrightarrow{P}=moverrightarrow{g}) выполняется, если подвес или опора покоятся или движутся относительно Земли прямолинейно и равномерно.
Если движение подвеса или опоры равноускоренное с ускорением (overrightarrow{a}ne 0), то (overrightarrow{P}ne moverrightarrow{g}), вес будет больше (при (overrightarrow{a}) направленном вверх) или меньше (при (overrightarrow{a}) направленном вниз) силы тяжести. Подробней этот случай будет рассмотрен в курсе физики для 9 класса.
п.4. Невесомость
Если опора свободно падает вместе с телом, то под действием силы тяжести каждая частица опоры и тела двигается вниз с одним и тем же ускорением (overrightarrow{g}). Ни в опоре, ни в теле не возникают сжатия или растяжения, нет сил упругости, а значит, вес тела равен нулю.
Состояние, при котором в свободно падающих телах исчезают деформации и взаимные давления частиц тел друг на друга, называют невесомостью.
Состояние невесомости можно испытать, если подпрыгнуть – с момента отрыва от земли до момента приземления. В первые моменты прыжка до раскрытия парашюта, парашютисты также находятся в состоянии невесомости.
Движение космического корабля по орбите вокруг Земли представляет собой непрерывное свободное падение, поэтому космонавты испытывают состояние невесомости в течение всего полета, кроме тех моментов, когда передвигаются по кораблю или включают двигатели для маневрирования.
п.5. Задачи
Задача 1. Какой вес имеет человек массой 65 кг, который стоит на земле?
Дано:
(m=65 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(P-?)
Вес равен силе тяжести (P=mg) $$ Papprox 65cdot 10=650 (text{Н}) $$ Ответ: 650 Н
Задача 2. Парашютист равномерно опускается на землю. Сила сопротивления воздуха 900 Н. Масса парашюта 15 кг. Найдите массу парашютиста.
Дано:
(F_{text{сопр}}=900 text{Н})
(m_1=15 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(m_2-?)

На раскрытый парашют действуют две силы: сила сопротивления воздуха, направленная вверх, и суммарный вес (парашюта и парашютиста), направленный вниз.
Т.к. движение равномерное, ускорение (a=0). Значит, вес равен силе тяжести, и begin{gather*} F_{text{сопр}}=P=F_{text{т}}=(m_1+m_2)g\[6pt] m_1+m_2=frac{F_{text{сопр}}}{g}Rightarrow m_2=frac{F_{text{сопр}}}{g}-m_1 end{gather*} Подставляем $$ m_2=frac{900}{10}-15=75 (text{кг}) $$ Ответ: 75 кг.
Задача 3. На сколько сантиметров растянется пружина жесткостью k=267 Н/м, если подвесить к ней медный брусок размерами 5 см х 6 см х 10 см. Плотность меди 8900 кг/м3.
Дано:
(V=5 text{см}times 6 text{см}times 10 text{см}=300 text{см}^3=3cdot 10^{-4} text{м}^3)
(rho=8900 text{кг/м}^3)
(k=1000 text{Н/м})
(gapprox 10 text{м/с}^2)
__________________
(m_2-?)

Вес бруска равен силе тяжести и уравновешивается силой упругости: begin{gather*} mg=F_{text{упр}}=kDelta lRightarrow Delta l=frac{mg}{k}, m=rho V\[6pt] Delta l=frac{rho Vg}{k} end{gather*} Получаем: $$ Delta l=frac{8900cdot 3cdot 10^{-4}cdot 10}{267}=0,1 (text{м}=10 (text{см}) $$ Ответ: 10 см.
Задача 4*. При подвешивании гирьки массой 450 г пружина динамометра растягивается до 8 см. А при подвешивании гирьки массой 300 г – до 6 см. Найдите длину пружины динамометра без груза (ответ запишите в см).
Дано:
(m_1=450 text{г}=0,45 text{кг})
(l_1=8 text{см}=0,8 text{м})
(m_2=300 text{г}=0,3 text{кг})
(l_2=6 text{см}=0,6 text{м})
__________________
(l_0-?)

Вес гирьки равен силе тяжести и уравновешивается силой упругости: begin{gather*} mg=F_{text{упр}}=kDelta lRightarrow k=frac{mg}{Delta l} end{gather*} где (Delta l=l-l_0) – растяжение пружины.
Жесткость пружины begin{gather*} k=frac{m_1g}{Delta l_1}=frac{m_1g}{l_1-l_0}, k=frac{m_2g}{Delta l_2}=frac{m_2g}{l_2-l_0}\[6pt] frac{m_1g}{l_1-l_0}=frac{m_2g}{l_2-l_0} Rightarrow frac{m_1}{l_1-l_0}=frac{m_2}{l_2-l_0} Rightarrow m_2(l_2-l_0)=m_2(l_1-l_0)\[6pt] m_1l_2-m_1l_0=m_2l_1-m_2l_0 Rightarrow m_1l_2-m_2l_1=(m_1-m_2)l_0\[6pt] l_0=frac{m_1l_2-m_2l_1}{m_1-m_2} end{gather*} Получаем $$ l_0=frac{0,45cdot 0,06-0,3cdot 0,08}{0,45-0,3}=frac{0,027-0,024}{0,15}=0,02 (text{м}=2 (text{см}) $$ Ответ: 2 см.
п.6. Лабораторная работа №7. Градуирование шкалы динамометра и измерение силы тяжести
Цель работы
Исследовать зависимость силы упругости от величины деформации. Изготовить шкалу динамометра. Измерить силу тяжести для двух тел неизвестной массы; рассчитать их массу.
Теоретические сведения
 |
При подвешивании груза на пружину, его вес уравновешивается силой упругости. Для неподвижной пружины вес равен силе тяжести. Получаем $$ P=F_{text{т}}=mg=F_{text{упр}} =kDelta l $$ Удлинение пружины $$ Delta l=frac gk m $$ При постоянном ускорении свободного падения (g) и постоянной жесткости (k), удлинение прямо пропорционально массе подвешенного груза. |
В данной работе считаем, что грузу массой 100 г соответствует показание динамометра (F=1 text{Н}), т.е. (overline{g}=frac{1 text{Н}}{100 text{г}}=10frac{text{Н}}{ text{кг}}=10frac{ text{м}}{ text{с}^2}). Более точное стандартное значение (g_0=9,80665frac{ text{м}}{ text{с}^2})
Ошибка метода, связанная с величиной (g) $$ delta_g=frac{|overline{g}-g_0|}{g_0}approx 0,02=2text{%} $$ Тогда грузу массой 200 г соответствует показание 2 Н, 300 г – 3 Н и т.д.
После градуирования в целых значениях Н на динамометре наносятся промежуточные деления с ценой деления (d=0,1 text{Н}).
Ошибка градуирования определяется как степень отклонения от равномерности шкалы, (delta_{text{шк}}).
Теперь с помощью полученного прибора можно непосредственно измерять силу тяжести, действующую на тела. Ошибка метода при определении сил равна сумме (delta=delta_g+delta_{text{шк}}).
Т.к. шкала изготовлена для (overline{g}=10frac{ text{м}}{ text{с}^2}), массу тел находим по формуле (m=frac{F}{overline{g}}), где (F) – показание динамометра. При этом ошибка метода равна (delta=delta_{text{шк}}), т.к. ошибка (delta_g) нивелируется за счет пропорциональности массы и растяжения пружины.
Таким образом, за счет сокращения (overline{g}), полученный прибор позволяет точнее измерять массы по сравнению с измерениями сил.
Приборы и материалы
Лабораторный динамометр на 5Н со шкалой, закрытой чистой бумагой; набор грузиков по 100 г; линейка; карандаш; 2 тела неизвестной массы.
Ход работы
1. Закрепите динамометр в штативе.
2. Подвесьте грузик массой 100 г, сделайте отметку 1Н на шкале.
3. Сделайте отметки 2Н, 3Н, 4Н и 5Н для грузов 200 г, 300 г, 400 г и 500 г соответственно.
4. Снимите динамометр со штатива и проверьте с помощью линейки, насколько равномерной получилась шкала. Оцените относительную ошибку (delta_{text{шк}})
5. С помощью линейки нанесите по 10 промежуточных делений между основными делениями шкалы.
6. Снова закрепите динамометр в штативе и проведите измерения силы тяжести для двух тел неизвестной массы. Найдите абсолютную и относительную погрешность измерений.
7. Рассчитайте массы для обоих тел. Найдите абсолютную и относительную погрешность расчетов. 8. Сделайте выводы.
Результаты измерений и вычислений
Расчетная таблица для оценки равномерности шкалы
| Отрезок шкалы | Длина отрезка, мм | (|x-x_{text{ср}}|) |
| 0-1 Н | 25 | 0 |
| 1-2 Н | 25 | 0 |
| 2-3 Н | 26 | 1 |
| 3-4 Н | 24 | 1 |
| 4-5 Н | 25 | 0 |
| Всего | 125 | 2 |
Средняя длина отрезка $$ x_{text{ср}}=frac{125}{5}=25 (text{мм}) $$ Среднее линейное отклонение $$ Delta =frac 25=0,4 (text{мм}) $$ Цена деления линейки (d_{text{л}}=1 text{мм}), абсолютная погрешность измерений (Delta_{text{л}}=0,5 text{мм})
Т.к. (Delta_{text{л}}gt Delta), принимаем погрешность равномерности шкалы (Delta=Delta_{text{л}}=0,5 text{мм})
Относительная погрешность равномерности шкалы $$ delta_{text{шк}}=frac{0,5}{25}=0,02=2text{%} $$
Относительная погрешность равномерности шкалы
| Показание динамометра (F, text{Н}) |
Ошибка метода (delta=delta_g+delta_{text{шк}}, text{%}) |
Абсолютная погрешность (Delta F=deltacdot F, text{Н}) |
|
| 1-е тело | 2,7 | 4% | 0,11 ≈ 0,1 |
| 2-е тело | 1,9 | 4% | 0,08 ≈ 0,1 |
Цена деления динамометра (d=0,1 text{Н}); погрешность прямых измерений (Delta_0=frac d2=0,05 text{Н})
Полученные абсолютные погрешности больше (Delta_0).
Сила тяжести для первого тела (F_1=(2,7pm 0,1) text{Н}, delta=4text_%)
Сила тяжести для второго тела (F_2=(1,9pm 0,1) text{Н}, delta=4text_%)
Расчет массы $$ m=frac{F}{10} (text{кг})=100F (text{г}) $$
| Масса (m=100F, text{г}) |
Ошибка метода (delta=delta_{text{шк}}, text{%}) |
Абсолютная погрешность (Delta m=deltacdot m, text{г}) |
|
| 1-е тело | 270 | 2% | 5 |
| 2-е тело | 190 | 2% | 4 |
Масса первого тела (m_1=(270pm 5) text{г}, delta=2text{%})
Масса второго тела (m_2=(190pm 4) text{г}, delta=2text{%})
Выводы
На основании проделанной работы можно сделать следующие выводы.
Для градуирования динамометра в ньютонах использовалось значение $$ overline{g}=10 frac{text{м}}{text{с}^2} $$
По сравнению со стандартным значением (g_0=9,80665 text{м/с}^2) это приводит к вкладу в ошибку метода (delta_gapprox 2text{%}).
При градуировании равномерность шкалы дала составляющую ошибки метода (delta_{text{шк}}=2text{%}).
При определении силы тяжести с помощью полученного динамометра ошибка метода равна сумме (delta+delta_g+delta_{text{шк}}=4text{%}).
Для двух тел неизвестной массы были получены следующие значения сил тяжести: $$ F_1=(2,7pm 0,1) text{Н}, F_2=(1,9pm 0,1) text{Н}, delta=4text{%} $$
При расчете массы по формуле (m=frac Fg), ошибка (delta_g) нивелируется за счет пропорциональности растяжения пружины. Ошибка метода уменьшается (delta=delta_{text{шк}}=2text{%}).
Получаем следующие значения масс: $$ m_1=(270pm 5) text{г}, m_2=(190pm 4) text{г}, delta=2text{%} $$ Таким образом, полученный в ходе работы динамометр позволяет измерять силы тяжести в интервале от 0 до 5 Н с погрешностью 4% и рассчитывать массы тел в интервале от 0 до 500 г с погрешностью 2%.
ВИДЕО УРОК
Силу тяжести, как и всякую другую силу, можно измерять динамометрами.
Динамометры, специально предназначенные для измерения силы тяжести, называют пружинными весами, потому что с их помощью
можно измерить вес тела. Что это за
величина – вес ?
ОПЫТ:
Рассмотрим процесс деформации
пружины динамометра, когда к ней подвешен некоторый груз. Обратим внимание не
только на то, что происходит с пружиной, но и на то, что происходит с самим
грузом, подвешенным к пружине.
На рисунке

изображена пружина динамометра
до того, как к ней был подвешен груз. Это недеформированная пружина (массой пружины
пренебрегаем).
Подвесим к пружине груз. При своём падении он
увлекает за собой и нижний конец пружины, вследствие чего пружина
деформируется, как это показано на рисунке.
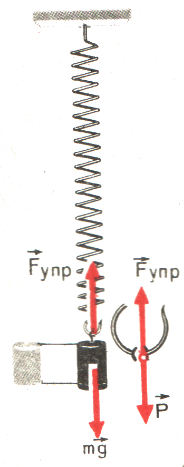
Возникающая при этом
сила упругости

тоже приложена к телу,
но направлена вверх. При определенном значении удлинения пружины сила упругости

по абсолютному значению
становится равной силе тяжести

Под действием этих двух сил,
равнодействующая которых равна нулю, груз устанавливается в состоянии покоя.
Но если пружина динамометра действует на груз,
то по третьему закону Ньютона и груз действует на пружину с такой же по
абсолютному значению силой, но направленной в противоположную сторону, то есть
вниз. Это тоже сила упругости. Возникает она из-за того, что и груз (а не только пружина)
деформируется. В сильно увеличенном виде эта деформация (удлинение) показана на рисунке

Вот эту силу, приложенную не к
телу, а к пружине, и называют весом тела. Вес тела принято обозначать
буквой Р.
Если тело не подвешивать, а поместить на
горизонтальную опору,

то оно и на опору действует с
силой, тоже называемой весом.
Весом тела называется сила, с которой неподвижное
относительно Земли тело давит на горизонтальную подставку, на которой оно
лежит, или растягивает нить, на которой оно висит.
Вес тела приближённо равен силе притяжения тела Землёй. Согласно второму
закону Ньютона, вес тела
P = mg.
Вес тела в системе СИ измеряется теми же единицами, что и сила – ньютонами.
На практике часто пользуются единицей силы (веса)
1 кГ.
1
кГ – это сила, сообщающая
массе 1
кг ускорение
g = 9,80665 м/сек2.
Очевидно,
1 кГ = 1 кг × 9,80665 м/сек2
≈ 9,8 н = 9,8 × 105 дин.
Вес тела – это сила, приложенная не к телу, а к опоре или подвесу.
Не обязательно, чтобы опора или подвес представляли собой спиральную
пружину. Тело можно подвесить на нити, на проволоке или поместить на стол. На
нить, проволоку или стол будет действовать вес тела.
В рассмотренных примерах вес тела, очевидно равен силе тяжести. Но это
верно только тогда, когда опора или подвес находятся в покое относительно Земли
(или движутся прямолинейно и равномерно).
Вес и сила тяжести не одно и то же: вес и сила
тяжести всегда приложены к разным телам.
Измерение массы тел взвешиванием.
Массу тела можно
определить, измеряя отношение ускорений при взаимодействии этого тела с телом,
принятым за эталон массы. Этот способ очень неудобен и на практике обычно не
применяется. Рассмотрим другой, более удобный способ измерения массы. Этот
способ называют взвешиванием. Определение
массы методом взвешивания основано на том, что сила тяжести, действующая на
тело, и масса этого тела пропорциональны друг другу:

А силу тяжести можно измерять на весах, так как
она по абсолютному значению равна весу тела, если весы вместе с взвешиваемым
телом покоятся относительно Земли. Поэтому, измерив вес тела

пружинными весами и зная ускорение свободного
падения

в месте, где производится взвешивание, можно
вычислить массу по формуле:

Ещё удобнее определять массу взвешиванием на рычажных весах. На рычажных
весах сравнивают веса тел и гирь. Когда весы уравновешены, можно утверждать,
что вес тела равен весу гирь. Но если равны веса тел, то равны их массы. Так
как на гирях (разновесках) указаны именно их массы, то массу тела мы
определяем, просто сложив числа, указанные на разновесках.
Рычажные весы очень чувствительный прибор. Наименьшая масса, которую можно
измерить наиболее чувствительными весами, составляет несколько миллионных долей
грамма.
Вес тела, движущегося с ускорением.
Мы знаем, что вес тела –
это сила, с которой тело действует на опору или на подвес. Если опора или
подвес покоятся относительно Земли или движутся относительно её прямолинейно и
равномерно, то вес тела равен силе тяжести

Но вес тела может существенно отличаться от значения силы тяжести, если
опора или подвес движутся с ускорением вверх или вниз. Почему ?
Посмотрим, что покажут пружинные весы, если они вместе с подвешенным к ним
телам движутся с ускорением вверх или вниз.
ОПЫТ:
Подвесим к пружинным весам какой-нибудь груз и
дадим им возможность двигаться с некоторым ускорением

Для этого можно взять
весы с грузом в руку и резко отпустим их вниз,

сообщив им ускорение,
направленное вниз. Мы увидим, что во время опускания весов их стрелка
перемещается вверх. Это значит, что вес груза во время опускания стал меньше,
чем он был в случае покоящихся весов. Если, наоборот, резко поднять весы,
стрелка опустится, показывая, что вес груза увеличивается.

Чем объясняется это уменьшение
или увеличение веса при ускоренном движении динамометра с грузом ?
Ответ на это даёт второй закон Ньютона.
Посмотрим, какие силы действуют на груз. На него действуют сила тяжести

направленная вниз, и
сила упругости

пружины весов,
направленная вверх. Под действием этих двух сил тело и движется с ускорением

которое может быть направлено
как вниз, так и вверх в зависимости от того, будем ли мы опускать весы или
поднимать их.
По второму закону Ньютона

Отсюда

С такой же по модулю
силой, но направленной противоположно силе

груз действует на
пружину. А эта сила и есть вес груза

Следовательно,

Векторы

параллельны вертикальной примой. Направив
координатную ось Х по вертикали вниз, можно формулу

написать в алгебраической форме для проекций этих векторов на вертикальную
ось:
P = m(g – a).
Если весы движутся с
ускорением

вниз, то проекция этого вектора на координатную ось положительна. Если a < g, то из формулы
P = m(g – a)
cледует, что P < mg.
Вес тела, направление ускорения которого совпадает с
направлением ускорения свободного падения, меньше веса покоящегося тела.
Это видно на рисунке

Если же весы движутся с ускорением

вверх, то проекция вектора ускорения на координатную ось отрицательна, и
согласно формуле
P = m(g – a)
P ˃ mg.
Если
ускорение тела направлено в сторону, противоположную ускорению свободного
падения, его вес больше веса покоящегося тела.

Увеличение веса тела, вызванное его ускоренным движением, называют перегрузкой.
Вес уменьшается или увеличивается не только тогда, когда тело подвешено к
пружинным весам. То же самое относится и к любому подвесу, и к любой опоре.
ПРИМЕР:
Автомобиль, движущийся по выпуклому мосту, легче
того же автомобиля, неподвижно стоящего на том же мосту.

Действительно, движение
по выпуклому мосту – это движение по части окружности. Поэтому автомобиль
движется с центростремительным ускорением, равным по по абсолютной величине:

где V –
линейная скорость автомобиля, r –
радиус кривизны.
В момент, когда автомобиль находится в высшей
точке моста, это ускорение направлено по вертикали вниз. Оно сообщается
автомобилю равнодействующей силы тяжести

и силы

реакции моста.
Направим координатную ось Х вертикально вниз. Тогда по второму закону
Ньютона

откуда

Вес автомобиля (сила, с
которой он давит на мост) по третьему закону Ньютона равен –

Следовательно,

P < mg.
Точно также уменьшается и вес
пассажиров, едущих в автомобиле по выпуклому мосту. Уменьшение веса тем больше,
чем больше скорость автомобиля.
ПРИМЕР:
Любые тела, покоящиеся на экваторе, благодаря
вращению Земли находятся в состоянии, аналогичном состоянию пассажиров
автомобиля, движущегося по выпуклому мосту. Их вес вычисляется по формуле:

где R –
радиус Земли ω – угловая скорость её вращения. На полюсе вес тех же тел
был бы равен mg. Так как
𝜔2R ≈ 8,6 ∙ 10-4 м/сек2,
то при грубых расчётах
величиной 𝜔2R обычно пренебрегают и считают, что и на
экваторе вес тела равен mg.
ПРИМЕР:
Лётчик, выводящий самолёт из пикирования,

в нижней части
траектории подвергается перегрузке. В самом деле, в этой части траектории
самолёт движется по окружности с центростремительным ускорением, направленным к
её центру по вертикали вверх. Абсолютное значение ускорения равно:

Но его проекция на
вертикальную ось, направленную вниз, отрицательна:

Следовательно, вес
лётчика, то есть сила, с которой он действует на опору (сиденье), определяется
формулой:

P ˃ mg.
Таким образом, вес лётчика больше <<нормального>>
веса, равного силе тяжести mg, на величину

Если при выходе из
пикирования центростремительное ускорение

превышает по абсолютному
значению ускорение свободного падения
в g и n раз

то вес лётчика
P = m(g + ng) = mg(n + 1),
то есть он будет в n + 1 раз больше <<нормального>>
веса лётчика.
При перегрузке увеличивают свой вес и внутренние
органы лётчика, увеличивается сила, с которой они действуют друг на друга и на
его остов (скелет). Это вызывает болезненные ощущения, а при чрезмерной
перегрузке может стать опасным для здоровья. Тренированные пилоты выдерживают
перегрузку до 10 mg (обычно перегрузку выражают не через величину mg, а через величину g и
говорят, что перегрузка равна, например, 10 g).
Тип 10 № 1862 

i
К динамометру подвесили груз (см. рис.). Укажите, чему равен вес груза с учётом того, что погрешность измерения равна половине цены деления шкалы прибора.
Запишите в ответ показания динамометра с учётом погрешности измерений. В ответе укажите значение и погрешность измерения слитно без пробела. Ответ приведите в ньютонах.
Спрятать решение
Решение.
Заметим, что цена деления динамометра равна 0,5 Н. Из рисунка видно, что динамометр даёт показания (8,50 ± 0,25) Н.
Ответ: 8,500,25.
Источник: ВПР 2019 год по физике 11 класс. Вариант 13
