Лабораторная работа № 5
Тема: «ИЗМЕРЕНИЕ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТИ»
Цель: определить коэффициент поверхностного натяжения воды методом отрыва капель.
Оборудование: сосуд с водой, шприц, сосуд для сбора капель.
Теория.
Молекулы поверхностного слоя жидкости обладают избытком потенциальной энергии по сравнению с энергией молекул, находящихся внутри жидкости
Как и любая механическая система, поверхностный слой жидкости стремится уменьшить потенциальную энергию и сокращается. При этом совершается работа А:
![]()
где σ – коэффициент поверхностного натяжения. Единицы измерения Дж/м2 или Н/м
![]() или
или ![]()
где F – сила поверхностного натяжения, l – длина границы поверхностного слоя жидкости.
Поверхностное натяжение можно определять различными методами. В лабораторной работе используется метод отрыва капель.
Опыт осуществляют со шприцом, в котором находится исследуемая жидкость. Нажимают на поршень шприца так, чтобы из отверстия узкого конца шприца медленно падали капли. Перед моментом отрыва капли сила тяжести Fтяж=mкапли·g равна силе поверхностного натяжения F, граница свободной поверхности – окружность капли
l=π·dкапли
Следовательно:
![]()
Опыт показывает, что dкапли =0,9d, где d – диаметр канала узкого конца шприца.
Массу капли можно найти, посчитав количество капель n и зная массу всех капель m.
Масса капель m будет равна массе жидкости в шприце. Зная объем жидкости в шприце V и плотность жидкости ρ можно найти массуm=ρ·V
Ход работы.
1. Подготовьте оборудование: Начертите таблицу:
Начертите таблицу:
|
№ опыта |
Масса капель m, кг |
Число капель n |
Диаметр канала шприца d, м |
Поверхност-ное натяжение σ, Н/м |
Среднее значение поверхностного натяжения σср, Н/м |
Табличное значение σтаб, Н/м |
Относительная погрешность δ % |
|
1 |
1*10-3 |
2,5*10-3 |
0,072 |
||||
|
2 |
2*10-3 |
2,5*10-3 |
|||||
|
3 |
3*10-3 |
2,5*10-3 |
Опыт 1
- Наберите в шприц 1 мл воды («один кубик»).
- Подставьте под шприц сосуд для сбора воды и, плавно нажимая на поршень шприца, добейтесь медленного отрывания капель. Подсчитайте количество капель в 1 мл и результат запишите в таблицу.
- Вычислите поверхностное натяжение по формуле
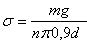
Результат запишите в таблицу.
- Повторите опыт с 2 мл и 3 мл воды.
- Найдите среднее значение поверхностного натяжения
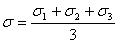
Результат запишите в таблицу.
- Сравните полученный результат с табличным значением поверхностного натяжения с учетом температуры.
- Определите относительную погрешность методом оценки результатов измерений.
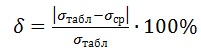
Результат запишите в таблицу.
- Сделайте вывод.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
- Почему поверхностное натяжение зависит от рода жидкости?
- Почему и как зависит поверхностное натяжение от температуры?
- Изменится ли результат вычисления поверхностного натяжения, если опыт проводить в другом месте Земли?
- Изменится ли результат вычисления, если диаметр капель трубки будет меньше?
- Почему следует добиваться медленного падения капель?
Вариант выполнения лабораторной работы.
Результаты измерений:
Количество капель в 1 мл – 21
Количество капель в 2 мл – 40
Количество капель в 3 мл – 59
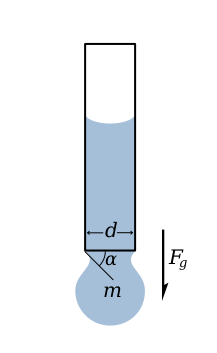
На представленной здесь картинке, капля задерживается на конце трубки за счет силы поверхностного натяжения. Сила эта пропорциональна длине границы между жидкостью и трубкой и равна
,
где — коэффициент поверхностного натяжения, измеряемый в ньютонах на метр, Н/м.
Капля не отрывается, очевидно, пока эта сила способна нейтрализовать силу тяжести, действующую на каплю в вертикальной проекции, то есть
При увеличении массы капли, то есть при ее росте, угол альфа будет стремиться к 90 градусам, и, в состоянии равновесия сил, формула примет вид
, откуда
масса капли
Рассчитав подобным образом массу и зная плотность жидкости, объем посчитать тривиально.
На самом деле, конечно, не вполне так, потому что место отрыва обычно немного ниже конца трубки, и отрыв происходит в месте формирования так называемой шейки, где диаметр несколько меньше чем диаметр трубки, но там, где не требуется очень большая точность, этим обычно пренебрегают.
Мне захотелось также оценить максимальный диаметр трубки, при котором еще возможно образование на ее конце капель. В оценке я исходил из того, что образование капли возможно тогда, когда силы поверхностного натяжения еще способны удерживать как минимум полусферу. Отсюда, опять же зная плотность жидкости, можно представить формулу следующим образом
и, соответственно,
Пара слов о калькуляторе ниже. Во первых, калькулятор не рассчитывает массу и объем капли при превышении диаметра трубки оценки, сделанной выше. Во-вторых, значения плотности и коэффициента поверхностного натяжения по умолчанию соответствуют воде.
![]()
Поверхностное натяжение. Масса и объем капли
Поверхностное натяжение, Н/м
Поверхностное натяжение жидкости, Н/м
Плотность жидкости, кг/м3
Ускорение св. падения, м/с2
Ускорение свободного падения, м/с2
Точность вычисления
Знаков после запятой: 3
Максимальная масса капли, г
Максимальный объем капли, cм3
Максимальный диаметр капилляра, м
Поверхностное натяжение. Масса и объем капли
Следующий калькулятор делает расчет массы и объема капли при отрыве ее от капиллярной трубки.
На картинке видно, что капля задержалась на конце трубки. Это явление за счет силы поверхностного натяжения. Данную силу можно выразить следующей формулой.
где y – это коэффициент поверхностного натяжения (Н/м).
Капля не отрывается от колбы, видимо, пока данная сила может противодействовать силе тяжести, которая действует на каплю в вертикальной проекции:
Когда масса капли увеличивается, то угол (а) будет тянуться к 90о, а когда силы будут примерно равны, то:
Высчитав таким способом массу, а также зная плотность воды, можно легко посчитать и объем.
Диаметр капилляра, м:
Поверхностное натяжение жидкости, Н/м:
Плотность жидкости, кг/м3:
Acceleration of gravity, м/с2:
Максимальная масса капли, г:
Максимальный объем капли, cм3:
Максимальный диаметр капилляра, м:
Получи верный ответ на вопрос 🏆 «Чтобы узнать массу одной капли воды, сначала взвешивают пустую посуду. Затем накапав в посуду 50 капель, снова взвешивают. Масса пустой …» по предмету 📕 Математика, используя встроенную систему поиска. Наша обширная база готовых ответов поможет тебе получить необходимые сведения!
Найти готовые ответы
Главная » Математика » Чтобы узнать массу одной капли воды, сначала взвешивают пустую посуду. Затем накапав в посуду 50 капель, снова взвешивают. Масса пустой посуды равнялась 45 г, а масса посуды с водой-48,5 г. Какова средняя масса одной капли?
Капля (физ.-хим.) — Под этим названием разумеется незначительное количество жидкости, принимающее округленную форму вследствие сцепления ее частиц. Содержание настоящей статьи составляют: 1) способы получения К., 2) форма К., 3) вес К., 4) связь между весом капли и поверхностным натяжением жидкости и, наконец, 5) приложение изучения веса К. к решению химических вопросов. Капля может быть получена весьма разнообразными способами. В опытах Гутри К. отделялись с шариков из различного материала или падали с медного кружка, в середине которого припаивалась проволока, имевшая во время опытов вертикальное положение. У Саллерона приборчик для получения К. представлял род Мариоттова сосуда. Широкая муфта, закрытая сверху, оканчивалась внизу капиллярной трубочкой. В верхнюю часть муфты впаивалась трубочка, опускающаяся ниже уровня жидкости в муфте и служащая для притока воздуха. Другой приборчик Саллерона состоял из маленького графина с припаянной ниже довольно длинного горла боковой узкой трубочкой, из которой и падали К. Дюпре для получения К. пользовался сифоном из капиллярных трубок, одно колено которого вставлялось в сосуд с испытуемою жидкостью. Подымая и опуская последний, можно ускорить или замедлить получение К. из другого колена сифона. В сосуд с испытуемою жидкостью вставлялась трубочка, снабженная каучуком с зажимом, посредством которого можно останавливать капание. В опытах Траубе с расплавленными солями — К., по мере расплавления соли, истекали через узкое (3—9 мм) отверстие платинового тигля. Форма К., по теории капиллярных явлений, основания коей изложены в статье Волосность (теории), должна быть шаровою в случае, когда размеры К. весьма малы. Когда же К. достаточно широка, то поверхность вблизи вершины мениска представляет параболоид вращения около вертикальной оси. Опыты подтверждают данные теории. Если в сифонную капиллярную трубку с неравными коленами наливать воду, то при прибавлении ее в большее колено поверхность, поднимаясь мало-помалу в меньшем колене, при выходе из трубки выпрямляется и становится даже выпуклой. Но, прежде чем принять полушаровую форму, вода стекает благодаря прилипанию ее к краям стеклянной трубки. Если же взять медную пластинку с узкой дырочкой, заменяющей капиллярную трубку, то вода, выступая из этого отверстия, образует шаровидную К., радиус которой примерно равен радиусу отверстия. Форма ртутных К. на стеклянной горизонтальной пластине представляет поверхность вращения вокруг вертикальной оси. В том месте, в котором К. касается пластинки, она сливается с горизонтальною плоскостью. Но, начиная отсюда, радиусы горизонтальных сечений постепенно увеличиваются, на некотором расстоянии достигают наибольшей величины и затем вновь уменьшаются. В больших К. верхняя часть поверхности совпадает с горизонтальной плоскостью, нижняя же часть составляет с изображением ее в стеклянной пластинке прямой угол, т. е. наклонение к горизонту касательной к поверхности К. равно 45°. Гей-Люссак в одном случае дает относительные размеры ртутной К.: при высоте 3,378 мм наибольший радиус горизонтального сечения 50 мм. Веса К. различных веществ определялись многими исследователями. Наблюдена зависимость веса К.: 1) от температуры, 2) от вещества того тела, с коего отделяется капля, 3) от размеров этого тела и 4) доказана связь между весом К. и поверхностным натяжением жидкости. По опытам Тэта, вес К. уменьшается с повышением температуры. В этих опытах К. падали с шарика термометра (радиуса 7,4 мм) и температура его принималась за температуру К. Вес К. воды в грм. найден:
| 40°,3 | 30°,6 | 20°,4 |
| 0,1298 | 0,1307 | 0,1326 |
Зависимость веса К. от вещества того тела, на коем образуется К., видна из опытов Гутри, который заставлял падать К. с шариков из различного материала. Капля воды при прочих одинаковых условиях (температура, радиус шарика) весила в граммах: сера 0,1202, цинк 0,1225, свинец 0,1226, пробка 0,1242, стекло 0,1297. Размеры тела, с которого отделяется К., также значительно влияют на ее вес. Опыты над образованием К. на медном кружке, припаянном в центре к проволоке, которая ставилась в вертикальное положение, показали, что веса К. возрастают приблизительно пропорционально радиусам кружков или их окружностям, что видно из следующих данных для воды:
| Радиус медного кружка r | Вес капли g | Отношение g/(2πr) |
|---|---|---|
| 6,35 мм | 0,1632 г | 0,0041 |
| 5,08 мм | 0,1491 г | 00047 |
| 3,81 мм | 0,0967 г | 0,0040 |
| 2,54 мм | 0,0733 г | 0,0046 |
| 1,27 мм | 0,0411 г | 0,0052 |
Связь между весом К. и поверхностным натяжением жидкости в первом приближении дается равенством g = 2πrf, где g вес К. в грам., падающей с кружка радиуса r, и f — поверхностное натяжение жидкости [1], представляющее количество жидкости в грам., прилипающей к единице длины тела. Если взять величину поверхностного натяжения из определений высот поднятия в волосных трубках и вычислить веса капель по приведенной формуле, то в большинстве случаев, хотя и не всегда, получается довольно удовлетворительное согласие, напр.:
| Наблюдено | Вычислено | |
|---|---|---|
| Вес капли ртути | 49,99 | 49,56—55,21 |
| Вес капли спирта | 2,509 | 2,509 |
Дюкло для определения поверхностного натяжения — вместо взвешивания К. измерял число капель, составляющее известный объем. По предыдущей формуле отношение объемов при одинаковой величине отверстия, из коего вытекает К., равно отношению 

где d плотность жидкости. Для тех жидкостей, кои дают n < 140, формула является применимой, но если n > 140, то, по Дюкло, следует вводить уже некоторые поправки. Вообще, определение веса К. хотя и не может служить для точного определения поверхностного натяжения жидкости, но пригодно во многих случаях. Так как поверхность натяжения жидкости резко изменяется от примеси даже ничтожных количеств постороннего вещества, то вес К., или число их в данном объеме, служит отличным критерием чистоты данной жидкости. В применении к химии веса К. изучались особенно Квинке и Траубе. Квинке определил веса К. 46 расплавленных тел и нашел, что объемы К. исследованных тел относятся как ряды целых чисел [2]. При радиусе трубки в 1 мм, из коей истекают К., получен: наименьший обем (в куб. миллим.) 3,89—4,84 у веществ: S, Se, P, Br, KJ; двойной обем 7,63—8,65 y Hg, Pb, Bi, Sb, KNO3; четырехкратный объем 14,44—17,86 у Н2О, Pt, Ag, Cd, Sn, Cu и, наконец, шестикратный объем 25,26—27,14 у Pd, Zn и Fe. Траубе исследовал веса К. (также при температуре плавления) солей калия KCl, KBr, KJ, KNO3, KNO2, KClO3 KBrO3, KCN, KCNO, KCNS, KCNSe, СНКО2 С2H3КО2, К2ClO4, KCr3О10, К2СО3, аналогичных солей натрия и многих других солей, отвечающих этим металлам. Сравнение веса К. солей минеральных кислот показало, что величины для солей одноосновных кислот, вообще близкие между собой значительно, отличаются от веса К. солей для кислот двуосновных. При переходе от солей калия к соответствующим солям натрия вес К. несколько возрастает. Таким образом, зная вес К. данной соли при температуре плавления, можно с некоторой достоверностью сделать заключение об основности кислоты, отвечающей этой соли.
В. Курилов.
Примечания[править]
- ↑ Между поверхностным натяжением f и коэффиц. а2 (см. Волосность) существует весьма простое соотношение. Вес жидкости, поднявшейся в трубке радиуса r, равен в первом приближении πr2hδ, где δ плотн. жидк., а h — высота поднятия, откуда вес жидкости, поднимаемой единицей длины,
- ↑ Вывод этот можно считать лишь приблизительным, ибо объемы тел при температуре плавления в большинстве случаев не вполне точны.

