
Если вы стоите перед выбором финансового решения из нескольких возможных вариантов, например, — в какую компанию из пяти предварительно отобранных наиболее выгодно инвестировать, советую Вам как следует все «взвесить».
Весовой коэффициент – это параметр, который отражает значимость (или «вес») данного фактора или показателя по сравнению с другими факторами, оказывающими влияние на изучаемый объект или явление.
Этот метод рекомендует нам для начала выявить и оценить все факторы или аргументы, влияющие на наши 5 компаний, и по специальной методике с помощью весовых коэффициентов определить степень конкурентного преимущества или уязвимости каждой компании и наметить соответствующие мероприятия.
Подробнее о методе – в статье.
Расчет весовых коэффициентов в сравнительном подходе
Согласно требованиям ФСО, контролирующих органов необходимо производить обоснование всех расчетов и результатов в отчете по оценке. В настоящее время практически отсутствуют методики обоснования весовых коэффициентов (ВК) в сравнительном подходе.

Весовой коэффициент это
Есть общие формулировки, что необходимо присваивать вес каждому аналогу в зависимости от произведенных корректировок, но при этом отсутствует конкретная информация, как это сделать.
В данной статье автор предлагает вариант распределения весовых коэффициентов достаточно простым обоснованным способом. Описываемый в статье вариант определения весовых коэффициентов предлагается для метода прямого поэлементного сравнения аналогов с объектом оценки.
Обычно в сравнительном подходе составляется сравнительная таблица аналогов, где проставляют корректировки по различным параметрам, рассчитанные тем или иным способом (уже на основании рыночных данных). В результате по каждому аналогу образуется сумма корректировок, которая может быть больше, меньше или равна нулю.
На этом этапе Оценщику необходимо распределить веса по каждому аналогу в зависимости от внесенных корректировок по ним и обосновать их согласно ФСО. Зачастую Оценщики прибегают к экспертному распределению весов с приведением каких-либо оснований. Данную процедуру можно упростить, применив математический способ расчета весовых коэффициентов.
Для этого необходимо рассчитать параметр, обратный удельному весу суммы корректировок по каждому аналогу в общей сумме корректировок аналогов (чем больше удельный вес, тем меньше весовой коэффициент и наоборот). Производить расчет предлагается по следующей формуле:

Очевидно, что не линейная, иначе распределение весов было бы гораздо проще по прямой пропорции. Рассмотрим пример расчета с использованием формулы (2),

Распределение весов показывает, что при двух стопроцентно идентичных аналогов оцениваемому объекту, первому аналогу с минимальной корректировкой присвоен вес в 20% и разница с другими аналогами составляет также 20%.

В другом случае различие в корректировках в 1 единицу дает разницу в 3% в весах. Это говорит о том, что аналоги, имеющие большую величину сумм корректировок, одинаково плохи, и разница в весах между ними соответственно невелика.
Графически зависимость веса от суммы корректировок (при нулевых корректировках для трех аналогов) выглядит так:

Из графика видно, что чем больше корректировка, тем меньше ее вес, и при увеличении величин корректировок разница в весах снижается. Вид графика функции не меняется от величины корректировок. Известно также, что величины корректировок могут быть как положительные, так и отрицательные, поэтому параметр S берется по модулю, так как значения корректировок, например -1 и +1 равнозначны.
В случае, когда сумма корректировок (S) равна нулю, в формулу введен минимальный параметр 1, который дает определять вес при нулевых значениях сумм корректировок и избежать математической ошибки деления на ноль.
Таким образом, предлагаемая формула, по мнению автора, наиболее близко к истине объясняет распределение весов в зависимости от сумм корректировок по аналогам.
Приведенная формула была написана для сравнительного подхода при распределении весов по аналогам. Однако ее также можно применять и в других областях, где применяются аналогичные приемы расчетов.
Источник: "top-ocenka.com"
Весовой коэффициент — это величина, характеризующая важность критерия
Обычно вторым этапом анализа ключевых факторов успеха (КФУ) является оценка устойчивости конкурентной позиции, которая осуществляется с помощью весовых коэффициентов.
Весовым коэффициентом называют величину, используемую для характеристики важности критерия.
Конечная цель – провести многокритериальное сравнение альтернативных вариантов. Для этого используют метод взвешенной суммы, когда критерий полезности альтернативы определяется как сумма произведений весовых коэффициентов (весов) критериев и оценки этого критерия. При этом сумма весовых коэффициентов должна быть равна единице.
Метод «весовых коэффициентов» для определения позиций компании в отрасли состоит из следующих этапов:
- выявление ключевых факторов успеха для организаций, работающих в этой отрасли; обычно не более 10 характеристик;
- производится оценка организации и ее прямых конкурентов по каждому ключевому фактору успеха (оi);
- далее определяется весовой коэффициент каждой характеристики, учитывающий степень важности ключевых факторов успеха для достижения устойчивой конкурентной позиции; сумма весовых коэффициентов по всем показателям должна равняться единице;
- определяется ранг характеристик для каждой из компаний: это взвешенная оценка по отдельным факторам, вычисляемая как произведение оценки компании по данному показателю на ее вес;
- рассчитывается общая сумма оценок характеристик по каждой компании, определяющая показатель конкурентной силы каждой компании; чем больше конкурентная сила отдельной компании по сравнению с другими компаниями, тем более устойчива ее позиция;
- составляется заключение о масштабах и степени конкурентного преимущества или уязвимости исследуемой организации с выявлением конкретных областей, где она опережает конкурентов или отстает от них;
- выделяются ключевые факторы успеха, которые нужно развивать в организации, составляется план по развитию ключевых факторов успеха до нужного уровня, разрабатываются мероприятия для этого:
- составляется цепочка дальнейших действий: цель → индикатор → целевое значение → мероприятия → эффективность. Например:
- цель: повысить известность бренда 1 →
- индикатор: измерять известность бренда 1 будем с помощью узнавания бренда с подсказкой (покажем логотип или дизайн упаковки) →
- целевое значение (значение, к которому стремится организация): в конце рассматриваемого периода 90% жителей страны должны узнавать бренд 1 →
- мероприятия: в рассматриваемый период должны быть проведены следующие… рекламные и PR-кампании →
- эффективность: была ли достигнута цель.
Оценка может производиться по любой балльной шкале, но для упрощения вычислений обычно используют только положительные оценки, например используют 10-балльную шкалу, где «1» обозначает абсолютную неразвитость характеристики в организации, «10» – максимально возможную представленность значения характеристики в организации для отрасли;
Пример:

В результате анализа «Компания 5» имеет самые устойчивые позиции на рассматриваемом рынке. В тоже время «Компания 1» – самая неустойчивая из рассматриваемых.
Вторым этапом исследования является составление профиля конкурентных преимуществ и недостатков организации. После определения компании с самыми устойчивыми позициями идет сравнение характеристик КФУ лидера с интересующей нас компанией. Предположим, нашей компанией является «Компания 4»:

Чем ниже взвешенная оценка КФУ, тем значимее проблема, т.е. можно выставить приоритет решения проблем (повышения характеристики) в организации.
Для «Компании 4» самой важной задачей является уменьшение издержек, для любой компании данная характеристика очень значима, так как напрямую влияет на прибыль организации. Второй наиболее значимой проблемой является повышение имиджа.
Возможно, эти две характеристики будут конфликтовать друг с другом, если «Компания 4» выберет стратегию, где для снижения издержек потребуется снизить качество товаров, что еще сильнее может испортить имидж организации. Возможно, «Компании 4» стоит снизить издержки за счет более качественного использования своего технологического уровня.
Очевидно, что «Компания 4» является наиболее конкурентоспособной, но даже у нее есть характеристики, которые требуют внимания.
Источник: "studme.org"
О расчетном методе определения весовых коэффициентов
При оценке качестве функционирования и оптимизации сложных систем, обычно характеризующихся совокупностью частных критериев, может возникнуть задача формирования обобщенного критерия качества.
При решении практических задач весьма часто обобщенный критерий качества формируют на основе принципа абсолютной уступки с учетом гибкого приоритета в виде взвешенной суммы частных показателей качества:
y = Syj*aj,
где: уj — нормированные частные показатели;
аj — весовые коэффициенты.
Однако процедура задания вектора весовых коэффициентов связана с серьезными трудностями, плохо поддается формализации и обычно выполняется методами экспертного опроса, которые требуют больших затрат и неизбежно привносят элемент субъективности.
Формализовать процесс получения весовых коэффициентов удается в том случае, если воспользоваться методикой изучения влияния весовых коэффициентов на величину обобщенного критерия качества, применяемую при сравнении характеристик совокупности вариантов Si, исследуемой системы, получаемых варьированием параметров системы х в процессе зондирования области Х при реализации матрицы плана активного эксперимента.
Получаемая при этом характеристическая матрица частных показателей || yij || отражает свойства системы во всей области варьирования параметров Х и служит, с одной стороны, основой для отыскания оптимальных значений х, а с другой — базой для формализованного расчета весовых коэффициентов, учитывающих относительную важность каждого j-го локального критерия.
В основу расчетного определения весовых коэффициентов положен принцип объективного сравнения вариантов системы, который может быть сформулирован следующим образом.
Если выбранная совокупность весовых коэффициентов доставляет максимум обобщенным критериям всех вариантов системы maxyi, то нет каких-либо оснований считать, что варианты системы сравниваются не объективно.
Q = 1 — yi/maxyi
Это соотношение характеризует степень объективности сравнения i-го варианта системы при данных значениях весовых коэффициентов а по отношению к максимально возможной при любых возможных а. Максимальная степень объективности сравнения достигается в том случае, если некоторый вектор а для всех вариантов Si одновременно доставляет Qi = 0.
Однако при рассмотрении всех вариантов Si образующаяся система неоднородных уравнений yi = Syij*aj является несовместной и переопределенной, так как обычно количество вариантов системы превышает количество частных показателей.
Поэтому условие Qi = 0 практически оказывается недостижимым и функция потерь имеет некоторый разброс:
p = maxQi — minQi.
Следовательно, вектор а, минимизирующий функцию разброса, будет обеспечивать наиболее объективное сравнение вариантов системы. Отсюда следует, что формализованное определение весовых коэффициентов должно строиться на исследовании их влияния на величину разброса и отыскании такого значения, которое обеспечивает min p.
Рассмотренная методика определения весовых коэффициентов легко поддается алгоритмизации и реализации на ЭВМ. Блок-схема алгоритма расчета представлена на рисунке:

Источник: "mstu.edu.ru"
Матрица приоритетов
Матрица приоритетов (матрица критериев) — это инструмент, с помощью которого можно ранжировать по степени важности данные и информацию, полученную в результате мозгового штурма или матричных диаграмм. Ее применение позволяет выявить важные данные в ситуации, когда нет объективных критериев для определения их значимости или когда люди, вовлеченные в процесс принятия решения, имеют различные мнения по поводу приоритетности данных.
Основное назначение матрицы приоритетов — это распределение различных наборов элементов в порядке значимости, а также установление относительной важности между элементами за счет числовых значений. Матрица приоритетов может быть построена тремя способами.
Варианты построения зависят от метода определения критериев, по которым оценивается приоритетность данных, — аналитический метод, метод определения критериев на основе консенсуса, и матричный метод.
- Аналитический метод применяется, когда относительно невелико число критериев (не больше 6), необходимо получить полное согласие всех экспертов, принимающих участие в оценке, число экспертов не превышает 8 человек, возможны большие потери в случае ошибки с расстановкой приоритетов.
- Метод определения критериев на основе консенсуса применяется, когда число экспертов составляет более 8 человек, существует значительное число критериев (от 6 до 15), имеется большое число ранжируемых данных (порядка 10-20 элементов).
- Матричный метод применяется в основном, когда между ранжируемыми элементами есть сильная взаимосвязь, а нахождение элемента с наибольшим влиянием является критичным для решения поставленной задачи.
Порядок действий, по которым строится матрица приоритетов для всех трех вариантов в основном, одинаковый. Различия заключаются в определении значимости критериев.
Матрица приоритетов строится в следующем порядке:
- Шаг 1. Определяется основная цель, ради которой строится матрица приоритетов.
- Шаг 2. Формируется команда экспертов, которая будет работать над поставленной задачей.
Эксперты должны понимать область решаемой проблемы и иметь представление о методах коллективной работы (например, о методе мозгового штурма, методе «дельфи» и т.п.)
- Шаг 3. Составляется список возможных решений поставленной проблемы.
Список может быть составлен за счет применения других инструментов качества, например мозгового штурма, диаграммы Исикавы и пр.
- Шаг 4. Определяется состав критериев. Изначально, он может быть достаточно большим. Матрица приоритетов будет включать в себя только часть этих критериев, т.к. в дальнейшем он сократится за счет выбора наиболее важных и существенных.
Для определения состава критериев можно использовать следующие подходы:
- провести анализ поставленной цели. Это можно сделать с помощью древовидной диаграммы или диаграммы Исикавы;
- определить существующие ограничения по достижению цели (например, финансовые ограничения или временные);
- определить выгоды от достижения поставленной цели;
- формулировать названия критериев таким образом, чтобы их можно было легко и объективно измерить.
- Шаг 5. Далее назначается весовой коэффициент для каждого критерия. Назначение весового коэффициента производится в зависимости от выбранного метода.
- Для аналитического метода:
- устанавливается рейтинговая шкала для каждого критерия;
- для каждого числового значения шкалы дается определение значимости.
Для того, чтобы различие в весовых коэффициентах были более заметны обычно применяют шкалу с числовыми значениями 1-3-9, где 1 – малая значимость, 3 – средняя значимость, 9 – большая значимость).
- Для метода консенсуса:
- устанавливается некоторое количество баллов, которые эксперты должны распределить между критериями. Количество баллов должно быть не меньше числа критериев;
- каждый из экспертов распределяет назначенные баллы между критериями;
- определяется суммарное число баллов по каждому из критериев. Это значение и будет являться весовым коэффициентом каждого из критериев.
- Для матричного метода:
- критерии располагаются в виде L-матрицы;
- устанавливается шкала для попарного сравнения критериев. Например, «0» — критерий А менее значим, чем критерий Б; «1» — критерий А и критерий Б равнозначны; «2» — критерий А более значим, чем критерий Б.
- проводится попарное сравнение всех критериев.
- определяется весовой коэффициент каждого критерия (весовой коэффициент подсчитывается как сумма всех значений в строке матрицы).
- Для аналитического метода:
- Шаг 6. Отбираются наиболее значимые критерии. Это можно сделать, отбросив критерии с наименьшими значениями весовых коэффициентов. Если же количество критериев не велико, то для дальнейшей работы могут быть сохранены все критерии.
- Шаг 7. Устанавливается метод подсчета значимости каждого из решений матрицы приоритетов (определены на шаге 3) на основе выбранных критериев (определены на шаге 6).
Для этого можно воспользоваться следующими вариантами:
- берется ограниченный набор возможных числовых значений со взаимосвязанным текстом (аналогично аналитическому методу, указанному на шаге 5);
- используется система голосования, как для метода консенсуса (шаг 5), когда каждый эксперт имеет ограниченное число баллов, которые можно распределить между решениями;
- используются отрицательные числовые значения для отрицательных взаимосвязей;
- используется процентная шкала вместо прямого подсчета баллов по каждому из решений.
- Шаг 8. Проводится оценка каждого решения по отношению к каждому критерию.
- Шаг 9. Оценка перемножается на весовой коэффициент соответствующего критерия.
- Шаг 10. Полученный список решений сортируется по порядку приоритетности. В случае необходимости приоритетность решений может быть представлена в виде диаграммы Парето.
- изменить технологию изготовления;
- увеличить число точек контроля;
- провести обучение мастеров;
- изменить конструкцию изделия.
- требуется не более 100 челчас на реализацию решения
- низкая стоимость реализации решения
- количество вовлекаемого персонала не более 50 чел.
- снижение затрат на брак не менее чем в 1,5 раза.
- Провести обучение мастеров — 118
- Изменить технологию изготовления — 100
- Увеличить число точек контроля — 90
- Изменить конструкцию изделия — 72
- в первую группу входят три самых весомых критерия,
- во вторую, соответственно, пять последующих,
- остальные составляют третью группу.
- Приростная капиталоотдача;
- Приростная капиталоемкость;
- Прирост прибыли на единицу капиталовложений.
- Ввод основных фондов на 1 рубль капиталовложений;
- Ввод производственных мощностей на 1 рубль капитальных вложений;
- Лаговые характеристики, в том числе лаг ввода основных фондов;
- Лаг ввода производственных мощностей;
- Лаг освоения мощностей.
- Ввод активной части основных фондов в расчете на 1 рубль инвестиций в машины и оборудование;
- Ввод пассивной части основных фондов на 1 рубль инвестиций в здания и сооружения;
- Доля инвестиций, не переходящих во вводы основных фондов, в общем объеме инвестиционных затрат;
- Соотношение инвестиций в машины и оборудование и инвестиций в здания и сооружения;
- Снижение удельных материальных затрат на производство в результате инвестирования;
- Снижение удельных трудовых затрат на производство в результате инвестирования.
- Первое значение весового коэффициента состоит в его влиянии на целеполагание и финансовое планирование.
- Второе значение – определение весового коэффициента позволяет составить прогноз о том, что произойдет в исследуемой области вследствие того или иного явления.
- Третье значение – весовые коэффициенты обязательно используются при создании компании, которая нуждается в инвестиционной поддержке.
- Четвертое значение – расчет весового коэффициента может быть подвержен изменениям с течением времени, по изменениям можно судить о переустройстве экономической системы.
- частоту встречаемости термина в документе: чем чаще встречается термин в документе, тем больше отношений он образует с другими терминами;
- категорию текста, в которую входит термин: термины тематической цепочки текста будут более значимы, чем термины текстовой модальности;
- содержательно-смысловой блок, в котором термин встречается: термин, который встретился в основном блоке, будет более полезен для отражения смысла, чем термин, который встретился во вспомогательном блоке.
- оценка степени влияния фактора, который характеризует каждый критерий;
- определение интегрального показателя весового коэффициента термина.
- предмет речи;
- субъект(-ы) речи, то есть автор(-ы) текста в целом;
- оценочная точка зрения субъекта;
- его эмоционально-психологический настрой;
- пространство и время как неотъемлемые атрибуты ситуации, в которой порождается текст;
- адресат общения.
- для описания общеизвестного и доказанного факта (Факт);
- для выражения убежденности автора (Убежденность);
- для обеспечения межфразовой связи (Коннектор);
- для отражения информации, противоположной претексту (Противоположность);
- для отражения информации о часто/редко повторяющихся событиях (Повторяемость);
- для отражения развития информации (Развитие); для уточнения информации (Уточнение).
- Проблема,
- Опыт,
- Решение,
- Итог.
- достаточно важен;
- скорее важен, чем не важен;
- скорее не важен, чем важен;
- совершенно не важен;
- затрудняюсь ответить.
- Насколько важен критерий «Частота встречаемости термина в научном тексте» для определения значимости термина текста?
- Насколько важен критерий «Термин отражает тему научного текста» для определения значимости термина текста?
- Насколько важен критерий «Содержательно-смысловой блок» для определения значимости термина текста?
- 1 Расчет весовых коэффициентов в сравнительном подходе
- 2 Весовой коэффициент — это величина, характеризующая важность критерия
- 3 О расчетном методе определения весовых коэффициентов
- 4 Матрица приоритетов
- 4.1 Пример
- 5 Работа планировщика и весовой коэффициент сервера
- 6 Определение ВК критериев эффективности инвестиций
- 7 Весовой коэффициент в экономической науке
- 8 Способ расчета ВК вершин семантической сети научного текста
- 8.1 Частота встречаемости термина в документе
- 8.2 Категория текста
- 8.3 Содержательно-смысловой блок
- 8.4 Вычисление интегрального весового коэффициента термина
- 8.5 Определение коэффициентов важности критериев
- 8.6 Вычислительные эксперименты
- 8.7 Заключение
Полученные значения суммируются по каждому из решений, что дает окончательную оценку приоритетности решений.
Итоговая оценка, которую содержит матрица приоритетов, может быть оставлена как есть, или переведена в проценты.
Пример
Шаг 1. Определяем цель составления матрицы приоритетов: уменьшить количество дефектов в изделии.
Шаг 2. Формируем команду экспертов: для примера состав команды экспертов будет состоять из 3 человек. Каждый из них знаком с методом выработки решений на основе мозгового штурма.
Шаг 3. Составляем список возможных решений проблемы: список решений поставленной проблемы сформированный командой экспертов:
Шаг 4. Определяем состав критериев для оценки приоритетности решений:
Шаг 5. Назначаем весовой коэффициент для каждого критерия. Рассмотрим назначение критериев для каждого из 3-х методов — аналитического, метода консенсуса и матричного метода:
Для аналитического метода:
Устанавливаем, что каждый эксперт может распределить между критериями 4 балла.

Для метода консенсуса:

Для матричного метода:

Шаг 6. Определяем наиболее значимые критерии: т.к. количество выбранных для примера критериев составляет всего 4, то оставляем все критерии.
Шаг 7. Выбираем метод подсчета значимости каждого из предложенных ранее (на шаге 3) решений.
Для определения значимости воспользуемся шкалой «1»-«3»-«9», где 9 — наиболее значимое решение, 3 — значимое решение, 1 — малозначимое решение.
Шаг 8. Проведем оценку значимости каждого решения по отношению к каждому критерию: для оценки значимости решений воспользуемся аналитическим методом. Весовые коэффициенты критериев определены на шаге 5.

Шаг 9. Определяем приоритетность каждого решения: оценка каждого решения перемножается на весовой коэффициент каждого критерия и значения суммируются.

Шаг 10. Распределяем решения по порядку приоритетности:
Матрица приоритетов, по сравнению с другими метода ранжирования, дает возможность более объективно оценить значимость данных и установить величину этой значимости.
Вместе с тем, очевиден и недостаток этого инструмента качества – он достаточно трудоемкий, особенно когда необходимо провести ранжирование большого количества данных по большому количеству критериев.
Источник: "kpms.ru"
Работа планировщика и весовой коэффициент сервера
Администратор LVS может назначить весовой коэффициент каждому узлу пула реальных серверов.
Этот коэффициент представляет собой целое число, которое используется в любом алгоритме, основанном на весовых коэффициентах и способствует более равномерному распределению нагрузки LVS-маршрутизатором при наличии реальных серверов с различной производительностью.
Весовые коэффициенты работают как множители.
Рассмотрим пример. Имеется два реальных сервера, весовой коэффициент первого — 5, весовой коэффициент второго — 1. В этом случае на каждый запрос, направленный второму серверу приходится 5 запросов, направленных первому. Значение весового коэффициента для реального сервера по умолчанию равно 1.
Хотя добавление весовых коэффициентов для различных аппаратных конфигураций в пуле реальных серверов может повысить эффективность балансировки нагрузки, оно также может привести к временной разбалансировке в случае добавления реального сервера в пул при использовании алгоритма «Минимум подключений c использованием весовых коэффициентов».
Рассмотрим пример: в пуле 3 реальных сервера. Серверы A и B имеют весовой коэффициент 1, сервер С — весовой коэффициент 2. Если сервер C выходит из строя по каким-либо причинам, нагрузка равномерно распределяется между серверами A и B.
Но как только сервер C начинает функционировать снова, LVS-маршрутизатор определяет, что подключения к серверу отсутствуют, и начинает все поступающие запросы направлять серверу C до тех пор, пока тот по количеству подключений не уравняется с серверами A и B.
Для предотвращения этого явления администратор может выполнить фиксацию виртуального сервера — каждый раз, когда включается узел в пуле реальных серверов таблица подключений обнуляется и LVS-маршрутизатор распределяет запросы как если бы все серверы были только что добавлены в пул.
Источник: "rhd.ru"
Определение ВК критериев эффективности инвестиций
Исследования по проблемам эффективности инвестиционной деятельности разнообразны и многочисленны. Особенно важны разработки по определению критериев эффективности инвестиций на макроуровне (например, для экономики страны).
Единого критерия на данный момент не выявлено, поэтому используется набор (система) критериев, рассматривающих проблему эффективности инвестиционной деятельности с разных сторон, что приближает нас к объективной оценке.
Однако взаимозависимость (корреляция) экономических критериев всегда создает большие трудности в решении задач многокритериальной оптимизации.
Как правило, приходится создавать некий интегральный критерий, включающий в себя весь набор локальных критериев с их весовыми коэффициентами.
При этом, возникает проблема определения значений весовых коэффициентов, т.е. веса (значимости) каждого критерия по отношению к интегральному, вес которого равен единице, и он же равен сумме весов всех составляющих его критериев. Для расчета весовых коэффициентов групп показателей может быть использован алгоритм применения АВ и АВС анализов Парето.
Для этого сначала критерии нумеруются в порядке убывания их значимости и разбиваются на группы:
При АВ анализе вторая и третья группа объединяются в одну. Далее оптимальный весовой коэффициент первого (самого значимого) критерия можно получить по формуле:

где n — общее число локальных критериев, используемых в интегральном критерии. Оптимальные весовые коэффициенты всех остальных критериев определяется формулой:

При этом, в случае n>15, согласно (1) можно брать n=15, так как ai незначительны при i>15. Полученные по формулам (1) и (2) требования к весовым коэффициентам ai соответствующих критериев i, где i=1,…n, должны обеспечиваться на практике наборами соответствующих мероприятий по повышению эффективности инвестиционного проекта, которые в каждом конкретном случае специально разрабатываются и обеспечиваются.
При этом важно последовательное обеспечение требований к а1, а2, а3 и т.д., поскольку нет смысла повышать вес несущественных критериев эффективности инвестиций.
В качестве примера рассмотрим некий набор критериев эффективности инвестиционного процесса на макроуровне. Пронумеруем в порядке убывания значимости все группы критериев.
В первую группу критериев соберем показатели эффективности инвестиций, ориентируемые на конечный результат:
Затем показатели инвестиций, ориентированных на непосредственный результат:
В третью группу поместим показатели эффективности, учитывающие видовую структуру инвестиций:
И показатели инвестиций, оценивающие инновационную компоненту:
Результаты расчета по формулам (1) и (2) весовых коэффициентов ai, (где i=1,14), представим в табличном виде:

Таблица 1.
Согласно данным Таблицы 1, вес первой группы (из трех критериев) равен 76,5% относительно 100% веса интегрального критерия. Для второй группы (из 5 критериев) имеем величину веса 21,5%, а для третьей соответственно 2%.
То есть для АВ анализа Парето имеем соотношение 76,5%:23,5%, а для АВС анализа соотношение будет 76,5%:21,5%:2%, что близко к рекомендуемым в мировой литературе соотношениям 80%:20% и 75%:20%:5% и несколько уточняет их, ибо соотношения эти получены эмпирическим путем и являются приближенными.
Таким образом, рассмотрен пример расчета оптимальных значений весовых коэффициентов критериев эффективности инвестиционного проекта при построении интегрального критерия эффективности.
Источник: "konspekt.biz"
Весовой коэффициент в экономической науке
Весовым коэффициентом называется число или степень числа, которая выражает значимость определенного предмета или явления. Например, оценивая перспективы вложения средств, инвестор анализирует различные экономические факторы и распределяет их по степени значимости. У наиболее значимого фактора будет самый высокий весовой коэффициент.
Расчет весового коэффициента какого-либо явления может производиться только при наличии других явлений, с которыми оно будет сравниваться.
Если у человека есть выбор между различными моделями поведения в финансовой сфере, он должен выбирать ту, весовой коэффициент аргументов которой больше, чем у других.
Вероятнее всего будет происходить то событие, у составляющих (аргументов) которого больший весовой коэффициент. На основании прогнозов вырабатывается план действий, что особенно часто наблюдается в макроэкономике (экономические отношения на внутригосударственном и международном уровнях).
Когда предприниматель обратится к инвесторам за помощью, он перечислит им причины, по которым стоит вкладывать деньги в его компанию, у каждой причины будет свой весовой коэффициент.
Чем больше будет суммарное значение весового коэффициента, тем выше вероятность получения предпринимателем инвестиционной поддержки.
Ведь весовой коэффициент определенного фактора может повышаться или понижаться только в том случае, если будет расти или падать значимость других факторов, а это может происходить только в случае преобразований в экономике.
Источник: "utmagazine.ru"
Способ расчета ВК вершин семантической сети научного текста
Одной из задач, решаемых при построении семантической сети текстового документа, является задача определения значимости терминов текста, которые влияют на определение его смысла. При решении данной задачи необходимо учесть множество факторов, влияние которых на значимость терминов различно и не всегда можно определить закономерности этого влияния.
Под понятием «значимость» будем понимать, во-первых, «наличие значения, смысла», и, во-вторых, как принято в семиотике и языкознании, отношение знака к другим знакам в рамках языковой системы. Определение значимости неразрывно связано с критериями значимости, роль которых сводится к обнаружению и установлению самого факта наличия значения или смысла термина, который здесь играет роль знака.
К основным критериям значимости можно отнести:
Для количественного представления значимости терминов обычно используются весовые коэффициенты.
Весовой коэффициент — числовой коэффициент, параметр, отражающий значимость, относительную важность, «вес» данного фактора, показателя в сравнении с другими факторами, оказывающими влияние на изучаемый процесс.
Вычислению весовых коэффициентов терминов предшествуют:
Рассмотрим определение степени влияния фактора, характеризующего каждый из вышеназванных критериев, на весовой коэффициент термина.
Частота встречаемости термина в документе
Статистический показатель термина документа невозможно использовать без предварительной обработки. Это связано с тем, что значение частоты встречаемости термина, который чаще других был употреблен в документе, абсолютно не влияет на его значимость.
Бóльшее значение будет иметь ранг частоты, который позволяет уравнивать значимости самых встречаемых терминов любых текстов и одновременно распределяет значимости терминов внутри одного текста.
При этом термины с одинаковой частотой встречаемости, имея одинаковый ранг частоты, будут одинаково значимы для передачи смысла.
Для учета частоты встречаемости при определении весового коэффициента термина предлагаем использовать формулу (1):
![]()
Она позволяет получить нормализованное значение w1 за счет вычисления логарифмической функции с основанием, равным максимальному рангу частоты.
Вычитание из единицы позволяет терминам с наибольшим рангом частоты иметь большее значение w1, а для терминов с максимальным рангом, т.е. которые редко используются в тексте, этот показатель будет равен нулю, что означает его неважность для отражения смысла текста.
Категория текста
Это одна из существенных характеристик текста, представляющая собой отражение определенной части общетекстового смысла различными языковыми, речевыми и собственно текстовыми (композитивными) средствами.
Категория текста имеет знаковую природу, план содержания такого знака — это единый текстовой смысл (например, целостность, тема, тональность, пространство, проспекция), а план выражения — функционально ориентированная типовая композиция разноуровневых языковых средств. Категория текста является единицей анализа, несущей в себе основные свойства целого, а именно целенаправленность и композитивность.
Каждая текстовая категория воплощает в себе отдельную смысловую линию текста, выраженную группой языковых средств, особым образом организованной в относительную внутритекстовую целостность.
Совокупность категорий текста, дополняющих друг друга и переплетающихся между собой, создают текст в качестве коммуникативной системы.
В соответствии с категориально-текстовой концепцией, основанной на принципе отражательности, категория текста как смысловая часть текста отражает один из компонентов коммуникативного акта, в число которых входит:
Соответственно выделяются текстовые категории темы, субъекта (авторизации), оценочности, тональности (текстовой модальности), текстового пространства и времени, адресата.
В силу объективно дробного выражения каждой категории в тексте к ним добавляется структурная текстовая категория композиции.
На наш взгляд, именно текстовые категории темы и композиции являются в настоящий момент наиболее важными для определения значимости терминов, и, кроме того, более прозрачными для исследования.
Тема — существенный и необходимый признак всякого текста. Это экстралингвистический фактор, который входит в ядро текста и определяет его структуру. Тема выражается в тематических группах, которые составляют тематическое поле тематического единства.
Тематическую группу научного текста, в частности научной статьи, можно сформировать, выделив термины из заголовка и подзаголовков. При этом если частота встречаемости выделенных терминов будет высокой в тексте, то их с полной уверенностью можно включить в текстовую категорию темы.
Тогда вклад в значение весового коэффициента термина можно принять равным 1, если термин отражает тему текста, и 0 в противном случае:
![]()
Говоря о второй текстовой категории, выбранной в работе, то композиция текста представляет собой единство внутренней структуры содержания, внешнего его деления на части и сами эти части. Для выделения такой структуры можно использовать выделение формальных текстовых признаков.
Содержательно-смысловой блок
Текстовая категория композиции соотносится с понятием содержательно-смысловой блок. Научный текст состоит из логически выделенных содержательных блоков: блок постановки и понимания проблемы (Проблема), блок изучения опыта предшественников (Опыт), блок изложения варианта решения проблемы, доказательства и аргументов (Решение), блок обобщения полученных данных и подведения итогов (Итог).
Для идентификации каждого блока применяется метод выделения формальных текстовых признаков, которые с высокой вероятностью используются в конкретном блоке.
Кроме вышеперечисленных блоков в текстах можно выделить, так называемые, дополнительные блоки, которые играют большую роль для отражения коммуникативной, аспектной, семантической, информативной, функционально-смысловой структуры научного текста:
Для достаточно небольших текстов, которыми являются научные статьи, наличие дополнительных блоков является не характерным: некоторые блоки могут отсутствовать, некоторые блоки могут быть очень маленькими и содержать в себе только 1-2 термина.
В связи с этим на данном этапе работы будут рассмотрены термины четырех основных блоков:
Очевидно, что для передачи основного замысла научной статьи существенную роль играют блоки Проблема, Решение и Итог. При этом блок Решение составляет зачастую большую половину текста. Это видно по результатам исследования корпуса научных статей объемом 100 единиц по различным областям знаний.
На этот же факт указывает существующее большое число маркеров и индикаторов, характерных для рассматриваемого блока. В связи со сказанным весовые коэффициенты терминов блока примем равными согласно (3):

Исследование научных текстов статей позволило выделить наиболее характерные индикаторы и маркеры каждого содержательно-смыслового блока.
Если термин используется в предложении, содержащем формальный признак того или иного блока, то его вес корректируется на соответствующую величину.
При этом если термин встретился в более, чем одном блоке, его вес изменяется на сумму соответствующих величин. Частота встречаемости термина в пределах одного блока здесь не играет роли, поскольку этот показатель был учтен в формуле (1).
Вычисление интегрального весового коэффициента термина
Бесспорно, что вышеуказанные три критерия значимости термина по-разному влияют на значение его весового коэффициента.
Тогда интегральный весовой коэффициент может быть рассчитан по формуле:
![]()
где ki — весовой коэффициент критерия i, i = 1..3.
Для определения весовых коэффициентов критериев воспользуемся процедурой взвешивания, предложенной в работе.
Для реализации данной процедуры необходимо осуществить две операции: вычислить критериальные индексы qi, на основе которых затем определяются весовые коэффициенты ki для всех критериев.
Исходной информацией для определения степени важности каждого критерия значимости термина служит следующая вопросная конструкция: насколько важен i-й критерий для определения значимости термина текста? Формат возможных ответов может быть представлен следующим множеством:
Тогда индекс важности каждого критерия может быть вычислен по формуле:

где i — индекс критерия;
j — индекс варианта ответа респондентов на вопрос относительно важности i-го критерия;
n — общее число предусмотренных вариантов ответа на вопрос (в нашем случае 5);
yij — доля респондентов (в процентах), указавших j-й вариант ответа для i-го критерия;
ai — весовой коэффициент j-го варианта ответа (для всех критериев используется единая шкала весовых коэффициентов;
0 ≤ ai ≤ 1); p — нормирующий коэффициент, величина которого определяется в ходе вычислительных экспериментов.
Для показателя a система весовых коэффициентов для всех критериев одинакова: a1 = 1,0; a2 = 0,6; a3 = 0,4; a4 = 0. Их значения интерпретируются как степени принадлежности рассматриваемого критерия к нечеткому множеству «важный критерий для определения значимости термина текста.
Идентификация индексов позволяет установить иерархию критериев. Для последующего включения всех критериев в интегральный весовой коэффициент необходимо от величин qi перейти к весовым коэффициентам важности каждого критерия, которые вычисляются по формуле:

где m — общее число критериев.
Процедура (6) позволяет пронормировать все критерии таким образом, что выполняется классическое балансовое условие:
![]()
Имея оценки критериальных весовых коэффициентов wi и коэффициентов их важности ki, можно рассчитать интегральный весовой коэффициент значимости термина W.
Определение коэффициентов важности критериев
В рамках выполнения вычислительных экспериментов была составлена анкета, включающая вопросы:
Формат возможных ответов был представлен выше. Рассчитанные по формуле (5) индексы важности каждого критерия соответственно равны q1 = 0,675; q2 = 0,887; q3 = 0,625.
Вычислив по формуле (6) весовые коэффициенты важности критериев, находим k1 = 0,309; k2 = 0,406; k3 = 0,285.
Вычислительные эксперименты
Рассмотрим на примере взвешивание терминов семантической сети научного текста. Для этого выберем одну статью «Технология многомерных баз данных» из коллекции статей по предметной области «Базы данных». На рисунке приведен фрагмент семантической сети рассматриваемого текста:

Для терминов данного фрагмента в табл. 1 приведены частота их встречаемости, ранг частоты и весовые коэффициенты w1 первого критерия значимости, рассчитанные по формуле (1). В последнем столбце этой таблицы приведены весовые коэффициенты w2 второго критерия значимости термина, определенные по формуле (2).
Для расчета весового коэффициента третьего критерия значимости необходимо идентифицировать содержательно-смысловые блоки текста по формальным текстовым признакам, характерным для каждого блока.
Будем выделять предложения с характерными индикаторами и маркерами, и в отношении терминов этих предложений будут задаваться весовые коэффициенты по третьему критерию в соответствии с формулой (3), представленные в последнем столбце табл. 1:

Таблица 1. Характеристики и весовые коэффициенты терминов
По формуле (4) с учетом вычисленных весовых коэффициентов важности критериев k1 = 0,309; k2 = 0,406; k3 = 0,285 находим значения интегральных весовых коэффициентов терминов (табл. 2):

Таблица 2. Результаты определения интегральных весовых коэффициентов W
Данные в табл. 2 отсортированы по убыванию значений интегральных весовых коэффициентов. Термин «Многомерные базы данных», имея пятый ранг частоты, встречаясь в названии статьи и относясь к содержательно-смысловому блоку «Итог», получил наибольшее значение весового коэффициента, что было ожидаемо. Анализируя другие термины, мы также видим проявление закономерностей, соответствующих выдвинутым предположениям.
Заключение
Полученные результаты являются достаточно правдоподобными и отражают значимость терминов научного текста для определения его смысла. В результате выполненной работы предлагается модифицировать формулу (5), так как в рамках данной задачи можно пренебречь степенью (1 — pyin), поскольку погрешность вычисления, оцененная в сотых долях, вполне приемлема и практически не влияет на результат дальнейших вычислений.
В перспективе требуется обосновать выбор системы весовых коэффициентов вариантов ответов при обработке результатов экспертного опроса, применяя методы нечеткой логики.
Источник: "fundamental-research.ru"
Содержание:
В
MAUT существенно используются веса
(коэффициенты важности) критериев.
Считается, что ЛПР может найти коэффициенты
– числа, которые определяют важность
критериев. Отношения между весами
критериев устанавливаются поиском
точек безразличия на плоскостях двух
критериев. В отличие от проверки условий
независимости по предпочтению по осям
упорядочиваются значения критериев от
худших к лучшим.
На
рис. 4.5 показана плоскость критериев C
1 , C 2 . Альтернативы А и К находятся в
отношении безразличия, которое
определяется так же, как и при проверке
условия независимости по предпочтению
(см. рис. 4.4).
Рис.
4.5. Определение
отношения
между
весами критериев C 1 и C 2
В
точке равновесия полезности альтернатив
равны, что позволяет записать U ($200 млн,
40 мин.) = U ($170 млн, 90 мин.). Это означает,
что критерий стоимости важнее для ЛПР:
w 1 > w 2 .
Используя
полученные ранее однокритериальные
функции полезности (рис. 4.2), находим w 2
= 0,4 w 1 . Аналогичным образом определяется
соотношение между весами критериев C 1
и C 3 . Пусть w 3 = w 1 , U ($150 млн) = 0,6 w 1 . Итак,
мы выразили веса всех критериев через
вес наиболее важного из них и упорядочили
критерии по важности: w 1 > w 3 > w 2 .
Для
нахождения численного значения веса
критерия C 1 (и, следовательно, всех
критериев) ЛПР предлагается сравнить
две стратегии, представленные на рис.
4.6, и определить вероятность р, при
которой обе стратегии равноценны. Первая
стратегия – это альтернатива, имеющая
лучшую оценку по первому критерию и
худшую – по двум другим. Вторая стратегия
– это лотерея, дающая с вероятностью р
альтернативу со всеми лучшими оценками
и с вероятностью (1– p ) – альтернативу
со всеми худшими оценками.
Рис
4. 6. Определение
коэффициента w 1
Предположим,
что такое р найдено. Тогда U ( A ) = U ( B ),
или w 1 = р. Пусть w 1 = 0,55. Тогда w 2 = 0,22; w 3 =
0,33.
4.7. Определение полезности альтернатив
После
нахождения весов критериев и построения
однокритериальных функций полезности
мы имеем всю необходимую информацию. В
соответствии с теоретическими результатами
остается установить вид функции
полезности. В нашем примере сумма
коэффициентов важности критериев
Считая
полученное значение достаточно близким
к единице, выбираем аддитивную форму
представления функции полезности:
Зная
оценки альтернатив (вариантов площадок),
можем подставить их в эту формулу,
определить полезность каждой альтернативы,
сравнить полезности и выбрать альтернативу
с наибольшей полезностью.
Пусть
заданы четыре альтернативы со следующими
оценками:
А
($180 млн, 70 мин., 10 тыс.);
В
($170 млн, 40 мин., 15 тыс.);
С
($160 млн, 55 мин., 20 тыс.);
D
($150 млн, 50 мин., 25 тыс.).
Подставляя
в формулы для вычисления полезности
альтернатив значения полезностей оценок
и веса критериев, получаем:
U(A)=0,55
? 0,25+0,22 ? 0,4+0,33 ? 0,89=0,52;
U(B)=0,684;
U(C)=0,66; U(D)=0,705;
U
( D ) => U ( B ) => U ( C ) => U ( A ).
Итак,
альтернатива D — лучшая .
5. Метод smart – простой метод многокритериальной оценки
Подход,
основанный на теории многокритериальной
полезности, требует достаточно много
усилий при практическом применении. В
детальном примере из книги [7] приведено
множество вопросов к ЛПР, ответы ЛПР в
многочасовом диалоге с консультантом.
Как реакцию на сложность методов,
основанных на MAUT , можно оценить появление
ряда эвристических методов, не имеющих
строго математического обоснования,
но использующих простые процедуры
получения информации и ее агрегации в
общую оценку альтернативы.
Одним
из наиболее известных методов такого
типа является метод SMART [10], предложенный
В. Эдвардсом. Метод можно представить
как совокупность следующих этапов:
• Упорядочить
критерии по важности.
• Присвоить
наиболее важному критерию оценку 100
баллов. Исходя из попарного отношения
критериев по важности, дать в баллах
оценку каждому из критериев.
• Сложить
полученные баллы. Произвести нормировку
весов критериев, разделив присвоенные
баллы на сумму весов.
• Измерить
значение каждой альтернативы по каждому
из критериев по шкале от 0 до 100 баллов.
• Определить
общую оценку каждой альтернативы,
используя формулу взвешенной суммы
баллов.
• Выбрать
как лучшую альтернативу, имеющую
наибольшую общую оценку.
• Произвести
оценку чувствительности результата к
изменениям весов.
По
признанию автора, метод SMART не учитывает
возможную зависимость измерений и
неаддитивность при определении общей
ценности альтернативы [10]. Однако, по
его мнению, метод прост и надежен при
практических применениях, что более
существенно. Проверка чувствительности
к изменениям весов позволяет учесть
влияние неточностей при измерениях и
возможной зависимости между критериями.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как математический анализ помогает в сравнении ИБ-решений
Время на прочтение
9 мин
Количество просмотров 2.3K
В этом году российским компаниям было непросто решить, чем заменить средства защиты иностранных вендоров, которые ушли из страны. В отечественных продуктах многих классов не оказалось привычной корпоративным пользователям многофункциональности зарубежных решений, к тому же не все из них успели завоевать доверие специалистов. Но со временем отрицание сменяется принятием, а принятие перетекает в действие. Казалось бы, осталось дело за малым — выбрать нужный продукт.
Но как подступиться к этой задаче? Ведь нужно сравнить слишком много критериев: провести функциональное и нагрузочное тестирование, проанализировать архитектуру, не упустить из виду экономические показатели и много чего еще. К тому же критерии могут иметь разную важность, в зависимости от конкретной задачи и внутренних требований компании. Даже если у компаний из одной отрасли со схожим профилем бизнеса будет одна цель — выбрать систему межсетевого экранирования, результаты могут оказаться кардинально разными.
В статье я не буду рассуждать о том, какие системы лучше, а какие хуже. Вместо этого поделюсь методикой сравнения продуктов, которую мы в «Solar Интеграция» часто применяем на практике. Эта методика позволяет не только детально оценить десятки критериев, но и учесть значимость каждого критерия по сравнению с другими, что очень важно для итогового анализа сравнения.

Знакомьтесь: метод попарного сравнения, или основа методики
В 1980 году математик Томас Лори Саати в своей книге «Принятие решений. Метод анализа иерархий» описал метод попарного сравнения. В его основе лежат математический анализ и сопоставление критериев по принципу значимости одного над другим. Что это означает на практике?
Цель метода в том, чтобы помогать руководителям анализировать потребности компании и принимать взвешенные решения с учетом конкретных задач и требований по их реализации. Метод позволяет точно сформулировать ожидания от продукта, структурировать и оценить наиболее важные аспекты, влияющие на принятие решения, и построить свою матрицу значимости одного критерия над другим.
Применению этого метода для решения задач в различных областях нашей повседневной жизни посвящено достаточно много работ. Я не буду останавливаться на повторении общедоступного материала, а сразу перейду к разбору использования метода при сравнении продуктов по кибербезопасности.
Для наглядности буду рассматривать применение метода на примере наиболее распространенной в этом году задачи по подбору системы межсетевого экранирования отечественного производства. Весь процесс оценки можно разделить на несколько этапов, давайте пройдемся по каждому из них.
Этап №1. Определение требований к системе и критериев оценки
Этот этап многим знаком, ведь без постановки целей и задач невозможно оценить результат от внедрения любой ИТ-системы или системы защиты информации. Но в отличие от классического бинарного подхода «работает — не работает», метод попарного сравнения дает возможность более гибко оценить, насколько та или иная система подходит под конкретные задачи. При подготовке к сравнению необходимо максимально четко сформулировать свои потребности. Возвращаясь к примеру с межсетевыми экранами: когда такая задача стояла у нашей команды, перед сравнением продуктов мы сначала составляли расширенный список требований, а затем сокращали его до наиболее важных для нашего проекта.
Для удобства сравнения все критерии оценки можно разделить на группы. Для сравнения систем защиты информации наиболее применимы три группы критериев:
-
Функциональность системы. Эта группа имеет среднюю степень важности, ведь никто не отменял требования по приведению в соответствие.
-
Технологии — наименее важная из трех, но существенная группа критериев, особенно если смотреть на перспективу развития системы защиты.
-
Экономические показатели — наиболее важная группа критериев с учетом ограниченности бюджетов.
Давайте посмотрим, какие критерии может включать каждая из этих групп.
Функциональность системы
Для примера возьму наиболее востребованную функциональность межсетевых экранов, при этом критерии с заведомо равной реализацией у сравниваемых решений включать не буду. Вот что у меня получится.
-
Идентификация и аутентификация пользователей: здесь важно посмотреть, могут ли решения получать полную информацию о пользователях и инициируемых ими процессах, реализована ли в них возможность интеграции с Active Directory и создания правил на основе данных из AD.
-
Контроль доступа из внешних информационных (автоматизированных) систем: в этой части стоит сосредоточиться на функции по блокировке трафика по приложениям.
-
Управление сетевыми соединениями: здесь важно обратить внимание на возможность маршрутизации трафика пользователей и журналирование соединений.
-
Защита от спама.
-
URL-фильтрация.
-
Использование эмулятора среды функционирования программного обеспечения (поведенческий анализ или «песочница»): в этой части полезно проверить наличие встроенной функциональности по анализу трафика эвристическими методами.
-
Защищенный удаленный доступ для пользователей.
В зависимости от особенностей конкретного проекта, приведенные критерии оценки могут меняться.
Технологии
-
Архитектура: важно проверить возможность отказоустойчивого физического исполнения, необходимость внесения изменений в схему построения сети и наличие централизованной системы управления и отчетности.
-
Масштабирование: здесь речь идет о возможности и удобстве использования одного решения как для одного офиса компании, так и для всей группы компаний с обеспечением индивидуальных настроек для отдельных обществ.
-
Внедрение: с этой точки зрения стоит сравнить механизмы и протоколы, применяемые для имплементации политик безопасности.
-
Лицензионная политика: важно проверить гибкость лицензирования (пользователи/устройства/целевые системы).
-
Интерфейс пользователя: стоит обратить внимание на эргономичность, качество и функциональность дизайна интерфейса, проверить наличие мониторинга за основными параметрами системы.
Экономические показатели
В зависимости от финансовых требований компании можно рассматривать разовые и операционные затраты с разными весами или сравнивать совокупную стоимость владения решением.
-
Инвестиционные затраты: важно сравнить объем инвестиций, которые понадобятся на закупку оборудования и ПО, внедрение решения и в случае необходимости его доработку.
-
Операционные затраты: здесь речь идет о затратах после внедрения, которые компания будет нести в течение всего жизненного цикла продукта.
Этап №2. Оценка критериев
После определения перечня критериев можно приступить непосредственно к сравнению критериев между собой. Для этого я применю девятибалльную шкалу, в которой единица означает равнозначность критериев, а оценка в девять баллов, напротив, говорит о максимальном превышении значимости одного критерия над другим. Для наглядности приведу распределение значений по оценочной шкале для критериев A и B.
|
Оценка |
Значение |
|
1 |
А и В одинаково важны |
|
3 |
А незначительно важнее В |
|
5 |
А значительно важнее В |
|
7 |
А явно важнее В |
|
9 |
А по своей значительности абсолютно превосходит В |
|
2, 4, 6, 8 |
Соответствующие промежуточные значения |
Для начала давайте оценим вес каждой группы выбранных критериев. Для автоматизации процесса в интернете можно найти специальные программы, но я применю «калькулятор» в таблице Excel. Как показано в приведенной ниже таблице, оценка критериев из первого столбца по отношению к критериям в верхней строке проставляется в ячейках, подсвеченных зеленым цветом. В нижней части оценка будет обратной, то есть высчитывается как единица, деленная на оценку в верхней части таблицы.
Итак, в моем примере с межсетевыми экранами стоимость играет важную роль, поэтому при оценке пар «Стоимость» — «Функциональность системы» и «Стоимость» — «Технологии» я поставлю пять баллов, то есть в этом случае стоимость значительно важнее других параметров. Оценивая пару «Функциональность системы» — «Технологии», я приму за аксиому тот факт, что функциональность будет явно важнее для решения поставленных задач, поэтому оценка будет семь баллов.
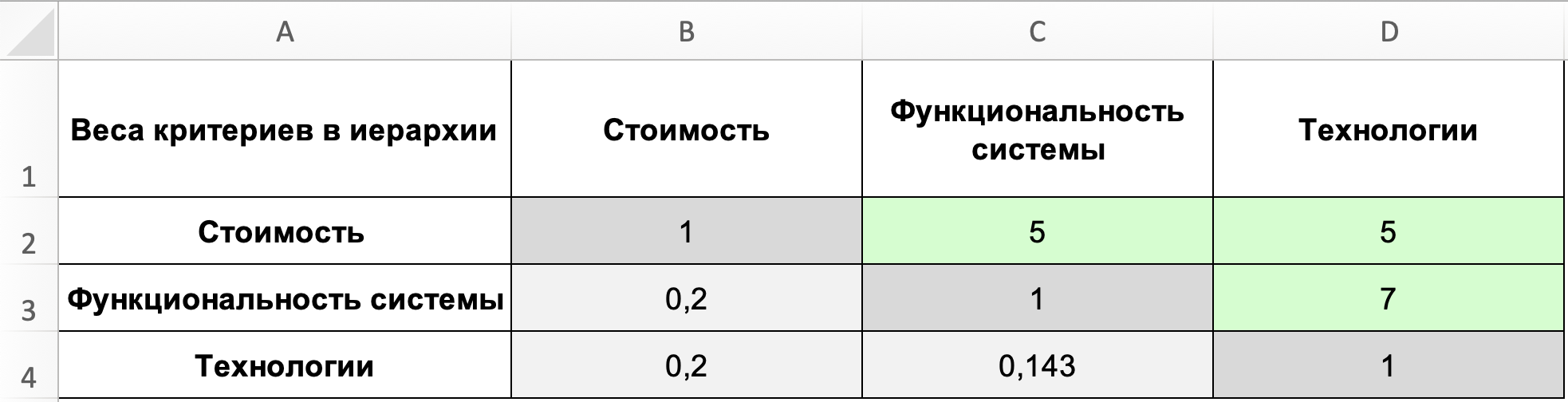
Затем необходимо оценить вес критерия среди всех рассматриваемых в группе. На языке математики это значит, что нужно определить вектор приоритетов по матрицам, то есть вычислить главный собственный вектор, который после нормализации становится вектором приоритетов. Сделать это можно четырьмя способами с различной степенью точности. Я воспользуюсь одним из самых точных вариантов, который можно реализовать без специализированных ЭВМ путем усреднения по нормализованным столбцам.
-
Выполню нормализацию столбца. Для этого разделю значения элементов в выбранной строке на сумму значений элементов в соответствующих им столбцах.
-
Затем сложу полученные значения и разделю результат на количество элементов в строке.
Для примера рассчитаю по описанному выше методу вес критерия «Стоимость» в группе критериев «Стоимость», «Функциональность системы» и «Технологии». Получится следующая формула:
Результаты оценки для каждого критерия представлены в таблице ниже в столбце «Вес критерия в группе, %».

Аналогичным образом необходимо оценить значимость и проставить вес каждого критерия во всех группах критериев.
Сравнение экономических показателей
Для тех, кто сталкивался в своей работе с задачей экономического обоснования решений, оценка показателей этой группы будет привычной. Достаточно запросить у вендоров данные о стоимости владения решением на один год, три и пять лет, и можно приступить к оценке показателей:
-
Первичные инвестиции (САРЕХ) — могут включать затраты на поставку оборудования и лицензий, обучение специалистов, закупку сопутствующего оборудования, например серверов и коммутаторов.
-
Операционные затраты (ОРЕХ) — на продление лицензий и поддержки оборудования производителем.
Поскольку в приведенном примере стоимость системы будет являться наиболее важным фактором принятия решения, я буду проводить сравнение по суммарной стоимости без разделения на САРЕХ и ОРЕХ.
Сравнение функциональности решений
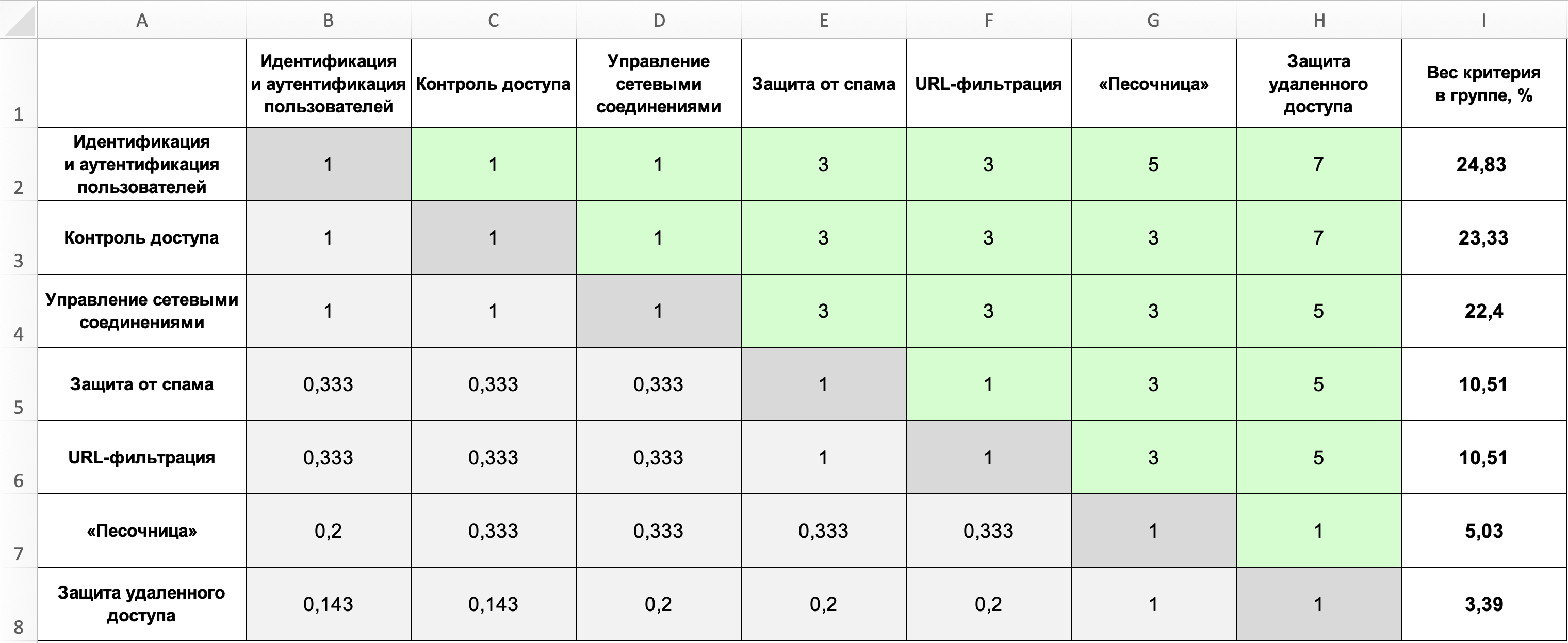
Попарное сравнение функциональных критериев я разберу на примере сравнения первого критерия из списка — идентификации и аутентификации пользователей — с другими критериями в группе. Результаты оценки показаны в матрице ниже, где критерии из первого столбца сравниваются с каждым из критериев по вертикали.
-
«Идентификация и аутентификация» пользователей равнозначна «Контролю доступа из внешних информационных (автоматизированных) систем», поэтому этой паре критериев я поставлю единицу.
-
«Управление сетевыми соединениями» является равнозначной задачей, так что и здесь поставлю один балл.
-
«Идентификация пользователей» незначительно важнее «Защиты от спама» и «URL-фильтрации», поэтому здесь оценка будет три балла.
-
Поведенческий анализ («Песочница») является значительно менее приоритетной задачей для выбираемого межсетевого экрана, поэтому в этом случае поставлю пять баллов.
-
Представьте, что количество удаленных пользователей в рамках проекта будет минимальным. В таком случае «Идентификация пользователей» будет значительно важнее «Защищенного удаленного доступа», и здесь я поставлю семь баллов.
Аналогичным образом необходимо сравнить оставшиеся пары критериев. При этом важно помнить, что с каждым шагом количество сравниваемых между собой пар будет уменьшаться, так как их сравнение уже было проведено ранее. В таблице пересечения критериев отмечены зеленым цветом.
При формировании матрицы нужно учитывать, что чем больше она получится, тем сложнее будет сделать попарное сравнение критериев, поэтому я рекомендую выбирать не более 10–15 самых важных критериев.
Сравнение критериев по группе «Технологии»
Аналогичным образом нужно заполнить матрицу для критериев группы «Технологии». Подробное пояснение расчетов в этом случае я опущу и сразу приведу получившийся результат.
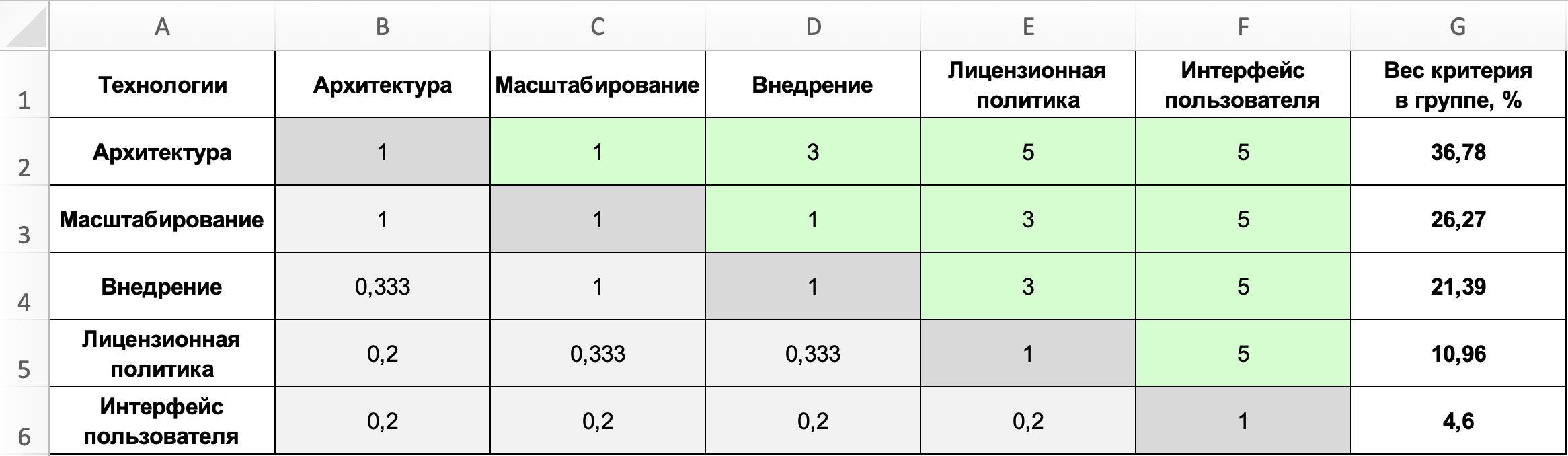
На этом этапе я определил вес каждого критерия в соответствующей группе. Но не стоит забывать, что собственный вес имеет и каждая группа критериев. Таким образом, при подведении итогов будет учитываться вес критерия с учетом веса его группы, то есть итоговый вес критерия будет равен произведению веса группы на вес критерия в группе. Например, итоговый вес критерия «Контроль доступа», входящего в группу критериев «Функциональность системы», будет равен:
Этап 3. Проверка выполнимости критериев
Перейду к заключительной, самой важной и трудоемкой, стадии. Теперь необходимо оценить выполнимость критериев. По моему опыту проведения аналогичных сравнений, максимально объективный и точный результат можно получить только после проведения функционального и нагрузочного тестирований сравниваемых решений.
Как заведено, результаты проведенных тестирований заносятся в протоколы, на основании которых можно заполнить последний раздел матрицы — критерии выполнимости. Для наибольшей эффективности оценки я снова не буду использовать триггеры в виде фраз «да» или «нет», а применю градацию по степени достижимости результатов тестов, при этом приведенные ниже баллы будут служить коэффициентом для финальной оценки. Это позволит оценить промежуточные значения, например, если функциональность имеется, но не отвечает вашим требованиям или находится в стадии разработки производителем.
|
Оценка |
Балл |
|
Полностью соответствует |
10 |
|
Соответствует со значительными отступлениями |
7 |
|
Соответствует на приемлемом уровне |
5 |
|
Во многом не соответствует |
3 |
|
Полностью не соответствует |
0 |
После внесения полученных результатов в сравнительную таблицу я получаю итоговый балл для каждого критерия и решения выбранного производителя. Он будет равен произведению итогового веса критерия и баллу оценки. Приведу пример для одного из сравниваемых решений по группе критериев «Функциональность системы».
|
Функциональность системы |
Итоговый вес критерия |
Производитель 1 |
||
|
Результат тестирования |
Оценка |
Итоговый балл критерия |
||
|
Идентификация и аутентификация пользователей |
6,99% |
Соответствует с незначительными отступлениями |
7 |
0,49 |
|
Контроль доступа |
6,57% |
Соответствует с незначительными отступлениями |
7 |
0,46 |
|
Управление сетевыми соединениями |
6,30% |
Соответствие на приемлемом уровне |
5 |
0,32 |
|
Защита от спама |
2,96% |
Соответствует с незначительными отступлениями |
7 |
0,21 |
|
URL-фильтрация |
2,96% |
Соответствует с незначительными отступлениями |
7 |
0,21 |
|
Поведенческий анализ |
1,42% |
Полностью не соответствует |
0 |
0,00 |
|
Защита удаленного доступа |
0,95% |
Во многом не соответствует |
3 |
0,03 |
|
Итоговый балл решения по группе критериев: |
1,71 |
Этап 4. Подведение итогов
Таким образом, в результате весьма кропотливой и трудоемкой работы можно получить объективную оценку результатов сравнения.
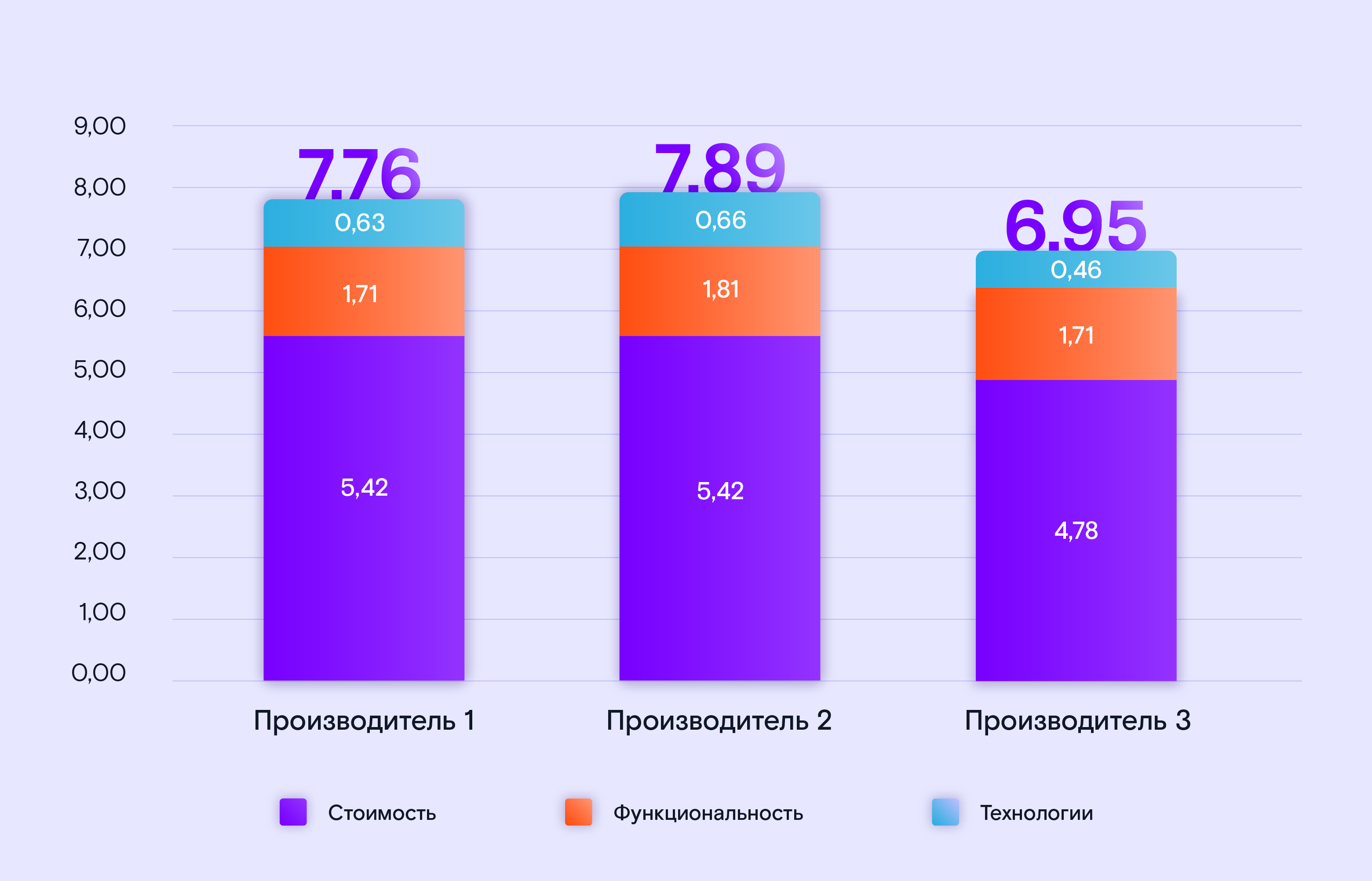
|
Производитель 1 |
Производитель 2 |
Производитель 3 |
|
|
Стоимость |
5,42 |
5,42 |
4,78 |
|
Функциональность |
1,71 |
1,81 |
1,71 |
|
Технологии |
0,63 |
0,66 |
0,46 |
|
Общий рейтинг |
7,76 |
7,89 |
6,95 |
Для наглядности при презентации результатов руководству компании можно представить их в виде диаграммы.
Проведенное сопоставление решений методом попарного сравнения стоит воспринимать как результат выполнения частной задачи. Рассмотренный подход не дает финальную оценку о том, что одно решение лучше или хуже другого. При изменении параметров сравнения вес критериев, критерии достижимости результата и ранжирование производителей поменяются.
При подготовке статьи я рассматривал гипотетическую задачу. Совпадения в критериях, оценках и баллах с проведенными сравнениями случайны.
Автор: Андрей Бондарев, руководитель направления сетевой безопасности центра «Solar Интеграция» компании «РТК-Солар»
Как выбрать из множества вариантов и не ошибиться? Рассказываем об эффективной технике принятия решений.

Используем таблицы
Для работы с методом откройте электронную таблицу или возмите бумагу и ручку. Так закрепить материал будет проще 😉
Представьте, что вы покупаете новый смартфон и разрываетесь между тремя приглянувшимися моделями. Или что вы планируете отправиться в отпуск, но никак не можете выбрать куда. Стандартные методы расстановки приоритетов (например, матрица Эйзенхауэра) здесь не работают. Как быть?
Здесь вам может пригодиться метод многокритериальной оценки. Это техника, которая как раз и помогает принимать решения в ситуациях выбора.
Сегодня расскажем, в чем суть метода многокритериальной оценки, и покажем на простых примерах, как его применять. Обратите внимание: для анализа вариантов мы будем использовать электронные таблицы (это очень удобно), однако все то же самое можно проделать и на бумаге.
Пример 1. Выбор квартиры
Предположим, мы планируем арендовать жилье. Мы почитали объявления, обошли несколько квартир и остановились на четырех вариантах. Чтобы выбрать наилучший вариант, воспользуемся методом.
Метод многокритериальной оценки состоит из четырех шагов:
Шаг 1. Определяем критерии. По каким параметрам мы будем оценивать квартиры? Что для нас наиболее важно?
Предположим, мы выбрали такие критерии:
- Стоимость аренды.
- Расстояние до работы.
- Общие впечатления от квартиры (насколько она нам понравилась).
Составляем таблицу и заносим в нее эти критерии:

Шаг 2. Определяем веса. Критерии редко бывают одинаково важны. Например, в нашем случае стоимость аренды может быть важнее, чем расстояние до работы.
Чтобы учесть эту разницу, каждому критерию присваивают свой вес. Вес — это число от 0 до 1, которое зависит от важности критерия. В сумме эти веса должны составлять единицу.
Пусть в нашем примере веса будут такими:

Шаг 3. Оцениваем варианты. Каждую квартиру нужно оценить по каждому из критериев. В этом примере мы будем ставить оценки по трехбалльной шкале (1 — плохо, 2 — нормально, 3 — хорошо), однако шкала может быть какой угодно.

Шаг 4. Считаем результат. Умножаем каждую оценку на вес критерия и суммируем результат. Если вы выполняете расчеты на бумаге, это будет выглядеть так:

В электронных таблицах просто вводим формулу для первого варианта и копируем ее на нижние ячейки с помощью перетаскивания.

Итого: победила квартира на улице Внучкина. По результатам анализа она набрала максимальную оценку.
Пример 2. Создание сайта
Мы планируем создать свой сайт, но не можем выбрать тематику. Снова используем метод многокритериальной оценки.
Шаг 1. Определяем критерии. Оценивать каждый вариант мы будем по четырем критериям:
- Интерес. Насколько эта тема нам интересна?
- Компетентность. Разбираемся ли мы в этом?
- Популярность. Интересно ли это людям?
- Конкуренция. Много ли в интернете ресурсов на эту тему?
Таблица будет выглядеть так:

Шаг 2. Определяем веса. Предположим, что самыми важными критериями для нас будут популярность и компетентность, а менее важными — интерес и конкуренция.

Шаг 3. Оцениваем варианты. На этот раз для разнообразия будем использовать 5-балльную шкалу.
Обратите внимание: конкуренция — это негативный параметр. Чем выше конкуренция, тем ниже должна быть оценка.

Шаг 4. Считаем результат. Все то же самое, что и в прошлом примере.

Итого: победил сайт о тайм-менеджменте. Именно его нам и следует создать.
Пример 3. Выбор цели
Предположим, у нас есть несколько важных целей, и мы никак не можем расставить приоритеты. Здесь снова поможет метод многокритериальной оценки.
Шаг 1. Определяем критерии. В этой ситуации критериями приоритетности становятся наши главные ценности. Пусть это будут семья, саморазвитие и материальное благосостояние.

Шаг 2. Определяем веса. Предположим, что материальное благосостояние немного важнее остальных ценностей.

Шаг 3. Оцениваем варианты. Насколько каждая цель важна с точки зрения той или иной ценности? Используем трехбалльную шкалу: 3 — очень важно, 2 — менее важно, 1 — не важно.

Шаг 4. Считаем результат. Вот что у нас получится:


Приоритетная цель
Максимально влияет на главные ценности
Итого: приоритетная цель — стать начальником отдела. Эта цель максимально влияет на главные ценности.
Заметим, что это был очень упрощенный пример. Целей и ценностей у человека обычно гораздо больше.
Тонкости
1. Определите минимальные требования. Если перед вами слишком много вариантов, задайте минимальные требования, чтобы «отфильтровать» лишнее.
Предположим, вы выбираете стиральную машину на Озоне. Минимальные требования могут быть такими:
- Загрузка от 5 кг.
- Стоимость — не более 50 тысяч.
- Оценка пользователей — не менее 4,5 звезд.
- Отзывов о товаре — не менее 50.
Такой отбор уменьшит количество вариантов и упростит дальнейший анализ.

Чарльз Дарвин
Жениться или нет?
2. Прислушайтесь к своим ощущениям после выбора. Если вы испытываете разочарование («Эх… А мне так хотелось другой вариант…»), возможно, вам стоит пересмотреть свое решение. Выбор не всегда должен быть рациональным.
Рассказывают, что однажды Чарльз Дарвин решил «по-научному» подойти к очень важному вопросу: жениться ему или нет. Он взял лист бумаги и скрупулезно записал на нем все за и против. Из этого анализа следовало, что жениться ему ни в коем случае нельзя.
В этот момент Дарвину стало настолько тоскливо, что он поспешил сделать предложение Эмме Веджвуд. С этой женщиной он счастливо прожил до конца своих дней.
П. Горский
В данной статье рассматриваются возможности корректного получения оценки сотрудника, часто называемой “рейтингом”. Предлагаются также методы оценки достоверности рейтинга, постановка задачи оценки денежных затрат на работу по оцениванию при заданном уровне достоверности.
Я решил написать эту статью, потому что почти везде и почти всегда сталкивался (и сталкиваюсь!) с “рейтингом” в виде взвешенной суммы:
R = S wi ri (1)
где ri – оценка сотрудника по i-му критерию,
wi – вес i-го критерия.
Беда в том, что эта формула не всегда дает верный результат! Неискушенного читателя это утверждение обычно приводит в недоумение. Следуют заявления вроде того, что приведенная формула “соответствует здравому смыслу”, или “отвечает интуитивному представлению о сравнительном качестве сотрудников” и т.п. Однако, все не так очевидно.
Обратимся, прежде всего, к оценкам . Условно разделим оценки на “объективные” и “экспертные”. Эксперта упрощенно можно рассматривать как некий “измерительный прибор”. Возникает вопрос о точности, с которой этот “прибор” может измерять. Ответ на этот вопрос дан в классической работе Миллера (Г. Миллер. Магическое число семь плюс минус два. Инженерная психология. – М.: Прогресс, 1964). Там показано, что эксперт чаще всего не способен различать более 7 градаций. Однако, сплошь и рядом приходится сталкиваться с ситуацией необоснованного использования шкал размерностью выше 7. Например, очень популярна 10-балльная шкала.
Нередки попытки получить от эксперта информацию в такой форме, в которой он не может дать ее с достаточной надежностью. Последние результаты исследований по этому вопросу приведены в книге: Ларичев О.И., Мошкович Е.М. Качественные методы принятия решений. – М.: Физматлит, 1996.
Не менее серьезные проблемы связаны с критериями. Прежде всего, не всегда удается обосновать тот набор критериев, который необходим и достаточен для решения конкретной задачи оценивания. Может показаться, что набор критериев “естественно” возникает в каждой конкретной задаче. Но, увы, это далеко не так.
Еще сложнее обстоит дело с весами критериев. Можно даже сказать, что веса критериев – самое тонкое место в проблеме критериального анализа. Чаще всего веса назначают, исходя из интуитивного представления о сравнительной важности критериев. Однако исследования показывают, что человек (эксперт) не способен непосредственно назначать критериям корректные численные веса. Необходимы специальные процедуры получения весов.
Итак, при серьезном рассмотрении выходит, что и оценки по критериям и сами критерии с их весами зачастую имеют весьма сомнительное происхождение. Вне поля критики осталась одна операция суммирования. Неужели и она может подвести? Еще как! Оказывается, что операция суммирования в данном случае не всегда корректна! В классической книге американских математиков Р.Л. Кини и Х. Райфа “Принятие решений при многих критериях: предпочтения и замещения” (Москва, изд-во “Радио и связь”, 1981) строго доказано, что подобная формула корректна только тогда, когда все критерии попарно независимы по предпочтению. Что такое “зависимость” критериев, какие виды зависимости бывают, и что из этого следует – все это выходит за рамки данной статьи.
Более того, оказывается, что сумма оценок основана на следующем неявном постулате: “низкая оценка по одному критерию может быть компенсирована высокой оценкой по другому”. Однако, этот постулат верен отнюдь не всегда. Например, пусть качество оператора ввода текстов оценивается двумя критериями: 1) скорость ввода (символов в минуту) и 2) среднее количество ошибок на страницу текста. Очевидно, что ухудшение качества ввода (увеличение количества ошибок) не может быть компенсировано увеличением скорости ввода. Можно даже сказать, что в области оценки персонала такая ситуация типична. Скажем, недостаток компетентности не может быть компенсирован повышенным уровнем активности. Скорее наоборот! Вспомним шутливое изречение: “Кто может быть хуже дурака? Дурак с инициативой!”
В итоге, можно сказать, что ценность подобных “рейтингов” не дотягивает даже до ценности выеденного яйца, которое само по себе все же имеет цену, хотя бы как минеральное удобрение. Более того – они даже вредны, поскольку дают искаженную картину реальности.
Почему же происходят все эти неприятности? Почему с таким постоянством применяется формула (1)? Ответ очевиден – кадровики и консультанты не знакомы с корректными методами построения рейтингов.
Причем речь идет не только о численных методах. Понятно, что слово “математический” прежде всего ассоциируется с понятием “число”. Однако, современная математика научилась оперировать не только числами. Как пишет профессор А.И.Орлов: “С начала 70-х годов под влиянием запросов прикладных исследований в технических, медицинских и социально- экономических науках в России активно развивается статистика объектов нечисловой природы, известная также как статистика нечисловых данных или нечисловая статистика. В создании этой сравнительно новой области прикладной математической статистики приоритет принадлежит российским ученым.”
Нетрудно показать, что при оценивании персонала применимы как числовые так и нечисловые (например, ранговые) подходы. Только делать это надо грамотно, подбирая подходящий метод к конкретной ситуации. Поскольку рамки статьи не позволяют рассмотреть все подходы, сосредоточим внимание только на численных методах, а точнее – на одной числовой модели.
Определение терминов
Не являясь специалистом по работе с персоналом, я все же для определенности вынужден уточнить используемую мной терминологию. Надеюсь, специалисты простят мне возможные “художества”.
Когда говорят “оценка” подразумевают использование какого-либо инструмента измерения. Оценить по существу означает измерить . Если мы оцениваем, к примеру, квартиру, то мы пытаемся “измерить” ее в денежных единицах. Что же измеряют при оценивании персонала? Условно можно считать, что измеряется некоторое “качество” сотрудника. Это качество определяется одним или несколькими критериями. Дадим следующие определения.
Оценивание – процедура получения числа, выражающего “качество” сотрудника. Условимся называть это число рейтингом сотрудника.
Объект оценивания – сотрудник предприятия.
Субъекты оценивания:
· сам сотрудник (если используется самооценка)
· сослуживцы (того же административного уровня, что и сотрудник)
· руководители сотрудника
· подчиненные сотрудника
· психологи
· специалисты предметной области, знание которой необходимо сотруднику в его работе
· сотрудники кадровой службы
В случае использования компьютерного тестирования можно условно считать субъектом оценивания также автора (авторов) теста. Оценку сослуживцев коллегами, начальниками и подчиненными назовем взаимооценкой .
Критерии – факторы, показатели, определяющие “качество” сотрудника.
Примеры критериев:
· Степень владения профессиональными навыками.
· Умение работать в коллективе.
ЛПР – “лицо, принимающее решение” (или группа таких лиц). Этой аббревиатурой будем обозначать тех руководителей предприятия и кадровых служб, которые будут принимать все ответственные решения, связанные с организацией и проведением работ по оценке сотрудников.
Уточнение задачи оценивания
Прежде всего зададимся вопросом: сколько рейтингов мы хотим получить? Один интегральный (обобщенный) или несколько частных? Например, можно получить два частных рейтинга: 1) рейтинг профессиональных качеств и 2) рейтинг качеств личности. Стоит ли объединять их в один обобщенный? При этом важен и другой вопрос: можно ли корректно построить обобщенную оценку на основе частных? На второй вопрос ответ есть: можно. Область прикладной математики, в которой исследуются и развиваются подобные методы, получила наименование “Decision Science” (в русскоязычной литературе часто переводится как “Поддержка принятия решений”). Что же касается первого вопроса, то, вообще говоря, однозначного ответа на него нет. Все определяется целью оценивания. Для определенности, в данной статье условимся считать, что нам нужен один обобщенный рейтинг.
Достоверность оценивания
При обсуждении любого рейтинга неизменно встает вопрос о его достоверности. В этом разделе я без доказательства опишу один математически корректный способ оценки достоверности рейтинга.
Прежде всего займемся взимооценкой. Предложим всем сотрудникам предприятия заполнить следующую анкету.
Таблица 1.
|
Перечислите сотрудников, которых Вы знаете |
|
| Профессиональные качества | Качества личности |
|
Знаю очень хорошо: |
Знаю очень хорошо: |
|
(фамилии) |
(фамилии) |
|
… |
… |
|
Знаю хорошо: |
Знаю хорошо: |
|
(фамилии) |
(фамилии) |
|
… |
… |
|
Знаю удовлетворительно: |
Знаю удовлетворительно: |
|
(фамилии) |
(фамилии) |
|
… |
… |
На основе таких анкет можно построить базу данных, содержащую степень знания сотрудниками друг-друга. Будем считать, что степень знания – это безразмерная величина в диапазоне от 0 (полное незнание) до 1 (абсолютно полное знание). Договоримся, что абсолютным знанием не может обладать никто и никогда. Тогда, к примеру, можно предложить такую шкалу:
Таблица 2
|
степень знания |
числовой эквивалент |
|
очень высокая |
0.9 |
|
высокая |
0.7 |
|
средняя (невысокая) |
0.5 |
Заметим, что низкая степень знания или отсутствие такового нас не интересуют и поэтому не рассматриваются.
Если мы собираемся использовать взаимооценку, то очевидно, во-первых, что чем выше степень знания субъектов оценивания об объекте, тем выше достоверность оценки.
Далее, пусть некоторого сотрудника Х будут оценивать N других сотрудников. Тогда нам понадобиться также следующая таблица.
Таблица 3
|
Субъект оценивания |
степень знания объекта X |
степень доверия ЛПР |
|
Субъект-1 |
P1 |
T1 |
|
… |
… |
… |
|
Субъект-N |
Pn |
Tn |
Нетрудно заметить, что в последней таблице появилась новая величина – степень доверия ЛПР. Определим ее как безразмерную величину в диапазоне от 0 (отсутствие доверия) до 1 (полное доверие). Будем считать, что эта величина выражает степень доверия ЛПР к степени знания конкретного субъекта о конкретном объекте. Например, в последней таблице величина t1 выражает степень доверия ЛПР к тому, что степень знания субъектом-1 объекта Х равна p1. Поскольку каждый объект оценивания в данной технологии оценивается несколькими субъектами, то для сведения набора степеней доверия объекта оценки к одной (интегральной) степени доверия нам потребуется соответствующая функция. Обозначим ее как
V = f (p,t) , (2)
т.е. аргументами функции являются наборы степеней знания и степеней доверия.
Важно отметить, что функция (2) позволяет не только получить интегральную степень доверия для каждого объекта оценивания, но и рассчитать обобщенную степень доверия для всей работы . Полученную таким образом величину можно рассматривать как степень достоверности рейтинга.
Я догадываюсь, что в этом месте у большинства читателей может возникнуть вопрос: для чего весь этот “огород”? Нельзя ли, к примеру, обойтись без такой неочевидной величины, как t ? Рискую огорчить большинство читателей, но должен со всей ответственностью заявить, что все, что приведено выше и все, что появится далее – не бред распоясавшихся математиков, а тщательно продуманная и выверенная схема. Все, что может показаться излишним – на самом деле жестко требуется для обеспечения корректности оценивания.
Критерии: их шкалы и веса
Ясно, что набор критериев оценки управленцев не может совпадать с набором критериев для оценки рабочих и/или специалистов. Стало быть, для каждого типа объекта оценивания должен быть разработан перечень критериев оценки объектов этого типа. Технологию формирования наборов критериев оставим за рамками данной статьи. Отметим только, что набор критериев должен быть достаточно стабилен, чтобы имелась возможность сравнивать рейтинги, полученные в разное время. Вообще говоря, однократный рейтинг полезен разве что для аутплейсмента (принятия решений по сокращению штатов). В остальных случаях интерес представляет именно динамика рейтинга.
Также существенно для нас и то, что для каждого критерия, по которому предполагается получать экспертную оценку, должна быть разработана шкала. Причем, если нет возможности четкой привязки градаций шкалы к какому-то объективному показателю, число градаций не должно превышать 7-ми. Каждая градация шкалы должна иметь содержательное значение (расшифровку). Приведу пример шкалы для критерия “степень владения профессиональными навыками”.
Таблица 4
| Значение градации |
Балл |
|
очень высокая |
5 |
|
высокая |
4 |
|
средняя |
3 |
|
низкая |
2 |
|
очень низкая |
1 |
Перейдем к весам критериев. Как отмечалось выше, веса критериев – самое тонкое место в проблеме критериального оценивания. Чаще всего веса назначают, исходя из интуитивного представления о сравнительной важности критериев. Однако исследования показывают, что человек (эксперт, ЛПР) не способен непосредственно назначать критериям корректные численные веса. Более того, есть данные, (они еще не опубликованы) которые свидетельствуют о том, что человек не может корректно назначать веса даже на базе нечисловых шкал. В рамках прикладной дисциплины Decision Science разработаны надежные методы получения весов критериев, однако их рассмотрение выходит за рамки данной статьи.
Читателям с хорошей математической подготовкой, желающим познакомиться с последними результатами в этой области, рекомендую статью В.В.Подиновского “Количественная важность критериев” (Автоматика и телемеханика, №5, 2000 г).
Об одном методе получения численных весов критериев все же следует упомянуть. Метод, о котором пойдет речь, особенно интересен и полезен в том случае, если задача выявления сравнительной важности критериев ставится как отдельная, самостоятельная проблема. В этом случае, наряду с оценками по критериям, каждый субъект оценивания должен выставить каждому объекту, который он оценивает, некую интегральную оценку. Такая “оценка сотрудника в целом” выставляется отдельно от оценок по критериям и никак не должна на них опираться. Если мы говорим “отличный работник” и не детализируем эту оценку, то можно считать, что мы дали человеку некую интегральную оценку. Если у нас есть набор таких интегральных оценок и набор оценок по критериям, то существуют корректный математический метод, позволяющий на основе только этой информации получить веса критериев. Причем, в рамках метода можно получить также оценку надежности численных значений весов.
Рейтинг
Представим результаты оценок в виде набора следующих таблиц (таблиц будет столько, сколько субъектов оценивания задействовано).
Таблица оценок объектов субъектом Sk
Таблица 5
|
Объекты оценивания |
K1 |
K2 |
… |
Km |
|
объект – 1 |
X11 |
X12 |
… |
X1m |
|
объект – 2 |
X21 |
X22 |
… |
X2m |
|
… |
… |
… |
… |
… |
|
объект – n |
Xn1 |
Xn2 |
… |
Xnm |
Через Kj обозначен j-й критерий. Через хij обозначена оценка i-го объекта по j-му критерию.
Ранее мы договорились получить одну интегральную оценку объекта. В этом случае нам понадобится функция
R = f(x,w) . (3)
где R – рейтинг объекта, x – вектор критериальных оценок, w – вектор весов критериев.
Поскольку мы также ввели в рассмотрение понятие “достоверность оценки”, то в итоге оценка каждого объекта будет представлена двумя числами: R – рейтингом объекта и V – степенью достоверности этого рейтинга. Будем записывать это следующим образом
O = {R,V} (4)
Возникает естественный вопрос: каков может быть вид функций (2) и (3)? В начале статьи уже говорилось о том, что функция (2) не может быть аддитивной. То же самое, оказывается, справедливо и для функции (3). Вообще говоря, несложно сформулировать систему условий (аксиом), которым должны удовлетворять указанные функции. Труднее подобрать конкретный вид функций, удовлетворяющий всем условиям. Однако, все эти сугубо математические вопросы приходится оставить за рамками данной статьи.
Необходимые базы данных
Какие данные нужны для реализации предлагаемых методов оценивания? Вот примерный перечень:
1. База данных о сотрудниках предприятия, содержащая следующие сведения:
-
стоимость 1 часа работы сотрудника;
-
степень знания сотрудниками друг-друга (отдельно в области профессиональной деятельности и отдельно в области личностных характеристик).
2. База данных о психологах, которых можно привлекать к оценке, содержащая номенклатуру методов тестирования с указанием необходимого времени и стоимости по каждой позиции. В эту же базу нужно поместить данные, характеризующие степень доверия для оценок каждого психолога (см. Таблицу 3).
3. База экспертов по специальностям, степень владения которыми предполагается тестировать. Формат тот же, что и для базы психологов (вид тестирования, время, стоимость, степень доверия).
4. База данных сотрудников, которых предполагается оценивать.
5. База данных, определяющая для каждого объекта оценивания список оценивающих его субъектов.
Оценка и оптимизация затрат
Совокупность указанных выше баз данных позволяет достаточно точно определить общие затраты S на выполнение всего комплекса работ по оцениванию и достигаемую при этом степень достоверности V полученных результатов. Обратим внимание на то обстоятельство, что первые 3 базы данных являются справочными, тогда как базы данных 4 и 5 собственно определяет конкретный профиль работы, т.е. указывают кого нужно оценивать и кто должен это делать.
Предположим, что базы данных с 1-й по 4-ю неизменны и перед нами поставлена задача проектирования базы данных №5. При этом можно решать две важные для практики задачи:
Задача 1
При заданном бюджете S подобрать совокупность субъектов оценивания таким образом, чтобы степень достоверности V результата была максимальна.
Задача 2
При заданной степени достоверности V результата подобрать совокупность субъектов оценивания таким образом, чтобы бюджет S был минимальным.
Обе задачи являются по сути оптимизационными. Для их решения понадобится набор ограничений, например, следующего вида:
-
количество психологов, привлекаемых для оценки определенного набора объектов не должно быть менее 2 (вариант – должно быть больше нуля);
-
количество оценок для определенного набора объектов не должно быть менее 5;
-
и т.п.
Важно, что планирование и разработка проекта по оценке персонала в приведенных выше терминах позволяет обоснованно, так сказать “с открытыми глазами”, а не на пальцах или на уровне интуиции (как это часто бывает) говорить о соотношении стоимости и эффективности работ.
Типичные ошибки
Большинство рейтинговых оценок по моим наблюдениям содержат одни и те же ошибки. Мне показалось полезным свести типичные ошибки в один список. Некоторые ошибки были уже описаны в начале статьи. Здесь их описание повторяется. 1. Неверный выбор шкал.
В технологии экспертного оценивания эксперта упрощенно можно рассматривать как некий измерительный прибор. Возникает вопрос о точности, с которой этот прибор может измерять. Ответ на этот вопрос дан в классической работе [1]. Там показано, что эксперт не способен различать более 9 градаций. Можно сказать, что в области обработки экспертных оценок закон Миллера играет роль закона Ома в электротехнике. Однако, буквально в последнее время появилась возможность использовать шкалы с большим, чем 9 числом градаций. Но для этого нужно применять метод оптимального шкалирования. 2. Незнание особенностей получения данных от экспертов. Часто делается попытка получить от эксперта такую информацию и в такой форме, которую он не может дать с достаточной надежностью. Последние результаты исследований по этому вопросу приведены в [14]. 3. Непосредственное назначение численных весов критериям.
Во многих работах показано, что такая процедура некорректна. Есть гипотеза (еще не проверенная), что человек не может правильно назначать критериям веса даже в вербальных шкалах. В работе В.В. Подиновского [12] приведена корректная процедура определения весов критериев на базе экспертизы цены замещения критериальных оценок. 4. Агрегирование критериальных оценок с использованием взвешенной суммы.
Строго доказано [3], что взвешенная сумма критериальных оценок корректна только тогда, когда критерии попарно независимы по предпочтению. Это – формальное ограничение для взвешенной суммы. Но есть и содержательные ограничения (см. следующий пункт). 5. Неудачный выбор способа агрегирования.
Любая аддитивная операция (в том числе и взвешенная сумма) может применяться только тогда, когда выполнено условие взаимной компенсации. В противном случае следует рассмотреть другие способы агрегирования [9]. Вообще говоря, строгий подход к выбору методов агрегирования требует детальной проработки аксиоматики, которая должна формализовать цель агрегирования в конкретном проекте. 6. Отсутствие анализа согласованности оценок экспертов. Если оценки в большой степени рассогласованы, возникает опасность получить так называемую “среднюю температуру по больнице”. В зависимости от количества оценок и вида их распределения следует выбирать адекватные способы анализа согласованности.
Литература
Не стоит пристально рассматривать год выхода в свет того или иного источника. Поскольку речь идет о математических методах, то уместно напомнить, что теорема Пифагора не устарела и по сей день.
1. Г. Миллер. Магическое число семь плюс минус два. Инженерная психология. – М.: Прогресс, 1964.
2. Литвак Б.Г. Экспертная информация: методы получения и анализа. – М.: Радио и связь, 1981.
3. Кини Р.Л., Райфа Х. Принятие решений при многих критериях: предпочтения и замещения. -М. : Радио и связь, 1981.
4. Садовский А.Л. Применение экспертных методов в задачах принятия решений в условиях нечеткой информации. В сб.”Вопросы кибернетики. Принятие решений и анализ экспертной информации.” – М.: АН СССР, Научный совет по комплексной проблеме “Кибернетика”, 1989.
5. Миркин Б.Г. Проблема группового выбора. -М.: Наука, 1974.
6. Емельянов С.В., Ларичев О.И. Многокритериальные методы принятия решений. -М.: Знание, 1985.
7. Глотов В.А., Павельев В.В. Векторная стратификация. -М. : Наука, 1985.
8. Юдин Д.Б. Вычислительные методы теории принятия решений. -М.: Наука, 1989.
9. Березовский Б.А. и др. Многокритериальная оптимизация. Математические аспекты. -М.: Наука, 1989.
10. Гафт М.Г. Принятие решений при многих критериях. -М.: Знание, 1979.
11. Гафт М.Г., Подиновский В.В. О построении решающих правил в задачах принятия решений. -Автоматика и телемеханика, №6, 1981.
12. Подиновский В.В. Многокритериальные задачи с упорядоченными по важности ресурсами. – Автоматика и телемеханика, 1976, №11.
13. Белкин А.Р., Левин М.Ш. Принятие решений: комбинаторные модели аппроксимации информации. – М.: Наука, 1990.
( в книге подробно рассмотрены некритериальные методы работы с информацией)
14. Ларичев О.И., Мошкович Е.М. Качественные методы принятия решений. – М.: Физматлит, 1996.
Об авторе
Павел Горский, кандидат технических наук, ведущий научный сотрудник Российского института экономики, политики и права (РИЭПП). Специализируется в областях: поддержка принятия решений, аналитические рейтинги, экспертные опросы, хранение и обработка больших массивов данных. До 2002 года – исполнительный директор Центра экспертных технологий.
Член Международного общества многокритериального принятия решений International Society on Multiple Criteria Decision Making.
Автор нескольких методик аналитических рейтингов, нашедших практическое применение. Среди них:
методика рейтинга компьютерных фирм России
методика рейтинга менеджеров информационных технологий
методика рейтинга российских предприятий (совместно с экспертами Moody’s)
Методики Павла прошли апробацию и были одобрены экспертами таких компаний как:
“Interfax” (АФИ)
Российская ассоциация туристических агентств (РАТА)
Евроазиатское рейтинговое агентство (EA Ratings)
Павел является консультантом рейтинговых проектов журналов: “Карьера”, “Бизон” (“Бизнес-он-лайн”).
Имеет 4 авторских свидетельства на системы поддержки принятия решений в разных областях, получил сертификат компании “Ernst & Young” по курсу “Корпоративные финансы”.
