Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Минимальные остовы
Рассмотрим следующую задачу:
Авиакомпания содержит (m) рейсов между (n) городами, (i)-ый из них обходится в (w_i) рублей, причём из любого города можно добраться до любого другого. В стране наступил кризис, и нужно отказаться от как можно большего числа из них таким образом, что содержание оставшиъся рейсов будет наиболее дешевым.
Иными словами, нужно найти дерево минимального веса, которое является подграфом данного неориентированного графа. Такие деревья называют остовами (каркас, скелет; ударение на первый слог, но так мало кто произносит). По-английски — minimum spanning tree (дословно, минимальное покрывающее дерево).
Почему дерево? Потому что в противном случае там был бы цикл, из которого можно удалить какое-то ребро и получить более оптималный ответ. А если это больше, чем одно дерево, то какие-то две вершины остаются несвязны.
Вообще, следующие утверждения про деревья являются эквивалентными:
- Граф — дерево.
- В графе из (n) вершин есть (n-1) рёбер и нет циклов.
- Из любой вершины можно дойти в любую другую единственным образом.
Лемма о безопасном ребре
Назовем подграф (T) графа (G) безопасным, если они является подграфом какого-то минимального остова.
Назовем ребро безопасным, если при добавлении его в подграф (T) получившийся подграф (T’) тоже является безопасным, то есть подграфом какого-то минимального остова.
Все алгоритмы для поиска минимального остова опираются на следующее утверждение:
Лемма о безопасном ребре. Рассмотрим произвольный разрез (удалили некоторые рёбра так, что граф распался на две части) какого-то подграфа минимального остова. Тогда ребро минимального веса, пересекающее этот разрез (то есть соединяющее их при добавлении) является безопасным.
Доказательство: Рассмотрим какой-то минимальный остов, в котором этого ребра нет. Если его добавить, то образуется цикл, из которого можно выкинуть ребро не меньшего веса, получив ответ точно не хуже. Противоречие.
Получается, что мы можем действовать жадно — на каждом шаге добавлять ребро минимального веса, которое увеличивает наш остов.
Алгоритм Прима
Один из подходов — строить минимальный остов постепенно, добавляя в него рёбра по одному.
- Изначально остов — одна произвольная вершина.
- Пока минимальный остов не найден, выбирается ребро минимального веса, исходящее из какой-нибудь вершины текущего остова в вершину, которую мы ещё не добавили. Добавляем это ребро в остов и начинаем заново, пока остов не будет найден.
Этот алгоритм очень похож на алгоритм Дейкстры, только тут мы выбираем следующую вершину с другой весовой функцией — вес соединяющего ребра вместо суммарного расстояния до неё.
Совсем наивная реализация за (O(nm)) — каждый раз перебираем все рёбра:
const int maxn = 1e5, inf = 1e9;
vector from, to, weight;
bool used[maxn]
// считать все рёбра в массивы
used[0] = 1;
for (int i = 0; i < n-1; i++) {
int opt_w = inf, opt_from, opt_to;
for (int j = 0; j < m; j++)
if (opt_w > weight[j] && used[from[j]] && !used[to[j]])
opt_w = weight[j], opt_from = from[j], opt_to = to[j]
used[opt_to] = 1;
cout << opt_from << " " << opt_to << endl;
}Реализация за (O(n^2)):
const int maxn = 1e5, inf = 1e9;
bool used[maxn];
vector< pair<int, int> > g[maxn];
int min_edge[maxn] = {inf}, best_edge[maxn];
min_edge[0] = 0;
// ...
for (int i = 0; i < n; i++) {
int v = -1;
for (int u = 0; u < n; j++)
if (!used[u] && (v == -1 || min_edge[u] < min_edge[v]))
v = u;
used[v] = 1;
if (v != 0)
cout << v << " " << best_edge[v] << endl;
for (auto e : g[v]) {
int u = e.first, w = e.second;
if (w < min_edge[u]) {
min_edge[u] = w;
best_edge[u] = v;
}
}
}Можно не делать линейный поиск оптимальной вершины, а поддерживать его в приоритетной очереди, как в алгоритме Дейкстры. Получается реализация за (O(m log n)):
set< pair<int, int> > q;
int d[maxn];
while (q.size()) {
v = q.begin()->second;
q.erase(q.begin());
for (auto e : g[v]) {
int u = e.first, w = e.second;
if (w < d[u]) {
q.erase({d[u], u});
d[u] = w;
q.insert({d[u], u});
}
}
}Про алгоритм за (O(n^2)) забывать не стоит — он работает лучше в случае плотных графов.
Система непересекающихся множеств
Система непересекающихся множеств (англ. disjoint set union) — структура данных, которая используется для хранения информации о связности компонент. Она нам потребуется для описания следующего подхода — алгоритма Крускала.
Изначально имеется несколько элементов, каждый из которых находится в отдельном (своём собственном) множестве. Структура поддерживает две операции:
- Объединить два каких-либо множества.
- Запросить, в каком множестве сейчас находится указанный элемент.
Обе операции выполняются в среднем почти за (O(1)) (но не совсем — этот сложный вопрос будет разъяснен позже).
Множества элементов мы будем хранить в виде деревьев: одно дерево соответствует одному множеству. Корень дерева — это представитель (лидер) множества. Заведём массив _p, в котором для каждого элемента мы храним номер его предка в дереве. Для корней деревьев будем считать, что их предки — они сами.
Наивная реализация, которую мы потом ускорим:
int _p[maxn];
int p(int v) {
if (_p[v] == v)
return v;
else
return p(_p[v]);
}
void unite(int a, int b) {
a = p(a), b = p(b);
_p[a] = b;
}
for (int i = 0; i < n; i++)
_p[i] = i;Эвристика сжатия пути. Оптимизируем работу функции p. Давайте перед тем, как вернуть ответ, запишем его в _p от текущей вершины, то есть переподвесим его за самую высокую.
Следующие две эвристики похожи по смыслу и стараются оптимизировать высоту дерева, выбирая оптимальный корень для переподвешивания.
Ранговая эвристика. Будем хранить для каждой вершины её ранг — высоту её поддереа. При объединении деревьев будем делать корнем нового дерева ту вершину, у которой ранг больше, и пересчитывать ранги (ранг у лидера должен увеличиться на единицу, если он совпадал с рангом другой вершины). Эта эвристика оптимизирует высоту дерева напрямую.
Весовая эвристика. Будем вместо ранга хранить размеры поддеревьев для каждой вершины, а при объединении — подвешивать за более «тяжелую».
Финальная реализация, использующая весовую эвристику и эвристику сжатия путей:
int _p[maxn], s[maxn];
int p (int v) { return (_p[v] == v) ? v : _p[v] = p(_p[v]); }
void unite(int a, int b) {
a = p(a), b = p(b);
if (s[a] > s[b])
swap(a, b);
s[b] += s[a];
_p[a] = b;
}
// где-то в main:
for (int i = 0; i < n; i++)
_p[i] = i;Автор предпочитает именно весовую эвристику, потому что часто в задачах размеры компонент требуются сами по себе.
Асимптотика
Эвристика сжатия путей улучшает асимптотику до (O(log n)) в среднем. Здесь используется именно амортизированная оценка — понятно, что в худшем случае нужно будет сжимать весь бамбук за (O(n)).
Индукцией несложно показать, что весовая и ранговая эвристики ограничивают высоту дерева до (O(log n)), а соответственно и асимптотику тоже.
При использовании эвристики сжатия плюс весовой или ранговой асимптотика будет (O(a(n))), где (a(n)) — обратная функция Аккермана (очень медленно растущая функция, для всех адекватных чисел не превосходящая 4).
Тратить время на изучения доказательства или даже чтения статьи на Википедии про функцию Аккермана автор не рекомендует.
Алгоритм Крускала
Отсортируем рёбра и будем пытаться добавлять их в остов в порядке возрастания их весов. Если ребро соединяет какие-то две уже соединенные вершины, то проигнорируем его, иначе оно является безопасным, и его можно добавить.
Звучит очень просто — отсортировать все рёбра, пройтись по ним циклом и делать проверку, что вершины в разных компонентах. Наивная проверка будет работать за (O(m log m + n^2)), но асимптотику можно улучшить до (O(m log m)) (до стоимости сортировки), если для проверок использовать систему непересекающихся множеств.
// (w, (a, b))
vector< pair< int, pair<int, int> > > edges;
sort(edges.begin(), edges.end());
for (auto e : edges) {
int a = e.first.first, b = e.first.second;
// компоненты разные, если лидеры разные
if (p(a) != p(b)) {
// добавим ребро (a, b)
unite(a, b);
}
}Алгоритм Борувки
Лемма. Для любой вершины минимальное инцидентное ей реборо является безопасным.
Доказательство. Пусть есть минимальный остов, в котором для какой-то вершины (v) нет её минимального инцидентного ребра. Тогда, если добавить это ребро, образуется цикл, из которого можно удалить другое ребро, тоже инцидентное (v), но имеющее не меньший вес.
Алгоритм Борувки опирается на этот факт и заключается в следующем:
- Для каждой вершины найдем минимальное инцидентное ей ребро.
- Добавим все такие рёбра в остов (это безопасно — см. лемму) и сожмем получившиеся компоненты, то есть объединим списки смежности вершин, которые эти рёбра соединяют.
- Повторяем шаги 1-2, пока в графе не останется только одна вершина-компонента.
Алгоритм может работать неправильно, если в графе есть ребра, равные по весу. Пример: «треугольник» с одинаковыми весами рёбер. Избежать это можно введя какой-то дополнительный порядок на рёбрах — например, сравнивая пары из веса и номера ребра.
Асимптотика
Заметим, что на каждой итерации каждая оставшаяся вершина будет задействована в «мердже». Это значит, что количество вершин-компонент уменьшится хотя бы вдвое, а значит всего итераций будет не более (O(log n))
На каждой итерации мы можем просматриваем почти все рёбра, так что конечное время работы составит (O(m log n)).
Зачем это нужно?
Алгоритм неприятно реализовывать. Настолько неприятно, что автор это делать не будет. Однако, алгоритм очень полезен на практике, потому что в «реальных» графах он работает за линейное время.
Утверждение. В случае планарных графов алгоритм работает за (O(n)).
Доказательство. Из формулы Эйлера нам известно, что рёбер в планарном графе (O(n)). Так как подграф планарного графа тоже всегда планарен, то после каждой итерации размер нашей задачи уменьшается в честные 2 раза — меньше становится не только вершин, но и рёбер тоже. Значит, алгоритм будет работать за (O(n) + O(frac{n}{2}) + O(frac{n}{4}) + ldots = O(n)).
Также, в отличие от алгоритмов Прима и Крускала, его можно легко распараллелить. «Параллельная сложность» у него (O(log v)): нужно каждую итерацию просто искать минимум по оставшимся рёбрам.
Полезные свойства и классические задачи
- Если веса всех рёбер различны, то остов будет уникален.
- Минимальный остов является также и остовом с минимальным произведением весов рёбер (замените веса всех рёбер на их логарифмы)
- Минимальный остов является также и остовом с минимальным весом самого тяжелого ребра.
- Если вы решаете задачу, где ребра не добавляются, а удаляются, и нужно поддерживать минимальный остов, то можно попробовать решать задачу «с конца» и применить алгоритм Крускала.
- Алгоритм Крускала — частный случай алгоритма Радо-Эдмондса.
Персистентная СНМ
СНМ — структура данных на ссылках, и её тоже можно сделать персистентной. В СНМ мы изменяем массивы, а массивы можно сделать персистентными через персистентное ДО (только так, проще не получается — многие пытались).
Здесь есть нюанс — амортизированные структуры не очень хорошо дружат с персистентностью. Поэтому нам придется отказаться от эвристики сжатия путей, и поэтому асимптотика составит (O(n log^2 n)) времени и памяти — один логарифм от самого СНМа, другой от персистентного ДО.
Динамическая связность
Dynamic Connectivity Problem:
Даны (n) запросов добавления ребра (
+), удаления ребра (-и какого-то запроса про граф (?), например, о связности двух вершин.
О решении этой задачи в online и в offline можете почитать в этом посте.
Привет, Хабр!
В свободное от учебы время пишу статьи, которых мне не хватало несколько лет назад.
Алгоритмы нахождения MST применимы в различных областях, начиная от кластеризации данных до построения компьютерных, транспортных сетей.
Я надеюсь, что вы после прочтения данной статьи, примерно понимали, как работают жадные алгоритмы нахождения MST.
Визуализация графов проводится с помощью graphonline.
Формальная постановка задачи
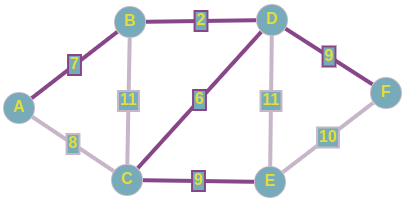
Имеется следующий неориентированный взвешенный граф. Назовем остовным деревом подграф, содержащий все вершины исходного графа, который является деревом. И задача состоит в том, чтобы найти такое остовное дерево, сумма рёбер которого минимальна.
Неформальная постановка задачи
Представьте исходный граф без рёбер, теперь вам нужно как-то соединить все вершины между собой, чтобы можно было бы попасть из любой вершины в другую, не имея при этом циклов в получившемся графе с минимально возможной суммой весов включенных рёбер.
Алгоритм Краскала
Механизм, по которому работает данный алгоритм, очень прост. На входе имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева. Будем рассматривать только связные графы, в другом случае при применении алгоритма Краскала мы будем получать не минимальное остовное дерево, а просто остовной лес.
-
Вначале мы производим сортировку рёбер по неубыванию по их весам.
-
Добавляем
i-оеребро в наш подграф только в том случае, если данное ребро соединяет две разные компоненты связности, одним из которых является наш подграф. То есть, на каждом шаге добавляется минимальное по весу ребро, один конец которого содержится в нашем подграфе, а другой – еще нет. -
Алгоритм завершит свою работу после того, как множество вершин нашего подграфа совпадет с множеством вершин исходного графа.
Данный алгоритм называется жадным из-за того, что мы на каждом шаге пытаемся найти оптимальный вариант, который приведет к оптимальному решению в целом.
Разбор конкретного примера по шагам
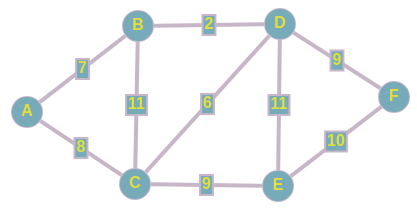
Из представленного сверху графа, выпишем все его ребра в отсортированном порядке:
1) D <--> B; w = 2
2) D <--> C; w = 6
3) A <--> B; w = 7
4) A <--> C; w = 8
5) C <--> E; w = 9
6) D <--> F; w = 9
7) F <--> E; w = 10
8) B <--> C; w = 11
9) D <--> E; w = 11
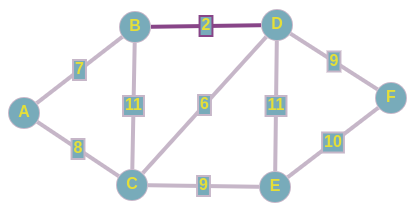
И начнем по списку добавлять эти ребра в наш остов:
При добавлении в наше остовное дерево ребра A <--> C, как вы можете заметить, образовывается цикл, поэтому мы просто пропускаем данное ребро.
По итогу у нас образовывается следующий подграф, и как вы заметили, мы соединили все вершины ребрами с минимально-возможными весами, а значит, нашли минимальное остовное дерево для нашего исходного графа.
Проводим проверку с помощью встроенного алгоритма для нахождения MST на graphonline, и видим, что подграфы идентичны.
И да, из-за того, что при равенстве весов рёбер мы можем выбрать любое из них, конечные подграфы, являющиеся минимальными остовными деревьями, могут различаться с точностью до некоторых рёбер.
Суммарный вес искомого MST равен 33.
Реализация
Реализовать представленный алгоритм проще всего с помощью СНМ(система непересекающихся отрезков).
Вначале, как мы уже раннее говорили, необходимо отсортировать ребра по неубыванию по их весам. Далее с помощью вызовов функции make_set()мы каждую вершину можем поместить в свое собственное дерево, то есть, создаем некоторое множество подграфов. Дальше итерируемся по всем ребрам в отсортированном порядке и смотрим, принадлежат ли инцидентные вершины текущего ребра разным подграфам с помощью функции find_set() или нет, если оба конца лежат в разных компонентах, то объединяем два разных подграфа в один с помощью функции union_sets().
Псевдокод
vector<int> parent, rank;
void make_set(int v) {
parent[v] = v;
rank[v] = 0;
}
int find_set(int v) {
if (v == parent[v])
return v;
return parent[v] = find_set(parent[v]);
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (rank[a] < rank[b])
swap(a, b);
parent[b] = a;
if (rank[a] == rank[b])
rank[a]++;
}
}
struct Edge {
int u, v, weight;
bool operator<(Edge const& other) {
return weight < other.weight;
}
};
int n;
vector<Edge> edges;
int cost = 0;
vector<Edge> result;
parent.resize(n);
rank.resize(n);
for (int i = 0; i < n; i++)
make_set(i);
sort(edges.begin(), edges.end());
for (Edge e : edges) {
if (find_set(e.u) != find_set(e.v)) {
cost += e.weight;
result.push_back(e);
union_sets(e.u, e.v);
}
}Алгоритм Прима
Суть самого алгоритма Прима тоже сводится к жадному перебору рёбер, но уже из определенного множества. На входе так же имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева.
-
Изначально наш подграф состоит из одной любой вершины исходного графа.
-
Затем из рёбер инцидентных этой вершине, выбирается такое минимальное ребро, которое связала бы две абсолютно разные компоненты связности, одной из которых и является наш подграф. То есть, как только у нас появляется возможность добавить новую вершину в наш подграф, мы тут же включаем ее по минимальмально возможному весу.
-
Продолжаем выполнять предыдущий шаг до тех пор, пока не найдем искомое MST.
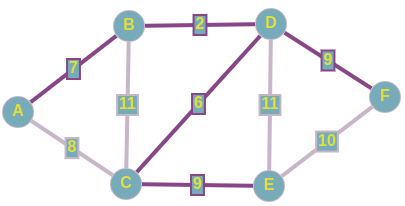
Разбор конкретного примера
Выбираем чисто случайно вершину E,далее рассмотрим все ребра исходящие из нее, включаем в наше остовное дерево ребро C <--> E; w = 9, так как данное ребро имеет минимальный вес из всех рёбер инцидентных множеству вершин нашего подграфа. Имеем следующее:
Теперь выборка производится из рёбер:
D <--> C; w = 6
A <--> C; w = 8
F <--> E; w = 10
B <--> C; w = 11
D <--> E; w = 11
То есть, в данный момент, мы знаем только о двух вершинах, соответственно, знаем о всех ребрах, исходящих из них. Про связи между другими вершинами, которые не включены в наш подграф, мы ничего не знаем, поэтому они на этом шаге не рассматриваются.
Добавляем в наш подграф реброD <--> C и по аналогии добаляем ребро D <--> B. Получаем следующее:
Давайте добьем наш подграф до минимального остовного дерева. Вы, наверное, уже догадались о том, по каким ребрам мы будем связывать наши оставшиеся вершины: A и F.
Проводим последние штрихи и получили тот же самый подграф в качестве минимального остовного дерева. Но как мы раннее говорили, сам подграф ничего не решает, главное тут – множество рёбер, которые включены в наше остовное дерево.
Суммарный вес искомого MST равен 33.
Источники
Инструмент для работы с графами
Лекция Павла Маврина
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Насколько подробно я расписываю? (Учтите, что приоритетом данных статей является разжевывание)
3.03%
Имхо, не стоит так подробно расписывать.
1
33.33%
Чего-то не хватает. Возможно, стоит по-лучше прорабатывать каждый шаг.
11
63.64%
Все плюс-минус неплохо, можно что-то понять.
21
Проголосовали 33 пользователя.
Воздержались 6 пользователей.
Минимальное остовное дерево
Остовным деревом графа называется дерево, которое можно получить из него
путём удаления некоторых рёбер. У графа может существовать несколько остовных
деревьев, и чаще всех их достаточно много.
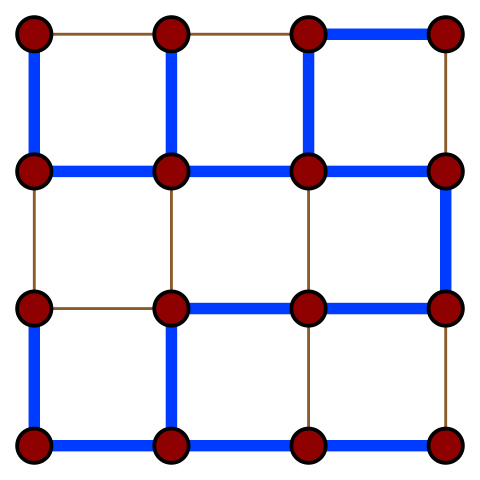
На иллюстрации приведено одно из остовных деревьев (рёбра выделены синим
цветом) решёткообразного графа.
Для взвешенных графов существует понятие веса остовного дерева,
которое определено как сумма весов всех рёбер, входящих в остовное дерево.
Из него натурально вытекает понятие минимального остовного
дерева – остовного дерева с минимальным возможным весом.
Для нахождения минимального остовного дерева графа существуют два основных
алгоритма: алгоритм Прима и алгоритм Крускала. Они оба имеют сложность
(O(M log N)), поэтому выбор одного из них зависит от ваших личных предпочтений.
В этой лекции мы разберём оба.
Алгоритм Прима
Алгоритм Прима в идее и реализации очень похож на алгоритм Дейкстры. Как и
в алгоритме Дейкстры, мы поддерживаем уже обработанную часть графа (минимального
остовного дерева), и постепенно её расширяем за счёт ближайших вершин.
Утверждается, что если разделить вершины графа на два множества (обработанные
и необработанные), первое из которых составляет связную часть минимального
остовного дерева, то ребро минимальной длины, связывающее эти два множества
гарантированно будет входить в минимальное остовное дерево.
Таким образом, для нахождения минимального остовного дерева начнём с
произвольной вершины и будем постепенно добавлять ближайшие к уже имеющимся.
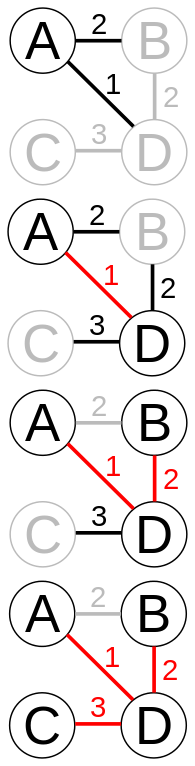
На иллюстрации красным цветом выделены рёбра, уже вошедшие в минимальный
остов, а чёрным – текущие кандидаты, из которых выбирается ребро с
минимальным весом.
Реализация алгоритма Прима
Будем искать вес минимального остовного дерева. Для нахождения ближайшей
вершины воспользуемся очередью с приоритетом (аналогично алгоритму Дейкстры),
в которой будем хранить пары (расстояние от остова до вершины, номер вершины).
Алгоритм Крускала
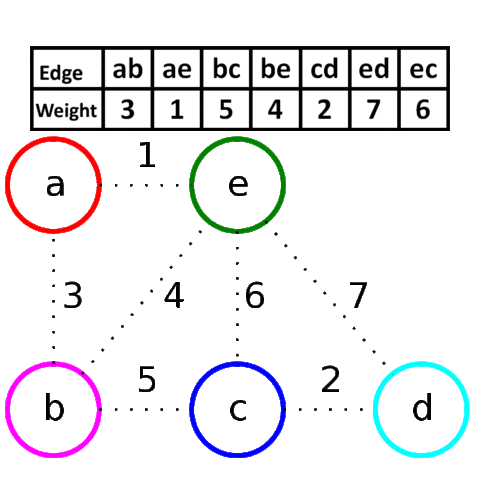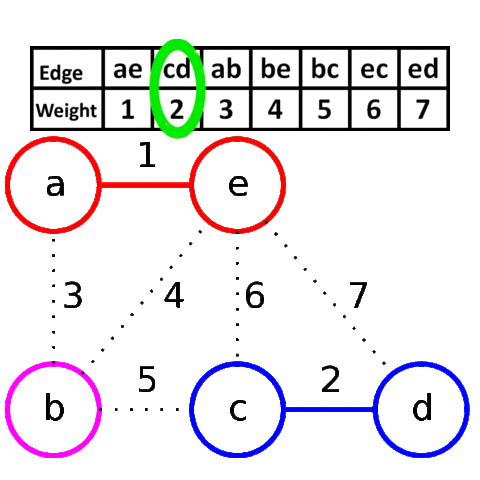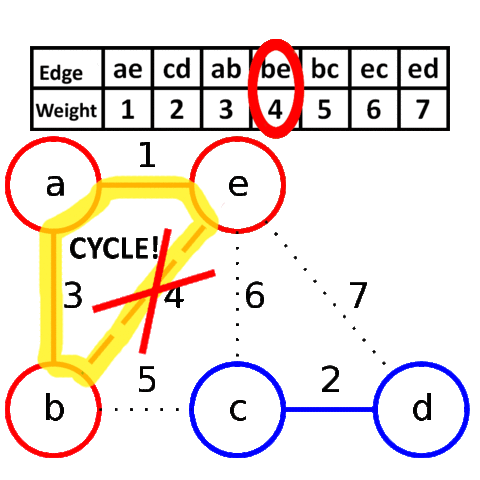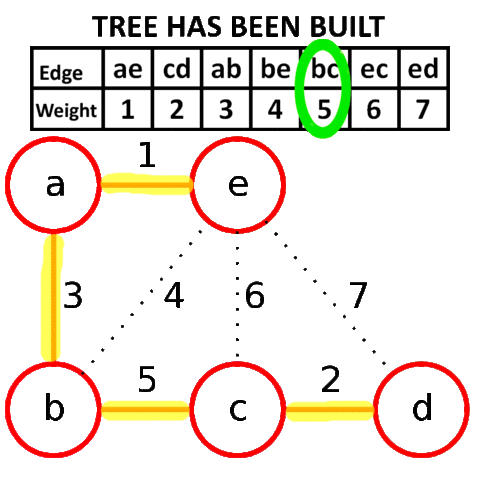
Алгоритм Крускала достаточно прост в своей идее и реализации. Он заключается
в сортировке всех рёбер в порядке возрастания длины, и поочерёдному добавлению
их в минимальный остов, если они соединяют различные компоненты связности.Более формально: пусть мы уже нашли некоторые рёбра, входящие в минимальный остов.
Утверждается, что среди всех рёбер, соединяющих различные компоненты связности,
в минимальный остов будет входить ребро с минимальной длиной.Для реализации алгоритма Крускала необходимо уметь сортировать рёбра по
возрастанию длины (для этого воспользуемся собственным типом данных) и проверять,
соединяет ли ребро две различных компоненты связности. Для этого будем
просто поддерживать текущие компоненты связности с помощью структуры данных DSU.Визуализация работы алгоритма Крускала:
Реализация алгоритма Крускала
Используем реализацию DSU со всеми оптимизациями из соответствующей лекции:
Различия в скорости работы
Хотя оба алгоритма работают за (O(M log N)), существуют константные различия
в скорости их работы. На разреженных графах (количество рёбер примерно равно
количеству вершин) быстрее работает алгоритм Крускала, а на насыщенных (количество
рёбер примерно равно квадрату количеству вершин) – алгоритм Прима (при
использовании матрицы смежности).На практике чаще используется алгоритм Крускала.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 ноября 2020 года; проверки требуют 5 правок.
Минимальное остовное дерево (или минимальное покрывающее дерево) в (неориентированном) связном взвешенном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.
Пример[править | править код]
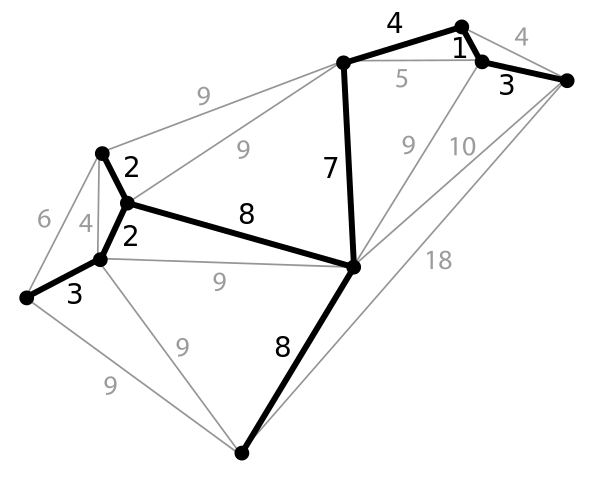
Пример минимального остовного дерева в графе. Числа на ребрах обозначают вес ребер.
Задача о нахождении минимального остовного дерева часто встречается в подобной постановке: допустим, есть n городов, которые необходимо соединить дорогами так, чтобы можно было добраться из любого города в любой другой (напрямую или через другие города). Разрешается строить дороги между заданными парами городов и известна стоимость строительства каждой такой дороги. Требуется решить, какие именно дороги нужно строить, чтобы минимизировать общую стоимость строительства.
Эта задача может быть сформулирована в терминах теории графов как задача о нахождении минимального остовного дерева в графе, вершины которого представляют города, рёбра — это пары городов, между которыми можно проложить прямую дорогу, а вес ребра равен стоимости строительства соответствующей дороги.
Алгоритмы[править | править код]
Существует несколько алгоритмов для нахождения минимального остовного дерева. Некоторые наиболее известные из них перечислены ниже:
- Алгоритм Прима,
- Алгоритм Краскала (или алгоритм Крускала),
- Алгоритм Борувки,
- Алгоритм обратного удаления (получение минимального остовного дерева из связного рёберно взвешенного графа).
Родственные задачи[править | править код]
На задачу о нахождении минимального остовного дерева похожа задача о дереве Штейнера. В ней задано несколько точек на плоскости и требуется проложить между ними граф путей так, чтобы минимизировать сумму длин путей. Главное отличие от задачи о минимальном остовном дереве при этом заключается в том, что разрешается добавлять дополнительные точки ветвления с целью ещё сильнее уменьшить сумму длин рёбер. Задача о дереве Штейнера является NP-полной.
Литература[править | править код]
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Глава 23. Минимальные остовные деревья // Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4.
Дерево
– это граф без циклов.
Понятие дерева
широко используется во многих областях
математики и информатики. Например, как
инструмент при вычислениях, как удобный
способ хранения данных, способ сортировки
или поиска данных.
Достаточно
развитое генеалогическое дерево образует
дерево.
Типичное
частичное организационное дерево для
университета.
Если
дерево имеет хотя бы одно ребро, оно
имеет две вершины со степенью 1. Вершины
со степенью 1 называются листьями.
Другие вершины называются внутренними
вершинами.
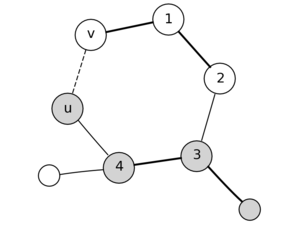
Предположим, что
дерево представляет физический объект,
подвижный в вершинах, и подвесим дерево
за одну из его вершин:
Если
подвесить за вершину V3
или V4
Вершина
в верхней части называется корнем
дерева, если корень определен, то дерево
называется корневым.
При необходимости корневое дерево Т
можно заменить на ориентированное
корневое дерево Т’,
порожденное корневым деревом Т.
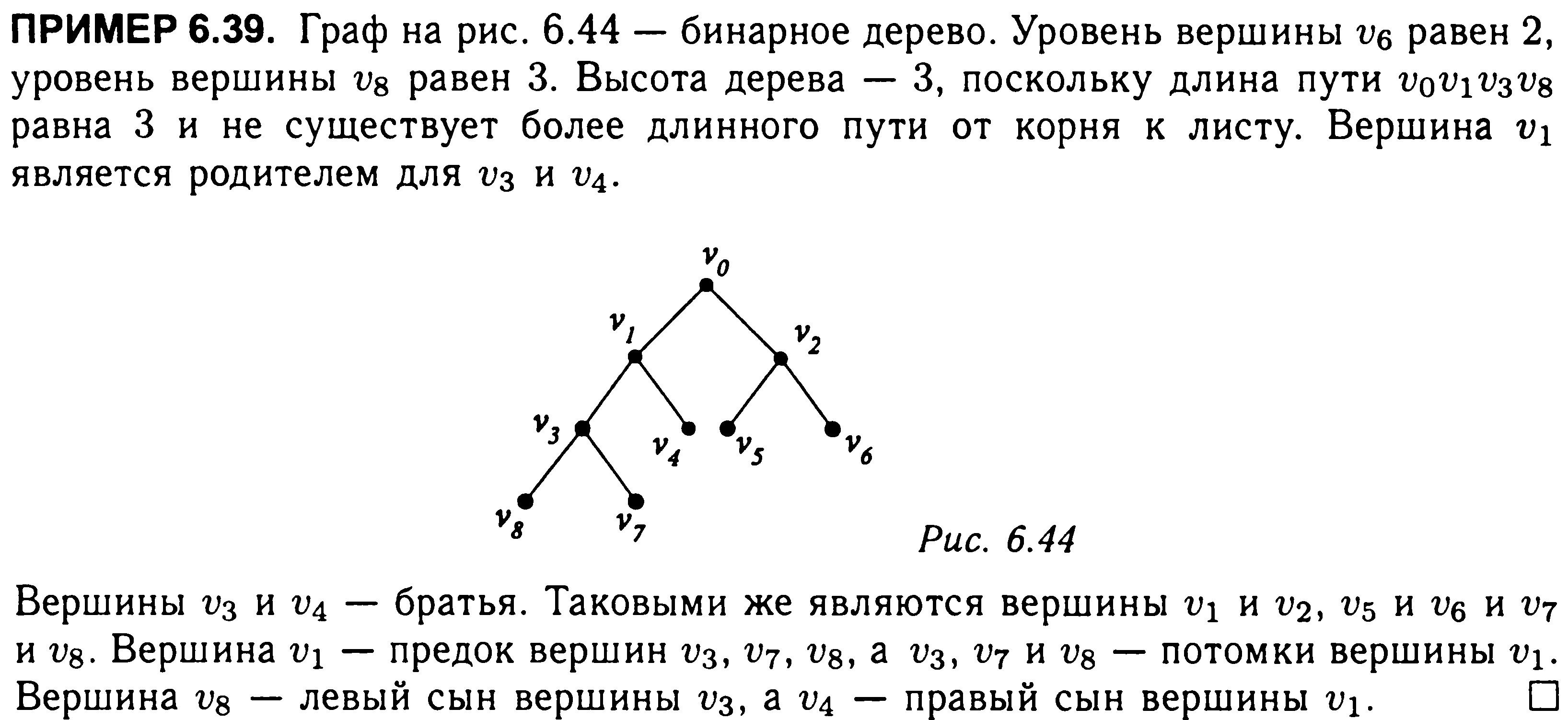
Если корень выбран,
уровень
вершины V
определяется длиной единственного пути
из корня в вершину V.
Высотой
дерева называется длина самого длинного
пути от корня дерева до листа.
Если рассматривается
корневое
ориентированное дерево Т’,
порожденное данным корневым деревом
Т, тогда вершина u
называется родителем
вершины v;
a v
называется сыном вершины u,
если существует ориентированное ребро
из u
в v.
Если u
— родитель v
и v1,
тогда v и
v1
называются братьями.
Если существует
ориентированный путь из вершины u
в вершину v,
тогда u
называется предком
вершины v,
a v
называется потомком
вершины u.
Если наибольшая
из степеней выхода для вершин дерева
равна m,
тогда дерево называется m
– арным
деревом.
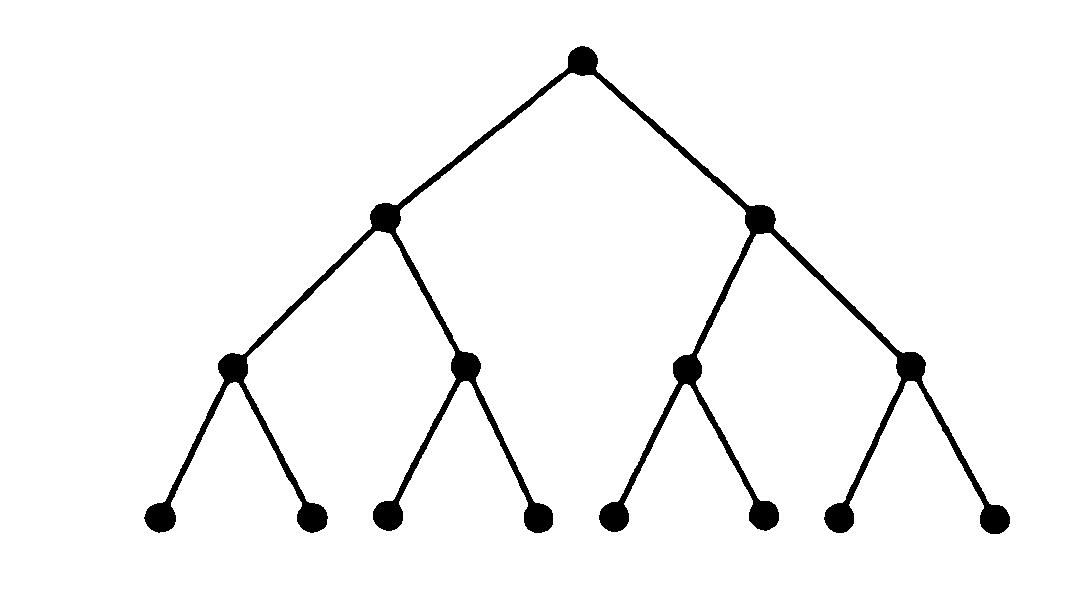
В частном случае,
когда m
= 2, дерево называется бинарным
деревом.
В каждом бинарном
дереве каждый сын родителя обозначается
либо как левый сын, либо как правый сын
(но не то и другое одновременно).
Связный
граф G(V,E),
не имеющий циклов, называется деревом.
ТЕОРЕМА (основные свойства
деревьев):
Пусть граф G(V,E)
имеет n
вершин. Тогда следующие утверждения
эквивалентны:
-
G
является деревом; -
G
не содержит циклов и имеет n-1
рёбер; -
G
связен и имеет n-1
рёбер; -
G
связен, но удаление ”
ребра нарушает связность; -
”
две вершины графа G
соединены ровно одним путём; -
G
не имеет циклов, но добавление ”
ребра порождает ровно один цикл.
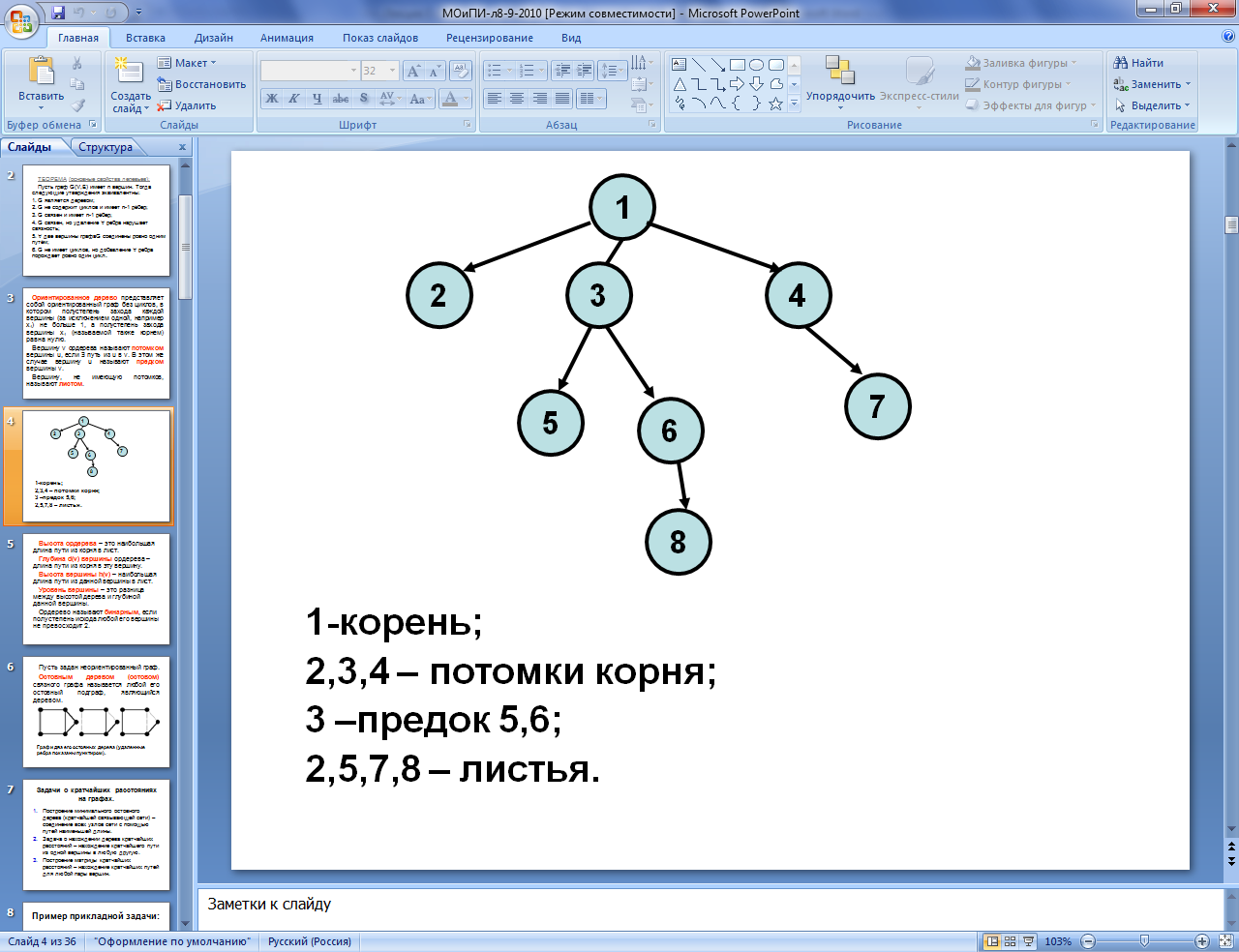
Ориентированное
дерево
представляет собой ориентированный
граф без циклов, в котором полустепень
захода каждой вершины (за исключением
одной, например v1)
не больше 1, а полустепень захода вершины
v1
(называемой также корнем)
равна нулю.
Вершину v
ордерева называют потомком
вершины u,
если $
путь из u
в v.
В этом же случае вершину u
называют предком
вершины v.
Вершину, не имеющую
потомков, называют листом.
Высота ордерева
– это наибольшая длина пути из корня
в лист.
Уровень вершины
ордерева – длина пути из корня в эту
вершину.
Ордерево называют
бинарным,
если полустепень исхода любой его
вершины не превосходит 2.
Пусть задан
неориентированный граф.
Остовным деревом
(остовом)
связного графа называется любой его
остовный подграф, являющийся деревом.
Граф и два его
остовных дерева (удаленные ребра
показаны пунктиром).
Задачи о кратчайших
расстояниях на графах.
-
Построение
минимального остовного дерева
(кратчайшей связывающей сети) –
соединение всех узлов сети с помощью
путей наименьшей длины. -
Задача
о нахождении дерева кратчайших
расстояний – нахождение кратчайшего
пути из одной вершины в любую другую. -
Построение
матрицы кратчайших расстояний –
нахождение кратчайших путей для любой
пары вершин.
Необходимо
проложить линии коммуникаций (дороги,
линии связи, электропередач и т.п.) между
n
заданными “точечными” объектами,
при условии:
во-первых,
известны “расстояния” между каждой
парой объектов (это может быть
геометрическое расстояние или стоимость
прокладки коммуникаций между ними),
во-вторых,
объекты могут быть связаны как
непосредственно, так и с участием
произвольного количества промежуточных
объектов.
При допущении,
что разветвления возможны только в
этих же n
объектах, задача сводится к нахождению
кратчайшего остовного дерева (SST –
shortest spanning tree, или MST – minimal spanning tree) во
взвешенном графе, вершины которого
соответствуют заданным объектам, а
веса ребер равны “расстояниям”
между ними.
Определение.
Вес
остовного
дерева взвешенного графа G
равен сумме весов, приписанных ребрам
остовного дерева. Будем обозначать
(T).
Минимальным
остовным деревом
(МОД) называется такое остовное дерево
графа G,
что вес T
меньше или равен весу любого другого
остовного дерева графа G.
Вес минимального остовного дерева
будем обозначать min(T).
Задача 1:
найти кратчайшее остовное дерево
(минимальный покрывающий остов)
взвешенного графа.
Пусть дан
неориентированный связный граф со
взвешенными ребрами. Вес ребра (xi,xj)
обозначим cij.
Из всех остовов графа необходимо найти
один, у которого сумма весов на ребрах
наименьшая.
Стоимость остовного
дерева вычисляется как сумма стоимостей
всех рёбер, входящих в это дерево.
Построение остова
графа G,
имеющего наименьший вес, имеет широкое
применение при решении некоторого
класса задач прикладного характера.
Например:
Пусть, например,
G=(V,
E,
)
служит моделью железнодорожной сети,
соединяющей пункты v1,
v2,
…, vnV,
а (vi,
vj)
– расстояние между пунктами vi
и vj.
Требуется проложить
сеть телеграфных линий вдоль
железнодорожной сети так, чтобы все
пункты v1,
v2,
…, vn
были связаны между собой телеграфной
сетью, протяженность которой была бы
наименьшей.
Рассмотрим два
способа построения минимального
остовного дерева взвешенного графа:
алгоритм Крускала и алгоритм Прима.
Алгоритм
Крускала:
1) Выбрать в графе
G
ребро e
минимального веса, не принадлежащее
множеству E
и такое, что его добавление в E
не создает цикл в дереве T.
2) Добавить это
ребро во множество ребер E.
3) Продолжить,
пока имеются ребра, обладающие указанными
свойствами.
Пример.
Для данного взвешенного графа найти
минимальное корневое остовное дерево,
используя алгоритм Крускала. Определить
высоту построенного дерева.
Алгоритм
Крускала.
Выбираем
ребро с минимальным весом. Это ребро,
(,
)
с весом, равным 4.
Пусть
вершина
будет корнем дерева. Далее выбираем
ребра, инцидентные вершинам
,
и имеющие минимальный вес.
Это
ребро (,
)
с весом 5. Затем к вершине
присоединяем ребро (,
)
с весом 7.
Далее,
добавляем ребро (,
)
с весом 7 и ребро (,
)
с весом 6.
Минимальный
вес построенного дерева равен:
min(T)=4+5+7+7+6=29.