Полное условие задачи
Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Шар наполняют гелием при нормальном атмосферном давлении. Определите минимальную массу оболочки, при которой шар начнет поднимать сам себя. Температура гелия и окружающего воздуха одинакова и равна 0 °С.
Краткое условие задачи
Решение задачи
Запишем второй закон Ньютона в векторной форме:
Перепишем его в проекциях на вертикальную ось OY:
или
Распишем силы, входящие в выражение (1). Сила Архимеда равна:
Объем шара равен:
Тогда:
Сила тяжести, действующая на гелий равна:
Подставляем формулу для объема шара и получим:
Сила тяжести, действующая на оболочку равна:
Площадь сферы находим по следующей формуле:
Тогда:
С учетом выражений (2), (3) и (4) перепишем выражение (1):
Выразим из последнего выражения радиус шара. Для этого разделим обе стороны уравнения на величину:
и получим:
Плотности гелия и воздуха получим из уравнения состояния идеального газа:
Так как
то
или
откуда находим плотность:
Плотность гелия:
Плотность воздуха:
Таким образом, радиус шара равен:
Находим теперь массу оболочки шара:
Подставляем данные и находим численный результат:
Ответ: 93 кг.
Пример заполнения шаров различными газами
Рассмотрим движение тел, погруженных в газ. Так как сила Архимеда действует на тела, не только погруженные в жидкость, но и в газ, то, используя её действие, можно сконструировать, по аналогии с водными судами, и летательные аппараты, например воздушные шары.
Для воздухоплавания необходимо, чтобы выталкивающая «архимедова сила» была больше силы тяжести. Попробуем отпустить два воздушных шарика: один из них опустился на землю, а второй устремился в небо. Почему? Воздушные шары делают из прочной оболочки, а внутренность наполняют газом. Для того чтобы шар поднимался в небо, плотность этого газа должна быть меньше плотности воздуха. Это может быть гелий, водород или тёплый нагретый воздух.
Объяснение подъемной силы шара
То есть можно подобрать сочетание выталкивающей силы и силы тяжести, чтобы шар как бы завис в воздухе. Воздушный шар может поднимать в небо различные грузы: кабину, людей, разные приборы, таким образом, шар может поднять в воздух вес груза, называемый подъемной силой шара. Для того чтобы рассчитать подъёмную силу шара, нам необходимо вспомнить некоторые понятия.
Формулы расчета подъемной силы
Итак, вес газа мы можем рассчитать по формуле: Pг = mг ∙ g, масса газа, умноженная на свободное падение.
Необходимо также помнить, что масса газа рассчитывается следующим образом: mг = ϱ ∙ V, плотность газа, умноженная на объём оболочки шара.
Получается, что для расчета веса газа мы должны умножить плотность газа на ускорение свободного падения и на объём: Pг = ϱг ∙ g ∙V.
Также необходимо вспомнить, что сила Архимеда рассчитывается по формуле: Fа = ϱв ∙ g ∙ V, плотность воздуха, в который погружён шар, на ускорение свободного падения и на объём шара.
Вес шара будет складываться из веса газа, заполняющего оболочку, и веса самой оболочки: Pш= Pг+ Pо.
Итак, для того чтобы рассчитать подъемную силу шара, нам необходимо из величины силы Архимеда вычесть вес шара Fпод = Fа– Pш.
Решение задачи
Рассмотрим решение задачи:
Радиозонд объёмом 10 кубических метров заполнен газом, плотность которого составляет 0,09 кг на метр кубический. Необходимо найти вес аппаратуры, который может поднять этот радиозонд, если известно, что вес оболочки радиозонда составляет 6 ньютонов. Запишем краткое условие задачи:
V = 10 м3
ϱг = 0,09 кг/ м3–плотность газа, которым заполнена оболочка 0,09 кг на метр кубический
ϱв = 1,29 кг/ м3– табличные данные плотности воздуха – 1,29 кг на метр кубический
P0 = 6 H – вес оболочки 6 Н
———————-
Fпод= ? – найти вес аппаратуры, численно он будет равен подъёмной силе радиозонда.
Итак:
Для расчета подъёмной силы нам необходимо из силы Архимеда вычесть вес шара, Fпод = Fа– Pш , который будет состоять из веса газа, заполнившего оболочку, плюс вес самой оболочки Pш= Pг+ Pо .
А для расчета силы Архимеда понадобится: Fа = ϱв ∙ g ∙ V.
Необходимо помнить, что вес газа рассчитывается по формуле: Pг = ϱг ∙ g ∙ V.
Получим конечную формулу, подставив все выражения в исходную:
![]() ,
,
подставим числовые данные:
![]()
Ответ: Fпод = 114 Н
Подъёмная сила радиозонда составит 114 Н, это и есть вес аппаратуры, который может поднять этот радиозонд.
Развитие воздухоплавания
В заключение хочется отметить, что люди мечтали подняться под облака с древних времен. Международным сообществом признано, что первым это удалось французским изобретателям – братьям Монгольфье в 1783 году. Они сделали огромный шар из бумаги, наполнили его горячим воздухом, и эксперимент состоялся. Именно этот опыт положил начало развития воздухоплавания.
Впоследствии появились и другие воздушные аппараты: аэростаты, дирижабли, и по сей день в небо поднимаются шары и зонды, которые исследуют верхние слои атмосферы. Воздухоплавание на сегодняшний день не только развлечение и не только спорт, но и инструмент научных исследований.
Список литературы
- Перышкин А. В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
- Перышкин А. В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
- Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «Files.school-collection.edu.ru» (Источник)
- Интернет-портал «Class-fizika.narod.ru» (Источник)
Домашнее задание
- Тело, находящееся внутри воды, выталкивается с силой 2 Н. С какой силой это тело будет выталкиваться керосином, плотность которого – 0,8 г/см3?
- В сосуд прямоугольной формы с площадью дна 20 х 30 см налит керосин до высоты 50 см. Определите массу и давление керосина на дно.
- Дать определение «архимедовой силе».
Максим
Ученик
(226),
на голосовании
10 лет назад
Наполненный водородом воздушный шар объемом 0,2 м^3 находится во взвешенном состоянии в воздухе плотностью 1,45 кг/м^3
Дополнен 10 лет назад
Помогите пожалуйста
Голосование за лучший ответ
Алина Александровна Фетисова
Знаток
(346)
10 лет назад
Плотность воздуха ρ при нормальных условиях – температура t = 0 C (273 К) и атмосферное давление P = 101 325 Па) равна 1,29 кг/м3.
PV = (m/M)RT,
M = mRT/(PV) = ρRT/P = 1,29 *8,31 * 273/ 101325 = 0,029 кг/моль или 29 г/моль
То есть, чтобы получить молярную массу воздуха, надо умножить плотность воздуха на газовую постоянную и температуру (К) и разделить на давление.
Баканина Л.П. Задачи о воздушных шарах // Квант. — 1975. — № 1. — С. 60-63.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В наш век самолетов и ракет, для которых доступны любые высоты над поверхностью Земли, воздушные шары, громоздкие, ненадежные и неуправляемые, уже отошли в прошлое, хотя когда-то именно они дали человеку возможность подняться в воздух. Впрочем, в некоторых случаях воздушные шары очень удобны, они используются и сейчас. Например, с аэростата удобно обучать прыжкам с. парашютом, а метеорологи исследуют давление, температуру и воздушные потоки в атмосфере с помощью шаров-зондов.
Задачи о воздушных шарах даются иногда на вступительных экзаменах. Обычно их можно разделить на два типа:
1) задачи, в которых нужно найти связь между габаритами и наполнением шара и подъемной силой, действующей на шар у поверхности Земли;
2) задачи, в которых нужно определить максимальную высоту подъема шара; при этом задается какая-нибудь модель атмосферы, то есть закон изменения давления и температуры с высотой.
По существу, задачи обоих типов – это задачи на статику. Для их решения нужно уметь применять уравнение состояния газов и найти условие равновесия шара, на который действует сила притяжения Земли и выталкивающая сила со стороны окружающего шар воздуха. Если выталкивающая сила больше силы притяжения (разность этих сил называют подъемной силой), шар поднимается вверх. Но по мере подъема уменьшается плотность окружающего воздуха, а, следовательно, уменьшается и выталкивающая сила, по закону Архимеда равная
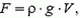
где ρ — плотность воздуха, а V — объем шара. На некоторой высоте выталкивающая сила окажется равной силе притяжения – это и будет максимальной высотой подъема шара.
Разберем теперь несколько конкретных задач, которые в разные годы предлагались на вступительных экзаменах в Московский физико-технический институт.
Задача 1. Сферическая оболочка воздушного шара сделана из материала, квадратный метр которого имеет массу b = 1 кг/м2. Шар наполнен гелием при нормальном атмосферном давлении. При каком минимальном радиусе шар поднимает сам себя? Температура гелия и температура окружающего воздуха одинаковы и равны 0 ºС. Молекулярная масса воздуха 29 кг/кмоль, молекулярная масса гелия 4 кг/кмоль.
При увеличении радиуса шара выталкивающая сила растет пропорционально кубу радиуса, а вес оболочки – пропорционально квадрату радиуса. Следовательно, выталкивающая сила растет быстрее и, начиная с какого-то значения радиуса, станет больше, чем вес оболочки. Тогда шар начнет подниматься. Обозначим этот радиус оболочки через r. При этом
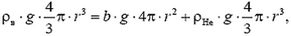
откуда
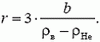
Плотности воздуха ρв и гелия ρНе при данных условиях найдем с помощью закона Менделеева–Клапейрона 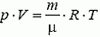 :
:
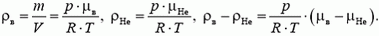
Окончательно получаем
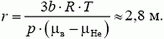
Задача 2. Объем воздушного шара равен V = 230 м3, масса оболочки М = 145 кг. Шар наполнен горячим воздухом при нормальном атмосферном давлении. Какую температуру должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Температура наружного воздуха t0 = 0 оС.
При нагревании воздуха его плотность уменьшается, так как 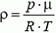 (см. задачу 1). Шар начнет подниматься, если
(см. задачу 1). Шар начнет подниматься, если 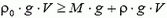 (ρ0 – плотность наружного воздуха). Подставляя выражения для плотности наружного воздуха и воздуха внутри шара ρ, получаем
(ρ0 – плотность наружного воздуха). Подставляя выражения для плотности наружного воздуха и воздуха внутри шара ρ, получаем
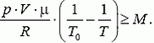
Отсюда
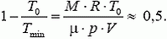
значит,
Tmin » 2T0 = 546 ºK = 273 ºC.
Задача 3. Для удержания на поверхности Земли метеорологического шара-зонда с массой М = 20 кг необходимо приложить силу F = 1000 Н. Шар поднимается до такой высоты, где его объем увеличивается в два раза. Температура воздуха, измеренная на этой высоте с помощью зонда, оказалась равной t = –43 ºС. Вычислить давление воздуха на этой высоте, если на поверхности Земли давление р0 = 754 мм рт. ст., а температура t0= +17 °С.
Условие равновесия шара у поверхности Земли записывается так:
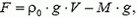 (1)
(1)
где V — объем шара у поверхности Земли, а 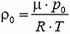 — плотность воздуха. При этом масса шара М включает в себя массу оболочки, приборов и газа, заключенного внутри оболочки. Из условия известно, что объем шара при подъеме увеличивается. Следовательно, оболочка шара мягкая и герметичная. Объем увеличивается потому, что при мягкой оболочке давление газа внутри должно быть таким же, как давление окружающего воздуха, которое уменьшается с высотой. Если оболочка герметичная, масса шара не изменяется при подъеме и максимальная высота его подъема определяется условием
— плотность воздуха. При этом масса шара М включает в себя массу оболочки, приборов и газа, заключенного внутри оболочки. Из условия известно, что объем шара при подъеме увеличивается. Следовательно, оболочка шара мягкая и герметичная. Объем увеличивается потому, что при мягкой оболочке давление газа внутри должно быть таким же, как давление окружающего воздуха, которое уменьшается с высотой. Если оболочка герметичная, масса шара не изменяется при подъеме и максимальная высота его подъема определяется условием
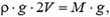 (2)
(2)
где 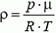 . Решая совместно уравнения (1) и (2), находим
. Решая совместно уравнения (1) и (2), находим
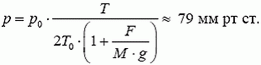
Задача 4. Шар-зонд, наполненный водородом, имеет герметичную оболочку постоянного объема V = 50 м3. Масса шара вместе с водородом М = 5 кг. Определить, на какую максимальную высоту он сможет подняться, если известно, что атмосферное давление уменьшается в два раза через каждые h = 5 км высоты. Температура в стратосфере t = –60 ºС. Молекулярная масса воздуха 29 кг/кмоль. Давление у поверхности Земли р0 = 1 атм.
На максимальной высоте выталкивающая сила равна весу шара- зонда:
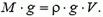
Выразив плотность окружающего воздуха через давление и температуру, получим
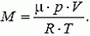
Таким образом, давление воздуха на этой высоте равно
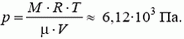
Посмотрим теперь, во сколько раз давление р меньше давления у поверхности Земли р0: 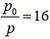 .
.
Из условия известно, что давление падает в два раза через каждые 5 км подъема, то есть 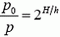 , где Н — высота подъема, a h = 5 км. В нашем случае
, где Н — высота подъема, a h = 5 км. В нашем случае
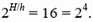
Отсюда
H = 4h = 20 км.
Задача 5. Нерастяжимая оболочка шара-зонда объема V = 75 м3 имеет в нижней части небольшое отверстие. Масса оболочки t = 7 кг. Шар наполнен водородом. Определить, на какую максимальную высоту сможет подняться этот шар-зонд, если известно, что атмосферное давление уменьшается в два раза через каждые h = 5 км высоты. Температура воздуха в стратосфере t = –60 °С, температура водорода равна температуре окружающего воздуха. Давление у поверхности Земли р0 = 1 атм.
Эта задача отличается от предыдущей тем, что оболочка шара не герметична, а имеет отверстие. Следовательно, давление внутри шара все время равно давлению в атмосфере, и по мере увеличения высоты подъема шара водород вытекает из отверстия. Будем, считать, что подъем происходит достаточно быстро и можно пренебречь диффузией воздуха внутрь оболочки, тогда условие равновесия шара на максимальной высоте
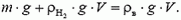
Плотности водорода и воздуха можно найти из уравнения Менделеева-Клапейрона:
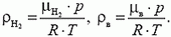
Таким образом, давление на максимальной высоте
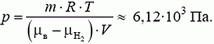
Отношение 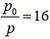 , и, следовательно, высота подъема Н = 20 км (см. решение предыдущей задачи).
, и, следовательно, высота подъема Н = 20 км (см. решение предыдущей задачи).
Высота подъема в задаче 5 получилась такая же, как для герметичного шара в задаче 4, но не следует забывать, что мы рассматривали разные шары, с разными объемами и массами. А если оба шара совершенно одинаковы и отличаются только тем, что у одного оболочка герметичная, а у другого имеет отверстие, — какой из шаров поднимется выше в этом случае?
Выталкивающая сила будет одинакова для обоих шаров, так как их объемы равны. Если начальные массы шаров были одинаковы, то после подъема шар с отверстием окажется легче, так как часть наполняющего его газа вытечет при подъёме. Следовательно, шар с отверстием сможет подняться на большую высоту.
Обычно человеку, впервые задумавшемуся над этим вопросом, такой результат кажется странным. Часто задают вопрос: «Как вообще в шаре с отверстием возникает подъемная сила? Ведь снизу, там, где отверстие, воздух и газ внутри шара находятся в равновесии».
Давайте рассмотрим верхнюю точку шара. Если в нижней точке шара давление воздуха и газа равно р0, в верхней точке давление воздуха 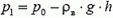 , а давление газа
, а давление газа 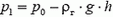 (h — высота шара). Если
(h — высота шара). Если 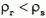 , то
, то 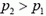 и, следовательно, на оболочку снизу действует большая сила, чем сверху — возникает подъемная сила. Легко убедиться (вы сможете это сделать сами для тела достаточно простой формы), что именно эта разница давлений и дает результирующую выталкивающую силу, определяемую законом Архимеда. Недоумение часто возникает потому, что при расчетах плотности газа внутри шара обычно считают давление в шаре всюду одинаковым. Не нужно забывать, что это всего лишь приближение. Если мы определяем саму величину
и, следовательно, на оболочку снизу действует большая сила, чем сверху — возникает подъемная сила. Легко убедиться (вы сможете это сделать сами для тела достаточно простой формы), что именно эта разница давлений и дает результирующую выталкивающую силу, определяемую законом Архимеда. Недоумение часто возникает потому, что при расчетах плотности газа внутри шара обычно считают давление в шаре всюду одинаковым. Не нужно забывать, что это всего лишь приближение. Если мы определяем саму величину
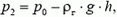
то, так как h мало — всего несколько метров, 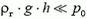 , и мы можем считать
, и мы можем считать 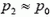 . Если же нас интересует разность
. Если же нас интересует разность
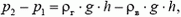
то здесь оба члена одинаковы по порядку величины, и учитывать их надо оба. Кстати сказать, то, что мы считаем ρв и ρг постоянными, — тоже приближение, на самом деле они уменьшаются с высотой по мере уменьшения давления. Но учет этого обстоятельства дал бы значительно меньшую поправку к выталкивающей силе, этой поправкой можно пренебречь.
Упражнения
1. Определить подъемную силу воздушного шара, в котором находится t г водорода. Оболочка шара герметичная и сделана из легкого неупругого материала, который может свободно растягиваться.
2. На сколько градусов надо нагреть воздух внутри сообщающегося с атмосферой воздушного шара, сферическая оболочка которого имеет диаметр 10 м и весит 10 кг, для того чтобы шар взлетел? Атмосферное давление 735 мм. рт. ст., температура окружающего воздуха +27 °С.
3. Воздушный шар представляет собой баллон постоянного объема, наполненный гелием. Через отверстие в нижней части шар сообщается с атмосферой. Как изменится максимальная высота подъема шара, если гелий нагреть до температуры t1? Температуру атмосферы считать постоянной и равной t0, а давление изменяющимся по закону 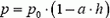 , где а — постоянная, h — высота подъема, р0 — давление у поверхности Земли.
, где а — постоянная, h — высота подъема, р0 — давление у поверхности Земли.
Ответы.
1. 13,5m·g.
2. Не менее чем на 5º.
3. 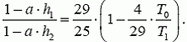 .
.
Содержание:
- § 1 Первый воздушный шар
- § 2 Движение воздушного шара
- § 3 Пример решения задачи на определение подъемной силы воздушного шара
- § 4 Конструкция воздушного шара
- § 5 Краткие итоги по теме урока
§ 1 Первый воздушный шар

Еще на заре цивилизации, наблюдая за полетом птиц, люди мечтали так же свободно парить в воздухе. Истории известны попытки создать разные летательные аппараты. В 1783 году был запущен воздушный шар, созданный братьями Монгольфье во Франции. Он был сделан из двух сшитых кусков ткани и наполнен теплым воздухом и дымом. Шар поднялся на высоту 300 метров и продержался в воздухе 10 минут, пролетев расстояние около километра. Сейчас воздушные шары наполняют водородом или гелием, оболочку шара делают из легких, прочных, морозоустойчивых, огнестойких материалов.
§ 2 Движение воздушного шара
Известно, что на тела, погруженные в жидкость или газ, действует выталкивающая – архимедова сила. Для того чтобы шар поднялся в воздух, нужно, чтобы архимедова сила была больше силы тяжести. Плотность теплого воздуха, плотность водорода, гелия меньше плотности окружающего шар воздуха, поэтому шар поднимается вверх. По мере поднятия плотность атмосферного воздуха уменьшается и архимедова сила, действующая на шар, становится меньше. Шар постепенно достигает максимальной высоты полета.
Воздушный шар может не только сам подниматься вверх, но и поднять груз: людей, приборы для проведения исследований и пассажиров. Сколько груза может поднять воздушный шар? Для этого нужно определить его подъемную силу.
§ 3 Пример решения задачи на определение подъемной силы воздушного шара
З А Д А Ч А :Запущен воздушный шар объемом 40 м3, наполненный гелием. Масса оболочки шара составляет 10 кг. Рассчитать подъемную силу шара.

По условию задачи И З В Е С Т Н О :
– объем шара V= 40 м3,
– плотность гелия ρ гелия =0,19 кг/м3,
– плотность воздуха ρ воздуха =1,29 кг/м3,
– масса оболочки шара m = 10 кг.
Н А ЙТ И :подъемную силу F подъемн.
Р Е Ш Е Н И Е :На шар действуют две силы: сила тяжести и архимедова сила. Архимедову силу определим по формуле: Fa = g ⋅ ρ воздуха ⋅ Vшара
Подставим числовые значения и вычислим: Fa = 516 Н.
Из-за действующей силы тяжести шар обладает весом. Вес шара складывается из веса гелия, которым шар наполнен, и веса оболочки. Вес гелия определим по формуле mg, где масса гелия равна произведению его плотности на объем шара. Подставив числовые значения, получим
76 Н. Итак, вес гелия 76 Н.
![]()
Вес оболочки также определим по формуле mg, что составит 100 Н.
![]()
Видим, что архимедова сила значительно больше веса воздушного шара, поэтому шар поднимается вверх. Подъемная сила шара равна разности между архимедовой силой и весом шара и составляет 340 Н.
Fподъемн. = Fa – (P гелия+ Pоболочки) = 516 Н – (76 Н + 100 Н) = 340 Н

§ 4 Конструкция воздушного шара
Шар такого же объема, но наполненный водородом, может поднять груз большей массы, так как плотность водорода меньше плотности гелия. Но воздушные шары обычно наполняют гелием, так как он не горит и потому безопаснее. Водород – горючий газ, он может взорваться.
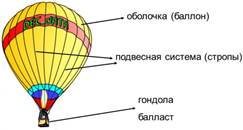
Воздушные шары, наполненные теплым воздухом, удобны тем, что можно регулировать высоту подъема шара, изменяя температуру воздуха внутри шара, при этом меняется его плотность, следовательно, объем шара и архимедова сила. Для этого под отверстием в нижней части шара помещают газовую горелку. Если сильно нагреть газ, то шар поднимается выше. Если уменьшить пламя горелки, то воздух внутри шара остывает и шар опускается вниз.
Для увеличения высоты подъема воздушного шара, наполненного водородом или гелием, с шара скидывают специально взятый груз – балласт. Для спуска шара из его оболочки выпускают часть газа, для этого служит специальный клапан.

В горизонтальном направлении воздушный шар перемещается под действием ветра, поэтому он называется аэростатом (от греческих слов аэр – воздух, стато – стоящий). Для исследования верхних слоев атмосферы служат стратостаты. Управляемые аэростаты – дирижабли – применялись для перевозки пассажиров и грузов по воздуху.
Воздушные шары используются для метеонаблюдений, изучения потоков воздуха в атмосфере, географических, биологических исследований в нижних слоях атмосферы. Аэростаты и дирижабли в настоящее время широко применяются в рекламных целях. Большой интерес вызывают соревнования по полету на воздушных шарах.
§ 5 Краткие итоги по теме урока
Аэростат – летательный аппарат легче воздуха, использующий для полёта подъёмную силу заключённого в оболочке газа, плотность которого меньше, чем плотность окружающего воздуха.
Подъемная сила аэростата равна разности между архимедовой силой и весом шара (газа и оболочки).
Управляемые аэростаты называются дирижаблями.
Аэростаты используются для метеонаблюдений, географических, биологических исследований в нижних слоях атмосферы, в рекламных целях.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября», 2002. – 272 с.
Использованные изображения:
