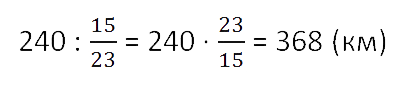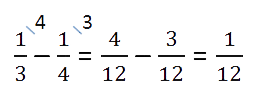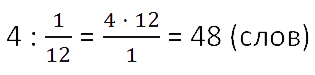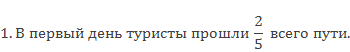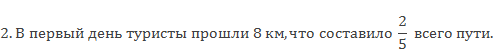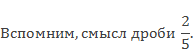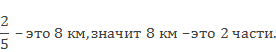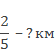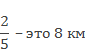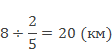Если известно сколько составляет часть от целого, то по известной части можно “восстановить”
целое.
Для этого пользуемся правилом нахождения целого (числа)
по его дроби (части).
Запомните!
Чтобы найти число по его части, выраженной дробью, нужно данное число
разделить на дробь.
Пример. Рассмотрим задачу.
Поезд прошёл 240 км, что составило
всего пути.
Какой путь должен пройти поезд?
Решение. 240 км — часть всего пути. Эти же километры
выражены дробью 15/23
от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части,
и 15 таких частей составляют 240 км
(числитель дроби равен 15).
Значит, можно найти, сколько составляет
часть пути.
240 : 15 = 16 (км)
Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью
.
Значит, чтобы найти весь путь (23 части, каждая из которых по
16 км) нужно:
16 · 23 = 368 (км)
Кратко запись решения такой задачи можно сделать следующим образом.
Ответ: поезд должен пройти 368 км.
Сложные задачи на нахождение числа по его части
Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.
Рассмотрим задачу.
При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?
Решение. Как обычно подчеркнём в условии задачи все важные данные.
Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.
Такую часть всех слов составляют 4 слова.
Итак, 4 слова — это
от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь
.
Ответ: всего 48 слов надо было выучить к диктанту.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
На уроке математики, на улице, в магазине, в быту и профессиональной деятельности, науке и технике часто приходится встречаться с дробями и решать различные задачи с ними.
Эта информация доступна зарегистрированным пользователям
Так, например, в кулинарии очень часто используют дробные числа, отмеряя те или иные ингредиенты в соответствии с рецептом: пол чайной ложки соли, треть стакана, четверть пачки, полкилограмма сахара и т.д.
Определяя время по часам, приходится находить часть от часа, от минуты, например, 30 минут равняется ½ часа, четверть часа (15 минут)- это ¼ часа, 30 секунд равняются ½ минуты, 15 секунд составляют ¼ минуты.
Эта информация доступна зарегистрированным пользователям
В медицине и фармацевтике используют дробные числа.
В состав лекарственного средства чаще всего включают дробное количество различных действующих и вспомогательных веществ.
Эта информация доступна зарегистрированным пользователям
Для корректного лечения врач устанавливает эффективную дозировку лекарственного препарата, которая иногда представлена в виде дробного числа.
Дозировку или концентрацию лекарственного средства приходится выражать в виде дроби: полтаблетки (1/2), четверть (1/4) таблетки и т.д.
Особенно важно учитывать количество медицинского препарата для пациентов детского возраста.
Часто дозировку лекарства для детей рассчитывают относительно взрослой дозы на основе данных о массе ребенка, количестве лет и др.
Обыкновенные дроби широко используются в строительстве и архитектуре.
Создавая надежную конструкцию, важно соблюдать соизмеримость и определенные соотношения частей сооружения.
Эта информация доступна зарегистрированным пользователям
Начертить чертеж, построить здание, возвести мост, положить асфальт, приготовить бетонную смесь невозможно без знаний о дробях.
В спортивных состязаниях вам, наверное, не раз приходилось слышать такие фразы: «состоялся четверть финал» или «полуфинал чемпионата», «одна восьмая финала».
Дроби используют в искусстве, например, в музыке, живописи и др.
Одним из примеров внедрения дробей в музыкальное искусство может служить нотная грамота.
Еще древнегреческий ученый Пифагор установил связь между длительностью музыкального звучания и дробей.
Дроби применяют для обозначения длительности нот.
Так, например, существует длинная нота.
Кроме нее есть половинная нота, четвертная, восьмая, шестнадцатая и т.д.
Эта информация доступна зарегистрированным пользователям
Такое обозначение нот удобно, так как явно видно насколько одна нота длиннее или короче другой.
Существует еще одна важная роль дробного числа в музыке.
Музыкальный размер (количество ритмических единиц в такте) так же обозначают в виде дроби (только без дробной черты) вначале нотной строки.
Эта информация доступна зарегистрированным пользователям
С помощью музыкального размера музыканты понимают с каким ритмом и темпом нужно играть музыкальное произведение.
В картографии и географии с помощью дроби указывают масштаб карты.
Деление целого на доли встречается в юридической практике при делении наследства.
В повседневной жизни мы часто делим целое на части, например, плитку шоколада ломаем на дольки, чтобы угостить друзей, режем на кусочки торт на празднике, делим мандарин на дольки и т.д.
Мы можем привести бесконечное множество примеров деления чего-либо на части.
Сегодня на уроке вспомним, что называют долей числа и, что представляет собой дробь от числа.
Эта информация доступна зарегистрированным пользователям
Научимся решать задачи, в которых необходимо находить часть от целого и целое по его части.
Рассмотрим алгоритм и примеры решения таких задач.
В математике дробью обозначают часть некоторой рассматриваемой величины, часть от целого.
Каждую равную часть одного целого называют долей числа.
Дробь представляет собой число, которое состоит из одной или нескольких долей (равных частей) целого.
Математическая запись обыкновенной дроби оформляется в виде двух чисел, разделенных чертой, которая называется дробной (она может быть горизонтальной и наклонной).
Число, стоящее над дробной чертой, называют числителем.
Числитель показывает, сколько долей взяли от целого.
Число, стоящее под дробной чертой, называют знаменателем.
Знаменатель показывает, на сколько всего равных долей разделили целое.
Зная целое, можно найти его часть.
Рассмотрим такую задачу.
Эта информация доступна зарегистрированным пользователям
Ленту, длиной 12 дм, разрезали на 2 равные части.
Что значит разрезать на две равные части?
Это значит, что ленту нужно разделить на две доли, каждая из которых является половиной этой ленты.
Эта информация доступна зарегистрированным пользователям
Итак, каждая доля- это половина всей ленты, по-другому такую часть от целого называют одна вторая часть ленты, обозначают ½.
В нашем примере половина всей ленты, т.е. одна вторая часть ее составляет 6 дм.
Запишем равенство: 12 ÷ 2 = 6 (дм).
Ленту такой же длины разделим на четыре равные части.
Эта информация доступна зарегистрированным пользователям
Получим 4 доли, каждая из которых равна одной четвертой всей длины ленты, обозначается 1/4.
Четверть (одна четвертая) ленты составляет: 12 ÷ 4 = 3 (дм).
Попробуем найти одну шестую ленты все той же длины- 12 дм.
Эта информация доступна зарегистрированным пользователям
1/6 доля этой ленты будет составлять: 12 ÷ 6 = 2 (дм).
Итак, нам становится ясно, чтобы найти долю от числа, необходимо разделить это число на количество долей (равных частей).
Рассмотрим ситуацию посложней.
Полоску бумаги, длиной 15 см, разделим на 5 равных частей (пять долей).
Эта информация доступна зарегистрированным пользователям
Определим, чему будет равны (mathbf{frac{3}{5}}) этой полоски бумаги.
Одна доля ((mathbf{frac{1}{5}}) этой полоски)- это 15 ÷ 5 = 3 (см).
Возьмем три таких доли.
Так как одна доля составляет 3 см, то три доли будут равны 3 ∙ 3 = 9 (см).
В данном случае получилось, что три пятых полоски бумаги составляют 9 см.
Сформулируем правило нахождения части от целого.
Чтобы найти несколько долей целого (дробь от числа), необходимо найти величину одной доли, затем умножить ее на количество долей.
Запишем алгоритм нахождения части от числа (несколько долей целого).
1. Найти величину одной доли.
2. Величину одной доли умножить на количество взятых долей.
В буквенном виде данное правило можно представить так:
Пусть А– это исходное число.
В– неизвестная часть числа А, выраженная дробью (mathbf{frac{m}{n}}).
m– числитель, показывает сколько долей взяли.
n– знаменатель, показывает на сколько долей разделили число А.
Чтобы найти часть числа А, необходимо это число А разделить на знаменатель (n) и умножить на числитель (m) дроби, которая выражает эту часть.
Эта информация доступна зарегистрированным пользователям
В качестве примера рассмотрим решение нескольких задач.
Задача №1.
Туристы за все время своего путешествия из пункта А в пункт В должны пройти 54 км.
Туристы прошли (mathbf{frac{1}{2}}) всего пути по лесу.
Сколько километров прошли туристы по лесу? Сколько им осталось пройти?
Решение:
Вспомним правило.
Чтобы найти долю от числа, необходимо число разделить на количество долей.
Прошли (mathbf{frac{1}{2}}) всего пути- это значит туристы преодолели половину своего пути.
Разделим весь путь на 2 равные доли, т.е. на 2, в результате получим (mathbf{frac{1}{2}}) пути, которую туристы прошли по лесу.
Этот путь будет составлять: 54 ÷ 2 = 27 (км).
Определим путь, который им осталось пройти, для этого из общего пути вычтем пройденный по лесу путь:
54 – 27 = 27 (км) туристам осталось пройти.
Ответ: 27 (км), 27 (км).
Задача №2
За три дня туристы прошли 54 километра.
За первый день они прошли половину всего пути.
За второй день преодолели (mathbf{frac{2}{3}}) оставшегося пути.
Сколько километров туристы прошли в каждый из трех дней?
Решение:
Весь трехдневный путь туристов составляет 54 км.
Первый день туристы прошли половину- это (mathbf{frac{1}{2}}) всего пути.
Выше в задаче №1 мы уже находили (mathbf{frac{1}{2}}) от 54 (км), у нас получился следующий результат:
54 ÷ 2 = 27 (км) прошли туристы в первый день.
Так как в первый день пройдена половина пути, то вторая половина- это оставшийся путь.
Он будет равен: 54 – 27 = 27 (км).
Второй день- это (mathbf{frac{2}{3}}) оставшегося пути, т.е. (mathbf{frac{2}{3}}) от 27 (км).
Чтобы найти дробь от числа, необходимо найти величину одной доли, затем умножить ее на количество частей (долей).
Найдем величину одной доли, для этого весь оставшийся путь (27 км) разделим на знаменатель дроби (в нашем случае это число 3), данное выражение будет описываться выражением 27 ÷ 3.
Полученный результат умножим на количество, пройденных туристами долей, на которые нам указывает числитель дроби (он равен 2).
В результате получим равенство:
27 ÷ 3 ∙ 2 = 9 ∙ 2 = 18 (км) туристы прошли во второй день.
Так как во второй день туристы прошли 18 км от пути, оставшегося после первого туристического дня (т.е. 18 км из 27 км), то за третий день им осталось пройти:
27 – 18 = 9 (км) туристы прошли в третий день.
Проверим полученные результаты.
Найдем весь туристический путь за три дня, он должен быть равен 54 км.
Для этого сложим путь первого, второго и третьего дня.
27 + 18 + 9 = 45 + 9 = 54 (км) прошли туристы за три дня.
Задача решена верно.
Ответ: 27 (км), 18 (км), 9 (км).
Эта информация доступна зарегистрированным пользователям
Если известно сколько составляет часть от целого, то по известной части можно найти целое.
Рассмотрим задачу:
Пусть длина (mathbf{frac{1}{2}}) ленты составляет 10 дм.
Определим, чему равна длина всей ленты.
Эта информация доступна зарегистрированным пользователям
Так как (mathbf{frac{1}{2}}) ленты- это ее половина, и она составляет 10 дм, то вторая половина так же равна 10 дм.
В таком случае, чтобы найти длину всей ленты, мы можем сложить длины этих двух половинок или, заменив сложение одинаковых слагаемых умножением, можем по 10 дм взять два раза, в результате получим равенство:
10 ∙ 2 = 20 (дм) длина всей ленты.
Ответ: 20 (дм).
Рассмотрим еще одну задачу, в которой будет известна длина одной четвертой части ленты.
Ленту подарочную разделили на четыре части.
Длина (mathbf{frac{1}{4}}) ленты составляет 5 дм.
Эта информация доступна зарегистрированным пользователям
Определим, чему равна длина всей ленты.
Целое, т.е. всю ленту разделили на 4 доли.
Известно, что одна доля- это (mathbf{frac{1}{4}}) ленты, она составляет 5 дм.
Чтобы найти длину всей ленты, необходимо длину одной доли (в нашем случае 5 дм) умножить на количество долей (в нашем примере их 4).
Получим следующее равенство:
5 ∙ 4 = 20 (дм) длина всей ленты.
Ответ: 20 (дм).
Рассмотрев эти два примера, можно сделать вывод:
Чтобы найти неизвестное число по его доле, необходимо долю этого числа умножить на число долей.
Усложним задачу про ленту и попробуем ее решить.
Пусть подарочную ленту разделили на 5 равных частей.
Определим, какова длина всей ленты, если (mathbf{frac{3}{5}}) этой ленты составляет 12 дм.
Эта информация доступна зарегистрированным пользователям
Из условия задачи известно, что разделили ленту на 5 долей, а 3 таких доли составляют 12 дм.
Для того чтобы найти длину всей ленты, необходимо найти длину одной доли.
Следовательно, известную длину трех долей (12 дм) разделим на количество этих долей (3 доли).
Данное действие будет описывать следующее выражение: 12 ÷ 3.
Затем умножим длину одной доли на количество всех долей (в нашем случае всю ленту разделили на 5 долей).
В результате получим равенство:
12 ÷ 3 ∙ 5 = 4 ∙ 5 = 20 (дм) длина всей ленты.
Ответ: 20 (дм).
Сформулируем правило нахождения целого по его части.
Чтобы найти целое по его части, необходимо определить величину одной доли, затем полученный результат умножить на общее количество долей (на которое поделено целое).
Запишем алгоритм нахождения числа по его дроби.
1. Найти величину одной доли.
2. Величину одной доли умножить на количество всех долей, на которое разделено число.
В буквенном виде данное правило можно представить так:
Пусть А– это исходное число, оно неизвестно.
В– часть числа А, выраженная дробью (mathbf{frac{m}{n}}).
m– числитель, показывает сколько долей взяли.
n– знаменатель, показывает на сколько долей разделили число.
Чтобы найти исходное число А, необходимо число В, соответствующее части числа А, разделить на числитель (m) и полученный результат умножить на знаменатель (n) дроби, которая выражает эту часть.
Эта информация доступна зарегистрированным пользователям
Рассмотрим, как данное правило применяется при решении задач.
Задача №1.
Дима потратил на сладости 120 рублей, что составляет (mathbf{frac{2}{4}}) всех накопленных им денег.
Сколько всего денег было у Димы накоплено?
Решение:
Общее количество денег, которое было у Димы не известно.
Известно только то, что 120 рублей- это часть всех денег Димы.
Эта же часть денег выражена дробью (mathbf{frac{2}{4}}) от всех денег.
Знаменатель данной дроби показывает на то, что все накопленные деньги разделены на 4 части, а числитель дроби указывает на то, что две части из четырех составляют 120 рублей.
Найдем величину одной доли (одной части из четырех), т.е. сколько составляет (mathbf{frac{1}{4}}) (четверть) всех денег Димы.
120 ÷ 2 = 60 (руб.) составляет четверть всех денег Димы.
Чтобы найти общее количество денег, которые накопил Дима (а это четыре части по 60 рублей), нужно:
4 ∙ 60 = 240 (руб.) было накоплено у Димы.
Кратко решение данной задачи можно записать следующим образом:
120 ÷ 2 ∙ 4 = 240 (руб.) было накоплено у Димы.
Ответ: 240 (руб.)
Очень часто задачи такого типа имеют более сложные условия и их приходится решать в несколько действий.
Задача №2.
Дима купил шоколадку. Он за нее заплатил 60 рублей, что составило (mathbf{frac{1}{3}}) всех его денег.
От оставшейся суммы (mathbf{frac{2}{3}}) он потратил на мороженное, остальные деньги положил в копилку.
Сколько денег Дима положил в копилку?
Решение:
Первым делом определим первоначальную сумму, которая была у Димы.
Будем считать, что искомое число состоит из трех долей.
По условию задачи одна доля составляет 60 рублей.
Чтобы найти число (целое) по его доле, необходимо долю этого числа умножить на число долей.
В таком случае получаем:
60 ∙ 3 = 180 (руб.) всего было накоплено у Димы- это первоначальная сумма, которая у него была.
Следующим действием найдем часть денег, которые потратил Дима на мороженное.
Из общей суммы денег вычтем 60 рублей, которые были потрачены на шоколадку.
180 – 60 = 120 (руб.) оставшееся сумма денег у Димы.
От полученного остатка найдем (mathbf{frac{2}{3}})
Чтобы найти (mathbf{frac{2}{3}}) от 120 (дробь от числа), нужно число 120 разделить на знаменатель и умножить на числитель этой дроби.
120 ÷ 3 ∙ 2 = 40 ∙ 2 = 80 (руб.) Дима потратил на мороженное.
Из первоначальной суммы (180 рублей) вычтем деньги, потраченные на шоколадку, (60 рублей), вычтем деньги, потраченные на мороженное, (80 рублей) и получим остаток денег, который Дима положил в копилку.
180 – 60 – 80 = 100 – 60 = 40 (руб.) Дима положил в копилку.
Ответ: 40 (руб.)
Эта информация доступна зарегистрированным пользователям
Читайте также
Математика
5 класс
Урок № 50
Нахождение целого по его части
Перечень рассматриваемых вопросов:
- обыкновенная дробь;
- числитель, знаменатель обыкновенной дроби;
- сократимая, несократимая дробь;
- задачи на дроби.
Тезаурус
Дробь в математике – это число, состоящее из одной или нескольких равных частей (долей) единицы.
Правильные дроби – это дроби, в которых числитель меньше знаменателя.
Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя.
Обязательная литература
- Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
«Без знания дробей никто не может быть сведущим в математике», – однажды сказал древнеримский философ Марк Туллий Цицерон. И трудно с ним не согласиться, ведь дроби в нашей жизни встречаются очень часто.
Убедимся в этом, решая задачи на нахождение целого по его части.
В окружающем нас мире очень часто приходится находить не только часть от чего-либо, но и, наоборот, целое по его части. Например, мы можем услышать в прогнозе погоды такую фразу «Сегодня выпало 20 миллиметров осадков, что составляет половину месячной нормы». А сколько тогда составляет месячная норма? Если половина нормы это 20 миллиметров, тогда норма в два раза больше, т. е. 40 миллиметров.
А теперь немного изменим условие задачи. Найдём всю месячную норму, если известно, что за день выпало 20 миллиметров, что составляет 
Для решения этой задачи воспользуемся следующими рассуждениями.
Будем считать, что месячная норма это 



20 : 2 = 10 мм – одна треть нормы. 10 мм · 3 = 30 мм – три трети нормы.
Ответ: месячная норма равна 30 мм.
Итак, сформулируем правило нахождения целого по его части: если часть искомого целого выражена дробью, то чтобы найти целое, можно эту часть разделить на числитель дроби, а результат умножить на её знаменатель.
Решим задачу.
Два путешественника отправились в поход, который длился несколько дней. В первый день они преодолели 

Какой путь должны преодолеть путешественники, если во второй день они прошли 20 км?
Решение.
Составим схему, на основе которой будем выполнять решение этой задачи.
Нам известно, что 20 километров это четыре пятых маршрута, пройденного в первый день. Соответственно, найдём длину маршрута в первый день.
20 : 4 · 5 = 25 км – расстояние, пройденное за 1 день.
Теперь, зная, что 25 = 
Ответ: весь путь равен 65 км.
Решим задачу. Младшей сестре исполнилось 9 лет, что составляет 

Решение: для решения этой задачи составим следующую схему.
По известному возрасту младшей сестры найдём возраст старшей.
9 : 3 · 5 =15 (лет) – возраст старшей из дочерей.
Теперь найдём возраст матери.
15 : 5 · 12 = 36 (лет) – возраст матери.
Ответ: 15 лет; 36 лет.
Тренировочные задания
№ 1. За один день бригада заасфальтировала 5 км дороги, что составило 
Решение: для решения этой задачи нужно использовать правило нахождения части от целого: чтобы найти целое по части, нужно эту часть разделить на числитель дроби, а результат умножить на её знаменатель.
Т. е. 5 : 5 · 7 = 7 км
Ответ: 7 км.
№ 2. Первая сторона треугольника равна 12 см, что составляет 

Решение: для решения этой задачи сначала нужно вспомнить, что периметр – это сумма длин всех сторон треугольника, т. е. сумма длин трёх сторон.
Теперь найдём периметр, исходя из условия задачи.
1) 12 : 3 · 10 = 60 см – периметр.
12 : 2 · 3 = 18 см – вторая сторона.
Теперь от периметра отнимем сумму длин двух сторон и получим третью сторону.
40 – (18 + 12) = 10 см – третья сторона. Ответ: 10 см.
§ 1 Правила нахождения части от целого и целого по его части
В этом занятии сформулируем правила отыскания части от целого и целого по его части, а также рассмотрим решение задач с использованием этих правил.
Рассмотрим две задачи:
Сколько километров прошли туристы в первый день, если весь туристический маршрут 20 км.?
Найдите длину всего пути туристов.
Сравним эти задачи – в обеих за целое принят весь путь. В первой задаче целое известно – 20 км, а во второй – неизвестно. В первой задаче необходимо найти часть от целого, а во второй – целое по его части. Величина, известная в первой задаче 20 км, неизвестна во второй задаче, и наоборот, известное во второй задаче – 8 км, в первой необходимо найти. Такие задачи называются взаимно обратными, так как в них известные и искомые величины меняются местами.
Рассмотрим первую задачу:
Знаменатель 5 показывает, на сколько частей разделили целое, т.е. если целое 20 разделить на 5, узнаем, сколько километров составляет одна часть, 20: 5 = 4 км. Числитель 2 показывает, что туристы прошли 2 части пути, значит 4 надо умножить на 2, получится 8 км. В первый день туристы прошли 8 км.
Получилось выражение 20 : 5 ∙ 2 = 8.
Перейдем ко второй задаче.
Следовательно, одна часть будет равна частному 8 и 2, получится 4, знаменатель 5, значит, всего частей 5.
4 умножить на 5, получится 20. Ответ 20 км длина всего пути.
Запишем выражение: 8 : 2 ∙ 5 = 20
Используя смысл умножения и деления числа на дробь, правила отыскания части от целого и целого по его части можно сформулировать так:
Чтобы найти часть от целого, надо число, соответствующее целому, умножить на дробь, соответствующую этой части;
чтобы найти целое по его части, надо число, соответствующее этой части, разделить на соответствующую части дробь.
Соответственно решение задач можно записать теперь по другому:
для первой задачи 20 ∙ 2/5 = 8 (км),
для второй задачи 8 : 2/5 = 20 (км).
Чтобы не было затруднений, решение подобных задач записываем так:
Целое: весь путь, известно – 20 км.
Ответ: 8 км.
Целое: весь путь – неизвестно.
Ответ: 20 км.
§ 2 Алгоритм решения задач на нахождение целого по его части и части целого
Составим алгоритм решения подобных задач.
Сначала проанализируем условие и вопрос задачи: выясним, что является целым, известно оно или нет, далее выясним, как представлена часть целого и что нужно найти.
Если необходимо найти часть от целого, то целое умножим на дробь, соответствующую этой части, если надо найти целое по его части, то число, соответствующее части разделим на дробь, соответствующую этой части. В результате получим выражение. Далее найдем значение выражения и запишем ответ, прочитав перед этим еще раз вопрос задачи.
Итак, прежде чем решать подобные задачи, необходимо ответить на следующие вопросы:
Какая величина прията за целое?
Известна ли эта величина?
Что требуется найти: часть от целого или целое по его части?
Подведем итоги: в этом уроке Вы познакомились с правилами отыскания части от целого и целого по его части, а также научились решать задачи по этим правилам.
Урок 30. Нахождение числа по его части
Гипермаркет знаний>>Математика>>Математика 4 класс>> Урок 30. Нахождение числа по его части
Задача 1. Какова длина дороги, если .ее составляют 8 км?
Решение:
В двух пятых долях дороги 8 км, поэтому ее часть составляет 8 : 2 = 4 км. Во всей дороге пять пятых долей, или 4 • 5 = 20 км. Решение можно записать короче: 8 : 2 • 5 = 20 (км).
Чтобы найти число по его части, выраженной дробью, надо разделить эту часть на числитель и умножить на знаменатель дроби.
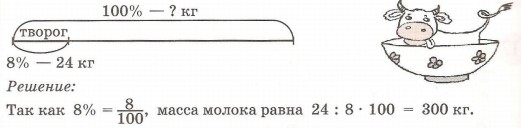
Задача 2. Из молока получается 8% творога. Сколько молока требуется для изготовления 24 кг творога?
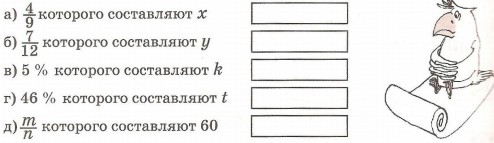
1. Запиши число:
2. Найди число, которого составляют 8, 32, 60, 240.
3. Дорисуй схемы и реши задачи:
а) Продолжительность жизни белки б лет, что составляет продолжительности жизни зайца. Сколько лет может жить заяц?
б) Бурый медведь весит около 320 кг, что составляет 40 % массы белого медведя. Какова масса белого медведя?
4. Найди число:
а) которого составляют 25; в) 7% которого составляют 56;
б) которого составляют 120; г) 4% которого составляют 200.
5. В городе 75 000 жителей. Дети составляют 24% всех его жителей. Сколько детей живет в этом городе?
6. Велогонщики проехали в первый день соревнований 130 км, что — составляет 26% всего пути. Сколько километров им еще осталось преодолеть?
7. Сравни дроби:
8. Нарисуй числовой луч с единичным отрезком, равным 14 клеточкам. Отметь на нем дроби . Найди среди них равные дроби. Придумай свои примеры равных дробей.
9. а) Максим задумал число, вычел его из 740 и полученную разность умножил на 57. В результате у него получилось 40 185. Какое число задумал Максим?
б) Аня задумала число, прибавила его к числу 789 и полученную сумму разделила на 8. В результате у нее получилось 4005. Какое число задумала Аня?
10. За 6 часов автомобиль проехал 552 км, а поезд — 336 км. Каксе расстояние проедет за это время мотоциклист, если его скорость 5 4 раза меныпе суммы скоростей автомобиля и поезда?
11. а) (16 250 : 130 – 86) • 9040 – 7008 • (25 094 – 24 786) : 704;
б) 30 303 – (76 ‘ 507 + 68 400 : 450) : 76 + 2350 • (1050 – 441).
12. Верно или неверно высказывание:
а) 45 кратно 5; г) 4 является делителем 20;
б) 32 не кратно 7; д) 18 является делителем 2;
в) 57 кратно 9; е) 25 не является делителем 5?
13. Выбери из множества {8, 16, 24, 35, 40, 48, 54, 64} числа, которые:
14*. Литературная викторина.
В каждой задаче найди значение буквенного выражения для всех значений переменной. В полном алфавите найди соответствующие им буквы и составь из полученных букв имя героя литературного произведения. Назови это литературное произведение и его автора.
1) 20 – а : 3, если а € {57, 15, 48, 42}
2) 0 + 63 • 0 + b • l, если b € {10, 13, 15, 19, 30}
3) 94 + с : 1 – 94, если c € {6, 16, 17, 18, 30}
4) 1 • d – 65 : 65 + 0 : 6, если d € {27, 2, 17, 10, 22, 14, 13}
Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 1. – М.: Издательство “Ювента”, 2005, – 64 с.: ил.
Материалы по математике за 4 класс скачать, конспект по математике, учебники и книги скатать бесплатно, школьная программа онлайн
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: