На прошлом уроке мы доказали с помощью опытов существование силы, действующей на тела, погруженные в жидкость или газ — выталкивающей силы. Также мы теперь знаем, что ее можно рассчитать по формуле: $F_{выт} = gm_ж = P_ж$. Но какое еще есть значение у этой силы? На этом уроке мы более подробно рассмотрим выталкивающую силу.
Выталкивающая сила и вес тела
Как можно на опыте определить, с какой силой тело, погруженное целиком в жидкость, выталкивается из жидкости?
Давайте познакомимся с таким опытом. Он представлен на рисунке 1.
Подвесим на пружину небольшую емкость для жидкости и тело цилиндрической формы ниже. На конце пружины у нас расположена стрелка-указатель. Она отмечает растяжение пружины на штативе (рисунок 1, а). Таким образом, мы видим вес тела в воздухе.
Теперь опустим наше тело в большой сосуд. Сосуд имеет трубку для слива и наполнен жидкостью до уровня этой трубки (рисунок 1, б).
Когда мы полностью опустим тело в сосуд, часть жидкости из него выльется через трубку для слива в стакан. Объем этой жидкости будет равен объему тела. Мы уже знаем, что на тело действует выталкивающая сила: пружина сокращается, стрелка-указатель поднимается, вес тела в жидкости становится меньше.
А теперь возьмем жидкость, которая вылилась в стакан. Зальем ее в емкость, которая также подвешена к пружине (рисунок 1, в). Теперь стрелка-указатель вернулась к своему изначальному положению.
Так чему равна эта сила? Сделаем вывод из данного опыта.
Сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела.
Если провести подобный опыт с газом, а не с жидкостью, то мы получим, что сила, выталкивающая тело из газа, равна весу газа, взятого в объеме тела.
Сила Архимеда
Как называют силу, которая выталкивает тела, погруженные в жидкости и газы?
Теперь мы добавим, что эту выталкивающую силу называют архимедовой силой. Архимед (рисунок 2) — древнегреческий ученый и инженер, сделавший множество открытий и в математике, и в физике. Именно он первый обнаружил наличие выталкивающей силы и рассчитал ее значение.
Как подсчитать архимедову силу?
В прошлом уроке мы получили формулу $F_{выт} = P_ж = g m_ж$. Теперь мы будем называть эту силу архимедовой $F_A$.
Из выше рассмотренных опытов мы можем выразить массу вытесненной жидкости через ее плотность и объем тела, который эту жидкость вытеснил (они одинаковы): $m_ж = rho_ж cdot V_т$. Получим формулу для архимедовой силы.
$F_A = g rho_ж V_т$.
От чего зависит архимедова сила?
Взгляните еще раз на формулу: $F_A = g rho_ж V_т$.
Ясно видно, что архимедова сила зависит только от плотности жидкости и от объема тела, которое мы погружаем в эту жидкость.
Если мы будем погружать в одну и ту же жидкость тела разной плотности и разной формы (рисунок 3), то значение силы меняться не будет (при условии, что эти тела будут обладать одинаковым объемом).
Определение веса тела, погруженного в жидкость или газ
На тело, погруженное в жидкость (или в газ), действуют две силы: сила тяжести и архимедова сила. Направлены они в противоположные стороны. Вес тела в жидкости $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_A$. То есть:
$P_1 = P space − space F_A = gm space − space gm_ж$.
Если тело погружено в жидкость или газ, то его вес уменьшается на вес вытесненной им жидкости или газа.
Пример задачи
Определите выталкивающую силу, которая будет действовать на камень объемом $2.6 space м^3$, лежащий на морском дне.
Дано:
$V_т = 2.6 space м^3$
$rho_ж = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$F_A — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Сила Архимеда рассчитывается по формуле:
$F_A = g rho_ж V_т$.
Подставим численные значения величин и рассчитаем эту силу:
$F_A = 9.8 frac {Н}{кг} cdot 1030 frac{кг}{ м^3} cdot 2.6 space м^3 approx 26 244 space Н approx 26.2 space кН$.
Ответ: $F_A approx 26,2 space кН$.
Забавное дополнение: легенда об Архимеде
Архимед, великий изобретатель, шокировал своих современников гениальными открытиями. Его имя упоминается во множестве легенд, но одна из них стала наиболее известной: легенда о том, как Архимед пришел к открытию выталкивающей силы.
Царь Гиерон поручил Архимеду проверить работу мастера, который изготовил для него золотую корону.
Долгое время ученый не мог найти ответ: как определить количество некачественных примесей? Проблема заключалась в том, что определить ее объем — сложная задача. По легенде озарение настигло Архимеда, когда он принимал ванну.
Ученый заметил, что из ванны вылилась вода, когда он залез в нее. И здесь его посетила гениальная мысль. Все вы слышали его известную цитату: «Эврика! Эврика!» (в переводе означает: «Нашел! Нашел!»).
Так Архимед победно выкрикивал свою фразу, потрясенный своим открытием, что она дошла в виде легенды и до наших времен.
Упражнения
Упражнение №1
К коромыслу весов подвешены два цилиндра одинаковой массы: свинцовый и алюминиевый (рисунок 4). Весы находятся в равновесии. Нарушится ли равновесие весов, если оба цилиндра одновременно погрузить в воду; в спирт? Ответ обоснуйте. Проверьте его на опыте. Как зависит выталкивающая сила от объема тела?
Посмотреть ответ
Скрыть
Ответ:
Когда мы погрузим цилиндры в жидкость, на каждый их них будет действовать сила Архимеда. Если эти силы будут равны, то весы останутся в равновесии.
Запишем формулы архимедовой силы для каждого цилиндра.
Для свинцового цилиндра:
$F_{A1} = g rho_ж V_1$.
Для алюминиевого цилиндра:
$F_{A2} = g rho_ж V_2$.
Мы видим, что равенство этих сил зависит от объемов цилиндров. Они равны? Нет, они имеют одинаковые массы, но разные плотности. Цилиндр из алюминия будет обладать большим объемом, чем свинцовый цилиндр ($V = frac{m}{rho}$). Значит, на алюминиевый цилиндр будет действовать большая выталкивающая сила, чем на свинцовый.
Если мы проверим это на опыте, то увидим подтверждение нашим выводам (рисунок 5).
При этом весы выйдут из равновесия в случае и с водой (рисунок 5, а), и со спиртом (рисунок 5, б). Так как мы опускаем цилиндры одновременно в один и тот же тип жидкости, значение архимедовой силы, действующей на цилиндры, будет различаться только в зависимости от объемов этих цилиндров — свинцовый перевесит алюминиевый в любой жидкости.
Заметим, что в случае погружения в воду, архимедова сила будет больше, чем в случае погружения в спирт. Это объясняется тем, что вода имеет большую плотность, чем спирт.
Упражнение №2
К коромыслу весов подвешены два алюминиевых цилиндра одинакового объема. Нарушится ли равновесие весов, если один цилиндр погрузить в воду, а другой — в спирт? Ответ обоснуйте. Зависит ли выталкивающая сила от плотности жидкости?
Посмотреть ответ
Скрыть
Ответ:
Если один цилиндр погрузить в воду, а другой — в спирт, то равновесие весов нарушится (рисунок 6). На цилиндр, находящийся в воде, будет действовать большая архимедова сила.
Так происходит, потому что архимедова сила зависит от объема погруженного тела (а они у нас одинаковые: $V_1 = V_2 = V$) и от плотности жидкости:
$F_А = g rho_ж V$.
Плотность спирта ($800 frac{кг}{м^3}$) меньше плотности воды ($1000 frac{кг}{м^3}$). Значит, на цилиндр, погруженный в воду, будет действовать большая архимедова сила, чем на тот, что погружен в спирт.
Упражнение №3
Объем куска железа равен $0.1 space дм^3$. Какая выталкивающая сила будет на него действовать при полном его погружении в воду; в керосин?
Дано:
$V = 0.1 space дм^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
СИ:
$V = 0.1 cdot 10^{-3} space м^3$
$F_{А1} — ?$
$F_{А2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Рассчитаем архимедову силу, которая будет действовать на кусок железа в воде:
$F_{А1} = g rho_1 V$,
$F_{А1} = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.98 space Н approx 1 space Н$.
Теперь рассчитаем архимедову силу, которая будет действовать на кусок железа в керосине:
$F_{А2} = g rho_2 V$,
$F_{А2} = 9.8 frac{Н}{кг} cdot 800 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.784 space Н approx 0.8 space Н$.
Ответ: $F_{А1} approx 1 space Н$, $F_{А2} approx 0.8 space Н$.
Упражнение №4
Бетонная плита объемом $2 space м^3$ погружена в воду. Какую силу необходимо приложить, чтобы удержать ее в воде; в воздухе?
Дано:
$V = 2 space м^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 1.29 frac{кг}{м^3}$
$rho_б = 2300 frac{кг}{м^3}$
$F_1 — ?$
$F_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Бетонная плита находится в воде. На нее действует сила тяжести и архимедова сила. Они направлены противоположно друг другу и будут иметь разные величины. Разность этих сил — и будет искомая сила $F_1$, которую нужно приложить, чтобы удержать бетонную плиту в воде (чтобы она не опускалась на дно и не всплывала):
$F_1 = F_{тяж} space − space F_{А1}$.
Сила тяжести рассчитывается по формуле:
$F_{тяж} = gm$.
Массу бетонной плиты мы можем выразить через ее плотность и объем:
$m = rho_б V$,
$F_{тяж} = g rho_б V$.
Архимедова сила, действующая на бетонную плиту в воде:
$F_{А1} = g rho_1 V$.
Подставим силу тяжести и архимедову силу в формулу и рассчитаем $F_1$:
$F_1 = F_{тяж} space − space F_{А1} = g rho_б V space − space g rho_1 V = gV cdot (rho_б space − space rho_1)$,
$F_1 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1000 frac{кг}{м^3}) = 25 space 480 space Н approx 25 space кН$.
Используем ту же формулу для того, чтобы рассчитать силу $F_2$, которую нужно приложить, чтобы удержать бетонную плиту в воздухе:
$F_2 = gV cdot (rho_б space − space rho_2)$,
$F_2 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3}) approx 45 space 054 space Н approx 45 space кН$.
Ответ: $F_1 approx 25 space кН$, $F_2 approx 45 space Н$.
Упражнение №5
Предположив, что корона царя Гиерона в воздухе весит $20 space Н$, а в воде — $18.75 space Н$, вычислите плотность вещества короны. Полагая, что к золоту было подмешано только серебро, определите, сколько в короне было золота и сколько серебра. При решении задачи плотность золота считайте равной $20 space 000 frac{кг}{м^3}$, плотность серебра — $10 space 000 frac{кг}{м^3}$. Каков был бы объем короны из чистого золота?
Дано:
$P_1 = 20 space Н$
$P_2 = 18.75 space Н$
$rho_з = 20 space 000 frac{кг}{м^3}$
$rho_с = 10 space 000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1.29 frac{кг}{м^3}$
$rho_2 = 1000 frac{кг}{м^3}$
$rho — ?$
$m_з — ?$
$m_с — ?$
$V_1 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Вес короны в воздухе $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_{A1}$. То есть:
$P_1 = P space − space F_{A1}$.
Значит, вес короны в вакууме будет равен сумме ее веса в воздухе и архимедовой силы:
$P = P_1 space + space F_{А1}$,
$gm = P_1 space + space g rho_1 V$.
Теперь запишем такое же уравнение для веса короны в воде:
$gm = P_2 space + space g rho_2 V$.
Левые части уравнений у нас равны, поэтому мы можем приравнять правые части друг к другу:
$P_1 space + space g rho_1 V = P_2 space + space g rho_2 V$.
Перенесем элементы, содержащие неизвестный объем вправо:
$P_1 space − space P_2 = g rho_2 V space − space g rho_1 V$,
$P_1 space − space P_2 = gV (rho_2 space − space rho_1)$.
Выразим отсюда объем короны и рассчитаем его:
$V = frac{P_1 space − space P_2}{g (rho_2 space − space rho_1)}$,
$V = frac{20 space Н space − space 18.75 space Н}{9.8 frac{Н}{кг} (1000 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3})} = frac{1.25}{9787} space м^3 = 12.8 cdot 10^{-5} space м^3$.
Используем одно из первых уравнений для веса короны в вакууме и в воздухе:
$gm = P_1 space + space g rho_1 V$.
Выразим отсюда массу короны и рассчитаем ее:
$m = frac{P_1 space + space g rho_1 V}{g}$,
$m = frac{20 space Н space + space 9.8 frac{Н}{кг} cdot 1.29 frac{кг}{м^3} cdot 12.8 cdot 10^{-5} space м^3}{9.8 frac{Н}{кг}} approx 2.04 space кг$.
Теперь мы знаем массу и объем короны. Рассчитаем ее плотность:
$rho = frac{m}{V}$,
$rho = frac{2.04 space кг}{12.8 cdot 10^{-5} space м^3} approx 16 space 000 frac{кг}{м^3}$.
Корона состоит из серебра и золота. Это означает, что ее общий объем мы можем записать в виде суммы объемов серебра и золота, ее составляющих:
$V = V_с space + space V_з$.
То же самое с общей массой короны:
$m = m_с space + space m_з$.
Запишем объемы через массы и плотности (а также выразим массу золота через общую массу короны и массу серебра):
$V_с = frac{m_с}{rho_с}$,
$V_з = frac{m_з}{rho_з} = frac{m space − space m_с}{rho_з}$.
Подставим эти объемы в формулу для общего объема короны и выразим из нее массу серебра:
$V = frac{m_с}{rho_с} space + space frac{m space − space m_с}{rho_з} = frac{m_с (rho_з space − space rho_с) space + space rho_с m}{rho_с rho_з} = m_с cdot frac{rho_з space − space rho_с}{rho_с rho_з} space + space frac{m}{rho_з}$,
$m_с = frac{V space − space frac{m}{rho_з}}{frac{rho_з space − space rho_с}{rho_с rho_з}} = frac{rho_с (V rho_з space − space m)}{rho_з space − space rho_с}$.
Рассчитаем массу серебра, содержащегося в короне:
$m_с = frac{10 space 000 frac{кг}{м^3} (12.8 cdot 10^{-5} space м^3 cdot 20 space 000 frac{кг}{м^3} space − space 2.04 space кг)}{20 space 000 frac{кг}{м^3} space − space 10 space 000 frac{кг}{м^3}} = frac{5200 frac{кг^2}{м^3}}{10 space 000 frac{кг}{м^3}} = 0.52 space кг$.
Теперь мы можем вычислить и количество золота в короне:
$m_з = m space − space m_с$,
$m_з = 2.04 space кг space − space 0.52 space кг = 1.52 space кг$.
Если бы вся корона была из золота, то ее объем был бы равен:
$V_1 = frac{m}{rho_з}$,
$V_1 = frac{2.04 space кг}{20 space 000 frac{кг}{м^3}} = 10.2 cdot 10^{-5} space м^3$.
Ответ: $rho approx 16 space 000 frac{кг}{м^3}$, $m_з = 1.52 space кг$, $m_с = 0.52 space кг$, $V_1 = 10.2 cdot 10^{-5} space м^3$.
Упражнение №6
По мелким камешкам ходить босыми ногами больно. Почему человек не испытывает боли, если ходит по таким же камням в воде?
Посмотреть ответ
Скрыть
Ответ:
Что означает фраза «ходить по камням»? Со стороны физики, когда мы наступаем на камни, мы давим на них своим весом: $p = frac{F}{S} = frac{P}{S}$.
Когда мы оказываемся в воде, наш вес уменьшается. Это следствие действия на нас архимедовой силы. Уменьшается вес — уменьшается и давление наших стоп на камни.
Вы замечали, что предметы в воде становятся легче? Существует много сказок и легенд, когда смекалистые герои поднимали вещи, которые на суше поднять было невозможно.
Мы знаем, что сила тяжести не изменяется, но вес тела может зависеть от множества причин. Когда тело погружается в воду, его сила тяжести не изменяется, но появляется новая сила (открытая Архимедом), которая уменьшает вес этого тела.
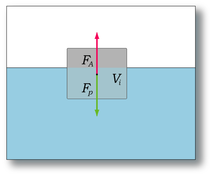
- Вес тела в воздухе: P=mg. Вес тела направлен вниз.
- Архимедова сила: FА=mж⋅g. Сила направлена вверх.
- Вес тела в жидкости: P1=P−FА=mg−mжg. Результирующая сил (1) и (2).
Тело, погружённое в жидкость, уменьшается в весе пропорционально весу вытесненной жидкости.
Пример:
определить, сколько весит в воде стеклянная пластина объёмом (1,5) дм³.
| Дано | Решение |
|
V=1,5дм3=0,0015м3ρж=1000кг/м3ρт=2600кг/м3g=9,8Н/кг ________________ |
P1=mтg−mжgmт=ρт⋅V;mж=ρж⋅V⇒⇒P1=ρтVg−ρжVg=Vgρт−ρжP1=0,0015м3⋅9,8Н/кг⋅2600кг/м3−1000кг/м3≈24Н |
Ответ: стеклянная пластина в воде весит (24) Н.
Вес тела,полностью погружённого в жидкость,в 2 раза меньше веса этого тела в воздухе.Сравните плотность тела и плотность жидкости. Вес тела в жидкости равен разнице двух прямо противоположных сил: силы тяжести и силы Архимеда.Fт = m*g, где m — масса тела (m = ρт*V, ρт — плотность тела, V — объем тела), g — ускорение свободного падения.Fa = ρж*g*V, где ρж — плотность жидкости.Вес тела в воздухе:Р1 = Fт = ρт*V*g.Вес тела в жидкости:Р2 = Fт — Fa = ρт*V*g — ρж*g*V.Так как Р1/Р2 = 2, тоρт*V*g/(ρт*V*g — ρж*g*V) = 2;ρт/(ρт — ρж) = 2;ρт = 2ρт — 2ρж;ρт = 2ρж.
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Вес тела,полностью погружённого в жидкость,в 2 раза меньше веса этого тела в воздухе.Сравните плотность тела и плотность
Чему равна масса тела в воде?
В воде вес тела Рв определяется формулой: Рв = Р — Fарх. Р = Рв + Fарх. m = (Рв + Fарх)/g. m = (2 Н + 0,5 Н)/9,8 м/с 2 = 0,255 кг.
Чему равен вес тела?
Чему равен вес тела, массой 10 кг?
Для нахождения значения веса указанного тела, необходимо использовать формулу: P = mт * g.Постоянные и переменные: mт — масса указанного тела (mт = 10 кг); g — ускорение свободного падения (g = 9,81 м/с 2 ).Вычисление: P = mт * g = 10 * 9,81 = 98,1 Н.Ответ: Вес указанного тела составляет 98,1 Н.
Знаешь ответ? Как написать хороший ответ? Будьте внимательны!
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Чему равен вес тела, массой 10 кг?
Сколько человек весит под водой?
Жидкость — Это 40-70% веса нашего тела. Причем, в мужчинах жидкости «содержится» больше, чем в женщинах. Если вы весите 68 кг и вы мужчина — то жидкости в вас может быть от 34 до 48 кг. Если вы женщина с тем же весом — то чуть меньше — от 27 до 41 кг воды.
Исключите углеводы — вода будет уходить, поскольку начнет расходоваться гликоген, запасенный в мышцах. Будете есть много соленого, вода будет задерживаться. Жидкость теряется ночью (до 1,4 кг за ночь), поэтому рекомендуется взвешиваться именно по утрам. В это время вы весите меньше всего.
Как найти вес тела формула?
По какой формуле можно определить вес тела? Формула, по которой определяется вес тела, записывается следующим образом: Р=mg, где Р-вес тела, m-масса тела, g-ускорение свободного падения. При решении задач, когда не требуется большой точности, g~9,8 Н/кг округляют до 10 Н/кг. Знаешь ответ? Как написать хороший ответ? Будьте внимательны!
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: По какой формуле можно определить вес тела?
Как посчитать вес тела в жидкости?
Вес тела,полностью погружённого в жидкость,в 2 раза меньше веса этого тела в воздухе.Сравните плотность тела и плотность жидкости. Вес тела в жидкости равен разнице двух прямо противоположных сил: силы тяжести и силы Архимеда.Fт = m*g, где m — масса тела (m = ρт*V, ρт — плотность тела, V — объем тела), g — ускорение свободного падения.Fa = ρж*g*V, где ρж — плотность жидкости.Вес тела в воздухе:Р1 = Fт = ρт*V*g.Вес тела в жидкости:Р2 = Fт — Fa = ρт*V*g — ρж*g*V.Так как Р1/Р2 = 2, тоρт*V*g/(ρт*V*g — ρж*g*V) = 2;ρт/(ρт — ρж) = 2;ρт = 2ρт — 2ρж;ρт = 2ρж.
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Вес тела,полностью погружённого в жидкость,в 2 раза меньше веса этого тела в воздухе.Сравните плотность тела и плотность
Как найти массу тела в жидкости?
Вы замечали, что предметы в воде становятся легче? Существует много сказок и легенд, когда смекалистые герои поднимали вещи, которые на суше поднять было невозможно. Мы знаем, что сила тяжести не изменяется, но вес тела может зависеть от множества причин. Когда тело погружается в воду, его сила тяжести не изменяется, но появляется новая сила (открытая Архимедом), которая уменьшает вес этого тела.
Вес тела в воздухе: P = mg, Вес тела направлен вниз.Архимедова сила: F А = m ж ⋅ g, Сила направлена вверх.Вес тела в жидкости: P 1 = P − F А = mg − m ж g, Результирующая сил (1) и (2).
Тело, погружённое в жидкость, уменьшается в весе пропорционально весу вытесненной жидкости. Пример: определить, сколько весит в воде стеклянная пластина объёмом (1,5) дм³.
| Дано | Решение |
| V = 1,5 д м 3 = 0,0015 м 3 ρ ж = 1000 кг / м 3 ρ т = 2600 кг / м 3 g = 9, 8 Н / кг _ | P 1 = m т g − m ж g m т = ρ т ⋅ V ; m ж = ρ ж ⋅ V ⇒ ⇒ P 1 = ρ т Vg − ρ ж Vg = Vg ρ т − ρ ж P 1 = 0,0015 м 3 ⋅ 9, 8 Н / кг ⋅ 2600 кг / м 3 − 1000 кг / м 3 ≈ 24 Н |
Ответ: стеклянная пластина в воде весит (24) Н.
Как изменяется вес в воде?
Вес тела в воде и в воздухе Вес тела в воде и в воздухе На весах закреплены одинаковые грузы. Один из них погружен в воду. Почему тот груз, который весит в воздухе перевешивает? Причина заключается в том, что на грузы действует выталкивающая (архимедова) сила.
Эта сила направлена против силы тяжести и действует тогда, когда тело окружено какой-нибудь средой (т.е. в вакууме она действовать не будет). Чем больше плотность среды и чем больше объём погруженного туда тела, тем больше и архимедова сила. Вода намного плотнее воздуха, поэтому в воде архимедова сила больше, чем в воздухе.
Соответственно, вес груза в воде меньше. Широко известна легенда о том, как Архимед сделал свое открытие выталкивающей силы, принимая ванну. Но мало кто знает, почему это открытие было так важно для Архимеда. Оказывается, он догадался, как измерить объем короны царя Гиерона, чтобы определить, из чего она сделана.
Как измеряется масса тела?
Единицы измерения массы — Килограмм является одной из семи основных единиц СИ, По современному определению, его величина выражается через величины трёх выбранных физических постоянных: постоянная Планка, скорость света и частота определённого электронного перехода. В Международной системе единиц (СИ) масса измеряется в килограммах,
Единицей измерения массы в системе СГС является грамм ( 1 ⁄ 1000 килограмма). Вообще говоря, в любой системе измерения выбор основных (первичных) физических величин, их единиц измерения и их числа произволен — зависит от принимаемого соглашения и масса не всегда входит в их состав — так в системе МКГСС единица массы была производной единицей и измерялась в кГс ·с²/м (называлась «техническая единица массы» или « инерта »).
В атомной физике и химии принято сравнивать массу с относительной атомной массой ( а.е.м.), в физике твёрдого тела — с массой электрона ( Атомная система единиц ), в физике элементарных частиц массу измеряют в электронвольтах, Кроме этих единиц, используемых в науке, существует большое разнообразие исторических единиц измерения массы, которые сохранили свою отдельную сферу использования: фунт, унция, карат, тонна и др.
- В астрофизике единицей для сравнения масс небесных тел служит масса Солнца,
- В некоторых естественных системах единиц в качестве единицы массы используются массы элементарных частиц: электрона или протона,
- В планковской системе единиц, также относящейся к естественным системам, единицей массы является планковская масса,
Массы очень мелких частиц могут быть определены с помощью величины, обратной к комптоновской длине волны : 1 см -1 ≈ 3,52⋅10 -41 кг, Масса очень большой звезды или чёрной дыры может быть отождествлена с её гравитационным радиусом : 1 см ≈ 6,73⋅10 24 кг,
Как записать вес тела?
Загрузить PDF Загрузить PDF Вес — сила, с которой тело действует на опору (или другой вид крепления), возникающая в поле силы тяжести. Масса связана с энергией и импульсом тела и эквивалентна энергии его покоя. Масса не зависит от силы тяжести (точнее от ускорения свободного падения).
- 1 Для вычисления веса используйте формулу Р = mg. Вес — это сила, с которой тело действует на опору, и его можно рассчитать, зная массу тела., где Р — вес тела (измеряется в ньютонах, Н), m, g — ускорение свободного падения (измеряется в м/с 2 ).
- Так как вес является силой, эту формулу можно записать и как F = mg,
- P или F — соответственно, вес или сила (измеряется в ньютонах, Н ).
- m — масса тела (измеряется в килограммах, кг ).
- g — ускорение свободного падения (измеряется в метрах на секунду в квадрате, м/с 2 ).
- Ускорение свободного падения на поверхности Земли равно 9,8 м/с 2, Это стандартное значение, принятое в международной системе единиц.
- 2 Определите массу тела. Так как ускорение свободного падения — это стандартная величина, то необходимо знать массу тела, чтобы найти его вес. Масса должна быть выражена в килограммах.
- 3 Узнайте величину ускорения свободного падения. На Земле, как уже было сказано выше, g = 9,8 м/с 2, В других местах вселенной ускорение гравитации меняется. Если в задаче требуется найти вес тела на другой планете (или другом космическом объекте), выясните ускорение свободного падения на этом объекте.
- Ускорение свободного падения на поверхности Луны примерно равно 1,622 м/с 2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.
- Ускорение свободного падения на Солнце примерно равно 274,0 м/с 2 (примерно в 28 раз больше, чем на Земле). Поэтому ваш вес на Солнце будет в 28 раз больше вашего земного веса (если конечно вы выживете на Солнце, что еще не факт!).
- 4 Подставьте значения в формулу. В формулу P=mg подставьте известные значения массы и ускорения свободного падения и найдите вес тела (измеряется в ньютонах, Н ). Реклама
- 1 Задача № 1. Найдите вес тела массой 100 кг на поверхности Земли.
- В этой задаче m = 100 кг, g = 9,8 м/с 2 (так как нужно найти вес тела на Земле).
- Р = 100 * 9,8 = 980 Н.
- Вы решили задачу. Ответ: вес тела массой 100 кг на поверхности Земли равен 980 Н, или Р = 980 Н.
- 2 Задача № 2. Найдите вес тела массой 40 кг на поверхности Луны.
- В этой задаче m = 40 кг, g = 1,6 м/с 2 (так как нужно найти вес тела на Луне).
- Р = 40 * 1,6 = 64 Н.
- Вы решили задачу. Ответ: вес тела массой 40 кг на поверхности Луны равен 64 Н, или Р = 64 Н.
- 3 Задача № 3. Найдите массу тела, которое на поверхности Земли весит 549 Н.
- В этой задаче Р = 549 Н, g = 9,8м/с 2 (так как дан вес тела на Земле).
- Выведите m из формулы P = mg. Получится m = P/g. Подставьте известные значения: m = 549/9,8 = 56 кг.
- Вы решили задачу. Ответ: масса тела, которое весит 549 Н (на поверхности Земли) равна 56 кг, или m = 56 кг.
Реклама
- 1 Не путайте массу и вес. Самая распространенная ошибка — перепутать вес и массу (что немудрено, ведь в повседневной жизни мы обычно называем массу весом). Но в физике все не так. Запомните, масса — это постоянное свойство объекта, то, сколько в нем вещества (килограммов), где бы он ни находился. Вес — это сила, с которой объект всеми своими килограммами давит на поверхность, и эта сила на разных небесных телах будет различной.
- 2 Используйте правильные единицы измерения. В задачах по физике вес или силу измеряют в ньютонах (Н), ускорение свободного падения — в метрах на секунду в квадрате (м/с 2 ), а массу — в килограммах (кг). Если для какой-либо из этих величин вы возьмете не ту единицу измерения, воспользоваться формулой будет нельзя, Если масса в условиях задачи указана в граммах или тоннах, не забудьте перевести ее в килограммы.
- 3 Проверяйте единицы измерения. Если вы решаете сложную задачу в несколько действий, следите, чтобы у вас получались правильные единицы. Запомните, что 1 ньютон эквивалентен 1 (кг*м)/с 2, При необходимости подставляйте этот эквивалент вместо ньютонов, чтобы путем сокращения получить нужную единицу.
- Задача. Вес Игоря на Земле составляет 880 ньютонов. Какова его масса?
- масса = (880 Н)/(9,8 м/с 2 )
- масса = 90 Н/(м/с 2 )
- масса = (90 кг*м/с 2 )/(м/с 2 )
- Сокращаем м/с 2 и получаем: масса = 90 кг.
- Масса должна быть выражена в килограммах, а значит, вы правильно решили задачу.
Реклама
- Ньютон — это единица измерения силы в международной системе единиц СИ. Нередко сила выражается в килограмм-силах, или кгс (в системе единиц МКГСС). Эта единица очень удобна для сравнения весов на Земле и в космосе.
- 1 кгс = 9,8166 Н.
- Разделите вес, выраженный в ньютонах, на 9,80665.
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне.
- Международная система единиц СИ — система единиц физических величин, которая является наиболее широко используемой системой единиц в мире.
Сколько весит 1 литр жира?
Сколько килограммов можно сбросить после операции? — За одну операцию откачивают, как правило, не больше 2,5 литра жира. Один литр весит около 900 граммов. То есть глобального похудения не будет.
Сколько жидкости на кг?
Сколько воды нужно пить в течение дня? — Здоровому взрослому человеку требуется около 35 мл воды в день на килограмм массы тела — в соответствии с общими рекомендациями научных организаций. Для человека весом 50 кг необходимо 1,7 л, 60 кг — 2,1 л, 70 кг — 2,4 л, 80 кг — 2,8 л воды каждый день.
- Основное правило: чем больше вы весите, тем больше воды нужно пить.
- Думаете, невозможно выпить слишком много воды? Слишком большое количество воды так же опасно для организма, как и обезвоживание.
- Рекомендуемый суточный объем отражает количество воды, которое ваши почки и сердце могут выдержать.
- Ежедневный объем воды также зависит от возраста, диеты, уровня активности и климата.
Активный ребенок, который гуляет на улице весь день, должен пить больше воды, чем ребенок, проводящий весь день в своей комнате за компьютером или книгами. Тем не менее, здоровому ребенку рекомендуется выпивать около 1,1 литра в день — независимо от чувства жажды.
Сколько воды в теле человека весом 60 кг?
Вычисли и запиши, сколько воды в теле человека, если его масса составляет. a)60кг-, б) 90кг-, Известно, что содержание воды в теле человека зависит от его возраста. Чем старше человек, тем меньше процентное содержание воды в его организме. Тело взрослого человека на 65% состоит из воды.
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Вычисли и запиши, сколько воды в теле человека, если его масса составляет. a)60кг-, б) 90кг-,
В чем измеряется вес тела?
У этого термина существуют и другие значения, см. Вес (значения), Не следует путать с массой, Вес — сила, с которой тело действует на опору (или подвес, или другой вид крепления), препятствующую падению, возникающая в поле сил тяжести, Единица измерения веса в Международной системе единиц (СИ) — ньютон, иногда используется единица СГС — дина,
Как найти вес через объем?
Вес можно рассчитать по формуле: m=V*p, где р – плотность, V – объем материала. Например, 10 м3 речного песка весят 13 тонн.
Чему равно g?
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 августа 2022 года; проверки требует 1 правка,
Ускорение свободного падения на поверхности некоторых небесных тел, м/с 2 и g
| Земля | 9,81 м/с 2 | 1,00 g | Солнце | 273,1 м/с 2 | 27,85 g |
| Луна | 1,62 м/с 2 | 0,165 g | Меркурий | 3,70 м/с 2 | 0,378 g |
| Венера | 8,88 м/с 2 | 0,906 g | Марс | 3,86 м/с 2 | 0,394 g |
| Юпитер | 24,79 м/с 2 | 2,528 g | Сатурн | 10,44 м/с 2 | 1,065 g |
| Уран | 8,86 м/с 2 | 0,903 g | Нептун | 11,09 м/с 2 | 1,131 g |
| Эрида | 0,82 ± 0,02 м/с 2 | 0,084 ± 0,002 g | Плутон | 0,617 м/с 2 | 0,063 g |
Ускоре́ние свобо́дного паде́ния ( ускорение силы тяжести ) — ускорение, придаваемое телу силой тяжести, при исключении из рассмотрения других сил. В соответствии с уравнением движения тел в неинерциальных системах отсчёта ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы,
Ускорение свободного падения на поверхности Земли g (обычно произносится как «же» ) варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах, Стандартное («нормальное») значение, принятое при построении систем единиц, составляет 9,80665 м/с², Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле: оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря,
В приблизительных расчётах его обычно принимают равным 9,81, 9,8 или более грубо 10 м/с².
Сколько воды в теле человека массой 60 кг?
Сколько воды в теле человека если его масса составляет 60 кг 42 кг 100:70=42(кг) ответ:42 килограмма в теле человека. (хорошего дня!!!) Содержание воды в теле человека зависит от многих факторов, в том числе и от возраста. Так, ребенок почти на 90% состоит из воды. Человек среднего возраста — уже на 70%.Предположим, нам надо рассчитать количество воды в теле человека среднего возраста, если его вес составлет 60 кг.Расчет будет выглядеть следующим образом:60:100х70=42 кг.Ответ: в теле человека среднего возраста весом 60 кг содержится 42 кг воды.
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Сколько воды в теле человека если его масса составляет 60 кг
Когда тело массой 10 кг опустили в воду оно потеряло в весе 25 Н?
Вес тела в воздухе найдем по формуле: P = m * g = 10 * 10 = 100 Ньютон. По условию задачи, при погружении в воду тело потеряло в весе 25 Ньютон, то есть: P1 = P — 25 = 100 — 25 = 75 Ньютон.
Сколько воды в теле если его масса составляет 60 кг?
Вычисли и запиши, сколько воды в теле человека, если его масса составляет. a)60кг-, б) 90кг-, Известно, что содержание воды в теле человека зависит от его возраста. Чем старше человек, тем меньше процентное содержание воды в его организме. Тело взрослого человека на 65% состоит из воды.
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Вычисли и запиши, сколько воды в теле человека, если его масса составляет. a)60кг-, б) 90кг-,
Чему равна масса и объем тела?
Содержание:
- § 1 Расчет массы и объема вещества по его плотности
- § 2 Решение задач
- § 3 Важно запомнить
§ 1 Расчет массы и объема вещества по его плотности В этом уроке мы изучим, как можно определить массу и объем тела, если известна плотность вещества. Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Из формулы плотности следует, что масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V. Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: v = m : p. Для правильного решения задач нужно уметь верно переводить единицы измерения величин в Международную систему единиц: 1 г = 0,001 кг, 1 л = 1 дм3 = 0,001 м3, 1 см3 = 0,000 001 м3, 1 г/см3 = 1000 кг/м3.
§ 2 Решение задач Какова масса подсолнечного масла в бутылке объемом 3 л, если плотность масла равна 930 кг/м3? Запишем условие задачи. Нам известны объем бутылки (обозначается буквой V) 3 л, и плотность подсолнечного масла (обозначается буквой ρ) 930 кг/м3. Сколько штук строительного кирпича размером 250 мм х 120 мм х 65 мм допускается перевозить на автомашине грузоподъемностью 4 т? Плотность кирпича 1800 кг/м3. Запишем условие задачи и выразим данные в Международной системе единиц. Известны размеры кирпича: длина а = 250 мм = 0,25 м, ширина b= 120 мм = 0,12 м, высота с = 60 мм = 0,06 м, плотность кирпича ρ = 1800 кг/м3, грузоподъемность – наибольшая масса груза, которую может перевезти автомобиль – m = 4 т = 4000 кг.
Найти количество кирпичей – обозначим латинской буквой N. Решение: Количество кирпичей можно найти, поделив общую массу всех кирпичей на массу одного кирпича: N = m/m1. Чтобы найти массу одного кирпича, нужно плотность умножить на его объем: m1 = ρ · V. Кирпич имеет форму прямоугольного параллелепипеда, следовательно, его объем равен произведению длины, ширины и высоты кирпича.
Подставим числовые значения известных величин и вычислим. Объем кирпича равен 0,0018 м3. Масса одного кирпича m1 равна 1800 кг/м3, умножим на 0,0018 м3, равно 3,24 кг. Тогда число кирпичей равно N 4000 кг, разделим на 3,24 кг и получим 1234, 567 штук или число целых кирпичей 1234 штуки. Медный шар имеет массу 840 г при объеме 120 см3. Сплошной этот шар или полый? Плотность меди 8900 кг/м3. Запишем условие задачи. Известна масса шара m 840 г, что в системе СИ составляет 0,84 кг, объем шара V=120 см3, в СИ 0,00 012 м3, плотность меди ρ = 8900 кг/м3.
- Определить, сплошной шар или содержит внутри пустое пространство? Решение.
- Представим, что на рычажных весах лежат два медных шара, один сплошной, второй содержит внутри пустое пространство, то есть полый шар.
- Если у них массы одинаковы, то объем полого шара должен быть больше, чем объем сплошного шара (рис 1).
Определим, каков объем шара, состоящего полностью из меди. Если объем окажется равным 120 см3, то шар сплошной и пустот не содержит. Если же вычисленный объем окажется меньше 120 см3, значит, внутри есть полость. Чтобы найти объем сплошного медного шара, массу шара разделим на его плотность. § 3 Важно запомнить Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v. Масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V. Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: V = m : p. Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. — М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика.7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика.7 класс — М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
Использованные изображения:
Профи
(535),
закрыт
7 лет назад
Светлана *******
Гуру
(2877)
7 лет назад
вес в воздухе – масса * 10
сила архимеда 1000*10*объем
вес в воде= вес в воздухе минус сила архимеда
При 211Ученик (123)
12 месяцев назад
Вес тела не может измениться в воде, просто вес будет приложен к воде
Необходимо объем тела умножить на плотность вещества и умножить на ускорение свободного падения
АС
Высший разум
(140971)
7 лет назад
P = Pо – Fа = Ро – Pж (вес тела, погруженного в жидкость или газ, уменьшается на величину выталкивающей силы, действующей на тело)
P = Pо – Fа = Ро – Pж =mg-qж*g*V (qж – плотность жидкости, которая для воды ≈1, g -ускорение свободного падения, V – объем тела, Ро- вес тела в вакууме, Pж – вес вытесненной жидкости)
Видеоурок: закон Архимеда
Зако́н Архиме́да — закон гидростатики и аэростатики: на тело, погружённое в жидкость или газ, действует выталкивающая сила, численно равная весу объема жидкости или газа, вытесненного телом. Закон открыт Архимедом в III веке до н. э. Выталкивающая сила также называется архимедовой силой или гидростатической подъёмной силой[1][2] (её не следует путать с аэро- и гидродинамической подъёмной силой, возникающей при обтекании тела потоком газа или жидкости).
Так как сила Архимеда обусловлена силой тяжести, то в невесомости она не действует.
В соответствии с законом Архимеда для выталкивающей силы выполняется[3]:
где:
Описание[править | править код]
Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.
Если тело плавает (см. плавание тел) или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа.
Плавание тела. Сила Архимеда (
) уравновешивает вес тела (
):
ρж g Vж = ρт g Vт
Например, воздушный шарик объёмом 
, наполненный гелием, летит вверх из-за того, что плотность гелия (
) меньше плотности воздуха (
):
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела, погруженного в жидкость или газ. В силу симметрии прямоугольного тела, силы давления, действующие на боковые грани тела, уравновешиваются. Давление (
) и сила давления (), действующие на верхнюю грань тела, равны:
где:
Давление (
) и сила давления (
), действующие на нижнюю грань тела, равны:
где:
Сила давления жидкости или газа на тело определяется разностью сил и :
где:
Разница давлений:
В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляцию жилых отсеков космических аппаратов необходимо производить принудительно вентиляторами.
Обобщения[править | править код]
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы[править | править код]
Вывод через мысленный эксперимент[править | править код]
Если мысленно заменить погружённое в жидкость тело той же жидкостью, мысленно размещённая в том же объёме порция воды будет находиться в равновесии и действовать на окружающую воду с силой, равной силе тяжести, действующей на порцию воды. Так как перемешивания частиц воды не происходит, можно утверждать, что окружающая вода действует на выделенный объём с той же силой, но направленной в противоположном направлении, то есть с силой, равной 
[4][5][6].
Расчёт силы[править | править код]
Гидростатическое давление 
на глубине 
, оказываемое жидкостью с плотностью 
на тело, есть 
. Пусть плотность жидкости () и напряжённость гравитационного поля (
) — постоянные величины, а — параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат 
, причём выберем направление оси z совпадающим с направлением вектора 
. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку 
. На неё будет действовать сила давления жидкости, направленная внутрь тела, 
. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.
Получаем, что модуль силы Архимеда равен 
, и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Вывод через закон сохранения энергии[править | править код]
Закон Архимеда можно также вывести из закона сохранения энергии. Работа силы, действующей со стороны погружённого тела на жидкость, приводит к изменению её потенциальной энергии:
где 
— масса вытесненной части жидкости, 
— перемещение её центра масс. Отсюда модуль вытесняющей силы:
По третьему закону Ньютона эта сила, равна по модулю и противоположна по направлению силе Архимеда, действующей со стороны жидкости на тело. Объём вытесненной жидкости равен объёму погруженной части тела, поэтому массу вытесненной жидкости можно записать как:
где — объем погружённой части тела.
Таким образом, для силы Архимеда имеем:
Условие плавания тел[править | править код]
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести 
и силы Архимеда , которые действуют на это тело. Возможны следующие три случая:
- — тело тонет;
- — тело плавает в жидкости или газе;
- — тело всплывает до тех пор, пока не начнёт плавать.
Другая формулировка (где 
— плотность тела, 
— плотность среды, в которую тело погружено):
- — тело тонет;
- — тело плавает в жидкости или газе;
- — тело всплывает до тех пор, пока не начнёт плавать.
Примечания[править | править код]
- ↑ Архимеда закон : [арх. 1 января 2023] // Анкилоз — Банка. — М. : Большая российская энциклопедия, 2005. — С. 331. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 2). — ISBN 5-85270-330-3.
- ↑ Архимеда закон // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 123. — 707 с. — 100 000 экз.
- ↑ Всё написанное ниже, если не оговорено иное, относится к однородному полю силы тяжести (например, к полю, действующему вблизи поверхности планеты).
- ↑ Перышкин А. , Оригинальное доказательство закона Архимеда. Дата обращения: 28 сентября 2020. Архивировано 20 июля 2020 года.
- ↑ Доказательство закона Архимеда для тела произвольной формы. Дата обращения: 28 сентября 2020. Архивировано 21 сентября 2020 года.
- ↑ Buoyancy (англ.). Архивировано 14 июля 2007 года.
Ссылки[править | править код]
- Архимедов закон // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Закон Архимеда // Энциклопедия «Кругосвет».
