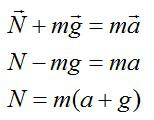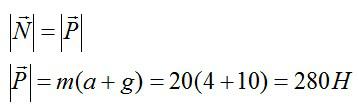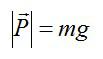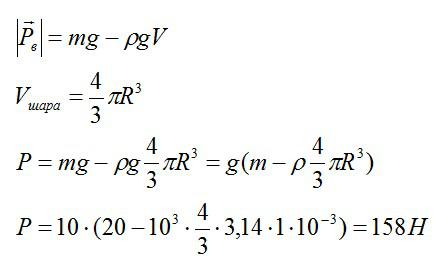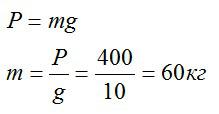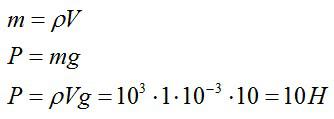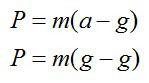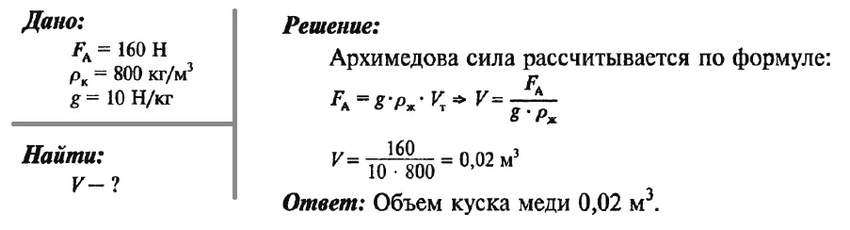Как найти вес шара в воздухе

Сегодняшняя тема – задачи на вес и невесомость. Разберем несколько примеров и вопросов, которые нужно знать при решении таких задач.

Больше разнообразной и полезной информации для учащихся ежедневно ждет вас на нашем телеграм-канале. 

Задачи на вес и невесомость с решениями

Задача №1. Задача на расчет веса тела, движущегося с ускорением

Условие

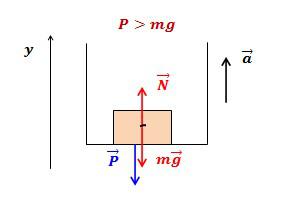
Груз массой 20 кг лежит на полу лифта, который движется вверх с ускорением а=4 м/с^2. Найти вес тела.

Решение

По второму закону Ньютона (в векторной форме и в проекции на ось y):

По третьему закону Ньютона:

Ответ: 280 Ньютонов

Задача №2. Задача на вычисление веса тела в жидкости

Условие

Шар радиусом 10 сантиметров имеет массу 20 килограмм. Сколько она будет весить в воде?

Решение

Вес шара в воздухе:

На тело, погруженное в жидкость, действует сила Архимеда:

Ответ: P=158 Н.

Задача №3. Нахождение веса тела при известной массе

Условие

Тело весит 400 Ньютонов. Какова его масса?

Решение

Ответ: 60 кг.

Задача №4. Вычисление веса жидкости

Условие

Какой вес имеет вода, полностью заполнившая литровую бутылку?

Решение

Зная объем воды и взяв из справочника ее плотность, вычислим массу воды:

Ответ: Р=10 Н.

Задача №5. Нахождение веса при свободном падении. Невесомость на Земле

Условие

Лифт с человеком срывается в шахте и свободно падает вниз, пока не сработает система безопасности. Чему в момент падения равен вес человека.

Решение

Лифт и человек движутся с ускорением a=g. Согласно второму и третьему законам Ньютона, вес человека в этом случае будет вычисляться по формуле:

Другими словами, человек никак не действует на опору, так она падает одновременно с ним. Типичный пример, когда вес равен нулю.

Ответ: P=0 Н.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Вопросы на тему «вес и невесомость»

Вопрос 1. В каком случае вес тела равен силе тяжести, действующей на него?

Ответ. Вес равен силе тяжести, если тело покоится или движется равномерно и прямолинейно (с нулевым ускорением).

Вопрос 2. В каких еще случаях можно испытывать состояние невесомости?

Ответ. Состояние невесомости также достигается при свободном падении.

Вопрос 3. Вредно ли длительное воздействие невесомости на здоровье?

Ответ. Длительное пребывание в невесомости влечет адаптивные изменения в сердечно-сосудистой и опорно-двигательной системах. Поэтому, по прибытии на Землю, космонавтам необходима реабилитация.

Вопрос 4. Где вес 100-киллограммового тела будет больше: на Земле, на Марсе или на Сатурне?

Ответ. Вес тела будет больше на Сатурне, так как там сильнее гравитационное взаимодействие.

Вопрос 5. От чего зависит вес тела?

Ответ. Вес зависит от ускорения, с которым движется тело, а также от физической среды, в которой тело находится. Например, в воде вес будет меньше, так как на тело действует выталкивающая сила Архимеда, которая частично компенсирует силу тяжести.

Все мы слышали слово «перегрузка». Перегрузка – противоположность невесомости. Это значит, что вес тела увеличивается из-за ускоренного движения опоры или подвеса.

Вес и невесомость: что есть что

Понятие веса широко используется в повседневной жизни. Но, решая задачи по физике, очень важно различать вес и массу.

Вес – это сила, к которой тело действует на опору или подвес вследствие притяжения к Земле.

Обозначается латинской буквой P, как и любая механическая сила, измеряется в Ньютонах. Вес – векторная физическая величина.

Не путайте вес с массой а также с силой тяжести! Это важно при решении задач.

Невесомость – отсутствие веса, то есть состояние тела, когда сила взаимодействия с опорой или подвесом отсутствует.

Космонавты на орбите испытывают состояние невесомости. Но не следует путать невесомость с отсутствием гравитации.

Примеры проявления невесомости:

• автомобиль подскакивает на ухабе и отрывается колесами от дороги;
• самолет проваливается в воздушную яму;
• десантник свободно падает, прежде чем раскрыть парашют;
• космонавт находится в космическом корабле, который движется по орбите с выключенным двигателем.

Нужна помощь в решении задач и выполнении других заданий? Обращайтесь в профессиональный студенческий сервис.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Задачи на силу Архимеда с решениями

Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Тело объемом 2 м³ погружено в воду. Найдите архимедову силу, действующую на тело.

Задача № 2.
Определить выталкивающую силу, действующую на деревянный плот объемом 12 м³, погруженный в воду на половину своего объема.

Задача № 3.
 Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?

Задача № 4.
 Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?

Задача № 5.
 Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?

Задача № 6.
Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?

Задача № 7.
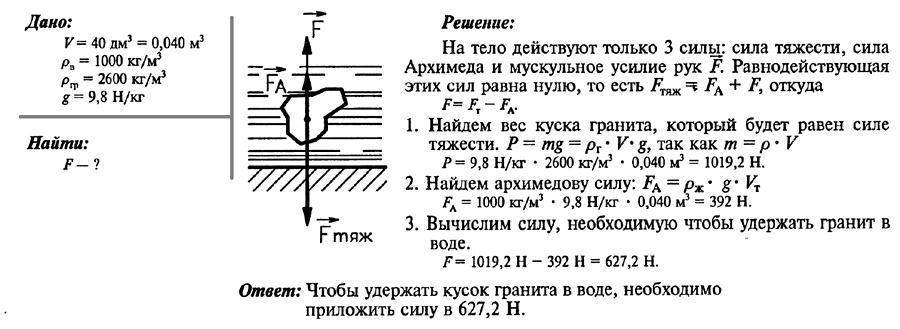
Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм³?

Задача № 8.
Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.

Задача № 9 (повышенной сложности).
 Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?

Задача № 10 (повышенной сложности).
 Рассчитайте, какой груз сможет поднять шар объемом 1 м³, наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)

Задача № 11.
  Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м³.

Дано: V – объем цилиндра (V = Sh);  h – высота цилиндра;  S – площадь основания цилиндра;  V₁ – объем цилиндра, погруженного в масло (V₁ = V – V₂ = Sh₁);  h₁ – высота части цилиндра, погруженной в масло;  V₂ – объем цилиндра, погруженного в воду после добавления масла;  р_в – плотность воды (1000 кг/м³);  р_м – плотность масла (800 кг/м³)

Найти:  (h – h₁) / h — ?

Решение.  F – сила, выталкивающая цилиндр из воды до добавления масла  F = 0,9p_вgV
F₁ – сила, выталкивающая цилиндр из масла   F₁ = p_мgV₁
F₂ – сила, выталкивающая цилиндр из воды после добавления масла  F₂ = p_вgV₂
Баланс сил: F – F₁ = F₂
0,9p_вgV – p_мgV₁ = p_вgV₂       V₁ = V – V₂   ⇒    0,9p_вV – p_м(V – V₂) = p_вV₂

V(0,9p_в – p_м) = V₂(p_в – p_м)         V = Sh;  V₁ = Sh₁    ⇒

Ответ: 1/2 часть цилиндра будет погружена в воду (50%).

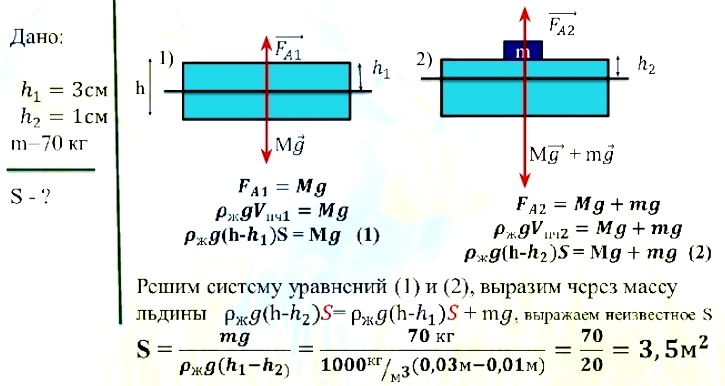
Задача № 12.
 Плоская льдина плавает в воде, выступая над уровнем воды на 3 см. Человек массой 70 кг зашел на льдину. В результате, высота выступающей части над льдиной уменьшилась в 3 раза. Найти площадь льдины.

Ответ: 3,5 м³.

Теория для решения задач.

Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = р_атм  + p*g*h

Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.

Конспект урока «Задачи на силу Архимеда с решениями».

Следующая тема: «Задачи на механическую работу».

Условия плавания тел. Воздухоплавание

1. Условия плавания тел
2. Плавание судов
3. Ареометр
4. Воздухоплавание
5. Задачи
6. Лабораторная работа №12. Изучение условий плавания тела в жидкости

На тело, погруженное в жидкость, действует выталкивающая сила $$ F_A=rho_text{ж}V_text{т}g $$ где (rho_text{ж}) – плотность воды; (V_text{т}) – объем тела (части тела), погруженного в жидкость; (g) – ускорение свободного падения (см. §33 данного справочника).

Выталкивающая сила (F_A) направлена вертикально вверх, сила тяжести (V_text{тяж}) направлена вертикально вниз. В зависимости от соотношения абсолютных величин этих двух сил, тело будет плавать иди тонуть.

• Если сила тяжести больше архимедовой силы (F_text{тяж}gt F_A), тело тонет.
• Если сила тяжести меньше архимедовой силы (F_text{тяж}lt F_A), тело всплывает.
• Если сила тяжести равна архимедовой силе (F_text{тяж}=F_A), и тело полностью погружено в воду, тело плавает на любой глубине.
• Если сила тяжести равна архимедовой силе (F_text{тяж}=F_A), и тело не полностью погружено в воду, тело плавает на поверхности.

В зависимости от соотношения плотности жидкости и плотности тела, получаем:

• Если плотность тела больше плотности жидкости (rho_text{т}gt rho_text{ж}) тело тонет.
• Если плотность тела меньше плотности жидкости (rho_text{т}lt rho_text{ж}), тело всплывает и плавает на поверхности. Чем меньше плотность тела по сравнению с плотностью жидкости, тем меньшая часть тела погружена в жидкость.
• Если плотность тела равна плотности жидкости (rho_text{т}=rho_text{ж}), и тело полностью погружено в воду, тело плавает на любой глубине.

п.2. Плавание судов

Чтобы судно держалось на воде, вес воды, вытесняемой подводной частью судна, должен быть равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом: begin{gather*} F_A=rho_text{в}V_text{подв}g \[7pt] P=Mg\[7pt] P=F_ALeftrightarrow M=rho_text{в}V_text{подв} end{gather*} В подводной части корабля есть большие полости, поэтому подводная часть имеет большой объем (V_text{подв}), который обеспечивает большую величину выталкивающей силы, достаточную для уравновешивания суммарного веса корабля и груза.

Глубину погружения судна в воду называют осадкой. Поскольку плотность речной воды меньше, чем плотность морской воды, при заходе в реку осадка увеличивается.

Наибольшую допустимую осадку называют ватерлинией; как правило, её отмечают на корпусе красной линией.

Водоизмещение судна – это вес воды, вытесняемой судном с грузом при погружении до ватерлинии, равный силе тяжести, действующей на судно с максимальным допустимым грузом.

п.3. Ареометр

Ареометр – прибор для измерения плотности жидкостей или концентрации растворов, принцип работы которого основан на законе Архимеда.

п.4. Воздухоплавание

Если наполнить шар газом, плотность которого меньше, чем плотность воздуха, то за счет действия выталкивающей силы можно подняться над поверхностью Земли. Плотность воздуха при (t=0^circ C), (p=760 text{мм рт.ст.}) $$ rho_text{возд}=1,290 text{кг/м}^3 $$ При тех же условиях плотность водорода $$ rho_{mathrm{H_2}}=0,090 text{кг/м}^3, $$ плотность гелия $$ rho_{mathrm{He}}=0,179 text{кг/м}^3, $$

Поскольку (rho_{mathrm{H_2}}lt rho_text{возд}) и (rho_{mathrm{He}}lt rho_text{возд}), воздушные шары, наполненные этими газами, будут подниматься наверх в атмосфере; сила Архимеда, действующая на них, будет больше силы тяжести.

Подъемная сила воздушного шара – это разность между силой Архимеда, действующей на шар в воздухе, и весом шара.

Можно также заполнять шар обычным воздухом, только горячим. Плотность воздуха заметно уменьшается с ростом температуры. Например, при (t=20^circ C), (rho_text{возд}=1,205 text{кг/м}^3), а при (t=120^circ C), (rho_text{возд}=0,898 text{кг/м}^3). С повышением температуры, плотность воздуха внутри шара уменьшается, становится меньшим вес шара, а его подъёмная сила увеличивается. Если хотим подняться наверх, включаем горелку. Если хотим опуститься, выключаем горелку.

п.5. Задачи

Задача 1. Определите наименьшую площадь плоской льдины толщиной 40 см, способной удержать на себе человека массой 72 кг. Плотность льда 900 кг/м³.

Дано:
(h=40 text{см}=0,4 text{м})
(rho=900 text{кг/м}^3)
(m=72 text{кг})
(rho_text{в}=1000 text{кг/м}^3)
__________________
(S-?)

Общий вес льдины и человека begin{gather*} P=(M_text{л}+m)g=(rho V+m)g end{gather*} Объем льдины (V=Sh)
При полном погружении льдины в воду на нее будет действовать выталкивающая сила (F_A=rho_text{в}Vg). Чтобы льдина больше не погружалась, должно выполняться условие begin{gather*} P=F_A\[7pt] (rho V+m)g=rho_text{в}Vg\[7pt] rho V+m=rho_text{в}V\[7pt] m=(rho_text{в}-rho)V=(rho_text{в}-rho)Sh end{gather*} Площадь льдины begin{gather*} S=frac{m}{(rho_text{в}-rho)h} end{gather*} Получаем begin{gather*} S=frac{72}{(1000-900)cdot 0,4}=1,8 (text{м}^2) end{gather*} Ответ: 1,8 м²

Задача 2. Найдите вес, архимедову силу и подъемную силу воздушного шара объемом (V=40 text{м}^3), наполненного гелием. Плотность воздуха (rho_text{возд}=1,29 text{кг/м}^3), плотность гелия (rho_{mathrm{He}}=0,18 text{кг/м}^3); (g=9,8 text{м/с}^2). Ответы округлите до десятых долей ньютона.
Может ли шар поднять груз весом (400 text{Н})?

Дано:
(rho_text{возд}=1,29 text{кг/м}^3)
(rho_{mathrm{He}}=0,18 text{кг/м}^3)
(g=9,8 text{м/с}^2)
(P_{text{гр}}=400 text{Н})
__________________
(P, F_A, F_{text{под}}-?)

Вес шара: begin{gather*} P=mg=rho_{mathrm{He}}Vg=0,18cdot 40cdot 9,8approx 70,6 (text{Н}) end{gather*} Архимедова сила, действующая на шар в воздухе: $$ F_A=rho_text{возд}Vg=1,29cdot 40cdot 9,8approx 505,7 (text{Н}) $$ Подъёмная сила шара: begin{gather*} F_{text{под}}=F_A-P=505,7-70,6=435,1 (text{Н}) end{gather*} Вес груза меньше подъемной силы: $$ 400 text{Н}lt 435,1 text{Н}, P_{text{гр}}lt F_{text{под}} $$ Шар может поднять этот груз.
Ответ: 70,6 Н; 505,7 Н; 435,1 Н; может

Задача 3. Льдина плавает в пресной воде. Объем ее надводной части 20 м³. Каков объем подводной части? Плотность льда 900 кг/м³.

Дано:
(rho=900 text{кг/м}^3)
(V_text{над}=20 text{м}^3)
(rho_{text{в}}=1000 text{кг/м}^3)
__________________
(V_{text{под}}-?)

Вес льдины в воздухе: begin{gather*} P=Mg=rho Vg=rho(V_text{над}+V_{text{под}})g end{gather*} Сила Архимеда, действующая на подводную часть: begin{gather*} F_A=rho_{text{в}}V_{text{под}}g end{gather*} Силы уравновешивают друг друга begin{gather*} P=F_A\[7pt] rho(V_text{над}+V_{text{под}})g= rho_{text{в}}V_{text{под}}g\[7pt] rho(V_text{над}+V_{text{под}})= rho_{text{в}}V_{text{под}}\[7pt] (rho_{text{в}}-rho)V_{text{под}}=rho V_text{над} end{gather*} Объем подводной части begin{gather*} V_{text{под}}=frac{rho}{rho_{text{в}}-rho}V_text{над} end{gather*} Для льда и воды в общем случае begin{gather*} V_{text{под}}=frac{900}{1000-900}V_text{над}=9V_text{над} end{gather*} Объем подводной части льда в воде в 9 раз больше объема надводной части.
В данном случае: $$ V_{text{под}}=9cdot 20=180 (text{м}^3) $$ Ответ: 180 м³

Задача 4*. Наполненный теплым воздухом воздушный шар объемом 1600 м³ парит на высоте 5,5 км, где плотность воздуха в два раза меньше, чем на уровне моря. Какова плотность воздуха внутри шара, если общая масса его оболочки и груза 150 кг? Ответ округлите до сотых долей кг/м³.

Дано:
(V=1600 text{м}^3)
(rho=frac 12rho_0)
(M=150 text{кг})
(rho_0=1,29 text{кг/м}^3)
__________________
(rho_{text{ш}}-?)

Масса шара – сумма массы оболочки с грузом и воздуха внутри: begin{gather*} M_{text{ш}}=M+rho_{text{ш}}V end{gather*} Вес шара: begin{gather*} P=M_{text{ш}}g=(M+rho_{text{ш}}V)g end{gather*} Выталкивающая сила на данной высоте begin{gather*} F_A=rho Vg=frac 12rho_0 Vg end{gather*} Условие равновесия begin{gather*} P=F_A\[6pt] (M+rho_{text{ш}}V)g=frac 12rho_0 Vg\[6pt] M+rho_{text{ш}}V=frac 12rho_0 V\[6pt] rho_{text{ш}}V=frac 12rho_0 V-M end{gather*} Плотность воздуха в шаре begin{gather*} rho_{text{ш}}=frac 12rho_0-frac MV end{gather*} Получаем begin{gather*} rho_{text{ш}}=frac 12cdot 1,29-frac{150}{1600}approx 0,55 text{кг/м}^3 end{gather*} Ответ: ≈55 кг/м³

Задача 5*. Льдинка плавает на границе между водой и керосином. Какая часть её объема находится ниже этой границы, если керосин покрывает льдинку полностью?

Дано:
(rho_1=800 text{кг/м}^3)
(rho_2=1000 text{кг/м}^3)
(rho=900 text{кг/м}^3)
__________________
(frac{V_text{под}}{V}-?)

Пусть высота слоя керосина над границей с водой равна (h_1), высота льдинки над границей равна (h_text{над}), высота льдинки под границей равна (h_text{под}).
Сверху на льдинку действует сила (F_1), которая равна давлению столба керосина высотой (h_1-h_text{над}) на площадь верхней поверхности льдинки: begin{gather*} F_1=rho g(h_2-h_text{над})S. end{gather*} Снизу по закону Паскаля на льдинку действует сила (F_2), которая равна сумме давлений всего столба керосина высотой (h_1) и столба воды высотой (h_text{под}) на площадь нижней поверхности льдинки: begin{gather*} F_2=rho_1 gh_1S+rho_2gh_text{под}S. end{gather*} На любом промежуточном уровне силы, действующие на боковые поверхности, равны по значению и противоположны по направлению, т.е. взаимно уравновешивают друг друга.
Равнодействующая всех сил, действующих на тело со стороны жидкости, является выталкивающей силой и равна: begin{gather*} F_A=F_2-F_1=rho_1gh_1S+rho_2gh_text{под}S-rho_1g(h_1-h_text{над})S=\[7pt] =(rho_1H_1rho_2h_text{под}-rho_1h_1+rho_1h_text{над})gS=(rho_1h_text{над}+rho_2h_text{под})gS=\[7pt] =(rho_1V_text{над}+rho_2V_text{под})g end{gather*} Учитывая, что (V_text{над}=V-V_text{под}), получаем begin{gather*} F_Aleft(rho_1(V-V_text{под})+rho_2V_text{под}right)g=left(rho_1V+(rho_2-rho_1)V_text{под}right)g end{gather*} Вес льдинки (P=rho Vg). Условие равновесия begin{gather*} P=F_A\[7pt] rho Vg=left(rho_1V+(rho_2-rho_1)V_text{под}right)g\[7pt] rho V=rho_1V+(rho_2-rho_1)V_text{под}\[7pt] (rho-rho_1)V=(rho_2-rho_1)V_text{под} end{gather*} Часть объема льдинки под границей между керосином и водой: begin{gather*} frac{V_text{под}}{V}=frac{rho-rho_1}{rho_2-rho_1} end{gather*} Подставляем: begin{gather*} frac{V_text{под}}{V}=frac{900-800}{1000-800}=frac 12 end{gather*} Под границей находится половина льдинки.
Ответ: 1/2

п.6. Лабораторная работа №12. Изучение условий плавания тела в жидкости

Цель работы
Изучить условия плавания тел в жидкости.

Теоретические сведения

Выталкивающая сила (F_A) направлена вертикально вверх, сила тяжести (F_text{тяж}) направлена вертикально вниз. В зависимости от соотношения абсолютных величин этих двух сил, тело будет плавать иди тонуть.

Выталкивающая сила в работе определяется весом вытесненной телом воды.

Чтобы определить этот вес, отметьте уровни воды в измерительном цилиндре до погружения тела в воду и после погружения. Разность уровней даст вам объем вытесненной телом воды (V_text{т}), по которому находится (F_A=rho_text{в}V_text{т}g).

Масса тела (m) определяется взвешиванием. Вес рассчитывается по формуле (P=mg).

Значение (g) в работе можно принять (gapprox 10 text{м/с}^2).

Приборы и материалы
Весы с разновесами, измерительный цилиндр, пробирка-поплавок с пробкой, сухой песок, сухая ткань.

Ход работы
1. Насыпьте в пробирку песка так, чтобы она в мерном цилиндре плавала вертикально, и часть ее была над водой.
2. Отметьте уровни воды в измерительном цилиндре до погружения пробирки в воду ((V_1)) и после погружения ((V_2)). Найдите объем вытесненной пробиркой воды (V_text{т}=V_2-V_1).
3. Выньте пробирку из воды, тщательно протрите ее сухой тканью. Определите взвешиванием массу пробирки с точностью до 1 г.
4. Рассчитайте выталкивающую силу и вес пробирки, занесите данные в таблицу.
5. Насыпьте в пробирку еще немного песка и повторите процедуру, начиная с п.2. Проделайте так несколько раз, пока пробирка не утонет.
6. Сделайте выводы об условиях плавания тел в жидкости.

Результаты измерений и вычислений

№ опыта	V1, мл	V2, мл	Vт, мл	m, г	FA, мН	P, мН	Поведение пробирки
1	200	234	34	34	340	340	(F_A=P) плавает на поверхности, выступает на 1/3
2	200	245	45	45	450	450	(F_A=P) плавает на поверхности, выступает на 1/5
3	200	254	54	54	540	540	(F_A=P) плавает на любой глубине
4	200	254	54	67	540	670	(F_Alt P) тонет

$$ 1 text{мл}=10^{-3} text{л}=10^{-3} text{дм}^3=10^{-6} text{м}^3 $$
Вычисления для первого опыта: begin{gather*} F_A=rho_text{в}V_text{т}g=1000cdot 34cdot 10^{-6}cdot 10=340cdot 10^{-3} (text{Н})=340 (text{мН})\[7pt] P=mg=34cdot 10^{-3}cdot 10=340cdot 10^{-3} (text{Н})=340 (text{мН}) end{gather*} Вычисления для остальных опытов проводятся аналогично.

Выводы
На основании проведенных экспериментов можно сделать следующие выводы.

Если вес равен архимедовой силе (P=F_A=540 text{мН}), пробирка полностью погружена в воду и плавает на любой глубине. Средняя плотность пробирки при этом равна плотности воды.

Если вес равен архимедовой силе (P=F_Alt 540 text{мН}), пробирка не полностью погружена в воду, она плавает на поверхности. Чем меньше P, тем большая часть пробирки выступает над водой; тем меньше средняя плотность пробирки по сравнению с плотностью воды.

Если вес больше архимедовой силы (Pgt F_A=540 text{мН}), пробирка тонет. Её средняя плотность становится больше плотности воды.