Как найти вес сплава

При решении задач на сплавы и смеси считают, что сумма масс сплавляемых веществ равна массе получаемого сплава, что сумма масс вещества, входящего в сплавы равна массе этого вещества в полученном сплаве. Аналогичное допущение принимаем и для сумм масс (объёмов) при смешивании жидкостей.

Рассмотрим подготовительную задачу.

Задача 1. Имеется уксусный раствор массой 1,5 кг, содержащий 40 % уксуса. Сколько килограммов воды нужно добавить в раствор, чтобы новый раствор содержал 10 % уксуса?

Решение. I способ.
1) 40 : 10 = 4 (раза) — во столько раз уменьшилась концентрация уксуса в растворе и увеличилась масса раствора,
2) 1,5 * 4 = 6 (кг) — масса нового раствора,
3) 6 – 1,5 = 4,5 (кг) — воды надо добавить.

II способ. 1) 0,4 * 1,5 = 0,6 (кг) — масса уксуса в первом растворе.
2) Пусть добавили x кг воды. Составим уравнение:
0,1(1,5 + x) = 0,6.
Оно имеет единственный корень 4,5. Значит, надо добавить 4,5 кг воды.
Ответ. 4,5 кг.

Рассмотрим способы решения задач на смеси и сплавы из сборников вариантов для подготовки к ЕГЭ.

Задача 2. (2017) В сосуд, содержащий 7 литров 15-процентного водного раствора некоторого вещества, добавили 8 литров воды. Определите процентную концентрацию того же вещества в новом растворе.

Задача 3. (2018) Имеется два сплава. Первый содержит 25 % никеля, второй — 30 % никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 28 % никеля. На сколько килограммов масса первого сплава меньше массы второго?

Решение. Пусть масса первого сплава x кг, второго (150 – x) кг, третьего — 150 кг. Найдём массу никеля в каждом из трёх сплавов. Никеля было
в первом сплаве 0,25x кг,
во втором — 0,3(150 – x) кг,
в третьем — 0,28 *150 = 42 (кг).

Составим уравнение:
0,25x + 0,3(150 – x) = 42.
Решив уравнение, получим его единственный корень x = 60. Теперь ответим на вопрос задачи. Масса первого сплава 60 кг, масса второго сплава 90 кг, первая меньше второй на 30 кг.

Ответ. На 30 кг.

Задача 4. (2019) Первый сплав содержит 5 % меди, второй — 14 % меди. Масса второго сплава больше массы первого сплава на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найдите массу третьего сплава.

Решение. Пусть масса первого сплава x кг, второго (x + 7) кг, третьего — (2x + 7) кг. Меди было в первом сплаве 0,05x кг, во втором — 0,14(x + 7) кг, в третьем — 0,1(2x + 7) кг. Составим уравнение:
0,05x + 0,14(x + 7) = 0,1(2x + 7).
Решив уравнение, получим его единственный корень x = 28. При x = 28 масса третьего сплава 2x + 7 равна 63 кг.
Ответ. 63 кг.

Задача 5. (2017) Смешав 70 %-й и 60 %-й растворы кислоты и добавив 2 кг чистой воды, получили 50 %-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90 %-го раствора той же кислоты, то получили бы 70 %-й раствор кислоты. Сколько килограммов 70 %-го раствора кислоты использовали для получения смеси?

Решение. Пусть масса первого раствора x кг, второго y кг. Приравняв массы кислоты до смешивания и после смешивания, составим два уравнения:
0,7x + 0,6y = 0,5(x + y + 2),
0,7x + 0,6y + 0,9*2 = 0,7(x + y + 2).
Решив систему этих двух уравнений, получим её единственное решение:
x = 3, y = 4. Использовали 3 кг 70 %-го раствора кислоты.
Ответ. 3 кг.

Задача 6. (2017) Имеется два сосуда. Первый содержит 100 кг, а второй — 50 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 28 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?

Для второго смешивания возьмём 1 кг первого раствора и 1 кг второго, получим 2 кг смеси. Составим первое уравнение:

Решив систему уравнений (1) и (2), получим её единственное решение: x = 12, y = 60. В первом сосуде содержится x * 100 / 100 = 12 (кг) кислоты. Ответ. 12 кг.

Для самостоятельного решения

7. Имеется 400 г морской воды, содержащей 4 % соли. Сколько граммов чистой воды нужно добавить в эту морскую воду, чтобы новый раствор содержал 2 % соли?

8. (2016) В сосуд, содержащий 10 литров 24-процентного водного раствора некоторого вещества, добавили 5 литров воды. Определите процентную концентрацию того же вещества в новом растворе.

9. (2009) В бидон налили 4 литра молока трёхпроцентной жирности и 6 литров молока шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне?

10. (2017) Имеется два сплава. Первый содержит 5 % никеля, второй — 20 % никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 15 % никеля. На сколько килограммов масса первого сплава меньше массы второго?

11. (2017) Первый сплав содержит 5 % меди, второй — 11 % меди. Масса второго сплава больше массы первого сплава на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найдите массу третьего сплава.

12. В первом сплаве отношение массы олова к массе свинца 2 : 3, во втором 1 : 5. В каком отношении надо взять массы этих сплавов, чтобы получить третий сплав с отношением массы олова к массе свинца 1 : 2?

13. В первом сплаве отношение массы олова к массе свинца 2 : 3, во втором 1 : 5. В каком отношении надо взять массы этих сплавов, чтобы получить третий сплав с отношением массы олова к массе свинца 1 : 2?

Ответы. 7. 400 г. 8. 16 %. 9. 4,8 %. 10. На 75 кг. 11. 6 кг. 12. 5 : 2. 13. 5 : 2.

Для работы с задачами в классе можно использовать вариант заметки в виде презентации: Сплавы и смеси. Задачи 11 из ЕГЭ.

Кто не видел белого медведя? В зоопарках он – обычный гость. Нет нужды описывать, каков он на вид. Напомним лишь, что у него только нос черный, сам медведь белый и зимой, и летом (а не как, скажем, песец или заяц-беляк – те лишь зимой белые). Подошвы лап у белого медведя густой шерстью поросли, а пальцы примерно на половину своей длины соединены плавательными перепонками. 

Плавают и ныряют белые медведи отлично. Две минуты могут пробыть под водой, но погружаются в нее редко глубже двух метров. Далеко в открытом море не раз видели белых медведей, даже медведиц с медвежатами. Плывут со скоростью 5 километров в час, не беспокоясь, что ни земли, ни льдов нигде вблизи не видно.

Белый медведь и тюленей ловит не только на льду, украдкой к ним подползая. Обычный его прием, так сказать, атаки с моря такой: поблизости от лежбищ тюленей медведь осторожно, без плеска и шума, сползает в воду, плывет туда, где заметил тюленей. Затем он бесшумно ныряет и выныривает уже у самого лежбища, быстро карабкается на лед, отрезая тем самым тюленям путь к спасительной воде. По отвесным ледяным стенам медведь может прямо из воды выпрыгнуть на льдину, даже если высота ее над водой два метра.

Тюлени – главная охотничья добыча белого медведя весной. За год ловит и съедает он примерно 50 тюленей. Летом меню его более разнообразно. Ловит он рыбу на мелкой воде, на берегу – леммингов, песцов, лакомится яйцами птиц. Когда голоден, ест ягоды, водоросли, мхи, лишайник, грибы.

Белый медведь – самый могучий из сухопутных хищных зверей. Лев и тигр в сравнении с ним легковесы: средний вес медведиц 310 килограммов, медведей-самцов – 420 килограммов. Если медведь матерый и хорошо упитанный, то он может весить целую тонну!

Акимушкин И.И. Мир животных: Млекопитающие, или звери. – М., 1988 г

IV. Тест по русскому языку

1. В тексте про белых медведей больше всего предложений:

а) повествовательных; б) вопросительных

2. Восклицательное предложение находится: 

а) в начале текста; б) в конце текста

3. Вопросительное предложение находится 

а) в начале текста; б) в конце текста

4. Выпиши из второй части текста (из второго абзаца) первое предложение. Разбери его по членам предложения. Что ты можешь сказать о сказуемых? Они являются

а) родственными словами; б) однородными членами предложения 

5. Что можно сказать о глаголах, которыми выражены сказуемые? Эти глаголы:

а) I спряжения; б) II спряжения

6. Эти глаголы стоят в форме:

а) настоящего времени; б) будущего времени; в) прошедшего времени

7. Эти глаголы стоят в форме:

а) единственного числа; б) множественного числа

8. Эти глаголы стоят в форме:

а) 1-го лица;     б) 2-го лица;  в) 3-го лица;    г)нельзя определить лицо

9. Эти глаголы стоят в форме:

а) ж.р.; б) м.р.; в) ср.р.; г) нельзя определить род

10. Найди во второй части текста (во втором абзаце) все слова, которые являются родственными существительному, являющемуся подлежащим в первом предложении. Запиши их столбиком, поставив в начальную форму. У тебя получилось:

а) два слова; б) три слова  

11. Найди во второй части текста (во втором абзаце) другую форму слова, которое является подлежащим в первом предложении. Выпиши такое словосочетание с формой этого слова, из которого можно определить его падеж. Этот падеж: 

а) Р.п.; б) В.п.

Бутко Сергей Васильевич-учитель математики высшей категории К.Г.У. Вечерняя средняя общеобразовательная школа при Е.С. учреждение 1643 г Петропавловска Сев.Каз.обл.

В школьном курсе математики предлагается очень мало задач на «смеси и сплавы». Эти задачи предлагаются на ЕНТ, вступительных экзаменах в вузы на экономические специальности на факультетах, связанных с легкой промышленностью и народным хозяйством. Задачи на «смеси и сплавы» встречаются на олимпиадах.

Учимся решать задачи на «смеси и сплавы»

Цель: объяснить решение задач на «смеси и сплавы»

Методы: объяснение, решение задач.

Ход занятия

Объяснение нового материала.

Задача 1. Имеется кусок сплава меди с оловом общей мас­сой 12 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы получившийся сплав содержал 40% меди?

Решение.

1. 12 • 0,45 = 5,4 (кг) — чистой меди в первом сплаве;

2. 5,4 : 0,4 = 13,5 (кг) — вес нового сплава;

3. 13,5 – 12 = 1,5 (кг).

Ответ: надо добавить 1,5 кг олова.

Задача 2. Имеется два сплава, состоящие из меди, цинка
и олова. Известно, что первый сплав содержит 40%
олова, а второй—26% меди. Процентное содержа­ние цинка в первом и втором сплавах одинаково. Спла­вив 150 кг первого сплава и 250 кг второго, получи­ли новый сплав, в котором оказалось 30% цинка.
Определите, сколько килограммов олова содержится в получившемся новом сплаве.

Для решения задачи полезно составить таблицу:

	Медь	Цинк	Олово	Масса
1-й сплав		30%	40%	150 кг
2-й сплав	26%	30%		250 кг
3-й сплав		30%	? кг	400 кг

Так как процентное содержание цинка в первом и втором сплавах и в третьем сплаве оказалось 30%, то в первом и втором сплавах процентное содержание цинка 30%.

Дальше задача легко решается по действиям:

1. 250 · 0,3 = 75 (кг) — цинка во втором сплаве;

2. 250 · 0,26 = 65 (кг) — меди во втором сплаве;

1. 250 – (75 + 65) = 110 (кг) — олова во втором сплаве;

1. 150-0,4 = 60 (кг) — олова в первом сплаве;

5) 110 + 60 = 170 (кг) — олова в третьем сплаве.
Ответ: 170 кг.

3. В сплаве весом 10 кг отношение меди к цинку равно 4 : 1, во втором сплаве весом 16 кг отношение меди к цинку равно 1:3. Сколько надо добавить чи­стой меди к этим сплавам, чтобы получить сплав, в котором отношение меди к цинку равно 3 : 2?

Таблица поможет решить задачу.

Пусть добавили Х кг чистой меди.

Медь Цинк Масса

1-й сплав 4 части 1 часть 10 кг

2-й сплав 1 часть 3 части 16 кг

3-й сплав 3 части 2 части (10 + 16 + Х) кг

1) 10 : 5 • 4 = 8 (кг) — чистой меди в 1-м сплаве;

2) 16 • =4 (кг) — чистой меди во 2-м сплаве.

12+х = (26+х), х=9.

Ответ: 9 кг.

Задача 4. Кусок сплава меди с цинком массой 36 кг содержит 45% меди. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60% меди?

36∙0,45 =16,2 (кг) – меди в 1-м сплаве.

Пусть добавили х кг меди.

Меди во 2-м сплаве (16,2+х) или (36+х)0,6.

16,2+х = 0,6(36+х), х=13,5

Ответ: 13,5 кг.

.

Задача 5. Имеется лом стали двух сортов содержание никеля 5% и 40%. Сколько нужно взять металла каждого из этих сортов, чтобы получить 140 т стали с содержанием 30% никеля?

5% никеля 40% никеля

х т у т

30 % никеля

140 т

По схеме учащиеся легко составляют систему уравнений

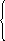х+у=140,

0,05х+0,4у=0,3∙140

Решая систему, получаем 40 т и 100 т.

Задача 6. В двух различных сплавах железо и олово на­ходятся в отношении 2:5 и 4:3.Сколько килограм­мов каждого сплава нужно взять, чтобы получить 14 кг нового сплава с равным содержанием железа и олова?

Учащиеся по условию задачи делают вывод, что железа и олова в сплаве должно быть по 7 кг. Отсюда легко получается система

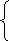
х +у = 7,

х +у = 7.

где х кг и у кг — массы первого и второго сплавов.

Ответ: 3,5 кг железа и 10,5 кг олова.

Задача 7. В сплаве золота на 200 г больше, чем серебра. После того, как из сплава выделили золота и 80% серебра, вес сплава оказался равным 80 г. Сколь­ко весил сплав первоначально?

Разберем подробно решение.

Пусть в сплаве х г золота, серебра — у г. Разница в весе (х – у) г, или по условию 200 г.

Имеем уравнение х – у = 200 . В сплаве золота осталось

Х – Х = х.

Серебра осталось у – 0,8у = 0,2у. Вес сплава стал (х +0,2у) г, или 80 г.

Имеем уравнение х + 0,2у = 80.

Так как х в каждом уравнении имеет один и тот же смысл и у обозначает в каждом уравнении одно и то же, то имеем систему

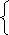х – у = 200,

х+0,2у = 80.

Решая эту систему, получим: у = 25, х = 225. Итак, первона­чально сплав весил 250 г.

Ответ: 250 г

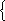Задача 8. Имеется смесь из двух веществ массой 900 г. После того как выделили первого вещества и 70% второго, то второго вещества осталось на 18 г боль­ше, чем первого в смеси. Сколько осталось каждого вещества? х + у = 900,

0,Зу – х = 18; х = 540, у = 360.

1) 540 ∙ = 90 (г); 2) 360 ∙ 0,3 = 108 (г).

Ответ: 90г и 108г.

Задача 9 . 36 г цинка в воде весят 31г, а 23г свинца в воде весят 21 г. Сплав цинка и свинца весом 118г весит в воде 104 г. Сколько цинка и сколько свинца содержится в сплаве?

Эту задачу можно решать так.

х — частей цинка в сплаве;

у — частей свинца в сплаве.

Тогда сплав весит 36х + 23у или 118 г. Имеем уравнение 36х + 23у= 118. В воде этот сплав весит 31х + 21у, или 104. Имеем второе уравнение:

31х + 21у= 104.

Р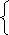ешая систему 36х + 23у = 118,

31х +21у = 104. х = 2, у =2

Значит, 36 • 2 = 72 (г) цинка и 23 • 2 = 46 (г) свин­ца в сплаве.

Ответ: 72 г цинка, 46 г свинца.

Эту задачу можно решить, если за неизвестное обозначить массу металлов.

х (г) — цинка в сплаве,

у (г) — свинца в сплаве.

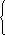Составляем систему х + у = 118,

х + у = 104, решаем ее и получаем ответ.

Задача 10. 24г одного металла в воде весят 21г, а 14г другого металла в воде весят12г. Сплав из этих ме­таллов весом 100 г весит в воде 87 г. Сколько каждого­ металла содержится в сплаве?

24x + 14у= 100,

21х + 12у = 87;

х = 3, у = 2.

1) 24 • 3 = 72 (г);

2) 14-2 = 28 (г).

Ответ: 72 г и 28 г.

Задача 11.Имеются три слитка массой в 5 кг,3 кг и 2 кг. Каждый представляет собой сплав серебра и меди. Если сплавить первый и второй слитки, то в этом
сплаве будет 75% серебра; если сплавить первый и третий слитки, то в этом сплаве будет 78% серебра; если же сплавить второй и третий слитки, то в этом сплаве будет 85,2% серебра. Сколько процентов се­ребра содержится в каждом слитке? (Потери при пе­реплавке не учитывать.)

Пусть а, в и с — процентное содержание серебра в каждом слитке.

Тогда составляем уравнения по мас­се серебра в слитках.

5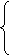а + 2с = 7 ∙ 0,78,

3в + 2с = 5∙ 0,852,

5а + 3в = 8 ∙ 0,75: а = 0,72, в = 0,8, с = 0,93.

Получаем: 72%, 80%, 93%.

Задача 12. Если к сплаву меди и цинка прибавить 20 г меди, то содержание меди в сплаве станет равным 70%. Если к первоначальному сплаву добавить 70 г сплава, содержащего 40% меди, то содержание меди станет равным 52%. Найдите первоначальный вес сплава.

Решить задачу помогут схемы.

1.

Медь, цинк

медь

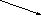
х г 20 г

70 % меди, цинк

(х + 20) г

2.

Медь, цинк

40% меди, цинк

х г 70 г

52% меди, цинк

(х + 70) г

Пусть у процентное содержание меди в первоначальном сплаве, тогда:

1. 0,7 ∙ (х + 20) = 20 + 0,01ух,

или 14 + 0,7х = 20 + 0,01ху;

1. 0,52 ∙ (х + 70) = 0,4 ∙ 70 + 0,01ух,

или 36,4 + 0,52х = 28 + 0,01ху.

Имеем:14 + 0,7х = 20 + 0,01ху,

36,4 + 0,52х = 28 + 0,01ху;

1400 + 70х = 2000 + ху, х ∙ (52 – у) = -840,

36400 + 52х = 2800 + ху; х ∙ (70 – у) = 600;

х = 80, у = 62,5.

Ответ: 80 г.

7