Как найти вес тела движущегося с ускорением

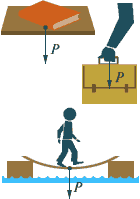
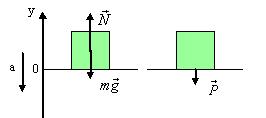
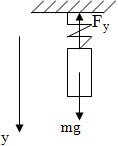
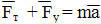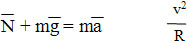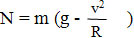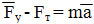Вес тела — это сила, с которой тело, вследствие притяжения к Земле, действует на опору или подвес.

P=N = mg

В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес – это упругая сила, приложенная к опоре или подвесу (т.е. к связи).

Вес тела в различных условиях движения.

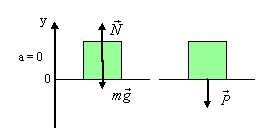
1) опора покоится или движется равномерно

N=mg – сила реакции опоры

P=N значит P=mg Вес тела равен действующей на тело силе тяжести.

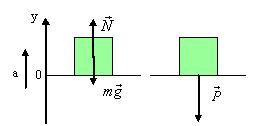
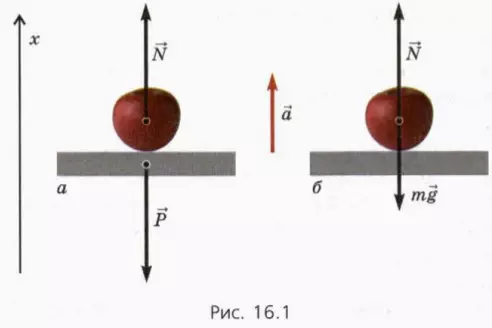
2) опора движется с ускорением a вверх.

N–mg=ma – второй закон Ньютона

N=mg+ma

P=N=m·(g+a)

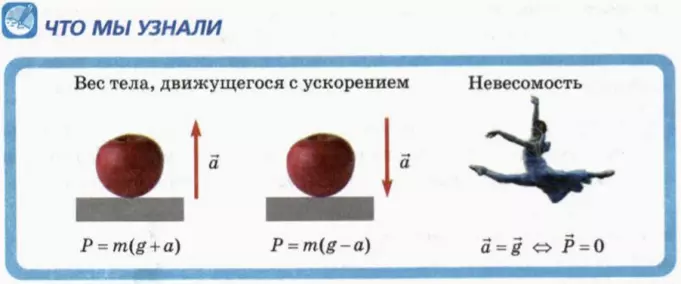
P>mg  Вес тела, движущегося с ускорением направленным вверх больше силы тяжести.

Увеличение веса тела, вызванное его ускоренным движением, называется перегрузкой.

3) опора движется с ускорением а вниз.

mg-N=ma – второй закон Ньютона

N=mg-ma

P=N=m·(g-a)

P<mg Вес тела, движущегося с ускорением вниз уменьшается.

Падение тел в вакууме без начальной скорости называется свободным падением. При свободном падении a=g из P=m·(g-a) следует, что P=0, т.е. вес отсутствует.

Если тела движутся только под действием силы тяжести, т.е. свободно падают, то они находятся в состоянии невесомости – состояние, при котором вес тела отсутствует (НО! масса у тела есть всегда).

Обозначения:

N – сила реакции опоры

P – вес тела

m – масса тела

g – ускорение свободного падения

a – ускорение, с которым движется тело

1. Вес тела, движущегося с ускорением

В § 12 мы доказали, что вес покоящегося тела равен действующей на это тело силе тяжести. Рассмотрим теперь вес тела, движущегося с ускорением. Это ускорение телу сообщает равнодействующая силы тяжести и силы, действующей со стороны опоры (или подвеса).

Поэтому, говоря далее об ускорении тела, мы должны понимать, что оно равно ускорению опоры (или подвеса).

Ускорение тела направлено вверх. Докажем, что в таком случае модуль веса тела

P = m(g + a),     (1)

где m – масса тела, a – модуль ускорения тела.

Пусть тело массой m лежит на опоре, движущейся с ускорением , направленным вверх (рис. 16.1, а).

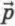
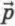
Тело давит на опору своим весом , а опора действует на груз с силой нормальной реакции ). По третьему закону Ньютона

= –. (2)

Отсюда следует, что

P = N.     (3)

На тело действуют сила тяжести mg_vec и сила нормальной реакции (рис. 16.1, б). Их равнодействующая = + m вызывает ускорение тела .
Следовательно, согласно второму закону Ньютона

+ m = m.

Запишем эту формулу в проекциях на направленную вверх ось x:

N – mg = ma.

Отсюда

N = m(g + a)     (4)

Из формул (3) и (4) следует, что

P = m(g + a).

Доказательство завершено: мы получили формулу (1).

Обратите внимание: если ускорение тела направлено вверх, вес груза больше действующей на него силы тяжести.

Когда вес тела больше силы тяжести, говорят, что оно испытывает перегрузку. Здоровый человек без вреда выдерживает кратковременные трехкратные перегрузки, то есть увеличение веса в три раза.

Космонавтам при старте и посадке космического корабля приходится выдерживать многократные перегрузки. Чтобы это не нанесло ущерба здоровью космонавтов, их тренируют с помощью специального аппарата – центрифуги (см. § 8).

Ускорение направлено вниз. Будем считать,что ускорение тела не превышает по модулю ускорения свободного падения.

? 1. Докажите, что в этом случае

P = m(g – a).     (5)

Итак, если ускорение тела направлено вниз, то вес тела меньше действующей на него силы тяжести.

Из формулы (5) следует, что при a = g, то есть когда тело движется с ускорением свободного падения, вес тела равен нулю. Подробнее мы рассмотрим это в пункте «Невесомость».

Обратите внимание: в формулы (1) и (5) для веса тела, движущегося с ускорением, не входит скорость тела. Это означает, что вес тела не зависит от модуля и направления скорости тела.

Например, если ускорение тела в некоторый момент направлено вверх, то вес будет больше действующей на это тело силы тяжести независимо от того, куда направлена скорость тела: вверх, вниз, горизонтально или под углом к горизонту!

? 2. Через 2 с после начала движения с постоянным ускорением скорость лифта стала равной 6 м/с. В лифте на весах стоит пассажир массой 60 кг. Каковы во время разгона лифта показания весов (в кг), если лифт едет вверх? вниз?

? 3. Лифт, двигавшийся со скоростью 4 м/с, начал тормозить. Во время торможения с постоянным ускорением вес находящегося в лифте человека массой 50 кг был равен 400 Н.
а) Куда направлено ускорение лифта?
б) Чему равно ускорение лифта?
в) Куда ехал лифт до остановки – вверх или вниз?

? 4. Подвешенный на нити длиной 1 м груз массой 0,5 кг совершает колебания в вертикальной плоскости (рис. 16.2). В нижней точке скорость груза равна 2 м/с.
а) Как направлено в нижней точке ускорение груза?
б) Чему равно ускорение груза в нижней точке?
в) Чему равна сила натяжения нити в нижней точке?

? 5. Автомобиль массой 1 т едет по выпуклому мосту, имеющему форму дуги окружности радиусом 40 м. Какой должна быть скорость автомобиля в верхней точке моста, чтобы в этой точке:
а) вес автомобиля был равен 2 кН?
б) автомобиль не давил на мост?

? 6. К пружине жесткостью 400 Н/м подвешивают груз массой 200 г, в результате чего пружина растягивается. Какова кратность перегрузки для груза в момент, когда удлинение пружины равно 2 см?

2. Невесомость

В предыдущем пункте была получена формула для веса тела, находящегося на опоре, движущейся с ускорением а, направленным вниз:

P = m(g – a).

(Мы считаем, что модуль ускорения тела не превышает ускорения свободного падения.)

Из этой формулы следует, что, когда ускорение опоры приближается к ускорению свободного падения у, вес тела стремится к нулю.

При a = g тело совсем перестает давить на опору. В этот момент вес тела становится ровным нулю. Такое состояние называют невесомостью.

Итак, тело находится в состоянии невесомости, когда оно под действием силы тяжести движется с ускорением свободного падения . При этом оно не давит на опору и не растягивает подвес, поэтому их можно вообще убрать.

Однако находящееся в состоянии невесомости тело не обязательно должно падать вниз! Вспомним, что ускорение брошенного произвольным образом тела во время всего полета равно ускорению свободного падения (если можно пренебречь сопротивлением воздуха). Следовательно, брошенное тело находится в состоянии невесомости во время всего полета.

? 7. Шарик брошен вертикально вверх. В какие моменты он находится в состоянии невесомости: при подъеме, в верхней точке траектории или когда он падает вниз?

Чтобы испытать кратковременное состояние невесомости, достаточно просто подпрыгнуть (рис. 16.З).

Длительное состояние невесомости испытывают космонавты при выключенных двигателях космического корабля. При этом как корабль, так и космонавты находятся под действием только силы тяжести, то есть движутся с ускорением свободного падения.

Поставим опыт

Нальем воду в пластиковую бутылку с отверстием в дне. Вода будет вытекать из отверстия. Но если бросить бутылку (в любом направлении), то во время полета бутылки вода из нее не выливается! Дело в том, что бутылка н вода в ней находятся в невесомости: вода не давит на дно бутылки и поэтому не выливается.

? 8. Шарик скатывается по «мертвой петле» радиусом 20 см (рис. 16.4), не отрываясь от нее. Чему равна скорость шарика в верхней точке окружности, если в этой точке он находится в состоянии невесомости?

Подсказка. Если шарик находится в состоянии невесомости, центростремительное ускорение ему сообщает только сила тяжести.

Дополнительные вопросы и задания

9. К пружине жесткостью k подвешивают груз массой m и отпускают без толчка. Чему равен вес груза в тот момент когда:
а) пружина не деформирована?
б) удлинение пружины равно x?

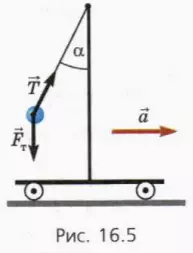
10. На тележке укреплен штатив, на котором на нити подвешен груз (рис. 16.5). Какой угол α с вертикалью составляет нить, когда тележка движется с ускорением a = 5 м/с²?

Подсказка. Ускорение грузу сообщает равнодействующая силы тяжести m и силы натяжения нити .

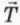
В В параграфе “Вес тел” мы выяснили, что вес тела – это сила, с которой тело действует на опору или на подвес. Если опора или подвес покоятся относительно Земли или движутся относительно нее прямолинейно и равномерно, то вес тела равен силе тяжести $mg$. Но вес тела может существенно отличаться от значения силы тяжести, если опора или подвес движется с ускорением вверх или вниз. Почему?

Вспомним, что вес – это сила, измеряемая, например, пружинными весами. Посмотрим, что покажут пружинные весы, если они вместе с подвешенным к ним телом движутся с ускорением вверх или вниз.

рис. 1



рис. 2

Подвесим к пружинным весам какой-нибудь груз и дадим им возможность двигаться с некоторым ускорением $vec{a}$. Для этого можно взять весы с грузом в руку и резко опустить их вниз (рис. 1), сообщив им ускорение, направленное вниз. Мы увидим, что во время опускания весов стрелка перемещается вверх. Это значит, что вес груза во время опускания стал меньше, чем он был в случае покоящихся весов. Если, наоборот, резко поднять весы вверх, стрелка опустится, показывая, что вес груза увеличился (рис. 2). Чем объясняется это уменьшение или увеличение веса при ускоренном движении динамометра с грузом?

Ответ на это дает второй закон Ньютона. Посмотрим, какие силы действуют на груз. На него действуют сила тяжести $m vec{g}$, направленная вниз, и сила упругости $vec{F}$ пружины весов, направленная вверх. Под действием этих двух сил тело и движется с ускорением $vec{a}$, которое может быть направлено как вниз, так и вверх в зависимости от того, будем ли мы опускать весы или поднимать их.

По второму закону Ньютона

$m vec{a} = m vec{g} + vec{F}$.

Отсюда

$vec{F} = m vec{a} – m vec{g}$. (1)

С такой же по модулю силой, но направленной противоположно силе $vec{F}$, груз действует на пружину. А эта сила и есть вес груза $vec{P}$:

$vec{P} = – vec{F}$.

Следовательно,

$vec{P} = – ( m vec{a} – m vec{g}) = m( vec{g} – vec{a})$. (2)

Векторы $vec{P}, vec{g}$ и $vec{a}$ параллельны вертикальной прямой. Направив координатную ось $X$ по вертикали вниз (см. рис. 1 и 2), мы можем формулу (2) написать в алгебраической форме для проекций этих векторов на вертикальную ось:

$P = m(g – a)$. (3)

Если весы движутся с ускорением $vec{a}$ вниз, то проекция этого вектора на координатную ось положительна. Если $a < g$, то из формулы (3) следует, что $P < mg$.

Вес тела, направление ускорения которого совпадает с направлением ускорения свободного падения, меньше веса покоящегося тела. Это мы и видели на опыте (рис. 1).

Если же весы движутся с ускорением $vec{a}$ вверх, то проекция вектора ускорения на координатную ось отрицательна н формула (3) тогда примет вид:

$P = m[g – (- | vec{a} | )] = m (g + | vec{a} | )$, (4)

т. е. $P > mg$.

Таким образом, если ускорение тела направлено в сторону, противоположную ускорению свободного падения, его вес больше веса покоящегося тела. Это мы и наблюдали на опыте (рис. 2).

Увеличение веса тела, вызванное его ускоренным движением, называют перегрузкой.

Вес уменьшается или увеличивается не только тогда, когда тело подвешено к пружинным весам. То же самое относится и к любому подвесу, и к любой опоре.

Приведем некоторые примеры изменения веса тела при его ускоренном движении.

рис. 3

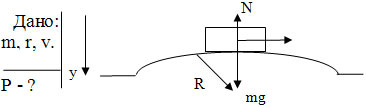
1. Автомобиль, движущийся по выпуклому мосту, легче того же автомобиля, когда он стоит на том же мосту (рис. 3).

Действительно, движение по выпуклому мосту – эго движение по части окружности. Поэтому автомобиль движется с центростремительным ускорением, равным по абсолютной величине:

$a_{цс} = frac{v^{2} }{r}$,

где $v$ – скорость автомобиля, $r$ – радиус кривизны. В момент, когда автомобиль находится в высшей точке моста, это ускорение направлено по вертикали вниз. В таком случае вес автомобиля, т. е. сила, с которой он давит на мост, будет равен:

$P = m(g – a) = m left ( g – frac{v^{2} }{r} right ), P < mg$.

Пассажиры, проезжающие в автомобиле с большой скоростью по выпуклому мосту, ощущают эго уменьшение веса.

рис. 4

2. Летчик, выводящий самолет из пикирования (рис. 4), в нижней части траектории подвергается перегрузке. В самом деле, в этой части траектории самолет движется по окружности с центростремительным ускорением, направленным к ее центру по вертикали вверх. Абсолютное значение ускорения по-прежнему равно:

$a_{цс} = frac{v^{2} }{r}$.

Но его проекция на вертикальную ось, направленную вниз, отрицательна:

$a = – a_{цс} = – frac{v^{2} }{r}$.

Следовательно, вес летчика, т. е. сила, с которой он действует на опору (сиденье), определяется формулой:

$P = m(g – a) = m left ( g + frac{v^{2} }{r} right ), P > mg$.

Таким образом, вес летчика больше «нормального» веса, равного силе тяжести $mg$, на величину $frac{mv^{2} }{r}$. Если при выходе из пикирования центростремительное ускорение $frac{ v^{2} }{r}$ превышает по абсолютному значению ускорение свободного падения $g$ в $n$ раз $left ( frac{v^{2} }{r} = ng right )$, то вес летчика

$P = m(g + ng) = mg(n + 1)$,

т. е. он будет в $n + 1$ раз больше нормального веса летчика.

При перегрузке увеличивают свой вес и внутренние органы летчика, увеличивается сила, с которой они действуют друг на друга и на его остов (скелет). Это вызывает болезненные ощущения, а при чрезмерной перегрузке может стать опасным для здоровья. Тренированные пилоты выдерживают перегрузку до $10mg$ (обычно перегрузку выражают не через величину $mg$, а через величину $g$ и говорят, что перегрузка равна, например, $10g$).

Цели урока:

• Повторить понятия изученных сил (тяжести, упругости, веса покоящегося тела).
• Повторить формулы этих сил.
• Вывести формулы для веса тела движущегося с ускорением вертикально вверх и вниз.
• Закрепить их на примерах из жизни.
• Сформировать представления учащегося, где эти знания применяются.

Оборудование урока:

1. картонки на магнитной доске с указанием сил.
2. динамометр, набор грузов на столе у каждого учащегося и у учителя.

Ход урока

1. Организационный момент (3-5 мин)
2. Проговаривание цели урока и темп урока, для чего эту тему вы выбрали.

А) Повторяем рани изученные темы (7-10 мин)

Сила упругости – Что ребята вы знаете о F_упр.?

План ответа:      

а) что называется силой упругости.

б) когда возникает сила упругости.

в) куда направлена.

г) чему пропорциональна, формула.

Сила тяжести – Что ребята вы знаете о F_тяж.?

а) что называется?

б) куда направлена.

в) от чего зависит? Формула.

е) что такое g? g = ? Особенности g ?

ж) к чему прикладывается? Куда направлена?

Вес тела        

а) что называется весом покоящегося тела?

б) какая природа этой силы?

в) на что действует? (к чему приложена)

г) формула. P = mg – если тело покоится или равномерно движется.

Б) P = mg  и  F = mg

– Одинаковы ли эти силы?

1. разная природа
2. действуют на разные тела
3. различны точки приложения.

В) работа с карточками (они повешены на магнитной доске)

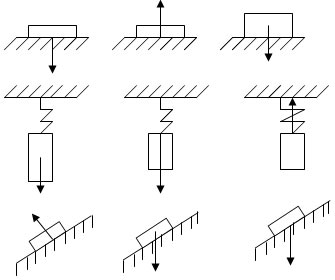
Вопросы:

1. Какая сила изображена?            
2. Чем отличаются изображённые силы?

Г) От чего зависит 

F_т ? – зависит от m тела

F_у?  – зависит от x-удлинения

P ? – от массы тела, при условии

1. Новый материал:

Выясним, что происходит с 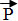(весом), когда тело движется по вертикали вниз.

Учащиеся самостоятельно проделывают опыт на столах и убеждаются в результате опыта.

Учитель проговаривает: а) учащиеся держат динамометр с грузом в руке

– Что происходит под действием груза?

– Какие силы возникают?

– Чему по модулю равен вес?

– Сравнить можно силы только … (одной природы)

– Что происходит со стрелкой динамометра, когда опускают динамометр с грузом вниз?

– Стрелка возвращается на «0» т.е. вес уменьшается.

– Докажем это.

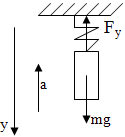
Сделаем рисунок, обозначим все действующие силы.

–  Выберем ось по направлению ускорения.

– Какой закон описывает это движение?

– Какие силы действуют?

Запишем уравнение второго закона Ньютона.

F_т   + F_y = ma

О_y: F_т – F_y = ma                      

mg – F_y = ma                  

F_y = – ma + mg

m(g – a) = P

Чему равна проекция вектора, как она определяется? | F_y | = | P |

Вес уменьшился, т.е. P₀ = mg >  P = m(g – a), так как  g > (g – a)

Вывод (сами учащиеся формируют):

Если тело вместе с опорой или подвесом движется с ускорением, которое направлено вниз, то его вес уменьшается по сравнению с весом покоящегося тела.

– Это тело двигалось по вертикали, а изменится ли вес тела движущегося по окружности?

Задача:

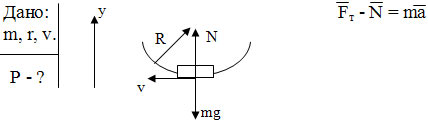
Автомобиль массой m  движется по выпуклому мосту, радиусом  r, со скоростью v. Чему равен вес автомобиля в верхней точке моста.

Учащийся сам выполняет эту задачу у доски, проговаривая каждый шаг.

О_y: mg – N = ma

N = m (g – a)

Вывод:  Если тело движется по выпуклой окружности вниз, то его вес уменьшается по сравнению с весом покоящегося тела.

Рассмотрим второй способ движения.

Когда груз вместе с динамометром движется вверх. Учащиеся самостоятельно проделывают этот опыт и убеждаются, что стрелка отклоняется вниз.

– Что пронаблюдали?

Меняется  F_y  т. е. меняется и P – он увеличивается – докажем.

Запишем II закон Ньютона – уравнение

F_y – F_т = ma

О_y: – F_y  + mg   = – ma

mg + ma = F_y                                           | F_y | = | P |

m (g + a) = P

Сравним P₀= mg    и   P = m(g + a)

P₀ < P т.к. g < (g + a)

Вывод (дети сами): Если тело движется с ускорением вверх, то его вес больше веса покоящегося тела.

– Может ли уменьшиться вес тела, движущегося по окружности? (да)

– А в какой точке больше в верхней или в нижней?

Задача:

Рассчитать вес летчика массой m, выводящего самолёт из пикирования  со скоростью v, и радиусом окружности r?

Учащиеся самостоятельно выполняют эту задачу, один у доски проговаривая каждый шаг.

О_y: – mg + N  =  ma            | N | = | P |

P = m (g + a)             a = v²/R                             

Вывод: вес лётчика увеличится.

Если вес человека, в данном случае лётчика, увеличивается, при движении вверх, то этот человек испытывает перегрузку.

Привести примеры перегрузки.

а) космонавт при старте ракеты – испытывает 10P₀.

– Мы с вами на поверхности Земли можем испытывать перегрузку?

б) качели – «лопенги».

в) поднимаемся на 5-й, 9-й этажи.

г) прыгаем на физкультуре, подымаемся по шведской стенке.

Но эти перегрузки незначительны.

Рассмотрим ещё один вид движения.

Опыт (проделывают учащиеся самостоятельно и наблюдают):

Динамометр с грузом подняли и выпустили из рук. Что произошло со стрелкой?

– Она вернулась на «0»?

– Что это значит?

Нет F_y = 0 > P = 0 т. е.  вес отсутствует.

Это явление называется невесомостью.

– При каком условии P = 0 – свободном падении. т. е. а = g

P = (g – g) = 0.

Каждый из вас был на поверхности Земли в состоянии невесомости (прыжки с вышки).

1. Итог урока.

Итак, мы с вами сегодня на уроке вывели формулы веса тел движущихся вертикально вверх и вниз, и увидели, что при подъёме вверх вес увеличивается, а при опускании вниз вес уменьшается. Вывести алгоритм таких задач и всё это закрепили.

Д/з: § 30 (II ч) – 31. упр. 15 (2).

Спасибо за урок!

До свидания.

§ 6. Закон всемирного тяготения. Вес тела

Анализируя законы Кеплера, описывающие движение планет, И. Ньютон в 1667 году пришёл к открытию закона всемирного тяготения:

В такой форме закон справедлив только для двух тел, которые можно считать материальными точками. Однако можно доказать, что для двух однородных тел шарообразной формы эта форма записи закона тоже справедлива.

Измерить величину гравитационной постоянной удалось английскому физику Г. Кавендишу в 1798 году.

С помощью крутильных весов и свинцовых шаров ему удалось получить значение гравитационной постоянной:

Второй закон Ньютона позволяет записать для силы, с которой тело притягивается к Земле: `F=G(Mm)/(R^2)=mg`, тогда `g=GM/R^2` – ускорение свободного падения на поверхности Земли (измерено Галилеем и Ньютоном), на расстоянии, большем радиуса на величину `h`, ускорение свободного падения находится по формуле:

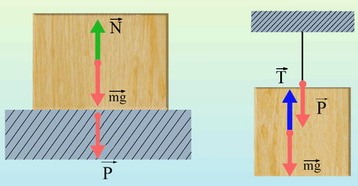
Рассмотрим твёрдое тело, расположенное на горизонтальной неподвижной опоре: под действием силы тяжести тело деформируется. Если тело находится на опоре, то на нижний слой действуют все верхние слои, и, как следствие,  этот  слой деформируется наибольшим образом. На предпоследний слой действует меньшее количество слоёв, и он деформируется  меньше. Таким образом, тело, бывшее прямоугольным, примет вид трапеции. Нижний слой приблизился при такой деформации к центру тела, а значит, возникла сила упругости, направленная в сторону, противоположную направлению смещения частиц при деформации. Сила упругости, возникшая внутри данного тела, направлена перпендикулярно опоре. Эту силу, созданную деформированным телом и приложенную к опоре, называют весом тела. Опора под действием веса деформируется. Противоположная весу сила упругости действует на данное тело со стороны деформированной опоры и тоже направлена перпендикулярно опоре, но называется силой реакции опоры `N` (от слова normal – перпендикуляр).

На рисунке 9 тело не касается опоры для того, чтобы показать, что вес приложен к опоре, а сила реакции опоры к телу. В действительности площадь реального соприкосновения твёрдых тел невелика. Большей частью между телами находится тонкий слой воздуха.

Вполне очевидно, что если опоры нет, то и веса тело иметь не будет. Такое случится в том случае, если тело движется под действием только одной силы – силы тяготения.

Также легко понять, что если на тело действует две силы (сила тяжести и сила реакции опоры), то эти силы не обязательно равны друг другу. Одна из них может быть больше другой.

Рассмотрим движение тела, помещённого в лифт. Пусть сам лифт движется с ускорением `veca`. 

Такое ускорение будет в двух случаях:

1) лифт поднимается равноускорено,

2) лифт опускается равнозамедленно.

Второй закон Ньютона для данного тела примет вид:

`vecN+mvecg=mveca`.

При рассмотрении данного движения из лабораторной неподвижной системы отсчёта `Oy` увидим, что в проекции на вертикальную ось `Oy` второй закон запишется следующим образом:

`N-mg=ma`, 

откуда   

`N=ma+mg=m(g+a)`.

Но по третьему закону Ньютона знаем, что сила реакции опоры и вес тела равны и противоположны, следовательно:

`N=P`, 

тогда:

Не трудно проследить за тем, что мы получим, если ускорение тела будет направлено вниз.

В проекции на ось `Oy` ускорение проецируется со знаком «`-`», что даст окончательную формулу для веса:

Или в общем случае:

Подобным образом можно получить выражение для веса тела, движущегося равномерно по выпуклому участку дороги.

Важное дополнение:

Для рассматриваемой силы, называемой весом, важно понимать и уметь правильно изображать точку приложения этой силы.

На рисунке 11а показан лифт, у которого нет ускорения. Тогда сила тяжести равна силе реакции опоры. А по третьему закону Ньютона, сила реакции опоры равна весу тела. Точка приложения силы тяжести расположена в геометрическом центре тела, если тело однородно и правильной формы. Точка приложения силы реакции опоры должна быть изображена внутри тела вблизи с нижней поверхностью тела на линии действия силы тяжести. Последнее свойство на рисунке не выдержано для удобства изображения (иначе силы на рисунке будут накладываться друг на друга). Точка приложения веса тела находится внутри опоры (пола лифта) вблизи поверхности на линии действия силы реакции опоры.

   

На рисунке 11б ускорение лифта направлено вниз. Тогда сила реакции опоры меньше силы тяжести. А вес снова равен силе реакции опоры.

На рисунке 11в ускорение лифта направлено верх. Тогда сила реакции опоры больше силы тяжести. А вес снова равен силе реакции опоры.