Вес тела
Весом тела называется сила, с которой данное тело давит на опору или растягивает подвес вследствие притяжения данного тела к Земле.
Установим основные характеристики этой силы – причину ее возникновения, модуль и направление. Рассмотрим тело, подвешенное на пружине (Рис. 1.). Под действием силы тяжести тело стремится двигаться вниз, увлекая за собой нижний конец пружины. В свою очередь, пружина деформируется, что вызывает появление в ней силы упругости.
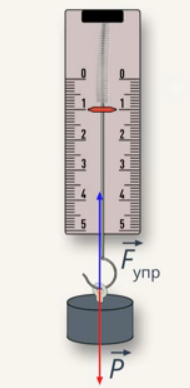
Рис. 1. Тело, подвешенное на пружине
Под действием силы упругости, которая приложена к верхнему краю тела, это тело, в свою очередь, также деформируется, возникает другая сила упругости, обусловленная деформацией тела. Эта сила приложена к нижнему краю пружины. Кроме того, она равна по модулю силе упругости пружины и направлена вниз. Именно эту силу упругости тела мы и будем называть его весом, то есть вес тела приложен к пружине и направлен вниз.
После того как колебания тела на пружине затухнут, система придет в состояние равновесия, в котором сумма сил, действующих на тело, будет равна нулю. Это значит, что сила тяжести рана по модулю и противоположна по направлению силе упругости пружины (Рис. 2). Последняя равна по модулю и противоположна по направлению весу тела, как мы уже выяснили. Значит, сила тяжести по модулю равна весу тела. Данное соотношение не универсально, но в нашем примере – справедливо.
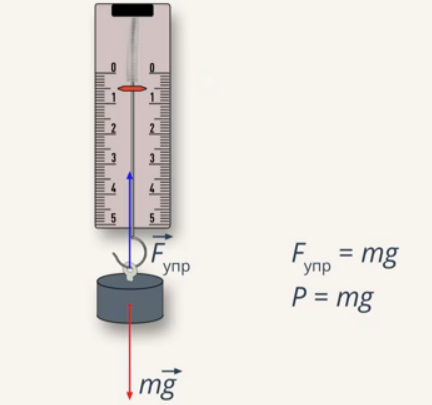
Рис. 2. Вес и сила тяжести
Приведенная формула не означает, что сила тяжести и вес – одно и то же. Эти две силы разные по своей природе. Вес – это сила упругости, приложенная к подвесу со стороны тела, а сила тяжести – это сила, приложенная к телу со стороны Земли.

Рис. 3. Вес и сила тяжести тела на подвесе и на опоре
Невесомость
Выясним некоторые особенности веса. Вес – это сила, с которой тело давит на опору или растягивает подвес, из этого следует, что если тело не подвешено или не закреплено на опоре, то его вес равен нулю. Данный вывод кажется противоречивым нашему повседневному опыту. Однако он имеет вполне справедливые физические примеры.
Если пружину с подвешенным к ней телом отпустить и позволить ей свободно падать, то указатель динамометра будет показывать нулевое значение (Рис. 4). Причина этого проста: груз и динамометр движутся с одинаковым ускорением (g) и одинаковой нулевой начальной скоростью (V0). Нижний конец пружины движется синхронно с грузом, при этом пружина не деформируется и силы упругости в пружине не возникает. Следовательно, не возникает и встречной силы упругости, которая является весом тела, то есть тело не обладает весом, или является невесомым.
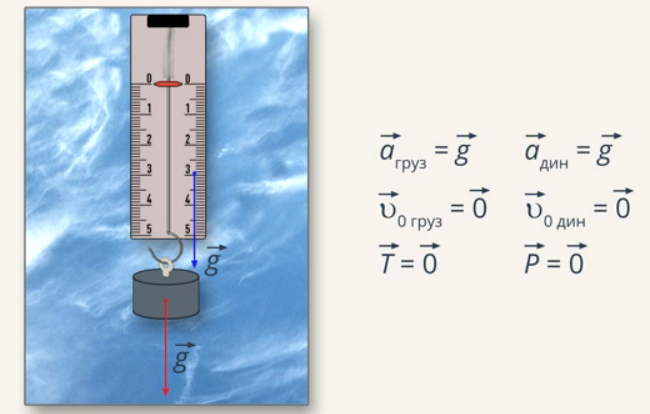
Рис. 4. Свободное падение пружины с подвешенным к ней телом
Состояние невесомости возникает благодаря тому, что в земных условиях сила тяжести сообщает всем телам одинаковое ускорение, так называемое ускорение свободного падения. Для нашего примера мы можем сказать, что груз и динамометр движутся с одинаковым ускорением. Если на тело действует только сила тяжести или только сила всемирного тяготения, то это тело находится в состоянии невесомости. Важно понимать, что в этом случае исчезает только вес тела, но не сила тяжести, действующая на это тело.
Состояние невесомости – не экзотика, довольно часто многие из вас его испытывали – любой человек, подпрыгивающий или спрыгивающий с какой либо высоты, до момента приземления находится в состоянии невесомости.
Рассмотрим случай, когда динамометр и прикрепленное к его пружине тело движутся вниз с некоторым ускорением, но не совершают при этом свободного падения. Показания динамометра уменьшатся по сравнению с показаниями при неподвижном грузе и пружине, значит, вес тела стал меньше, чем он был в состоянии покоя. В чем причина такого уменьшения? Дадим математическое объяснение, опираясь на второй закон Ньютона.

Рис. 5. Математическое объяснение веса тела
На тело действуют две силы: сила тяжести, направленная вниз, и сила упругости пружины, направленная вверх. Эти две силы сообщают телу ускорение. и уравнение движения будет иметь вид:
m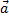 =
= 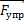 + m
+ m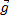
Выберем ось y (Рис. 5), поскольку все силы направлены вертикально, нам достаточно одной оси. В результате проецирования и переноса слагаемых получим – модуль силы упругости будет равен:
ma = mg – Fупр
Fупр = mg – ma,
где в левой и правой части уравнения стоят проекции сил, указанных во втором законе Ньютона, на ось y. Согласно определению, вес тела по модулю равен силе упругости пружины, и, подставив ее значение, получим :
P = Fупр = mg – ma = m( g – а)
Вес тела равен произведению массы тела на разность ускорений. Из полученной формулы видно, что если модуль ускорения тела меньше модуля ускорения свободного падения, то вес тела меньше силы тяжести, то есть вес тела, движущегося ускоренно, меньше веса покоящегося тела.
Рассмотрим случай, когда тело с грузиком движется ускоренно вверх (Рис. 6).
Стрелка динамометра покажет значение веса тела большее, чем покоящегося груза.
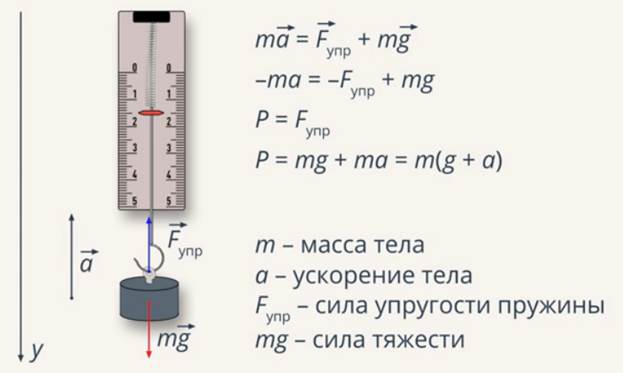
Рис. 6. Тело с грузиком движется ускоренно вверх
Тело движется вверх, и его ускорение направлено туда же, следовательно, нам необходимо поменять знак проекции ускорения на ось у.
Из формулы видно, что теперь вес тела больше силы тяжести, то есть больше веса покоящегося тела.
Увеличение веса тела, вызванное его ускоренным движением, называется перегрузкой.
Это справедливо не только для тела, подвешенного на пружине, но и для тела, укрепленного на опоре.
Рассмотрим пример, в котором проявляется изменение тела при его ускоренном движении (Рис. 7).
Автомобиль движется по мосту выпуклой траектории, то есть по криволинейной траектории. Будем считать форму моста дугой окружности. Из кинематики мы знаем, что автомобиль движется с центростремительным ускорением, величина которого равна квадрату скорости, деленной на радиус кривизны моста. В момент нахождения его в наивысшей точке, это ускорение будет направлено вертикально вниз. Согласно второму закону Ньютона это ускорение сообщается автомобилю равнодействующей силой тяжести и силой реакции опоры.
m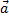 =
= 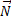 + m
+ m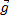
Выберем координатную ось у, направленную вертикально вверх, и запишем это уравнение в проекции на выбранную ось, подставим значения и проведем преобразования:
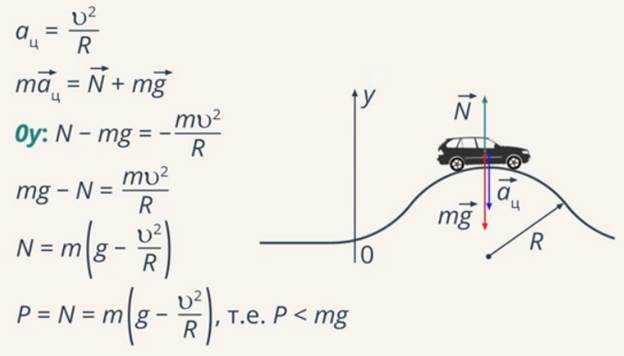
Рис. 7. Наивысшая точка нахождения автомобиля
Вес автомобиля, по третьему закону Ньютона, равен по модулю силе реакции опоры (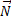 ), при этом мы видим, что вес автомобиля по модулю меньше силы тяжести, то есть меньше веса неподвижного автомобиля.
), при этом мы видим, что вес автомобиля по модулю меньше силы тяжести, то есть меньше веса неподвижного автомобиля.
Пример задачи
Ракета при старте с Земли движется вертикально вверх с ускорением а=20 м/с2. Каков вес летчика-космонавта, находящегося в кабине ракеты, если его масса m=80 кг?
Совершенно очевидно, что ускорение ракеты направлено вверх и для решения мы должны использовать формулу веса тела для случая с перегрузом (Рис. 8).
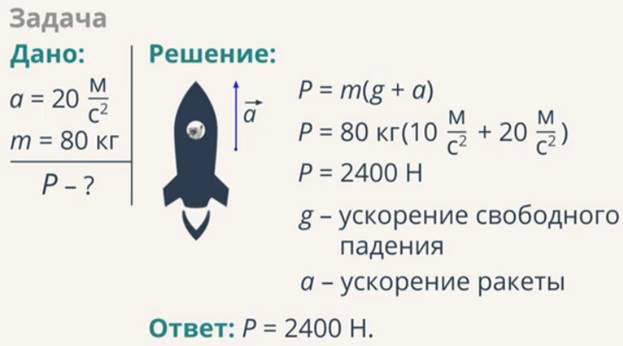
Рис. 8. Иллюстрация к задаче
Необходимо отметить, что если неподвижное относительно Земли тело имеет вес 2400 Н, то его масса составляет 240 кг, то есть космонавт ощущает себя в три раза массивнее, чем есть на самом деле.
Заключение
Мы разобрали понятие веса тела, выяснили основные свойства этой величины и получили формулы, которые позволяют нам рассчитать вес тела, движущегося с ускорением.
Если тело движется вертикально вниз, при этом модуль его ускорения меньше ускорения свободного падения, то вес тела уменьшается по сравнению со значением веса неподвижного тела.
Если тело движется ускоренно вертикально вверх, то его вес возрастает и при этом тело испытывает перегруз
Сила тяжести. Вес
- Движение тел вблизи поверхности Земли
- Сила тяжести
- Вес тела
- Невесомость
- Задачи
- Лабораторная работа №7. Градуирование шкалы динамометра и измерение силы тяжести
п.1. Движение тел вблизи поверхности Земли
Вблизи поверхности Земли все тела, предоставленные самим себе, падают вниз, независимо от направления начальной скорости.
Такое движение тел называют свободным падением.
п.2. Сила тяжести
Многочисленные эксперименты показали, что в свободном падении все тела вблизи поверхности Земли падают с одинаковым ускорением (overrightarrow{g}), которое направлено вниз, к центру Земли.
В системе отсчета, связанной с Землей, на любое тело массой (m) действует сила тяжести $$ overrightarrow{F_{text{тяж}}}=m overrightarrow{g} $$
 |
Сила тяжести прямо пропорциональна массе тела. Точка приложения силы тяжести – центр масс тела. Сила тяжести всегда направлена вертикально вниз, к центру Земли. |
 |
Измерения показывают, что на средних географических широтах ускорение свободного падения (gapprox 9,81 text{м/с}^2). Т.е., скорость при падении увеличивается на (9,81 text{м/с}) каждую следующую секунду.
В общем случае, ускорение свободного падения зависит от широты рассматриваемого места, высоты над уровнем моря, времени суток и ещё нескольких более «тонких» факторов. В школьных задачах, если другое не оговорено, для вычислений используют приблизительное значение (gapprox 10 text{м/с}^2). |
п.3. Вес тела
Если подвесить тело или положить его на опору, сила тяжести, действующая на тело, будет уравновешена силой, которую называют силой реакции подвеса или силой реакции опоры.
Т.к. силы уравновешивают друг друга, выполняется соотношение $$ moverrightarrow{g}=-overrightarrow{N} $$ где (moverrightarrow{g}) – сила тяжести, (overrightarrow{N}) – реакция подвеса или опоры.
По третьему закону Ньютона, если подвес или опора действуют на тело с силой (overrightarrow{N}), то и тело действует на подвес или опору с силой (overrightarrow{P}=-overrightarrow{N})
Вес тела – это сила, с которой тело действует на подвес или опору.
Получаем, что (overrightarrow{P}=moverrightarrow{g}), вес и сила тяжести равны по величине и направлению, но приложены к разным точкам: сила тяжести – к центру масс тела, вес – к подвесу или опоре.
По своей природе реакции подвеса или опоры являются силами упругости: под действием веса тела подвес или опора деформируются, и силы упругости стремятся восстановить их форму и размеры.
Равенство (overrightarrow{P}=moverrightarrow{g}) выполняется, если подвес или опора покоятся или движутся относительно Земли прямолинейно и равномерно.
Если движение подвеса или опоры равноускоренное с ускорением (overrightarrow{a}ne 0), то (overrightarrow{P}ne moverrightarrow{g}), вес будет больше (при (overrightarrow{a}) направленном вверх) или меньше (при (overrightarrow{a}) направленном вниз) силы тяжести. Подробней этот случай будет рассмотрен в курсе физики для 9 класса.
п.4. Невесомость
Если опора свободно падает вместе с телом, то под действием силы тяжести каждая частица опоры и тела двигается вниз с одним и тем же ускорением (overrightarrow{g}). Ни в опоре, ни в теле не возникают сжатия или растяжения, нет сил упругости, а значит, вес тела равен нулю.
Состояние, при котором в свободно падающих телах исчезают деформации и взаимные давления частиц тел друг на друга, называют невесомостью.
Состояние невесомости можно испытать, если подпрыгнуть – с момента отрыва от земли до момента приземления. В первые моменты прыжка до раскрытия парашюта, парашютисты также находятся в состоянии невесомости.
Движение космического корабля по орбите вокруг Земли представляет собой непрерывное свободное падение, поэтому космонавты испытывают состояние невесомости в течение всего полета, кроме тех моментов, когда передвигаются по кораблю или включают двигатели для маневрирования.
п.5. Задачи
Задача 1. Какой вес имеет человек массой 65 кг, который стоит на земле?
Дано:
(m=65 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(P-?)
Вес равен силе тяжести (P=mg) $$ Papprox 65cdot 10=650 (text{Н}) $$ Ответ: 650 Н
Задача 2. Парашютист равномерно опускается на землю. Сила сопротивления воздуха 900 Н. Масса парашюта 15 кг. Найдите массу парашютиста.
Дано:
(F_{text{сопр}}=900 text{Н})
(m_1=15 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(m_2-?)

На раскрытый парашют действуют две силы: сила сопротивления воздуха, направленная вверх, и суммарный вес (парашюта и парашютиста), направленный вниз.
Т.к. движение равномерное, ускорение (a=0). Значит, вес равен силе тяжести, и begin{gather*} F_{text{сопр}}=P=F_{text{т}}=(m_1+m_2)g\[6pt] m_1+m_2=frac{F_{text{сопр}}}{g}Rightarrow m_2=frac{F_{text{сопр}}}{g}-m_1 end{gather*} Подставляем $$ m_2=frac{900}{10}-15=75 (text{кг}) $$ Ответ: 75 кг.
Задача 3. На сколько сантиметров растянется пружина жесткостью k=267 Н/м, если подвесить к ней медный брусок размерами 5 см х 6 см х 10 см. Плотность меди 8900 кг/м3.
Дано:
(V=5 text{см}times 6 text{см}times 10 text{см}=300 text{см}^3=3cdot 10^{-4} text{м}^3)
(rho=8900 text{кг/м}^3)
(k=1000 text{Н/м})
(gapprox 10 text{м/с}^2)
__________________
(m_2-?)

Вес бруска равен силе тяжести и уравновешивается силой упругости: begin{gather*} mg=F_{text{упр}}=kDelta lRightarrow Delta l=frac{mg}{k}, m=rho V\[6pt] Delta l=frac{rho Vg}{k} end{gather*} Получаем: $$ Delta l=frac{8900cdot 3cdot 10^{-4}cdot 10}{267}=0,1 (text{м}=10 (text{см}) $$ Ответ: 10 см.
Задача 4*. При подвешивании гирьки массой 450 г пружина динамометра растягивается до 8 см. А при подвешивании гирьки массой 300 г – до 6 см. Найдите длину пружины динамометра без груза (ответ запишите в см).
Дано:
(m_1=450 text{г}=0,45 text{кг})
(l_1=8 text{см}=0,8 text{м})
(m_2=300 text{г}=0,3 text{кг})
(l_2=6 text{см}=0,6 text{м})
__________________
(l_0-?)

Вес гирьки равен силе тяжести и уравновешивается силой упругости: begin{gather*} mg=F_{text{упр}}=kDelta lRightarrow k=frac{mg}{Delta l} end{gather*} где (Delta l=l-l_0) – растяжение пружины.
Жесткость пружины begin{gather*} k=frac{m_1g}{Delta l_1}=frac{m_1g}{l_1-l_0}, k=frac{m_2g}{Delta l_2}=frac{m_2g}{l_2-l_0}\[6pt] frac{m_1g}{l_1-l_0}=frac{m_2g}{l_2-l_0} Rightarrow frac{m_1}{l_1-l_0}=frac{m_2}{l_2-l_0} Rightarrow m_2(l_2-l_0)=m_2(l_1-l_0)\[6pt] m_1l_2-m_1l_0=m_2l_1-m_2l_0 Rightarrow m_1l_2-m_2l_1=(m_1-m_2)l_0\[6pt] l_0=frac{m_1l_2-m_2l_1}{m_1-m_2} end{gather*} Получаем $$ l_0=frac{0,45cdot 0,06-0,3cdot 0,08}{0,45-0,3}=frac{0,027-0,024}{0,15}=0,02 (text{м}=2 (text{см}) $$ Ответ: 2 см.
п.6. Лабораторная работа №7. Градуирование шкалы динамометра и измерение силы тяжести
Цель работы
Исследовать зависимость силы упругости от величины деформации. Изготовить шкалу динамометра. Измерить силу тяжести для двух тел неизвестной массы; рассчитать их массу.
Теоретические сведения
 |
При подвешивании груза на пружину, его вес уравновешивается силой упругости. Для неподвижной пружины вес равен силе тяжести. Получаем $$ P=F_{text{т}}=mg=F_{text{упр}} =kDelta l $$ Удлинение пружины $$ Delta l=frac gk m $$ При постоянном ускорении свободного падения (g) и постоянной жесткости (k), удлинение прямо пропорционально массе подвешенного груза. |
В данной работе считаем, что грузу массой 100 г соответствует показание динамометра (F=1 text{Н}), т.е. (overline{g}=frac{1 text{Н}}{100 text{г}}=10frac{text{Н}}{ text{кг}}=10frac{ text{м}}{ text{с}^2}). Более точное стандартное значение (g_0=9,80665frac{ text{м}}{ text{с}^2})
Ошибка метода, связанная с величиной (g) $$ delta_g=frac{|overline{g}-g_0|}{g_0}approx 0,02=2text{%} $$ Тогда грузу массой 200 г соответствует показание 2 Н, 300 г – 3 Н и т.д.
После градуирования в целых значениях Н на динамометре наносятся промежуточные деления с ценой деления (d=0,1 text{Н}).
Ошибка градуирования определяется как степень отклонения от равномерности шкалы, (delta_{text{шк}}).
Теперь с помощью полученного прибора можно непосредственно измерять силу тяжести, действующую на тела. Ошибка метода при определении сил равна сумме (delta=delta_g+delta_{text{шк}}).
Т.к. шкала изготовлена для (overline{g}=10frac{ text{м}}{ text{с}^2}), массу тел находим по формуле (m=frac{F}{overline{g}}), где (F) – показание динамометра. При этом ошибка метода равна (delta=delta_{text{шк}}), т.к. ошибка (delta_g) нивелируется за счет пропорциональности массы и растяжения пружины.
Таким образом, за счет сокращения (overline{g}), полученный прибор позволяет точнее измерять массы по сравнению с измерениями сил.
Приборы и материалы
Лабораторный динамометр на 5Н со шкалой, закрытой чистой бумагой; набор грузиков по 100 г; линейка; карандаш; 2 тела неизвестной массы.
Ход работы
1. Закрепите динамометр в штативе.
2. Подвесьте грузик массой 100 г, сделайте отметку 1Н на шкале.
3. Сделайте отметки 2Н, 3Н, 4Н и 5Н для грузов 200 г, 300 г, 400 г и 500 г соответственно.
4. Снимите динамометр со штатива и проверьте с помощью линейки, насколько равномерной получилась шкала. Оцените относительную ошибку (delta_{text{шк}})
5. С помощью линейки нанесите по 10 промежуточных делений между основными делениями шкалы.
6. Снова закрепите динамометр в штативе и проведите измерения силы тяжести для двух тел неизвестной массы. Найдите абсолютную и относительную погрешность измерений.
7. Рассчитайте массы для обоих тел. Найдите абсолютную и относительную погрешность расчетов. 8. Сделайте выводы.
Результаты измерений и вычислений
Расчетная таблица для оценки равномерности шкалы
| Отрезок шкалы | Длина отрезка, мм | (|x-x_{text{ср}}|) |
| 0-1 Н | 25 | 0 |
| 1-2 Н | 25 | 0 |
| 2-3 Н | 26 | 1 |
| 3-4 Н | 24 | 1 |
| 4-5 Н | 25 | 0 |
| Всего | 125 | 2 |
Средняя длина отрезка $$ x_{text{ср}}=frac{125}{5}=25 (text{мм}) $$ Среднее линейное отклонение $$ Delta =frac 25=0,4 (text{мм}) $$ Цена деления линейки (d_{text{л}}=1 text{мм}), абсолютная погрешность измерений (Delta_{text{л}}=0,5 text{мм})
Т.к. (Delta_{text{л}}gt Delta), принимаем погрешность равномерности шкалы (Delta=Delta_{text{л}}=0,5 text{мм})
Относительная погрешность равномерности шкалы $$ delta_{text{шк}}=frac{0,5}{25}=0,02=2text{%} $$
Относительная погрешность равномерности шкалы
| Показание динамометра (F, text{Н}) |
Ошибка метода (delta=delta_g+delta_{text{шк}}, text{%}) |
Абсолютная погрешность (Delta F=deltacdot F, text{Н}) |
|
| 1-е тело | 2,7 | 4% | 0,11 ≈ 0,1 |
| 2-е тело | 1,9 | 4% | 0,08 ≈ 0,1 |
Цена деления динамометра (d=0,1 text{Н}); погрешность прямых измерений (Delta_0=frac d2=0,05 text{Н})
Полученные абсолютные погрешности больше (Delta_0).
Сила тяжести для первого тела (F_1=(2,7pm 0,1) text{Н}, delta=4text_%)
Сила тяжести для второго тела (F_2=(1,9pm 0,1) text{Н}, delta=4text_%)
Расчет массы $$ m=frac{F}{10} (text{кг})=100F (text{г}) $$
| Масса (m=100F, text{г}) |
Ошибка метода (delta=delta_{text{шк}}, text{%}) |
Абсолютная погрешность (Delta m=deltacdot m, text{г}) |
|
| 1-е тело | 270 | 2% | 5 |
| 2-е тело | 190 | 2% | 4 |
Масса первого тела (m_1=(270pm 5) text{г}, delta=2text{%})
Масса второго тела (m_2=(190pm 4) text{г}, delta=2text{%})
Выводы
На основании проделанной работы можно сделать следующие выводы.
Для градуирования динамометра в ньютонах использовалось значение $$ overline{g}=10 frac{text{м}}{text{с}^2} $$
По сравнению со стандартным значением (g_0=9,80665 text{м/с}^2) это приводит к вкладу в ошибку метода (delta_gapprox 2text{%}).
При градуировании равномерность шкалы дала составляющую ошибки метода (delta_{text{шк}}=2text{%}).
При определении силы тяжести с помощью полученного динамометра ошибка метода равна сумме (delta+delta_g+delta_{text{шк}}=4text{%}).
Для двух тел неизвестной массы были получены следующие значения сил тяжести: $$ F_1=(2,7pm 0,1) text{Н}, F_2=(1,9pm 0,1) text{Н}, delta=4text{%} $$
При расчете массы по формуле (m=frac Fg), ошибка (delta_g) нивелируется за счет пропорциональности растяжения пружины. Ошибка метода уменьшается (delta=delta_{text{шк}}=2text{%}).
Получаем следующие значения масс: $$ m_1=(270pm 5) text{г}, m_2=(190pm 4) text{г}, delta=2text{%} $$ Таким образом, полученный в ходе работы динамометр позволяет измерять силы тяжести в интервале от 0 до 5 Н с погрешностью 4% и рассчитывать массы тел в интервале от 0 до 500 г с погрешностью 2%.
Вес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.
Вес тела имеет электромагнитную природу (не путать с силой тяжести – она возникает между двумя телами и имеет гравитационную природу!). Обозначается P. Измеряется динамометром. Единица измерения — Н (Ньютон).
Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P↑↓N или P↑↓T.
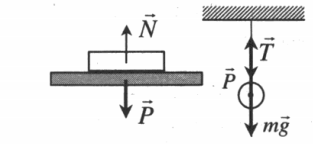
Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:
P = T; P = N; P = Fупр.
Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:
P0 = Fтяж = mg
Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.
Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.
Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:
P = mg = 16,38∙10 = 163,8 (Н)
Перегрузка
Перегрузка — отношение абсолютной величины линейного ускорения, вызванного негравитационными силами, к стандартному ускорению свободного падения на поверхности.
Перегрузка определяется отношением:
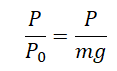
Перегрузка возникает, когда система, в которой находится тело, движется с ускорением.
Вес тела в движущейся равноускоренно системе
Вес тела в движущейся системе может быть больше или меньше веса того же тела в системе, которая находится в состоянии покоя:
- Если система движется равноускоренно в направлении ускорения свободного падения, вес тела меньше веса тела в неподвижной системе: при a↑↑g — P < P0.
- Если система движется равноускоренно в направлении, противоположном ускорению свободного падения, вес тела больше веса тела в неподвижной системе: при a↑↓g — P > P0.
- Если система движется с равномерной скоростью (ускорение равно нулю) в любом направлении по отношению к ускорению свободного падения, вес тела равен весу тела в неподвижной системе: при a = 0 — P = P0.
Применение законов Ньютона для определения веса тела
Опора или подвес неподвижны |
|
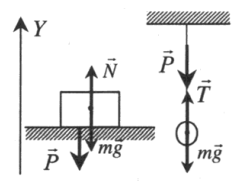 |
Второй закон Ньютона в векторной форме:
N + mg = ma или T + mg = ma Проекция на ось ОУ: N – mg = 0 или T — mg = 0 |
Ускорение опоры направлено вверх |
|
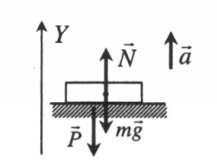 |
Второй закон Ньютона в векторной форме:
N + mg = ma Проекция на ось ОУ: N – mg = ma Вес тела: P = N = ma + mg = m(a + g) |
Ускорение опоры направлено вниз |
|
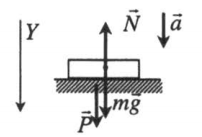 |
Второй закон Ньютона в векторной форме:
N + mg = ma Проекция на ось ОУ: mg – N = ma Вес тела: P = N = mg – ma = m(g – a) |
Вершина выпуклого моста |
|
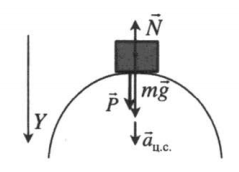 |
Второй закон Ньютона в векторной форме:
N + mg = maц.с. Проекция на ось ОУ: mg – N = m aц.с. Вес тела: P = N = mg – m aц.с. = m(g – aц.с.) |
Нижняя точка вогнутого моста |
|
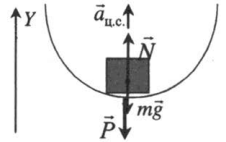 |
Второй закон Ньютона в векторной форме:
N + mg = maц.с. Проекция на ось ОУ: N – mg = maц.с. Вес тела: P = N = maц.с. + mg = m(aц.с. + g) |
Полный оборот на подвесе |
|
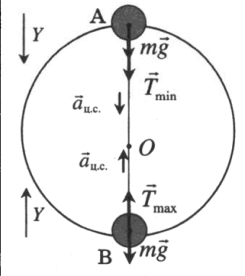 |
Второй закон Ньютона в векторной форме:
T + mg = ma Проекция на ось ОУ в точке А: T + mg = maц.с. Вес тела в точке А: P = T = maц.с. – mg = m (aц.с. – g) Проекция на ось ОУ в точке В: T – mg = maц.с. Вес тела в точке В: P = T = maц.с. + mg = m (aц.с. + g) Важно! Центростремительное ускорение всегда направлено к центру окружности. |
Пример №2. Автомобиль массой 1000 кг едет по выпуклому мосту с радиусом кривизны 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали невесомость?
Вес тела в верхней точке выпуклого моста равен:
P = m(g – aц.с.)
Чтобы пассажиры почувствовали состояние невесомости, вес тела должен быть равен 0:
m(g – aц.с.) = 0
Масса не может быть нулевой, поэтому:
g – aц.с. = 0
g = aц.с
Значит, пассажиры в верхней точке моста почувствуют невесомость, если центростремительное ускорение будет равно ускорению свободного падения. Центростремительное ускорение определяется формулой:
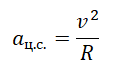
Отсюда скорость автомобиля в верхней точке моста должна быть равна:
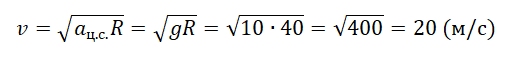
Задание EF18133
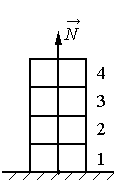 Четыре одинаковых кирпича массой m каждый сложены в стопку (см. рисунок). Если убрать два верхних кирпича, то модуль силы N, действующей со стороны горизонтальной опоры на первый кирпич, уменьшится на…
Четыре одинаковых кирпича массой m каждый сложены в стопку (см. рисунок). Если убрать два верхних кирпича, то модуль силы N, действующей со стороны горизонтальной опоры на первый кирпич, уменьшится на…
Алгоритм решения
1.Вычислить силу, с которой оставшиеся кирпичи давят на опору.
2.Применить третий закон Ньютона.
3.Определить силу, с которой действует горизонтальная опора на первый кирпич.
Решение
Так как кирпичи покоятся, вес каждого равен:
P = mg
Вес двух кирпичей равен:
2P = 2mg
Опора действует на первый кирпич с такой же силой, с какой на него действует два кирпича, оставшихся после того, как два верхних кирпича убрали.
Следовательно:
N = 2P = 2mg
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17624
Подъёмный кран поднимает груз с постоянным ускорением. На груз со стороны каната действует сила, равная по величине 8⋅103 H. На канат со стороны груза действует сила, которая:
а) 8∙103 Н
б) меньше 8∙103 Н
в) больше 8∙103 Н
г) равна силе тяжести, действующей на груз
Алгоритм решения
1.Сформулировать третий закон Ньютона.
2.Применить закон Ньютона к канату и грузу.
3.На основании закона сделать вывод и определить силу, которая действует на канат со стороны груза.
Решение
Третий закон Ньютона формулируется так:
«Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны».
Математически он записывается так:
FA = –FB
Если на груз со стороны каната действует некоторая сила, то и груз действует на канат с этой силой, которая называется весом этого груза, или силой натяжения нити. Следовательно, груз действует на канат с силой 8∙103 Н.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22586
Мальчик медленно поднимает гирю, действуя на неё с силой 100 Н. Гиря действует на руку мальчика с силой:
а) больше 100 Н, направленной вниз
б) меньше 100 Н, направленной вверх
в) 100 Н, направленной вниз
г) 100 Н, направленной вверх
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж, иллюстрирующий ситуацию.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций.
5.Вычислить силу, с которой гиря действует на руку мальчика.
Решение
Запишем исходные данные: мальчик поднимает гирю вверх с силой F = 100 Н.
Сделаем рисунок. В данном случае рука мальчика выступает в роли подвеса. Так как мальчик поднимает гирю медленно, можно считать, что он поднимает ее равномерно (равнодействующая всех сил равна нулю). Выберем систему координат, направление оси которой совпадает с направлением движения руки и гири.
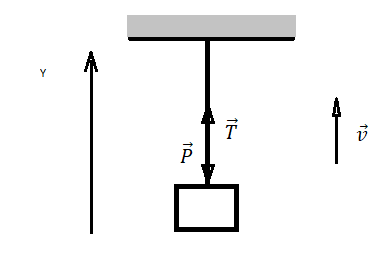
На руку (подвес) действуют только две силы. Поэтому второй закон Ньютона выглядит следующим образом:
P + T = 0
Запишем этот же закон в проекции на ось ОУ:
–P + T = 0
Отсюда:
P = T
Следовательно, на руку мальчика действует вес гири, который по модулю равен силе, с которой мальчик действует на эту гирю.
Внимание! Существует второй способ решения задачи через третий закон Ньютона. Согласно ему, тела действуют друг на друга с силами, равными по модулю, но противоположными по направлению.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.5k
Сила упругости. Закон Гука
«Без сомнения, всё наше
знание начинается с опыта»
Иммануил Кант
В данной теме будет рассмотрен еще один вид силы – сила упругости.
Ранее говорилось о том, что сила, действующая на тело, является причиной изменения скорости этого тела. На любое тело, находящееся на Земле, действует сила тяжести. Остановимся на этом поподробнее. Например, если человек сидит на лавочке, то на него действует сила тяжести, хотя его скорость не изменяется. Таким образом, хотя на тело действует сила, но при этом, скорость этого тела не меняется (то есть, остаётся нулевой в данном случае). Как же это можно объяснить? Объяснение может быть только одно: на тело действует какая-то другая сила, которая уравновешивает силу тяжести. Эта сила называется силой упругости. Сила упругости – это сила, возникающая при деформации и стремящаяся вернуть тело в исходное положение, придать ему исходную форму. То есть, из-за силы тяжести, действующей на лавочку, возникает сила упругости, которая препятствует тому, чтобы лавочка прогибалась, и стремится вернуть лавочку в исходное положение. То же самое можно сказать и о книге, лежащей на столе. На неё действует сила тяжести со стороны Земли и сила упругости со стороны стола.
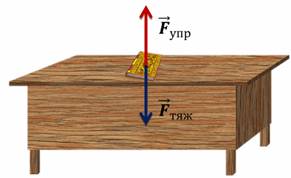
Проведем следующий опыт: подвесим тело на пружине. Чем больше пружина будет растягиваться, тем больше будет сила упругости. В какой-то момент, сила упругости станет равной силе тяжести, и тогда растяжение прекратится. Зависимость силы упругости от степени деформации тела была исследована Робертом Гуком.

Он установил, что изменение длины тела при растяжении (или сжатии) прямо пропорционально модулю силы упругости. В этом и заключается закон Гука.
Fупр = kDl
где Dl – изменение длины тела;
k – жёсткость тела.
Жесткость зависит от размеров и формы тела и, конечно, от вещества, из которого тело состоит. Жесткость тела определяется экспериментальным путем. Если выразить жесткость из формулы, описывающей закон Гука, то можно убедиться, что она равна отношению силы упругости к удлинению тела.
k = Fупр / Dl
Поскольку в системе СИ сила измеряется в Н (ньютонах), а длина в м (метрах), следуя формуле, жесткость измеряется в ньютонах на метр.
[k] = [Н/м]
Необходимо отметить, что существуют упругие и неупругие деформации. Под упругой деформацией подразумевается деформация, после которой тело восстанавливает исходную форму, как только перестают действовать силы, вызвавшие деформацию. Неупругая деформация – это деформация, после которой тело не восстанавливает форму, даже после окончания действия сил, вызвавших деформацию. Например, если растянуть пружину, а потом отпустить её, то пружина восстановит свою форму. Это будет называться упругой деформацией. А вот если расплющить монету ударом молотка, то монета не восстановит свою форму. Это пример неупругой деформации. Так вот, закон Гука применим только к упругим деформациям.
Действие сил упругости используется для создания такого прибора, как динамометр. Динамометр – это прибор для измерения силы.

У каждого динамометра есть крючок, на который укрепляется груз, а также пружина, степень деформации которой позволяет судить о приложенной силе. Также на динамометр нанесена шкала, чтобы можно было считывать его показания. Например, если подвесить грузик на пружину динамометра, то прибор покажет нам силу тяжести, действующую на этот грузик. Допустим по шкале прибора видно, что эта сила составляет 1 Н. Если подвесить еще один такой же грузик, то динамометр покажет силу, вдвое большую, то есть, 2 Н. Добавив еще один грузик, можно убедится, что сила уже равна 3 Н. Таким образом, сила упругости, возникающая при деформации пружины, уравновешивает суммарную силу тяжести грузиков. На динамометре есть и другая шкала – шкала, с помощью которой можно измерить удлинение пружины. Если повторить тот же опыт, то можно убедиться, что удлинение увеличивается пропорционально увеличению силы упругости. То есть, подтверждается закон Гука.
Таким образом, когда тело висит на каком-то подвесе, или стоит на опоре, на него действует сила тяжести, которая уравновешивается силой упругости. Сила, действующая на опору или подвес, вследствие притяжения тела к Земле, называется весом тела. Вес тела обозначается большой латинской буквой 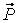 и является векторной величиной (как и любая другая сила). Вес направлен перпендикулярно опоре или вдоль подвеса. В том случае, если тело и опора находятся в состоянии покоя или движутся равномерно и прямолинейно, вес тела равен силе тяжести. В чем же тогда разница между весом тела и силой тяжести? Разница довольно существенная: сила тяжести действует на тело (то есть, сила тяжести приложена к телу). Вес – это сила, с которой тело действует на опору (то есть, вес приложен к опоре). Сила тяжести – это сила, возникающая в результате взаимодействия тела с Землёй. Вес – это сила, возникающая в результате взаимодействия тела с опорой или подвесом.
и является векторной величиной (как и любая другая сила). Вес направлен перпендикулярно опоре или вдоль подвеса. В том случае, если тело и опора находятся в состоянии покоя или движутся равномерно и прямолинейно, вес тела равен силе тяжести. В чем же тогда разница между весом тела и силой тяжести? Разница довольно существенная: сила тяжести действует на тело (то есть, сила тяжести приложена к телу). Вес – это сила, с которой тело действует на опору (то есть, вес приложен к опоре). Сила тяжести – это сила, возникающая в результате взаимодействия тела с Землёй. Вес – это сила, возникающая в результате взаимодействия тела с опорой или подвесом.

Рассмотрим пример: тело находится в свободном падении. Почему оно падает? Потому что на него действует сила тяжести. Но вес тела в этот момент равен нулю, потому что тело не действует, ни на опору, ни на подвес.
Необходимо обратить внимание на распространенную ошибку: часто люди спрашивают «сколько ты весишь?» и получают ответ, например, 50 кг. В килограммах измеряется масса, и именно о ней следует спрашивать. А вес – это сила, и она измеряется в ньютонах. Опять же, при падении тела, его вес равен нулю. Но вот масса тела не зависит от того, падает тело или покоится.
Упражнения.
Задача 1. Ученик прицепил динамометр к пружине. Когда он растянул пружину на 10 см, он посмотрел на динамометр. Оказалось, что для такого растяжения потребовалось приложить силу, равную 4 Н. Найдите жесткость данной пружины.

Задача 2. Шнур длиной 2 м имеет жесткость, 120 Н/м. Какую силу нужно приложить к шнуру, чтобы его длина составила 205 см?

Задача 3. На опоре стоит куб, сторона которого равна 15 см. На подвесе висит шар, сделанный из того же материала, что и куб. Найдите объём этого шара, если его вес вдвое больше, чем вес куба.

Основные выводы:
– Сила упругости – это сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.
– Деформации бывают упругими и неупругими.
– Упругая деформация – это деформация, после которой тело восстанавливает исходную форму, как только перестают действовать силы, вызвавшие деформацию.
– Неупругая деформация – это деформация, после которой тело не восстанавливает форму, даже после окончания действия сил, вызвавших деформацию.
– Закон Гука (для упругих деформаций)
Fупр = kDl
– Коэффициентом пропорциональности в этом законе является такая величина, как жёсткость тела. Эта величина определяется экспериментально.
– Вес – это сила, действующая на опору или подвес вследствие действия на тело силы тяжести. Вес направлен перпендикулярно опоре или вдоль подвеса. В случае если и тело, и опора (или подвес) покоятся или двигаются равномерно и прямолинейно, вес тела равен силе тяжести.
P = Fтяж
Домашнее задание
Стр. 71 — 86 читать, Упр. №10 письменно фот в WhatsApp!
3.1. Вес тела
Вес тела – это сила, с которой
тело, вследствие его притяжения к Земле,
действует на опору или подвес.
Рассмотрим, например, тело, подвешенное
к пружине, другой конец которой закреплен
(рис. 6). На тело действует сила тяжести
![]() направленная
направленная
вниз. Оно поэтому начинает падать,
увлекая за собой нижний конец пружины.
Пружина окажется из-за этого деформированной,
и появится сила упругости
![]() пружины.
пружины.
Она приложена к верхнему краю тела и
направлена вверх. Верхний край тела
будет поэтому «отставать» в своем
падении от других его частей, к которым
сила упругости пружины не приложена.
Вследствие этого и тело деформируется.
Возникает еще одна сила упругости –
сила упругости деформированного тела.
Она приложена к пружине и направлена
вниз. Вот эта сила и есть вес тела.

Рис. 6.
По третьему закону Ньютона обе эти силы
упругости равны по модулю и направлены
в противоположные стороны. После
нескольких колебаний тело на пружине
оказывается в покое. Это значит, что
сила тяжести
![]()
по модулю равна силе упругости Fynp
пружины. Но этой же силе равен и
вес тела.
Таким
образом, в нашем примере вес тела, который
мы обозначим буквой
![]() ,
,
по модулю равен силе тяжести:
![]()
Второй пример. Пусть тело А
находится на горизонтальной опоре
В (рис. 7). На тело А действует
сила тяжести
![]() и
и
сила реакции опоры
![]() .
.
Но если опора действует на тело с силой
![]() то
то
и тело действует на опору с силой
![]() ,
,
которая в соответствии с третьим законом
Ньютона равна по модулю и противоположна
по направлению
![]() :
:
![]() .
.
Сила
![]() и
и
есть вес тела.

Рис. 7.
Если тело и опора неподвижны или движутся
равномерно и прямолинейно, т. е. без
ускорения, то, согласно второму закону
Ньютона,
![]()
Так как
![]() то
то
![]()
Следовательно,
![]()
Значит, если ускорение а = 0, то
вес тела равен силе тяжести.
Но это не значит, что вес тела и сила
тяжести, приложенная к нему, одно и то
же. Сила тяжести приложена к телу, а
вес приложен к опоре или подвесу. Природа
силы тяжести и веса тоже различна. Если
сила тяжести является результатом
взаимодействия тела и Земли (сила
тяготения), то вес появляется в результате
совсем другого взаимодействия:
взаимодействия тела А и опоры В.
Опора В и тело А при этом
деформируются, что приводит к появлению
сил упругости. Таким образом, вес тела
(как и сила реакции опоры) является
частным видом силы упругости.
Вес обладает особенностями, существенно
отличающими его от силы тяжести.
Во-первых, вес определяется всей
совокупностью действующих на тело сил,
а не только силой тяжести (так, вес тела
в жидкости или воздухе меньше, чем в
вакууме, из-за появления выталкивающей
(архимедовой) силы). Во-вторых, вес тела,
существенно зависит от ускорения, с
которым движется опора (подвес).
Вес тела при движении опоры или подвеса
с ускорением
Можно ли увеличить или уменьшить вес
тела, не изменяя самого тела? Оказывается,
да. Пусть тело находится в кабине лифта,
движущегося с ускорением
![]() (рис.
(рис.
8 а, б). Согласно второму закону
Ньютона
![]() (4)
(4)
где N – сила реакции опоры (пола
лифта), m – масса тела.

а

б
Рис. 8.
По третьему закону Ньютона вес тела
![]() .
.
Поэтому, учитывая (4), получим
![]()
Направим координатную ось Y системы
отсчета, связанной с Землей, вертикально
вниз. Тогда проекция веса тела на эту
ось будет равна
![]()
Так как векторы
![]() и
и
![]() сонаправлены
сонаправлены
с осью координат Y, то Ру
= Р и gy = g. Если
ускорение
![]() направлено
направлено
вниз (см. рис. 8, а), то аy
= а, и равенство принимает следующий
вид:
![]()
Из формулы следует, что лишь при а = 0
вес тела равен силе тяжести. При
![]() вес
вес
тела отличается от силы тяжести. При
движении лифта с ускорением, направленным
вниз (например, в начале спуска лифта
или в процессе его остановки при движении
вверх) и по модулю меньшим ускорения
свободного падения, вес тела меньше
силы тяжести. Следовательно, в этом
случае вес тела меньше веса того же
тела, если оно находится на покоящейся
или равномерно движущейся опоре
(подвесе). По этой же причине вес тела
на экваторе меньше, чем на полюсах Земли,
так как вследствие суточного вращения
Земли тело на экваторе движется с
центростремительным ускорением.
Рассмотрим теперь, что произойдет, если
тело движется с ускорением
![]() ,
,
направленным вертикально вверх (см.
рис. 8, б). В данном случае получаем
![]()
Вес тела в лифте, движущемся с ускорением,
направленным вертикально вверх, больше
веса покоящегося тела. Увеличение веса
тела, вызванное ускоренным движением
опоры (или подвеса), называется перегрузкой.
Перегрузку можно оценить, найдя отношение
веса ускоренно движущегося тела к весу
покоящегося тела:
![]()
Тренированный человек способен
кратковременно выдерживать примерно
шестикратную перегрузку. Значит,
ускорение космического корабля, согласно
полученной формуле, не должно превосходить
пятикратного значения ускорения
свободного падения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
