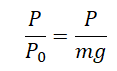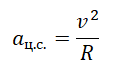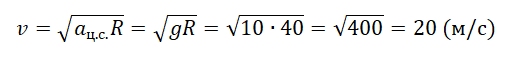Как найти вес в ньютонах физике - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Вес — сила, с которой тело действует на опору (или другой вид крепления), возникающая в поле силы тяжести. Масса связана с энергией и импульсом тела и эквивалентна энергии его покоя. Масса не зависит от силы тяжести (точнее от ускорения свободного падения). Поэтому тело, на Земле имеющее массу 20 кг, на Луне будет иметь массу 20 кг, но совсем другой вес (потому что ускорение свободного падения на Луне в 6 раз меньше, чем на Земле).

1

Для вычисления веса используйте формулу . Вес — это сила, с которой тело действует на опору, и его можно рассчитать, зная массу тела. В физике используется формула .^[1]
2

Определите массу тела. Так как ускорение свободного падения — это стандартная величина, то необходимо знать массу тела, чтобы найти его вес. Масса должна быть выражена в килограммах.
3
Узнайте величину ускорения свободного падения. На Земле, как уже было сказано выше, g = 9,8 м/с². В других местах Вселенной эта величина меняется.^[3]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с² (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.^[4]
- Ускорение свободного падения на Солнце приблизительно равно 274,0 м/с² (примерно в 28 раз больше, чем на Земле). Поэтому ваш вес на Солнце будет в 28 раз больше вашего земного веса (если, конечно, вы выживете на Солнце, что еще не факт!).^[5]
4

Подставьте значения в формулу . Теперь, когда вы знаете массу и ускорение свободного падения , подставьте их значения в формулу . Так вы найдете вес тела (измеряется в ньютонах, Н).

Реклама

1

Задача № 1. Найдите вес тела массой 100 кг на поверхности Земли.
2

Задача № 2. Найдите вес тела массой 40 кг на поверхности Луны.
3

Задача № 3. Найдите массу тела, которое на поверхности Земли весит 549 Н.

Реклама

1
Не путайте массу и вес. Самая распространенная ошибка — перепутать вес и массу (что немудрено, ведь в повседневной жизни мы обычно называем массу весом). Но в физике все не так. Запомните, масса — это постоянное свойство объекта, то, сколько в нем вещества (килограммов), где бы он ни находился. Вес — это сила, с которой объект всеми своими килограммами давит на поверхность, и эта сила на разных небесных телах будет различной.
- Масса измеряется в килограммах или граммах. Запомните, что в этих словах, как и в слове «масса», есть буква «м».
2

Используйте правильные единицы измерения. В задачах по физике вес или силу измеряют в ньютонах (Н), ускорение свободного падения — в метрах на секунду в квадрате (м/с²), а массу — в килограммах (кг). Если для какой-либо из этих величин вы возьмете не ту единицу измерения, воспользоваться формулой будет нельзя. Если масса в условиях задачи указана в граммах или тоннах, не забудьте перевести ее в килограммы.

Реклама

Приложение: вес, выраженный в кгс

Ньютон — это единица измерения силы в международной системе единиц СИ. Нередко сила выражается в килограмм-силах, или кгс (в системе единиц МКГСС). Эта единица очень удобна для сравнения весов на Земле и в космосе.
1 кгс = 9,8166 Н.
Разделите вес, выраженный в ньютонах, на 9,80665.
Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне.
Международная система единиц СИ — система единиц физических величин, которая является наиболее широко используемой системой единиц в мире.

Советы

Самая трудная задача — уяснить разницу между весом и массой, так как в повседневной жизни слова «вес» и «масса» используются как синонимы. Вес — это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу.
Ускорение свободного падения также может быть выражено в Н/кг. 1 Н/кг = 1 м/с².
Плечевые весы измеряют массу (в кг), в то время как весы, работа которых основана на сжатии или расширении пружины, измеряют вес (в кгс).
Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне. На нейтронной звезде он будет весить еще больше, но он, вероятно, этого не заметит.
Единица измерения «Ньютон» применяется намного чаще (чем удобная «кгс»), так как можно найти множество других величин, если сила измеряется в ньютонах.

Предупреждения

Выражение «атомный вес» не имеет ничего общего с весом атома, это масса. В современной науке оно заменено на выражение «атомная масса».

Об этой статье

Эту страницу просматривали 113 467 раз.

Была ли эта статья полезной?

Источник

Определение

Вес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.

Вес тела имеет электромагнитную природу (не путать с силой тяжести – она возникает между двумя телами и имеет гравитационную природу!). Обозначается P. Измеряется динамометром. Единица измерения — Н (Ньютон).

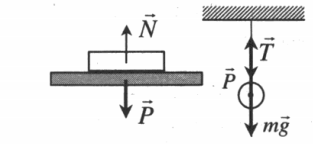
Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P↑↓N или P↑↓T.

Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:

P = T; P = N; P = F_упр.

Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:

P₀ = F_тяж = mg

Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.

Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.

Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:

P = mg = 16,38∙10 = 163,8 (Н)

Перегрузка

Перегрузка — отношение абсолютной величины линейного ускорения, вызванного негравитационными силами, к стандартному ускорению свободного падения на поверхности.

Перегрузка определяется отношением:

Перегрузка возникает, когда система, в которой находится тело, движется с ускорением.

Вес тела в движущейся равноускоренно системе

Вес тела в движущейся системе может быть больше или меньше веса того же тела в системе, которая находится в состоянии покоя:

Если система движется равноускоренно в направлении ускорения свободного падения, вес тела меньше веса тела в неподвижной системе: при a↑↑g — P < P₀.
Если система движется равноускоренно в направлении, противоположном ускорению свободного падения, вес тела больше веса тела в неподвижной системе: при a↑↓g — P > P₀.
Если система движется с равномерной скоростью (ускорение равно нулю) в любом направлении по отношению к ускорению свободного падения, вес тела равен весу тела в неподвижной системе: при a = 0 — P = P₀.

Применение законов Ньютона для определения веса тела

Опора или подвес неподвижны
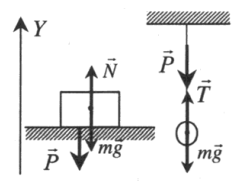	Второй закон Ньютона в векторной форме: N + mg = ma или T + mg = ma Проекция на ось ОУ: N – mg = 0 или T — mg = 0
Ускорение опоры направлено вверх
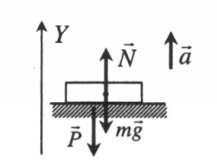	Второй закон Ньютона в векторной форме: N + mg = ma Проекция на ось ОУ: N – mg = ma Вес тела: P = N = ma + mg = m(a + g)
Ускорение опоры направлено вниз
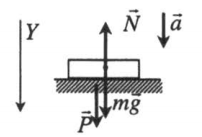	Второй закон Ньютона в векторной форме: N + mg = ma Проекция на ось ОУ: mg – N = ma Вес тела: P = N = mg – ma = m(g – a)
Вершина выпуклого моста
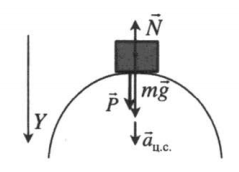	Второй закон Ньютона в векторной форме: N + mg = ma_ц.с. Проекция на ось ОУ: mg – N = m a_ц.с. Вес тела: P = N = mg – m a_ц.с. = m(g – a_ц.с.)
Нижняя точка вогнутого моста
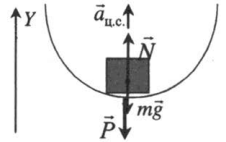	Второй закон Ньютона в векторной форме: N + mg = ma_ц.с. Проекция на ось ОУ: N – mg = ma_ц.с. Вес тела: P = N = ma_ц.с. + mg = m(a_ц.с. + g)
Полный оборот на подвесе
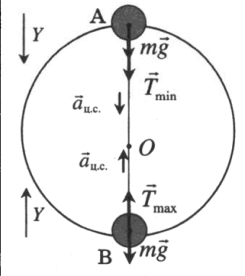	Второй закон Ньютона в векторной форме: T + mg = ma Проекция на ось ОУ в точке А: T + mg = ma_ц.с. Вес тела в точке А: P = T = ma_ц.с. – mg = m (a_ц.с.– g) Проекция на ось ОУ в точке В: T – mg = ma_ц.с. Вес тела в точке В: P = T = ma_ц.с. + mg = m (a_ц.с.+ g) *Важно!* Центростремительное ускорение всегда направлено к центру окружности.

Пример №2. Автомобиль массой 1000 кг едет по выпуклому мосту с радиусом кривизны 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали невесомость?

Вес тела в верхней точке выпуклого моста равен:

P = m(g – a_ц.с.)

Чтобы пассажиры почувствовали состояние невесомости, вес тела должен быть равен 0:

m(g – a_ц.с.) = 0

Масса не может быть нулевой, поэтому:

g – a_ц.с.= 0

g = a_ц.с

Значит, пассажиры в верхней точке моста почувствуют невесомость, если центростремительное ускорение будет равно ускорению свободного падения. Центростремительное ускорение определяется формулой:

Отсюда скорость автомобиля в верхней точке моста должна быть равна:

Задание EF18133

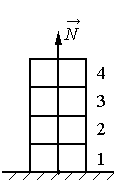
Четыре одинаковых кирпича массой m каждый сложены в стопку (см. рисунок). Если убрать два верхних кирпича, то модуль силы N, действующей со стороны горизонтальной опоры на первый кирпич, уменьшится на…

Алгоритм решения

1.Вычислить силу, с которой оставшиеся кирпичи давят на опору.

2.Применить третий закон Ньютона.

3.Определить силу, с которой действует горизонтальная опора на первый кирпич.

Решение

Так как кирпичи покоятся, вес каждого равен:

P = mg

Вес двух кирпичей равен:

2P = 2mg

Опора действует на первый кирпич с такой же силой, с какой на него действует два кирпича, оставшихся после того, как два верхних кирпича убрали.

Следовательно:

N = 2P = 2mg

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17624

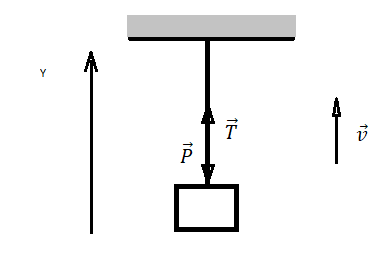
Подъёмный кран поднимает груз с постоянным ускорением. На груз со стороны каната действует сила, равная по величине 8⋅10³H. На канат со стороны груза действует сила, которая:

а) 8∙10³ Н

б) меньше 8∙10³ Н

в) больше 8∙10³ Н

г) равна силе тяжести, действующей на груз

Алгоритм решения

1.Сформулировать третий закон Ньютона.

2.Применить закон Ньютона к канату и грузу.

3.На основании закона сделать вывод и определить силу, которая действует на канат со стороны груза.

Решение

Третий закон Ньютона формулируется так:

«Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны».

Математически он записывается так:

F_A = –F_B

Если на груз со стороны каната действует некоторая сила, то и груз действует на канат с этой силой, которая называется весом этого груза, или силой натяжения нити. Следовательно, груз действует на канат с силой 8∙10³ Н.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22586

Мальчик медленно поднимает гирю, действуя на неё с силой 100 Н. Гиря действует на руку мальчика с силой:

а) больше 100 Н, направленной вниз

б) меньше 100 Н, направленной вверх

в) 100 Н, направленной вниз

г) 100 Н, направленной вверх

Алгоритм решения

1.Записать исходные данные.

2.Сделать чертеж, иллюстрирующий ситуацию.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в виде проекций.

5.Вычислить силу, с которой гиря действует на руку мальчика.

Решение

Запишем исходные данные: мальчик поднимает гирю вверх с силой F = 100 Н.

Сделаем рисунок. В данном случае рука мальчика выступает в роли подвеса. Так как мальчик поднимает гирю медленно, можно считать, что он поднимает ее равномерно (равнодействующая всех сил равна нулю). Выберем систему координат, направление оси которой совпадает с направлением движения руки и гири.

На руку (подвес) действуют только две силы. Поэтому второй закон Ньютона выглядит следующим образом:

P + T = 0

Запишем этот же закон в проекции на ось ОУ:

–P + T = 0

Отсюда:

P = T

Следовательно, на руку мальчика действует вес гири, который по модулю равен силе, с которой мальчик действует на эту гирю.

Внимание! Существует второй способ решения задачи через третий закон Ньютона. Согласно ему, тела действуют друг на друга с силами, равными по модулю, но противоположными по направлению.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 6.5k

Источник

Из-за притяжения Земли все тела имеют вес.

Сила, с которой тело давит на опору или растягивает подвес, называют весом.

Рис. (1). Тело на опоре, тело на подвесе

Вес тела обозначают (P) и измеряют в ньютонах ((H)).

Вес неподвижного тела равен

P=mg

Формула определения веса неподвижного тела точно такая же, как и формула силы тяжести (см. предыдущую тему «Сила. Сила тяжести»). Однако вес тела и сила тяжести — не одно и то же.

Рис. (2). Сила тяжести и вес тела

Например, сила тяжести свободно падающего трёхкилограммового кирпича приблизительно составляет (30) (H), ((F = mg)), а его вес (P) в момент падения равен (0) (H) (так как кирпич находится в состоянии невесомости).

Если помещённое на опору или подвешенное тело неподвижно по отношению к Земле или находится в равномерном движении вверх или вниз, тогда вес тела не меняется.

Вес меняется, когда тело перемещается вверх или вниз с ускорением.

Во время поездки в лифте, если мы двигаемся с ускорением вверх, наш вес увеличивается, хотя сила тяжести остаётся неизменной.

Состояние невесомости — это состояние, когда тело не давит на опору и не растягивает подвес. Такое происходит, когда тело свободно падает под воздействием только силы гравитации.

Почему в космическом корабле есть состояние невесомости?

Потому что космический корабль, обращаясь вокруг Земли, находится в свободном падении (он всё время как бы падает на Землю, но пролетает мимо). Это происходит, когда космический корабль достигает 1-й космической скорости — 7,9 км/с.

Если скорость космического корабля была бы меньше, он упал бы на Землю, а если корабль достиг бы 2-й космической скорости — 11,2 км/с, он стал бы искусственным спутником Солнца.

Если скорость космического корабля достигнет 3-й космической скорости — 16,7 км/с, тогда корабль направится из Солнечной системы к другим звёздам.

К сожалению, до ближайшей звёздной системы Альфа Центавра нужно лететь (18000) лет, так как она находится на расстоянии (4) световых лет.

Интересно, что для того, чтобы достичь Луны, ракета должна развить скорость, равную (0,992) от второй космической скорости.

Источники:

Рис. 1. Тело на опоре, тело на подвесе. © ЯКласс.
Рис. 2. Сила тяжести и вес тела. © ЯКласс.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 апреля 2023 года; проверки требует 1 правка.

У этого термина существуют и другие значения, см. Вес (значения).

Не следует путать с массой.

Вес — сила, с которой тело действует на опору (или подвес, или другой вид крепления), препятствующую падению, возникающая в поле сил тяжести^[1]^[2].
Единица измерения веса в Международной системе единиц (СИ) — ньютон, иногда используется единица СГС — дина.

Помимо приведённого определения, укоренившегося в советской и постсоветской педагогике, встречается трактовка веса как синонима силы тяжести, то есть силы притяжения тела Землёй. В англоязычной литературе существует частично похожее по звучанию слово weight, которое в физике означает силу тяжести^[3], но в быту имеет и другие значения, в том числе «масса» и «вес».

Терминология и значимость[править | править код]

В случае покоящегося в инерциальной системе отсчёта тела, его вес равен силе тяжести, действующей на тело, и пропорционален массе и ускорению свободного падения в данной точке:

{displaystyle mathbf {P} =mmathbf {g} .}

Широтное уменьшение силы тяжести mg

Ускорение свободного падения зависит от высоты над земной поверхностью и — ввиду несферичности Земли, а также ввиду её вращения — от географических координат точки измерения. В результате суточного вращения Земли существует широтное уменьшение веса: на экваторе вес примерно на 0,3 % меньше, чем на полюсах. Другим фактором, влияющим на значение и, соответственно, вес тела, являются гравитационные аномалии, обусловленные особенностями строения земной поверхности и недр в окрестностях точки измерения. Если тело находится вблизи другой планеты, а не Земли, то ускорение свободного падения будет определяться массой и размерами этой планеты, наряду с расстоянием между её поверхностью и телом.

При движении системы «тело» — «опора или подвес» относительно инерциальной системы отсчёта с ускорением вес перестаёт совпадать с силой тяжести^[1]:

{displaystyle mathbf {P} =m(mathbf {g} -mathbf {w} ).}

Например, если ускорение (независимо от скорости) лифта направлено вверх, то вес находящегося в нём груза увеличивается, а если вниз, то уменьшается. Ускорение за счёт вращения Земли не входит в , оно уже учтено в . Состояние отсутствия веса (невесомость) наступает вдали от притягивающего объекта, либо когда тело находится в свободном падении, то есть при .

Тело массой , вес которого анализируется, может стать субъектом приложения дополнительных сил, косвенно обусловленных присутствием гравитационного поля, в том числе силы Архимеда и трения.

В определении, приведённом в преамбуле, отсутствует конкретизация, должны ли учитываться подобные факторы. Не оговорено также, обязательно ли роль опоры-подвеса должно играть упругое твёрдое тело и что если опор несколько. Кроме того, в публикациях встречаются и неэквивалентные дефиниции веса^[4]^[5]^[6].

Так, при учёте только вклада силы тяжести покоящемуся на наклонной поверхности телу приписывается направленный по нормали к опоре вес , где alpha — угол наклона^[5]. Но если учесть ещё и силу трения покоя (а она, по третьему закону Ньютона, приложена и к телу, и к опоре), то вектор веса станет равным ^[4]. Аналогично с силой Архимеда: в жидкости или газе с плотностью rho на тело действует подъёмная сила ${displaystyle mathbf {F} _{A}=-rho mathbf {g} V}$ (где — объём тела), из-за которой, скажем, воздействие тела на неровное^[7] дно водоёма ослабляется. Если считать жидкость или газ опорой и учитывать (в соответствии с третьим законом Ньютона) действие со стороны тела силы Архимеда на жидкость, вектор веса останется равным . При подходе, при котором учитывается действие тела на всё, действующее на само тело, вес тела с точностью до знака равен векторной сумме всех сил (кроме силы тяжести), действующих на тело, включая силы Архимеда («жидкая опора»^[4]) и трения, при учёте всех имеющихся опор-подвесов совместно.

В английском языке существует частично похожее по звучанию слово “weight”, которое в физике означает силу тяжести^[3] , но в быту имеет и другие значения, в том числе “масса” и “вес”. В немецком и французском языках слова, обозначающие силу тяжести, непохожи на русское “вес”. В англоязычной литературе для суммарной силы воздействия на опору — используют термин “apparent weight”, что иногда переводят как «кажущийся вес». Знание этой величины, например, может помочь оценить способность конструкции удержать изучаемое тело в данных условиях.

В ряде случаев — скажем, в ситуации привязанного на улице шарика, наполненного гелием, если под «опорой» имеется в виду только место крепления без включения атмосферы в понятие опоры — «кажущийся вес» (в англоязычной терминологии) может оказаться направленным против вектора ввиду влияния ${displaystyle mathbf {F} _{A}}$ .

Понятие «вес» в физике не является необходимым^[8]. В принципе, можно вообще отменить этот термин и говорить либо о «массе», либо о «силе»^[9] такой-то природы. Использование понятия «вес» во многом связано просто с привычкой^[8] и языковыми традициями.

Измерение[править | править код]

Вес можно измерять с помощью пружинных весов, которые могут служить и для косвенного измерения массы, если их соответствующим образом проградуировать; рычажные весы в такой градуировке не нуждаются, так как в этом случае сравниваются массы, на которые действует одинаковое ускорение свободного падения или сумма ускорений в неинерциальных системах отсчёта. При взвешивании с помощью технических пружинных весов вариациями ускорения свободного падения обычно пренебрегают, так как влияние этих вариаций обычно меньше практически необходимой точности взвешивания.

При нахождении в газообразной или жидкой среде измеренный вес тела может отличаться от измеренного при тех же условиях в вакууме из-за уменьшения веса за счёт действия силы Архимеда^[1].

Вес и масса[править | править код]

В физике вес и масса — разные понятия. Вес — векторная величина, сила, с которой тело действует на опору или подвес. Масса — скалярная величина, мера инертности тела (инертная масса) либо «заряд» гравитационного поля (гравитационная масса). У этих величин отличаются и единицы измерения (в СИ масса измеряется в килограммах, а вес — в ньютонах). Возможны ситуации с нулевым весом и ненулевой массой одного и того же тела, например, в условиях невесомости у всех тел вес равен нулю, а масса у каждого тела своя. И если в состоянии покоя тела показания весов будут нулевыми, то при ударе по весам тел с одинаковыми скоростями воздействие будет разным (см. закон сохранения импульса, закон сохранения энергии).

Вместе с тем строгое различение понятий веса и массы принято в основном в науке и технике, а во многих повседневных ситуациях слово «вес» продолжает использоваться, когда фактически речь идёт о «массе». Например, мы говорим, что какой-то объект «весит один килограмм», несмотря на то, что килограмм представляет собой единицу массы^[10]. Кроме того, термин «вес» в значении «масса» традиционно использовался в цикле наук о человеке — в словосочетании «вес тела человека», вместо современного «масса тела человека». В связи с этим метрологические организации отмечают, что неправильное использование термина «вес» вместо термина «масса» должно прекращаться, и во всех тех случаях, когда имеется в виду масса, должен использоваться термин «масса»^[11]^[12].

История[править | править код]

III Генеральная конференция по мерам и весам, проведённая в 1901 году, подчеркнула, что термин «вес» обозначает величину той же природы, что термин «сила». Конференция определила вес тела как произведение массы тела на ускорение, обусловленное гравитационным притяжением. Стандартный вес тела конференцией был определён как произведение массы тела на стандартное ускорение, обусловленное гравитационным притяжением. В свою очередь для стандартного ускорения было принято значение 980,665 см/с²^[13].

Примечания[править | править код]

↑ ¹ ² ³ Рудой Ю. Г. Вес // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 262. — 707 с. — 100 000 экз.
↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2005. — Т. I. Механика. — С. 373. — 560 с. — ISBN 5-9221-0225-7.
↑ ¹ ² Weight (англ.). Британская энциклопедия. — «Weight, gravitational force of attraction on an object, caused by the presence of a massive second object, such as the Earth… weight is the product of an object’s mass and either the gravitational field or the acceleration of gravity…» Дата обращения: 8 ноября 2020. Архивировано 17 ноября 2020 года.
↑ ¹ ² ³ И. Е. Каган «Вес тела» (IX класс) Архивная копия от 2 октября 2016 на Wayback Machine // Фізiка: праблемы выкладання. – 2001. – № 3. – С. 58-74.
↑ ¹ ² С. В. Задорожная «Вес тела» Архивная копия от 24 января 2021 на Wayback Machine // Сайт педаг. сообщ. «Урок.рф» (2016).
↑ Во многих иноязычных публикациях вес (см., например, Allen L. King. Weight and weightlessness (англ.) // American Journal of Physics : journal. — 1963. — Vol. 30. — P. 387. — doi:10.1119/1.1942032. — Bibcode: 1962AmJPh..30..387K., также начало немецкой версии статьи) синонимизируется с силой тяжести, что в российской педагогике считается ошибкой.
↑ Неровность нужна для подтекания воды под опору, см. Л. Г. Асламазов: Гидростатика Архивная копия от 6 апреля 2018 на Wayback Machine // Квант. – 1972. – № 12. (с. 57, рис. 9ав).
↑ ¹ ² В. Г. Зубов. Механика. М.: Наука, 1978. — 352 с. // см. § 71, с. 176 Архивная копия от 16 сентября 2017 на Wayback Machine: «В механике понятие веса является совершенно лишним. Но так как это слово простое, привычное, то им часто пользуются». (недоступная ссылка) Проверено 21 сентября 2020.
↑ The National Standard of Canada, CAN/CSA-Z234.1-89 Canadian Metric Practice Guide, January 1989: 5.7.3. Considerable confusion exists in the use of the term “weight”. <…> In scientific and technical work, the term “weight” should be replaced by the term “mass” or “force”, depending on the application.
↑ Ранее в технике широко использовалась единица силы килограмм-сила — одна из основных единиц системы МКГСС.
↑ ISO 80000-4:2006, Quantities and units — Part 4: Mechanics. “In common parlance, the name ‘weight’ continues to be used where ‘mass’ is meant, but this practice is deprecated.”
↑ SI Units: Mass (англ.). Weights and Measures. NIST. Дата обращения: 7 декабря 2016. Архивировано 17 декабря 2016 года.
↑ Declaration on the unit of mass and on the definition of weight; conventional value of g (англ.). Resolution of the 3rd CGPM (1901). BIPM. Дата обращения: 1 ноября 2015. Архивировано 25 июня 2013 года.

См. также[править | править код]

Масса
Геоид
Гравиметрия
Фигура Земли
Весы

Источник

Прежде чем отвечать на вопрос о количестве килограммов в одном ньютоне, необходимо разобраться с предложенными понятиями с точки зрения общепринятой системы СИ, учитывая, что ньютон является не столько базовой единицей системы СИ, сколько единицей метрической.

Содержание:

Порядок решения задачи
Алгоритм решения вопроса с учетом законов физики
- Формула для перевода величин

Порядок решения задачи

При решении физических задач значения физических величин измерения массы, представленные в единицах, отличных от единиц массы, необходимо перевести в единицы СИ, т. е. в килограммы.

Перевод осуществляем следующим образом:

1 Н = 1 кг x 1 м/с².

Если рассматривать поставленный вопрос буквально, то ответ будет следующим:

1 кг/1 Н = 1 кг/(1 кг x 1 м/с²) = 1/(1 м/с2) = 1 с²/м.

Получаем обратную единицу измерения ускорения. В этом нет здравого смысла.

Алгоритм решения вопроса с учетом законов физики

Если рассуждать здраво, то нужно исходить из позиции, что в системе СИ ньютон — единица силы, которую вы получаете при помещении тела в гравитационное поле. Фактически этот показатель используется для обозначения любых сил — гравитационных, электромагнитных, силы трения и других сил с привязкой к массе объекта, на который действуют любые силы. Килограмм же есть единица измерения массы.

Говоря проще, чтобы вытеснить тело весом один килограмм с ускорением один м/с², нам нужно приложить силу, равную одному ньютону.

Если ограничивать силу только гравитационной силой планетной массы для тела меньшей массы на ее поверхности, можно вывести пропорциональную зависимость между массой и указанной гравитационной силой, приводящей к постоянному ускорению для произвольной массы (пренебрегая другими силами, такими как сопротивление воздуха). Иначе говоря, числовое значение ньютонов в килограмме в любом месте будет равно силе ускорения объекта определенной массы.

Таким образом, в системе СИ значение в 1 Н определяется как сила, необходимая для ускорения массы в один килограмм с ускорением в один метр в секунду за секунду (то есть секунду в квадрате) в направлении действия силы.

Обратите внимание, что сила и ускорение являются векторными величинами, поэтому они имеют направление и величину, тогда как масса — скалярное значение, имеющее только заданную величину.

Сила (F) равна массе (m) раз на ускорение (a): F = m x a .

Такой вывод основан на втором законе ньютоновского движения, ускорение тела, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе этого тела.

Исходя из этого, вопрос о переводе ньютонов в килограммы изначально не имеет никакого смысла. По сути, это равносильно тому, как если бы вы спросили: «Сколько в одном часе метров?» или «Сколько байт в десяти литрах?» Поскольку сравнение различны физических величин, измеряемых в разных единицах, само по себе безосновательно.

Поэтому уместнее было бы рассматривать вопрос о том, как все-таки вычислить, сколько ньютонов в одном килограмме с позиции гравитации в определенном месте на Земле. Иными словами, чтобы найти массу в килограммах, нам нужно знать вес в ньютонах, поскольку масса фактически представляет собой вес тела. Приведя две физические величины с разными значениями к общему знаменателю — в данном случае утверждению о том, что масса равна весу, мы можем смело переводить ньютоны в килограммы и обратно, а также учитывать, насколько сильно гравитационное поле, которое напрямую связано с ускорением.

В частности, мы можем использовать формулу W = m x g (которая, по сути, является особым случаем выражения упомянутого второго закона: F = m x а), где W — вес объекта в ньютонах, m — масса объекта в килограммах, g — гравитационное ускорение объекта в ньютонах на килограмм.

Все по тому же второму закону получаем: F = m x g.

Если предположить, что объект весом 1 кг находится на Земле, поскольку один килограмм веса тяжелее на Земле, чем на Луне или, скажем, на Марсе, то мы учитываем значение g на поверхности Земли, которое составляет g = 9,8 Н/кг. Таким образом, получаем: W = 9,8 * 1 = 9,8 Н, то есть один килограмм составляет 9,8 ньютонов. Таким образом, мы с вами осуществили перевод килограммов в ньютоны:

Тело весом один килограмм имеет (стандартный) вес равный 9,8 Н.

Идем дальше. «Стандартная гравитация» или «стандартное ускорение свободного падения» (g ₀) составляет 9,80665 м/с² или 9,80665 Н/кг — среднее значение гравитации на поверхности планеты Земля.

Несмотря на то, что это значение является общепринятым для преобразования значений между массой и силой тяжести, это теоретическое значение, поскольку справедливо оно только для некоторых мест на Земле вблизи уровня моря.

Фактическая же сила тяжести на Земле изменяется на 0,7%. Но это частности. Хотя, как известно, из-за того, что не учитываются исключения и частности, могут возникать неточности при проведении измерений.

Формула для перевода величин

Отвечая на вопрос о переводе ньютонов в килограммы при стандартной гравитации (и это важно), получаем следующее значение:

1 Н ÷ g ₀ ≃ 0,101972 кг.

Округлив полученное значение, можно записать следующее:

1 Н = 0,101 кг.

Источник

Приложение: вес, выраженный в кгс

Советы

Предупреждения

Об этой статье

Была ли эта статья полезной?

Перегрузка

Применение законов Ньютона для определения веса тела

Опора или подвес неподвижны

Ускорение опоры направлено вверх

Ускорение опоры направлено вниз

Вершина выпуклого моста

Нижняя точка вогнутого моста

Полный оборот на подвесе

Терминология и значимость[править | править код]

Измерение[править | править код]

Вес и масса[править | править код]

История[править | править код]

Примечания[править | править код]

См. также[править | править код]

Порядок решения задачи

Алгоритм решения вопроса с учетом законов физики

Формула для перевода величин

Вам также может понравиться

Как найти площадь многоугольных фигур

Как составить цель командировки

Как составить задание на реконструкцию

Добавить комментарий Отменить ответ