Как найти входное напряжение цепи - Сайт, где вы сможете решить свои вопросы

Тема1 Расчет действующих значений токов и напряжений

P = R I~2 :

Изучение этой темы предоставляет возможность оперировать показаниями измерительных приборов электромагнитной и электродинамической систем, а также выполнять расчеты при последовательном или параллельном соединении приемников без использования комплексных чисел.

Занятие1

Цели занятия:

1.Научиться строить векторные диаграммы для цепей с последовательным и параллельным соединением приемников.

2.Научиться применять закон Ома для действующих значений.

3.Научиться вычислять потребляемую схемой мощность.

Рассмотрим первую целевую задачу занятия.

Действующим значением тока I считают такой постоянный ток, который производит тот же тепловой эффект, что и реальный переменный ток. Действующие значения обозначают заглавными печатными буквами:

I,U, E .

Законы Кирхгофа для действующих значений не выполняются. Оперировать действующими значениями позволяют прямоугольные треугольники, которые получаются при построении векторных диаграмм.

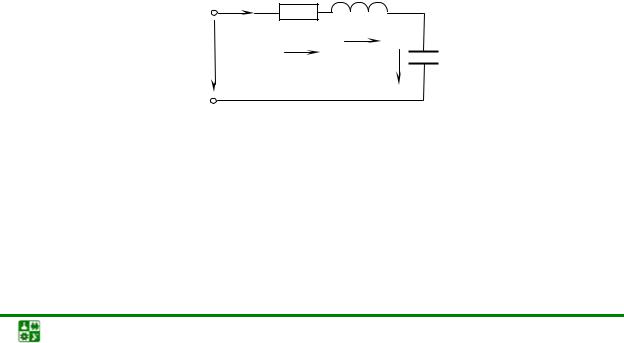
Схема замещения цепи с последовательным соединением приемников изображена на рис. 2.1.

I	R	X L
UL
	UR
U		X
	C
		UC

Рис. 2.1

Построим векторную диаграмму. Построение начнем с вектора величины, общей для данной цепи. При последовательном соединении элементов такой величиной является ток. Вид диаграммы зависит от характера цепи. Построение векторной диаграммы для цепи, имеющей активно-индуктивный характер, т. е.

 Теоретические основы электротехники. Практикум

-53-

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Тема 1 Расчет действующих значений токов и напряжений

X L > XC и X > 0, показано на рис. 2.2.

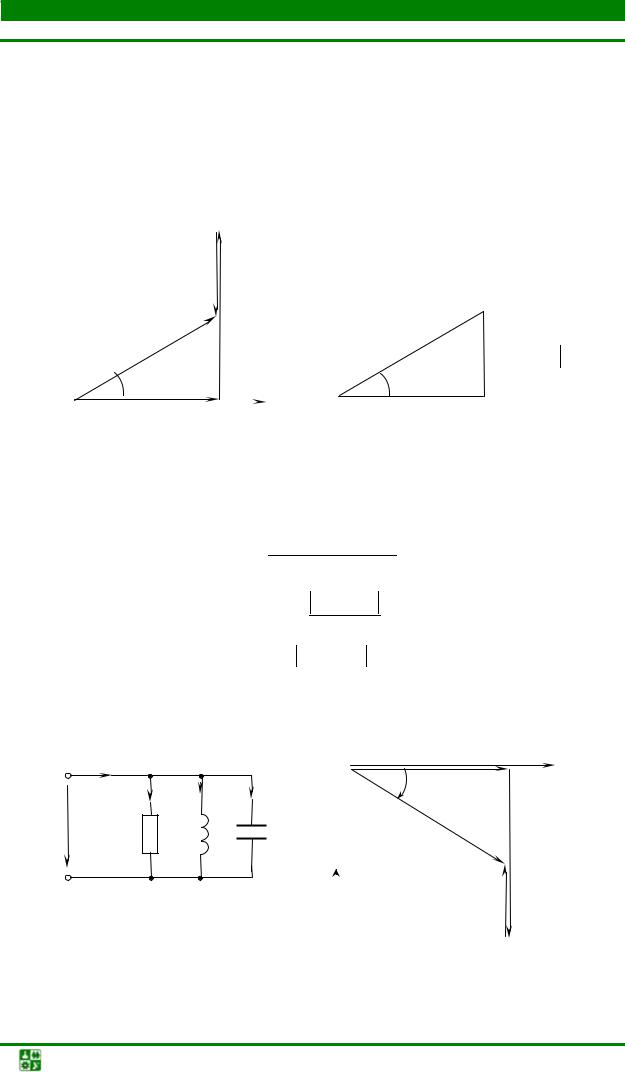
Входное напряжение складывается из напряжений на трех идеальных элементах при учете сдвига фаз. Напряжение на резисторе совпадает с током по фазе. Напряжение на индуктивном элементе опережает ток на 90°, на емкостном – отстает на 90°.

Полученный при построении векторной диаграммы треугольник ОАВ изображен на рис. 2.3.

		UL
		UC
		B				B
	U				U		UL −UC


0	ϕ	A		0	ϕ	A
	UR
		UR	I


		Рис. 2.2			Рис. 2.3

Угол ϕ = ψu − ψi – угол сдвига фаз тока и полного напряжения.

Треугольник ОАВ дает возможность оперировать действующими значениями:

U= 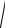UR2 +(UL −UC )2 ,

ϕ= arctg UL −UC ,

U R =U cosϕ, U L −UC =U sin ϕ.

Схема замещения цепи с параллельным соединением приемников изображена на рис. 2.4.

I			0	A U
I	I	IR

ϕ
IR	L	C

U	R	X L	XC	I

					B
				IC	IL
	Рис. 2.4
				Рис. 2.5

 Теоретические основы электротехники. Практикум

-54-

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Тема 1 Расчет действующих значений токов и напряжений

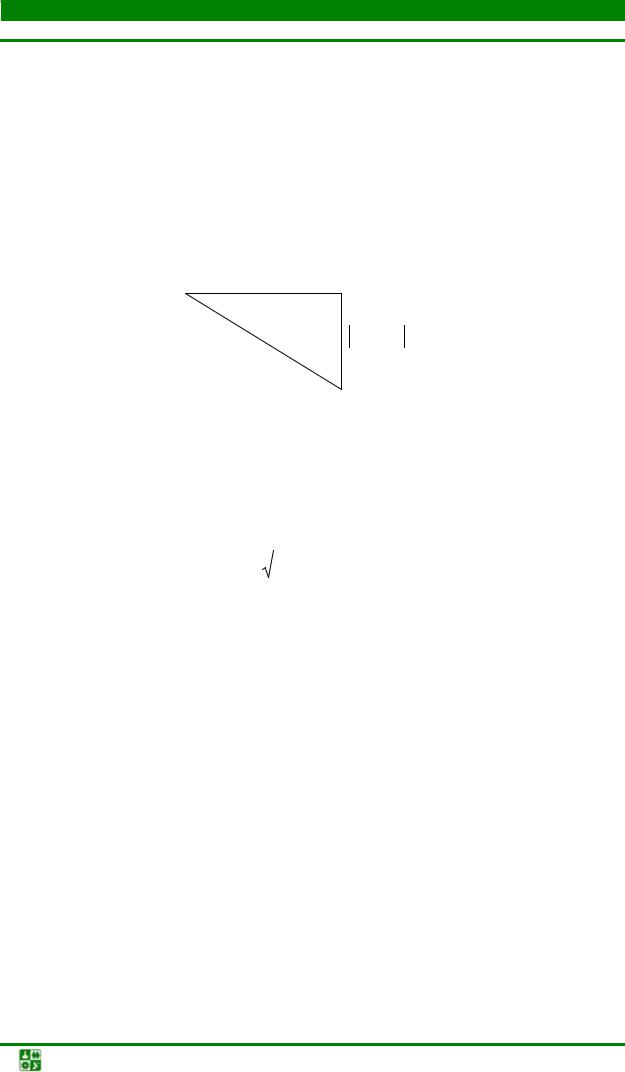
Построение векторной диаграммы начинаем с вектора напряжения, которое является одинаковым для всех элементов схемы. Векторная диаграмма для случая, когда X L < XC , приведена на рис. 2.5.

Ток в неразветвленной части схемы складывается из токов трех параллельных ветвей при учете сдвига фаз. Ток через резистор совпадает с напряжением по фазе, через индуктивный элемент отстает от напряжения на 90°, ток через конденсатор опережает его на 90°.

Полученный при построении векторной диаграммы треугольник токов ОАВ изображен на рис. 2.6.

IR A

0 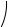ϕ

IL − IC

Рис. 2.6

Из свойств треугольника токов получаем следующие соотношения, позволяющие оперировать действующими значениями:

I =

;

IR2 + (IL − IC )2

ϕ = arctg

IL − IC

;

IR = I cosϕ;

I L − IC

= I sin ϕ.

Перейдем к рассмотрению второй целевой задачи.

I ,

Если разделить все стороны треугольника напряжений на ток

получим подобный ему треугольник сопротивлений (рис.

2.7), где

Z –

полное сопротивление цепи;

R – активное сопротивление; X – реактивное

сопротивление; X L = L ω

– индуктивное

сопротивление,

XC =

–

C ω

емкостное сопротивление.

 Теоретические основы электротехники. Практикум

-55-

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Тема 1 Расчет действующих значений токов и напряжений

U	= Z		UL −UC
I			=	X L − XC	= X


		I
ϕ

	UR	= R
	I

		Рис. 2.7

Закон Ома для действующих значений при последовательном соединении приемников примет вид

U = Z I .

Из свойств треугольника сопротивлений получаем соотношения

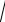
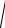
Z= R2 + X 2 = R2 + (X L − XC )2 ;

ϕ= arctg XR ;

R = Z cosϕ; X = Z sin ϕ.

Полное сопротивление любого количества последовательно соединенных приемников

Z = 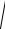(∑R)2 +(∑X L −∑XC )2 .

UIR =G

		I	− I

I			L	C	= B

=Y	U
U

Рис. 2.8

Разделив все стороны треугольника токов на напряжение, получим подобный ему треугольник проводимостей (рис. 2.8), где Y – полная

 Теоретические основы электротехники. Практикум

-56-

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Тема 1 Расчет действующих значений токов и напряжений

проводимость; G – активная проводимость; B = BL − BC – реактивная проводимость; BL – индуктивная проводимость; BC – емкостная проводимость.

Закон Ома для действующих значений при параллельном соединении примет вид

I = Y U .

Из свойств треугольника проводимостей получаем соотношения

Y = 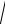G2 + B2 ;

G= Y cosϕ; B = Y sin ϕ;

ϕ= arctg GB

Полная проводимость любого количества параллельно соединенных приемников

Y = 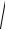(∑G)2 +(∑BL −∑BC )2 .

Перейдем к рассмотрению третьей целевой задачи.

Умножением всех сторон треугольника напряжений на ток получаем треугольник мощностей (рис. 2.9).

UR I = P

Рис. 2.9

Активная мощность

P =UR I = R I 2 =U I cosϕ

характеризует энергию, которая передается в одном направлении от генератора к приемнику. Она связана с резистивными элементами.

 Теоретические основы электротехники. Практикум

-57-

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Тема 1 Расчет действующих значений токов и напряжений

Реактивная мощность Q = UL −UC I = X I 2 =U I sinϕ характеризует

часть энергии, непрерывно циркулирующей в цепи и не совершающей полезной работы. Она связана с реактивными элементами.

Полная (кажущаяся) мощность S =U I = P2 +Q2 .

Активную мощность измеряют в ваттах (Вт), реактивную – в вольтамперах реактивных (вар), полную – вольтамперах (В А).

Задача1

Вычислить показание вольтметра, подключенного к зажимам индуктивной катушки, схема замещения которой представлена на рис. 2.10, если амперметр показывает ток I =10 А, R = 3 Ом, X L = 4 Ом.

A I

U V

X L

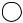
Рис. 2.10

Решение

1. Вольтметр показывает действующее значение входного напряжения U , которое можно вычислить по закону Ома:

U= Z I .

2.Полное сопротивление схемы

Z = 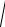R2 + X L2 = 32 + 42 =5 Ом.

Тогда напряжение на входе схемы

U = 5 10 = 50 В.

Входное напряжение можно вычислить другим путем, используя треугольник напряжений, полученный при построении векторной диаграммы

(рис. 2.11):

 Теоретические основы электротехники. Практикум

-58-

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Тема 1 Расчет действующих значений токов и напряжений

U UL I

Рис. 2.11

U = UR2 +UL2 = (R I )2 + (X L I )2 =

= 302 + 402 =50 В.

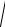
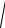
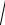
Следующие задачи решите самостоятельно.

Задача2

В схеме на рис. 2.12 первый вольтметр показывает напряжение 30 В, второй – 90 В, третий – 50 В.

Определить напряжение, которое показывает вольтметр на входе схемы.

Ответ: U = 50 В.

	V1	V2
	R	X L
U	UR	UL	XC V3
UC
V

Рис. 2.12

Задача3

В схеме на рис. 2.13 первый амперметр показывает ток 6 А, второй – 20 А, третий – 12 А. Определить ток, который показывает амперметр на входе схемы.

 Теоретические основы электротехники. Практикум

-59-

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Тема 1 Расчет действующих значений токов и напряжений

I A

	A1	A2	A3
		I
U	I	2	I	3
	1
	R	X L		XC

	Рис. 2.13

Ответ: I =10 А.

Задача4

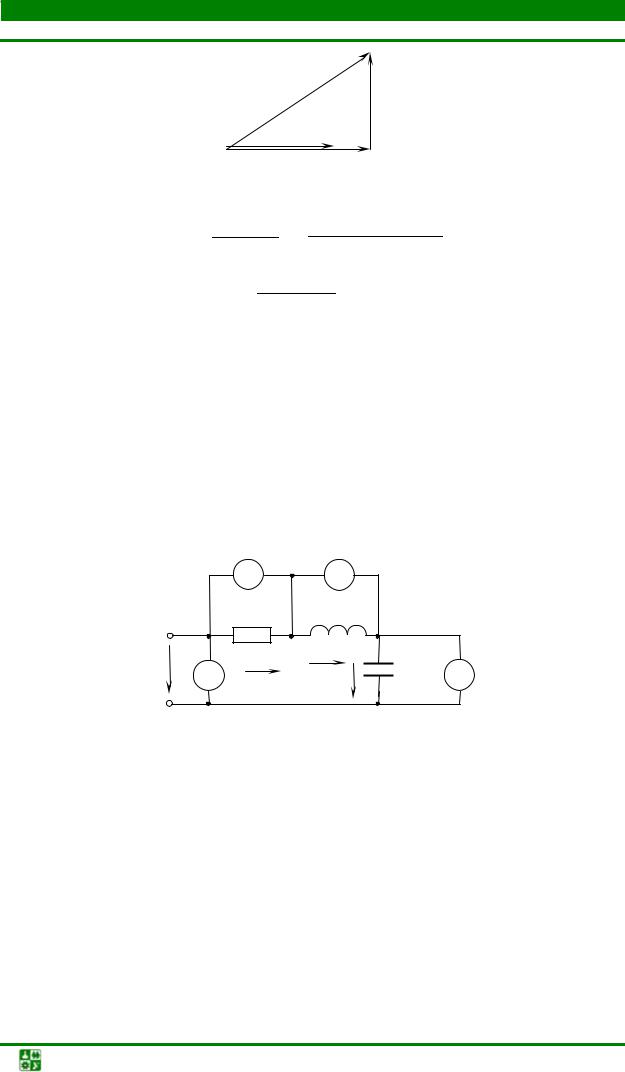
Определить, можно ли подключить цепь, схема замещения которой изображена на рис. 2.14, к сети с напряжением U = 66 В и частотой f = 50

Гц, если напряжения Uab		и Ubс не	должны превышать номинального
Uн =120 В, R1 = 8 Ом, R2 =3 Ом,
L = 0,1576 Гн, C = 64,34 мкФ.
a	I		R	X L	b
1

U

		XC
			R2
c

		Рис. 2.14

Решение

1. По закону Ома для действующих значений

Uаb = Zаb I ; Ubс = Zbc I .

2. Полное

сопротивление

аb

R2 + X

Индуктивное

сопротивление

X L = L ω= L 2π f = 0,1576 2 π 50 = 49,5

Ом.

Подставив

значения R

и X

, получим Z

аb

+ 49,52

= 50,1 Ом.

Полное сопротивлениеZ

bс

+ X 2

Емкостное

сопротивление

106

= 49,5 Ом.

Подставив значения

и X

C 2π f

64,34 2π 50

Cω

получим Zbс =

32 + 49,52

= 49,6 Ом.

 Теоретические основы электротехники. Практикум

-60-

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Тема 1 Расчет действующих значений токов и напряжений

3. Ток в цепи по закону Ома

I= UZ .

4.Полное сопротивление схемы

Z = (R1 + R2 )2 + (X L − XC )2 = (8 +3)2 +(49,5 − 49,5)2 =11 Ом.

Тогда	ток	I = 66 = 6	А.	Напряжение Uаb = 50,1 6 = 300,6 В,
	Ubс	11
напряжение	= 49,6 6 = 297,5	В. Следовательно,	такое	подключение
сделать нельзя, так как значения напряжений Uаb	и Ubс	значительно
превышают номинальное.
			Задача5
Вычислить ток в индуктивной катушке, подключенной к сети
переменного	тока с напряжением U = 220 В, если потребляемая мощность
P = 440 Вт,	коэффициент мощности cosϕ = 0,5. Какой ток будет в этой

катушке при подключении ее к сети постоянного тока того же напряжения?

Решение

1. Вычислим ток в катушке при подключении ее к сети переменного напряжения, воспользовавшись формулой активной мощности

P =U I cosϕ.

Отсюда

I~ = U P = 440 = 4 А.

cosϕ 220 0,5

2.Ток в катушке при подключении ее к сети постоянного напряжения можно найти по закону Ома I_ = UR , так как в схеме замещения (рис. 2.10)

остается только резистивный элемент (ω= 0, X L = L ω= 0).

3. Вычислим активное сопротивление из формулы активной мощности

 Теоретические основы электротехники. Практикум

-61-

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Тема 1 Расчет действующих значений токов и напряжений

Тогда I− = 27220,5 = 8 А.

Следующую задачу решите самостоятельно.

	Задача6
Вычислить	параметры схемы	замещения индуктивной катушки
(рис. 2.10), если	при подключении	к сети с напряжением U =120 В и

частотой f = 50 Гц ток I =100 А, активная мощность P =10000 Вт.

Пояснение к решению

Параметрами индуктивной катушки являются активное сопротивление R и индуктивность L .

Ответ: R =1 Ом, L = 0,002 Гн.

Для самоконтроля решите задачи 7–10.

Задача7

В цепь синусоидального тока (рис. 2.15) включены три амперметра электромагнитной системы. Определить показание амперметра А2 , если

амперметры А и А1 показывают соответственно I =10 А и I1 = 6 А.

A XC

Рис. 2.15

Ответ: I2 =8 А.

Задача8

Определить ток I и входное напряжение U схемы на рис. 2.16, если напряжение на емкостном элементе UC = 70,7 В, R =100 Ом, C = 2 мкФ,

ω= 5000 с-1.

 Теоретические основы электротехники. Практикум

-62-

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Домашнее задание № 3.2

Определить переходную и импульсную характеристику цепи. Входное напряжение подключено к зажимам 1-1’. Выходное напряжение снимается с зажимов 2-2’.
Пользуясь любой из найденных характеристик, определить реакцию цепи на заданное входное воздействие . : длительность импульса следует выбрать равной постоянной времени цепи,
Построить временную зависимость . Рассчитать значения , , ,

R1	R2	C2
10 Ом	10 Ом	20 мкФ

[image]

Определим переходную и импульсную характеристики цепи.

Входное сопротивление цепи:

Ток равняется:

Выходное напряжение найдём по второму закону Кирхгофа:

Тогда передаточная функция цепи:

Подставляя числовые значения, получим:

Переходная характеристика цепи – это реакция цепи на единичное входное воздействие:

Изображение единичной функции , поэтому мы можем найти изображение выходного напряжение при таком воздействии на входе цепи:

Теперь найдём оригинал этого изображения выходного напряжения – это и будет переходная характеристика цепи. Изображение имеет вид дроби , где корни уравнения равняются и . Повторяющихся корней нет. Производная знаменателя:

Так как дробь мы можем представить в виде дроби:

То в нашем случае:

Таким образом:

Оригинал , который и будет переходной функцией, имеет вид:

Импульсная характеристика четырёхполюсника определяется как реакция на входное воздействие, представляющее собой дельта-функцию . Изображение дельта-функции равняется 1, поэтому изображение выходного напряжения имеет вид:

Оригинал этого напряжения будет импульсной характеристикой цепи:

Импульсная характеристика – это производная от переходной характеристики:

Определим реакцию цепи на заданное входное воздействие.

Входное воздействие имеет вид:

[image]

Где – постоянная времени цепи. Постоянная времени цепи определяет время, в течении которого напряжение на выходе уменьшается в раз. В нашем случае

Это входное воздействие можно рассматривать как 3 следующих друг за другом этапа:

– скачок входного напряжения в момент времени от 0 до

– постоянное значение при

– скачок входного напряжения в момент времени от до 0

Воспользуемся для определения реакции цепи (нахождения ) интегралом Дюамеля:

при :

Первое слагаемое обусловлено скачком в момент времени , второе слагаемое – постоянным значением напряжения на входе цепи в период времени , равняется 0, так как.

при

Третье слагаемое обусловлено скачком напряжения в момент . Воспользовавшись единичной функцией , можем записать для :

Входной сигнал имеет вид:

Найдём изображение входного напряжения :

Определим реакцию цепи на такое входное воздействие. Изображение выходного напряжения :

Рассмотрим дробь:

Корни уравнения , откуда и . Первая производная . Таким образом:

Таким образом:

Оригинал выходного напряжения имеет вид:

Что совпадает с выходным напряжением, полученным с использованием переходной характеристики цепи.

Построим графически зависимость . Рассчитаем значения , , ,

График напряжения :

[image]

Рассчитаем значения в моменты времени . Для этого воспользуемся аналитическим выражением для .

Для :

Так как выходное напряжение – это напряжение на конденсаторе, поэтому согласно законам коммутации оно не может измениться скачком, а для оно было равно нулю, так как входное напряжение было равно нулю. Таким образом, .

Для моментов времени и также , потому что выходное напряжение – это напряжение на конденсаторе, и оно не может измениться скачком, согласно законам коммутации.

Заметим, что, если бы входное напряжение представляло собой единичный скачок амплитудой бесконечной длительности, то напряжение на конденсаторе для равнялось бы напряжению на резисторе в установившемся процессе: . Но так как длительность единичного импульса ограниченно временем , равным постоянной времени цепи, то конденсатор не успевает зарядиться до этого значения, и успевает зарядиться только до значения, на меньшее, а при разряжается через резистор .

Для :

При входное напряжение равняется нулю, поэтому при конденсатор разряжается через резистор и напряжение на нем, которое равняется выходному, стремится к нулю.

Ответ:

Переходная характеристика цепи:

_{Импульсная характеристика цепи:}

Реакция цепи на заданное входное воздействие:

Сайт управляется системой uCoz

Источник

ads

Одним из способов расчета цепей переменного тока является комплексный, или еще как говорят, символический метод расчета. Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений, используя для решения любые методы (эквивалентных преобразований, контурных токов, узловых потенциалов и т.п.). Но для начала необходимо иметь понятие, в каких именно формах может представляться синусоидальная величина. 1. Одна из форм представления – это вращающийся вектор (см. рис.1):

Рис.1. Вращающийся вектор

С помощью рисунка ясно видно, как с течением времени меняется значение синусоидальной величины. В нашем случае – это величина а на графике, которая может быть, например, входным напряжением. Величина имеет некоторое начальное значение при t = 0 при начальной фазе φ

имеет положительное максимальное значение при угле ωt₃, когда при времени t₃ сумма ωt₃ + φ = 90° и соответственно,

имеет отрицательное максимальное значение при угле ωt₇, когда при времени t₇ сумма углов ωt₇ + φ = 270° и, соответственно,

и имеет два нулевых значения при ωt_n + φ = 0, когда ωt_n = —φ (на рис.1 эта область не показана и находится слева от начала координат)

и тогда

и имеет нулевое значение при угле ωt₁₁, когда при времени t₁₁ сумма ωt₁₁ + φ = 360° и соответственно,

Именно по такому закону и меняется привычное нам переменное напряжение 220 В, изменяясь по синусоидальному закону от значения 0 В до максимальных 311 В и обратно.

2. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2)

Рис.2. Комплексное число на комплексной плоскости

Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины. С учетом начальной фазы φ такое число записывают как .

На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна

На рисунке выше этот вектор также показан.
Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли

При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.
Итак, три формы записи комплексного числа:

1) показательная форма в виде

2) тригонометрическая форма в виде

3) алгебраическая форма

где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая.

Например, имеем комплексное число в показательной форме вида

в тригонометрической форме записи это запишется как

при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что

В итоге получим

где

При переходе от алгебраической формы к показательной комплексное число вида

переходит к показательному виду по следующим преобразованиям

а угол

Таким образом, и получим

Перейдем к рассмотрению несложных примеров использования символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода:

1. - Составить комплексную схему, заменяя мгновенные значения ЭДС, напряжений и токов их комплексным видом
  - В полученной схеме произвольно выбирают направления токов в ветвях и обозначают их на схеме.
  - При необходимости составляют комплексные уравнения по выбранному методу решения.
  - Решают уравнения относительно комплексного значения искомой величины.
  - Если требуется, записывают мгновенные значения найденных комплексных величин.

Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.

Рис.3. Схема с последовательным соединением элементов

Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.4):

Рис.4. Схема с комплексными обозначениями

По закону Ома ток в цепи равен

где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как

Пояснение: здесь начальная фаза φ = 0°, так как общее выражение для мгновенного значения напряжение вида при φ = 0° равно

Соответственно, комплекс входного напряжения в показательной форме запишется как

Полное комплексное сопротивление цепи в общем виде

Находим комплексное сопротивление индуктивности

Находим комплексное сопротивление емкости

Соответственно, общее комплексное сопротивление цепи

Ток в цепи

Комплексные напряжения на элементах

Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство

Проверяем

С небольшим расхождением из-за округлений промежуточных вычислений всё верно.

Пример 2. В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1) полное сопротивление электрической цепи и его характер;
2) действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;

Рис.5.Цепь однофвзного синусоидального тока

Решение:
1. Находим комплексные сопротивления ветвей и всей цепи:
Учитываем, что

Комплексное сопротивление первой ветви:

Комплексное сопротивление второй ветви:

Комплексное сопротивление третьей ветви:

Общее сопротивление цепи

Откуда

— нагрузка носит активно-индуктивный характер

2. Находим действующие значения токов в ветвях:

Рис.6. Схема с обозначенными комплексными токами

Действующие значения, соответственно,

3. Определим показания приборов:
Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:
U=220 В
Ваттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом, активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания: