На чтение 15 мин Просмотров 10 Опубликовано 7 апреля 2023 Обновлено 7 апреля 2023
Содержание
- Что такое входное сопротивление и как его измерить
- Понятие входного сопротивления для постоянного тока
- Что такое внутреннее сопротивление при переменном токе
- Как измерить
- Выходное напряжение
- Практическое применение
- Видео по теме
- Электроника
- учебно-справочное пособие
- Входное и выходное сопротивление
- Входное сопротивление
- Измерение входного сопротивления
- Выходное сопротивление
- Выводы
- Источники:
Что такое входное сопротивление и как его измерить
При работе со сложными схемами нужно уметь определять характеристики их отдельных блоков и элементов. В частности, входное и выходное сопротивление. Важно знать, что они из себя представляют, как определяются и какую роль играют в работе устройства.

Понятие входного сопротивления для постоянного тока
Радиоэлектронные устройства могут быть не только относительно, но и очень сложными, состоящими из многих блоков. Однако независимо от сложности устройства, количества используемых в нем деталей, схему можно рассматривать в качестве совокупности простых частей с определенной разностью потенциалов на входе. На выходе блока имеется ещё два контакта, на которых также присутствует напряжение. В первом случае его называют входным, в другом — выходным. Сказанное можно пояснить следующим рисунком.

Входное сопротивление цепи можно легко измерить с помощью вольтметра. Также нетрудно определить силу тока, протекающего между контактами. Для этого достаточно к схеме последовательно подключить амперметр. Получив эти два параметра, по закону Ома можно определить сопротивление схемы. Его называют входным. Иногда при этом рассматривают входное сопротивление длинной линии. Его определяющим свойством является то, что при подключении нагрузки к клеммам источника питания электрические характеристики не меняются.
Устройство блока может быть достаточно сложным, но в рассматриваемом случае не принимаются во внимание особенности его конструкции. Фактически можно представить, что внутри как бы находится резистор с определенным активным сопротивлением, соответствующим измеренному.

Входное электрическое сопротивление рассматривается как общая характеристика конкретного блока. Напряжение на вход может поступать с выхода другого блока или, например, с клемм аккумулятора или батареи.
Что такое внутреннее сопротивление при переменном токе
В предыдущем разделе было рассмотрено чисто активное сопротивление. При наличии в цепи только активного сопротивления фазы напряжения и тока совпадают. В реальных схемах обязательно присутствует реактивное сопротивление, которое делится еще на ёмкостное и индуктивное. Для постоянного тока его значение принято считать пренебрежимо малым и не принимать во внимание при расчёте параметров.

Если используется переменное напряжение на входе, тогда рассматривается полное сопротивление, состоящее из активного и реактивного. Их суммируют, используя правило прямоугольного треугольника. В этом случае один катет соответствует активному сопротивлению, второй — реактивному, а гипотенуза — полному или импедансу.
Важно учитывать, что в цепи с переменным током фаза напряжения сдвигается относительно фазы тока. Сдвиг фаз зависит от соотношения активного и реактивного сопротивлений конкретной цепи.
При отсутствии конденсаторов и катушек индуктивности в цепи емкостным и индуктивным сопротивлениями можно пренебречь и учитывать только активное. В этом случае ток будет следовать за напряжением, одновременно принимая нулевые и максимальные значения.
Если же в цепь включить катушку или конденсатор, создающих индуктивное или емкостное сопротивление настолько большого значения, что активное становится пренебрежимо малым, то сдвиг фаз будет равен π/2.

Так как реактивное сопротивление зависит от частоты поступающего сигнала, то чтобы более точно определить импеданс, необходимо узнать нужные параметры при двух различных частотах.
Следует принимать во внимание, что входное полное сопротивление линии может быть различным в отличающихся температурных условиях. Характер и величина отличий зависит от конкретного устройства рассматриваемого блока. Также требуется учитывать обратное влияние самой процедуры измерения на электрические параметры схемы.
Входное сопротивление зависит еще и от того, каким способом вводится в цепь сигнал обратной связи (ОС). Если этот сигнал отсутствует, то входное сопротивление определяется напряжением и током, присутствующими на входе. В том случае, когда обратную связь вводят по последовательной схеме, сопротивление на входе увеличивается при отрицательной ОС и уменьшается при положительной ОС.
При использовании параллельной схемы введения ОС входное сопротивление уменьшается и при отрицательной, и при положительной ОС. При небольшом сопротивлении в цепи ОС оно может составлять десятые, и даже тысячные доли Ома.
Как измерить
При определении входных параметров блока его устройство не рассматривается, но при этом может возникнуть необходимость провести измерение входного сопротивления. Блок выглядит как чёрный ящик, имеющий две входных и две выходных клеммы. Наиболее простым решением является определение входного напряжения и силы тока. Для простоты можно предположить, что рассматривается постоянный ток. Определить входное электрическое сопротивление в этом случае можно способом, который описан далее.

Найти входное сопротивление можно, разделив напряжение на силу тока. Однако в рассматриваемом случае нужно понимать, что если напряжение подаётся с батареи, то на показания будет влиять внутреннее сопротивление источника тока.
Если в блоке используется конденсатор, то нужно учитывать, что через него ток проходить не будет. С другой стороны, для переменного тока он помехой не является. Для переменного тока в качестве входного сопротивления цепи рассматривается полное сопротивление (импеданс). Оно представляет собой векторную сумму активного (омического) и реактивного (индуктивного и ёмкостного) сопротивлений. Однако его значение будет отличаться при различных частотах. Поэтому процедура измерения является более сложной по сравнению с постоянным током. В этом случае может быть использована следующая схема.

В данной схеме применён генератор переменного тока, который расположен слева. Его соединяют с исследуемым блоком, подавая на него переменный ток. На одном из соединительных проводов ставится резистор с известным сопротивлением R.
Напряжение измеряют дважды — перед резистором и после него. Пусть его значение будет равно U1 и U2 соответственно. Как известно, при переменном входном токе I(вх) падение напряжения на этой детали составит U2 – U1. С другой стороны оно будет равно I(вх) × R. В результате может быть получена следующая формула:
Из этой формулы можно определить величину входного тока:
На вход исследуемого блока поступает напряжение U2:
Входное сопротивление R(вх) найдем, используя формулу:
Определяем значение сопротивления:
Все величины в правой части равенства являются известными или были измерены. Подставив их формулу, можно определить величину входного сопротивления схемы.
Применение описанного здесь способа позволяет точно вычислять входное сопротивление даже в тех случаях, когда оно очень велико.
Выходное напряжение
При рассмотрении упрощённой схемы блока видно, что у него имеется выходное напряжение. Оно появляется на контактах, указанных на изображении справа.

На рисунке показан идеальный источник тока, который, как предполагается, не имеет внутреннего сопротивления. Это означает, что может быть создан сколько угодно большой ток. Имеющийся на схеме резистор нарушает определенную идеальность, ограничивая величину тока при коротком замыкании.
Измерение выходного тока может быть выполнено следующим образом. Напряжение U является известной величиной. При коротком замыкании может быть измерен проходящий по контактам ток. Выходное сопротивление R(вых) определяется по закону Ома. Для его вычисления необходимо напряжение разделить на ток.
Однако этот способ неудобен, так как большой ток нарушает условия функционирования схемы и может привести к поломкам. Поэтому на практике между клеммами ставят дополнительный резистор с известной величиной сопротивления R и только после этого измеряют значение силы тока I и напряжения U2. Предварительно следует определить разность потенциалов U1 с помощью вольтметра. Исходя из закона Ома, получают следующую формулу:
Практическое применение
Понятие входного сопротивления играет важную роль при согласовании характеристик соединённых между собой блоков. Сказанное можно пояснить на следующем примере.
Предположим, что первым блоком является источник питания. Если к его клеммам присоединён следующий блок, то при практическом определении его входного сопротивления станет понятно, что оно немного меньше расчётной величины.
Это связано с наличием внутреннего сопротивления аккумулятора. Чем оно больше, тем искажение заметнее. Аналогичная ситуация наблюдается при соединении двух любых других блоков. Чтобы передача сопротивления проходила с минимальными потерями, необходимо, чтобы выходное сопротивление предыдущего блока было намного меньше входного у последующего.
С учетом этого обстоятельства необходимо уметь определять рассматриваемые величины, а при создании схемы обеспечивать их правильное соотношение. Если оно будет нарушено, то произойдёт значительное падение напряжения при передаче.
На практике обычно сталкиваются с очень большими значениями входных сопротивлений. В некоторых случаях они могут достигать 1 МОм. Это часто происходит при относительно небольшом входном напряжении. В результате сила рассматриваемого тока получается также небольшой.
В электронике входное и выходное сопротивление играют важную роль. Все качественные измерительные приборы стараются делать с очень высоким входным сопротивлением, чтобы оно минимально сказывалось на измеряемом сигнале и не гасило его амплитуду.
Что касается качественных источников питания, то их выпускают с очень небольшим выходным сопротивлением, чтобы при подключении низкоомной нагрузки напряжение на выходе «не проседало». Но даже если это случится, его можно подкорректировать вручную, используя регулировку выходного напряжения, присутствующую в каждом нормальном источнике питания.
Видео по теме
Источник
Электроника
учебно-справочное пособие
Входное и выходное сопротивление
Все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и т.д. Например, (рис. 1) состоит из двух блоков.
Рис. 1 — Схема источника питания
На рисунке 1 в левом блоке мы получаем постоянное напряжение, а в правом блоке его стабилизируем (рис. 2).
Рис. 2 — Блочная схема источника питания
Блочная схема — это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод «от простого к сложному» полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем — готовое устройство, например, телевизор.
Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.
На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.
Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением.
Если прислушаться фразам, то входное сопротивление — это сопротивление какого-то входа, а выходное — сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот «прячутся» они в самих блоках радиоэлектронных устройств.
Входное сопротивление
В блочной схеме вход блока располагается слева, выход — справа.
Рис. 3 — Входы и выходы в блочной схеме
Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение Uвх от другого блока или от источника питания, а на его выходе появится напряжение Uвых (или не появится, если блок является конечным).
Рис. 4 — Входное и выходное напряжения
Но раз уж мы подаем напряжение на вход (входное напряжение Uвх), следовательно, у нас этот блок будет потреблять какую-то силу тока Iвх.
Рис. 5 — Сила тока на входе
От чего зависит Iвх ? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи:
Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от. СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.
Рис. 6 — Входное сопротивление
То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет. Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока.
Измерение входного сопротивления
Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?
- Замерить напряжение Uвх , подаваемое на блок.
- Замерить силу тока Iвх , которую потребляет блок.
- По закону Ома найти входное сопротивление Rвх .

Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.
Рис. 7 — Измерение входного сопротивления
Мы с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).
Падение напряжения на резисторе R обозначим, как


Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!
Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление Rвх=1 МОм, а резистор взяли R = 1 КОм. Пусть генератор выдает постоянное напряжение U=10 В. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.
Рис. 8 — Делитель напряжения
Рассчитываем силу тока в цепи в амперах:
Получается, что падение напряжения на сопротивлении R в вольтах будет:
Грубо говоря 0,01 В. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем мультиметре.
Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также очень большого номинала. В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.
Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 В, и во включенном состоянии замеряем потребляемую силу тока. По схеме все это будет выглядеть вот так:
Итак, у нас получилось 22,5 миллиАмпер.
Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:
Выходное сопротивление
Яркий пример выходного сопротивления — это закон Ома для полной цепи, в котором есть так называемое «внутреннее сопротивление».
Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогеновую лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:
И как только подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.
Разница напряжения, то есть 0,3 В (12,09 -11,79) у нас падало на так называемом внутреннем сопротивлении r . Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.
У всех аккумуляторов есть это внутреннее сопротивление r, и «цепляется» оно последовательно с источником ЭДС ( Е ).
Рис. 13 — Внутреннее сопротивление аккумулятора
Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.
В теореме Тевенина говорилось, что любую цепь, которая имеет две клеммы и содержит в себе много различных источников ЭДС и резисторов разного номинала можно привести к источнику ЭДС с каким-то значением напряжения ( Eэкв ) и с каким-то внутренним сопротивлением ( Rэкв ).
Eэкв — эквивалентный источник ЭДС
Rэкв — эквивалентное сопротивление
То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.
В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС ( E ). С замером ЭДС вроде бы понятно, но вот как замерить Rвых ?
В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания Iкз .
Рис. 15 — Ток короткого замыкания
В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что
Но есть небольшая загвоздка. Теоретически — формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешенного значения, да вообще, вся схема ведет себя неадекватно.
Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогеновую лампочку, которая была нагрузкой R. В результате по цепи шел электрический ток. На лампочке и на внутреннем сопротивлении у нас падало напряжение, сумма которых равнялась ЭДС.
Итак, для начала замеряем напряжение на аккумуляторе без лампочки (рис. 17).
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E = 12,09 В.
Как только мы цепанули нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение
следовательно, на внутреннем резисторе падение напряжения составило
Сила тока в цепи равняется I =4,35 Ампер. ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи вычисляем, чему у нас будет равняться внутреннее сопротивление r:
r = (12,09 — 11,79)/4,35 = 0,069 [Ом]
Выводы
Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль при согласовании узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.
С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе. Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе «не проседало» при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается уже автоматически.

Источники:
Электроника © ЦДЮТТ • Марсель Арасланов • 2019
Источник
Электроника
учебно-справочное пособие
Входное и выходное сопротивление
Все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и т.д. Например, (рис. 1) состоит из двух блоков.
Рис. 1 — Схема источника питания
На рисунке 1 в левом блоке мы получаем постоянное напряжение, а в правом блоке его стабилизируем (рис. 2).
Рис. 2 — Блочная схема источника питания
Блочная схема — это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод «от простого к сложному» полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем — готовое устройство, например, телевизор.
Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.
На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.
Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением.
Если прислушаться фразам, то входное сопротивление — это сопротивление какого-то входа, а выходное — сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот «прячутся» они в самих блоках радиоэлектронных устройств.
Входное сопротивление
В блочной схеме вход блока располагается слева, выход — справа.
Рис. 3 — Входы и выходы в блочной схеме
Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение Uвх от другого блока или от источника питания, а на его выходе появится напряжение Uвых (или не появится, если блок является конечным).
Рис. 4 — Входное и выходное напряжения
Но раз уж мы подаем напряжение на вход (входное напряжение Uвх), следовательно, у нас этот блок будет потреблять какую-то силу тока Iвх.
Рис. 5 — Сила тока на входе
От чего зависит Iвх ? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи:
Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от. СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.
Рис. 6 — Входное сопротивление
То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет. Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока.
Измерение входного сопротивления
Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?
- Замерить напряжение Uвх , подаваемое на блок.
- Замерить силу тока Iвх , которую потребляет блок.
- По закону Ома найти входное сопротивление Rвх .

Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.
Рис. 7 — Измерение входного сопротивления
Мы с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).
Падение напряжения на резисторе R обозначим, как


Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!
Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление Rвх=1 МОм, а резистор взяли R = 1 КОм. Пусть генератор выдает постоянное напряжение U=10 В. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.
Рис. 8 — Делитель напряжения
Рассчитываем силу тока в цепи в амперах:
Получается, что падение напряжения на сопротивлении R в вольтах будет:
Грубо говоря 0,01 В. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем мультиметре.
Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также очень большого номинала. В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.
Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 В, и во включенном состоянии замеряем потребляемую силу тока. По схеме все это будет выглядеть вот так:
Итак, у нас получилось 22,5 миллиАмпер.
Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:
Выходное сопротивление
Яркий пример выходного сопротивления — это закон Ома для полной цепи, в котором есть так называемое «внутреннее сопротивление».
Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогеновую лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:
И как только подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.
Разница напряжения, то есть 0,3 В (12,09 -11,79) у нас падало на так называемом внутреннем сопротивлении r . Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.
У всех аккумуляторов есть это внутреннее сопротивление r, и «цепляется» оно последовательно с источником ЭДС ( Е ).
Рис. 13 — Внутреннее сопротивление аккумулятора
Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.
В теореме Тевенина говорилось, что любую цепь, которая имеет две клеммы и содержит в себе много различных источников ЭДС и резисторов разного номинала можно привести к источнику ЭДС с каким-то значением напряжения ( Eэкв ) и с каким-то внутренним сопротивлением ( Rэкв ).
Eэкв — эквивалентный источник ЭДС
Rэкв — эквивалентное сопротивление
То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.
В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС ( E ). С замером ЭДС вроде бы понятно, но вот как замерить Rвых ?
В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания Iкз .
Рис. 15 — Ток короткого замыкания
В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что
Но есть небольшая загвоздка. Теоретически — формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешенного значения, да вообще, вся схема ведет себя неадекватно.
Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогеновую лампочку, которая была нагрузкой R. В результате по цепи шел электрический ток. На лампочке и на внутреннем сопротивлении у нас падало напряжение, сумма которых равнялась ЭДС.
Итак, для начала замеряем напряжение на аккумуляторе без лампочки (рис. 17).
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E = 12,09 В.
Как только мы цепанули нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение
следовательно, на внутреннем резисторе падение напряжения составило
Сила тока в цепи равняется I =4,35 Ампер. ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи вычисляем, чему у нас будет равняться внутреннее сопротивление r:
r = (12,09 — 11,79)/4,35 = 0,069 [Ом]
Выводы
Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль при согласовании узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.
С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе. Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе «не проседало» при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается уже автоматически.

Источники:
Электроника © ЦДЮТТ • Марсель Арасланов • 2019
Источник
Найти входное напряжение
Найти входное напряжение
Есть задача и примерное решение. Как я понял, остаётся только U входное найти. Как это сделать?
Найти входное напряжение и ток четырехполюсника
Всем привет Дали задачу, помогите пожалуйста ее решить Rn — это нагрузка на резисторе? Как от.
Найти входное напряжение в параллельном диодном ключе
Определить величину входного напряжения в параллельном диодном ключе, представленный на схеме при.
Найти входное сопротивление цепи и напряжение катушки
Сопротивления всех элементов равны 2 Ом. Входное напряжение 10 В. Не могу разобраться как сложить.
Добавлено через 2 минуты
Схему нужно будет перерисовать. Назвать резисторы. И те 2 резистора, которые по 30(Ом) их объединить в 1 по формуле параллельных резисторов. R = (R1*R2)/(R1 + R2).
Ну так ты это сделай сначала.
Добавлено через 28 минут
Сопротивления могут включаться последовательно. Общее сопротивление — это сумма этих сопротивлений.
Добавлено через 24 минуты
В общем-то последние(крайние правые) 2 сопротивления тоже соединены параллельно и их нужно объединить в 1.
Входное напряжение
Здраствуйте. Помогите с задачей, надо определить входное напряжение и построить топографическую.
 входное напряжение
входное напряжение
Здравствуйте, подскажите пожалуйста какое будет входное напряжение двухполюсника, если P=1 кВт, Q=.
 Входное напряжение цепи
Входное напряжение цепи
Входное НАПРЯЖЕНИЕ на схеме так определяется ? U=I1*Rэкв, где Rэкв=R1+R2*R3/(R2+R3) ?
Входное напряжение в последовательной цепи
Дано: R = 5 Ом Xc = 4 Ома XL = 6 Ом Uc = 40В. цепь еще дана.. последовательно включены.
Каким будет входное и выходное напряжение
Каким в данной схеме будут входное и выходное напряжение. Формулы. Не могу понять, как их выразить.
Входное напряжение. Направление токов в цепи
Здравствуйте! Помогите пожалуйста разобраться с направлением токов в цепи. Верно ли они.
Источник
Что такое входное сопротивление и как его измерить
При работе со сложными схемами нужно уметь определять характеристики их отдельных блоков и элементов. В частности, входное и выходное сопротивление. Важно знать, что они из себя представляют, как определяются и какую роль играют в работе устройства.

Понятие входного сопротивления для постоянного тока
Радиоэлектронные устройства могут быть не только относительно, но и очень сложными, состоящими из многих блоков. Однако независимо от сложности устройства, количества используемых в нем деталей, схему можно рассматривать в качестве совокупности простых частей с определенной разностью потенциалов на входе. На выходе блока имеется ещё два контакта, на которых также присутствует напряжение. В первом случае его называют входным, в другом — выходным. Сказанное можно пояснить следующим рисунком.

Входное сопротивление цепи можно легко измерить с помощью вольтметра. Также нетрудно определить силу тока, протекающего между контактами. Для этого достаточно к схеме последовательно подключить амперметр. Получив эти два параметра, по закону Ома можно определить сопротивление схемы. Его называют входным. Иногда при этом рассматривают входное сопротивление длинной линии. Его определяющим свойством является то, что при подключении нагрузки к клеммам источника питания электрические характеристики не меняются.
Устройство блока может быть достаточно сложным, но в рассматриваемом случае не принимаются во внимание особенности его конструкции. Фактически можно представить, что внутри как бы находится резистор с определенным активным сопротивлением, соответствующим измеренному.

Входное электрическое сопротивление рассматривается как общая характеристика конкретного блока. Напряжение на вход может поступать с выхода другого блока или, например, с клемм аккумулятора или батареи.
Что такое внутреннее сопротивление при переменном токе
В предыдущем разделе было рассмотрено чисто активное сопротивление. При наличии в цепи только активного сопротивления фазы напряжения и тока совпадают. В реальных схемах обязательно присутствует реактивное сопротивление, которое делится еще на ёмкостное и индуктивное. Для постоянного тока его значение принято считать пренебрежимо малым и не принимать во внимание при расчёте параметров.

Если используется переменное напряжение на входе, тогда рассматривается полное сопротивление, состоящее из активного и реактивного. Их суммируют, используя правило прямоугольного треугольника. В этом случае один катет соответствует активному сопротивлению, второй — реактивному, а гипотенуза — полному или импедансу.
Важно учитывать, что в цепи с переменным током фаза напряжения сдвигается относительно фазы тока. Сдвиг фаз зависит от соотношения активного и реактивного сопротивлений конкретной цепи.
При отсутствии конденсаторов и катушек индуктивности в цепи емкостным и индуктивным сопротивлениями можно пренебречь и учитывать только активное. В этом случае ток будет следовать за напряжением, одновременно принимая нулевые и максимальные значения.
Если же в цепь включить катушку или конденсатор, создающих индуктивное или емкостное сопротивление настолько большого значения, что активное становится пренебрежимо малым, то сдвиг фаз будет равен π/2.

Так как реактивное сопротивление зависит от частоты поступающего сигнала, то чтобы более точно определить импеданс, необходимо узнать нужные параметры при двух различных частотах.
Следует принимать во внимание, что входное полное сопротивление линии может быть различным в отличающихся температурных условиях. Характер и величина отличий зависит от конкретного устройства рассматриваемого блока. Также требуется учитывать обратное влияние самой процедуры измерения на электрические параметры схемы.
Входное сопротивление зависит еще и от того, каким способом вводится в цепь сигнал обратной связи (ОС). Если этот сигнал отсутствует, то входное сопротивление определяется напряжением и током, присутствующими на входе. В том случае, когда обратную связь вводят по последовательной схеме, сопротивление на входе увеличивается при отрицательной ОС и уменьшается при положительной ОС.
При использовании параллельной схемы введения ОС входное сопротивление уменьшается и при отрицательной, и при положительной ОС. При небольшом сопротивлении в цепи ОС оно может составлять десятые, и даже тысячные доли Ома.
Как измерить
При определении входных параметров блока его устройство не рассматривается, но при этом может возникнуть необходимость провести измерение входного сопротивления. Блок выглядит как чёрный ящик, имеющий две входных и две выходных клеммы. Наиболее простым решением является определение входного напряжения и силы тока. Для простоты можно предположить, что рассматривается постоянный ток. Определить входное электрическое сопротивление в этом случае можно способом, который описан далее.

Найти входное сопротивление можно, разделив напряжение на силу тока. Однако в рассматриваемом случае нужно понимать, что если напряжение подаётся с батареи, то на показания будет влиять внутреннее сопротивление источника тока.
Если в блоке используется конденсатор, то нужно учитывать, что через него ток проходить не будет. С другой стороны, для переменного тока он помехой не является. Для переменного тока в качестве входного сопротивления цепи рассматривается полное сопротивление (импеданс). Оно представляет собой векторную сумму активного (омического) и реактивного (индуктивного и ёмкостного) сопротивлений. Однако его значение будет отличаться при различных частотах. Поэтому процедура измерения является более сложной по сравнению с постоянным током. В этом случае может быть использована следующая схема.

В данной схеме применён генератор переменного тока, который расположен слева. Его соединяют с исследуемым блоком, подавая на него переменный ток. На одном из соединительных проводов ставится резистор с известным сопротивлением R.
Напряжение измеряют дважды — перед резистором и после него. Пусть его значение будет равно U1 и U2 соответственно. Как известно, при переменном входном токе I(вх) падение напряжения на этой детали составит U2 – U1. С другой стороны оно будет равно I(вх) × R. В результате может быть получена следующая формула:
Из этой формулы можно определить величину входного тока:
I(вх) = ( U2 − U1 ) / R.
На вход исследуемого блока поступает напряжение U2:
Входное сопротивление R(вх) найдем, используя формулу:
( U2 − U1 ) / R = U2 / R(вх).
Определяем значение сопротивления:
R(вх) = R × U2 / ( U2 − U1 ).
Все величины в правой части равенства являются известными или были измерены. Подставив их формулу, можно определить величину входного сопротивления схемы.
Применение описанного здесь способа позволяет точно вычислять входное сопротивление даже в тех случаях, когда оно очень велико.
Выходное напряжение
При рассмотрении упрощённой схемы блока видно, что у него имеется выходное напряжение. Оно появляется на контактах, указанных на изображении справа.

На рисунке показан идеальный источник тока, который, как предполагается, не имеет внутреннего сопротивления. Это означает, что может быть создан сколько угодно большой ток. Имеющийся на схеме резистор нарушает определенную идеальность, ограничивая величину тока при коротком замыкании.
Измерение выходного тока может быть выполнено следующим образом. Напряжение U является известной величиной. При коротком замыкании может быть измерен проходящий по контактам ток. Выходное сопротивление R(вых) определяется по закону Ома. Для его вычисления необходимо напряжение разделить на ток.
Однако этот способ неудобен, так как большой ток нарушает условия функционирования схемы и может привести к поломкам. Поэтому на практике между клеммами ставят дополнительный резистор с известной величиной сопротивления R и только после этого измеряют значение силы тока I и напряжения U2. Предварительно следует определить разность потенциалов U1 с помощью вольтметра. Исходя из закона Ома, получают следующую формулу:
R(вых) = ( U2 – U1 ) / ( U2 / R ).
Практическое применение
Понятие входного сопротивления играет важную роль при согласовании характеристик соединённых между собой блоков. Сказанное можно пояснить на следующем примере.
Предположим, что первым блоком является источник питания. Если к его клеммам присоединён следующий блок, то при практическом определении его входного сопротивления станет понятно, что оно немного меньше расчётной величины.
Это связано с наличием внутреннего сопротивления аккумулятора. Чем оно больше, тем искажение заметнее. Аналогичная ситуация наблюдается при соединении двух любых других блоков. Чтобы передача сопротивления проходила с минимальными потерями, необходимо, чтобы выходное сопротивление предыдущего блока было намного меньше входного у последующего.
С учетом этого обстоятельства необходимо уметь определять рассматриваемые величины, а при создании схемы обеспечивать их правильное соотношение. Если оно будет нарушено, то произойдёт значительное падение напряжения при передаче.
На практике обычно сталкиваются с очень большими значениями входных сопротивлений. В некоторых случаях они могут достигать 1 МОм. Это часто происходит при относительно небольшом входном напряжении. В результате сила рассматриваемого тока получается также небольшой.
В электронике входное и выходное сопротивление играют важную роль. Все качественные измерительные приборы стараются делать с очень высоким входным сопротивлением, чтобы оно минимально сказывалось на измеряемом сигнале и не гасило его амплитуду.
Что касается качественных источников питания, то их выпускают с очень небольшим выходным сопротивлением, чтобы при подключении низкоомной нагрузки напряжение на выходе «не проседало». Но даже если это случится, его можно подкорректировать вручную, используя регулировку выходного напряжения, присутствующую в каждом нормальном источнике питания.
Калькулятор напряжения – расчет по току, сопротивлению, мощности
Расчет электрического напряжения по току, сопротивлению, мощности с помощью калькулятора – рассчитайте напряжение онлайн и по формулам.
- Расчёт
- Скачать



Используйте калькулятор напряжения для расчета вольтажа сети по известным значениям силы тока, сопротивления, мощности. Алгоритм программы выполняет подсчеты по формулам закона Ома для участка цепи. Чтобы получить результат, выберите необходимый тип операции, заполните поля и нажмите кнопку «Рассчитать».
Смежные нормативные документы:
- СП 256.1325800.2016 «Электроустановки жилых и общественных зданий. Правила проектирования и монтажа»
- СП 31-110-2003 «Проектирование и монтаж электроустановок жилых и общественных зданий»
- СП 76.13330.2016 «Электротехнические устройства»
- ГОСТ 31565-2012 «Кабельные изделия. Требования пожарной безопасности»
- ГОСТ 10434-82 «Соединения контактные электрические. Классификация»
- ГОСТ Р 50571.1-93 «Электроустановки зданий»
Формулы расчета напряжения
Электрическое напряжение (U) — это скалярная физическая величина, которая равна работе электрического поля по перемещению заряда из одной точки цепи к другой. Международная единица измерения — Вольт (В / V).
— Напряжение по току и сопротивлению: U = I × R
— Напряжение по току и мощности: U = P / I
— Напряжение по мощности и сопротивлению: U = √(P × R)
Делитель напряжения. Расчет делителя напряжения.
Делитель напряжения, одна из широко используемых схем соединения резисторов. Делитель напряжения позволяет уменьшить выходное напряжение. Например, на вход делителя подается 12 Вольт, а на выходе 3 Вольта, или сколько нужно, но не больше входного напряжения делителя. Схема соединения резисторов, о которой мы говорим, может использоваться только для слаботочной нагрузки, чуть позже я объясню почему. Вот собственно и сама схема делителя:

Делитель напряжения вы все ни один раз видели, например, регулятор громкости. Регулятором громкости является переменный резистор, соединенный по схеме потенциометра.
 Потенциометр, можно представить как два резистора, соединённых последовательно, при вращении рукоятки один резистор уменьшает свое сопротивление, другой увеличивает.
Потенциометр, можно представить как два резистора, соединённых последовательно, при вращении рукоятки один резистор уменьшает свое сопротивление, другой увеличивает.
В делителе напряжения, входное напряжение полностью падает на двух резисторах. Например, входное напряжение 40 Вольт и если на одном резисторе падает 3 Вольта, то на другом 37 Вольт.

Расчет делителя напряжения.
Сразу скажу одно правило, ток, протекающий через резистор R1 и R2 должен быть как минимум в 10 раз больше, чем ток нагрузки (иначе будет просадка напряжения на выходе). Например, если к нашему девайсу будет подсоединена лампа, потребляющая ток 40 мА, то делитель нужно рассчитывать так, чтобы ток, текущий через резисторы R1 и R2 был минимум 400 мА (в 10 и более раз больше).
И еще один нюанс. Ток делителя не только должен быть больше тока нагрузки в 10 раз, но и должен быть меньше тока, выдаваемого источником тока. Вот пример, мы посадили на выход делителя напряжения лампу, потребляющую 200 мА, соответственно ток через делитель потечет как минимум в 10 раз больше (2 Ампер), но если источник тока у нас рассчитан выдавать 1 Ампер, то он просто напросто не вытянет и сгорит, либо сработает защита.
Поэтому есть правило. При расчете делитель напряжения нужно рассчитывать так, чтобы ток через него был как минимум в 10 раз больше тока нагрузки и меньше максимального тока источника. Отсюда делитель напряжения используют для слаботочных нагрузок.
Входной ток (ток делителя) ищется по такой формуле:
Например, у меня входное напряжение 12 Вольт (10 Ампер), мне нужен делитель напряжения, у которого на выходе нагрузка напряжением 3 Вольта и током потребления 20 мА (зацеплю светодиод).

Ток делителя Iвх должен быть минимум в 10 раз больше тока нагрузки, возьму в 20 раз. Получается Iвх = 20 мА*20=400мА.
Найдем теперь сумму резисторов R1 и R2 (Rобщ) зная ток, текущий через них 0,4 Ампер и напряжение на них 12 Вольт. Rобщ=12 Вольт/0,4 Ампер = 30 Ом.
Далее нахожу номинал резистора R2 по следующей формуле:
R2 = (3 Вольта*30 Ом)/12 Вольт = 7,5 Ом.
Теперь нахожуу R1, R1 = Rобщ – R2 = 30 – 7,5 = 22,5 Ом.
Давайте проверим по этой формуле:
Iвх = 3 Вольт / 7,5 Ом = 0,4 Ампер.
Iвх = 12 Вольт / 30 Ом = 0,4 Ампер.
Рассчитаем мощность резисторов. Напряжение на R2 = 3 Вольт, значит напряжение на R1 = Uвх-Uвых = 9 Вольт (я уже говорил, если на одном падает 3 Вольта, то на втором резисторе делителя падает остальное напряжение).
Мощность ищется по следующей формуле:
![]()
P1 = 9 Вольт* 0,4 Ампер = 3,6 Вт (из стандартного ряда 5 Вт);
P2 = 3 Вольт* 0,4 Ампер = 1,2 Вт (из стандартного ряда 2 Вт);
Вот еще несколько формул, вы их можете использовать для расчета делителя напряжение в зависимости от того, какими известными значениями вы владеете.

- Проверка расчета практически.

При расчете мы получили следующие номиналы резисторов, R1 = 22,5 Ом (из стандартного рядя 22 Ом), R2 = 7,5 Ом.
По мощности у меня оба резистора 2 Вт, поэтому R1 у меня сильно греется.

Входное напряжение делителя 12 Вольт.

Напряжение, которое падает на R1 = 22 Ом почти 9 Вольт.

Напряжение, которое падает на R2 = 7,5 Ом (наше выходное напряжение делителя) = 3 Вольта.

Ток, текущий через R1 и R2 (входной ток делителя) = 430 мА.

Светодиод загорается и горит в нормальном режиме, не перегорая.
Содержание
- 1 Что такое входное напряжение?
- 2 Как рассчитать входное сопротивление усилителя?
- 3 Что такое выходное напряжение?
- 4 Что такое входное и выходное сопротивление?
- 5 Как найти коэффициент усиления операционного усилителя?
- 6 Как определить ток в цепи?
- 7 Что означает напряжение?
Что такое входное напряжение?
Смотреть что такое «входное напряжение» в других словарях:
входное напряжение — Udin Напряжение, определяемое напряжением в системе электроснабжения и коэффициентом преобразования измерительного преобразователя.
Как рассчитать входное сопротивление усилителя?
Но более точное измерение входного сопротивление прибора получается по двум измерениям для разных напряжений U1 и U2 и соответствующим измеренным токам I1 и I2; в этом случае входное сопротивление вычисляется по формуле: RВХ = (U1 − U2 ) / ( I1 − I2).
Что такое выходное напряжение?
3.1.9 выходное напряжение (output voltage) Ua: Напряжение на выходных зажимах измерительной аппаратуры, с которых эта аппаратура выдает или может выдавать электрическую энергию. …
Что такое входное и выходное сопротивление?
Если прислушаться к этим фразам, то входное сопротивление – это сопротивление какого-то входа, а выходное – сопротивление какого-либо выхода.
Как найти коэффициент усиления операционного усилителя?
Коэффициент усиления ОУ определяется отношением изменения входного напряжения к вызвавшему его изменению напряжения между дифференциальными входами усилителя при разомкнутой цепи обратной связи. В современных ОУ величина коэффициента усиления достигает десятков, а иногда и сотен тысяч.
Как определить ток в цепи?
Ток в амперах можно всегда определить, если разделить напряжение в вольтах на сопротивление в омах. Поэтому закон Ома для участка цепи записывается следующей формулой: I = U/R.
Что означает напряжение?
Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — скалярная физическая величина, значение которой равно работе эффективного электрического поля (включающего сторонние поля), совершаемой при переносе единичного пробного электрического заряда из точки A в точку B.
Тема1 Расчет действующих значений токов и напряжений
Изучение этой темы предоставляет возможность оперировать показаниями измерительных приборов электромагнитной и электродинамической систем, а также выполнять расчеты при последовательном или параллельном соединении приемников без использования комплексных чисел.
Занятие1
Цели занятия:
1.Научиться строить векторные диаграммы для цепей с последовательным и параллельным соединением приемников.
2.Научиться применять закон Ома для действующих значений.
3.Научиться вычислять потребляемую схемой мощность.
Рассмотрим первую целевую задачу занятия.
Действующим значением тока I считают такой постоянный ток, который производит тот же тепловой эффект, что и реальный переменный ток. Действующие значения обозначают заглавными печатными буквами:
I,U, E .
Законы Кирхгофа для действующих значений не выполняются. Оперировать действующими значениями позволяют прямоугольные треугольники, которые получаются при построении векторных диаграмм.
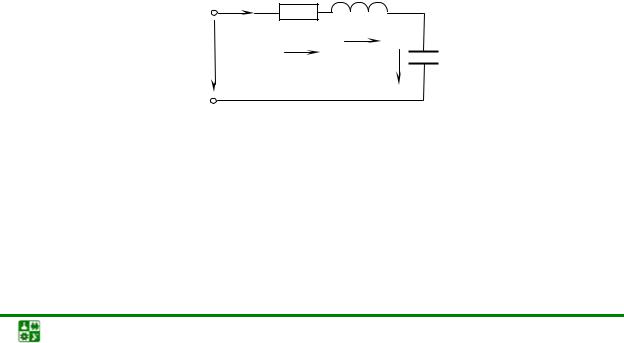
Схема замещения цепи с последовательным соединением приемников изображена на рис. 2.1.
|
I |
R |
X L |
||
|
UL |
||||
|
UR |
||||
|
U |
X |
|||
|
C |
||||
|
UC |
Рис. 2.1
Построим векторную диаграмму. Построение начнем с вектора величины, общей для данной цепи. При последовательном соединении элементов такой величиной является ток. Вид диаграммы зависит от характера цепи. Построение векторной диаграммы для цепи, имеющей активно-индуктивный характер, т. е.
|
Теоретические основы электротехники. Практикум |
-53- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 1 Расчет действующих значений токов и напряжений
X L > XC и X > 0, показано на рис. 2.2.
Входное напряжение складывается из напряжений на трех идеальных элементах при учете сдвига фаз. Напряжение на резисторе совпадает с током по фазе. Напряжение на индуктивном элементе опережает ток на 90°, на емкостном – отстает на 90°.
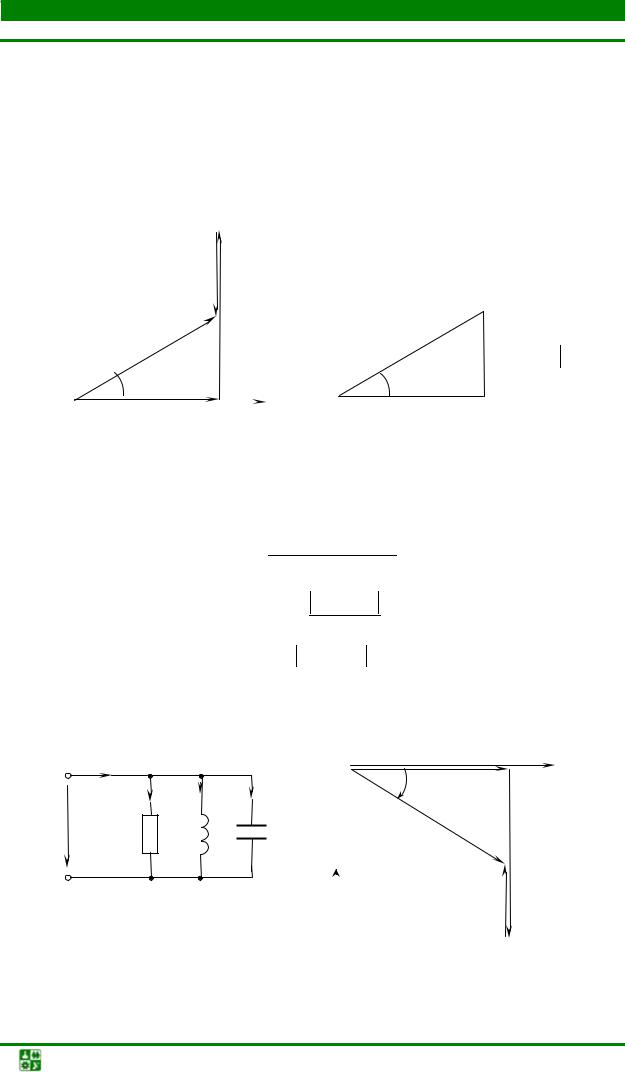
Полученный при построении векторной диаграммы треугольник ОАВ изображен на рис. 2.3.
|
UL |
||||||||
|
UC |
||||||||
|
B |
B |
|||||||
|
U |
U |
UL −UC |
||||||
|
0 |
ϕ |
A |
0 |
ϕ |
A |
|||
|
UR |
||||||||
|
UR |
I |
|||||||
|
Рис. 2.2 |
Рис. 2.3 |
Угол ϕ = ψu − ψi – угол сдвига фаз тока и полного напряжения.
Треугольник ОАВ дает возможность оперировать действующими значениями:
U= 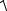
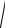 UR2 +(UL −UC )2 ,
UR2 +(UL −UC )2 ,
ϕ= arctg UL −UC ,
UR
U R =U cosϕ, U L −UC =U sin ϕ.
Схема замещения цепи с параллельным соединением приемников изображена на рис. 2.4.
|
I |
0 |
A U |
|||
|
I |
I |
IR |
|||
|
ϕ |
|||||
|
IR |
L |
C |
|
U |
R |
X L |
XC |
I |
|
|
B |
|||||
|
IC |
IL |
||||
|
Рис. 2.4 |
|||||
|
Рис. 2.5 |
|
Теоретические основы электротехники. Практикум |
-54- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 1 Расчет действующих значений токов и напряжений
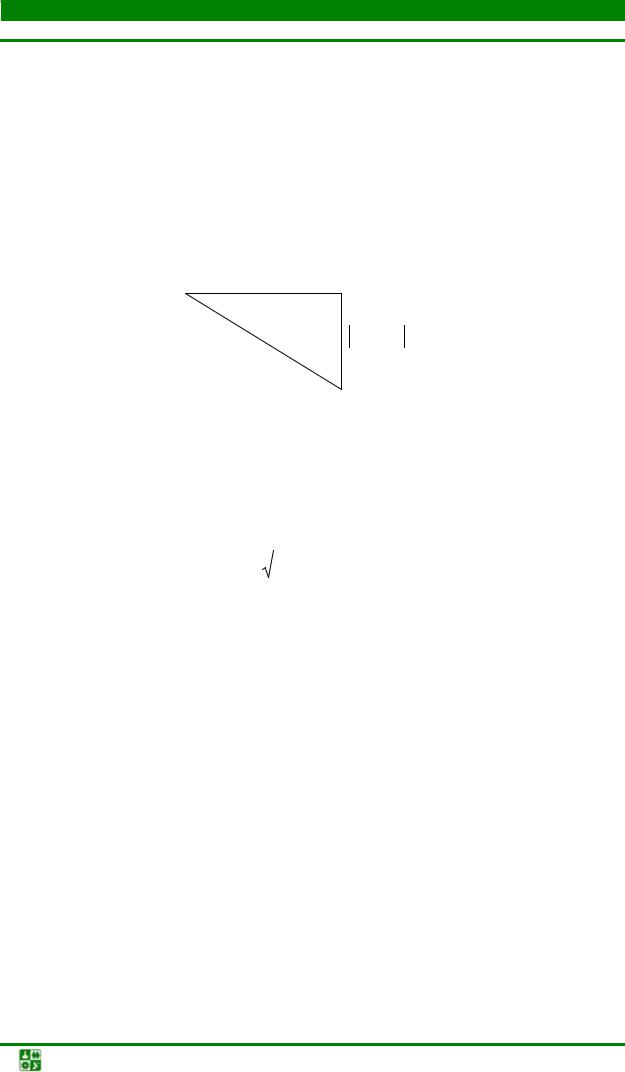
Построение векторной диаграммы начинаем с вектора напряжения, которое является одинаковым для всех элементов схемы. Векторная диаграмма для случая, когда X L < XC , приведена на рис. 2.5.
Ток в неразветвленной части схемы складывается из токов трех параллельных ветвей при учете сдвига фаз. Ток через резистор совпадает с напряжением по фазе, через индуктивный элемент отстает от напряжения на 90°, ток через конденсатор опережает его на 90°.
Полученный при построении векторной диаграммы треугольник токов ОАВ изображен на рис. 2.6.
IR A
0 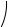 ϕ
ϕ
IL − IC
I
B
Рис. 2.6
Из свойств треугольника токов получаем следующие соотношения, позволяющие оперировать действующими значениями:
|
I = |
; |
||||||||||||
|
IR2 + (IL − IC )2 |
|||||||||||||
|
ϕ = arctg |
IL − IC |
; |
|||||||||||
|
IR |
|||||||||||||
|
IR = I cosϕ; |
I L − IC |
= I sin ϕ. |
|||||||||||
|
Перейдем к рассмотрению второй целевой задачи. |
I , |
||||||||||||
|
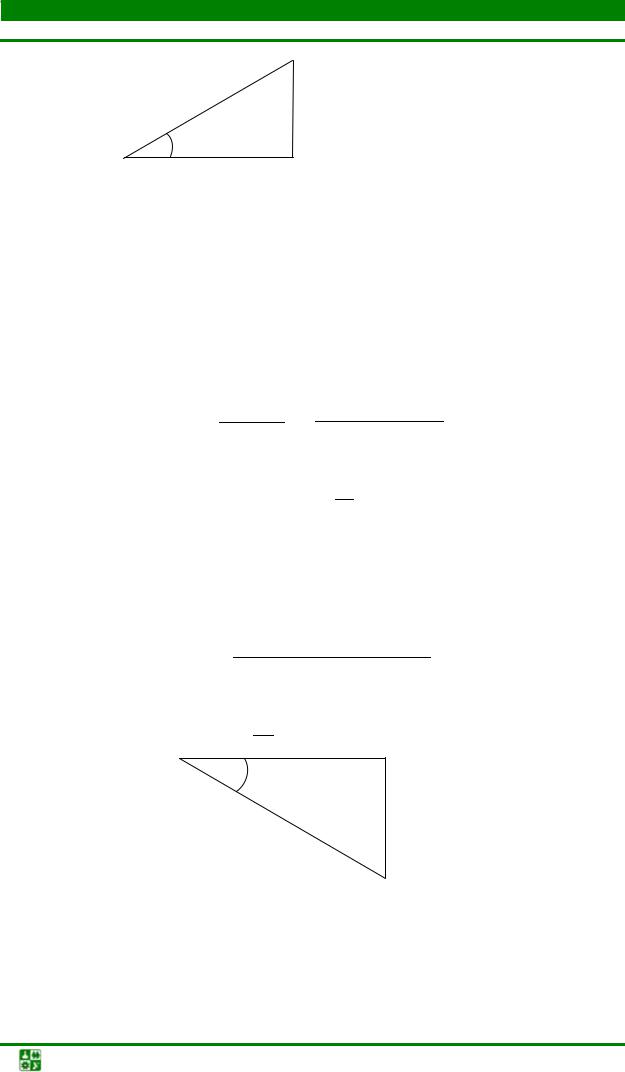
Если разделить все стороны треугольника напряжений на ток |
|||||||||||||
|
получим подобный ему треугольник сопротивлений (рис. |
2.7), где |
Z – |
|||||||||||
|
полное сопротивление цепи; |
R – активное сопротивление; X – реактивное |
||||||||||||
|
сопротивление; X L = L ω |
– индуктивное |
сопротивление, |
XC = |
1 |
– |
||||||||
|
C ω |
|||||||||||||
емкостное сопротивление.
|
Теоретические основы электротехники. Практикум |
-55- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 1 Расчет действующих значений токов и напряжений
|
U |
= Z |
UL −UC |
|||||||
|
I |
= |
X L − XC |
= X |
||||||
|
I |
|||||||||
|
ϕ |
|||||||||
|
UR |
= R |
||||||||
|
I |
|||||||||
|
Рис. 2.7 |
Закон Ома для действующих значений при последовательном соединении приемников примет вид
U = Z I .
Из свойств треугольника сопротивлений получаем соотношения
Z= 
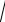 R2 + X 2 =
R2 + X 2 = 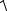
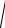 R2 + (X L − XC )2 ;
R2 + (X L − XC )2 ;
ϕ= arctg XR ;
R = Z cosϕ; X = Z sin ϕ.
Полное сопротивление любого количества последовательно соединенных приемников
Z = 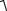
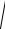 (∑R)2 +(∑X L −∑XC )2 .
(∑R)2 +(∑X L −∑XC )2 .
UIR =G
ϕ
|
I |
− I |
||||||
|
I |
L |
C |
= B |
||||
|
=Y |
U |
||||||
|
U |
Рис. 2.8
Разделив все стороны треугольника токов на напряжение, получим подобный ему треугольник проводимостей (рис. 2.8), где Y – полная
|
Теоретические основы электротехники. Практикум |
-56- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 1 Расчет действующих значений токов и напряжений
проводимость; G – активная проводимость; B = BL − BC – реактивная проводимость; BL – индуктивная проводимость; BC – емкостная проводимость.
Закон Ома для действующих значений при параллельном соединении примет вид
I = Y U .
Из свойств треугольника проводимостей получаем соотношения
Y = 
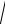 G2 + B2 ;
G2 + B2 ;
G= Y cosϕ; B = Y sin ϕ;
ϕ= arctg GB
Полная проводимость любого количества параллельно соединенных приемников
Y = 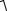
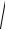 (∑G)2 +(∑BL −∑BC )2 .
(∑G)2 +(∑BL −∑BC )2 .
Перейдем к рассмотрению третьей целевой задачи.
Умножением всех сторон треугольника напряжений на ток получаем треугольник мощностей (рис. 2.9).
ϕ
UR I = P
Рис. 2.9
Активная мощность
P =UR I = R I 2 =U I cosϕ
характеризует энергию, которая передается в одном направлении от генератора к приемнику. Она связана с резистивными элементами.
|
Теоретические основы электротехники. Практикум |
-57- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 1 Расчет действующих значений токов и напряжений
Реактивная мощность Q = UL −UC I = X I 2 =U I sinϕ характеризует
часть энергии, непрерывно циркулирующей в цепи и не совершающей полезной работы. Она связана с реактивными элементами.
Полная (кажущаяся) мощность S =U I = 
 P2 +Q2 .
P2 +Q2 .
Активную мощность измеряют в ваттах (Вт), реактивную – в вольтамперах реактивных (вар), полную – вольтамперах (В А).
Задача1
Вычислить показание вольтметра, подключенного к зажимам индуктивной катушки, схема замещения которой представлена на рис. 2.10, если амперметр показывает ток I =10 А, R = 3 Ом, X L = 4 Ом.
A I
R
U V
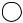 X L
X L
Рис. 2.10
Решение
1. Вольтметр показывает действующее значение входного напряжения U , которое можно вычислить по закону Ома:
U= Z I .
2.Полное сопротивление схемы
Z = 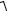
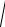 R2 + X L2 =
R2 + X L2 = 
 32 + 42 =5 Ом.
32 + 42 =5 Ом.
Тогда напряжение на входе схемы
U = 5 10 = 50 В.
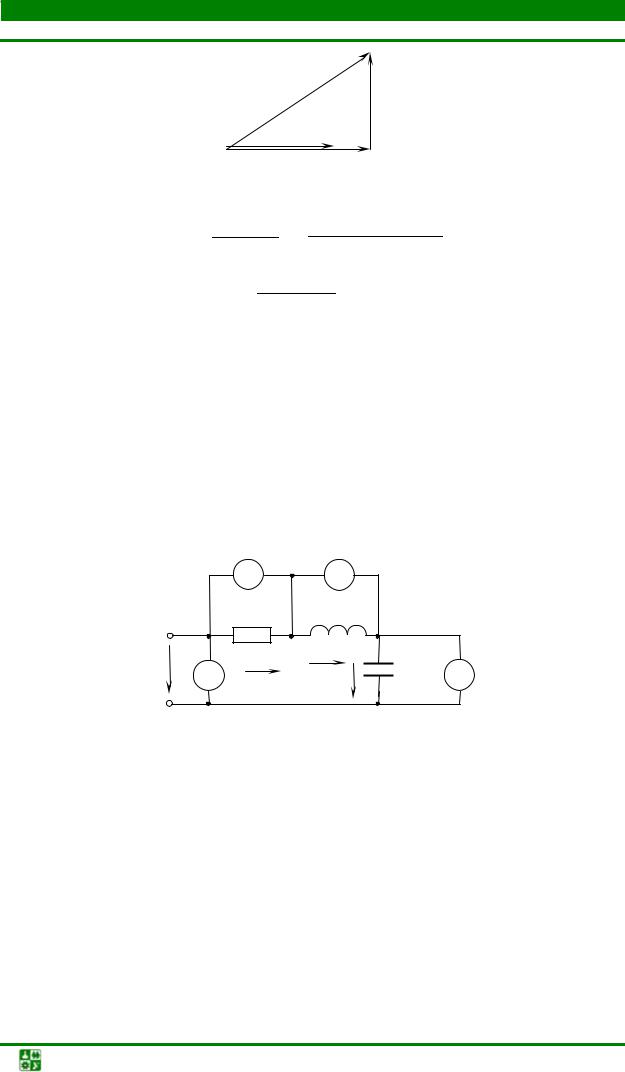
Входное напряжение можно вычислить другим путем, используя треугольник напряжений, полученный при построении векторной диаграммы
(рис. 2.11):
|
Теоретические основы электротехники. Практикум |
-58- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 1 Расчет действующих значений токов и напряжений
U UL I
UR
Рис. 2.11
U = 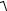
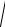 UR2 +UL2 =
UR2 +UL2 = 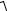
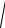 (R I )2 + (X L I )2 =
(R I )2 + (X L I )2 =
= 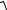
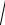 302 + 402 =50 В.
302 + 402 =50 В.
Следующие задачи решите самостоятельно.
Задача2
В схеме на рис. 2.12 первый вольтметр показывает напряжение 30 В, второй – 90 В, третий – 50 В.
Определить напряжение, которое показывает вольтметр на входе схемы.
Ответ: U = 50 В.
|
V1 |
V2 |
|||
|
R |
X L |
|||
|
U |
UR |
UL |
XC V3 |
|
|
UC |
||||
|
V |
Рис. 2.12
Задача3
В схеме на рис. 2.13 первый амперметр показывает ток 6 А, второй – 20 А, третий – 12 А. Определить ток, который показывает амперметр на входе схемы.
|
Теоретические основы электротехники. Практикум |
-59- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 1 Расчет действующих значений токов и напряжений
I A
A
|
A1 |
A2 |
A3 |
||
|
I |
||||
|
U |
I |
2 |
I |
3 |
|
1 |
||||
|
R |
X L |
XC |
||
|
Рис. 2.13 |
Ответ: I =10 А.
Задача4
Определить, можно ли подключить цепь, схема замещения которой изображена на рис. 2.14, к сети с напряжением U = 66 В и частотой f = 50
|
Гц, если напряжения Uab |
и Ubс не |
должны превышать номинального |
||||||
|
Uн =120 В, R1 = 8 Ом, R2 =3 Ом, |
||||||||
|
L = 0,1576 Гн, C = 64,34 мкФ. |
||||||||
|
a |
I |
R |
X L |
b |
||||
|
1 |
||||||||
|
U |
||||||||
|
XC |
||||||||
|
R2 |
||||||||
|
c |
||||||||
|
Рис. 2.14 |
||||||||
Решение
1. По закону Ома для действующих значений
Uаb = Zаb I ; Ubс = Zbc I .
|
2. Полное |
сопротивление |
Z |
аb |
= |
R2 + X |
2 |
. |
Индуктивное |
|||||||||||||||||||
|
1 |
L |
||||||||||||||||||||||||||
|
сопротивление |
X L = L ω= L 2π f = 0,1576 2 π 50 = 49,5 |
Ом. |
Подставив |
||||||||||||||||||||||||
|
значения R |
и X |
L |
, получим Z |
аb |
= |
82 |
+ 49,52 |
= 50,1 Ом. |
|||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||
|
Полное сопротивлениеZ |
bс |
= |
R2 |
+ X 2 |
. |
Емкостное |
сопротивление |
||||||||||||||||||||
|
2 |
C |
||||||||||||||||||||||||||
|
X |
= |
1 |
= |
1 |
= |
106 |
= 49,5 Ом. |
Подставив значения |
R |
и X |
C |
, |
|||||||||||||||
|
C 2π f |
64,34 2π 50 |
||||||||||||||||||||||||||
|
C |
Cω |
2 |
|||||||||||||||||||||||||
|
получим Zbс = |
32 + 49,52 |
= 49,6 Ом. |
|
Теоретические основы электротехники. Практикум |
-60- |

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 1 Расчет действующих значений токов и напряжений
3. Ток в цепи по закону Ома
I= UZ .
4.Полное сопротивление схемы
Z = 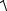
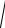 (R1 + R2 )2 + (X L − XC )2 =
(R1 + R2 )2 + (X L − XC )2 = 
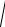 (8 +3)2 +(49,5 − 49,5)2 =11 Ом.
(8 +3)2 +(49,5 − 49,5)2 =11 Ом.
|
Тогда |
ток |
I = 66 = 6 |
А. |
Напряжение Uаb = 50,1 6 = 300,6 В, |
||
|
Ubс |
11 |
|||||
|
напряжение |
= 49,6 6 = 297,5 |
В. Следовательно, |
такое |
подключение |
||
|
сделать нельзя, так как значения напряжений Uаb |
и Ubс |
значительно |
||||
|
превышают номинальное. |
||||||
|
Задача5 |
||||||
|
Вычислить ток в индуктивной катушке, подключенной к сети |
||||||
|
переменного |
тока с напряжением U = 220 В, если потребляемая мощность |
|||||
|
P = 440 Вт, |
коэффициент мощности cosϕ = 0,5. Какой ток будет в этой |
катушке при подключении ее к сети постоянного тока того же напряжения?
Решение
1. Вычислим ток в катушке при подключении ее к сети переменного напряжения, воспользовавшись формулой активной мощности
P =U I cosϕ.
Отсюда
I~ = U P = 440 = 4 А.
cosϕ 220 0,5
2.Ток в катушке при подключении ее к сети постоянного напряжения можно найти по закону Ома I_ = UR , так как в схеме замещения (рис. 2.10)
остается только резистивный элемент (ω= 0, X L = L ω= 0).
3. Вычислим активное сопротивление из формулы активной мощности
|
P = R I~2 : |
P |
440 |
||||
|
R = |
= |
= 27,5 |
Ом. |
|||
|
I~2 |
16 |
|||||
|
Теоретические основы электротехники. Практикум |
-61- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 1 Расчет действующих значений токов и напряжений
Тогда I− = 27220,5 = 8 А.
Следующую задачу решите самостоятельно.
|
Задача6 |
||
|
Вычислить |
параметры схемы |
замещения индуктивной катушки |
|
(рис. 2.10), если |
при подключении |
к сети с напряжением U =120 В и |
частотой f = 50 Гц ток I =100 А, активная мощность P =10000 Вт.
Пояснение к решению
Параметрами индуктивной катушки являются активное сопротивление R и индуктивность L .
Ответ: R =1 Ом, L = 0,002 Гн.
Для самоконтроля решите задачи 7–10.
Задача7
В цепь синусоидального тока (рис. 2.15) включены три амперметра электромагнитной системы. Определить показание амперметра А2 , если
амперметры А и А1 показывают соответственно I =10 А и I1 = 6 А.
R


 A1
A1
 A
A  XC
XC

 A2
A2
Рис. 2.15
Ответ: I2 =8 А.
Задача8
Определить ток I и входное напряжение U схемы на рис. 2.16, если напряжение на емкостном элементе UC = 70,7 В, R =100 Ом, C = 2 мкФ,
ω= 5000 с-1.
|
Теоретические основы электротехники. Практикум |
-62- |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
