Главная
→
Примеры решения задач ТОЭ
→
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.
В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.
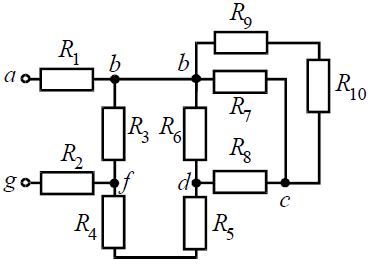
Рис. 1
Решение
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
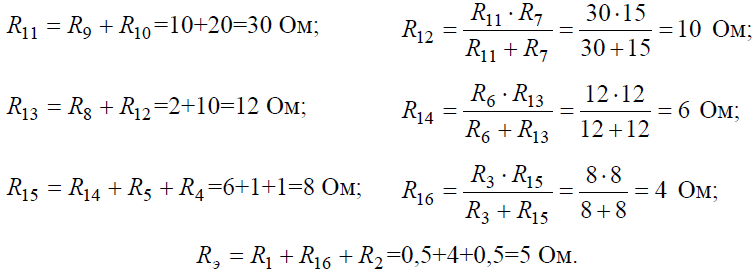
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.
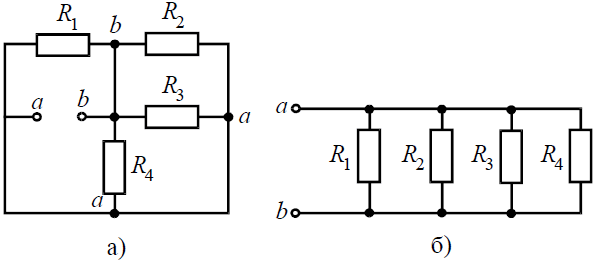 Рис. 2
Рис. 2
Решение
Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
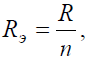 где R — величина сопротивления, Ом;
где R — величина сопротивления, Ом;
n — количество параллельно соединенных сопротивлений.
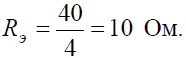
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R1 = R2 = R3 = R4 = R5 = R6 = 10 Ом (рис. 3, а).
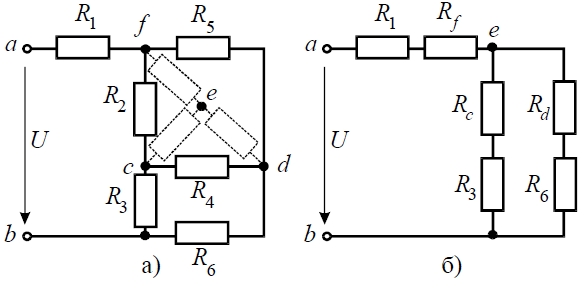
Рис. 3
Решение
Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
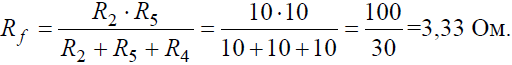 По условию задачи величины всех сопротивлений равны, а значит:
По условию задачи величины всех сопротивлений равны, а значит:
![]() На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
![]()
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
![]()
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
Решение
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
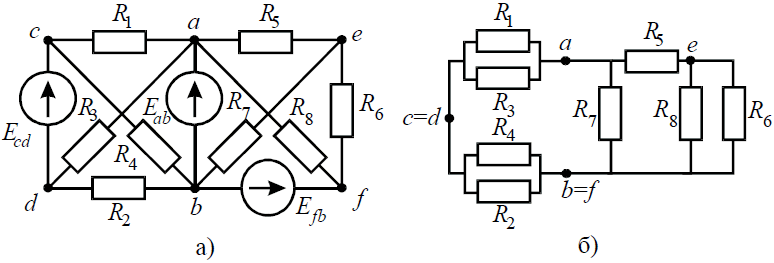
Рис. 4
Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
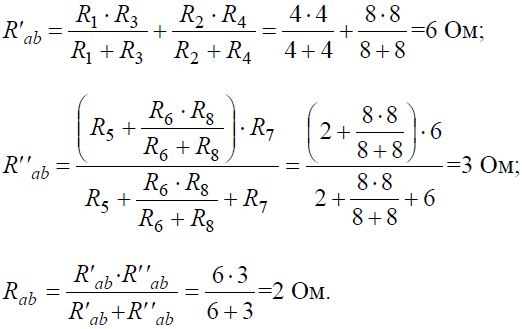
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
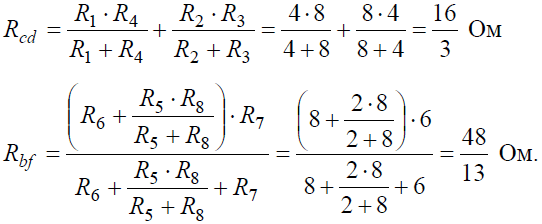
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I2, I3 и составить баланс мощностей, если известно: R1 = 12 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 120 В.
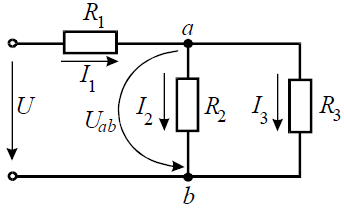
Рис. 5
Решение
Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
![]()
Эквивалентное сопротивление всей цепи:
американские сигареты парламент.
![]()
Ток в неразветвленной части схемы:
![]()
Напряжение на параллельных сопротивлениях:
![]()
Токи в параллельных ветвях:
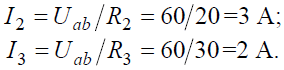
Баланс мощностей:
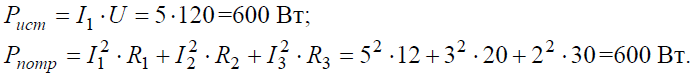
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
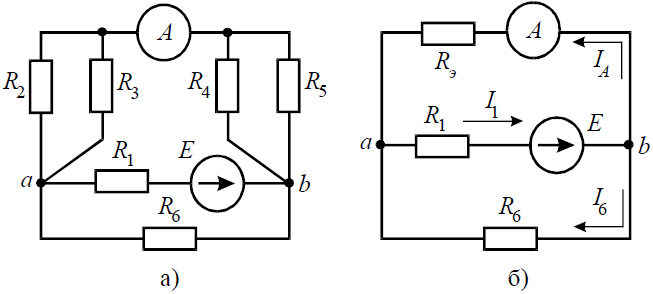
Рис. 6
Решение
Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б).
Величина эквивалентного сопротивления:
проститутки академическая. Смотри здесь строительство и ремонт деревянного дома.
![]()
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
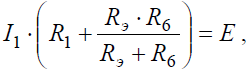
откуда ток I1:
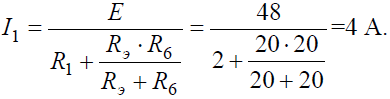
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
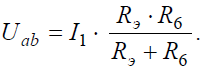
Тогда амперметр покажет ток:
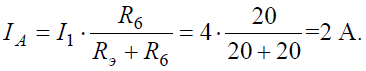
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
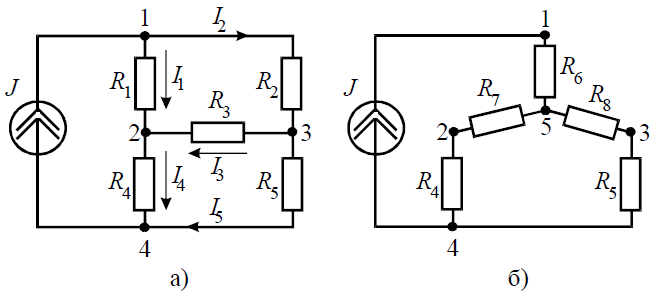
Рис. 7
Решение
Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
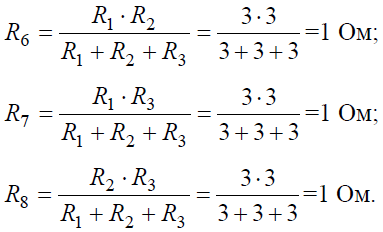
Преобразуем параллельное соединение ветвей между узлами 4 и 5
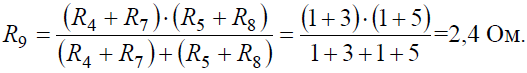
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
![]()
И теперь можно определить токи I4 и I5:

Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
![]()
Тогда ток в ветви с сопротивлением R3 определится:
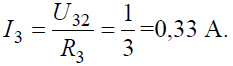
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
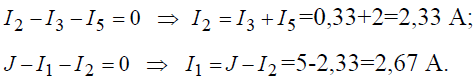
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
 Метод эквивалентных преобразований
Метод эквивалентных преобразований
Что такое входное сопротивление и как его измерить
Содержание
- 1 Понятие входного сопротивления для постоянного тока
- 2 Что такое внутреннее сопротивление при переменном токе
- 3 Как измерить
- 4 Выходное напряжение
- 5 Практическое применение
- 6 Видео по теме
При работе со сложными схемами нужно уметь определять характеристики их отдельных блоков и элементов. В частности, входное и выходное сопротивление. Важно знать, что они из себя представляют, как определяются и какую роль играют в работе устройства.

Понятие входного сопротивления для постоянного тока
Радиоэлектронные устройства могут быть не только относительно, но и очень сложными, состоящими из многих блоков. Однако независимо от сложности устройства, количества используемых в нем деталей, схему можно рассматривать в качестве совокупности простых частей с определенной разностью потенциалов на входе. На выходе блока имеется ещё два контакта, на которых также присутствует напряжение. В первом случае его называют входным, в другом — выходным. Сказанное можно пояснить следующим рисунком.

Входное сопротивление цепи можно легко измерить с помощью вольтметра. Также нетрудно определить силу тока, протекающего между контактами. Для этого достаточно к схеме последовательно подключить амперметр. Получив эти два параметра, по закону Ома можно определить сопротивление схемы. Его называют входным. Иногда при этом рассматривают входное сопротивление длинной линии. Его определяющим свойством является то, что при подключении нагрузки к клеммам источника питания электрические характеристики не меняются.
Устройство блока может быть достаточно сложным, но в рассматриваемом случае не принимаются во внимание особенности его конструкции. Фактически можно представить, что внутри как бы находится резистор с определенным активным сопротивлением, соответствующим измеренному.

Входное электрическое сопротивление рассматривается как общая характеристика конкретного блока. Напряжение на вход может поступать с выхода другого блока или, например, с клемм аккумулятора или батареи.
Что такое внутреннее сопротивление при переменном токе
В предыдущем разделе было рассмотрено чисто активное сопротивление. При наличии в цепи только активного сопротивления фазы напряжения и тока совпадают. В реальных схемах обязательно присутствует реактивное сопротивление, которое делится еще на ёмкостное и индуктивное. Для постоянного тока его значение принято считать пренебрежимо малым и не принимать во внимание при расчёте параметров.

Если используется переменное напряжение на входе, тогда рассматривается полное сопротивление, состоящее из активного и реактивного. Их суммируют, используя правило прямоугольного треугольника. В этом случае один катет соответствует активному сопротивлению, второй — реактивному, а гипотенуза — полному или импедансу.
Важно учитывать, что в цепи с переменным током фаза напряжения сдвигается относительно фазы тока. Сдвиг фаз зависит от соотношения активного и реактивного сопротивлений конкретной цепи.
При отсутствии конденсаторов и катушек индуктивности в цепи емкостным и индуктивным сопротивлениями можно пренебречь и учитывать только активное. В этом случае ток будет следовать за напряжением, одновременно принимая нулевые и максимальные значения.
Если же в цепь включить катушку или конденсатор, создающих индуктивное или емкостное сопротивление настолько большого значения, что активное становится пренебрежимо малым, то сдвиг фаз будет равен π/2.

Так как реактивное сопротивление зависит от частоты поступающего сигнала, то чтобы более точно определить импеданс, необходимо узнать нужные параметры при двух различных частотах.
Следует принимать во внимание, что входное полное сопротивление линии может быть различным в отличающихся температурных условиях. Характер и величина отличий зависит от конкретного устройства рассматриваемого блока. Также требуется учитывать обратное влияние самой процедуры измерения на электрические параметры схемы.
Входное сопротивление зависит еще и от того, каким способом вводится в цепь сигнал обратной связи (ОС). Если этот сигнал отсутствует, то входное сопротивление определяется напряжением и током, присутствующими на входе. В том случае, когда обратную связь вводят по последовательной схеме, сопротивление на входе увеличивается при отрицательной ОС и уменьшается при положительной ОС.
При использовании параллельной схемы введения ОС входное сопротивление уменьшается и при отрицательной, и при положительной ОС. При небольшом сопротивлении в цепи ОС оно может составлять десятые, и даже тысячные доли Ома.
Как измерить
При определении входных параметров блока его устройство не рассматривается, но при этом может возникнуть необходимость провести измерение входного сопротивления. Блок выглядит как чёрный ящик, имеющий две входных и две выходных клеммы. Наиболее простым решением является определение входного напряжения и силы тока. Для простоты можно предположить, что рассматривается постоянный ток. Определить входное электрическое сопротивление в этом случае можно способом, который описан далее.

Найти входное сопротивление можно, разделив напряжение на силу тока. Однако в рассматриваемом случае нужно понимать, что если напряжение подаётся с батареи, то на показания будет влиять внутреннее сопротивление источника тока.
Если в блоке используется конденсатор, то нужно учитывать, что через него ток проходить не будет. С другой стороны, для переменного тока он помехой не является. Для переменного тока в качестве входного сопротивления цепи рассматривается полное сопротивление (импеданс). Оно представляет собой векторную сумму активного (омического) и реактивного (индуктивного и ёмкостного) сопротивлений. Однако его значение будет отличаться при различных частотах. Поэтому процедура измерения является более сложной по сравнению с постоянным током. В этом случае может быть использована следующая схема.

В данной схеме применён генератор переменного тока, который расположен слева. Его соединяют с исследуемым блоком, подавая на него переменный ток. На одном из соединительных проводов ставится резистор с известным сопротивлением R.
Напряжение измеряют дважды — перед резистором и после него. Пусть его значение будет равно U1 и U2 соответственно. Как известно, при переменном входном токе I(вх) падение напряжения на этой детали составит U2 – U1. С другой стороны оно будет равно I(вх) × R. В результате может быть получена следующая формула:
U2 − U1 = I(вх) × R.
Из этой формулы можно определить величину входного тока:
I(вх) = ( U2 − U1 ) / R.
На вход исследуемого блока поступает напряжение U2:
I(вх) = U2 / R(вх).
Входное сопротивление R(вх) найдем, используя формулу:
( U2 − U1 ) / R = U2 / R(вх).
Определяем значение сопротивления:
R(вх) = R × U2 / ( U2 − U1 ).
Все величины в правой части равенства являются известными или были измерены. Подставив их формулу, можно определить величину входного сопротивления схемы.
Применение описанного здесь способа позволяет точно вычислять входное сопротивление даже в тех случаях, когда оно очень велико.
Выходное напряжение
При рассмотрении упрощённой схемы блока видно, что у него имеется выходное напряжение. Оно появляется на контактах, указанных на изображении справа.

На рисунке показан идеальный источник тока, который, как предполагается, не имеет внутреннего сопротивления. Это означает, что может быть создан сколько угодно большой ток. Имеющийся на схеме резистор нарушает определенную идеальность, ограничивая величину тока при коротком замыкании.
Измерение выходного тока может быть выполнено следующим образом. Напряжение U является известной величиной. При коротком замыкании может быть измерен проходящий по контактам ток. Выходное сопротивление R(вых) определяется по закону Ома. Для его вычисления необходимо напряжение разделить на ток.
Однако этот способ неудобен, так как большой ток нарушает условия функционирования схемы и может привести к поломкам. Поэтому на практике между клеммами ставят дополнительный резистор с известной величиной сопротивления R и только после этого измеряют значение силы тока I и напряжения U2. Предварительно следует определить разность потенциалов U1 с помощью вольтметра. Исходя из закона Ома, получают следующую формулу:
R(вых) = ( U2 – U1 ) / ( U2 / R ).
Практическое применение
Понятие входного сопротивления играет важную роль при согласовании характеристик соединённых между собой блоков. Сказанное можно пояснить на следующем примере.
Предположим, что первым блоком является источник питания. Если к его клеммам присоединён следующий блок, то при практическом определении его входного сопротивления станет понятно, что оно немного меньше расчётной величины.
Это связано с наличием внутреннего сопротивления аккумулятора. Чем оно больше, тем искажение заметнее. Аналогичная ситуация наблюдается при соединении двух любых других блоков. Чтобы передача сопротивления проходила с минимальными потерями, необходимо, чтобы выходное сопротивление предыдущего блока было намного меньше входного у последующего.
С учетом этого обстоятельства необходимо уметь определять рассматриваемые величины, а при создании схемы обеспечивать их правильное соотношение. Если оно будет нарушено, то произойдёт значительное падение напряжения при передаче.
На практике обычно сталкиваются с очень большими значениями входных сопротивлений. В некоторых случаях они могут достигать 1 МОм. Это часто происходит при относительно небольшом входном напряжении. В результате сила рассматриваемого тока получается также небольшой.
В электронике входное и выходное сопротивление играют важную роль. Все качественные измерительные приборы стараются делать с очень высоким входным сопротивлением, чтобы оно минимально сказывалось на измеряемом сигнале и не гасило его амплитуду.
Что касается качественных источников питания, то их выпускают с очень небольшим выходным сопротивлением, чтобы при подключении низкоомной нагрузки напряжение на выходе «не проседало». Но даже если это случится, его можно подкорректировать вручную, используя регулировку выходного напряжения, присутствующую в каждом нормальном источнике питания.
Видео по теме
Входным сопротивлением длинной линии (цепи с распределенными параметрами) называется
такое сосредоточенное сопротивление, подключение которого вместо линии к зажимам
источника не изменит режим работы последнего.
В общем случае для линии с произвольной нагрузкой ![]() для входного сопротивления можно
для входного сопротивления можно
записать
 . . |
(1) |
Полученное выражение показывает, что входное сопротивление является функцией
параметров линии ![]() и
и ![]() , ее длины
, ее длины ![]() и нагрузки
и нагрузки ![]() . При этом зависимость входного
. При этом зависимость входного
сопротивления от длины линии, т.е. функция ![]() , не является монотонной, а носит
, не является монотонной, а носит
колебательный характер, обусловленный влиянием обратной (отраженной) волны.
С ростом длины линии как прямая, так соответственно и отраженная волны затухают
все сильнее. В результате влияние последней ослабевает и амплитуда колебаний
функции ![]() уменьшается.
уменьшается.
При согласованной
нагрузке, т.е. при ![]() , как было показано ранее, обратная
, как было показано ранее, обратная
волна отсутствует, что полностью соответствует выражению (1), которое при ![]() трансформируется в соотношение
трансформируется в соотношение
![]() .
.
Такой же величиной определяется входное сопротивление при ![]() .
.
При некоторых значениях длины линии ее входное сопротивление может оказаться
чисто активным. Длину линии, при которой ![]() вещественно, называют резонансной.
вещественно, называют резонансной.
Как и в цепи с сосредоточенными параметрами, резонанс наиболее ярко наблюдается
при отсутствии потерь. Для линии без потерь на основании (1) можно записать
 . . |
(2) |
Из (2) для режимов холостого хода (ХХ) и короткого замыкания (КЗ), т.е. случаев,
когда потребляемая нагрузкой активная мощность равна нулю, соответственно получаем:
| (3) |
| (4) |
Исследование характера изменения ![]() в зависимости от длины
в зависимости от длины ![]() линии на основании (3) показывает,
линии на основании (3) показывает,
что при ![]()
![]() по модулю изменяется в пределах
по модулю изменяется в пределах
![]() и имеет емкостный характер, а
и имеет емкостный характер, а
при ![]() – в пределах
– в пределах ![]() и имеет индуктивный характер.
и имеет индуктивный характер.
Такое чередование продолжается и далее через отрезки длины линии, равные четверти
длины волны (см. рис. 1,а).
В соответствии с (4) аналогичный характер, но со сдвигом на четверть волны,
будет иметь зависимость ![]() при КЗ (см. рис. 1,б).
при КЗ (см. рис. 1,б).

Точки, где ![]() , соответствуют резонансу напряжений,
, соответствуют резонансу напряжений,
а точки, где ![]() , – резонансу токов.
, – резонансу токов.
Таким образом, изменяя длину линии без потерь, можно имитировать емкостное
и индуктивное сопротивления любой величины. Поскольку длина волны ![]() есть функция частоты, то аналогичное
есть функция частоты, то аналогичное
изменение ![]() можно обеспечить не изменением
можно обеспечить не изменением
длины линии, а частоты генератора. При некоторых частотах входное сопротивление
цепи с распределенными параметрами также становится вещественным. Такие частоты
называются резонансными. Таким образом, резонансными называются частоты,
при которых в линии укладывается целое число четвертей волны.
Переходные процессы в цепях с распределенными параметрами
Переходные процессы в цепях с распределенными параметрами имеют характер блуждающих
волн, распространяющихся по цепи в различных направлениях. Эти волны могут претерпевать
многократные отражения от стыков различных линий, от узловых точек включения
нагрузки и т.д. В результате наложения этих волн картина процессов в цепи может
оказаться достаточно сложной. При этом могут возникнуть сверхтоки и перенапряжения,
опасные для оборудования.
Переходные процессы в цепях с распределенными параметрами возникают при различных
изменениях режимов их работы: включении-отключении нагрузки, источников энергии,
подключении новых участков линии и т.д. Причиной переходных процессов в длинных
линиях могут служить грозовые разряды.
Уравнения переходных процессов в цепях с распределенными
параметрами
При рассмотрении схемы замещения цепи с распределенными параметрами были получены
дифференциальные уравнения в частных производных
| (5) |
| (6) |
Их интегрирование с учетом потерь представляет собой достаточно сложную задачу.
В этой связи будем считать цепь линией без потерь, т.е. положим ![]() и
и ![]() . Такое допущение возможно для
. Такое допущение возможно для
линий с малыми потерями, а также при анализе начальных стадий переходных процессов,
часто наиболее значимых в отношении перенапряжений и сверхтоков.
С учетом указанного от соотношений (5) и (6) переходим к уравнениям
| (7) |
| (8) |
Для получения уравнения (7) относительно одной переменной продифференцируем
(7) по х, а (8) – по t:
 ; ; |
(9) |
 . . |
(10) |
Учитывая, что для линии без потерь ![]() , после подстановки соотношения
, после подстановки соотношения
(10) в (9) получим
 . . |
(11) |
Аналогично получается уравнение для тока
 . . |
(12) |
Волновым уравнениям (11) и (12) удовлетворяют решения
![]() ;
;
 .
.
Как и ранее, прямые и обратные волны напряжения и тока связаны между собой
законом Ома для волн
![]() и
и ![]() ,
,
где ![]() .
.
При расчете переходных процессов следует помнить:
- В любой момент времени напряжение и ток в любой точке линии рассматриваются
как результат наложения прямой и обратной волн этих переменных на соответствующие
величины предшествующего режима. - Всякое изменение режима работы цепи с распределенными параметрами обусловливает
появление новых волн, накладываемых на существующий режим. - Для каждой волны в отдельности выполняется закон Ома для волн.
- Как указывалось, переходный процесс в цепях с распределенными параметрами
характеризуется наложением многократно отраженных волн. Рассмотрим многократные
отражения для двух наиболее характерных случаев: подключение источника постоянного
напряжения к разомкнутой и короткозамкнутой линии.
Переходные процессы при включении на постоянное напряжение
разомкнутой и замкнутой на конце линии
При замыкании рубильника (см. рис. 2) напряжение в начале линии сразу же достигает
величины ![]() , и
, и

возникают прямые волны прямоугольной
формы напряжения ![]() и тока
и тока ![]() , перемещающиеся вдоль линии со
, перемещающиеся вдоль линии со
скоростью V (см. рис. 3,а).Во всех точках линии, до которых волна еще не дошла,
напряжение и ток равны нулю.Точка, ограничивающая участок линии, до которого
дошла волна, называется фронтом волны. В рассматриваемом случае во всех
точках линии, пройденных фронтом волны, напряжение равно ![]() , а ток –
, а ток – ![]() .
.
Отметим, что в реальных условиях форма волны, зависящая от внутреннего сопротивления
источника, параметров линии и т.п., всегда в большей или меньшей степени отличается
от прямоугольной.

Кроме того, при подключении к линии источника с другим
законом изменения напряжения форма волны будет иной. Например, при экспоненциальном
характере изменения напряжения источника (рис. 4,а) волна будет иметь форму
на рис. 4,б.

В рассматриваемом примере с прямоугольной волной напряжения при первом пробеге
волны напряжения и тока (см. рис. 3,а) независимо от нагрузки имеют значения
соответственно ![]() и
и ![]() , что связано с тем, что волны
, что связано с тем, что волны
еще не дошли до конца линии, и, следовательно, условия в конце линии не могут
влиять на процесс.
В момент времени ![]() волны напряжения и тока доходят
волны напряжения и тока доходят
до конца линии длиной l, и нарушение однородности обусловливает появление обратных
(отраженных) волн. Поскольку в конце линия разомкнута, то
![]() ,
,
откуда ![]() и
и ![]() .
.
В результате (см. рис. 3,б) напряжение в линии, куда дошел фронт волны, удваивается,
а ток спадает до нуля.
В момент времени ![]() , обратная волна напряжения, обусловливающая
, обратная волна напряжения, обусловливающая
в линии напряжение ![]() , приходит к источнику, поддерживающему
, приходит к источнику, поддерживающему
напряжение ![]() . В результате возникает волна
. В результате возникает волна
напряжения ![]() и соответствующая волне тока
и соответствующая волне тока ![]() (см. рис. 3,в).
(см. рис. 3,в).
В момент времени ![]() волны напряжения и тока подойдут
волны напряжения и тока подойдут
к концу линии. В связи с ХХ ![]() и
и ![]() (см. рис. 3,г). Когда эти волны
(см. рис. 3,г). Когда эти волны
достигнут начала линии, напряжение и ток в ней окажутся равными нулю. Следовательно,
с этого момента переходный процесс будет повторяться с периодичностью ![]() .
.
В случае короткозамкнутой на конце линии в интервале времени ![]() картина процесса соответствует
картина процесса соответствует
рассмотренной выше. При ![]() , поскольку в конце линии
, поскольку в конце линии ![]() и
и ![]() , что приведет к возрастанию тока
, что приведет к возрастанию тока
в линии за фронтом волны до величины ![]() . При
. При ![]() от источника к концу линии будет
от источника к концу линии будет
двигаться волна напряжения ![]() и соответствующая ей волна тока
и соответствующая ей волна тока
![]() , обусловливающая ток в линии,
, обусловливающая ток в линии,
равный ![]() , и т. д. Таким образом, при каждом
, и т. д. Таким образом, при каждом
пробеге волны ток в линии возрастает на ![]() .
.
Отметим, что в реальном случае, т.е. при наличии потерь мощности, напряжение
в линии в режиме ХХ постепенно выйдет на уровень, определяемый напряжением
источника, а ток в режиме КЗ ограничится активным сопротивлением и проводимостью
линии, а также внутренним сопротивлением источника.
Литература
- Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. - Теоретические основы электротехники. Учеб. для вузов. В трех т. Под
общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные
электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с. - Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Контрольные вопросы и задачи
- Какой характер имеет зависимость входного сопротивления линии от ее длины
и почему? - С помощью чего можно изменять характер и величину входного сопротивления
цепи с распределенными параметрами? - Какое допущение лежит в основе анализа переходных процессов в длинных линиях?
- Каким законом связаны волны напряжения и тока в переходных режимах?
- Линия без потерь имеет длину
 , фазовая скорость волны
, фазовая скорость волны  . При каких частотах в ней будут
. При каких частотах в ней будут
иметь место минимумы и максимумы входного сопротивления? - При каких длинах линии без потерь в ней будут наблюдаться резонансные явления,
если фазовая скорость равна скорости света, а частота ?
? - Постройте эпюры распределения напряжения и тока вдоль линии, питаемой от
источника постоянного напряжения, при включении и отключении в ее конце резистивной
нагрузки.
Ответ: ![]() .
.
Ответ: ![]() .
.

Тема1 Метод эквивалентных преобразований
Изучение этой темы очень важно, так как в ней подробно рассматриваются вопросы, необходимые для решения задач всех последующих разделов курса. Учебной программой предусмотрены три практических занятия по данной теме.
Занятие1
Цели занятия:
1.Научиться применять законы Ома и Кирхгофа для расчета цепей
содним источником ЭДС.
2.Научиться рассчитывать эквивалентное сопротивление цепи при последовательно-параллельном соединении приемников.
3.Научиться использовать формулу для определения тока в одной из двух пассивных параллельных ветвей, когда общий ток известен.
Рассмотрим первую целевую задачу занятия.
В настоящее время под законом Ома понимают соотношения, связывающие напряжение и ток. В схемах замещения цепей постоянного тока имеется один вид приемников – резистор, обладающий сопротивлением R. По закону Ома напряжение на резисторе пропорционально току в нем.
Коэффициент пропорциональности и назван сопротивлением: U R = R I .
Первый закон Кирхгофа сформулирован для узла. Узел – это точка в схеме, где сходятся не менее трех ветвей. В настоящее время при использовании ЭВМ для ввода исходных данных узлами выделяют каждый элемент схемы замещения. Эти узлы называют ложными или устранимыми. В дальнейшем речь будет идти о неустранимых узлах.
Алгебраическая сумма токов в узле равна нулю:
n
∑I j = 0.
j=1
Второй закон Кирхгофа относится к контуру. Алгебраическая сумма напряжений на приемниках в любом контуре равна алгебраической сумме ЭДС, действующих в этом же контуре:
|
Теоретические основы электротехники. Практикум |
-6- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
При непосредственном использовании законов Ома и Кирхгофа решение получается громоздким. Расчет схемы с одним источником энергии и несколькими приемниками существенно упрощается при применении метода эквивалентных преобразований. Все приемники заменяют одним с эквивалентным сопротивлением. При этом токи и напряжения в частях схемы, не затронутых преобразованием, должны оставаться неизменными. Находят токи в свернутой схеме. Затем постепенно возвращаются к исходной схеме с определением остальных токов.
Перейдем ко второй целевой задаче.
Преобразование схемы проводят постепенно, выявляя участки с последовательными и параллельными соединениями приемников. Предварительно нужно выявить узлы и ветви. Узел – точка в схеме, где сходятся не менее трех ветвей. Ветвь – участок с одним током между двумя узлами. Элементы, принадлежащие одной ветви, соединены между собой последовательно. В них один ток. Эквивалентное сопротивление последовательно соединенных резисторов равно сумме их сопротивлений:
n
Rэ = i∑=1Ri .
При параллельном соединении элементы схемы замещения находятся под одним напряжением и соединены между собой двумя выходными зажимами. Эквивалентная проводимость параллельно соединенных резисторов равна сумме их проводимостей:
|
1 |
n |
1 |
||
|
= i∑=1 |
||||
|
R |
э |
R |
||
|
i |
При параллельном соединении двух резисторов с сопротивлениями R1 и R2 эквивалентное сопротивление
Rэ = R1 R2
R1 + R2
При параллельном соединении n одинаковых резисторов сопротивлением R эквивалентное сопротивление Rэ = Rn
Если способ соединения резисторов не совсем ясен, нужно перечертить схему, начиная с одного входного зажима и заканчивая другим, изображая узлы с одинаковыми потенциалами (соединенные ветвью с нулевым сопротивлением) как один узел.
|
Теоретические основы электротехники. Практикум |
-7- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
К третьей целевой задаче занятия переходим после того, как схема превращена в одноконтурную с током I, который определяют по закону Ома:
I = Е . Возвращаемся к исходной схеме с определением остальных токов.
Rэ
При этом удобно пользоваться формулой для определения тока в одной из двух параллельно соединенных пассивных ветвей. Ток в одной из двух
|
параллельно соединенных |
пассивных |
ветвей пропорционален току |
|||
|
в неразветвленной |
части |
схемы. |
В |
числителе |
коэффициента |
пропорциональности записываем сопротивление другой пассивной ветви, в знаменателе – сумму сопротивлений двух пассивных параллельных ветвей.
Рассмотрим алгоритм решения на примере конкретных задач.
Задача1
Напряжение между зажимами батареи измеряли три раза разными вольтметрами, отличающимися друг от друга величиной внутреннего
|
сопротивления: |
RV = |
400 Ом, |
RV |
= 2400 |
Ом, RV |
= ∞. ЭДС |
батареи |
|||||||||
|
1 |
2 |
3 |
||||||||||||||
|
Е = 75 В, |
Rвн =100 Ом. |
|||||||||||||||
|
Определить показания вольтметра. |
||||||||||||||||
|
Пояснение к решению |
||||||||||||||||
|
Если в условии задачи не приведена схема замещения цепи, то прежде |
||||||||||||||||
|
всего ее надо составить (рис. 1.1). |
||||||||||||||||
|
Схема одноконтурная, в ней один ток, |
I |
|||||||||||||||
|
направление |
которого |
определяет |
||||||||||||||
|
направление |
ЭДС. |
Стрелка |
источника |
|||||||||||||
|
E |
RV |
|||||||||||||||
|
показывает |
направление |
увеличения |
UV |
|||||||||||||
|
потенциала. Направление тока рекомендуют |
Rвн |
|||||||||||||||
|
указывать стрелкой на линии, обозначающей |
||||||||||||||||
|
провод. |
Ток |
направлен |
в |
сторону |
||||||||||||
|
уменьшения потенциала. |
||||||||||||||||
|
Рис. 1.1 |
||||||||||||||||
|
Знаки плюс и минус на схеме говорят |
||||||||||||||||
|
лишь о |
том, что |
потенциал |
точки, |
отмеченной знаком плюс, выше потенциала точки, отмеченной знаком минус.
Напряжение на вольтметре, равное напряжению на зажимах батареи, покажем стрелкой, параллельной резистору, учитывающему вольтметр. Напряжение направлено по току.
Решение
1. Напряжение вольтметра по закону Ома: UV = RV I .
|
Теоретические основы электротехники. Практикум |
-8- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
2. Ток в цепи по закону Ома: I = E
Rэ
3. В резисторах один ток, следовательно, они соединены
последовательно, Rэ = Rвн + RV .
Сделаем расчет для трех различных вольтметров:
|
а) R |
= 400 |
Ом; R |
э |
=100 + 400 = |
500 Ом; I = |
75 |
= 0,15 |
А; U |
V |
= 60 |
В. |
|||||||||
|
V |
500 |
|||||||||||||||||||
|
1 |
||||||||||||||||||||
|
б) R |
= 2400 Ом; R |
э |
=100 + 2400 = 2500 Ом; I = |
75 |
= 0,03 |
А; U |
V |
= 72 В. |
||||||||||||
|
V |
2500 |
|||||||||||||||||||
|
2 |
||||||||||||||||||||
|
в) R |
= ∞; |
R |
э |
=100 + ∞ = ∞; I = |
75 = 0 ; U |
V |
= ∞ 0 =неопределенность. |
|||||||||||||
|
V |
∞ |
|||||||||||||||||||
|
3 |
||||||||||||||||||||
Предложенный алгоритм не дает возможности определить показания третьего вольтметра. Обсудим результаты, полученные для двух первых вольтметров. ЭДС батареи Е = 75 В, однако первый вольтметр показал 60 В, второй – 72 В. Разница между ЭДС и показаниями вольт метра – падение напряжения на резисторе, учитывающем внутреннее сопротивление источника. Во втором случае оно меньше, следовательно, второй вольтметр лучше первого. Он отличается большим значением внутреннего сопротивления. Идеальным является вольтметр с RV3 = ∞. Ток в цепи равен
нулю, падение напряжения Uвн = Rвн I = 0 , UV3 = E = 75 В. Уравнение по второму закону Кирхгофа имеет вид Uвн +UV = E . После подстановки значений напряжений по закону Ома получим
Rвн I + RV I = E .
Для третьего вольтметра находим следующее значение:
100 0 + ∞ 0 = 75 , т. е. UV3 = ∞ 0 = 75 В.
Задача2
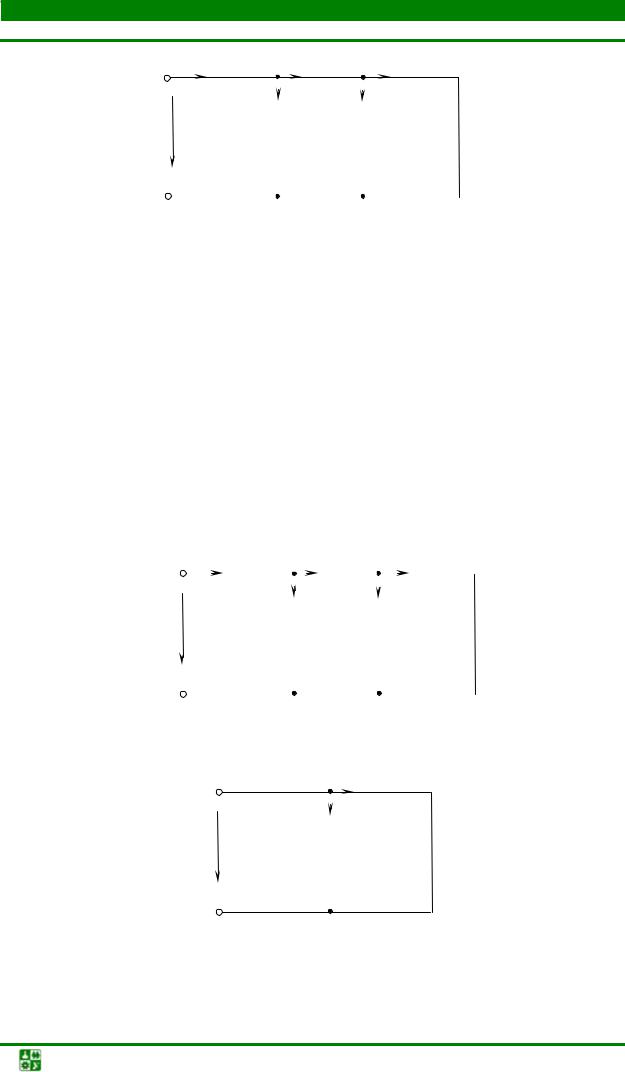
Найти эквивалентное сопротивление цепи, схема замещения которой изображена на рис. 1.2.
|
Теоретические основы электротехники. Практикум |
-9- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
I1 |
a I3 |
b |
I 5 |
|||||||||||||||||||||||||||||||||||||
|
I 4 |
||||||||||||||||||||||||||||||||||||||||
|
R1 |
I2 |
R3 |
R5 |
|||||||||||||||||||||||||||||||||||||
|
U |
R2 |
R |
R6 |
|||||||||||||||||||||||||||||||||||||
|
4 |
||||||||||||||||||||||||||||||||||||||||
|
c |
d |
|||||||||||||||||||||||||||||||||||||||
|
Рис. 1.2 |
||||||||||||||||||||||||||||||||||||||||
|
В схеме три узла, потому что точки с и d |
можно рассматривать как |
|||||||||||||||||||||||||||||||||||||||
|
одну. Узлы соединены между собой пятью ветвями. |
||||||||||||||||||||||||||||||||||||||||
|
Решение |
||||||||||||||||||||||||||||||||||||||||
|
В пятой ветви два резистора с сопротивлениями |
R5 |
и R6 |
соединены |
|||||||||||||||||||||||||||||||||||||
|
между собой последовательно. Их |
можно |
заменить |
одним |
резистором |
||||||||||||||||||||||||||||||||||||
|
с эквивалентным сопротивлением |
R56 = R5 + R6 (рис. |
1.3). |
В этой |
схеме |
||||||||||||||||||||||||||||||||||||
|
резисторы с сопротивлениями R4 |
и |
R56 |
соединены |
между |
собой |
|||||||||||||||||||||||||||||||||||
|
параллельно. |
Заменим их |
одним |
с |
эквивалентным |
сопротивлением |
|||||||||||||||||||||||||||||||||||
|
R |
= |
R4 R56 |
(рис. 1.4). |
|||||||||||||||||||||||||||||||||||||
|
bc |
R4 + R56 |
|||||||||||||||||||||||||||||||||||||||
|
I1 |
a I3 |
b |
I 5 |
|||||||||||||||||||||||||||||||||||||
|
I2 |
I |
|||||||||||||||||||||||||||||||||||||||
|
R |
R |
4 |
||||||||||||||||||||||||||||||||||||||
|
U |
1 |
3 |
||||||||||||||||||||||||||||||||||||||
|
R2 |
R |
R56 |
||||||||||||||||||||||||||||||||||||||
|
c |
4 |
|||||||||||||||||||||||||||||||||||||||
|
Рис. 1.3 |
||||||||||||||||||||||||||||||||||||||||
|
a I3 |
||||||||||||||||||||||||||||||||||||||||
|
I2 |
||||||||||||||||||||||||||||||||||||||||
|
R |
R3 |
|||||||||||||||||||||||||||||||||||||||
|
U |
1 |
|||||||||||||||||||||||||||||||||||||||
|
R2 |
R |
|||||||||||||||||||||||||||||||||||||||
|
bc |
||||||||||||||||||||||||||||||||||||||||
c
Рис. 1.4
|
Теоретические основы электротехники. Практикум |
-10- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
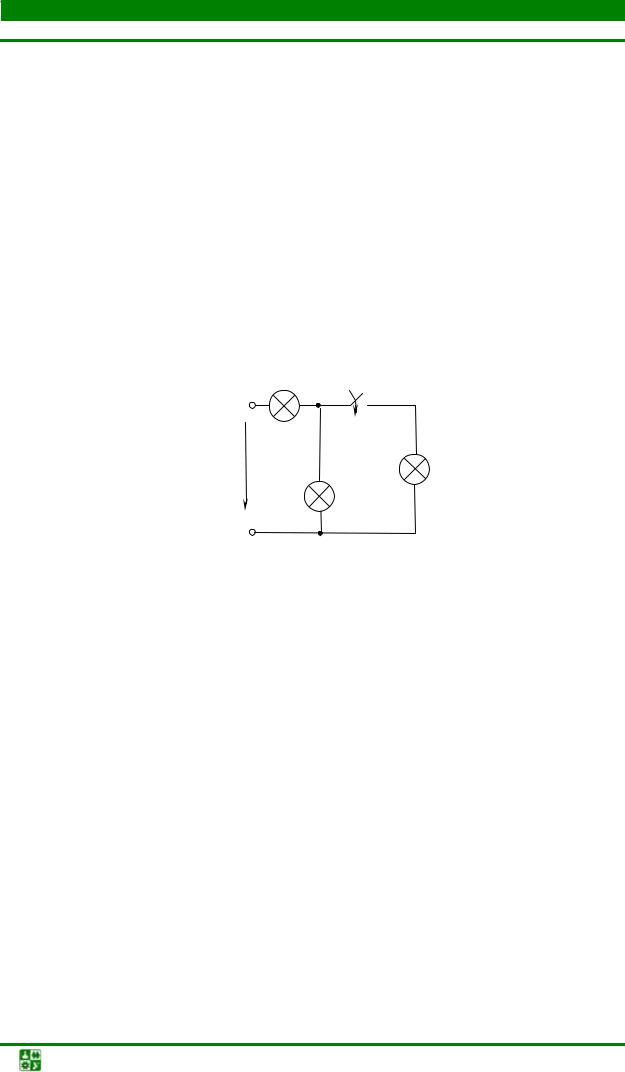
Резисторы с сопротивлениями R3 и Rbc соединены между собой
последовательно. Заменяем их одним резистором с эквивалентным сопротивлением, равным R3 + Rbc . Дальнейшие преобразования повторяют
предыдущие. Эквивалентное сопротивление схемы
|
R |
= R |
+ R2 (R3 + Rbc ) |
|||
|
э |
1 |
R2 |
+ R3 + Rbc |
||
Решите следующие задачи самостоятельно.
Задача3
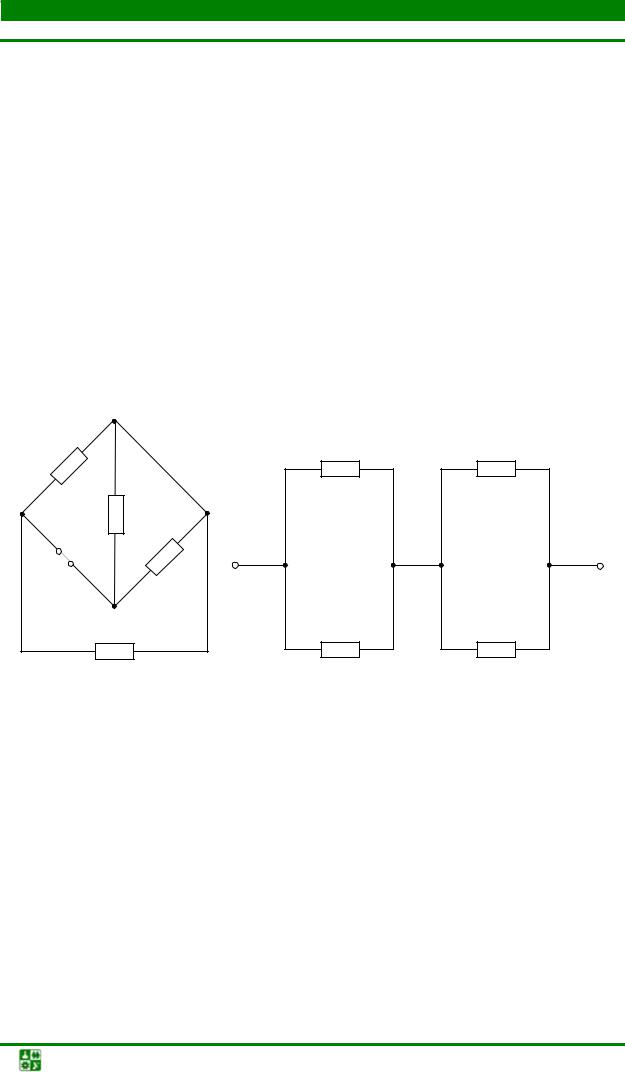
Как изменится яркость первой и второй лампочек после подключения третьей лампочки (рис. 1.5).
Рис. 1.5
Сопротивления всех лампочек одинаковы.
Примечание. Если вы получили ответ, в котором говорится, что яркость лампочки Л1 увеличилась, а лампочки Л2 – уменьшилась, переходите к решению следующей задачи. В противном случае (или для самоконтроля) прочтите решение задачи 3.
Решение
Яркость лампочек зависит от напряжения на них. По второму закону Кирхгофа напряжение на входе схемы U до и после замыкания ключа складывается из напряжений на первой и второй лампочках. Так как входное напряжение не изменялось, напряжения на лампочках Л1 и Л2 либо тоже не изменялись, либо изменялись противоположно. Если обозначим сопротивление одной лампочки R, то до замыкания ключа эквивалентное сопротивление последовательно соединенных Л1 и Л2 Rэ1 = 2R . После
замыкания ключа получилась схема со смешанным соединением: лампочки Л2 и Л3 соединены между собой параллельно, лампочка Л1 подключена к ним последовательно. Эквивалентное сопротивление
|
Теоретические основы электротехники. Практикум |
-11- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
Rэ2 = R + R2 =1,5 R .
Эквивалентное сопротивление уменьшилось, поэтому общий ток увеличился, увеличилось напряжение на первой лампочке, следовательно, и ее яркость. Яркость второй лампочки соответственно уменьшится.
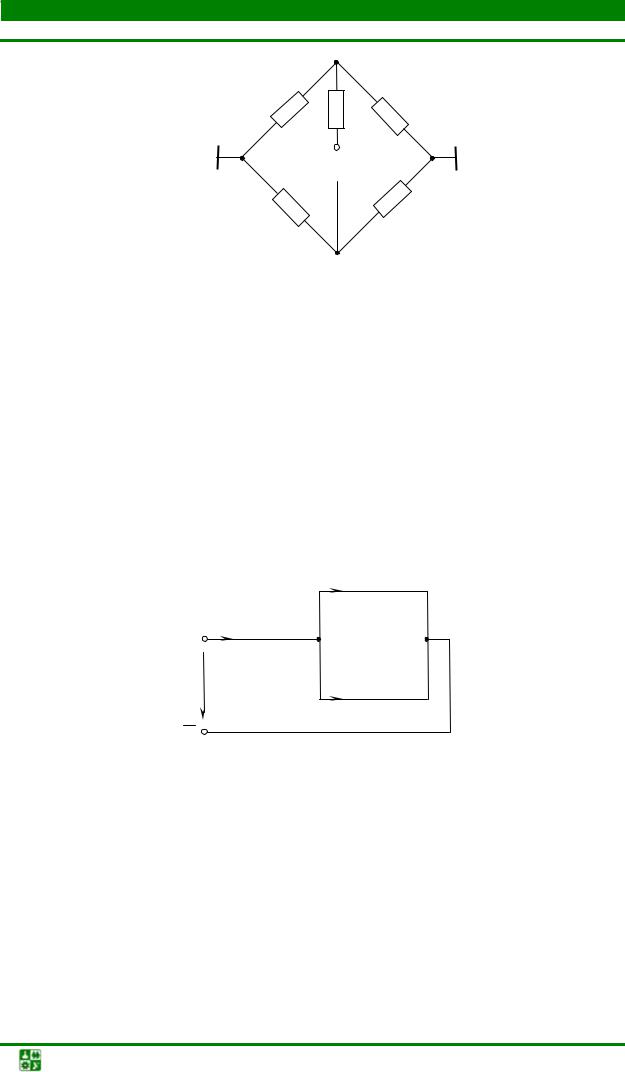
Задача4
Найти входное эквивалентное сопротивление схемы, изображенной на рис. 1.6.
Пояснение к решению
Если перерисовать схему (рис. 1.7) в соответствии с данными рекомендациями, то способ соединения резисторов становится очевидным.
|
R |
R |
R |
|
|
R |
|||
|
a b |
a |
b |
|
|
R |
|||
|
R |
R |
R |
|
|
Рис. 1.6 |
Рис. 1.7 |
Ответ: Rэ = R2 + R2 = R.
Задача5
Найти входное эквивалентное сопротивление схемы рис. 1.8.
|
Теоретические основы электротехники. Практикум |
-12- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
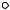 b
b
R R
Рис. 1.8
Пояснение к решению
Знак означает, что потенциал данной точки равен нулю. Ответ: Rэ = 2R.
|
Задача6 |
||||||
|
Вычислить токи в схеме |
рис. 1.9, |
если U =120 В, R1 = 18 Ом, |
||||
|
R2 = 30 Ом, R3 = 20 Ом. |
R2 |
|||||
|
I2 |
||||||
|
I1 |
R1 |
b |
||||
|
a |
||||||
|
+ |
I3 |
R3 |
||||
|
U |
||||||
Рис. 1.9
Пояснение к решению
Выявить в схеме узлы ( a и b), найти ветви, их соединяющие, указать направления токов. Цепь на входе не разорвана. Источник ЭДС на схеме часто не изображают, так как он находится на электростанции. Показывают напряжение на его зажимах. Ветвь с током I1 является активной, ветви с
токами I2 и I3 – пассивные.
Решение
|
Теоретические основы электротехники. Практикум |
-13- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
1. Эквивалентное сопротивление цепи
|
R |
э |
= R + |
R2 R3 |
=18 + |
30 20 |
= 30 Ом. |
|
1 |
R2 |
+ R3 |
30 + 20 |
|||
2. Ток в свернутой схеме I1 (так как источник ЭДС не подвергался преобразованиям) вычисляем по закону Ома:
I1 = U = 120 = 4 А.
Rэ 30
3. Вычислим ток в одной из двух пассивных параллельных ветвей:
I2 = R2R+3 R3 I1 = 3020+ 20 4 =1,6 А.
4. Ток I3 можно вычислить по аналогичной формуле либо с помощью первого закона Кирхгофа:
I3 = R2R+2R3 I1 = 3030+ 20 4 = 2,4 А,
либо I3 = I1 − I2 = 4 −1,6 = 2,4 А.
Следующие задачи решите для самоконтроля.
Задача7
Вычислить эквивалентное сопротивление схемы рис. 1.10. Ответ: Rэ =113 R .
R R  R R
R R
Рис. 1.10
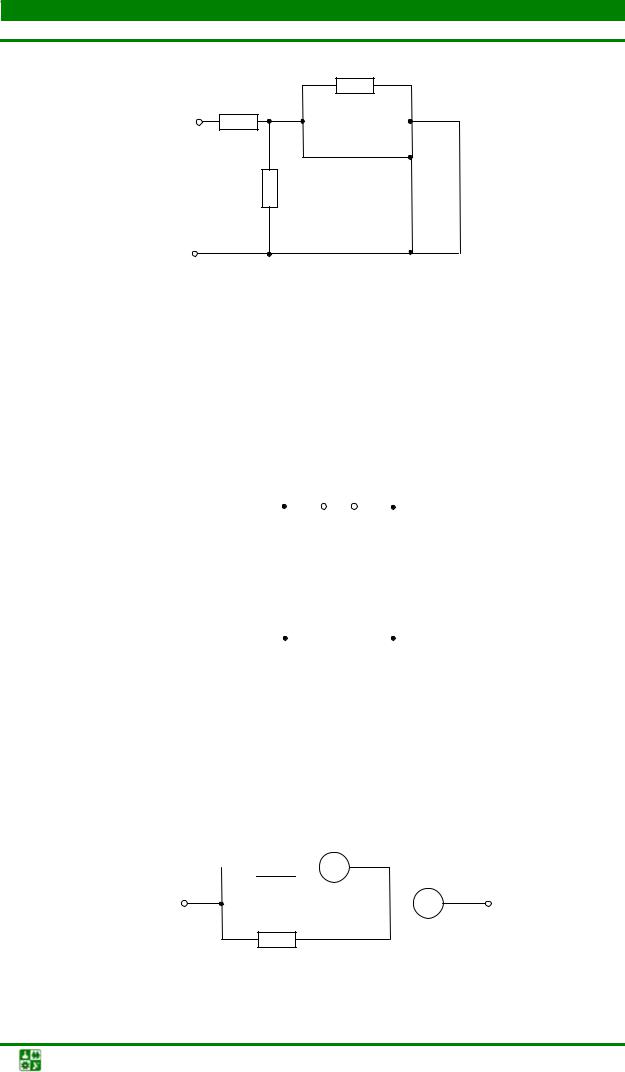
Задача8
Вычислить эквивалентное сопротивление схемы рис. 1.11.
|
Теоретические основы электротехники. Практикум |
-14- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
2R
R
2R
|
4R |
4R |
4R |
||||||
|
R |
||||||||
|
Рис. 1.11 |
Ответ: Rэ = 3R .
Задача9
Вычислить эквивалентное сопротивление схемы рис. 1.12.
3R
|
2R |
2R |
2R |
2R |
|||||||||||||
|
R |
||||||||||||||||
|
Рис. 1.12 |
||||||||||||||||
|
Ответ: Rэ =1,5R . |
||||||||||||||||
|
Задача10 |
||||||||||||||||
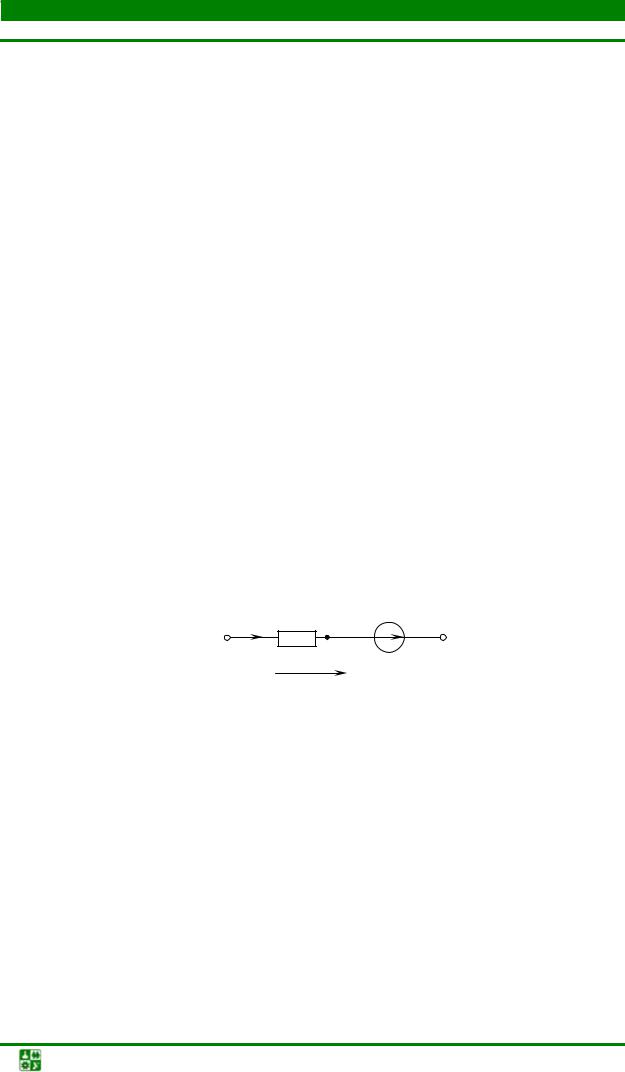
|
Вычислить сопротивление |
R2 в схеме рис. 1.13, если R1 = 3 Ом, |
|||||||||||||||
|
амперметр А показывает ток 25 А, амперметр |
A2 – ток 5 А. |
R2
 А2
А2
 А
А
R1
Рис. 1.13
|
Теоретические основы электротехники. Практикум |
-15- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
Ответ: R2 =12 Ом.
Задача11
Линия передачи электроэнергии расположена на двух опорах, сопротивление изоляции которых составляет 20 кОм. Напряжение на входе U = 480 В. Человек, стоя на земле, взялся одной рукой за провод. Сопротивление человека равно 5 кОм. Погибнет ли человек, если «убойный» ток порядка 0,1 А?
Пояснение к решению
Прежде чем решать задачу, следует составить схему замещения исследуемой цепи.
Ответ: нет, так как ток через человека Iч = 0,016 А.
Занятие2
Цели занятия:
1.Научиться определять напряжение между любыми точками схемы.
2.Научиться проверять правильность расчета токов, составляя уравнение баланса мощностей.
Рассмотрим первую целевую задачу занятия.
Активная ветвь, названная так из-за наличия источника ЭДС, изображена на рис. 1.14.
|
a |
I |
R |
c |
E |
|
|
b |
|||||
|
Uab |
|||||
Рис. 1.14
Между концами ветви возникает напряжение Uab . Индексация
показывает направление ко второму индексу. Напряжение – это разность потенциалов между двумя точками, т. е. Uab =Va −Vb .
Определим потенциал точки а, исходя из потенциала Vb . Рассчитаем изменение потенциала промежуточной точки c (рис. 1.14) по сравнению с Vb .
Между точками b и с расположен источник ЭДС, т. е. потенциал точки с отличается от потенциала точки b на величину E. Стрелка источника показывает направление увеличения потенциала. Следовательно, потенциал точки с ниже потенциала точки b. Между точками с и а находится резистор с сопротивлением R. Потенциал Va отличается от потенциала Vc величиной
напряжения на резисторе RI . Ток направлен от большего потенциала к
|
Теоретические основы электротехники. Практикум |
-16- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
меньшему. Так как на пути от с к а перемещение происходит навстречу току, потенциал Va выше потенциала Vc .
Итак, Va =Vb − E + RI ,
Va −Vb = −E + RI ,
но Va −Vb =Uab , т. е. Uab = −E + RI .
Можно определить напряжение между двумя любыми точками, рассчитав изменение потенциалов между ними. При этом нужно вести расчет в сторону увеличения потенциала, т. е. от второго индекса к первому.
Решим уравнение относительно тока:
I = UabR+ E = G(Uab + E),
где G = R1 – проводимость ветви. Это выражение называют законом
Ома для активной ветви.
Последнее выражение можно составить, исходя из следующих рассуждений. Для появления тока в ветви (рис. 1.14) есть два условия: наличие разности потенциалов между концами ветви и действие источника ЭДС. Если направление ЭДС совпадает с направлением тока, она способствует его появлению и должна быть записана в уравнение со знаком плюс. В противном случае – со знаком минус. Напряжение Uab и ток I
направлены одинаково (от точки а к точке b), поэтому напряжение Uab
должно быть записано в уравнение со знаком плюс. Рассуждая таким образом, получаем для тока ветви прежнее выражение.
Перейдем к рассмотрению второй целевой задачи.
Баланс мощностей – интерпретация закона сохранения энергии в электротехнике. Мощность источников энергии равна мощности потребителей: Pг = Rн, причем
|
n |
m |
||
|
Pг = ∑Ei Ii + ∑U j J j , |
|||
|
i=1 |
j=1 |
||
|
где |
n |
– мощность источников ЭДС; |
m |
|
∑Ei Ii |
∑U j I j – мощность источников |
||
|
i=1 |
j=1 |
тока; J j – токи источников тока.
Эти суммы алгебраические. Источник может вырабатывать и потреблять электрическую энергию (заряд аккумулятора).
Если направления ЭДС и тока через источник ЭДС совпадают, мощность источника записывают в уравнение баланса мощностей с положительным знаком. Он работает в режиме генератора. При
|
Теоретические основы электротехники. Практикум |
-17- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
противоположных направлениях ЭДС и тока мощность в уравнении баланса учитывают с отрицательным знаком (режим потребителя).
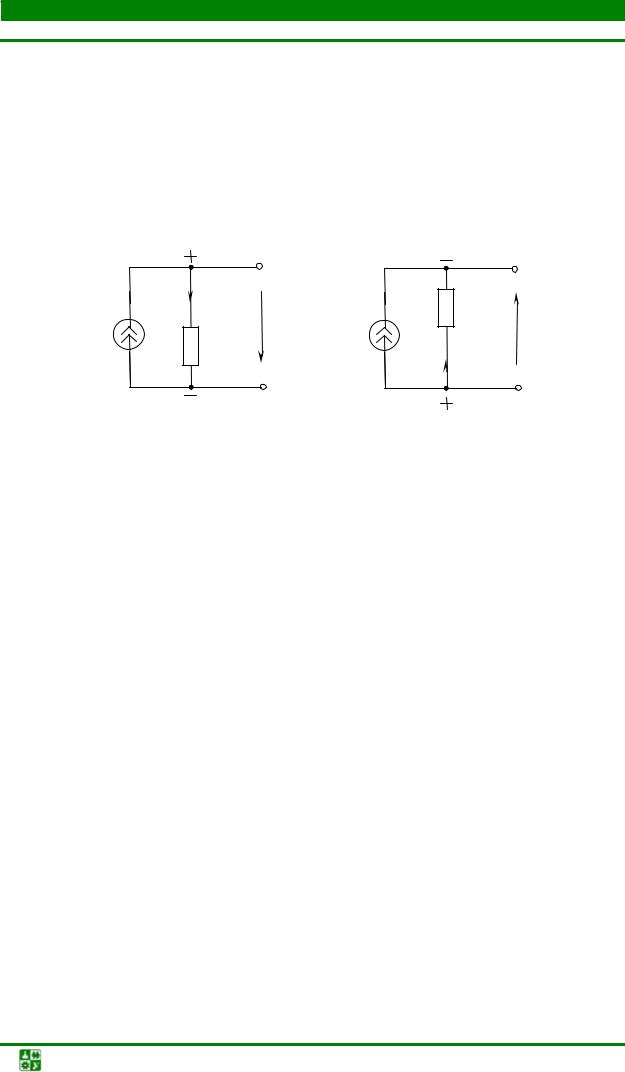
Определение знака мощности источника тока поясняет рис. 1.15, на котором показана разметка зажимов источника тока, вырабатывающего (а) или потребляющего (б) электрическую энергию.
Ток I0 и напряжение U направлены в сторону уменьшения потенциала, что и позволяет разметить зажимы источника.
|
I0 |
R0 |
|||
|
U |
||||
|
J |
J |
U |
||
|
R0 |
||||
|
I0 |
||||
|
а |
б |
Рис. 1.15
Мощность потребителей (нагрузок)
|
1 |
I |
1 |
I 2 . |
||||||
|
P = ∑U |
k |
k |
= ∑R |
k |
|||||
|
н |
k=1 |
k=1 |
k |
||||||
|
Эта сумма арифметическая. Погрешность расчета не |
должна |
||||||||
|
превышать |
|||||||||
|
(1–3) %. |
|||||||||
|
Задача1 |
|||||||||
|
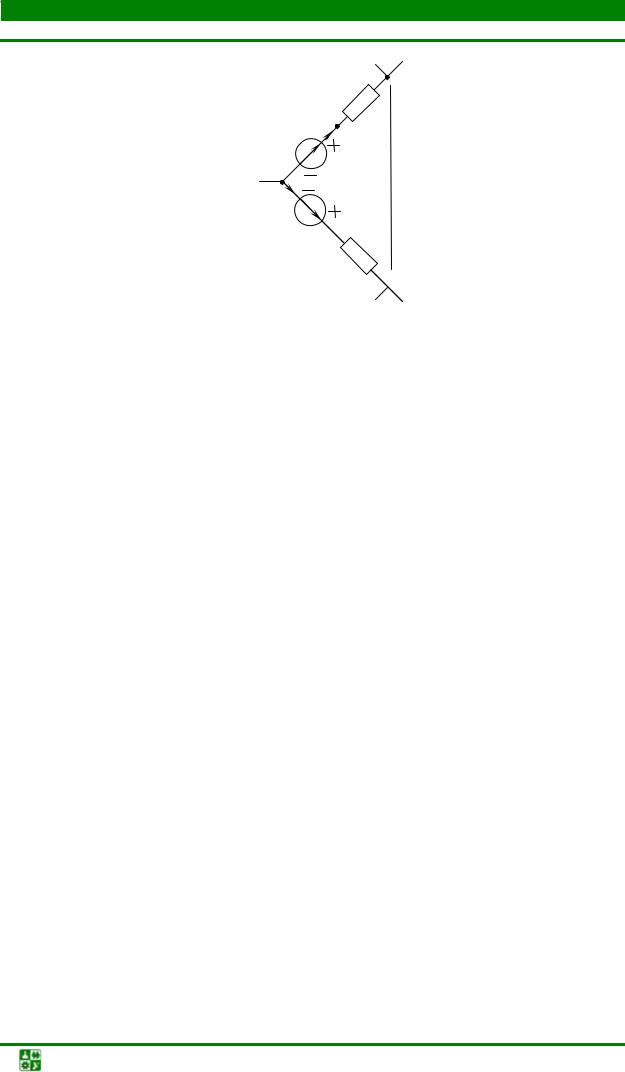
На рис. 1.16 показана часть схемы замещения электрической цепи. |
|||||||||
|
Вычислить напряжение Uab , если |
I1 = 3A, |
I2 = 2,4 А, E1 = 70В, |
R1 = 8Ом, |
||||||
|
R2 = 5Ом, E2 = 20 В. |
|
Теоретические основы электротехники. Практикум |
-18- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
a |
|
|
R1 |
|
|
I1 |
e |
|
E1 |
|
|
d |
Uab |
|
I2 |
E2  c
c
R2 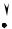 b
b
Рис. 1.16
Пояснение к решению
Нужно расставить на схеме промежуточные точки за каждым элементом. Расчет изменения потенциалов ведем от точки b к точке а, т. е. в сторону увеличения потенциала. Разметим зажимы у источников ЭДС.
Решение
Потенциал точки с изменился по сравнению с потенциалом Vb на величину напряжения R2 I2 Так как на пути от b к c перемещение происходит против тока, потенциал Vc выше потенциала Vb . Между точками с и d находится источник ЭДС E2 . Разметка зажимов источника показывает, что потенциал Vd меньше потенциала Vc на величину E2 . Потенциал точки е Ve больше потенциала Vd на величину E1. Потенциал Va меньше потенциала Ve на величину напряжения R1I1 , так как ток I1 направлен от точки е к
точке а.
Таким образом, Uab = R2 I2 − E2 + E1 − R1I1 = 5 2,4 −20 + 70 −8 3 = 38
В.
Задача2
Вычислить напряжение Uab в схеме рис. 1.17, если E = 45 В, R1 = 20 Ом, R2 = 30 Ом, R3 =10 Ом, R4 = 5 Ом.
|
Теоретические основы электротехники. Практикум |
-19- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
a |
R3 |
I3 c |
I2 |
|
I1 |
|||
|
Uab |
R1 |
R2 |
|
|
b |
|||
R4 
 E
E
d
Рис. 1.17
Пояснение к решению
Сначала нужно разобраться в топологии схемы, т. е. найти узлы и ветви. В схеме два неустранимых узла: с и d. Между ними находятся три ветви. Число токов равно числу ветвей. В схеме с одним источником энергии при последовательно-параллельном соединении приемников направления токов являются очевидными. Если направления токов указаны неверно, то при их расчете методом эквивалентных преобразований напряжение Uab
будет вычислено неправильно. Сначала укажем направление тока в активной ветви I1, которое определено направлением ЭДС источника. В узле с (рис.
1.17) ток I1 разветвляется на токи I2 и I3 .
Решение
1. Запишем выражение напряжения Uab как разность потенциалов Va
и Vb :
Uab = −R1I1 − R3I3,
либо так:
Uab = −E + R4 I3 .
2. Расчет нужных для вычисления напряжения Uab токов проведём
методом эквивалентных преобразований. В резисторах с сопротивлениями R 3 и R4 один ток, значит, они соединены последовательно. Их можно
заменить одним с эквивалентным сопротивлением R34 = R3 + R4.
Резистор с сопротивлением R 34 и резистор с сопротивлением R2 подключены к точкам с и d , т. е. находятся под одним напряжением Ucd ,
следовательно, соединены параллельно. После их замены одним резистором с эквивалентным сопротивлением получаем одноконтурную схему с последовательным соединением элементов. Таким образом,
|
Теоретические основы электротехники. Практикум |
-20- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
R |
э |
= R + |
R2 R34 |
= 20 + |
30 15 |
= 30 Ом. |
|
1 |
R2 |
+ R34 |
30 +15 |
|||
3. Вычислим ток I1 в свёрнутой схеме (ток в источнике ЭДС остался неизменным):
|
I1 = |
E |
= |
45 |
=1,5 |
А. |
|
30 |
|||||
|
Rэ |
4. Вычислим ток I3 по формуле для определения тока в одной из двух пассивных параллельных ветвей:
|
I3 |
= |
R2 |
I1 = |
30 |
=1А. |
||
|
R2 |
+ R34 |
30 +15 |
|||||
Напряжение Uab = −20 1,5 −10 1 = −40 В, либо Uab = −45 +5 1 = −40В.
Обратите внимание! Если ответ получился со знаком минус, это означает, что потенциал точки b выше потенциала точки а. Напряжение направлено противоположно указанному на рис. 1.17. Действительные направления токов и напряжений рекомендуется указывать пунктирными стрелками параллельно выбранным первоначально.
5. Для проверки правильности расчета токов составим уравнение баланса мощностей цепи:
E I1 = R1I12 + R2I22 + R3I32 + R4I32 .
Ток
I2 = I1 − I3 = 0,5 А.
Pг = 45 1,5 = 67,5Вт.
Pн = 20 1,52 +30 0,52 +10 12 +5 12 = 67,5 Вт.
67,5 Вт = 67,5 Вт.
Pг = Pн.
Следующую задачу решите самостоятельно.
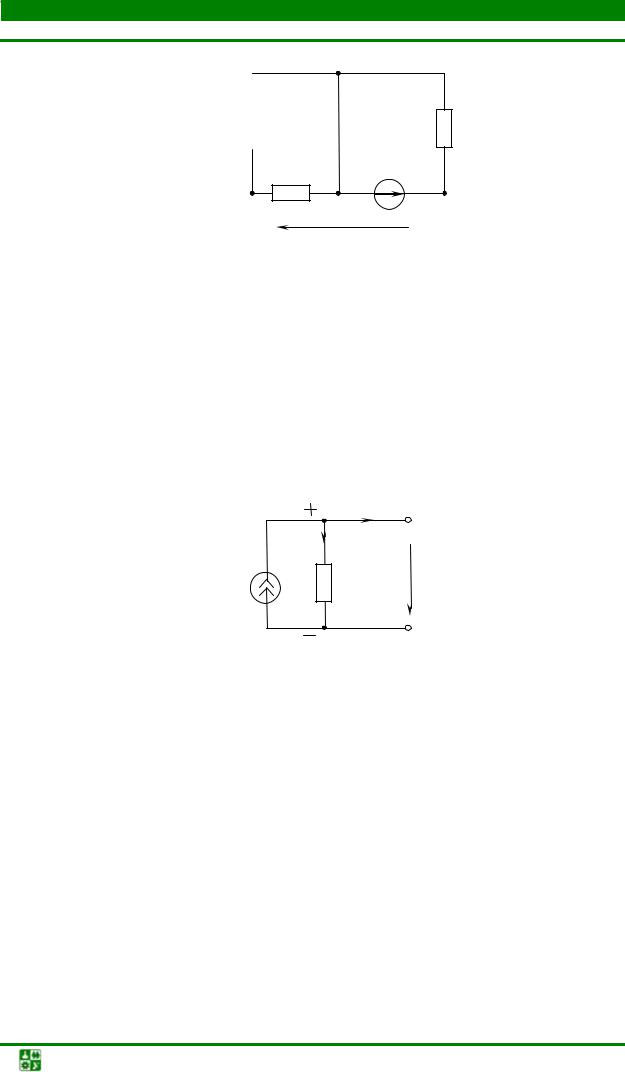
Задача3
Вычислить напряжение Uab в схеме рис. 1.18, если E = 90 B,
R1 = 20 Oм, R2 =10 Ом, R3 = 60 Ом, R4 = 40 Ом.
|
Теоретические основы электротехники. Практикум |
-21- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
R1 |
R3 |
R4 |
||||
|
R2 |
E |
||
|
b |
a |
||
|
Uab |
Рис. 1.18
Составить уравнение баланса мощностей. Ответ: Uab = 80 В.
Задача4
Вычислить мощность источника тока на рис. 1.19, если J = 0,1 A, G0 =10−3 Cм, I = 90 мА. Определить, в каком режиме работает источник тока: генератора или нагрузки.
b
Рис. 1.19
Решение
1. Произвольно направим ток I0 и вычислим его по первому закону Кирхгофа:
J − I0 − I = 0.
Отсюда
I0 = J − I = 0,1−0,09 = 0,01 А.
Знак плюс означает, что направление тока I0 выбрано верно.
2. Вычислим напряжение на зажимах источника тока по закону Ома:
|
Теоретические основы электротехники. Практикум |
-22- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
U = R0 I0 = I0 = 0,01 =10 В.
G0 10−3
|
3. Определим |
мощность |
источника |
тока |
по |
формуле |
||||||||||
|
P =U J =10 0,1 =1 Вт. Так как значение тока |
I0 получилось со знаком |
||||||||||||||
|
плюс, то потенциал Va |
выше потенциала Vb , следовательно, источник тока |
||||||||||||||
|
вырабатывает электроэнергию. |
|||||||||||||||
|
Следующие задачи предлагаем для самоконтроля. |
|||||||||||||||
|
Задача5 |
|||||||||||||||
|
Определить показания вольтметра в схеме рис. 1.20, если |
RV → ∞, |
||||||||||||||
|
I1 =1А, I3 = 2 А, R1 = 2Ом, R2 = 2 Ом, E1 =10В, E2 = 5 В. |
|||||||||||||||
|
E |
R1 |
R2 |
E2 |
||||||||||||
|
I1 |
1 |
||||||||||||||
|
I3 |
|||||||||||||||
|
V |
|||||||||||||||
|
Рис. 1.20 |
|||||||||||||||
|
Ответ: UV = 3В. |
|||||||||||||||
|
Задача6 |
|||||||||||||||
|
Вычислить напряжение |
Uab |
в |
схеме рис. 1.21, |
если |
E = 4 В, |
||||||||||
|
R1 = R4 =1Ом, R2 = R3 = 3Ом. |
|||||||||||||||
|
R1 |
R |
||||||||||||||
|
3 |
|||||||||||||||
|
a |
b |
||||||||||||||
|
Uab |
|||||||||||||||
|
R2 |
R4 |
Рис. 1.21
Пояснение к решению
При расчете токов, нужных для вычисления Uab , нет необходимости искать эквивалентное сопротивление. Напряжение между двумя узлами
|
Теоретические основы электротехники. Практикум |
-23- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
равно ЭДС, поэтому токи в пассивных ветвях могут быть найдены сразу по закону Ома.
Ответ: Uab = 2 В.
Задача7
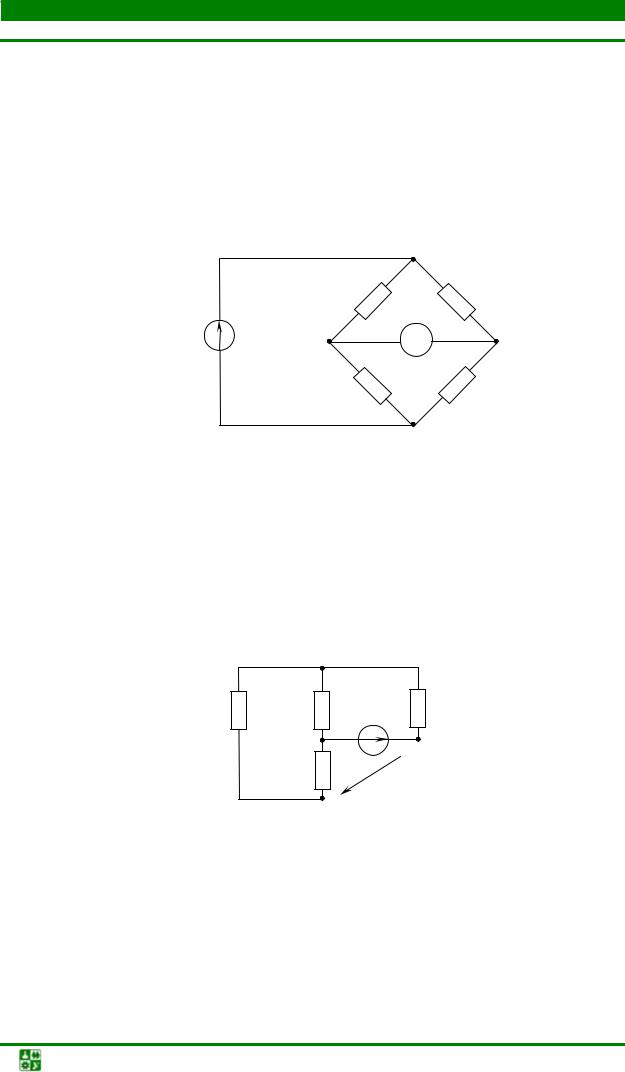
В схеме рис. 1.22 вольтметр показывает напряжение 1 В. Вычислить значение Е, если R1 = R4 = 2 Ом, R2 = R3 = 3Ом, RV → ∞.
Рис. 1.22
Ответ: Е = 5 В.
|
Задача8 |
||
|
Вычислить напряжение Uab в схеме рис. 1.23, |
если Е = 27 В, |
R1 = 3 |
|
Ом, R2 = 6 Ом, R3 =18 Ом, R4 =12 Ом. Проверить |
правильность |
расчета |
токов с помощью баланса мощностей.
|
R1 |
R3 |
E |
R4 |
|
a |
|||
|
R2 |
Uab |
||
|
b |
|||
|
Рис. 1.23 |
Ответ: Uab = 21 В.
Занятие3
Цели занятия:
1. Научиться рассчитывать токи методом эквивалентных преобразований в схемах с одним источником тока.
|
Теоретические основы электротехники. Практикум |
-24- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
2. Научиться рассчитывать токи методом эквивалентных преобразований в схемах, не содержащих последовательно-параллельных соединений резисторов.
Рассмотрим первую целевую задачу занятия.
Расчет схем с источником тока проще, чем с источником ЭДС, так как общий ток известен. Свертывание схемы производят до получения трех ветвей: активной с известным током источника и двух пассивных, токи которых находят по рассмотренным нами формулам.
Перейдем к рассмотрению второй целевой задачи.
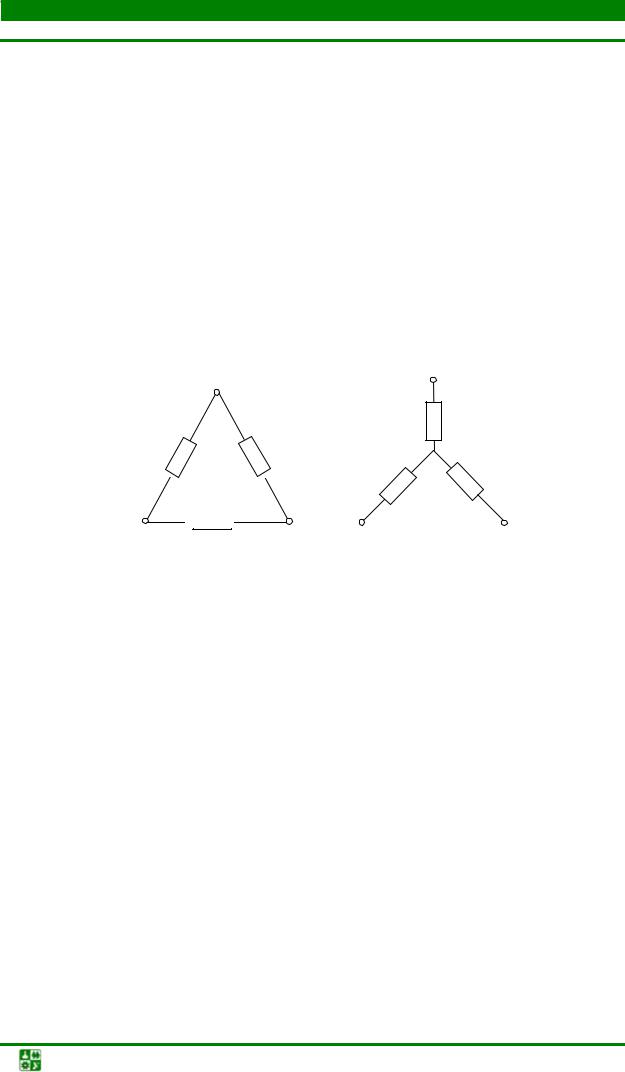
Если схема не содержит последовательно-параллельные соединения резисторов, необходимо соединение треугольником (рис. 1.24, а) заменить эквивалентным соединением звездой (рис. 1.24, б) или выполнить обратную замену.
|
Rca |
Rab |
Ra |
||
|
Rc |
Rb |
|||
|
Rbc |
||||
|
b |
b |
|||
|
c |
a |
c |
||
|
б |
||||
|
Рис. 1.24 |
Структура формул эквивалентных преобразований проста для запоминания:
|
Ra = |
Rab Rca |
, |
||||||
|
Rab + Rbc + Rca |
||||||||
|
Rc = |
Rca Rbc |
; |
||||||
|
Rab + Rbc + Rca |
||||||||
|
R = R + R + |
Rb Rc |
, |
||||||
|
bc b c |
Ra |
|||||||
|
Rb |
= |
Rbc |
Rab |
, |
|||
|
Rab + Rbc + Rca |
|||||||
|
R = R + R + Ra Rb , |
|||||||
|
ab |
a b |
Rc |
|||||
|
R = R + R |
a |
+ |
Rc Ra |
. |
|||
|
ca |
c |
Rb |
|||||
После преобразования резисторы в схеме будут соединены последовательно-параллельно, их можно заменить одним с эквивалентным сопротивлением.
Задача1
|
Теоретические основы электротехники. Практикум |
-25- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
Вычислить |
токи в цепи, схема |
замещения |
которой |
изображена |
||||||||||
|
на рис. 1.25, |
если J =120 мА, R1 =10 кОм, R2 = 0,5 кОм, |
R3 =12 кОм, |
||||||||||||
|
R4 =1,5 кОм, |
R5 = 6 кОм. |
R2 |
||||||||||||
|
a I2 |
b |
|||||||||||||
|
I5 |
||||||||||||||
|
I |
I3 |
|||||||||||||
|
1 |
||||||||||||||
|
J |
||||||||||||||
|
R1 |
R |
R5 |
||||||||||||
|
R4 |
3 |
|||||||||||||
|
c |
I4 |
d |
||||||||||||
|
Рис. 1.25 |
||||||||||||||
|
Пояснение к решению |
||||||||||||||
|
Сначала нужно разобраться в топологии схемы. Она содержит четыре |
||||||||||||||
|
узла (a, b, c, |
d) и шесть ветвей. Направления токов в них вполне |
определенны. Ток в ветви с источником тока известен. Ток I2 = I3 + I5 = I4 . Следовательно, нужно вычислить четыре неизвестных тока.
Решение
1. Для свертывания схемы выявляем последовательные и параллельные соединения резисторов. Ветвей, содержащих более одного резистора, в схеме нет, т. е. нет последовательных соединений. Резисторы с сопротивлениями R3 и R5 соединены параллельно, заменим их одним с эквивалентным
сопротивлением:
|
R R |
12 6 10 |
6 |
||||||
|
R |
= |
3 |
5 |
= |
= 4 |
кОм. |
||
|
35 |
R3 |
+ R5 |
(12 + 6) 103 |
|||||
2. Получившаяся после этого преобразования схема изображена на рис. 1.26. В ней три ветви.
c
Рис. 1.26
|
Теоретические основы электротехники. Практикум |
-26- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
Дальнейшее преобразование схемы не требуется. Наиболее рационально вычислить ток I2 по формуле для определения тока в пассивной
параллельной ветви:
|
I2 |
= |
R1 |
J = 75 мА. |
|||
|
R1 |
+ R2 |
+ R35 + R4 |
||||
3. По первому закону Кирхгофа вычислим ток I1:
I1 = J − I2 = 45мА.
4. Возвращаемся к исходной схеме с определением оставшихся токов. Ток I2 является общим для токов I3 и I5 , поэтому
|
R |
6 |
103 |
−3 |
|||||||||
|
I3 |
= |
5 |
I2 |
= |
103 |
75 10 |
= 25 мА, |
|||||
|
R3 |
6 |
+12 |
||||||||||
|
+ R5 |
I5 = I2 − I3 = 50 мА.
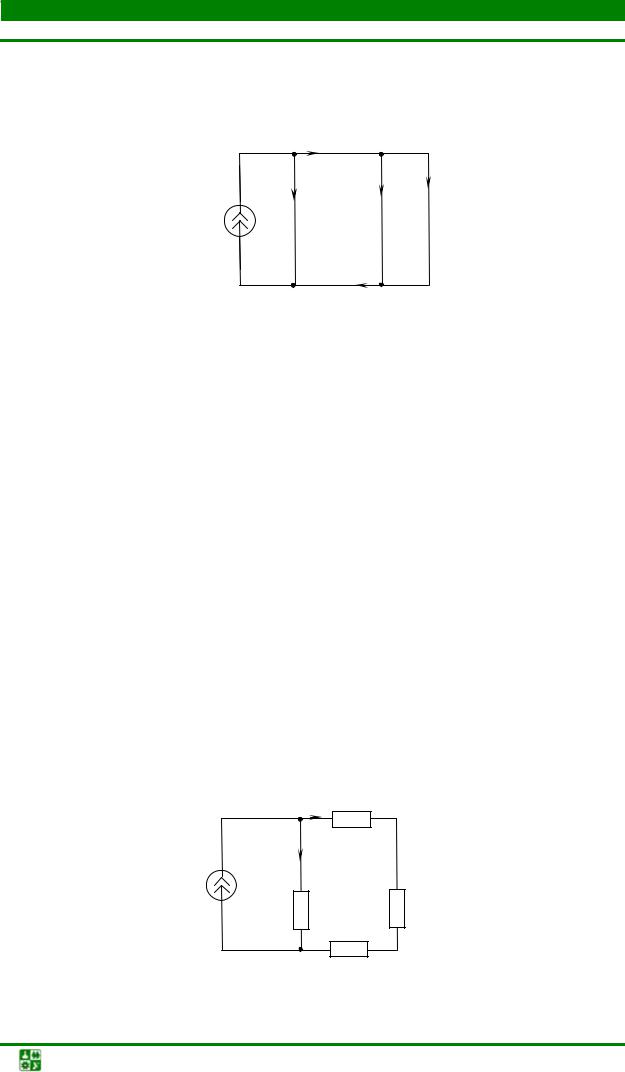
Следующую задачу решите самостоятельно.
|
Задача2 |
||
|
Вычислить напряжение |
Uab в схеме |
рис. 1.27, если J = 4 A, |
|
R1 = R4 =1 Ом, R2 = R3 = 3 Ом. |
||
|
R1 |
R |
|
|
3 |
||
|
J |
a |
b |
Uab
R2 R4
Рис. 1.27
Ответ: Uab = 4 В.
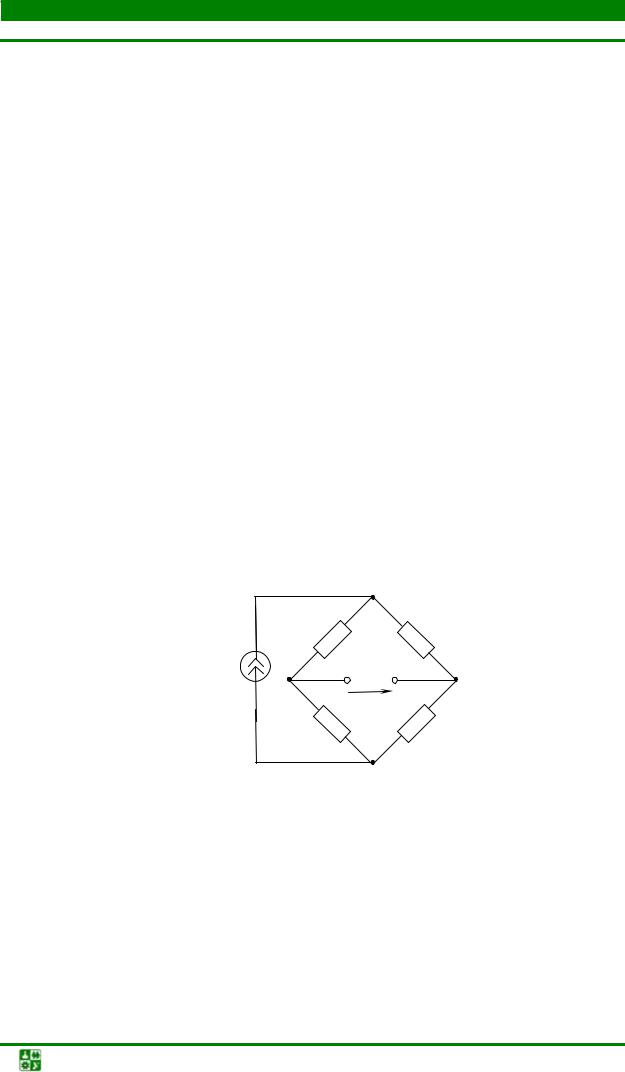
Задача3
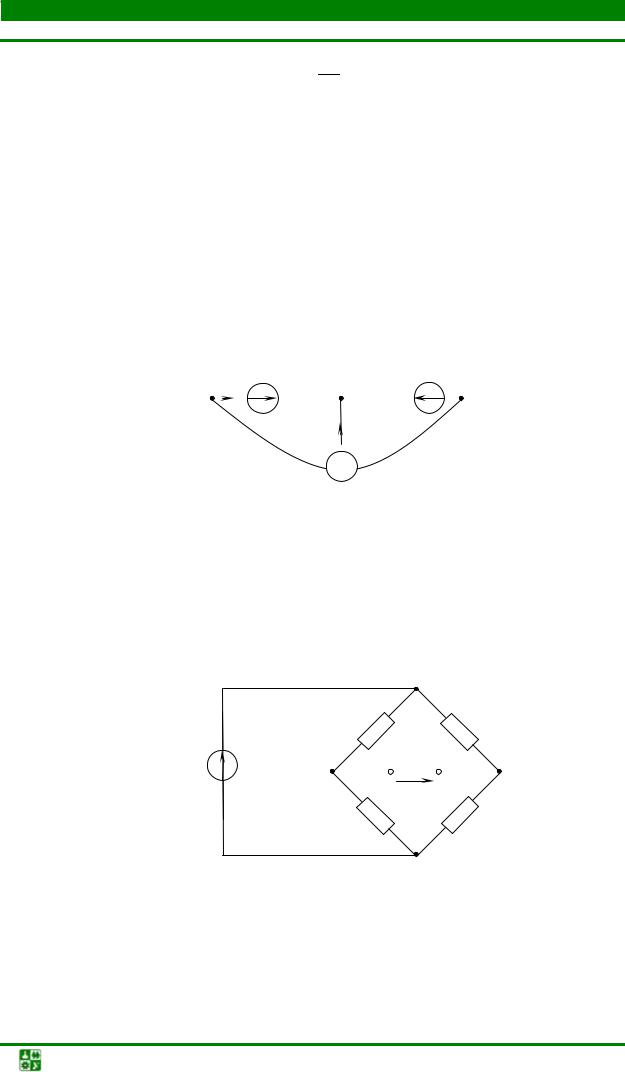
Вычислить токи в цепи, схема замещения которой представлена на
рис. 1.28, если Е = 30 В, R1 =180 Ом, R2 = 60 Ом, R3 =120 Ом, R4 = 80 Ом, R5 =120 Ом.
|
Теоретические основы электротехники. Практикум |
-27- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
I |
R1 |
A |
R2 |
|
I1 |
R3 |
I2 |
|
|
E C |
I3 |
||
|
B |
|||
|
R4 |
I4 |
R5 |
|
|
I5 |
D
Рис. 1.28
Пояснение к решению
Найдем узлы, ветви, направим токи. В этой схеме нет резисторов, которые были бы соединены между собой последовательно или параллельно. Резисторы с сопротивлениями R1, R2 и R3 соединены между собой
треугольником. К нему присоединены резисторы с сопротивлениями R4 и R5 .
Можно считать, что треугольником соединены резисторы с сопротивлениями R4 , R3 и R5 . К нему присоединены резисторы с сопротивлениями R1 и R2 .
Нередко студенты делают ошибки, полагая, что в предлагаемой схеме два треугольника. Но схема содержит только пять резисторов. Можно считать
|
соединенными звездой резисторы с сопротивлениями R1, R3 и R4 |
либо с |
|
сопротивлениями R2 , R3 и R5 . Нужно выбрать один из вариантов |
|
|
соединения. |
|
|
Решение |
|
|
1. Заменив соединенные треугольником резисторы с сопротивлениями |
|
|
R1, R2 и R3 эквивалентным соединением звездой, получим |
схему, |
|
изображенную на рис. 1.29. |
|
Теоретические основы электротехники. Практикум |
-28- |
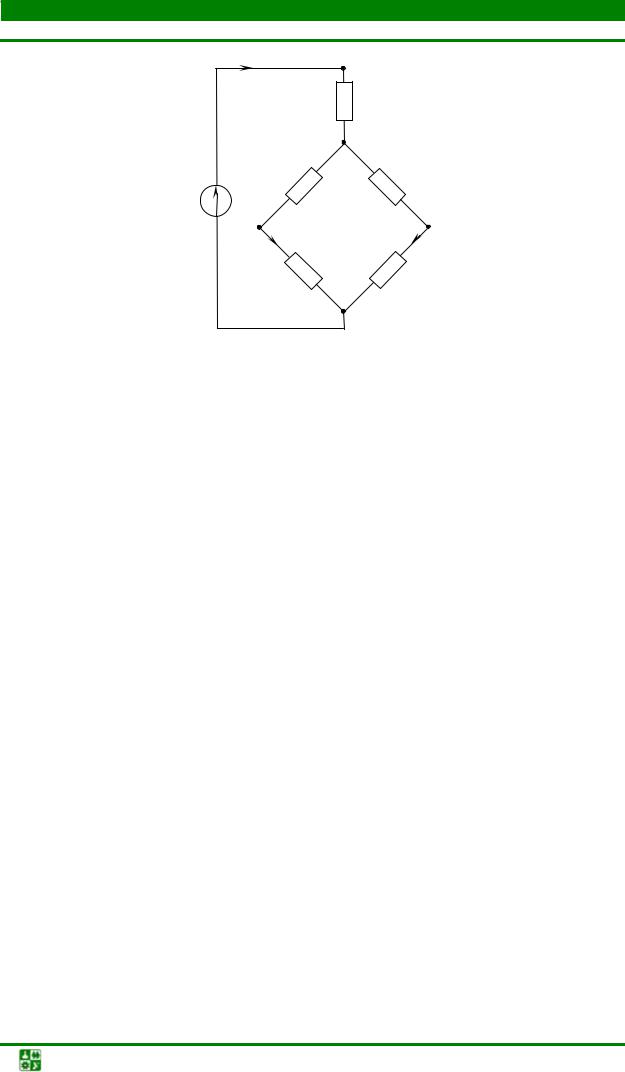
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
RC RB
E
|
C |
B |
|
|
I4 |
I5 |
|
|
R4 |
D |
R5 |
Рис. 1.29
В этой схеме два узла, соединенных между собой тремя ветвями. Так как источник ЭДС и резисторы с сопротивлениями R4 и R5 не подвергались
преобразованиям, токи в них не изменились.
В схеме рис. 1.29 резисторы соединены последовательно-параллельно, их можно заменить одним с эквивалентным сопротивлением:
|
R |
э |
= |
R |
А |
+ |
(RС + R4 ) (RB + R5 ) |
, |
|||||||||||||||
|
(R |
+ R |
4 |
+ R |
B |
+ R ) |
|||||||||||||||||
|
С |
5 |
|||||||||||||||||||||
|
где |
R |
A |
= |
R1 R2 |
= |
180 60 |
= 30 Ом, |
|||||||||||||||
|
R + R |
2 |
+ R |
180 +60 +120 |
|||||||||||||||||||
|
1 |
3 |
|||||||||||||||||||||
|
RB |
= |
R2 R3 |
= 60 120 |
= 20 |
Ом, |
|||||||||||||||||
|
R1 |
+ R2 + R3 |
|||||||||||||||||||||
|
360 |
||||||||||||||||||||||
|
R = |
R1 R3 |
= 180 120 = 60 Ом. |
||||||||||||||||||||
|
C |
R1 |
+ R2 + R3 |
360 |
|||||||||||||||||||
Тогда
Rэ = 30 + (60 +80) (20 +120)=100 Ом.
60 +80 + 20 +120
2. Вычислим ток в свернутой схеме по закону Ома:
|
Теоретические основы электротехники. Практикум |
-29- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
I = |
E |
= |
30 |
= 0,3 А. |
|
|
100 |
|||||
|
Rэ |
3. Определим токи в пассивных параллельных ветвях:
|
I4 |
= |
RB + R5 |
I = 0,15 А, |
|
|
RB + R5 |
+ RC + R4 |
|||
I5 = I − I4 = 0,15 А.
Так как сопротивления пассивных параллельных ветвей оказались одинаковыми, I4 = I5 = I/ 2, хотя сопротивления R4 и R5 не равны друг
другу.
4. Возвращаемся к исходной схеме с определением оставшихся токов.
По закону Ома ток I1 = U АС . Найдем напряжение U АС как изменение
R1
потенциала между точками А и С:
U АС = −R4I4 + E = −80 0,15 +30 =18 В.
Тогда
I1 = 18018 = 0,1 А.
5. Токи I2 и I3 можно найти по первому закону Кирхгофа. Для узла А
I − I1 − I2 = 0.
Отсюда
I2 = I − I1 = 0,2 А.
Для узла С
I1 − I3 − I4 = 0.
Отсюда
I 3 = I1 − I4 = 0,1−0,15 = −0,05 А.
Знак минус показывает, что направление тока I3 выбрано неправильно. Действительное направление тока I3 укажем пунктирной стрелкой.
Следующую задачу решите самостоятельно.
|
Теоретические основы электротехники. Практикум |
-30- |
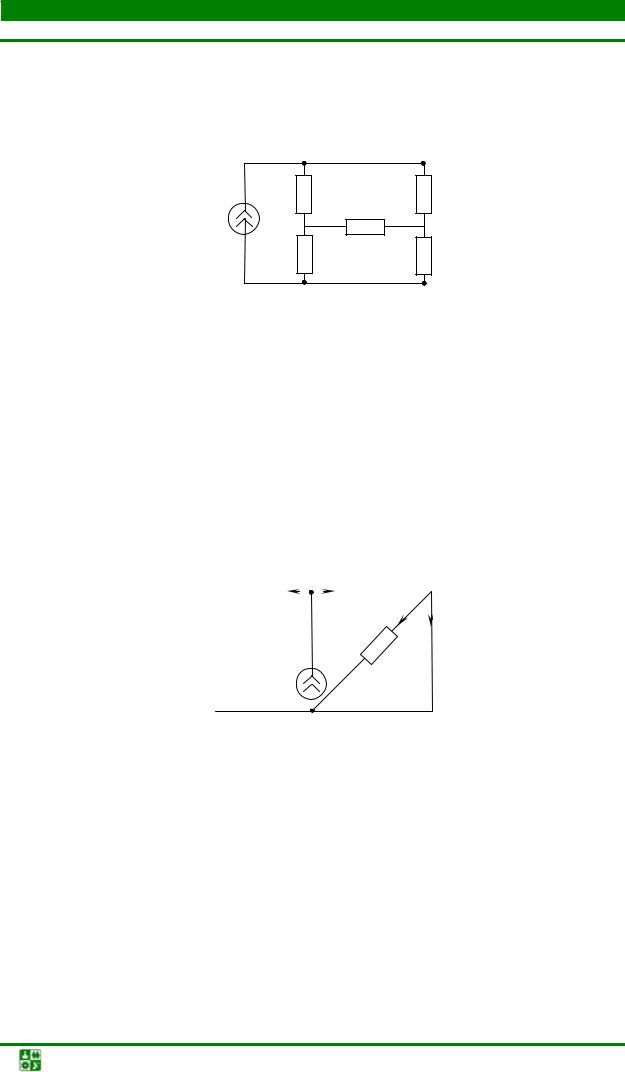
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
Задача4
Вычислить токи в схеме, представленной на рис. 1.30, если J = 5 А,
R1 = R2 = R3 = R4 = 3Ом, R5 = 5 Ом.
|
R1 |
R3 |
R |
|
J |
2 |
|
|
R4 |
R5 |
|
|
Рис. 1.30 |
Ответ:I1 = 2,67 А, I2 = 2,33 А, I3 = 0,33 А, I4 = 3 А, I5 = 2 А. Для самоконтроля решите задачи 5 и 6.
Задача5
Вычислить все токи в схеме, представленной на рис. 1.31, если J = 2
А, R5 = 20Ом, R1 = R2 = R3 = R4 = R6 = R7 = =10 Ом.
|
R2 |
I2 |
I4 |
R4 |
||||||||||||
|
I5 |
I6 |
||||||||||||||
|
R |
R5 |
||||||||||||||
|
1 |
|||||||||||||||
|
R3 |
R6 |
||||||||||||||
|
J |
|||||||||||||||
|
R7 |
|||||||||||||||
|
Рис. 1.31 |
|||||||||||||||
|
Ответ: I2 =1А, I4 =1А, I5 = 0,5 A, I6 |
= 0,5 А. |
||||||||||||||
|
Задача6 |
Рассчитать все токи в схеме, представленной на рис.1.32, если Е = 12
В, R = 3 Ом.
|
Теоретические основы электротехники. Практикум |
-31- |
Входное и выходное сопротивление является очень важным в электронике.
Предисловие
Ладно, начнем издалека… Как вы знаете, все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и тд. В нашей статье будем использовать понятие «блок». Например, источник питания, собранный по этой схеме:
состоит из двух блоков. Я их пометил в красном и зеленом прямоугольниках.

В красном блоке мы получаем постоянное напряжение, а в зеленом блоке мы его стабилизируем. То есть блочная схема будет такой:
Блочная схема — это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод «от простого к сложному» полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем — готовое устройство, например, телевизор.
Ладно, что-то отвлеклись. Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.
— Ага! Так что же получается? Я могу просто тупо взять готовые блоки и изобрести любое электронное устройство, которое мне придет в голову?
Да! Именно на это нацелена сейчас современная электроника 😉 Микроконтроллеры и конструкторы, типа Arduino, добавляют еще больше гибкости в творческие начинания молодых изобретателей.
На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.
Думаю, все помнят, что такое сопротивление и что такое резистор. Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением. Но что такое входное и выходное сопротивление? Это уже что-то новенькое. Если прислушаться к этим фразам, то входное сопротивление — это сопротивление какого-то входа, а выходное — сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот «прячутся» они в самих блоках радиоэлектронных устройств.
Входное сопротивление
Итак, имеем какой-либо блок. Как принято во всем мире, слева — это вход блока, справа — выход.
Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение Uвх от другого блока или от источника питания, а на его выходе появится напряжение Uвых (или не появится, если блок является конечным).
Но раз уж мы подаем напряжение на вход (входное напряжение Uвх), следовательно, у нас этот блок будет кушать какую-то силу тока Iвх.
Теперь самое интересное… От чего зависит Iвх ? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи :

Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от… СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.
То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет). Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока. Скажем так, совокупное сопротивление.
Как измерить входное сопротивление
Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?
1)Замерить напряжение Uвх, подаваемое на этот блок
2)Замерить силу тока Iвх, которую потребляет наш блок
3) По закону Ома найти входное сопротивление Rвх.

Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.
Мы с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).
Падение напряжения на резисторе R обозначим, как UR




Из всего этого получаем…

Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!
Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление Rвх=1 МегаОм, а резистор взяли R=1 КилоОм. Пусть генератор выдает постоянное напряжение U=10 Вольт. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.
В результате получается цепь:
Высчитываем силу тока в цепи в Амперах

Получается, что падение напряжения на сопротивлении R в Вольтах будет:

Грубо говоря 0,01 Вольт. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем китайском мультиметре.
Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также очень большого номинала. В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.
Измерение входного сопротивления на практике
Ну все, запарка прошла ;-). Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Мой взгляд сразу упал на Транзистор-метр. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 Вольт, и во включенном состоянии замеряем потребляемую силу тока. Как замерить силу тока в цепи, читаем в этой статье. По схеме все это будет выглядеть вот так:
А на деле вот так:
Итак, у нас получилось 22,5 миллиАмпер.
Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:

Получаем:

Выходное сопротивление
Яркий пример выходного сопротивления — это закон Ома для полной цепи, в котором есть так называемое «внутреннее сопротивление». Кому лень читать про этот закон, вкратце рассмотрим его здесь.
Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогенную лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:
И как только подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.
Разница напряжения, то есть 0,3 Вольта (12,09-11,79) у нас падало на так называемом внутреннем сопротивлении r 😉 Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.
У всех аккумуляторов есть это внутреннее сопротивление r, и «цепляется» оно последовательно с источником ЭДС (Е).
Но только ли аккумуляторы и различные батарейки обладают выходным сопротивлением? Не только. Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.
В теореме Тевенина (короче, умный мужик такой был) говорилось, что любую цепь, которая имеет две клеммы и содержит в себе туеву кучу различных источников ЭДС и резисторов разного номинала можно привести тупо к источнику ЭДС с каким-то значением напряжения (Eэквивалентное) и с каким-то внутренним сопротивлением (Rэквивалентное).
Eэкв — эквивалентный источник ЭДС
Rэкв — эквивалентное сопротивление
То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.
В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС (E). С замером ЭДС вроде бы понятно, но вот как замерить Rвых ?
В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания Iкз.
В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что

Но есть небольшая загвоздка. Теоретически — формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешеного значения, да вообще, вся схема ведет себя неадекватно.
Измерение выходного сопротивления на практике
Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогенную лампочку, которая была нагрузкой R. В результате по цепи шел электрический ток. На лампочке и на внутреннем сопротивлении у нас падало напряжение, сумма которых равнялась ЭДС.
Итак, для начала замеряем напряжение на аккумуляторе без лампочки.
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем резисторе падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r:


Заключение
Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль. В этом мы убедимся, когда начнем рассматривать статью по согласованию узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.
С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе. Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе «не проседало» при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается автоматически.
