Как найти вид плотности вероятности случайной величины

Как найти вид плотности вероятности случайной величины

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 августа 2021 года; проверки требуют 7 правок.

Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются[источник не указан 1058 дней] и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).

Прикладное описание понятия[править | править код]

Плотность распределения одномерной непрерывной случайной величины xi — это числовая функция f(x), отношение {displaystyle f(x_{1})/f(x_{2})} значений которой в точках x_{1} и x_{2} задаёт отношение вероятностей попаданий величины xi в узкие интервалы равной ширины {displaystyle [x_{1},x_{1}+Delta x]} и {displaystyle [x_{2},x_{2}+Delta x]} вблизи данных точек.

Плотность распределения неотрицательна при любом x и нормирована, то есть

{displaystyle int _{-infty }^{+infty }f(x),{mbox{d}}x=1}

При стремлении x к {displaystyle ,pm infty } функция f(x) стремится к нулю. Размерность плотности распределения всегда обратная к размерности случайной величины — если xi исчисляется в метрах, то размерностью f будет м-1.

Если в конкретной ситуации известно выражение для f(x), с его помощью можно вычислить вероятность попадания величины xi в интервал [a,b] как

{displaystyle P(xi in [a,b])=int _{a}^{b}f(x),{mbox{d}}x}.

Зная плотность вероятности, можно также определить наиболее вероятное значение (моду) случайной величины как максимум f(x).
Также с помощью плотности вероятности находится среднее значение случайной величины:

{displaystyle Exi =int _{-infty }^{+infty }xf(x),{mbox{d}}x}

и среднее значение измеримой функции {displaystyle g(xi )} случайной величины:

{displaystyle langle g(xi )rangle =int _{-infty }^{+infty }g(x)f(x),{mbox{d}}x}.

Чтобы перейти к плотности распределения {displaystyle {f}_{chi }(y)} другой случайной величины {displaystyle chi =z(xi )}, нужно взять

{displaystyle {f}_{chi }(y)=f(z^{-1}(y))cdot left|{frac {{mbox{d}}z^{-1}(y)}{{mbox{d}}y}}right|},

где {displaystyle z^{-1}(y)} — обратная функция по отношению к {displaystyle y=z(x)} (предполагается, что z — взаимно однозначное отображение).

Значение плотности распределения f(x_{1}) не является вероятностью принять случайной величиной значение x_{1}. Так, вероятность принятия непрерывной случайной величиной xi значения x_{1} равна нулю. При непрерывном распределении случайной величины xi вопрос может ставиться о вероятности её попадания в некий диапазон, а не о вероятности реализации её конкретного значения.

Интеграл

{displaystyle int _{-infty }^{x}f(t),{mbox{d}}t=F(x)}

называют функцией распределения (соответственно, плотность распределения вероятности — это производная функции распределения). Функция F является неубывающей и изменяется от 0 при {displaystyle xto -infty } до 1 при xto +infty .

Самым простым распределением является равномерное распределение на отрезке [a,b]. Для него плотность вероятности равна:

{displaystyle f(x)=left{{begin{matrix}{1 over b-a},&xin [a,b]\0,&xnot in [a,b]end{matrix}}right..}

Широко известным распределением является «нормальное», оно же гауссово, плотность которого записывается как

{displaystyle f(x)={frac {1}{{sqrt {2pi }}sigma }}exp left[-{frac {(x-mu )^{2}}{2sigma ^{2}}}right]},

где mu и sigma — параметры: математическое ожидание и среднеквадратичное отклонение. Другие примеры плотностей распределения — одностороннее лапласовское (lambda >0):

{displaystyle f(x)=Aexp left[-lambda ,xright],,(xgeq 0)} и {displaystyle f(x)=0,,(x<0)},

и максвелловское ({displaystyle alpha >0}):

{displaystyle f(x)=Ax^{2}exp left[-alpha x^{2}right],,(xgeq 0)} и {displaystyle f(x)=0,,(x<0)}.

В двух последних примерах множитель A подбирается в зависимости от параметра lambda или alpha так, чтобы обеспечить нормировку интеграла от плотности вероятности. В случае распределения Лапласа оказывается, что {displaystyle A=lambda }.

Как названные, так и другие распределения широко применяются в физике. Например, в случае распределения Максвелла роль случайной величины обычно играет абсолютная величина скорости молекулы в идеальном газе. При этом для аргумента функции f нередко используют тот же символ, что и для рассматриваемой в физической задаче случайной величины (как если бы выше на месте xi всюду стояло x). Так, в выражении максвелловской плотности распределения пишут не формальную переменную x, а символ скорости v. В простейших ситуациях такая вольность с обозначениями не приводит к недоразумениям.

Спадающий при стремлении аргумента к +infty или -infty участок графика плотности вероятности f(x) в областях, где {displaystyle fll f_{max}}, называется хвостом. Из упомянутых распределений, нормальное и лапласовское имеют по два хвоста (слева и справа), а максвелловское в выписанном виде — один (справа).

Выше была изложена суть понятия «плотность вероятности». Однако, такое изложение не является строгим — плотность f нередко является функцией нескольких величин, в рассуждениях неявно предполагались не всегда гарантируемые непрерывность и дифференцируемость функций и так далее.

Определение плотности вероятности в теории меры[править | править код]

Плотность вероятности можно рассматривать как один из способов задания вероятностной меры на евклидовом пространстве mathbb {R} ^{n}.
Пусть mathbb {P} является вероятностной мерой на mathbb {R} ^{n}, то есть определено вероятностное пространство left(mathbb{R}^n,mathcal{B}(mathbb{R}^n),mathbb{P}right), где mathcal{B}(mathbb{R}^n) обозначает борелевскую σ-алгебру на mathbb {R} ^{n}. Пусть m обозначает меру Лебега на mathbb {R} ^{n}.
Вероятность mathbb {P} называется абсолютно непрерывной (относительно меры Лебега) (mathbb{P} ll m), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

forall B in mathcal{B}(mathbb{R}^n),; ( m(B) = 0 ) Rightarrow ( mathbb{P}(B) = 0 ) .

Если вероятность mathbb {P} абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция fcolonmathbb{R}^n to [0,infty) такая, что

mathbb{P}(B) = intlimits_{B} f(x), dx,

где использовано общепринятое сокращение m(dx) equiv dx, и интеграл понимается в смысле Лебега.

В более общем виде, пусть (X, mathcal F) — произвольное измеримое пространство, а mu и nu  — две меры на этом пространстве. Если найдется неотрицательная f, позволяющая выразить меру nu через меру mu в виде

nu(A) = int_A f dmu,

то такую функцию называют плотностью меры nu по мере mu , или производной Радона-Никодима меры nu относительно меры mu , и обозначают

f=frac{dnu}{dmu}.

Плотность случайной величины[править | править код]

Пусть определено произвольное вероятностное пространство (Omega ,{mathcal {F}},mathbb {P} ), и Xcolon Omega to mathbb {R} ^{n} случайная величина (или случайный вектор). X индуцирует вероятностную меру mathbb {P} ^{X} на left(mathbb{R}^n,mathcal{B}(mathbb{R}^n)right), называемую распределением случайной величины X.

Если распределение mathbb {P} ^{X} абсолютно непрерывно относительно меры Лебега, то его плотность f_X = frac{dmathbb{P}^X}{dx} называется плотностью случайной величины X. Сама случайная величина X называется абсолютно непрерывной.

Таким образом для абсолютно непрерывной случайной величины имеем:

mathbb{P}(X in B) = intlimits_{B} f_X(x), dx.

Замечания[править | править код]

  • Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.
  • Функция распределения абсолютно непрерывной случайной величины X непрерывна и может быть выражена через плотность следующим образом:
F_X(x_1,ldots, x_n) = mathbb{P}left(X in prodlimits_{i=1}^n (-infty,x_i]right) = intlimits_{-infty}^{x_n} !! ldots !! intlimits_{-infty}^{x_1} f_X(x'_1,ldots, x'_n), dx'_1ldots dx'_n.

В одномерном случае:

F_X(x) = intlimits_{-infty}^x f_X(x'), dx'.

Если f_X in C(mathbb{R}^n), то F_X in mathcal{D}(mathbb{R}^n), и

frac{partial^n}{partial x_1 ldots partial x_n} F_X(x_1,ldots, x_n) = f_X(x_1,ldots, x_n).

В одномерном случае:

frac{d}{dx} F_X(x) = f_X(x).
  • Математическое ожидание функции от абсолютно непрерывной случайной величины может быть записано в виде:
mathbb{E}[g(X)] = intlimits_{mathbb{R}^n} g(x) , mathbb{P}^X(dx) = intlimits_{mathbb{R}^n} g(x), f_X(x), dx,

где gcolon mathbb{R}^n to mathbb{R} — борелевская функция, так что mathbb{E}[g(X)] определено и конечно.

Плотность преобразования случайной величины[править | править код]

Пусть Xcolon Omega to mathbb {R} ^{n} — абсолютно непрерывная случайная величина, и gcolonmathbb{R}^n to mathbb{R}^n — инъективная непрерывно дифференцируемая функция такая, что J_g(x) not=0,; forall xin mathbb{R}^n, где J_g(x) — якобиан функции g в точке x. Тогда случайная величина Y = g(X) также абсолютно непрерывна, и её плотность имеет вид:

f_Y(y) = f_Xleft(g^{-1}(y)right) vert J_{g^{-1}}(y) vert.

В одномерном случае:

f_Y(y) = f_Xleft(g^{-1}(y)right) leftvert frac{dg^{-1}}{dy}(y)rightvert.

Свойства плотности вероятности[править | править код]

  • Интеграл от плотности по всему пространству равен единице:
mathbb{P}left(mathbb{R}^nright) = intlimits_{mathbb{R}^n} f(x), dx = 1.

Обратно, если f(x) — неотрицательная почти всюду функция, такая что intlimits_{mathbb{R}^n}f(x), dx = 1, то существует абсолютно непрерывная вероятностная мера mathbb {P} на mathbb {R} ^{n} такая, что f(x) является её плотностью.

  • Замена меры в интеграле Лебега:
intlimits_{mathbb{R}^n} varphi(x), mathbb{P}(dx) = intlimits_{mathbb{R}^n}varphi(x), f(x), dx,

где {displaystyle varphi ::mathbb {R} ^{n}to mathbb {R} } любая борелевская функция, интегрируемая относительно вероятностной меры {displaystyle {}mathbb {P} }.

Примеры абсолютно непрерывных распределений[править | править код]

  • Бета-распределение
  • Гамма-распределение
  • Гиперэкспоненциальное распределение
  • Двумерное нормальное распределение
  • Логнормальное распределение
  • Многомерное нормальное распределение
  • Непрерывное равномерное распределение
  • Нормальное распределение
  • Обобщённое гиперболическое распределение
  • Полукруговой закон Вигнера
  • Распределение variance-gamma
  • Распределение Вейбулла
  • Распределение Гомпертца
  • Распределение Колмогорова
  • Распределение копулы
  • Распределение Коши
  • Распределение Лапласа
  • Распределение Накагами
  • Распределение Парето
  • Распределение Пирсона
  • Распределение Райса
  • Распределение Рэлея
  • Распределение Стьюдента
  • Распределение Трейси — Видома
  • Распределение Фишера
  • Распределение хи-квадрат
  • Частотное распределение
  • Экспоненциальное распределение

См. также[править | править код]

  • Распределение вероятностей
  • Сингулярное распределение
  • Функция вероятности

Литература[править | править код]

  • Плотность вероятности // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
Источник

Непрерывная
случайная величина может быть задана
не только с помощью функции распределения.
Введем понятие плотности
вероятности
непрерывной случайной величины.

Рассмотрим
вероятность попадания непрерывной
случайной величины на интервал [х,
х
+ Δх].
Вероятность такого события

P(х
≤ X
≤ х
+ Δх)
= F(х+
Δх)
– F(х),

т.е.
равна приращению функции распределения
F(х)
на этом участке. Тогда вероятность,
приходящаяся на единицу длины, т.е.
средняя плотность вероятности на участке
от х
до х+
Δх,
равна

.

Переходя к пределу
Δх
→ 0, получим плотность вероятности в
точке х:

,

представляющую
производную функции распределения
F(х).
Напомним, что для непрерывной случайной
величины F(х)
– дифференцируемая функция.

Определение.
Плотностью
вероятности
(плотностью
распределения)
f(x)
непрерывной
случайной величины Х называется
производная ее функции распределения

f(x)
= F′(x).

(4.8)

Про случайную
величину Х
говорят, что она имеет распределение с
плотностью f(x)
на определенном участке оси абсцисс.

Плотность вероятности
f(x),
как и функция распределения F(x)
является одной из форм закона распределения.
Но в отличие от функции распределения
она существует только для непрерывных
случайных величин.

Плотность вероятности
иногда называют дифференциальной
функцией
или дифференциальным
законом распределения.
График плотности вероятности называется
кривой
распределения.

Пример 4.4.
По данным примера 4.3 найти плотность
вероятности случайной величины Х.

Решение.
Будем находить плотность вероятности
случайной величины как производную от
ее функции распределения f(x)
= F‘(x).

◄

Отметим свойства
плотности вероятности непрерывной
случайной величины.

1.
Плотность
вероятности – неотрицательная функция,
т.е.

f(x)
≥ 0,

(4.9)

как
производная монотонно неубывающей
функции F(x).

2.
Вероятность
попадания непрерывной случайной величины
Х в интервал [α,
β,]
равна
определенному интегралу от ее плотности
вероятности в пределах от α
до β,
т.е.

(4.10)

Геометрически
вероятность попадания в интервал [α,
β,]
равна площади фигуры, ограниченной
сверху кривой распределения и опирающейся
на отрезок [α,
β,]
(рис.4.4).

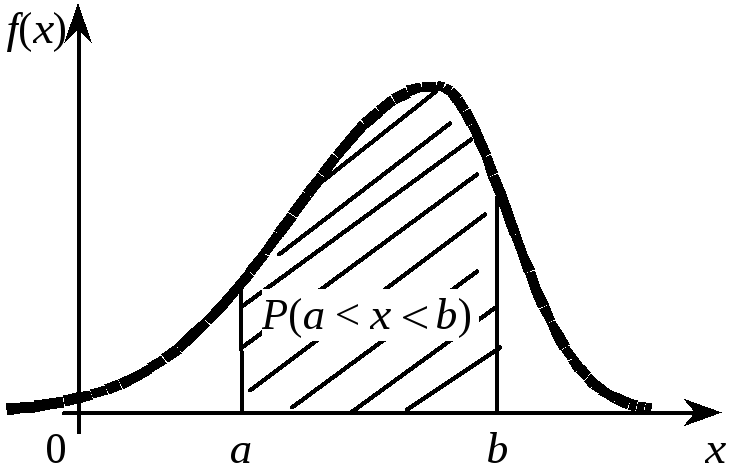
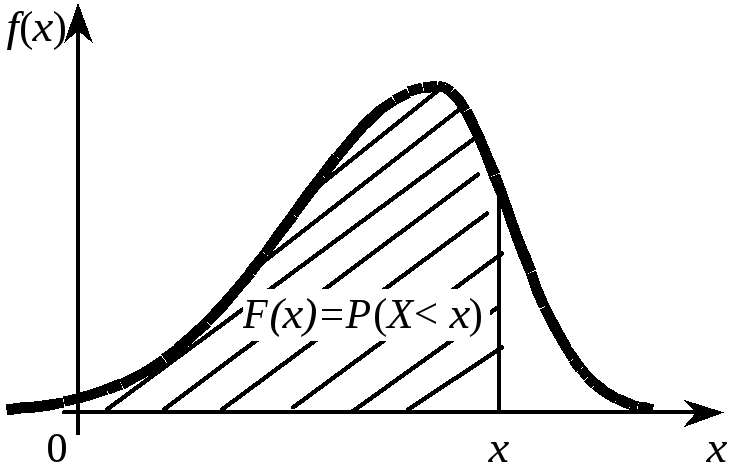
Рис. 4.4 Рис.
4.5

3.
Функция
распределения непрерывной случайной
величины может быть выражен через
плотность вероятности по формуле:

.

(4.11)

Геометрически
функция распределения равна площади
фигуры, ограниченной сверху кривой
распределения и лежащей левее точки х
(рис. 4.5).

4.
Несобственный
интеграл в бесконечных пределах от
плотности вероятности непрерывной
случайной величины равен единице:

.

(4.12)

Геометрически
свойства 1
и 4
плотности вероятности означают, что ее
график – кривая распределения – лежит
не ниже оси абсцисс, а полная площадь
фигуры, ограниченной кривой распределения
и осью абсцисс, равна единице.

Пример 4.5.
Функция f(x)
задана в виде:

Найти: а) значение
А;
б) выражение функции распределения
F(х);
в) вероятность того, что случайная
величина Х
примет значение на отрезке [0; 1].

Решение.
а) Для того, чтобы f(x)
была плотностью вероятности некоторой
случайной величины Х,
она должна быть неотрицательна,
следовательно, неотрицательным должно
быть и значение А.
С учетом свойства 4
находим:

,
откуда А
=
.

б) Функцию
распределения находим, используя
свойство 3:

Если x
≤ 0, то f(x)
= 0 и, следовательно, F(x)
= 0.

Если 0 < x
≤ 2, то f(x)
= х/2
и, следовательно,

.

Если х
> 2, то f(x)
= 0 и, следовательно

.

в) Вероятность
того, что случайная величина Х
примет значение на отрезке [0; 1] находим,
используя свойство 2:

=
0,25. ◄

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Определение плотности распределения

Автор статьи

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Как нам уже известно, случайную величину можно задавать с помощью таблицы или с помощью функции распределения вероятности. Предположим теперь, что случайная величина $X$ является непрерывной, а функция распределения вероятности $F(x)$ непрерывна и дифференцируема в своей области определения. Тогда для такой случайной величины существует еще один способ её задания — задания с помощью плотности распределения.

Определение 1

Плотностью распределения $varphi (x)$ непрерыной случайной величины называется первая производная от функции распределения вероятности $F(x)$.

Примечание 1

!!! Подчеркнем, что данное понятие не применимо к дискретной случайной величине.

Геометрически, плотность распределения связана с функцией распределения вероятностей следующим образом: площадь криволинейной трапеции, ограниченной графиком плотности распределения и находящейся по левую сторону от величины $x$ и есть функция распределения вероятности (рис. 1).

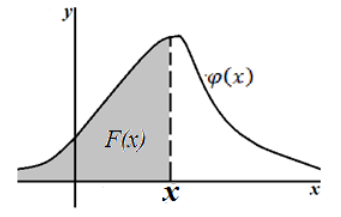
Связь функций $varphi (x)$ и $F(x)$.

Рисунок 1. Связь функций $varphi (x)$ и $F(x)$.

То есть:

Геометрический смысл: вероятность попадания непрерывной случайной величины в интервал $(alpha ,beta )$ равна площади криволинейной трапеции, ограниченной графиком функции распределения $varphi left(xright)$ и прямыми $x=alpha ,$ $x=beta $ и $y=0$ (рис. 2).

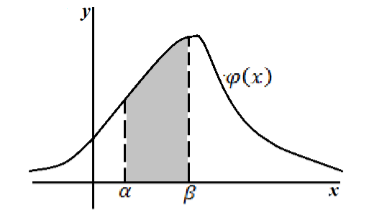
Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал $(alpha ,beta )$.

Рисунок 2. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал $(alpha ,beta )$.

«Определение плотности распределения» 👇

Примеры задач на понятие плотности распределения

Пример 1

Пусть функция распределения $F(x)$ случайной величины $X$ имеет следующий вид:

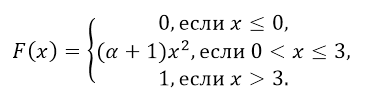
Рисунок 3.

а) Найти значение $alpha $.

б) Найти плотность распределения $varphi left(xright)$.

в) Построить график плотности распределения.

г) Найти вероятность попадания случайной величины в интервал $left(1,2right)$

Решение:

а) Так как необходимо найти плотность распределения, то случайная величина $X$ является непрерывной.

Тогда, при $x=3$, получим, что $(alpha +1)x^2=1$, то есть

[9alpha +9=1,] [9alpha =-8,] [alpha =-frac{8}{9}.]

То есть:

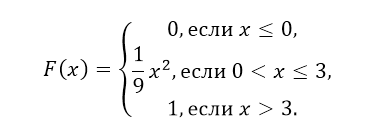
Рисунок 4.

б) Так как $varphi (x)$ = $F'(x)$, то получим:

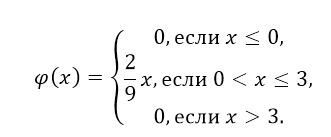
Рисунок 5.

в) Построим график функции $varphi left(xright)$.

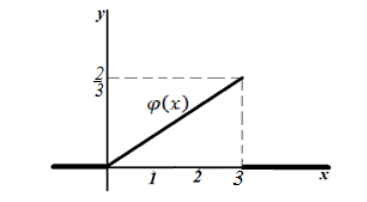
Рисунок 6.

г) Воспользовавшись геометрическим смыслом функции плотности распределения получим, что нам нужно найти площадь криволинейной трапеции, ограниченной функцией $y=frac{2}{9}x$ и прямыми $x=1,$ $x=2$ и $y=0$.

Таким образом, получим:

[Pleft(1

Пример 2

Найти функцию распределения непрерывной случайной величины и построить её график, если плотность распределения имеет вид:

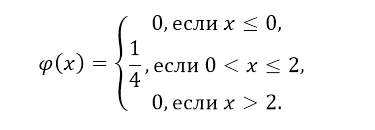
Рисунок 7.

Решение.

При решении будем использовать следующую формулу: $Fleft(xright)=intlimits^x_{-infty }{varphi (x)dx}$

begin{enumerate}
item При $xle 0$, по формуле, получим:

[Fleft(xright)=intlimits^x_{-infty }{varphi (x)dx}=intlimits^x_{-infty }{0dx}=0]

item При $0
[Fleft(xright)=intlimits^x_{-infty }{varphi (x)}=intlimits^0_{-infty }{0dx}+intlimits^x_0{frac{dx}{4}}=0+frac{x}{4}-0=frac{x}{4}]

item При $x>2$, по формуле, получим:

[Fleft(xright)=intlimits^x_{-infty }{varphi (x)}=intlimits^0_{-infty }{0dx}+intlimits^2_0{frac{dx}{4}}+intlimits^x_2{0dx}=0+frac{1}{2}-0+0=frac{1}{2}]

end{enumerate}

Таким образом, функция распределения имеет вид:

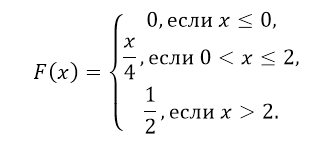
Рисунок 8.

Построим её график.

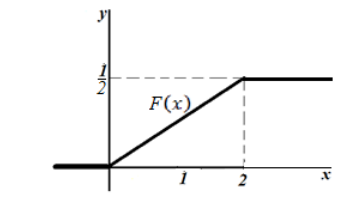
Рисунок 9.

Примечание 2

!!! Заметим, что, так как дана плотность распределения, то случайная величина является непрерывной. Следовательно, функция $F(x)$ также должна быть непрерывной (как и получилось в нашем примере). Это может служить косвенной проверкой правильности решения такого рода задач.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 20.02.2023

Источник

Добавить комментарий