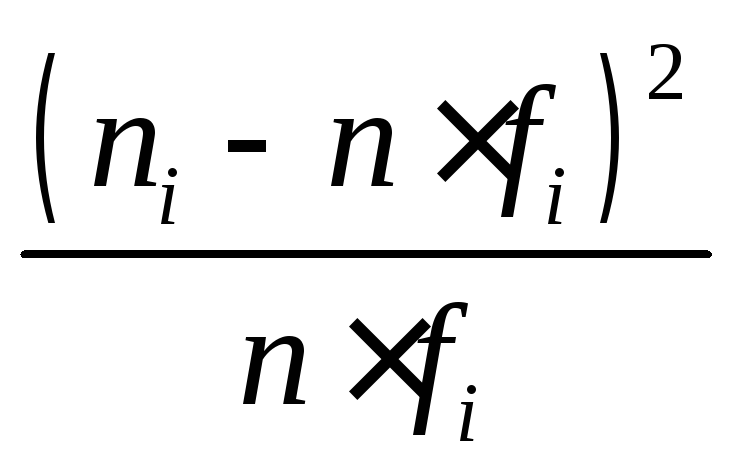Как найти вид распределения – Сайт, где вы сможете решить свои вопросы

Часто вопрос стоит следующим образом. Есть экспериментальные данные, и хочется понять, можно ли описывать как случайную величину с некоторым типом распределения (чаще всего нормальным). Как в такой ситуации поступать?

Есть очевидный путь — построить гистограмму распределения и сравнить ее с кривой нормального распределения. Какая возникает при этом проблема? Мы пытаемся подобрать адекватную модель для описания процесса. Отличие от подобных ситуаций с моделями другого типа состоит в том, что модель — случайная. Мы заведомо принимаем, что она может давать разные результаты при одних и тех же входных параметрах.

Если мы работаем с физическим объектом, мы говорим о том, что у него есть физические свойства и параметры — масса, теплоемкость и т.п. Эти параметры мы можем чаще всего напрямую измерить. Теперь же мы отказываемся от описания объекта как физического объекта. Мы говорим, что да, то, что происходит, определяется физическими процессами. То же образование трещин, например — физический процесс. Но процесс настолько сложный, что описание его как физического, становится нецелесообразным. Например, из-за того, что слишком много параметров определяют его ход, и мы не можем их контролировать. Эти рассуждения могут показаться банальными, когда мы говорим о погрешности, но иногда этот переход дается тяжело. Можно вспомнить наш разговор о моделировании погодных явлений — люди долго шли к тому, чтобы встроить в модели случайность и начать говорить о результатах расчета на языке теории вероятностей.

Модель случайной величины — это тоже модель, у нее есть свои законы: они описываются в теории вероятностей. У нее есть свои параметры — тип распределения, математическое ожидание, дисперсия. Но эти параметры мы не можем измерить напрямую, ведь при одних и тех же входных параметрах мы получаем разные результаты. А для работы с моделью эти параметры нужны.

Рассмотрим, например, нормальное распределение. Случайная величина, описывающаяся данным типом распределения, может принимать любые значения — от минус бесконечности до плюс бесконечности вне зависимости от того, каковы параметры распределения. Как же в такой ситуации измерить эти параметры? Идея следующая. Мы выдвигаем гипотезу — берем фиксированные тип распределения, математическое ожидание и дисперсию и пытаемся понять, насколько результаты измерений адекватны нашей гипотезе. Весь вопрос в том, как на количественный язык перевести понятие адекватности.

Рис. 1. Мы выдвинули гипотезу о том, что процесс можно описать как случайную величину с µ=10 и σ²=1. Результат B явно более адекватен гипотезе, чем результат A, но как охарактеризовать эту «адекватность» количественно?

Посмотрим на рис. 1 – здесь мы выдвинули гипотезу о нормальном распределении с мат. Ожиданием µ=10 и дисперсией σ²=1. Показаны два результата измерений: A=9 и B=6. Интуитивно мы понимаем, что для результата A гипотеза выглядит более-менее правдоподобной, а вот для результата B – нет. Результат B находится далеко от основной части колокола. Как количественно описать эту разницу?

Какие вообще количественные ответы дает модель случайной величины? Вероятности тех или иных событий. Возможно, стоит оценить вероятность событий «мы получили результат A» и «мы получили результат B» P({X=A}) и P({X=B}). К сожалению, различий мы не получим – вероятность получить любое конкретное значение равна нулю, поскольку мы имеем дело с непрерывной случайной величиной.

Тогда мы делаем следующий ход. Вместо события «мы получили результат A» мы рассмотрим событие «мы получили результат, отклоняющийся от мат.ождания не меньше, чем A». На языке математики это можно записать так: мы перейдем от P({X=A}) к P({|X-µ|>|A-µ|}), где X – случайная величина. Соответственно, эту вероятность мы будем сравнивать с P({|X-µ|>|B-µ|}). Эти вероятности уже конечны, и сильно отличаются: P({|X-µ|>|B-µ|}) > P({|X-µ|>|A-µ|}) (рис. 2).

Рис. 2. Мы будем сравнивать вероятности событий «мы получили результат, отклоняющийся от математического ожидания не меньше, чем A» и «мы получили результат, отклоняющийся от математического ожидания не меньше, чем B».

Если стоит задача оценить правдоподобность гипотезы для конкретного результата измерений A, можно сравнить вероятность события P({|X-µ|>|A-µ|}) (будем называть далее ее просто «тестовой вероятностью») с некоторым пороговым уровнем вероятности P₀ (его называют «уровнем значимости»). Часто берут P₀=0.05.

Следует иметь в виду, что часто рассматривают вероятность противоположного события P({|X-µ|<|A-µ|}). Тогда проверяют условие P({|X-µ|<|A-µ|}) < P₁, а характерное используемое значение P₁=1-P₀ (например, P₁=0.95).

На практике обычно мы имеем дело с ситуацией, когда есть не одно измерение, а набор [A₁, A₂, … , A_n]. Та же идея распространяется и на этот случай. Диапазон, в который попали измерения, делится на m частей, затем строится гистограмма [G₁,…,G_m], где G_j – число измерений, в который результат попал в j-й диапазон, деленное на число измерений n и на величину j-го диапазона (деление необходимо, чтобы получить плотность вероятности). Далее мы определяем степень отклонения гистограммы от гипотетической кривой T(x), соответствующей предполагаемому распределению (рис. 3):

В результате для набора измерений мы получили скалярную величину W – количественную характеристику отклонения от предполагаемого распределения. Далее вычисляется вероятность получить такое или большее отклонение.

Рис. 3. Гистограмма, построенная по выборке данных и ее сравнение с кривой нормального распределения.

На этом этапе возникает ряд вопросов к деталям алгоритма, в частности — как выбрать дискретные диапазоны, на базе которых строится гистограмма. Подходы к решению этих вопросов описаны в литературе — например, по теме «t-критерия Стьюдента». Здесь мы ограничимся описанием идеи метода. В Matlab он реализован в функции chi2gof.

Из приведенного описания ясно, что при проверке гипотезы нет цели получить вероятность, близкую к 100%. Однако слишком малые значения «тестовой вероятности» будут сигнализировать о том, что скорее всего, гипотеза неадекватна. Если мы получили «тестовую вероятность», например, 0.1%, это можно трактовать следующим образом – «приняв рассматриваемую статистическую гипотезу, в принципе, такой результат измерений можно было получить, однако настолько отклоняющиеся от наиболее ожидаемых результаты попадаются только в одном опыте из 1000».

Этот аспект важно понимать, поскольку часто люди интерпретируют вычисляемую при тесте «тестовую вероятность» как вероятность правильности гипотезы.

— Но ведь для построения гипотезы нам нужны некие исходные данные. С другой стороны, если мы используем все исходные данные, мы построим гипотезу, которая очень хорошо согласуется с известными данными, но вряд ли будет работать дальше. Получается, нам надо для построения гипотезы выбрать некую часть данных, а потом тестировать ее на остальных?

— Да, это один из вариантов. Он требует большого объема данных. Так логично действовать, если стоит задача построить функцию распределения вероятности. Есть другой вариант — выдвинуть гипотезу, исходя из физических соображений, и проверить ее на данных. В этом случае можно использовать для проверки все данные. Наиболее часто в этом случае в качестве гипотезы берут предположение о том, что распределение нормальное. Чем это обосновано? Предположением о том, что эксперимент хорошо поставлен, и источник отклонения будет описываться нормальным распределением.

— А если все-таки нужно определить функцию распределения, как действовать?

— Во-первых, важно определить цели, поскольку подобная задача потребует большого объема измерений. Следует помнить о том, что центральная предельная теорема гарантирует, что ты можешь определить математическое ожидание и дисперсию вне зависимости от формы распределения случайной величины, проведя измерение большое число раз. А для решения ряда задач кроме математического ожидания и дисперсии ничего не требуется (см. неравенство Чебышева). В таком случае усилия можно сэкономить. Если все же требуется определить функцию распределения — можно взять часть измерений, построить гистограмму, аппроксимировать ее некоей гладкой функцией и проверить эту гипотезу на других данных измерения. Проверка проводится по аналогии с описанным методом — вычисляется отклонение гистограммы от функции распределения, вычисляется вероятность получить такое или большее отклонение. В Matlab, например, есть функции, позволяющие реализовать такой тест для любого типа распределения, не только для нормального.

Хотя подобные тесты можно производить над очень небольшими выборками, результаты в такой ситуации может быть обманчивы.

Проведем следующий численный эксперимент. Возьмем генератор нормального распределения и генератор однородного распределения (уж оно-то сильно непохоже на нормальное, и их легко будет различить!). Заставим каждый из генераторов выдать последовательность из N чисел и проведем на этой парой последовательностей описанный выше тест на нормальность распределения. В качестве алгоритма используется функция Matlab

chi2gof с настройками по умолчанию (в частности, уровень доверия здесь P₀ = 0.05). На графике на рис. 4 показана зависимость доли положительных ответов теста в зависимости от длины последовательности N. Как видно, генератор нормального распределения проходит тест примерно в 95% случаев вне зависимости от N, как и можно было ожидать. Здесь следует отметить — в 5% случаев генератор случайной величины подчинялся нормальному распределению, однако тест на нормальность он не прошел, и такая доля «ложных несрабатываний» — неотъемлимое свойство теста. Снижая уровень доверия, мы уменьшим долю «ложных несрабатываний», однако одновременно повысится доля «ложных срабатываний» — положительных результатов теста в случае, если распределение не было нормальным.

Рис. 4. Результаты применения «Хи-квадрат» проверки нормальности распределения случайной величины. Тестируемые выборки сформированы генератором случайного распределения в Matlab. Синяя кривая получена при помощи генератором нормального распределения, красная — однородного распределения.

А вот результаты для генератора однородного распределения более интересны — при малой величине выборки он проходит тест на нормальное распределение! При длине последовательности N=50 генератор однородного распределения проходит тест на нормальность в 80% случаев! Чтобы при помощи этого теста надежно отличить нормальное распределение от однородного требуется порядка 300 измерений. Если же отличия между функциями распределения меньше, потребуются еще большие выборки.

Почему так происходит? Дело в том, что такого типа тесты помогает ответить на вопрос «могли ли данные результаты измерений быть получены при нормальном распределении?», а не на вопрос «было ли распределение случайной величины нормальным?»

Получается, что отличие от нормального распределения может ощущаться только при большом числе измерения. Отсюда следует, что часто даже если реальное распределение отличается от нормального, нет практической необходимости это учитывать — это очень трудоемко, а выигрыш невелик. И нормальное распределение применяется как хорошая и разработанная модель, позволяющая получить удовлетворительные по точности результаты.

— Я посчитала хи-квадрат тест руками, и у меня получилось, что распределение могло быть нормальным, а применение функции chi2gof в матлабе дало обратный результат.

— Такое возможно, поскольку подобные тесты сильно зависят от правил построения гистограммы и, разумеется, уровня доверия, с которым сравнивается условная вероятность. В

chi2gof по умолчанию зашиты конкретные правила — например, если в столбец попало меньше 5 значений, он объединяется с соседним. Если изменить это число — результат изменится. Поэтому результаты теста несколько субъективны. Есть рекомендуемые значения числа столбцов в зависимости от величины выборки, позволяющие получить наиболее значимые результаты.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 марта 2021 года; проверки требуют 33 правки.

Распределение вероятностей — это закон, описывающий область значений случайной величины и соответствующие вероятности появления этих значений.

Определение[править | править код]

Пусть задано вероятностное пространство $(Omega ,{mathcal {F}},mathbb {P} )$ , и на нём определена случайная величина $X:Omega to mathbb {R}$ . В частности, по определению, $X$ является измеримым отображением измеримого пространства $(Omega ,{mathcal {F}})$ в измеримое пространство $(mathbb {R} ,{mathcal {B}}(mathbb {R} ))$ , где ${mathcal {B}}(mathbb {R} )$ обозначает борелевскую сигма-алгебру на $mathbb {R}$ . Тогда случайная величина $X$ индуцирует вероятностную меру $mathbb {P} ^{X}$ на $mathbb {R}$ следующим образом:

$mathbb {P} ^{X}(B)=mathbb {P} (X^{-1}(B)),;forall Bin {mathcal {B}}(mathbb {R} ).$

Мера $mathbb {P} ^{X}$ называется распределением случайной величины $X$ .
Иными словами, $mathbb {P} ^{X}(B)=mathbb {P} (Xin B)$ , таким образом $mathbb {P} ^{X}(B)$ задаёт вероятность того, что случайная величина $X$ попадает во множество $Bin {mathcal {B}}(mathbb {R} )$ .

Классификация распределений[править | править код]

Функция $F_{X}(x)=mathbb {P} ^{X}((-infty ,x])=mathbb {P} (Xleqslant x)$ называется (кумулятивной) функцией распределения случайной величины $X$ . Из свойств вероятности вытекает теорема:

Функция распределения $F_{X}(x)$ любой случайной величины удовлетворяет следующим трем свойствам:

$F_{X}$ — функция неубывающая;
$lim _{xto -infty }F_{X}(x)=0,;lim _{xto infty }F_{X}(x)=1$ ;
$F_{X}$ непрерывна справа.

Из того факта, что борелевская сигма-алгебра на вещественной прямой порождается семейством интервалов вида ${(-infty ,x]}_{xin mathbb {R} }$ , вытекает теорема:

Любая функция $F(x)$ , удовлетворяющая трём свойствам, перечисленным выше, является функцией распределения для какого-то распределения $mathbb {P} ^{X}$ .

Для вероятностных распределений, обладающих определенными свойствами, существуют более удобные способы их задания. В то же время распределения (и случайные величины) принято классифицировать по характеру функций распределения^[1].

Дискретные распределения[править | править код]

Случайная величина $X$ называется простой или дискретной, если она принимает не более, чем счётное число значений. То есть $X(omega )=a_{i},;forall omega in A_{i}$ , где ${A_{i}}_{i=1}^{infty }$ — разбиение $Omega$ .

Распределение простой случайной величины тогда по определению задаётся: $mathbb {P} ^{X}(B)=sum _{i:a_{i}in B}mathbb {P} (A_{i})$ . Введя обозначение $p_{i}=mathbb {P} (A_{i})$ , можно задать функцию $p(a_{i})=p_{i}$ . В силу свойств вероятности $sum _{i=1}^{infty }p_{i}=1$ . Используя счётную аддитивность $mathbb {P}$ , легко показать, что эта функция однозначно определяет распределение $X$ .

Набор вероятностей $p(a_{i})=p_{i}$ , где $sum _{i=1}^{infty }p_{i}=1$ называется распределением вероятностей дискретной случайной величины $X$ . Совокупность значений ${displaystyle a_{i},i=1,2...infty }$ и вероятностей ${displaystyle p_{i},iin {1,2...infty }}$ называется дискретным законом распределения вероятностей^[2].

Для иллюстрации сказанного выше, рассмотрим следующий пример.

Пусть функция $p$ задана таким образом, что $p(-1)={frac {1}{2}}$ и $p(1)={frac {1}{2}}$ . Эта функция задаёт распределение случайной величины $X$ , для которой $mathbb {P} (X=pm 1)={frac {1}{2}}$ (см. распределение Бернулли, где случайная величина принимает значения ${displaystyle 0,1}$ ). Случайная величина $X$ является моделью подбрасывания уравновешенной монеты.

Другими примерами дискретных случайных величин являются распределение Пуассона, биномиальное распределение, геометрическое распределение.

Дискретное распределение обладает следующими свойствами:

$p_{i}geqslant 0$ ,
$sum _{i=1}^{n}p_{i}=1$ , если множество значений – конечное — из свойств вероятности,
Функция распределения $F_{X}(x)$ имеет конечное или счётное множество точек разрыва первого рода,
Если $x_{0}$ – точка непрерывности $F_{X}(x)$ , то существует ${displaystyle {frac {dF_{X}(x_{0})}{dx}}=0}$ .

Решётчатые распределения[править | править код]

Решётчатым называется распределение с дискретной функцией распределения и точки разрыва функции распределения образуют подмножество точек вида ${displaystyle a+nh}$ , где $a$ – вещественное, $h>0$ , $n$ – целое^[3].

Теорема. Для того, чтобы функция распределения $F$ была решётчатой с шагом $h$ , необходимо и достаточно, чтобы её характеристическая функция $f$ удовлетворяла соотношению $|f(2pi /h)|=1$ ^[3].

Абсолютно непрерывные распределения[править | править код]

Распределение случайной величины $X$ называется абсолютно непрерывным, если существует неотрицательная функция $f_{X}:mathbb {R} to mathbb {R} _{+}$ , такая что $mathbb {P} ^{X}(B)equiv mathbb {P} (Xin B)=int limits _{B}f_{X}(x),dx$ . Функция $f_{X}$ тогда называется плотностью распределения вероятностей случайной величины $X$ . Функция таких распределений абсолютно непрерывна в смысле Лебега.

Примерами абсолютно непрерывных распределений являются нормальное распределение, равномерное распределение, экспоненциальное распределение, распределение Коши.

Пример. Пусть $f(x)=1$ , когда $0leqslant xleqslant 1$ , и $f(x)=0$ в противном случае. Тогда $mathbb {P} (a<X<b)=int limits _{a}^{b}1,dx=b-a$ , если $(a,b)subset [0,1]$ .

Для любой плотности распределения $f_{X}$ верны свойства:

${displaystyle f_{X}(x)geqslant 0}$ ;
$int limits _{-infty }^{infty }f_{X}(x),dx=1$ .

Верно и обратное — если функция $f:mathbb {R} to mathbb {R}$ такая, что:

$f(x)geqslant 0,;forall xin mathbb {R}$ ;
$int limits _{-infty }^{infty }f(x),dx=1$ ,

то существует распределение $mathbb {P} ^{X}$ такое, что $f(x)$ является его плотностью.

Применение формулы Ньютона-Лейбница приводит к следующим соотношениям между функцией и плотностью абсолютно непрерывного распределения:

${displaystyle mathbb {P} (a<X<b)=F(b)-F(a)=int limits _{a}^{b}f(t),dt}$ .

Теорема. Если $f(x)$ — непрерывная плотность распределения, а $F(x)$ — его функция распределения, то

$F'(x)=f(x),;forall xin mathbb {R} ,$
$F(x)=int limits _{-infty }^{x}f(t),dt$ .

При построении распределения по эмпирическим (опытным) данным следует избегать ошибок округления.

Сингулярные распределения[править | править код]

Кроме дискретных и непрерывных случайных величин существуют величины, не являющиеся ни на одном интервале ни дискретными, ни непрерывными. К таким случайным величинам относятся, например, те, функции распределения которых непрерывные, но возрастают только на множестве лебеговой меры нуль^[4].

Сингулярными называют распределения, сосредоточенные на множестве нулевой меры (обычно меры Лебега).

Таблица основных распределений[править | править код]

Дискретные распределения

Название	Обозначение	Параметр	Носитель	Плотность (последовательность вероятностей)	Матем. ожидание	Дисперсия	Характеристическая функция
Дискретное равномерное	${displaystyle {text{R}}{1,dots ,N}}$	${displaystyle Nin mathbb {N} }$	${displaystyle {1,dots ,N}}$	${displaystyle mathrm {P} ({k})={frac {1}{N}},kin {1,dots ,N}}$	${displaystyle {frac {N+1}{2}}}$	${displaystyle {frac {N^{2}-1}{12}}}$	${displaystyle {frac {e^{it}-e^{i(N+1)t}}{N(1-e^{it})}}}$
Бернулли	${displaystyle {text{Bern}}(p)}$	${displaystyle pin (0,1)}$	${displaystyle {0,1}}$	${displaystyle mathrm {P} ({0})=1-p,mathrm {P} ({1})=p}$	${displaystyle p}$	${displaystyle p(1-p)}$	${displaystyle pe^{it}+1-p}$
Биномиальное	${displaystyle {text{Bin}}(n,p)}$	${displaystyle nin mathbb {N} ,pin (0,1)}$	${displaystyle {0,dots ,n}}$	${displaystyle mathrm {P} ({k})=C_{n}^{k}p^{k}(1-p)^{n-k}}$	${displaystyle np}$	${displaystyle np(1-p)}$	${displaystyle (pe^{it}+1-p)^{n}}$
Пуассоновское	${displaystyle {text{Pois}}(lambda )}$	$lambda >0$	${displaystyle mathbb {Z} _{+}}$	${displaystyle mathrm {P} ({k})={frac {lambda ^{k}}{k!}}e^{-lambda }}$	$lambda$	$lambda$	${displaystyle e^{lambda (e^{it}-1)}}$
Геометрическое	${displaystyle {text{Geom}}(p)}$	${displaystyle pin (0,1]}$	${displaystyle mathbb {N} }$	${displaystyle mathrm {P} ({k})=(1-p)^{k-1}p}$	${frac {1}{p}}$	${displaystyle {frac {1-p}{p^{2}}}}$	${displaystyle {frac {pe^{it}}{1-(1-p)e^{it}}}}$

Абсолютно непрерывные распределения

Название	Обозначение	Параметр	Носитель	Плотность вероятности $f(x)$	Функция распределения F(х)	Характеристическая функция	Математическое ожидание	Медиана	Мода	Дисперсия	Коэффициент асимметрии	Коэффициент эксцесса	Дифференциальная энтропия	Производящая функция моментов
Равномерное непрерывное	${displaystyle U(a,b)}$	${displaystyle a,bin mathbb {R} ,a<b}$ , $a$ — коэффициент сдвига, $b-a$ — коэффициент масштаба	${displaystyle [a,b]}$	${displaystyle {dfrac {1}{b-a}}I{xin [a,b]}}$	${displaystyle {dfrac {x-a}{b-a}}I{xin [a,b]}+I{x>b}}$	${displaystyle {dfrac {e^{itb}-e^{ita}}{it(b-a)}}}$	${displaystyle {frac {a+b}{2}}}$	${frac {a+b}{2}}$	любое число из отрезка $[a,b]$	${frac {(b-a)^{2}}{12}}$	${displaystyle 0}$	$-{frac {6}{5}}$	${displaystyle ln(b-a)}$	${frac {e^{{tb}}-e^{{ta}}}{t(b-a)}}$
Нормальное (гауссовское)	${displaystyle N(mu ,sigma ^{2})}$	${displaystyle mu in mathbb {R} }$ — коэффициент сдвига, ${displaystyle sigma >0}$ — коэффициент масштаба	${mathbb R}$	${displaystyle {frac {1}{sigma {sqrt {2pi }}}};e^{-{frac {left(x-mu right)^{2}}{2sigma ^{2}}}}}$	${displaystyle {frac {1}{2}}left(1+operatorname {erf} left({frac {x-mu }{sqrt {2sigma ^{2}}}}right)right)}$	${displaystyle e^{i,mu ,t-{frac {sigma ^{2}t^{2}}{2}}}}$	$mu$	$mu$	$mu$	$sigma ^{2}$	${displaystyle 0}$	${displaystyle 0}$	${displaystyle ln left(sigma {sqrt {2,pi ,e}}right)}$	${displaystyle e^{mu ,t+{frac {sigma ^{2}t^{2}}{2}}}}$
Логнормальное	${displaystyle LN(mu ,sigma ^{2})}$	${displaystyle mu in mathbb {R} ,sigma >0}$	${displaystyle (0;+infty )}$	${displaystyle {frac {1}{xsigma {sqrt {2pi }}}}e^{-{frac {1}{2}}left({frac {ln(x)-mu }{sigma }}right)^{2}}}$	${frac {1}{2}}+{frac {1}{2}}{mathrm {Erf}}left[{frac {ln(x)-mu }{sigma {sqrt {2}}}}right]$	$sum _{{n=0}}^{{infty }}{frac {(it)^{n}}{n!}}e^{{nmu +n^{2}sigma ^{2}/2}}$	$e^{{mu +sigma ^{2}/2}}$	$e^{{mu }}$	$e^{{mu -sigma ^{2}}}$	$(e^{{sigma ^{2}}}!!-1)e^{{2mu +sigma ^{2}}}$	$(e^{{sigma ^{2}}}!!+2){sqrt {e^{{sigma ^{2}}}!!-1}}$	$e^{{4sigma ^{2}}}!!+2e^{{3sigma ^{2}}}!!+3e^{{2sigma ^{2}}}!!-6$	${frac {1}{2}}+{frac {1}{2}}ln(2pi sigma ^{2})+mu$	${displaystyle e^{smu +{tfrac {1}{2}}s^{2}sigma ^{2}}.}$
Гамма-распределение	${displaystyle Gamma (alpha ,beta )}$	${displaystyle alpha >0,beta >0}$	${displaystyle mathbb {R} _{+}}$	${displaystyle {frac {alpha ^{beta }x^{beta -1}}{Gamma (beta )}}e^{-alpha x}}$	${displaystyle {frac {1}{Gamma (beta )}}gamma (beta ,alpha x)}$	${displaystyle left(1-{frac {it}{alpha }}right)^{-beta }}$	${displaystyle {frac {beta }{alpha }}}$		${displaystyle {frac {beta -1}{alpha }}}$ при ${displaystyle beta geq 1}$	${displaystyle {frac {beta }{alpha ^{2}}}}$	${displaystyle {frac {2}{sqrt {beta }}}}$	${displaystyle {frac {6}{beta }}}$	${displaystyle {begin{aligned}beta &-ln alpha +ln Gamma (beta )\&+(1-beta )psi (beta )end{aligned}}}$	${displaystyle left(1-{frac {t}{alpha }}right)^{-beta }}$ при ${displaystyle t<alpha }$
Экспоненциальное	${displaystyle {text{Exp}}(lambda )}$	${displaystyle lambda >0}$	${displaystyle mathbb {R} _{+}}$	${displaystyle lambda e^{-lambda x}I{x>0}}$	${displaystyle 1-e^{-lambda x}}$	${displaystyle {frac {lambda }{lambda -it}}}$	${displaystyle {frac {1}{lambda }}}$	${displaystyle ln(2)/lambda }$	${displaystyle 0}$	${displaystyle lambda ^{-2}}$	$2$	$6$	${displaystyle 1-ln(lambda )}$	${displaystyle left(1-{frac {t}{lambda }}right)^{-1}}$
Лапласа	${displaystyle {text{Laplace}}(alpha ,beta )}$	$alpha >0$ — коэффициент масштаба, $betainmathbb{R}$ — коэффициент сдвига	${mathbb R}$	$frac{alpha}{2},e^{-alpha\|x-beta\|}$	${displaystyle {begin{cases}{frac {1}{2}}e^{alpha (x-beta )},&xleqslant beta \1-{frac {1}{2}}e^{-alpha (x-beta )},&x>beta end{cases}}}$	${displaystyle {frac {alpha ^{2}}{alpha ^{2}+t^{2}}}e^{itbeta }}$	$beta$	$beta$	$beta$	${displaystyle {frac {2}{alpha ^{2}}}}$	${displaystyle 0}$	$3$	${displaystyle ln {frac {2e}{alpha }}}$	${displaystyle {frac {e^{beta t}}{1-alpha ^{2}t^{2}}}{text{ для }}\|t\|<1/alpha }$
Коши	${displaystyle {text{Cauchy}}(x_{0},gamma )}$	$x_{0}$ — коэффициент сдвига, $gamma > 0$ — коэффициент масштаба	${mathbb R}$	${displaystyle {1 over pi }left({gamma over gamma ^{2}+(x-x_{0})^{2}}right)}$	${frac {1}{pi }}{mathrm {arctg}}left({frac {x-x_{0}}{gamma }}right)+{frac {1}{2}}$	${displaystyle e^{i,x_{0},t-gamma ,\|t\|}}$	нет	$x_{0}$	$x_{0}$	$+infty$	нет	нет	${displaystyle ln(4,pi ,gamma )}$	нет
Бета-распределение	${displaystyle {text{Beta}}(alpha ,beta )}$	${displaystyle alpha >0,beta >0}$	${displaystyle [0,1]}$	${displaystyle {frac {x^{alpha -1}(1-x)^{beta -1}}{{text{B}}(alpha ,beta )}}}$	${displaystyle I_{x}(alpha ,beta )}$	${displaystyle {}_{1}F_{1}(alpha ;alpha +beta ;i,t)}$	${displaystyle {frac {alpha }{alpha +beta }}}$	${displaystyle I_{frac {1}{2}}^{[-1]}(alpha ,beta )approx {frac {alpha -{tfrac {1}{3}}}{alpha +beta -{tfrac {2}{3}}}}}$ для ${displaystyle alpha ,beta >1}$	${displaystyle {frac {alpha -1}{alpha +beta -2}}}$ для $alpha >1,beta >1$	${displaystyle {frac {alpha beta }{(alpha +beta )^{2}(alpha +beta +1)}}}$	${frac {2,(beta -alpha ){sqrt {alpha +beta +1}}}{(alpha +beta +2){sqrt {alpha beta }}}}$	${displaystyle 6,{frac {alpha ^{3}-alpha ^{2}(2beta -1)+beta ^{2}(beta +1)-2alpha beta (beta +2)}{alpha beta (alpha +beta +2)(alpha +beta +3)}}}$		$1+sum _{k=1}^{infty }left(prod _{r=0}^{k-1}{frac {alpha +r}{alpha +beta +r}}right){frac {t^{k}}{k!}}$
хи-квадрат	${displaystyle chi ^{2}(k)}$	$k>0$ — число степеней свободы	${displaystyle mathbb {R} _{+}}$	${displaystyle {frac {(1/2)^{k/2}}{Gamma (k/2)}}x^{k/2-1}e^{-x/2}}$	${displaystyle {frac {gamma (k/2,x/2)}{Gamma (k/2)}}}$	${displaystyle (1-2,i,t)^{-k/2}}$	$k$	примерно ${displaystyle k-2/3}$	${displaystyle k-2}$ если $kgeq 2$	${displaystyle 2,k}$	${displaystyle {sqrt {8/k}}}$	${displaystyle 12/k}$	${frac {k}{2}}!+!ln left[2Gamma left({k over 2}right)right]!+!left(1!-!{frac {k}{2}}right)psi left({frac {k}{2}}right)$	$(1-2,t)^{-k/2}$ , если ${displaystyle 2,t<1}$
Стьюдента	${displaystyle {text{t}}(n)}$	$n>0$ — число степеней свободы	${mathbb R}$	${displaystyle {frac {Gamma ({frac {n+1}{2}})}{{sqrt {npi }},Gamma ({frac {n}{2}})}}(1+{frac {x^{2}}{n}})^{-{frac {n+1}{2}}}}$	${displaystyle {frac {1}{2}}+{xGamma left({frac {n+1}{2}}right)}{frac {,_{2}F_{1}left({frac {1}{2}},{frac {n+1}{2}};{frac {3}{2}};-{frac {x^{2}}{n}}right)}{{sqrt {pi n}},Gamma ({frac {n}{2}})}}}$	${displaystyle {frac {K_{n/2}left({sqrt {n}}\|t\|right)cdot left({sqrt {n}}\|t\|right)^{n/2}}{Gamma (n/2)2^{n/2-1}}}}$ для $n>0$	${displaystyle 0}$ , если $n>1$	${displaystyle 0}$	${displaystyle 0}$	${frac {n}{n-2}}$ , если $n>2$	${displaystyle 0}$ , если $n>3$	${displaystyle {frac {6}{n-4}}}$ , если $n>4$	${begin{matrix}{frac {n+1}{2}}left[psi ({frac {1+n}{2}})-psi ({frac {n}{2}})right]\[0.5em]+log {left[{sqrt {n}}B({frac {n}{2}},{frac {1}{2}})right]}end{matrix}}$	Нет
Фишера	${displaystyle F(d_{1},d_{2})}$	${displaystyle d_{1}>0, d_{2}>0}$ – числа степеней свободы	${displaystyle mathbb {R} _{+}}$	${displaystyle {frac {sqrt {frac {(d_{1},x)^{d_{1}},,d_{2}^{d_{2}}}{(d_{1},x+d_{2})^{d_{1}+d_{2}}}}}{x,mathrm {B} !left({frac {d_{1}}{2}},{frac {d_{2}}{2}}right)}}}$	${displaystyle I_{frac {d_{1}x}{d_{1}x+d_{2}}}(d_{1}/2,d_{2}/2)}$	${displaystyle {frac {Gamma ({frac {d_{1}+d_{2}}{2}})}{Gamma ({tfrac {d_{2}}{2}})}}U!left({frac {d_{1}}{2}},1-{frac {d_{2}}{2}},-{frac {d_{2}}{d_{1}}}imath sright)}$	${displaystyle {frac {d_{2}}{d_{2}-2}}}$ , если $d_{2}>2$		${displaystyle {frac {d_{1}-2}{d_{1}}};{frac {d_{2}}{d_{2}+2}}}$ , если $d_{1}>2$	${displaystyle {frac {2,d_{2}^{2},(d_{1}+d_{2}-2)}{d_{1}(d_{2}-2)^{2}(d_{2}-4)}},}$ если $d_{2}>4$	${displaystyle {frac {(2d_{1}+d_{2}-2){sqrt {8(d_{2}-4)}}}{(d_{2}-6){sqrt {d_{1}(d_{1}+d_{2}-2)}}}},}$ если $d_{2}>6$	${displaystyle 12{frac {d_{1}(5d_{2}-22)(d_{1}+d_{2}-2)+(d_{2}-4)(d_{2}-2)^{2}}{d_{1}(d_{2}-6)(d_{2}-8)(d_{1}+d_{2}-2)}}}$	${displaystyle ln Gamma left({tfrac {d_{1}}{2}}right)+ln Gamma left({tfrac {d_{2}}{2}}right)-ln Gamma left({tfrac {d_{1}+d_{2}}{2}}right)+!}$ ${displaystyle left(1-{tfrac {d_{1}}{2}}right)psi left(1+{tfrac {d_{1}}{2}}right)-left(1+{tfrac {d_{2}}{2}}right)psi left(1+{tfrac {d_{2}}{2}}right)!}$ ${displaystyle +left({tfrac {d_{1}+d_{2}}{2}}right)psi left({tfrac {d_{1}+d_{2}}{2}}right)+ln {frac {d_{1}}{d_{2}}}!}$
Рэлея	${displaystyle mathrm {Rayleigh} (sigma )}$	${displaystyle sigma }$	${displaystyle mathbb {R} _{+}}$	${displaystyle {frac {x}{{sigma }^{2}}}e^{-{frac {{x}^{2}}{2{{sigma }^{2}}}}}}$	${displaystyle 1-e^{frac {-x^{2}}{2sigma ^{2}}}}$	$1!-!sigma te^{{-sigma ^{2}t^{2}/2}}{sqrt {{frac {pi }{2}}}}!left({textrm {erfi}}!left({frac {sigma t}{{sqrt {2}}}}right)!-!iright)$	${sqrt {{frac {pi }{2}}}}sigma$	${displaystyle sigma {sqrt {ln(4)}}}$	$sigma$	$left(2-pi /2right){{sigma }^{{2}}}$	${frac {2{sqrt {pi }}(pi -3)}{(4-pi )^{{3/2}}}}$	$-{frac {6pi ^{2}-24pi +16}{(4-pi )^{2}}}$	$1+ln left({frac {sigma }{{sqrt {2}}}}right)+{frac {gamma }{2}}$	${displaystyle 1+sigma t,e^{sigma ^{2}t^{2}/2}{sqrt {frac {pi }{2}}}left({textrm {erf}}left({frac {sigma t}{sqrt {2}}}right)!+!1right)}$
Вейбулла	${displaystyle mathrm {W} (k,lambda )}$	${displaystyle lambda >0}$ – коэффициент масштаба, $k>0$ – коэффициент формы	${displaystyle mathbb {R} _{+}}$	${displaystyle {frac {k}{lambda }}left({frac {x}{lambda }}right)^{k-1}e^{-left({frac {x}{lambda }}right)^{k}}}$	${displaystyle 1-e^{-left({frac {x}{lambda }}right)^{k}}}$	${displaystyle sum _{n=0}^{infty }{frac {(it)^{n}lambda ^{n}}{n!}}Gamma (1+n/k)}$	${displaystyle lambda Gamma left(1+{frac {1}{k}}right)}$	${displaystyle lambda ln(2)^{1/k}}$	$frac{lambda(k-1)^{frac{1}{k}}}{k^{frac{1}{k}}},$ для $k>1$	${displaystyle lambda ^{2}Gamma left(1+{frac {2}{k}}right)-mu ^{2}}$	$frac{Gamma(1+frac{3}{k})lambda^3-3muGamma(1+frac{2}{k})lambda^2+2mu^3}{sigma^3}$	${displaystyle {frac {lambda ^{4}Gamma left(1+{frac {4}{k}}right)-4lambda ^{3}mu Gamma left(1+{frac {3}{k}}right)+6lambda ^{2}mu ^{2}Gamma left(1+{frac {2}{k}}right)-3mu ^{4}}{sigma ^{4}}}}$	$gammaleft(1!-!frac{1}{k}right)+left(frac{lambda}{k}right)^k +lnleft(frac{lambda}{k}right)$	${displaystyle sum _{n=0}^{infty }{frac {t^{n}lambda ^{n}}{n!}}Gamma (1+n/k), kgeq 1}$
Логистическое	${displaystyle L(mu ,s)}$	$mu$ , ${displaystyle s>0}$	${mathbb R}$	${displaystyle {frac {e^{-(x-mu )/s}}{sleft(1+e^{-(x-mu )/s}right)^{2}}}}$	${displaystyle {frac {1}{1+e^{-(x-mu )/s}}}}$	${displaystyle e^{imu t},mathrm {B} (1-ist,;1+ist)}$ для ${displaystyle \|ist\|<1}$	$mu$	$mu$	$mu$	${displaystyle {frac {pi ^{2}}{3}}s^{2}}$	${displaystyle 0}$	${displaystyle 6/5}$	${displaystyle ln(s)+2}$	${displaystyle e^{mu ,t},mathrm {B} (1-s,t,;1+s,t)}$ для ${displaystyle \|s,t\|<1}$
Вигнера	${displaystyle rho (R)}$	$R>0$ – радиус	${displaystyle [-R;+R]}$	${displaystyle {frac {2}{pi R^{2}}},{sqrt {R^{2}-x^{2}}}}$	${displaystyle {frac {1}{2}}+{frac {x{sqrt {R^{2}-x^{2}}}}{pi R^{2}}}+{frac {arcsin !left({frac {x}{R}}right)}{pi }}}$ для $-Rleq xleq R$	$2,{frac {J_{1}(R,t)}{R,t}}$	${displaystyle 0}$	${displaystyle 0}$	${displaystyle 0}$	${displaystyle {frac {R^{2}}{4}}}$	${displaystyle 0}$	$-1$	${displaystyle ln(pi R)-{frac {1}{2}}}$	$2,{frac {I_{1}(R,t)}{R,t}}$
Парето	${displaystyle {text{Pareto}}(k,x_{text{m}})}$	${displaystyle x_{text{m}}>0}$ — коэффициент масштаба, $k>0$	${displaystyle [x_{text{m}};+infty )}$	${displaystyle {frac {k,x_{text{m}}^{k}}{x^{k+1}}}}$	${displaystyle 1-left({frac {x_{text{m}}}{x}}right)^{k}}$	${displaystyle k{big (}Gamma (-k){big [}x_{text{m}}^{k}(-it)^{k}-(-ix_{text{m}}t)^{k}{big ]}+E_{text{k+1}}(-ix_{text{m}}t){big )}}$	${displaystyle {frac {kx_{text{m}}}{k-1}}}$ , если $k>1$	${displaystyle x_{text{m}}{sqrt[{k}]{2}}}$	${displaystyle x_{text{m}}}$	${displaystyle left({frac {x_{text{m}}}{k-1}}right)^{2}{frac {k}{k-2}}}$ при $k>2$	${displaystyle {frac {2(1+k)}{k-3}},{sqrt {frac {k-2}{k}}}}$ при ${displaystyle k>3}$	${displaystyle {frac {6(k^{3}+k^{2}-6k-2)}{k(k-3)(k-4)}}}$ при ${displaystyle k>4}$	${displaystyle ln left({frac {k}{x_{text{m}}}}right)-{frac {1}{k}}-1}$	нет

где $Gamma$ – гамма-функция, $gamma$ – неполная гамма-функция, $psi =Gamma '/Gamma$ – дигамма-функция, $B$ – бета-функция, ${displaystyle I_{x}}$ – регуляризованная неполная бета-функция, ${displaystyle _{1}F_{1}}$ , ${displaystyle _{2}F_{1}}$ — гипергеометрическая функция, $J_{alpha }$ – функция Бесселя, ${displaystyle I_{nu }}$ – модифицированная функция Бесселя первого рода, ${displaystyle K_{nu }}$ – модифицированная функция Бесселя второго рода, ${displaystyle U(a,b,z)}$ – функция Трикоми.

Многомерные распределения

Название	Обозначение	Параметр	Носитель	Плотность (последовательность вероятностей)	Матем. ожидание	Дисперсия	Характеристическая функция
Гауссовское	${displaystyle N(a,Sigma )}$	${displaystyle ain mathbb {R} ^{n},Sigma in mathbb {R} ^{ntimes n}}$ – симм. и неотр. опр.	$mathbb {R} ^{n}$	${displaystyle p(x)={dfrac {1}{sqrt {(2pi )^{n}det Sigma }}}e^{-{frac {1}{2}}(x-a)^{T}Sigma ^{-1}(x-a)}}$	$a$	$Sigma$	${displaystyle e^{ia^{T}t-{frac {1}{2}}t^{T}Sigma t}}$

Примечания[править | править код]

↑ Маталыцкий, Хацкевич. Теория вероятностей, математическая статистика и случайные процессы, 2012. – С.69
↑ Маталыцкий, Хацкевич. Теория вероятностей, математическая статистика и случайные процессы, 2012. – С.68
↑ ¹ ² Рамачандран, 1975, с. 38.
↑ Маталыцкий, Хацкевич. Теория вероятностей, математическая статистика и случайные процессы, 2012. — С.76

Литература[править | править код]

Распределение вероятностей // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
Лагутин М.Б. Наглядная математическая статистика. — М.: Бином, 2009. — 472 с.
Жуковский М.Е., Родионов И.В. Основы теории вероятностей. — М.: МФТИ, 2015. — 82 с.
Жуковский М.Е., Родионов И.В., Шабанов Д.А. Введение в математическую статистику. — М.: МФТИ, 2017. — 109 с.
Рамачандран Б. Теория характеристических функций. — М.: Наука, 1975. — 224 с.
Королюк В.С., Портенко Н.И., Скороход А.В., Турбин А.Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.
Губарев В.В. Вероятностные модели: Справочник в 2-х частях. — Новосибирск.: Новосибир. электротехн. ин-т, 1992. — 422 с.

См. также[править | править код]

Маргинальное распределение

Источник

Формулы: законы распределения случайных величин

В данном разделе вы найдете формулы по теории вероятностей, описывающие законы распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, экспоненциальный, равномерный, нормальный.

Каталог формул по теории вероятности онлайн

Законы распределения на этой странице

Биномиальный
Пуассона
Геометрический
Гипергеометрический

Показательный
Равномерный
Нормальный

Понравилось? Добавьте в закладки

Дискретные случайные величины

Биномиальное распределение ДСВ

Пусть дискретная случайная величина $X$ – количество “успехов” в последовательности из $n$ независимых случайных экспериментов, таких что вероятность “успеха” в каждом из них равна $p$ (“неуспеха” – $q=1-p$).

Закон распределения $X$ имеет вид:

$x_k$	0	1	…	k	…	n
$p_k$	$q^n$	$ncdot p cdot q^{n-1}$		$C_n^k cdot p^k cdot q^{n-k}$		$p^n$

Здесь вероятности находятся по формуле Бернулли:

$$
P(X=k) = C_n^k cdot p^k cdot (1-p)^{n-k} = C_n^k cdot p^k cdot q^{n-k}, k=0,1,2,…,n.
$$

Числовые характеристики биномиального распределения:

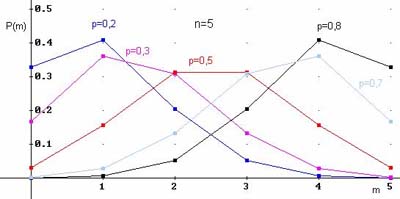
$$M(X)=np, quad D(X)=npq, sigma(X)=sqrt{npq}.$$

Примеры многоугольников распределения для $n=5$ и различных вероятностей:

Примеры решенных задач на биномиальный закон ДСВ

Пуассоновское распределение ДСВ

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

При условии $pto 0$, $n to infty$, $np to lambda = const$ закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность $p$ события $A$ в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Ряд распределения по закону Пуассона имеет вид:

$x_k$	0	1	…	k	…
$p_k$	$e^{-lambda}$	$lambda e^{-lambda}$	…	$frac{lambda^k}{k!}cdot e^{-lambda}$	…

Вероятности вычисляются по формуле Пуассона:

$$
P(X=k)=frac{lambda^k}{k!}cdot e^{-lambda}, k=0,1,2,…
$$

Числовые характеристики для распределения Пуассона:

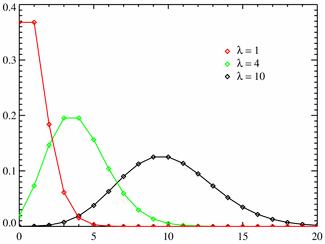
$$M(X)=lambda, quad D(X)=lambda, sigma(X)=sqrt{lambda}.$$

Разные многоугольники распределения при $lambda = 1; 4; 10$.

Примеры решенных задач на закон Пуассона

Геометрическое распределение ДСВ

Пусть происходит серия независимых испытаний, в каждом из которых событие может появится с одной и той же вероятностью $p$. Тогда случайная величина $X$ – количество испытаний до первого появления события, имеет геометрическое распределение вероятностей.

Формула для вероятностей:

$$
P(X=k) = q^k cdot p, k=0,1,2,…,n,…
$$

Ряд распределения геометрического закона:

$x_k$	0	1	2	…	k	…
$p_k$	$p$	$qcdot p$	$q^2 cdot p$	…	$q^k cdot p$	…

Числовые характеристики:

$$M(X)=frac{q}{p}, quad D(X)=frac{q}{p^2}.$$

Примеры решенных задач на геометрическое распределение

Гипергеометрическое распределение ДСВ

Из урны, в которой находятся $N$ шаров ($K$ белых и $N-K$ чёрных шаров), наудачу и без возвращения вынимают $n$ шаров ($n le N$). Найти закон распределения случайной величины $X$ – равной числу белых шаров среди выбранных.

Случайная величина $X$ может принимать целые значения от $0$ до $K$ (если $n lt K$, то до $n$). Вероятности вычисляются по формуле:
$$
P(X=k)=frac{C_K^k cdot C_{N-K}^{n-k}}{C_N^n}, quad 0le k le K.
$$

Числовые характеристики:

$$M(X)=frac{K}{N}cdot n, quad D(X)=frac{K}{N}cdot n cdot frac{N-n}{N} cdot frac{N-K}{N-1}.$$

Примеры задач на гипергеометрическое распределение

Решаем теорию вероятностей на отлично. Закажите сейчас!

Непрерывные случайные величины

Показательное распределение НСВ

Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Плотность распределения величины $X$(везде $ lambda gt 0)$:

$$
f(x)=
left{
begin{array}{l}
0, x lt 0\
lambda e^{-lambda x}, xge 0 \
end{array}
right.
$$

Функция распределения величины $X$:

$$
F(x)=
left{
begin{array}{l}
0, x lt 0\
1- e^{-lambda x}, xge 0 \
end{array}
right.
$$

Числовые характеристики можно найти по формулам:

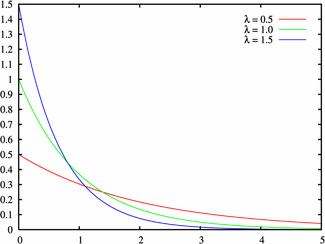
$$M(X)=frac{1}{lambda}, quad D(X)=frac{1}{lambda^2}, quad sigma= frac{1}{lambda}.$$

Плотность распределения при различных значениях $lambda gt 0$:

Примеры решенных задач на показательное распределение

Равномерное распределение НСВ

Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.

Плотность распределения на отрезке $(a;b)$:

$$
f(x)=
left{
begin{array}{l}
0, x le a\
frac {1}{b-a}, a lt x le b, \
0, x gt b, \
end{array}
right.
$$

Функция распределения:

$$
F(x)=
left{
begin{array}{l}
0, x le a\
frac {x-a}{b-a}, a lt x le b, \
1, x gt b, \
end{array}
right.
$$

Числовые характеристики равномерно распределенной случайной величины:

$$M(X)=frac{a+b}{2}, quad D(X)=frac{(b-a)^2}{12}, quad sigma=frac{b-a}{2sqrt{3}}.$$

График плотности вероятностей:

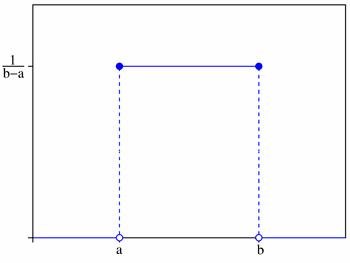
Примеры решенных задач на равномерное распределение

Нормальное распределение или распределение Гаусса НСВ

Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.

Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Плотность распределения нормальной случайной величины $X$ имеет вид:

$$f(x)= frac{1}{sigmasqrt{2pi}} expleft({-frac{(x-a)^2}{2sigma^2}}right). $$

При $a=0$ и $sigma=1$ эта функция принимает вид:

$$varphi(x)= frac{1}{sqrt{2pi}} e^{-x^2/2}.$$

Скачать таблицу для функции $varphi(x)$

Числовые характеристики для нормального распределения:

$$M(X)=a, quad D(X)=sigma^2.$$

Пример графика плотности распределения для различных значений среднего и СКО:

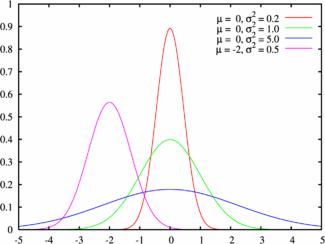
Нормальный закон распределения случайной величины с параметрами $a=0$ и $sigma=1$ называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.

Функция Лапласа определяется как:

$$Phi(x)= frac{1}{sqrt{2pi}}int_0^x e^{-t^2/2} dt$$

Скачать таблицу для функции Лапласа

Вероятность попадания нормально распределенной случайной величины $X$ в заданный интервал $(alpha, beta)$:

$$
P(alpha lt X lt beta) = Phileft( frac{beta-a}{sigma} right) – Phileft( frac{alpha-a}{sigma} right).
$$

Вероятность отклонения нормально распределенной случайной величины $X$ на величину $delta$ от математического ожидания (по модулю).

$$
P(|X -a|lt delta) = 2 Phileft( frac{delta}{sigma} right).
$$

Примеры решенных задач на нормальное распределение

Полезная страница? Сохрани или расскажи друзьям

Решенные задачи по теории вероятностей

Ищете готовые задачи по теории вероятностей? Посмотрите в решебнике:

Подробно решим теорию вероятностей. Закажите сейчас!

Полезные ссылки

Онлайн калькуляторы
Формулы комбинаторики

Статьи по теории вероятностей
Более 200 готовых примеров

Источник

Содержание:

Законы распределения:

Распределение случайных переменных: Каждая из случайных переменных имеет ряд возможных значений, могущих возникнуть с определенной вероятностью.

Случайные переменные величины могут носить прерывный (дискретный) и непрерывный характер. Возможные значения прерывной случайной переменной отделены друг от друга конечными интервалами. Возможные значения непрерывной случайной переменной не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.

Примерами прерывных случайных переменных могут служить:

число попаданий при п выстрелах, если известна вероятность попадания при 1 выстреле. Число попаданий может быть 0, 1, 2….. n;
число появлений герба при n бросаниях монеты.

Примеры непрерывных случайных переменных:

ошибка измерения;
дальность полета снаряда.

Если перечислить все возможные значения случайной переменной и указать вероятности этих значений, то получится распределение случайной переменной. Распределение случайной переменной указывает на соотношение между отдельными значениями случайной величины и их вероятностями.

Распределение случайной переменной будет задано законом распределения, если точно указать, какой вероятностью обладает каждое значение случайной переменной.

Закон распределения имеет чаще всего табличную -форму изложения. В этом случае перечисляются все возможные значения случайной переменной и соответствующие им вероятности:

Законы распределения случайных величин - определение и вычисление с примерами решения

Такая таблица называется также рядом распределения случайной переменной.

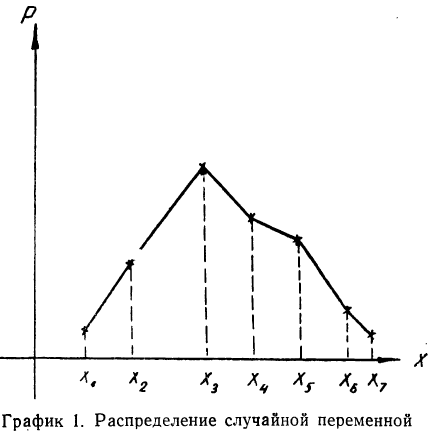
Для наглядности ряд распределения изображают графически, откладывая на прямоугольной системе координат по оси абсцисс возможные значения случайной переменной, а по оси ординат — их вероятности. В результате графического изображения получается многоугольник или полигон распределения (график 1). Многоугольник распределения является одной из форм закона распределения.

Функция распределения

Ряд распределения является исчерпывающей характеристикой прерывной случайной перемен-
Законы распределения случайных величин - определение и вычисление с примерами решения

Вероятность того, что Х<х, зависит от текущей переменной х и является функцией от х. Эта функция носит название функции распределения случайной переменной X.

F(x) = P(X

Функция распределения является одной из форм выражения закона распределения. Она является универсальной характеристикой случайной переменной и может существовать для прерывных и непрерывных случайных переменных.

Функция распределения F(x) называется также интегральной функцией распределения, или интегральным законом распределения.

Основные свойства функции распределения могут быть сформулированы так:

F(x) всегда неотрицательная функция, т. е.
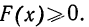
Так как вероятность не может быть больше единицы, то
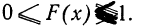
Ввиду того что F(x) является неубывающей функцией, то при
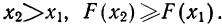
Предельное значение функции распределения при х= 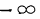равно нулю, а при х= 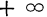равно единице.

Если случайная переменная X дискретна и задана рядом распределения, то для нахождения F(x) для каждого х необходимо найти сумму вероятностей значений X, которые лежат до точки х.

Графическое изображение функции распределения представляет собой некоторую неубывающую кривую, значения которой начинаются с 0 и доходят до 1.

В случае дискретной случайной переменной величины вероятность F(x) увеличивается скачками всякий раз, когда х при своем изменении проходит через одно из возможных значений 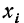Законы распределения случайных величин - определение и вычисление с примерами решения величины X. Между двумя соседними значениями функция F(x) постоянна. Поэтому графически функция F(x) в этом случае будет изображена в виде ступенчатой кривой (см. график 2).

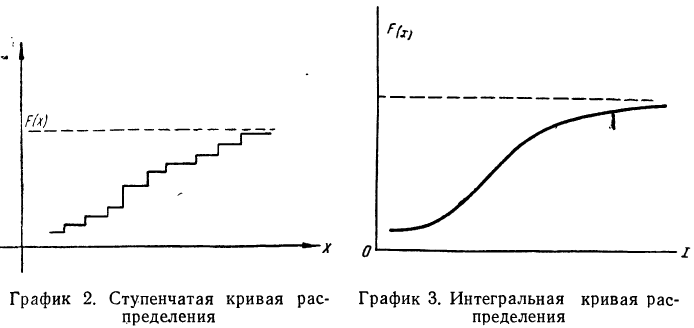
В случае непрерывной случайной переменной величины функция F(x) при графическом изображении дает плавную, монотонно возрастающую кривую следующего вида (см. график 3).

Обычно функция распределения непрерывной случайной переменной представляет собой функцию, непрерывную во всех точках. Эта функция является также дифференцируемой функцией. График функции распределения такой случайной переменной является плавной кривой и имеет касательную в любой ее точке.

Плотность распределения

Если для непрерывной случайной переменной X с функцией распределения F(x) вычислять вероятность попадания ее на участок от х до х+ 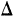Законы распределения случайных величин - определение и вычисление с примерами решения х, т. е. 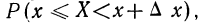то оказывается, что эта вероятность равна приращению функции распределения на этом участке, т. е.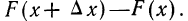 Законы распределения случайных величин - определение и вычисление с примерами решения

Если величину 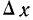Законы распределения случайных величин - определение и вычисление с примерами решения полагать бесконечно малой величиной и находить отношение вероятности попадания на участок к длине участка, то величину отношения в пределе можно выразить так:

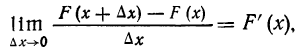
Законы распределения случайных величин - определение и вычисление с примерами решения

т. е. производной от функции распределения, которая характеризует плотность, с которой распределяются значения случайной переменной в данной точке. Эта функция называется плотностью распределения и часто обозначается f(x). Ее называют также дифференциальной функцией распределения, или дифференциальным законом распределения.
Законы распределения случайных величин - определение и вычисление с примерами решения
Таким образом, функция плотности распределения f(x) является производной интегральной функции распределения F(x).

Вероятность того, что случайная переменная X примет значение, лежащее в границах от а до 6, равна определенному интегралу в тех же пределах от плотности вероятности, или:

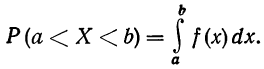
Законы распределения случайных величин - определение и вычисление с примерами решения

Кривая, изображающая плотность распределения случайной переменной, называется кривой распределения (дифференциальной).

Построим кривую некоторой заданной функции плотности вероятности и найдем участок, ограниченный абсциссами а и b. Площадь, ограниченная соответствующими ординатами кривой распределения самой кривой и осью абсцисс, и отобразит вероятность того, что случайная переменная будет находиться в данных пределах (см. график 4).

Плотность распределения является одной из форм закона распределения, но существует только для непрерывных случайных величин.

Основные свойства плотности распределения могут быть сформулированы так:

1. Плотность распределения есть функция, не могущая принимать отрицательных значений, т. е. 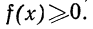Законы распределения случайных величин - определение и вычисление с примерами решения

Отсюда в геометрическом изображении плотности распределения (в кривой распределения) не может быть точек, лежащих ниже оси абсцисс.

2.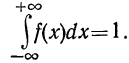 Законы распределения случайных величин - определение и вычисление с примерами решения Следовательно, вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

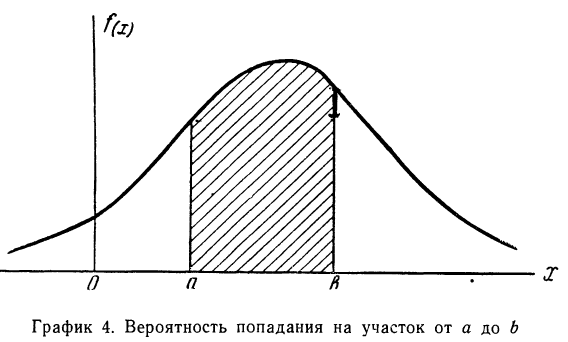
Законы распределения случайных величин - определение и вычисление с примерами решения
Среди законов распределения большое значение имеют биномиальное распределение, распределение Пуассона и нормальное распределение.

Биномиальное распределение

Если производится n независимых испытаний, в каждом из которых вероятность появления данного события А есть величина постоянная, равная р, и, следовательно, вероятность непоявления события А также постоянна и равна q=1—р, то число появлений события А во всех n испытаниях представляет собой случайную переменную. Вероятность того, что событие А появится в n испытаниях m раз, равна:

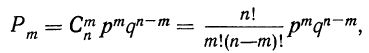
Законы распределения случайных величин - определение и вычисление с примерами решения
т. е. m+1, члену разложения бинома 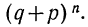Здесь q+p=1 и, следовательно,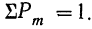 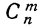—число сочетаний из n элементов по m. Теорема верна для любых m, в том числе и для m = 0 и m=n. Вероятность 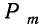Законы распределения случайных величин - определение и вычисление с примерами решения появления события А образует распределение вероятностей случайной переменной m.

Ввиду того что вероятности 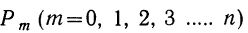Законы распределения случайных величин - определение и вычисление с примерами решения связаны с разложением бинома 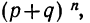распределение случайной переменной m называется биномиальным распределением. Биномиальное распределение является распределением дискретной случайной переменной, поскольку величины m могут принимать только вполне определенные целые значения.

График биномиального распределения, на котором по оси абсцисс откладываются числа наступлений события, а по оси ординат — вероятности этих чисел, представляет собой ломаную линию. Форма графика зависит от значений р, q и n.

Если р и q одинаковы, то график распределения симметричен. Если же р и q неодинаковы, то график распределения будет скошенным.

Одна из частот на графике имеет максимальное значение. Это наиболее вероятная частота. Ее значение можно определить приближенно, аналитически как произведение nр.

Найдем вероятности числа наступления события А при 20 испытаниях при p = 0,1 и р = 0,4 и построим график их распределений (см. график 5). Найдем вероятности частот при n = 20 для p = 0,1 и р=0,4.

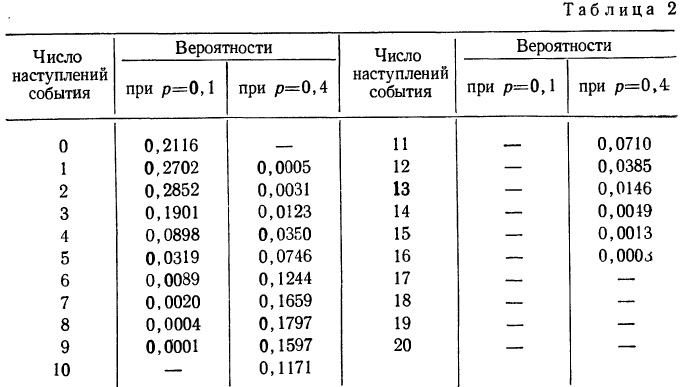
Законы распределения случайных величин - определение и вычисление с примерами решения

График показывает, что приближение р к 0,5 вносит в распределение большую симметрию. Оказывается также, что при увеличении n распределение становится симметричным и для 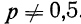Законы распределения случайных величин - определение и вычисление с примерами решения

Биномиальное распределение имеет широкое распространение в практической деятельности людей. Например, продолжительное наблюдение за качеством выпускаемой заводом продукции показало, что p-я часть ее является браком. Иначе говоря, мы выражаем через р вероятность для любого изделия оказаться бракованным. Биномиальное распределение показывает вероятность того, что в партии, содержащей n изделий, окажется m бракованных, где m = 0, 1, 2, 3 … n.
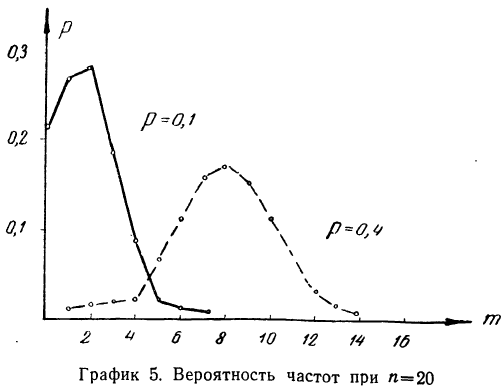
Законы распределения случайных величин - определение и вычисление с примерами решения
Предположим, имеется 100 изделий из партии изделий, в ко торой доля брака равна 0,05. Вероятность того, что из этих из делий окажется 10 бракованных, равна:

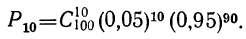
Законы распределения случайных величин - определение и вычисление с примерами решения

Закон биномиального распределения называется также схемой Бернулли. .

Нормальное распределение

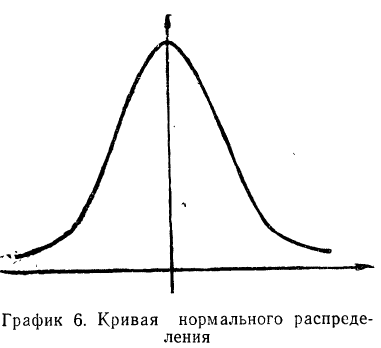
Расчет вероятностей по формуле биномиального распределения при больших n очень громоздок. При этом значении m прерывны, и нет возможности аналитически отыскать их сумму в некоторых границах. Лаплас нашел закон распределения, являющийся предельным законом при неограниченном возрастании числа испытаний n и называемый законом нормального распределения.

Плотность вероятности нормального распределения выражается при этом формулой:
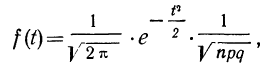
Законы распределения случайных величин - определение и вычисление с примерами решения
где t представляет собой нормированное отклонение частоты т от наиболее вероятной частоты nр, т. е. 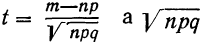Законы распределения случайных величин - определение и вычисление с примерами решения — среднее квадратическое отклонение случайной переменной m. Графическое изображение плотности распределения f(t) дает кривую нормального распределения (см. график 6).

Максимальная ордината кривой соответствует точке m=nр, т. е. математическому ожиданию случайной переменной m; величина этой ординаты равна 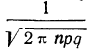Законы распределения случайных величин - определение и вычисление с примерами решения .

Для практического нахождения вероятностей используют таблицу значений f(t).

Эмпирические и теоретические распределения

В примерах распределений, приведенных в разделе I, мы пользовались данными, почерпнутыми из наблюдений.

Поэтому всякий наблюденный ряд распределения назовем эмпирическим, а график, изображающий распределение
частот этого ряда, — эмпирической кривой распределения. Эмпирические кривые распределения могут быть представлены полигоном и гистограммой. При этом изображение в виде полигона применяется для рядов с прерывными значениями признака, а гистограмма— для рядов с непрерывными значениями признака.

Законы распределения случайных величин - определение и вычисление с примерами решения

Наблюдая многочисленные ряды распределения, математики стремятся описать эти распределения путем анализа образования величины признака, пытаются построить теоретическое распределение, исходя из данных об эмпирическом распределении.

Мы уже видели на примере распределения случайной переменной, что распределение ее задается законом распределения. Закон распределения, заданный в виде функции распределения, позволяет математически описать ряды распределения некоторых совокупностей.

Теоретическим законом распределения многих совокупностей, наблюдаемых на практике, является нормальное распределение. Иначе говоря, многие эмпирические подчинены закону нормального распределения, функция плотности вероятности которого приведена в предыдущем параграфе.

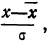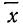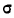Чтобы эту формулу применять для нахождения теоретических данных по некоторому эмпирическому ряду, необходимо вероятностные характеристики заменить данными эмпирического ряда. При этой замене величина стандартизованного отклонения t будет представлять собой Законы распределения случайных величин - определение и вычисление с примерами решения где х— текущие значения случайной переменной X, а и — соответствующие характеристики эмпирического распределения, а именно средняя арифметическая и среднее квадратическое отклонение.

Следовательно, нормальное распределение ряда распределения зависит от величин средней арифметической и его среднего квадратического отклонения.

Свойства кривой нормального распределения

Дифференциальный закон нормального распределения, заданный функцией:

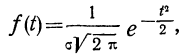
Законы распределения случайных величин - определение и вычисление с примерами решения
имеет ряд свойств. Полагая 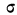=1, тем самым будем иметь измерение варьирующего признака в единицах среднего квадратического отклонения. Тогда функция нормального распределения упростится и примет вид:

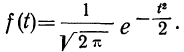
Законы распределения случайных величин - определение и вычисление с примерами решения

Рассмотрим ее свойства.

Кривая нормального распределения имеет ветви, удаленные в бесконечность, причем кривая асимптотически приближается к оси Ot.
Функция является четной: t(—t) = f(t). Следовательно, кривая нормального распределения симметрична относительно оси Оу.
Функция имеет максимум при t = 0. Величина этого максимума равна

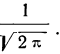
Следовательно, модального значения кривая
достигает при t = 0, а так как Законы распределения случайных величин - определение и вычисление с примерами решения то при
Наибольшую частоту кривая будет иметь при значении х, равном среднему арифметическому из отдельных вариантов. Средняя арифметическая является центром группирования частот ряда.

4. При t=±1 функция имеет точки перегиба. Это означает, что кривая имеет точки перегиба при отклонениях от центра

группирования 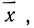Законы распределения случайных величин - определение и вычисление с примерами решения равных среднему квадратическому отклонению.

5. Сумма частостей, лежащих в пределах от а до b, равна определенному интегралу в тех же пределах от функции f(t), т. е.
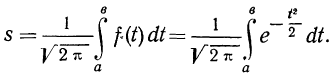
Законы распределения случайных величин - определение и вычисление с примерами решения

Если учесть действительную величину среднего квадратического отклонения, то окажется, что при больших величинах о значение f(t) мало, при малых, наоборот, велико. Отсюда изменяется и форма кривой распределения. При больших 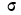Законы распределения случайных величин - определение и вычисление с примерами решения кривая нормального распределения становится плоской, растягиваясь вдоль оси абсцисс. При уменьшении 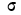Законы распределения случайных величин - определение и вычисление с примерами решения кривая распределения вытягивается вверх и сжимается с боков.

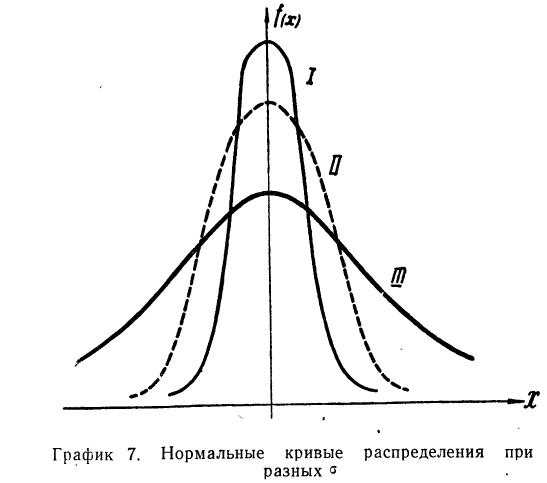
На графике 7 показаны 3 кривые нормального распределения (I, II, III) при 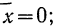Законы распределения случайных величин - определение и вычисление с примерами решения из них кривая I соответствует самому большому, а кривая III—самому малому значению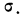 Законы распределения случайных величин - определение и вычисление с примерами решения

Зная общие свойства кривой нормального распределения, рассмотрим те условия, которые приводят к образованию кривых данного типа.

Формирование нормального распределения

Закон нормального распределения является наиболее распространенным законом не только потому, что он наиболее часто встречается, но и потому, что он является предельным законом распределения, к которому приближается ряд других законов распределения.

Нормальное распределение образуется в том случае, когда действует большое число независимых (или слабо зависимых), случайных причин. Подчиненность закону нормального распределения проявляется тем точнее, чем больше случайных величин действует вместе. Основное условие формирования нормального распределения состоит в том, чтобы все случайные величины, действующие вместе, играли в общей сумме примерно одинаковую роль. Если одна из случайных ошибок окажется по своему влиянию резко превалирующей над другими, то закон распределения будет обусловлен действием этой величины.

Если есть основания рассматривать изучаемую величину как сумму многих независимых слагаемых, то при соблюдении указанного выше условия ее распределение будет нормальным, независимо от характера распределения слагаемых.

Нормальное распределение встречается часто в биологических явлениях, отклонениях размеров изделий от их среднего размера, погрешностях измерения и т. д.

Если взять распределение людей по номеру носимой ими обуви, то это распределение будет нормальным. Но это правило применимо только в том случае, когда численность совокупности велика и сама совокупность однородна.

Из того факта, что нормальное распределение встречается нередко в разных областях, не следует, что всякий признак распределяется нормально. Наряду с нормальным распределением существуют другие различные распределения.

Но все же умение выявить нормальное распределение в некоторой эмпирической совокупности является важным условием для ряда практических расчетов и действий. Зная, что эмпирическое распределение является нормальным, можно определить оптимальные размеры предприятий, размеры резервов и т. д.

Важным условием определения характера данной эмпирической кривой является построение на основе эмпирических данных теоретического нормального распределения.

Построение кривой нормального распределения

Первый способ. Для того чтобы построить кривую нормального распределения, пользуются следующей егo формулой:

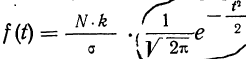
Законы распределения случайных величин - определение и вычисление с примерами решения
где N — число проведенных испытаний, равное сумме частот эмпирического распределения 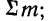Законы распределения случайных величин - определение и вычисление с примерами решения

k — величина интервала дробления эмпирического ряда распределения;

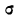Законы распределения случайных величин - определение и вычисление с примерами решения — среднее квадратическое отклонение ряда;

t—нормированное отклонение, т. е. 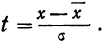Законы распределения случайных величин - определение и вычисление с примерами решения

Величина 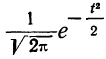Законы распределения случайных величин - определение и вычисление с примерами решения табулирована и может быть найдена по таблице (см. приложение II).

Для нахождения значений теоретических частот (см. пример 1) сначала необходимо найти среднюю арифметическую эмпирического ряда распределения, т. е. 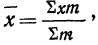Законы распределения случайных величин - определение и вычисление с примерами решения для чего находим произведения хm. 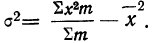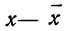Затем находим дисперсию ряда, вос-пользовавшись формулой Законы распределения случайных величин - определение и вычисление с примерами решения Поскольку средняя уже найдена, остается найти для чего по каждой строке находим Законы распределения случайных величин - определение и вычисление с примерами решения (графы 4 и 5). Затем определяем величину t, последовательно записывая для каждой строки Законы распределения случайных величин - определение и вычисление с примерами решения и 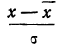(графы 6 и 7). Графа 7 дает величину t по строкам. Из таблицы значений f(t) (см. приложение II) для данных в графе 7 найдем соответствующие величины (графа 8). Осталось найденные величины умножить на общий для всех строк множитель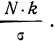 Законы распределения случайных величин - определение и вычисление с примерами решения

Найденная при умножении величина и составляет теоретическую частоту каждого варианта, записанного в строке (графа 9). Ввиду того что частоты могут быть только целыми числами, округляем их до целых и получим теоретические частоты, которые будем обозначать 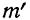Законы распределения случайных величин - определение и вычисление с примерами решения (графа 10).

Пример 1.

В таблице 3 приведено эмпирическое распределение веса 500 спиралей и расчет частот нормального распределения. (Вес спиралей х дан в миллиграммах.)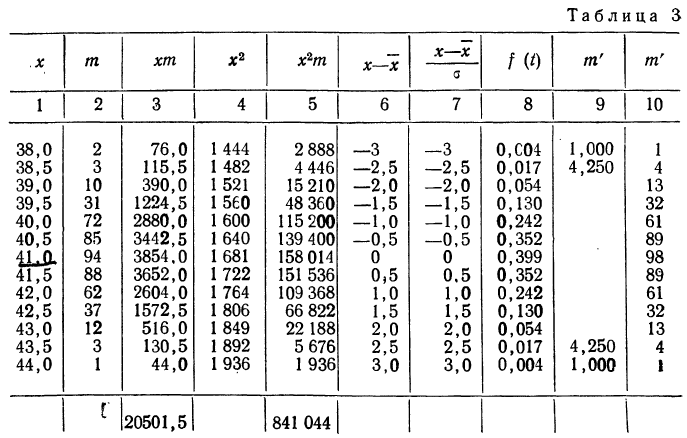 Законы распределения случайных величин - определение и вычисление с примерами решения

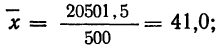
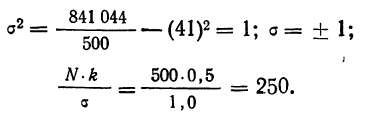
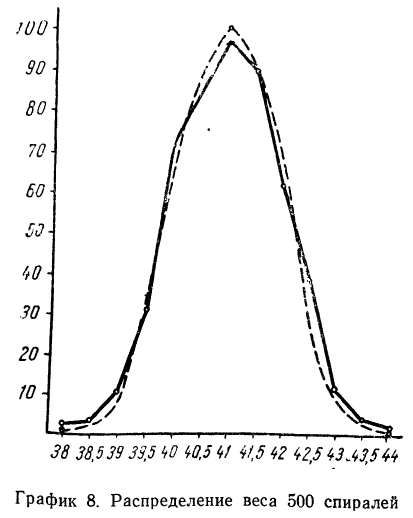
Из таблицы находим: Законы распределения случайных величин - определение и вычисление с примерами решения

Законы распределения случайных величин - определение и вычисление с примерами решения

Строим график эмпирических и теоретических данных. На графике 8 сплошной линией дано изображение эмпирического распределения, а пунктирной — построенного на его основе теоретического распределения.
Законы распределения случайных величин - определение и вычисление с примерами решения

Законы распределения случайных величин - определение и вычисление с примерами решения

Пример 2.

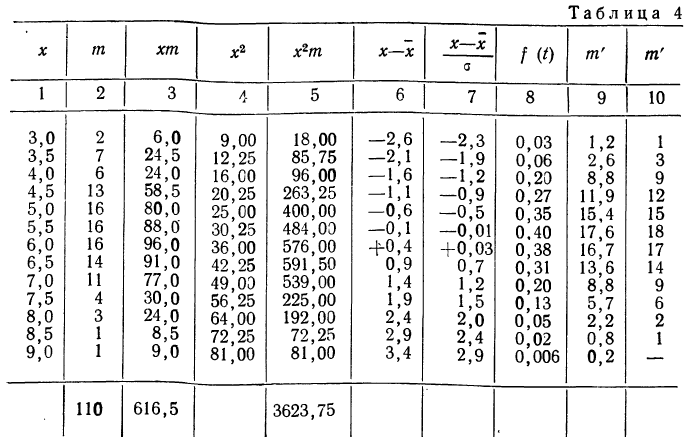
В таблице 4 дается эмпирическое распределение ПО замеров межцентрового расстояния при шевинговании зубцов динамомашины 110412 и расчет теоретических частот.

Исчислим:
Законы распределения случайных величин - определение и вычисление с примерами решения
Построим графики эмпирического и теоретического распределений (см. график 9).

Оба эмпирических распределения хорошо воспроизводятся теоретическим нормальным распределением.

Второй способ построения кривой нормального распределения основан на применении функции стандартизованного нормального распределения, в котором Законы распределения случайных величин - определение и вычисление с примерами решения = 1, т. е. величина наибольшей ординаты принимается за единицу.

За начало отсчета признака при этом способе построения берется его средняя арифметическая. Ей соответствует наибольшая ордината.

Законы распределения случайных величин - определение и вычисление с примерами решения

Вычисление ординат производится по формуле:

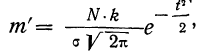
Законы распределения случайных величин - определение и вычисление с примерами решения
где N — число наблюдений;

k — величина интервала эмпирического распределения.

Так как значение наибольшей ординаты получается при

t = 0, когда 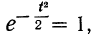Законы распределения случайных величин - определение и вычисление с примерами решения то величина наибольшей ординаты будет:

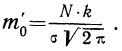
Придавая t последовательно значения 0,5; 1,0; 1,5; 2,0, т. е. сначала меньшие, а потом увеличивающиеся, находим в таблице стандартизованного нормального распределения для данных t соответствующие 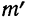Законы распределения случайных величин - определение и вычисление с примерами решения и, умножив полученную величину на значение наибольшей ординаты, будем иметь ординаты для этих значений t.

Например, при t = 0,5 величина стандартизованного нормального распределения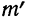 Законы распределения случайных величин - определение и вычисление с примерами решения = 0,8825. Так как величина наибольшей ординаты 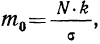то величина ординаты в точке t = 0,5 будет равна:

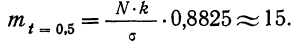
Законы распределения случайных величин - определение и вычисление с примерами решения

Пример 3.

Взяты результаты измерения 100 отклонений шага резьбы х от всей длины резьбы. Получен следующий ряд распределения, для которого по общим правилам производится расчет средней и дисперсии.

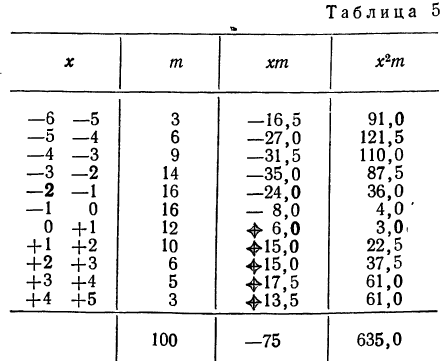
Законы распределения случайных величин - определение и вычисление с примерами решения

Отсюда;
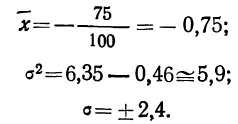
Законы распределения случайных величин - определение и вычисление с примерами решения
Рассчитаем наибольшую ординату:

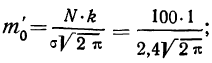
Законы распределения случайных величин - определение и вычисление с примерами решения
так как величина 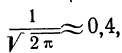то:

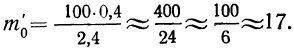
Законы распределения случайных величин - определение и вычисление с примерами решения

Взяв значение t = 0,5 по таблице стандартизованного нормального распределения, находим 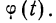Законы распределения случайных величин - определение и вычисление с примерами решения При t = 0,5 оно равно 0,88251. Это и есть коэффициент, который при умножении на значение наибольшей ординаты дает величину ординаты в этой точке. Потом аналогично находим ординаты для t = ± 1 и т. д.

Для данного примера будем иметь:

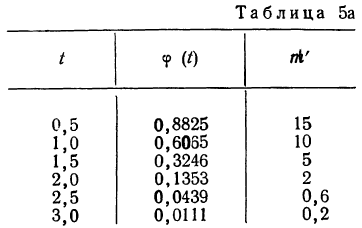
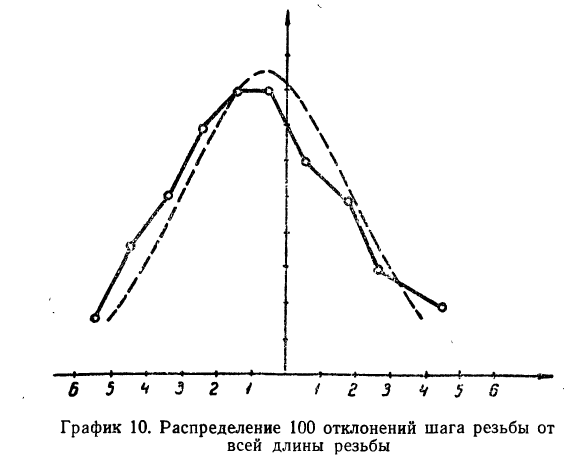
Законы распределения случайных величин - определение и вычисление с примерами решения

Полученный результат наносим на график, а для сравнения наносим на график и результаты непосредственных измерений отклонений (см. график 10).

Как видно из графика, теоретическая кривая довольно близко воспроизводит полигон эмпирического распределения.
Законы распределения случайных величин - определение и вычисление с примерами решения

Пример 4.

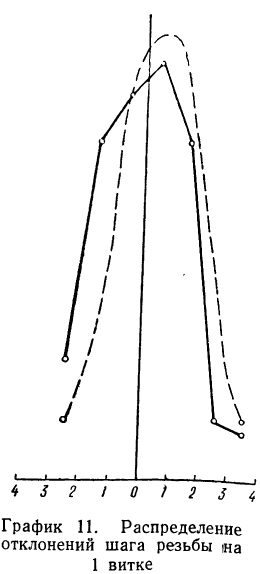
Даны результаты измерений отклонений шага резьбы (х) в микронах на 1 витке от среднего значения. Приводятся эти данные с соответствующими расчетами:
Законы распределения случайных величин - определение и вычисление с примерами решения

Законы распределения случайных величин - определение и вычисление с примерами решения

Теоретические частоты (ординаты) рассчитываются так же, как и в предыдущем примере. Сначала находится величина наибольшей частоты:

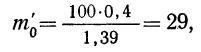
Законы распределения случайных величин - определение и вычисление с примерами решения
затем другие частоты:

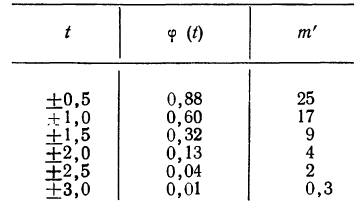
Эмпирические и теоретические частоты наносим на график (см. график 11) и убеждаемся, что эмпирическое распределение довольно близко воспроизводится теоретическим распределением.

Третий способ построения кривой нормального распределения (или вычисления теоретических частот) по имеющимся эмпирическим данным основан на применении функции:
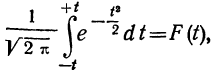
Законы распределения случайных величин - определение и вычисление с примерами решения

которая дает площадь нормальной кривой, заключенной между —t и +t.

Вообще говоря, можно находить площадь нормальной кривой, заключенную между любыми точками Законы распределения случайных величин - определение и вычисление с примерами решения как

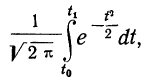
применяя функцию F(t). Искомая площадь будет представлять собой 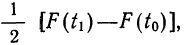причем для отрицательных t надо брать F(t) со знаком минус.

Пример 5.

Получены результаты 208 измерений межцентровых расстояний при шевинговании зубцов шестерни динамо-машины (см. табл. 7). Вычислим нужные параметры и теоретические частоты и построим графики эмпирического и теоретического распределений.

Колонки 1, 2, 3, 4 и 5 необходимы для расчетов 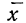Законы распределения случайных величин - определение и вычисление с примерами решения и 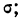в колонке 6 рассчитаны отклонения концов интервалов от средней, в колонке 7 — величина стандартизованного отклонения 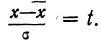Законы распределения случайных величин - определение и вычисление с примерами решения Колонка 8 содержит значения F(t), взятые из приложения III, умноженные на 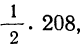т. е. на 104. В верхней строке приведено и значение t для конца интервала, предшествующего первому, т. е.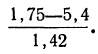 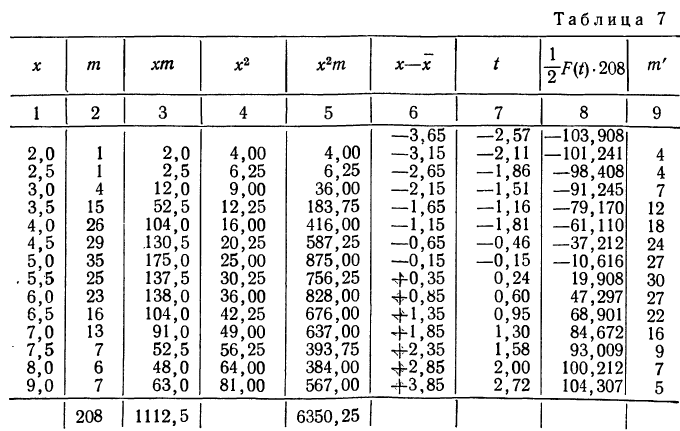Законы распределения случайных величин - определение и вычисление с примерами решения

Чтобы получить теоретическую частоту для каждого интервала, достаточно из верхней строки (в 8-й колонке) вычесть число той же колонки, стоящее строкой ниже.
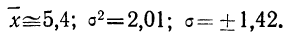
Законы распределения случайных величин - определение и вычисление с примерами решения

На графике 12 показано, что теоретическое распределение достаточно точно отражает эмпирически полученный материал, только наблюдается некоторое смещение теоретической кривой вправо, что, очевидно, вызвано большим удельным весом правого конца эмпирического распределения.

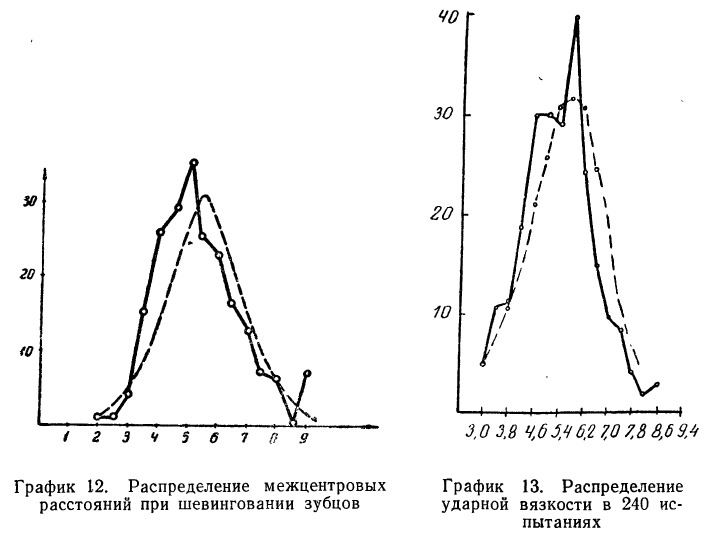
Законы распределения случайных величин - определение и вычисление с примерами решения

Пример 6.

Дается ряд распределения ударной вязкости в 240 испытаниях. Приведем этот ряд распределения и построим для него теоретическое распределение (см. график 13).

Законы распределения случайных величин - определение и вычисление с примерами решения

Критерии согласия

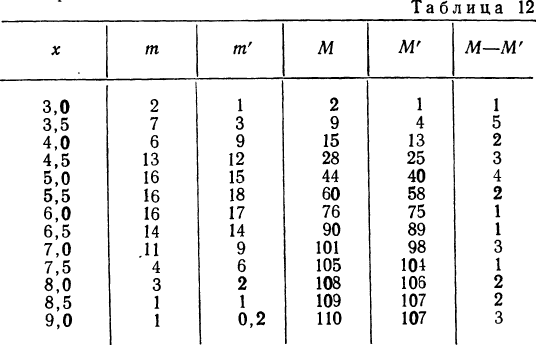
Определение близости эмпирических распределений к теоретическому нормальному распределению по графику может быть недостаточно точным, субъективным и по-разному оценивать расхождения между ними. Поэтому математики выработали ряд объективных оценок для того, чтобы определить, является ли данное эмпирическое распределение нормальным. Такие оценки называются критериями согласия. Критерии согласия были предложены разными учеными, занимавшимися этим вопросом. Рассмотрим критерии согласия Пирсона, Романовского, Колмогорова и Ястремского.

Критерий согласия Пирсона основан на определении величины 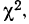Законы распределения случайных величин - определение и вычисление с примерами решения которая вычисляется как сумма квадратов разностей эмпирических и теоретических частот, отнесенных к теоретическим частотам, т. е.

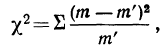
Законы распределения случайных величин - определение и вычисление с примерами решения

где m — эмпирические частоты;

m’ — теоретические частоты.

Для оценки того, насколько данное эмпирическое распределение воспроизводится нормальным распределением, исчисляют по распределению Пирсона вероятности достижения 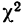Законы распределения случайных величин - определение и вычисление с примерами решения данного значения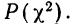

Значения 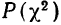Законы распределения случайных величин - определение и вычисление с примерами решения вычислены для разных 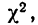табулированы и приводятся в приложении VI, в котором дается комбинационная таблица, где одним из аргументов (данные по строкам) являются значения 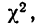Законы распределения случайных величин - определение и вычисление с примерами решения а по другим (по столбцам) —значения k — число степеней свободы варьирования эмпирического распределения. Число степеней свободы вариации определяется для данного ряда распределения и равно числу групп в нем минус число исчисленных статистических характеристик (средняя, дисперсия, моменты распределения и т. д.), использованных при вычислении теоретического распределения.

Пересечение данного столбца с соответствующей строкой дает искомую вероятность 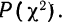Законы распределения случайных величин - определение и вычисление с примерами решения

При вероятностях, значительно отличающихся от нуля, расхождение между теоретическими и эмпирическими частотами можно считать случайным.

Проф. В. И. Романовский предложил более простой метод оценки близости эмпирического распределения к нормальному, используя величину 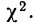Законы распределения случайных величин - определение и вычисление с примерами решения

Он предложил вычислять отношение:

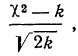
Законы распределения случайных величин - определение и вычисление с примерами решения
где k — число степеней свободы.

Если указанное отношение имеет абсолютное значение, меньшее трех, то предлагается расхождение между теоретическим и эмпирическим распределениями считать несущественным; если же это отношение больше трех, то расхождение существенно. Несущественность расхождения (когда величина отношения Романовского меньше трех) говорит о возможности принять за закон данного эмпирического распределения нормальное распределение.

По данным примера 2 рассчитаем величину Законы распределения случайных величин - определение и вычисление с примерами решения

Пример 7.

Вычисление Законы распределения случайных величин - определение и вычисление с примерами решения Для распределения межцентрового расстояния в НО наблюдениях:

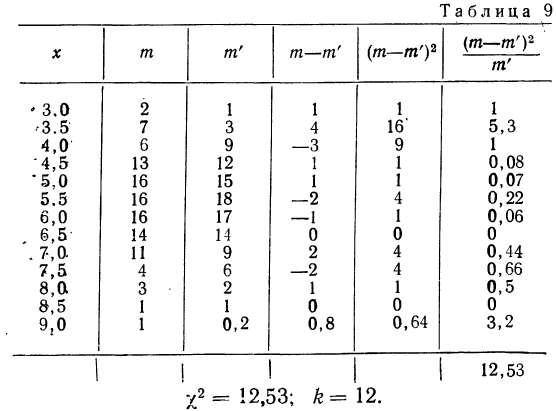
Из таблицы 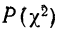Законы распределения случайных величин - определение и вычисление с примерами решения (приложение VI) для 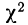= 12 и k = 12 находим вероятность 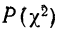=0,4457; она достаточно велика, значит расхождение между теоретическими и эмпирическими частотами можно считать случайными, а распределение — подчиняющимся закону нормального распределения.

Находим отношение Романовского:
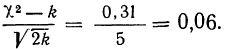
Законы распределения случайных величин - определение и вычисление с примерами решения

Это отношение значительно меньше трех, поэтому расхождение между теоретическими и эмпирическими частотами можно считать несущественными, и, таким образом, теоретическое распределение достаточно хорошо воспроизводит эмпирическое.

Пример 8.

Вычислим критерий 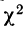Законы распределения случайных величин - определение и вычисление с примерами решения Для распределения веса 500 спиралей.

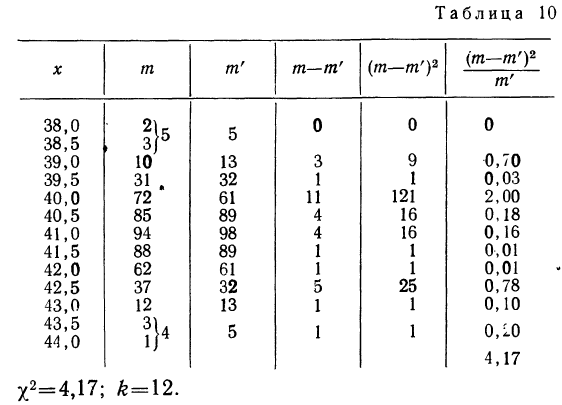
По таблице находим вероятность 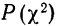Законы распределения случайных величин - определение и вычисление с примерами решения = 0,9834, которая близка к достоверности, и поэтому расхождение между теоретическим и эмпирическим распределением может быть случайным.

Отношение Романовского
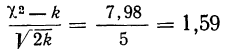
Законы распределения случайных величин - определение и вычисление с примерами решения
также значительно меньше трех, поэтому теоретическое воспро* изведение эмпирического ряда достаточно удовлетворительное.

Критерий 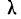Колмогорова. Критерий 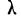Законы распределения случайных величин - определение и вычисление с примерами решения , предложенный А. Н. Колмогоровым, устанавливает близость теоретических и эмпирических распределений путем сравнения их интегральных распределений. 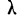Законы распределения случайных величин - определение и вычисление с примерами решения исчисляется исходя из D — максимального верхнего предела абсолютного значения разности их накопленных частот, отнесенного к квадратному корню из числа наблюдений N:

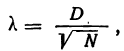
Законы распределения случайных величин - определение и вычисление с примерами решения
где D — максимальная граница разности: — накопленных теоретических частот и М— накопленных эмпирических частот.

Приведем таблицу значений 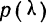Законы распределения случайных величин - определение и вычисление с примерами решения —вероятности того, что достигнет данной величины.

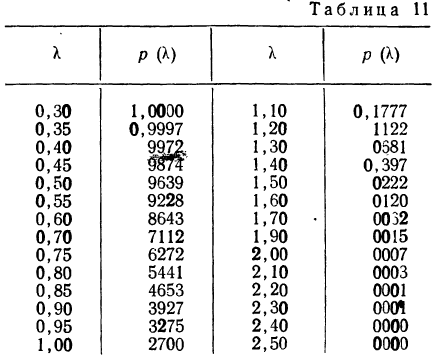
Законы распределения случайных величин - определение и вычисление с примерами решения

Если найденному значению 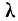Законы распределения случайных величин - определение и вычисление с примерами решения соответствует очень малая вероятность 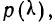то расхождение между эмпирическим и теоретическим распределением нельзя считать случайным и, таким образом, первое мало отражает второе. Наоборот, если 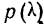Законы распределения случайных величин - определение и вычисление с примерами решения — величина значительная (больше 0,05), то расхождение между частотами может быть случайным и распределения хорошо соответствуют одно другому.

Рассмотрим применение этого критерия на двух примерах.

Пример 9.

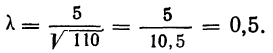
Законы распределения случайных величин - определение и вычисление с примерами решения

Законы распределения случайных величин - определение и вычисление с примерами решения
В таблице вероятностей 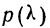находим для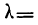

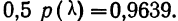
Эта большая вероятность указывает на то, что расхождение между наблюдением и теоретическим распределением вполне могло быть случайным.

Пример 10.

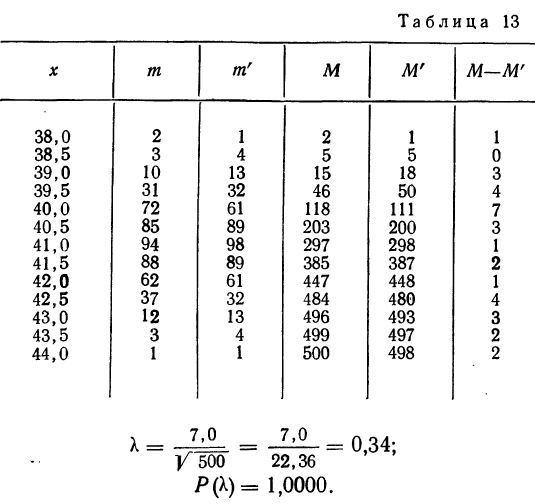
Законы распределения случайных величин - определение и вычисление с примерами решения
Величина вероятности 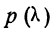показывает несущественность расхождений между теоретическим и эмпирическим распределением.

Критерий Б. С. Ястремского. В общем виде критерий Ястремского можно записать следующим неравенством:

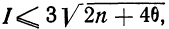
Законы распределения случайных величин - определение и вычисление с примерами решения

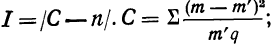
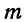где Законы распределения случайных величин - определение и вычисление с примерами решения

— эмпирические частоты;
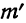— теоретические частоты;
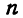— число групп.

Для числа групп, меньших 20, 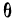Законы распределения случайных величин - определение и вычисление с примерами решения = 0,6; q = 1 — р.

Значение I, меньшее 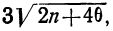Законы распределения случайных величин - определение и вычисление с примерами решения в критерии Ястремского показывает несущественность расхождения между эмпирическими и теоретическими частотами в данном распределении.

При значениях I, больших 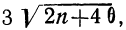Законы распределения случайных величин - определение и вычисление с примерами решения расхождение между теоретическим и эмпирическим распределением существенно.

Пример 11.

Определим величину I и оценим эмпирическое распределение 500 спиралей (m) по сравнению с соответствующим нормальным (m’).
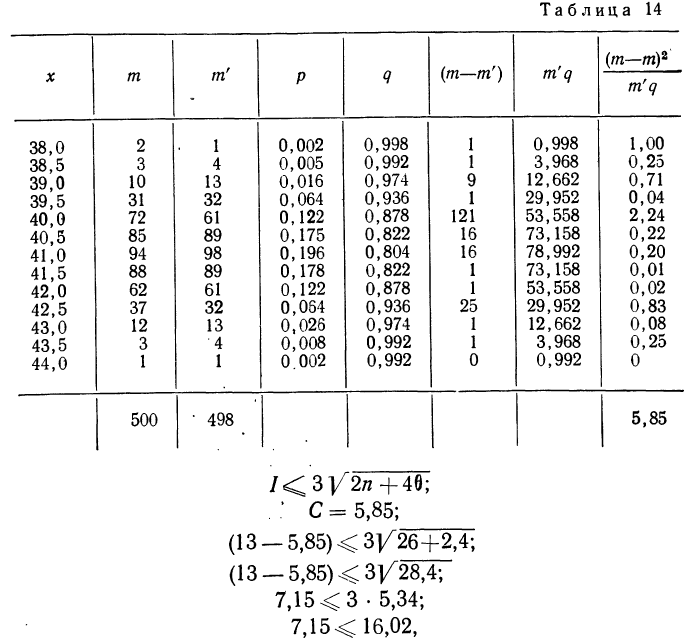
Законы распределения случайных величин - определение и вычисление с примерами решения
что говорит о нормальном распределении исследуемой совокупности.

Элементарные приемы определения «нормальности» распределения. Для определения элементарными способами близости данного опытного распределения к нормальному прибегают к числам Вестергарда и к сравнению средней арифметической, моды и медианы.

Числами Вестергарда являются: 0,3; 0,7; 1,1; 3. Для пользования ими определяют сначала основные характеристики — среднюю арифметическую 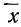Законы распределения случайных величин - определение и вычисление с примерами решения и среднее квадратическое отклонение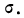

Для того чтобы данное эмпирическое распределение было подчинено закону нормального распределения, необходимо, чтобы распределение удовлетворяло следующим условиям:

в промежутке от 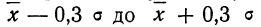была расположена 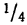часть всей совокупности;
в промежутке от 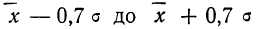была расположена 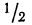часть всей совокупности;
в промежутке от 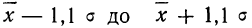было расположено 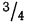всей совокупности;
в промежутках от —3 до +3 было расположено 0,998 всей совокупности.

Для приводимого распределения 500 спиралей по весу (пример 1) все эти условия соблюдаются, что говорит о подчинении данного распределения закону нормального распределения.

К элементарным приемам определения «нормальности» следует отнести применение графического метода, особенно удобное с помощью полулогарифмической сетки Турбина. На сетке накопленные эмпирические частоты при нормальном их распределении дают прямую линию. Всякое отклонение от прямой свидетельствует об отклонении эмпирического распределения от «нормального».

Распределение Пуассона

Вероятности частот событий, редко встречающихся при некотором числе испытаний, находят по формуле:

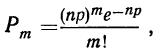
Законы распределения случайных величин - определение и вычисление с примерами решения

где m — частота данного события;

n — число испытаний;

р — вероятность события при одном испытании;

е= 2,71828.

Это выражение носит название закона распределения Пуассона.

Подставим вместо nр среднее число фактически наблюдавшихся случаев в эмпирическом материале. Теоретические ординаты кривой распределения по закону Пуассона m’ найдем по формуле:

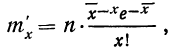
Законы распределения случайных величин - определение и вычисление с примерами решения
где х — переменное значение числа раз;

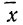Законы распределения случайных величин - определение и вычисление с примерами решения — среднее число раз в эмпирическом распределении;

n — число наблюдений.

При

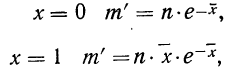
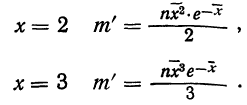
Законы распределения случайных величин - определение и вычисление с примерами решения

Пример 12.

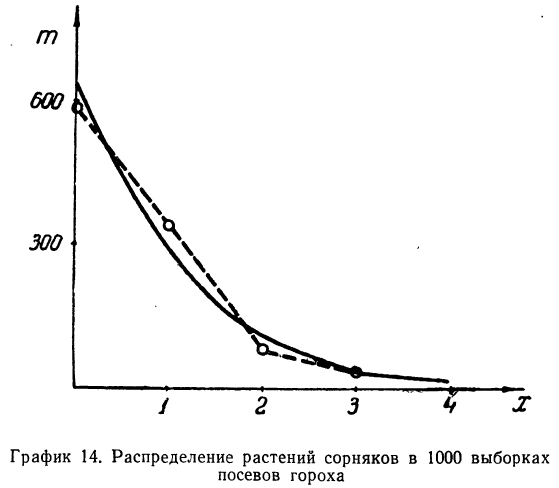
Наблюдалось следующее распределение растений сорняков в 1000 выборках посевов гороха. Результаты эксперимента записаны в следующей таблице:

Законы распределения случайных величин - определение и вычисление с примерами решения

Определим по закону Пуассона теоретические частоты разного числа растений сорняков. Для этого предварительно исчислим среднее число растений сорняков в одной выборке:

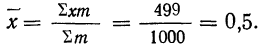
Законы распределения случайных величин - определение и вычисление с примерами решения

Из таблицы находим 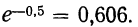Законы распределения случайных величин - определение и вычисление с примерами решения

Определим теоретическое число выборок, в которых число растений сорняков будет равно 0:

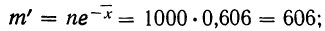
Законы распределения случайных величин - определение и вычисление с примерами решения

то же:

для числа растений сорняков, равного 1:

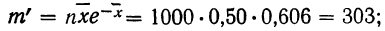
Законы распределения случайных величин - определение и вычисление с примерами решения

для числа растений сорняков, равного 2:

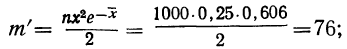
Законы распределения случайных величин - определение и вычисление с примерами решения

для числа растений сорняков, равного 3:

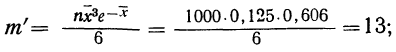
Законы распределения случайных величин - определение и вычисление с примерами решения

для числа растений сорняков более 3:

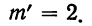
Законы распределения случайных величин - определение и вычисление с примерами решения

Графическое сопоставление обоих распределений говорит о соответствии между эмпирическим и теоретическим распределениями.
Законы распределения случайных величин - определение и вычисление с примерами решения

Распределение Максвелла

В технике часто встречается распределение по закону Максвелла. Это — распределение существенно положительных величин. Например, эмпирическое распределение эксцентриситетов биений теоретически воспроизводится распределением Максвелла.

Дифференциальный закон распределения Максвелла выражается следующей формулой:
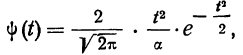
Законы распределения случайных величин - определение и вычисление с примерами решения
где 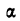— параметр распределения, равный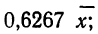

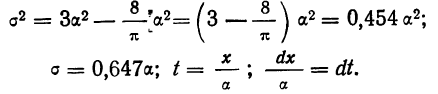
Законы распределения случайных величин - определение и вычисление с примерами решения
Интегральный закон распределения выразится тогда:

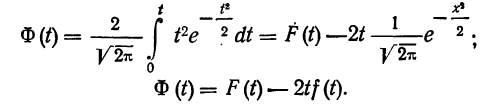
Законы распределения случайных величин - определение и вычисление с примерами решения

Пример 13.

Заимствуем из книги А. М. Длина таблицу распределения симметричности гнезд относительно торцов в круглых плашках (в 0,01 мм) и проведем дополнительные расчеты.
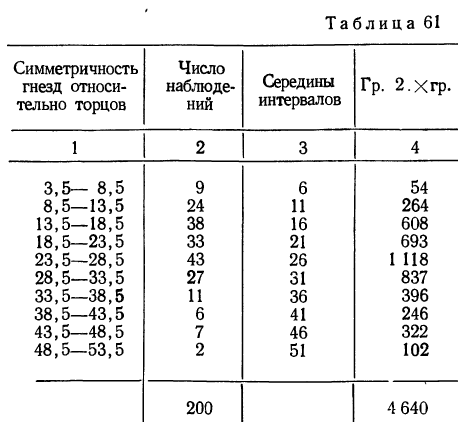
Законы распределения случайных величин - определение и вычисление с примерами решения

Из этой таблицы легко определим среднюю симметричность:
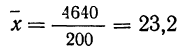
Законы распределения случайных величин - определение и вычисление с примерами решения
и параметр рассеяния:

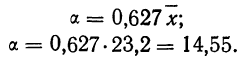
Законы распределения случайных величин - определение и вычисление с примерами решения

Формула интегрального распределения по закону Максвелла позволяет найти накопленные, а затем теоретические частости и частоты.
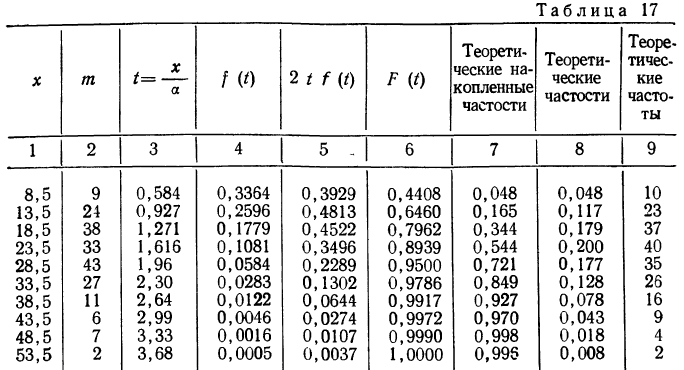
Законы распределения случайных величин - определение и вычисление с примерами решения

Изобразим на графике 15 данные эмпирического и теоретического рядов распределения.

Законы распределения случайных величин - определение и вычисление с примерами решения
Определим близость их по критерию согласия Ястремского. Для этого приведем в табл. 18 расчет величины С:

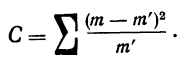
Законы распределения случайных величин - определение и вычисление с примерами решения

По критерию Ястремского находим
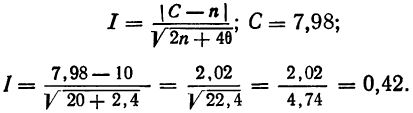
Законы распределения случайных величин - определение и вычисление с примерами решения
Величина I значительно меньше 3. Следовательно, данное эм лирическое распределение хорошо согласуется с законом распределения Максвелла.

Дисперсионный анализ
Математическая обработка динамических рядов
Корреляция – определение и вычисление
Элементы теории ошибок
Статистические оценки
Теория статистической проверки гипотез
Линейный регрессионный анализ
Вариационный ряд

Источник

Вернемся к исходной таблице рассматриваемого
примера, добавив еще одну строку в
которой проставим частость одинаковых
ответов

Размер,	39	40	41	42	43	44	45
Количество,	1	3	4	5	4	2	1	20
Частость,	0,05	0,15	0,2	0,25	0,2	0,1	0,05	1,00

П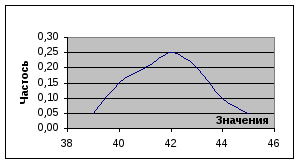редставим
имеющиеся данные в виде графика. Как
видно из графика: – численные значения
изменяются не беспредельно; – чем больше
отклонение от среднего значения, тем
меньше частость ее появления и наоборот.
Следовательно, имеют место элементы,
присущие нормальному закону.

Выдвигаем гипотезу (Высказываем
предположение): случайные величины
распределены по нормальному закону. Но
нормальный закон характерен для
генеральной совокупности, а у нас выборка
ограниченного объема. Насколько приемлема
наша гипотеза?

Вполне очевидно, что при нормальном
законе распределения частости будут
иные. Если они отличаются от опытных
данных несущественно, то можно согласиться
с выдвинутой гипотезой, если отличия
существенные, то придется опровергнуть
гипотезу. Но что значит «несущественно»?
Видимо придется установить какой-либо
критерий. Существуют различные способы
установления критерия, который принято
называть «Критерий согласия». К числу
наиболее распространенных способов
относятся: критерий согласия Пирсона
(
хи – квадрат); Романовского; Колмагорова
и Ястремского.

Сущность всех способов одинакова и
сводится к определению опытного значения
критерия согласия и сравнению его с
некоторым теоретическим значением.
Если опытное значение критерия согласия
превосходит теоретическое его значение,
то гипотеза отвергается, если не
превосходит, то принимается. Наиболее
распространенным является критерий
согласия Пирсона
(
хи – квадрат). Рассмотрим порядок
проведения расчетов при использовании
этого способа.

Формулируем основную гипотезу: опытное
распределение соответствуют теоретическому
распределению, что записывается в виде
.
Тогда конкурирующая гипотеза.

Опытное значение критерия согласия
рассчитывают по формуле
,

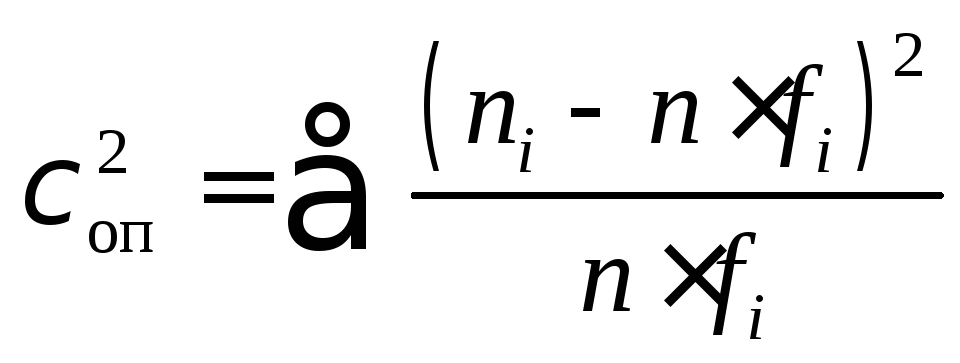где	n	– общее число опытов;
		– число значений, оказавшихся в i–м интервале по результатам опыта;
		– теоретическая частость попадания в i–ый интервал;
		– число значений в i–м интервале, которое соответствует теоретическому распределению.

По физическому смыслу критерий согласия
Пирсона–
это мера отклонений опытных данных от
теоретических.

Для того чтобы найти теоретическую
частость
попадания вi–ый
интервал, необходимо сначала вычислить
отклонения от среднего значения и это
отклонение выразить в среднем
квадратическом отклонении для генеральной
совокупности, т.е..
Например,.

Результаты аналогичных расчетов сведем
в таблицу

Размер,	39	40	41	42	43	44	45
	-1,86	-1,22	-0,58	0,06	0,71	1,35	1,99

Затем, используя таблицу функции
распределения нормального закона
найти соответствующие значения.
Например, первому столбцу должно
соответствовать значение

f(39)=F(-1,86)–F(-1,22),

второму столбцу f(40)=F(-0,58)-F(-1,22)
и т.д.

Примечание.При отсутствии таблицы
можно воспользоваться компьютером. Для
этого вExcelв какой-либо
столбец ввести значения.Выделить
ячейку рядом с первым числом, вызвать
Статистические функции, НОРМСТРАСП и
в появившемся подменю указать первое
числох = –1,86. Ок. В ячейке появится
0,031, соответствующее

F(-1,86). Аналогично дляF(-1,22)= 0,111.

Вычитая, имеем

f(39)=F(-1,26)–F(-1,52)=
0,111-0,031=0,080.

Аналогичные и последующие расчеты
заносим в таблицу

Размер,	39	40	41	42	43	44	45
	-1,86	-1,22	-0,58	0,06	0,71	1,35	1,99
	0,031	0,111	0,281	0,524	0,761	0,911	0,977
	0.080	0.170	0.243	0.237	0.150	0.065	0.019
	1	3	4	5	4	2	1
	0,222	0,046	0,152	0,014	0,328	0,371	1,008

Суммируя последнюю строку, получим

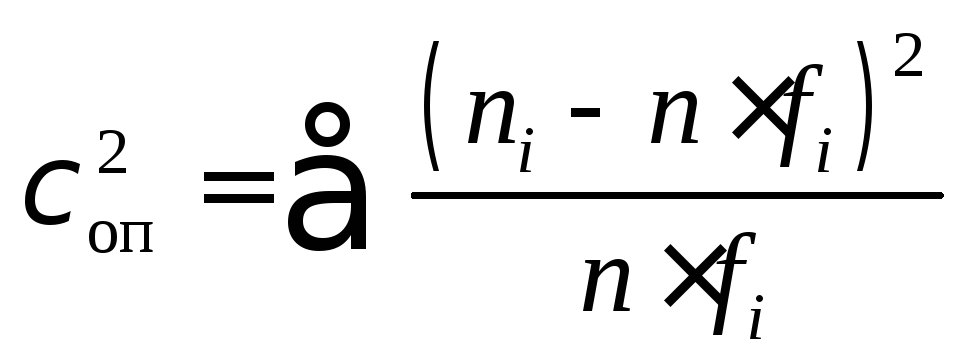=2,142.

Необходимо сравнить опытное значение
с теоретическим значением. Теоретическое
значениенаходят по специальным таблицам, Входом
в таблицу является гарантированная
вероятность и число степеней свободы.
Число степеней свободы находят по
формуле,
гдеk– число разрядов
в таблице (в нашем случае число столбцовk=7);s–
число наложенных связей. Одна связь
присутствует всегда. Действительно,
если сумма вероятностей равна единице,
тоn-1 значений могут
быть любыми, а одна всегда равна.
Если потребуем равенства,
то это еще одна связь. Если потребуем
равенства дисперсий, то это еще одна
связь. Итого три. Следовательно, число
степеней свободы.
По таблице, для уровня значимости,
при,
находим.

Вывод. Так как
,
то с вероятностью 90% можно утверждать,
что нет оснований для того, чтобы
отвергнуть гипотезу. Вероятность того,
что мы ошибаемся равна.

Примечание. При отсутствии таблицы
можно воспользоваться компьютером. Для
этого вExcel вызвать
Статистические функции, ХИ2ОБР и в
появившемся подменю указать Вероятность
0,1, Степеней свободы 4. Ок. Прочитать
ответ 7,77944.

Пример 1. 2.В казино поступила жалоба,
что игральная кость с неравномерным
выпадением очков. Необходимо проверить
следуют ли экспериментальные данные
закону равной вероятности. Для решения
этой задачи проведен эксперимент, в
котором произведено 600 бросаний.

Используем критерий χ². Основная
гипотезаНо:,
конкурирующая гипотеза.
Результаты эксперимента и промежуточные
расчеты отражены в таблице.

Число очков,	Их число в эксперименте,	Теоретическое значение		Примечание
1	101	100	0.01
2	86	100	1.96
3	107	100	0.49
4	94	100	0.36
5	97	100	0.09
6	115	100	2.25
Всего	600	600	5,16

Суммируя, находим

Число степеней свободы:
;k=6 – число строк;s=3.
Следовательно, r
=6-3=3.

.
Так как,
то нет оснований для того, чтобы отвергнуть
гипотезу о равномерном выпадении очков.
Отклонения–следствие случайности.
Вероятность того, что мы ошибаемся
составляет 5%.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Определение[править | править код]

Классификация распределений[править | править код]

Дискретные распределения[править | править код]

Решётчатые распределения[править | править код]

Абсолютно непрерывные распределения[править | править код]

Сингулярные распределения[править | править код]

Таблица основных распределений[править | править код]

Примечания[править | править код]

Литература[править | править код]

См. также[править | править код]

Формулы: законы распределения случайных величин

Каталог формул по теории вероятности онлайн

Законы распределения на этой странице

Дискретные случайные величины

Биномиальное распределение ДСВ

Пуассоновское распределение ДСВ

Геометрическое распределение ДСВ

Гипергеометрическое распределение ДСВ

Непрерывные случайные величины

Показательное распределение НСВ

Равномерное распределение НСВ

Нормальное распределение или распределение Гаусса НСВ

Решенные задачи по теории вероятностей

Полезные ссылки

Функция распределения

Плотность распределения

Биномиальное распределение

Нормальное распределение

Эмпирические и теоретические распределения

Свойства кривой нормального распределения

Формирование нормального распределения

Построение кривой нормального распределения

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Пример 5.

Пример 6.

Критерии согласия

Пример 7.

Пример 8.

Пример 9.

Пример 10.

Пример 11.

Распределение Пуассона

Пример 12.

Распределение Максвелла

Пример 13.

Вам также может понравиться

Майнкрафт как найти незеритовую крепость

Как мне найти подругу на ночь

Как найти свой арбитражный суд

Добавить комментарий Отменить ответ