Преподаватель который помогает студентам и школьникам в учёбе.
Определение видимости в начертательной геометрии с примерами
Определение видимости:
Точки, расположенные на одной проецирующей прямой, называются конкурирующими.
Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).
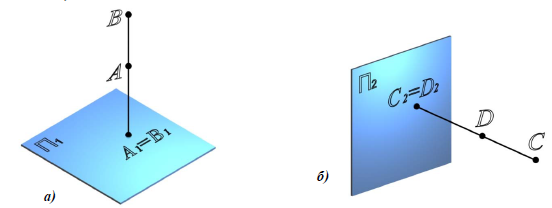
Рис. 7.1. Конкурирующие точки:
а – относительно горизонтальной плоскости проекций;
б – относительно фронтальной плоскости проекций
Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D – невидима).
Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).
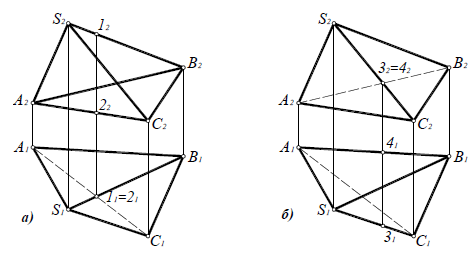
Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже:
а – относительно горизонтальной плоскости проекций;
б – относительно фронтальной плоскости проекций
Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П1, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П1.
- Заказать чертежи
Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П2.
- Конструктивное отображение пространства
- Чертежи точки, отрезка прямой
- Чертежи плоскости
- Взаимное положение двух плоскостей, прямой линии и плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Геометрические тела
- Комплексный чертеж
Определение видимости точек, прямых и плоских фигур.
Видимость
— это изображение на чертеже только
тех точек, прямых и поверхностей
(плоскостей) предметов, которые расположены
ближе к наблюдателю. Изображение
предметов с учетом видимости улучшает
восприятие их формы и размещения в
пространстве.
Определение
видимости — это определение точек
предмета, лежащих на одном луче
проецирования (называемых конкурирующими),
и обозначение на чертеже только тех из
них, которые расположены по этому лучу
ближе к наблюдателю.
в
F’
С’
Г
Рис. 3.16

Если
необходимо указать невидимые точки, их
обозначения на плоскости проекций, где
проекции точек совпадают, заключают в
круглые скобки. Невидимые линии
изображаются на чертеже штриховыми
линиями.
Определение
видимости осуществляется как при
центральном, так и при параллельном
проецировании.
Граничными точками
видимости называются точки, разделяющие
зоны видимости и невидимости прямых и
поверхностей (плоскостей).
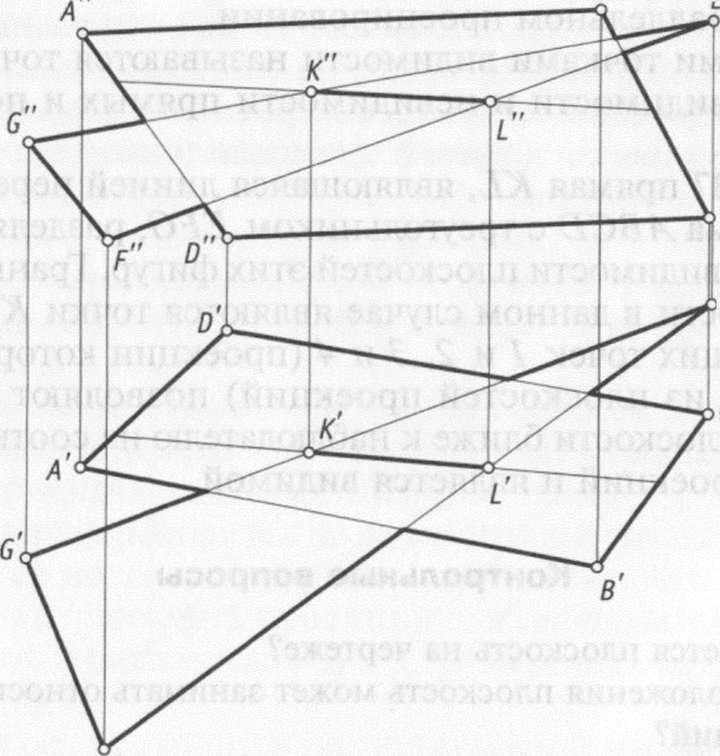
На
рис. 3.17 прямая АХ, являющаяся линией
пересечения параллелограмма ABCD с
треугольником EFG, разделяет зоны видимости
и невидимости плоскостей этих фигур.
Граничными точками видимости в данном
случае являются точки К и L, а пары
конкурирующих точек 1 и 2, 3 и 4 (проекции
которых совпадают на одной из
плоскостей проекций) позволяют определить,
какая часть плоскости ближе к наблюдателю
на соответствующей плоскости проекций
и является видимой.
Контрольные
вопросы
-
Как задается
плоскость на чертеже? -
Какие
положения плоскость может занимать
относительно плоскостей проекций? -
Как определить
на чертеже восходящую и нисходящую
плоскости общего положения? -
Какие положения
занимают горизонтально-проецирующая,
фрон- тально-проецирующая и
профильно-проецирующая плоскости? -
Как определить
углы между проецирующими плоскостями
и плоскостями проекций? -
Где располагается
проекция любой точки, находящейся в
проецирующих плоскостях? -
Какие положения
занимают плоскости уровня? -
Как определяются
углы наклона плоскости уровня к
плоскостям проекций? -
Каково условие
принадлежности точки плоскости? -
Дайте определения
горизонтали, фронтали и профильной
прямой плоскости. -
Каковы условия
параллельности прямой и плоскости? -
Как могут
располагаться две плоскости относительно
друг друга?
Глава 4. Способы преобразования чертежа
Использование
частных положений прямых линий и плоских
фигур относительно плоскостей проекций
значительно упрощает построение чертежа
и позволяет отобразить натуральные
размеры прямых линий, плоских фигур,
расположенных на одной плоскости
проекций, и расстояний между ними. Для
такого преобразования чертежа используют:
-
введение
дополнительных плоскостей проекций
таким образом, чтобы прямая линия или
плоская фигура, не изменяя своего
положения в пространстве, оказалась в
каком-либо частном положении в новой
системе плоскостей проекций — способ
перемены плоскостей проекций; -
изменение
положения прямой линии или плоской
фигуры посредством поворота вокруг
некоторой оси таким образом, чтобы
прямая или плоская фигура оказалась в
частном положении относительно
неизменной системы плоскостей проекций
— способ вращения.
Преобразование
чертежа (для достижения необходимого
результата) при определении натуральных
размеров отрезков и углов может
осуществляться многократно одним или
разными способами.
Способ
перемены плоскостей проекций.
При использовании способа перемены
плоскостей проекций (рис. 4.1) положение
точек, линий, плоских фигур, поверхностей
в пространстве остается неизменным, а
система щ, п2 дополняется плоскостями,
образующими с щ или п2, или между собой
системы двух взаимно-перпендикулярных
плоскостей, принимаемых за плоскости
проекций.
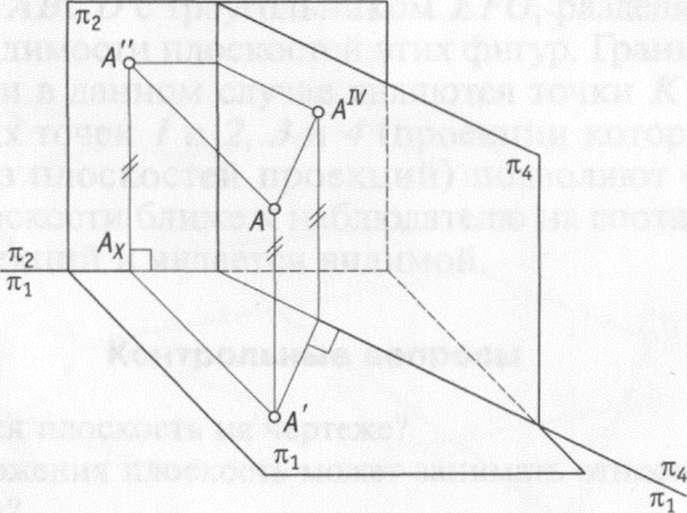
Рис. 4.1

При введении
дополнительной плоскости проекций
проводят новую ось системы проекций
(рис. 4.2), разделяющую две плоскости
проекций в новой системе проекций. При
этом новую ось проводят либо параллельно,
либо перпендикулярно проекциям прямых,
чтобы получить частное положение этих
прямых в новой системе проекций.
При построении в
новой системе плоскостей следует
соблюдать те же условия положения
наблюдателя, которые были установлены
в первоначальной системе проекций.
Если новая ось
проводится на горизонтальной плоскости,
значит, изменяется положение фронтальной
плоскости проекций и дополнительная
плоскость проекций для наблюдателя
становится фронтальной. Наблюдатель
при этом перемещается в горизонтальной
плоскости.
Если
новая ось проводится на фронтальной
плоскости, значит, изменяется положение
горизонтальной плоскости проекций и
дополнительная плоскость проекций для
наблюдателя становится горизонтальной.
Наблюдатель при этом перемещается в
фронтальной плоскости.
Таким образом,
наблюдатель может рассматривать предметы
с любой стороны.
Дополнительные
плоскости по мере построения обозначают
тг4, 7с5и т.д. Обозначения дополнительных
плоскостей представляют собой как бы
числитель и знаменатель дроби,
разделительной чертой которой является
ось проекций, причем их обозначения
располагаются по ту сторону оси, где
должны размещаться соответствующие
проекции.
На
рис. 4.2 показано определение угла наклона
плоскости треугольника к фронтальной
(введением дополнительной плоскости
я6) и горизонтальной (введением
дополнительной плоскости я4) плоскостям
проекций посредством одной их перемены
и определение натурального размера
треугольника ЛВС выполнением двух
перемен плоскостей проекций (введением
дополнительных плоскостей я4, тс5).
Способ
вращения.
При вращении вокруг некоторой неподвижной
прямой — оси вращения — каждая точка
вращаемой фигуры перемещается в
плоскости, перпендикулярной этой оси
(т.е. плоскости вращения).
Точка
вращаемой фигуры перемещается по
окружности, центр которой находится в
точке пересечения оси вращения этой
фигуры с плоскостью вращения, называемой
центром вращения, а радиус этой окружности
равен расстоянию от вращаемой точки до
центра вращения и называется радиусом
вращения.
Если какая-либо
из точек данной системы находится на
оси вращения, то при ее вращении эта
точка считается неподвижной.
Ось
вращения может быть задана или выбрана.
В последнем случае ее выгодно располагать
перпендикулярно одной из плоскостей
проекций, так как при этом упрощаются
построения.
Действительно,
если ось вращения перпендикулярна,
например, плоскости тс2, то плоскость,
в которой происходит вращение точки,
параллельна плоскости п2. Следовательно,
траектория этой точки на плоскость п2
проецируется в виде окружности без
искажения, а на плоскость 7Cj — в виде
отрезка прямой линии (рис. 4.3).
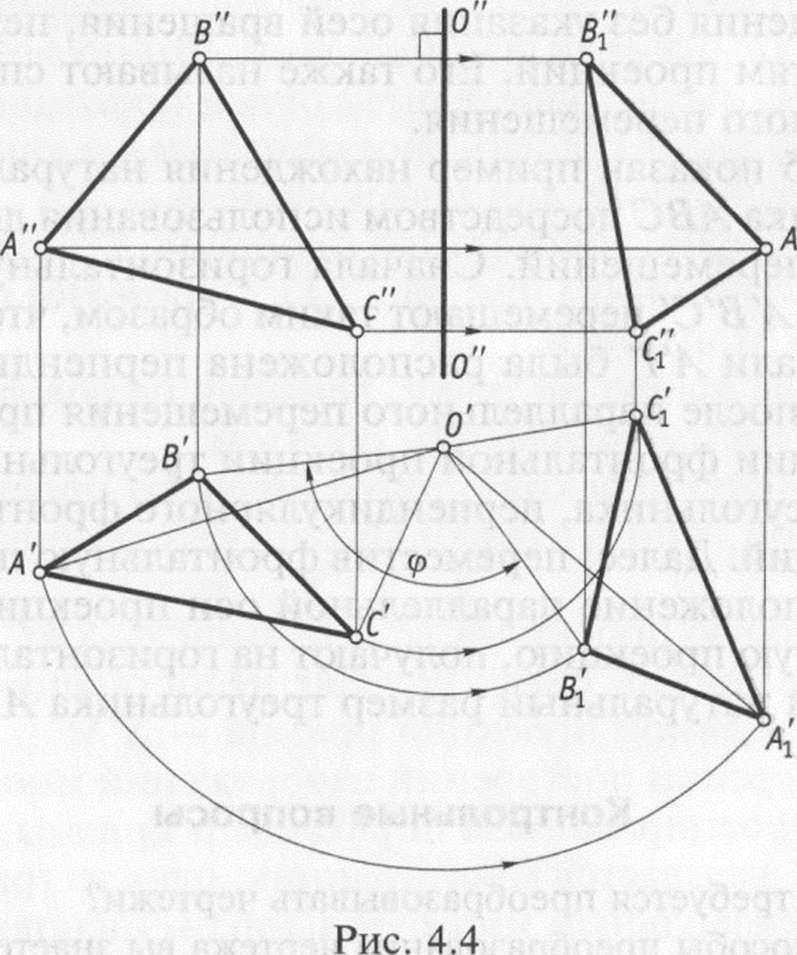
На
рис. 4.4 показан поворот треугольника
ABC вокруг выбранной оси О на угол ср.
Если
вращать отрезок прямой линии или плоскую
фигуру вокруг оси, перпендикулярной
плоскости проекций, то проекция на эту
плоскость не изменится ни по виду, ни
по размеру, изменится лишь положение
этой проекции относительно оси проекций.
Что же касается проекции на плоскость,
параллельную оси вращения, все ее точки
(за исключением, конечно, точек, проекции
которых расположены на оси вращения)
перемещаются по прямым, параллельным
оси проекций, и, следовательно, изменяются
ее форма и размер. В этом случае можно
не указывать проек цию оси вращения, не
устанавливать радиус вращения, а, не
изменяя вид и размер одной из проекций
заданной плоской фигуры, переместить
ее в требуемое положение и построить
другую проекцию с помощью линий,
параллельных оси проекций.
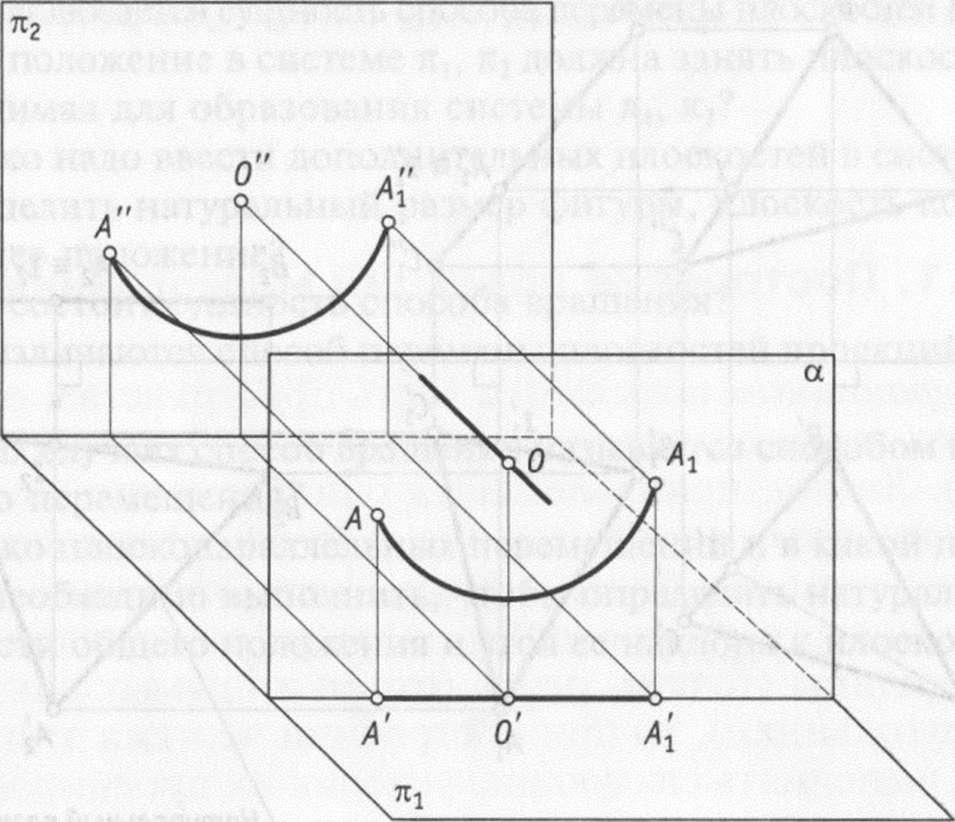
Рис. 4.3
33
Натуральный размер
Рис. 4.5
Данный
способ преобразования чертежа получил
название способа вращения без указания
осей вращения, перпендикулярных
плоскостям проекций. Его также называют
способом плоскопараллельного перемещения.
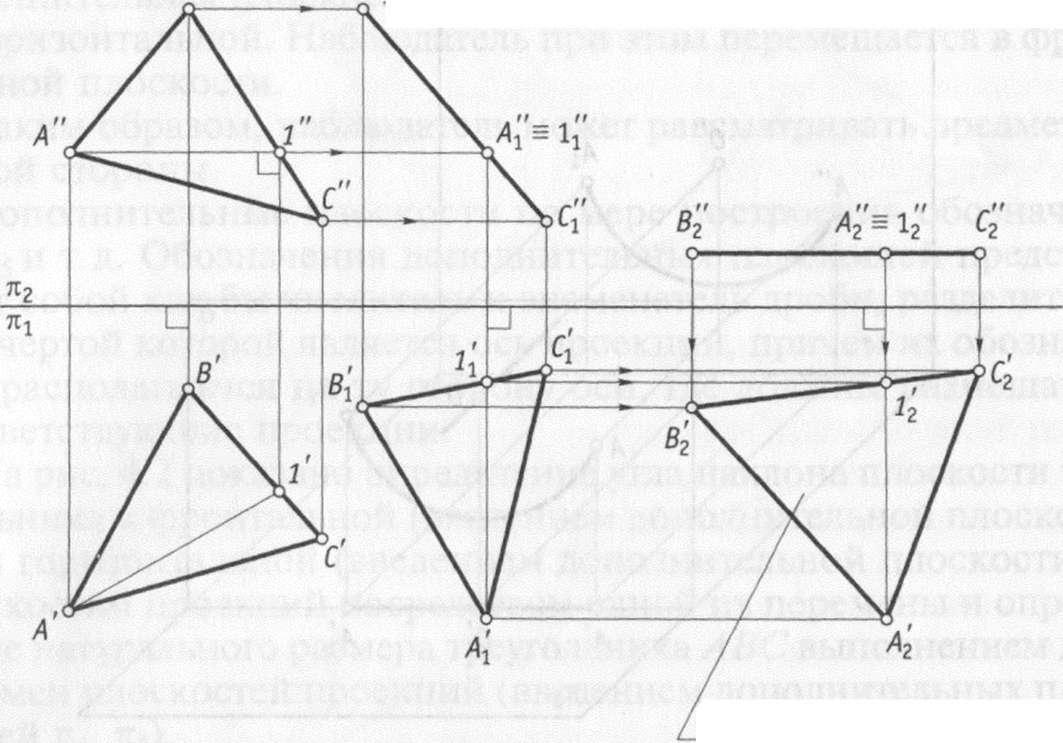
На
рис. 4.5 показан пример нахождения
натурального размера треугольника ABC
посредством использования двух
плоскопараллельных перемещений. Сначала
горизонтальную проекцию треугольника
А’В’С’ перемещают таким образом, чтобы
проекция его горизонтали AT была
расположена перпендикулярно оси
проекций, и после параллельного
перемещения проекций точек при построении
фронтальной проекции треугольника
получают плоскость треугольника,
перпендикулярного фронтальной плоскости
проекций. Далее, переместив фронтальную
проекцию треугольника в положение
параллельной оси проекций и построив
горизонтальную проекцию, получают на
горизонтальной плоскости проекций
натуральный размер треугольника ЛВС.
Контрольные
вопросы
-
Для чего требуется
преобразовывать чертежи? -
Какие способы
преобразования чертежа вы знаете? -
В чем заключается
сущность способа перемены плоскостей
проекции? -
Какое
положение в системе щ9 к2 должна занять
плоскость я3 проекций, вводимая для
образования системы я4, Я|? -
Сколько
надо ввести дополнительных плоскостей
в систему яь тс2, чтобы определить
натуральный размер фигуры, плоскость
которой занимает общее положение? -
В чем состоит
сущность способа вращения? -
Чем различаются
способ перемены плоскостей проекций
и способ вращения? -
В каких случаях
способ вращения называется способом
плоскопараллельного перемещения? -
Сколько
плоскопараллельных перемещений и в
какой последовательности необходимо
выполнить, чтобы определить натуральный
размер плоскости общего положения и
угол ее наклона к плоскостям проекций?
3.1. Способы задания плоскости на ортогональных чертежах
Положение плоскости в пространстве определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, взятой вне прямой;
- двумя пересекающимися прямыми;
- двумя параллельными прямыми;
- плоской фигурой.
В соответствии с этим на эпюре плоскость может быть задана:
- проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
- проекциями точки и прямой (Рисунок 3.1,б);
- проекциями двух пересекающихся прямых (Рисунок 3.1,в);
- проекциями двух параллельных прямых (Рисунок 3.1,г);
- плоской фигурой (Рисунок 3.1,д);
- следами плоскости;
- линией наибольшего ската плоскости.
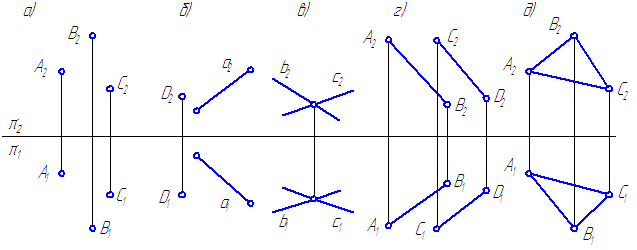
Рисунок 3.1 – Способы задания плоскостей
Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
Плоскость общего положения может иметь три следа: горизонтальный – απ1, фронтальный – απ2 и профильный – απ3, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π1, фронтальной π2 и профильной π3 (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения
3.2. Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости: все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения
3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости
α = m // n D ∈ n ⇒ D ∈ α

Рисунок 3.6 – Принадлежность прямой плоскости
left.begin{array}{l}alpha=mparallel n,\Dinalpha\Cinalpha\end{array}right} Longrightarrow CDinalpha
Упражнение
Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С.

Рисунок 3.7 – Решение задачи
Решение:
- ABCD – плоский четырехугольник, задающий плоскость.
- Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
- Согласно признаку пересекающихся прямых, построим фронтальную проекцию точки пересечения этих прямых — K: A2C2 ∩ B2D2=K2.
- Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD: на проекции диагонали B1D1 строим К1.
- Через А1К1 проводим проекцию диагонали А1С1.
- Точку С1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А1К1.
3.4. Главные линии плоскости
В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).
Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1) (Рисунок 3.8, а; 3.9).
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2) (Рисунок 3.8, б; 3.10).
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π3) (Рисунок 3.8, в; 3.11).
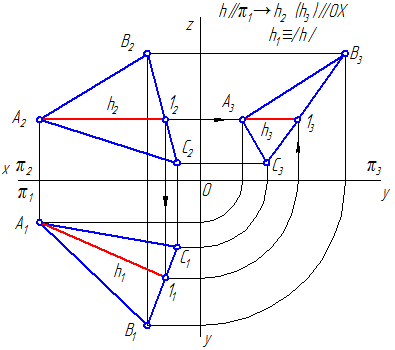
Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником
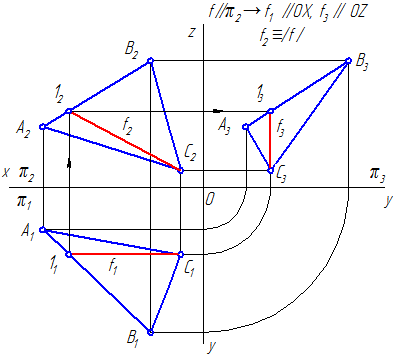
Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником
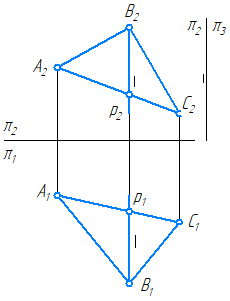
Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости: прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).
alpha=mcap n\left.begin{array}{l}a_2parallel m_2\a_1parallel m_1\end{array}right} Rightarrow aparallelalpha

Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
- Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
- Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
- Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.
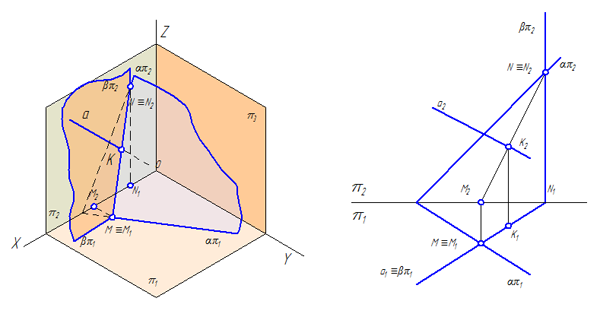
Рисунок 3.13 – Построение точки встречи прямой с плоскостью
Упражнение
Заданы: прямая АВ общего положения, плоскость σ⊥π1. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.
Решение:
-
- Точка К должна принадлежать прямой АВ ⇒ К1∈А1В и заданной плоскости σ ⇒ К1∈σ, следовательно, К1 находится в точке пересечения проекций А1В1 и σ1;
- Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ1 (горизонтальный след плоскости);
- Фронтальную проекцию точки К находим посредством линии проекционной связи: К2∈А2В2.
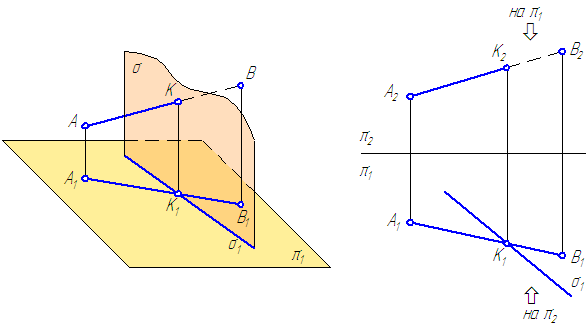
Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения
Упражнение
Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).
Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью
Решение:
- Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
- Если α⊥π1, то на плоскость проекций π1 плоскость α проецируется в прямую (горизонтальный след плоскости απ1 или α1), совпадающую с E1F1;
- Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
- Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.
Алгоритм решения задачи (Рисунок 3.15, б): Через EF проведем вспомогательную плоскость α:
- left.begin{array}{l}alpha perp pi_1\alphain EF\end{array}right} Longrightarrow alpha_1in E_1F_1
- alphacapsigma=(1-2)left.begin{array}{l}|alpha_1cap A_1C_1=1_1longrightarrow 1_2\|alpha_1cap A_1B_1=2_1longrightarrow 2_2\end{array}right.
- (1_2-2_2)cap E_2F_2=K_2\left.begin{array}{l}Kin EF\Kin (1-2)Rightarrow Kinsigma\end{array}right}Longrightarrow K=EFcap (sigma =triangle ABC)
3.6. Определение видимости методом конкурирующих точек
При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π1 или π2.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π2 (рис. 3.15)
Выберем точки, конкурирующие на π2 – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π2.
Направление взгляда на π2 показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π2, видно, что точка 41 располагается ближе к наблюдателю, чем 31.
41∈E1F1 ⇒ 4∈EF ⇒ на π2 будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π1.
Для определения видимости выберем точки, конкурирующие на π1 – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π1.
Направление взгляда на π1 показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π1, видно, что точка 22 располагается ближе к наблюдателю, чем 52.
22∈А2В2 ⇒ 2∈АВ ⇒ на π1 будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.
3.7. Перпендикулярность прямой плоскости
Признак перпендикулярности прямой плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости
Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)
Теорема доказывается через теорему о проецировании прямого угла в частном случае.
Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).
Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.
- Построим горизонталь и фронталь в плоскости σ=ΔАВС : σ=ΔАВС : A-1∈σ; A-1//π1; С-2∈σ; С-2//π2.
- Восстановим из точки K перпендикуляр к заданной плоскости: p1⊥h1 и p2⊥f2, или p1⊥απ1 и p2⊥απ2.
3.8. Взаимное положение двух плоскостей
3.8.1. Параллельность плоскостей
Две плоскости могут быть параллельными и пересекающимися между собой.
Признак параллельности двух плоскостей: две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Упражнение
Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).
Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной
Решение: В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.
- Через точку F проводим прямую m, параллельную, например, АВ.
- Через точку F, или же через любую точку, принадлежащую m, проводим прямую n, параллельную, например, ВС, причём m∩n=F.
- β = m∩n и β//α по определению.
3.8.2. Пересечение плоскостей
Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.
Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.
Упражнение
Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей. 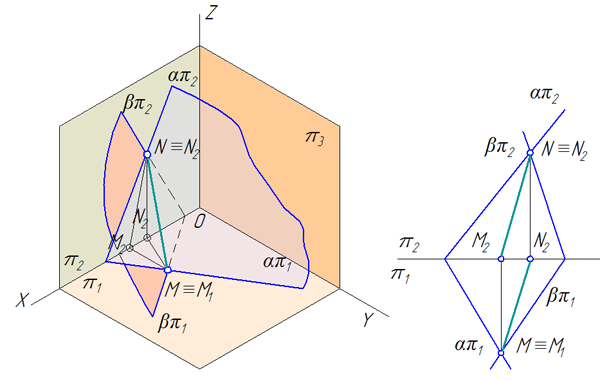
Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами
Порядок построения линии пересечения плоскостей:
- Найти точку пересечения горизонтальных следов — это точка М (её проекции М1 и М2, при этом М1=М, т.к. М – точка частного положения, принадлежащая плоскости π1).
- Найти точку пересечения фронтальных следов — это точка N (её проекции N1 и N2, при этом N2=N, т.к. N – точка частного положения, принадлежащая плоскости π2).
- Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М1N1 и М2N2.
МN – линия пересечения плоскостей.
Упражнение
Задана плоскость σ = ΔАВС, плоскость α – горизонтально- проецирующая (α⊥π1) ⇒α1 – горизонтальный след плоскости (Рисунок 3.19). Построить линию пересечения этих плоскостей.
Решение:
Так как плоскость α пересекает стороны АВ и АС треугольника АВС, то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L, то есть K1 и L1 , на пересечении горизонтального следа (α1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС: А1В1 и A1C1. После чего посредством линий проекционной связи находим фронтальные проекции этих точек K2 и L2 на фронтальных проекциях прямых АВ и АС. Соединим одноимённые проекции: K1 и L1; K2 и L2. Линия пересечения заданных плоскостей построена.
Алгоритм решения задачи:
left.begin{array}{l}ABcapsigma=K\ACcapsigma=L\end{array}right} left.begin{array}{l}Rightarrow A_1B_1capsigma_1=K_1 rightarrow K_2\Rightarrow A_1C_1cap sigma_1=L_1 rightarrow L_2\end{array}right.
KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения
Упражнение
Заданы плоскости α = m//n и плоскость σ = ΔАВС (Рисунок 3.20). Построить линию пересечения заданных плоскостей. Решение:
- Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
- В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π2; τ⊥π2.
- Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:
— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7); — результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).
- Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях σ и β, то есть на прямой пересечения этих плоскостей;
- Аналогично находим точку N, общую для плоскостей σ и β.
- Соединив точки M и N, построим прямую пересечения плоскостей σ и β.
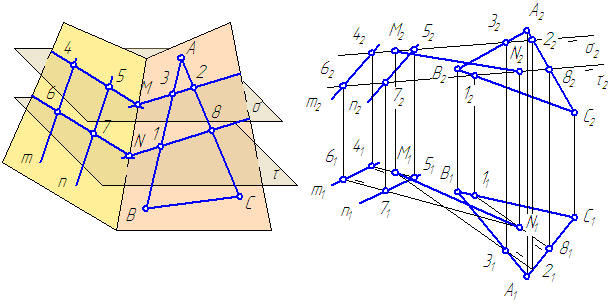
Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)
Алгоритм решения задачи:
left.begin{array}{l}alphacapsigma=(4-5)\betacapsigma=(3-2)\end{array}right}\left.begin{array}{l}alphacaptau=(6-7)\betacaptau=(1-8)\end{array}right}left.begin{array}{l}(4_1-5_1)cap(3_1-2_1)=M_1rightarrow M_2\(6_1-7_1)cap(1_1-8_1)=N_1rightarrow N_2\end{array}right}rightarrow\left.begin{array}{l}M_1N_1\M_2N_2\end{array}right}Rightarrowalphacapbeta=MN
Упражнение
Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей
Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π2, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π2 (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Упражнение
Задана плоскость σ⊥π2 и прямая общего положения – DE (Рисунок 3.22)
Требуется построить через DE плоскость τ⊥σ.
Решение.
Проведём перпендикуляр CD к плоскости σ – C2D2⊥σ2 (на основании теоремы о проецировании прямого угла).

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости
По теореме о проецировании прямого угла C1D1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.
Упражнение
Задана плоскость α = ΔАВС и точка K вне плоскости α. Требуется построить плоскость β⊥α, проходящую через точку K. Алгоритм решения (Рисунок 3.23):
- Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС;
- Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости: если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b2⊥f2; b1⊥h1;
- Задаём плоскость β любым способом, например, β = a∩b, таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.
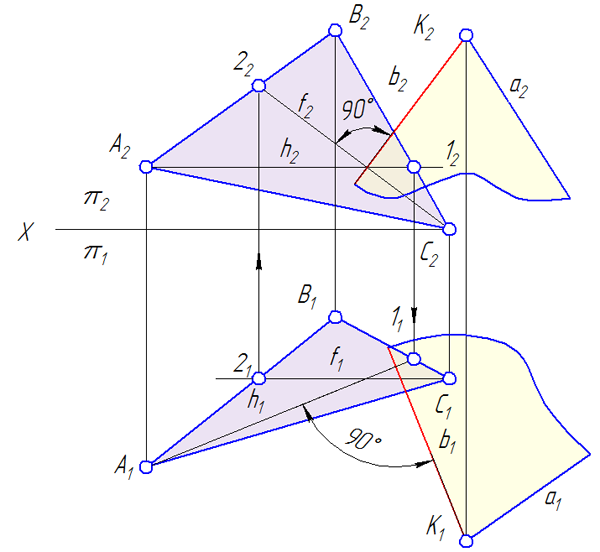
Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.
Постройте фронтальную проекцию точки К.

Рисунок 3.24
2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

Рисунок 3.25
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π2, если его диагональ MN //π2 (Рисунок 3.26).

Рисунок 3.26
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

Рисунок 3.27
5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

Рисунок 3.28
6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π1.
7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π1.
§11. Построение линии пересечения двух плоскостей. (Вторая позиционная задача).
Результатом пересечения двух плоскостей является прямая . Для построения этой прямой достаточно найти две точки, принадлежащие обеим плоскостям и провести через них прямую линию.
Если мы возьмем прямую, принадлежащую одной плоскости и найдем точку ее пересечения с другой плоскостью, то эта точка будет общей для обеих плоскостей. Таким образом, построение линии пересечения двух плоскостей сводится к решению первой позиционной задачи, повторенному дважды.
Задача 11.1. Построить линию пересечения плоскости α, заданной треугольником АВС, и плоскости β, заданной двумя пересекающимися прямыми МЕ и МК (рисунок 11.1). Определить видимость плоскостей.
Решение.
1. Возьмем прямую АВ, принадлежащую плоскости α, и найдем точку ее пересечения с плоскостью β. Для этого заключим ее в проецирующую плоскость и найдем точку пересечения, используя алгоритм для решения первой позиционной задачи (см. §7).
На рисунке 11.2 продемонстрирован этот этап решения – точка N является точкой пересечения прямой АВ и плоскости β(МК, МЕ). В данном случае мы заключили прямую в фронтально-проецирующую плоскость ФП, прямая 1-2 является результатом пересечения плоскости ФП и плоскостиβ.
Не нужно забывать о том, что все точки на чертеже отображены в проекциях. Так, например, на рисунке 11.2. точка N представлена проекциями N1 и N2.
2. Возьмем прямую МК, принадлежащую плоскости β, и найдем точку ее пересечения с плоскостью α. Заключив ее в горизонтально-проецирующую плоскость, и проведя аналогичные построения, найдем точку L (рисунок 11.3).
3. Проведем прямую NL, являющуюся линией пересечения плоскостей α и β (рисунок 11.4).
4. Определяем видимость плоскостей (рисунок 11.5).
Применяем метод конкурирующих точек – для определения видимости на фронтальной проекции берем конкурирующие точки, проекции которых совпадают с точкой 22, для определения видимости на горизонтальной проекции берем точки с проекцией в 41. Конкурирующие точки 22 принадлежат фронтальной проекции АВ и МК. Пройдя по стрелке взгляда вниз, видим, что точка, лежащая на прямой АВ находится ближе к наблюдателю, так как у нее координата у больше, поэтому в районе проекции прямая АВ видимая, а МК – невидимая. Следовательно, проекция М2К2 в точке 22 меняет свой вид с видимой на невидимую.
Точка 41 лежит на горизонтальной проекции ВС и МК. Видимой будет та прямая, которая по стрелке взгляда находится выше на фронтальной проекции, в данном случае это прямая ВС.
Нужно обратить внимание на то, что прямые АВ и ВС меняют видимость в точках пересечения с прямой NL. Линия пересечения плоскостей всегда видимая.
На рисунке 11.6 показано окончательное решение задачи, для наглядности плоскости затонированы.
Задача 11.2. Построить линию пересечения плоскостей α и β, заданных следами (рисунок 11.7). Определить видимость плоскостей.
Решение.
Поскольку следы плоскости – это прямые, принадлежащие этой плоскости, а точки пересечения 1 и 2 одноименных проекций следов являются общими для обеих плоскостей, то очевидно, что результат пересечения плоскостей – это прямая, проходящая через эти точки. На эпюре Монжа определяем фронтальные и горизонтальные проекции точек 1 и 2 (рисунок 11.8).
Как видно на рисунке 11.8, горизонтальная проекция точки 1, являющейся точкой пересечения фронтальных следов α и β, а также фронтальная проекция точки 2 – лежат она оси х, поскольку сами прямые принадлежат плоскостям проекций. Соединив одноименные проекции точек 1 и 2, получим линию пересечения плоскостей (рисунок 11.9).
Определив видимость плоскостей в проекциях, получим окончательное решение задачи (рисунок 11.10)
Построение линии пересечения плоскостей, заданных различными способами
Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.
Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L1 и L2, принадлежащих линии пересечения.

- Вводим вспомогательную горизонтальную плоскость γ1. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1”C” и 2”3”, совпадают с фронтальным следом пл. γ1. Он обозначен на рисунке как f0γ1 и расположен параллельно оси x.
- Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
- Находим горизонтальную проекцию точки L1 на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L1 лежит на фронтальном следе плоскости γ.
- Вводим вспомогательную горизонтальную плоскость γ2. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L2.
- Через L1 и L2 проводим искомую прямую l.
Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.
Пересечение плоскостей, заданных следами
Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П1 и П2.

- Находим точку L’1, расположенную на пересечении горизонтальных следов h0α и h0β. Точка L”1 лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’1.
- Находим точку L”2 на пересечении фронтальных следов пл. α и β. Точка L’2 лежит на оси x. Её положение определяется по линии связи, проведенной из L”2.
- Проводим прямые l’ и l” через соответствующие проекции точек L1 и L2, как это показано на рисунке.
Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.
Пересечение плоскостей треугольников
Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.

- Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3”=A”B”∩f0σ и 5”=A”С”∩f0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
- Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N” расположена на фронтальном следе f0σ на одной линии связи с N’.
Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.
Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π2. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π2. С противоположной стороны от линии N”K” видимость треугольников меняется.
Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π1. Так как (∙)6” находится выше, чем (∙)7”, то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π1. С противоположной стороны от линии N’K’ видимость треугольников меняется.
Построение линии пересечения поверхностей с примерами
Содержание:
Построение линии пересечения поверхностей:
Предложенные задания охватывают задачи не на все методы построения линий пересечения поверхностей, а только наиболее распространенные. Ниже приведены решения типовых задач, когда применены различные способы в зависимости от формы и расположения пересекающихся поверхностей.
Одна из поверхностей занимает частное (проецирующее) положение
Задание: даны две поверхности: 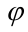
Решение: поверхность цилиндра перпендикулярна к 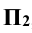
Ниже приводится построение горизонтальной проекции только одной точки 1 (рис. 13.1). Из этой точки вниз проводят линию проекционной связи. Одновременно из этой же точки радиусом 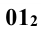 проводят дугу окружности, на которой лежит эта точка, как принадлежащая тору, и находят проекцию этой окружности на горизонтальной проекции тора – это прямая линия, параллельная оси x. Она проходит через точку
проводят дугу окружности, на которой лежит эта точка, как принадлежащая тору, и находят проекцию этой окружности на горизонтальной проекции тора – это прямая линия, параллельная оси x. Она проходит через точку 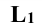 (точка пересечения окружности, проходящей через точку 1, с окружностью тора, лежащей на
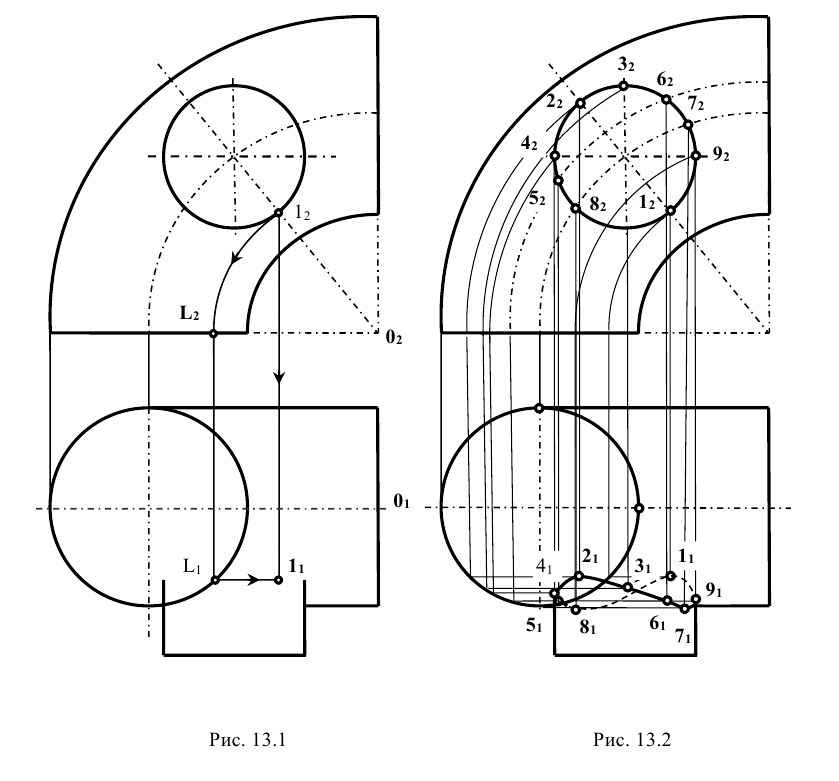
(точка пересечения окружности, проходящей через точку 1, с окружностью тора, лежащей на 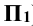 ). Горизонтальная проекция точки 1 находится на пересечении линии проекционной связи, проведенной из точки
). Горизонтальная проекция точки 1 находится на пересечении линии проекционной связи, проведенной из точки 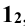 , с горизонтальной проекцией окружности тора, на которой лежит точка 1. Остальные точки строят аналогично точке 1 (рис. 13.2).
, с горизонтальной проекцией окружности тора, на которой лежит точка 1. Остальные точки строят аналогично точке 1 (рис. 13.2).
Точки 4 и 9 определяют видимость линии пересечения на горизонтальной проекции, а точки 1 и 2 наиболее удаленные от контура на горизонтальной проекции. Эту задачу можно решать и методом вспомогательных секущих плоскостей, который рассматривается далее.
Метод вспомогательных секущих плоскостей
Этот метод применяется для построения линии пересечения двух поверхностей, когда секущие (параллельные) плоскости при пересечении с данными поверхностями образуют простые для построения линии (прямую или окружность).
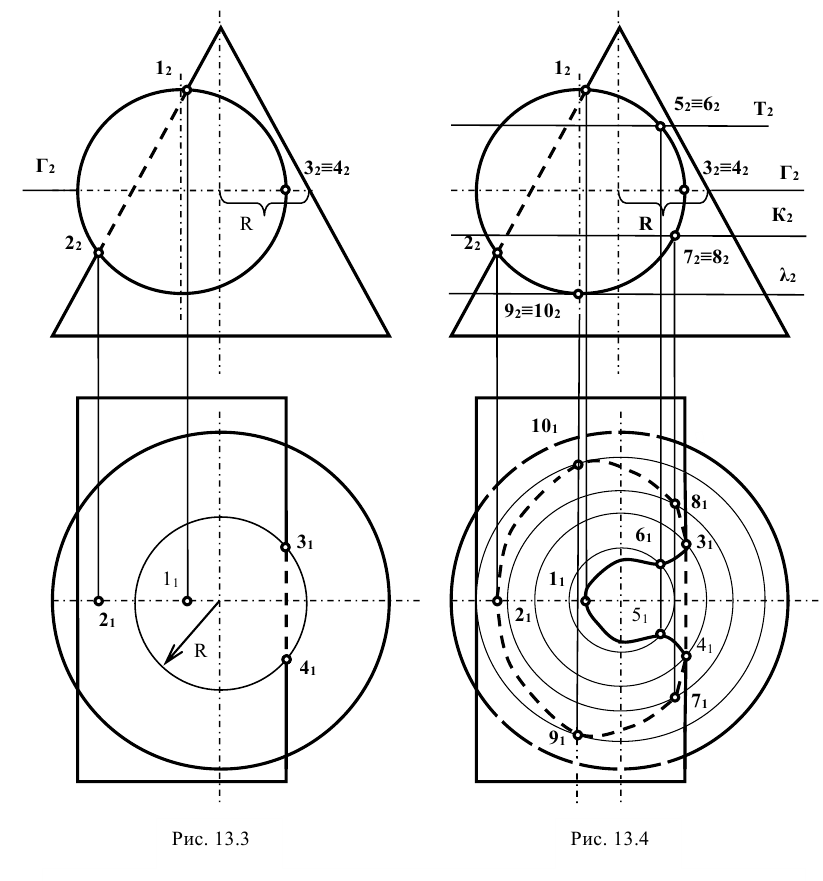
Задание: даны поверхности конуса 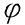 и цилиндра Ф (рис. 13.3). Требуется построить линию их пересечения.
и цилиндра Ф (рис. 13.3). Требуется построить линию их пересечения.
Решение: ось цилиндра перпендикулярна к плоскости 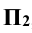 , следовательно, поверхность цилиндра – проецирующая. В этом случае задача может быть решена так, как это было разобрано в предыдущем (п. 13.1.1) примере. Для этого определяют характерные -наивысшую и низшую точки линии пересечения 1 и 2, лежащие на пересечении фронтальной проекции цилиндра с очерковой образующей конуса. Их горизонтальные проекции
, следовательно, поверхность цилиндра – проецирующая. В этом случае задача может быть решена так, как это было разобрано в предыдущем (п. 13.1.1) примере. Для этого определяют характерные -наивысшую и низшую точки линии пересечения 1 и 2, лежащие на пересечении фронтальной проекции цилиндра с очерковой образующей конуса. Их горизонтальные проекции 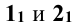 принадлежат горизонтальной проекции очерковой образующей конуса (
принадлежат горизонтальной проекции очерковой образующей конуса (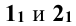 , совпадают с осевой линией конуса). Точки 3 и 4 определяют видимость линий пересечения на горизонтальной проекции.
, совпадают с осевой линией конуса). Точки 3 и 4 определяют видимость линий пересечения на горизонтальной проекции.
Для определения их горизонтальных проекций через ось цилиндра параллельно 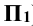 проводят вспомогательную секущую плоскость Г (ее фронтальный след
проводят вспомогательную секущую плоскость Г (ее фронтальный след 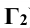 ).
).
Эта плоскость рассечет цилиндр по очерковым образующим, а конус по окружности радиуса R, которая на 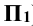 будет проецироваться в натуральную величину. Пересечение этой окружности с очерковыми образующими цилиндра есть не что иное, как горизонтальные проекции характерных точек
будет проецироваться в натуральную величину. Пересечение этой окружности с очерковыми образующими цилиндра есть не что иное, как горизонтальные проекции характерных точек 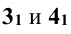 (рис. 13.3).
(рис. 13.3).
Построение промежуточных точек аналогично построению точек 3 и 4, только образующие, по которым вспомогательная плоскость будет рассекать цилиндр, не будут очерковыми (рис. 13.4).
Задание: Даны две поверхности вращения – конус и цилиндр, оси которых пересекаются и находятся в одной плоскости, параллельной 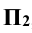 (рис. 13.5). Требуется построить линию их пересечения.
(рис. 13.5). Требуется построить линию их пересечения.
Решение: на фронтальной проекции фиксируют точки пересечения заданных поверхностей вращения 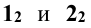 – они принадлежат искомой линии пересечения. Горизонтальные проекции этих точек находятся на осевой линии конуса и цилиндра –
– они принадлежат искомой линии пересечения. Горизонтальные проекции этих точек находятся на осевой линии конуса и цилиндра – 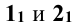 .
.
Другие точки линии пересечения можно построить, используя концентрические сферические поверхности. Из точки пересечения осей фронтальных проекций, как из центра, проводятся сферы. Первая – касательная к проекции конуса, а последующие – большим радиусом (рис. 13.6). Каждая сфера пересекает обе поверхности по окружностям, фронтальные проекции которых изображаются отрезками прямых линий. Эти проекции пересекаются в точках, являющихся фронтальными проекциями точек искомой линии пересечения поверхностей. 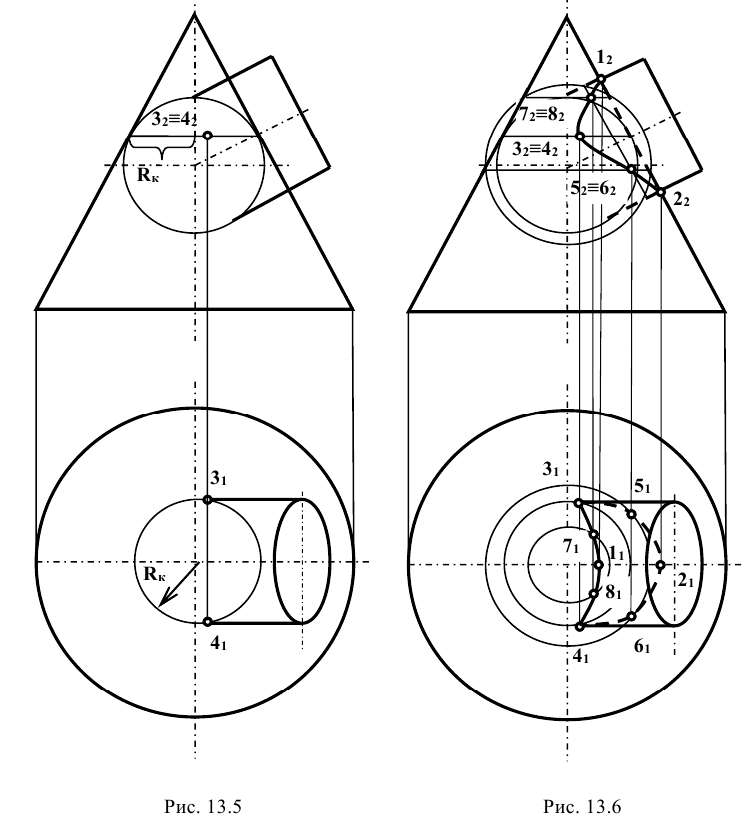
Горизонтальные проекции этих точек определяются по принадлежности одной из поверхностей. В данном случае удобнее их получать по принадлежности конусу. Например, точки 3 и 4 лежат на той же окружности, по которой вспомогательная сфера пересекает конус. Изменяя радиус вспомогательной секущей сферы, находят ряд точек линии пересечения, соединив которые, получают проекции искомой линии (рис. 13.6). Чтобы определить видимость горизонтальной проекции линии пересечения, на её фронтальной проекции отмечают точки, лежащие на проекции осевой линии цилиндра и принадлежащие линии пересечения.
Затем по линиям проекционной связи переносят их на очерковые образующие горизонтальной проекции цилиндра. Точки, лежащие ниже указанных, будут находиться на невидимой части цилиндра.
Метод эксцентрических сфер
Метод эксцентрических сфер применяется для построения линии пересечении поверхностей вращения, у которых оси расположены в одной плоскости, являющейся плоскостью симметрии. При этом пересекающиеся поверхности должны иметь семейство круговых сечений.
Задание: даны две поверхности вращения – тор и конус, оси которых находятся в одной плоскости, параллельной 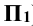 (рис. 13.7). Требуется построить линии их пересечения.
(рис. 13.7). Требуется построить линии их пересечения.
Решение: прежде всего, фиксируют опорные точки пересечения очерковых меридианов 1 и 2. Затем через ось вращения поверхности кольца проводят фронтальный след 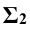 фронтально проецирующей плоскости Σ. Линия пересечения её с поверхностью тора – окружность. Центр сферы, пересекающей кольцо по окружности, находится на перпендикуляре, восстановленном из центра такой окружности к секущей проецирующей плоскости. Чтобы конус пересекался вспомогательной секущей сферой по окружности, её центр должен находиться на оси конуса. Точка пересечения перпендикуляра к проецирующей плоскости с осью конуса (
фронтально проецирующей плоскости Σ. Линия пересечения её с поверхностью тора – окружность. Центр сферы, пересекающей кольцо по окружности, находится на перпендикуляре, восстановленном из центра такой окружности к секущей проецирующей плоскости. Чтобы конус пересекался вспомогательной секущей сферой по окружности, её центр должен находиться на оси конуса. Точка пересечения перпендикуляра к проецирующей плоскости с осью конуса (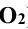 ) выбирается центром вспомогательной секущей сферы. Радиус ее равен расстоянию от центра до точки пересечения меридиана тора со следом плоскости
) выбирается центром вспомогательной секущей сферы. Радиус ее равен расстоянию от центра до точки пересечения меридиана тора со следом плоскости 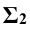 . Такая вспомогательная секущая сфера пересекает кольцо и конус вращения по окружностям, фронтальные проекции которых – проекции прямых. Точка пресечения этих отрезков
. Такая вспомогательная секущая сфера пересекает кольцо и конус вращения по окружностям, фронтальные проекции которых – проекции прямых. Точка пресечения этих отрезков 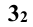 (рис. 13.7) принадлежит искомой линии пересечения поверхностей.
(рис. 13.7) принадлежит искомой линии пересечения поверхностей.
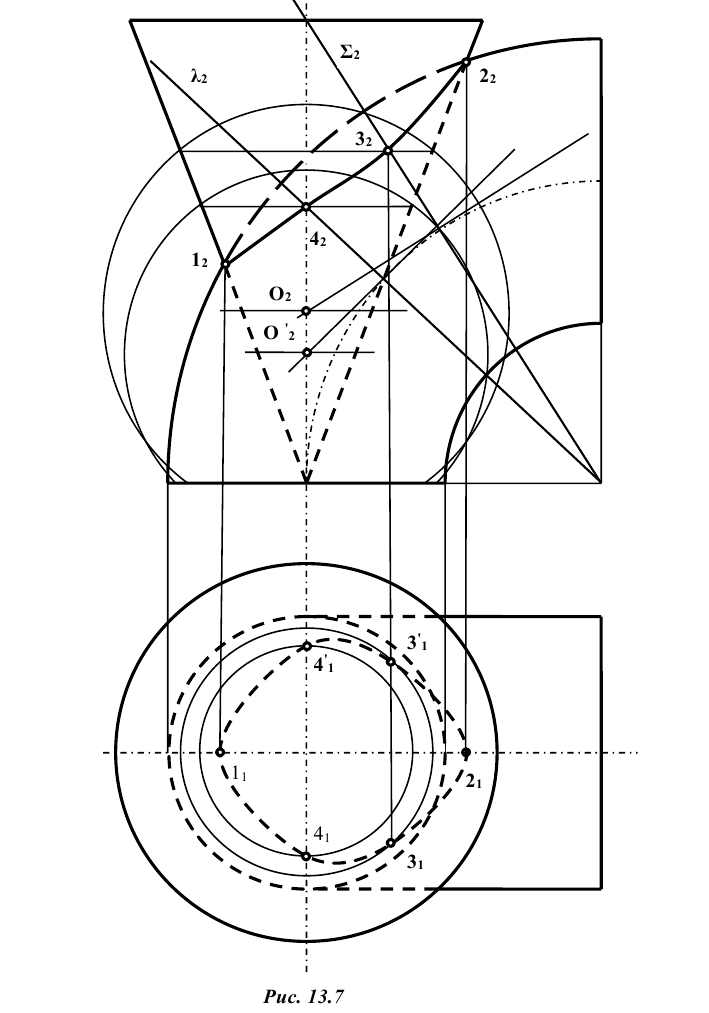
Вспомогательные сферы имеют различные центры на оси конуса вращения; так, при построении проекции – точки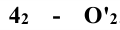 . Горизонтальные проекции точек пересечения строят по принадлежности этих точек к одной из поверхностей, используя параллели, например, конуса.
. Горизонтальные проекции точек пересечения строят по принадлежности этих точек к одной из поверхностей, используя параллели, например, конуса.
Пересечение линии с поверхностью
В общем случае для графического определения положения точек пересечения линии с поверхностью необходимо выполнить ряд геометрических построений в следующей последовательности: заключить линию во вспомогательную поверхность; определить линию пересечения этой поверхности с заданной поверхностью; отметить точки пересечения построенной линии с заданной.
Этот алгоритм является универсальным, пригодным для решения любых задач. Ранее (лекция 4, рис. 4.5 и 4.6) он применялся для построения проекций точки пересечения прямой с плоскостью, где в качестве вспомогательной секущей поверхности использовалась плоскость и строилась прямая линии пересечения ее с заданной плоскостью, а искомая проекция точки пересечения определялась как место пересечения этой линии с заданной прямой.
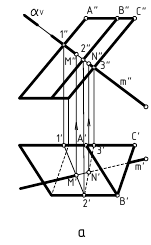
На рис. 12.1–12.3 проиллюстрирован тот же алгоритм применительно к построению точки пересечения кривой линии k с плоскостью α(∆ABC).
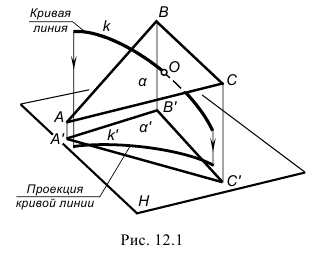
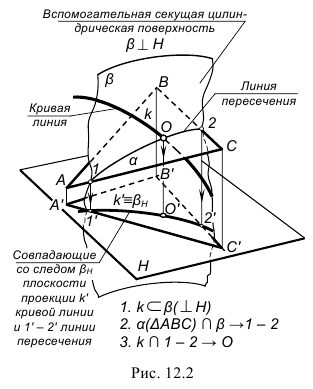
В качестве секущей поверхности в данном случае следует использовать проецирующую цилиндрическую поверхность, в частности, горизонтально-проецирующую β(βH)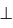 H, в которую должна быть заключена кривая k(k”,k’). Для этого на чертеже (рис. 12.3) обозначаем горизонтальный след этой поверхности βH. Горизонтальная проекция линии ее пересечения с заданной плоскостью α(∆ABC) совпадает с ним, располагаясь между точками 1′-2′. Для построения ее фронтальной проекции воспользуемся произвольными вспомогательными прямыми линиями, принадлежащими плоскости. Вначале задаем их горизонтальные проекции, например, через вершину C. Затем по точкам их пересечения со стороной AB находим фронтальные проекции вспомогательных прямых и определяем на них фронтальные проекции точек пересечения с ними заданной кривой. Проводим через найденные точки плавную кривую линию, являющуюся, таким образом, фронтальной проекцией линии пересечения, и отмечаем на ней место пересечения с фронтальной проекцией заданной кривой k(k”,k’) – точку O”. Это и будет фронтальная проекция искомой точки пересечения заданной кривой k(k”,k’) с плоскостью α(∆ABC). Затем, воспользовавшись линией связи, находим горизонтальную проекцию O’ точки пересечения.
H, в которую должна быть заключена кривая k(k”,k’). Для этого на чертеже (рис. 12.3) обозначаем горизонтальный след этой поверхности βH. Горизонтальная проекция линии ее пересечения с заданной плоскостью α(∆ABC) совпадает с ним, располагаясь между точками 1′-2′. Для построения ее фронтальной проекции воспользуемся произвольными вспомогательными прямыми линиями, принадлежащими плоскости. Вначале задаем их горизонтальные проекции, например, через вершину C. Затем по точкам их пересечения со стороной AB находим фронтальные проекции вспомогательных прямых и определяем на них фронтальные проекции точек пересечения с ними заданной кривой. Проводим через найденные точки плавную кривую линию, являющуюся, таким образом, фронтальной проекцией линии пересечения, и отмечаем на ней место пересечения с фронтальной проекцией заданной кривой k(k”,k’) – точку O”. Это и будет фронтальная проекция искомой точки пересечения заданной кривой k(k”,k’) с плоскостью α(∆ABC). Затем, воспользовавшись линией связи, находим горизонтальную проекцию O’ точки пересечения.
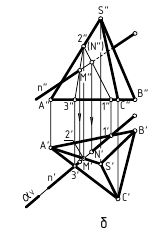
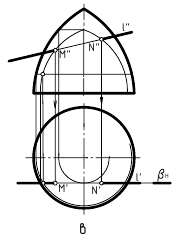
Этот алгоритм применен и для построения точек пересечения прямой линии с поверхностями геометрических тел – призмы, пирамиды и самопересекающегося тора (рис. 12.8, а, б, в). Поскольку поверхности этих тел являются замкнутыми, то необходимо найти по две точки пересечения на каждой из них.
При пересечении с призмой (рис. 12.8, а) в качестве секущей плоскости для заключения в нее заданной прямой m(m”,m’) использовалась фронтально-проецирующая плоскость αV. При пересечении с пирамидой (рис. 12.8, б) в качестве секущей плоскости для заключения в нее заданной прямой n(n”,n’) использовалась горизонтально-проецирующая плоскость αH. При пересечении с самопересекающимся тором (рис. 12.8, в) в качестве секущей плоскости для заключения в нее заданной прямой l(l”,l’) использовалась фронтальная плоскость βH. Далее все действия аналогичны рассмотренным. В каждом случае вначале строилась линия пересечения поверхности плоскостью, исходя из ее проецирующего положения, определялись на ней точки пересечения с заданной прямой, а при окончательном оформлении – видимость на чертеже.
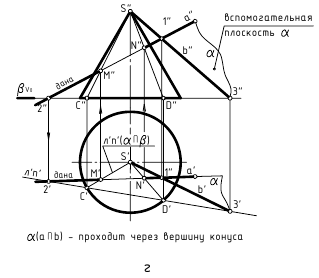
В качестве секущей плоскости при определении точек пересечения прямой с поверхностью могут использоваться также плоскости общего положения, пересекающие поверхность вдоль ее образующих (рис. 12.8, г, д). Так, для построения точек пересечения прямой a(a”,a’) общего положения с поверхностью прямого кругового конуса (рис. 12.8, г) показано использование плоскости общего положения α, проходящей через вершину конуса и заданную прямую. Плоскость задана двумя пересекающимися прямыми. Одна из них – это заданная прямая a(a”,a’), вторая – пересекающаяся с ней произвольная прямая b(b”,b’), проходящая через вершину конуса. Для построения проекций образующих, вдоль которых плоскость пересекает поверхность конуса, найден ее горизонтальный след, затем проекции C’ и D’ точек его пересечения с горизонтальным следом основания конуса и фронтальные проекции C” и D” этих точек. Искомые проекции точек M(M”,M’) и N(N”,N’) пересечения заданной прямой общего положения с поверхностью конуса находятся в местах пересечения с ней построенных образующих.
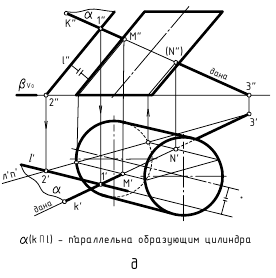
Аналогичные действия выполнены и для построения проекций M”,M’ и N”,N’ точек пересечения прямой общего положения k(k”,k’) с поверхностью наклонного эллиптического цилиндра (рис. 12.8, д). Для этого использовалось задание плоскости общего положения α(k∩l) также двумя пересекающимися прямыми, одна из которых, как и в предыдущем случае, – это заданная прямая k(k”,k’), а пересекающаяся с ней в произвольной точке 1(1″,1′) вторая прямая линия – это прямая l(l”,l’), параллельная образующим цилиндра. Строился горизонтальный след этой плоскости и по точкам пересечения его с горизонтальным следом заданного цилиндра находились образующие, по которым вспомогательная плоскость общего положения α(k∩l) пересекает цилиндр. В местах пересечения с проекциями этих образующих проекций прямой общего положения k(k”,k’) находятся искомые проекции M”,M’ и N”,N’ точек пересечения заданной прямой с поверхностью цилиндра.
Касательные плоскости и нормаль к поверхности
Плоскостью, касательной к поверхности в некоторой ее точке, называют плоскость, в которой можно провести две прямые линии, пересекающиеся в точке касания, касательные к двум пересекающимся в этой же точке линиям, принадлежащим поверхности.
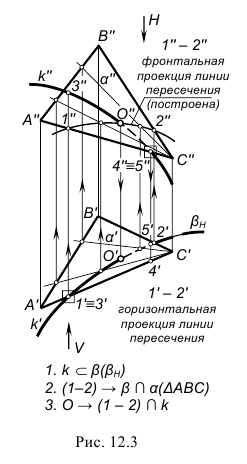
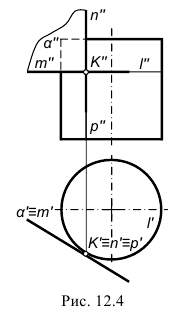
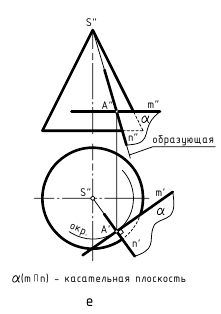
На чертеже касательную плоскость α(α”,α’) однозначно можно задать проекциями двух пересекающихся прямых m(m”,m’) и n(n”,n’). Эти линии строят касательно к проекциям двух пересекающихся в точке касания линий, принадлежащих поверхности. На рис. 12.4 линия m(m”,m’) является касательной к линии окружности l(l”,l’), проходящей через точку касания K(K”,K’) по поверхности цилиндра, а пересекающаяся с ней в этой точке линия n(n”,n’) сливается с линией р(р”,р’) – образующей цилиндра.
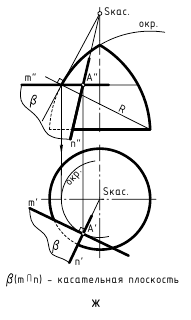
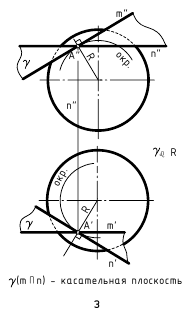
Аналогичные действия (рис. 12.8, е, ж, з) выполнены и при построении касательных плоскостей к поверхностям прямого кругового конуса, самопересекающегося тора и сферы, касающихся этих поверхностей в некоторой точке A(A”,A’). Пересекающиеся прямые m(m”,m’) и n(n”,n’), задающие касательные плоскости α(α”,α’) к ним, являются касательными к окружностям, построенным на этих поверхностях вращения и пересекающимся в точке касания A(A”,A’). Следует отметить одну особенность при построении прямой n(n”,n’), касательной к линии меридионального сечения поверхности самопересекающегося тора (рис. 12.8, ж). Для упрощения построений вначале строят касательную к этой линии, параллельной фронтальной плоскости проекций, определяют на оси вращения тора точку S, через которую проходят касательные ко всем точкам, расположенным на той же параллели поверхности, что и заданная точка касания A(A”,A’), а затем строят необходимую касательную n(n”,n’).
Эти построения использовались также для определения точки касания K(K”,K’) на поверхности самопересекающегося тора в задаче на рис. 12.5, где необходимо было задать общую касательную плоскость к поверхностям самопересекающегося тора и прямого кругового конуса. Ключом к решению задачи явилось заключение самопересекающегося тора в коническую поверхность с тем же углом наклона образующих, что и у заданного конуса (справа). Общая касательная плоскость задана пересекающимися прямыми, из которых m1(m1“,m1‘), являющаяся горизонтальным следом плоскости, построена, как касательная к следам указанных конических поверхностей, а прямая m2(m2“,m2‘), сливается с одной из образующих заданного конуса. Эта образующая является и геометрическим элементом касания построенной плоскости α(m1∩m2) с поверхностью заданного конуса. Поверхности самопересекающегося тора эта плоскость касается в точке K(K”,K’), которая найдена благодаря вышерассмотренным построениям и образующей второго конуса, охватывающего тор.
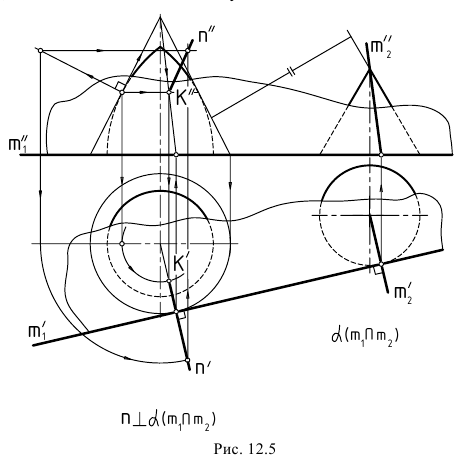
На рассматриваемом чертеже показано также построение нормали n(n”,n’), к поверхности самопересекающегося тора в точке K(K”,K’). Условием для построения нормали является ее перпендикулярность к плоскости, касательной к поверхности в той же точке. Вначале нормаль построена к очерковой образующей тора, затем на ней взята произвольная точка и выполнен ее поворот вокруг оси тора в положение, в котором она окажется расположенной в плоскости, перпендикулярной построенной касательной плоскости (направления указанных перемещений показаны стрелками).
На рис. 12.6 показано построение точек пересечения P(P”,P’) и T(T”,T’) фронтальной прямой MN(M”N”,M’N’) с поверхностью ¼ кольцевого тора и построение касательной плоскости к этой поверхности в одной из построенных точек, например, T(T”,T’).
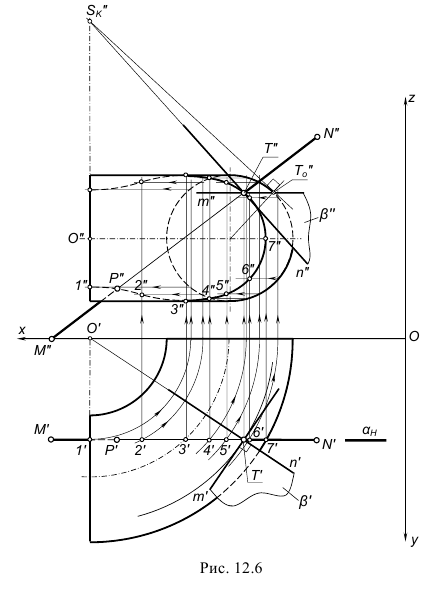
Точки P(P”,P’) и T(T”,T’) найдены благодаря заключению заданной прямой MN во фронтальную плоскость α(αH) и построению проекций линии пересечения по точкам 1′, 2′, 3′, … , 7′, крайние из которых 1′ и 7′ взяты в местах пересечения горизонтального очерка плоскостью тора, а остальные – произвольно на горизонтальном следе αH секущей плоскости. Для дальнейших построений использовались горизонтальные сечения поверхности тора плоскостями.
Для задания касательной плоскости β(m∩n) одна из задающих ее пересекающихся прямых m(m”,m’) построена как касательная к линии кольцевого сечения поверхности тора в точке T(T”,T’), а вторая – как касательная прямая n(n”,n’) к линии окружности осевого сечения поверхности тора. Для более точного построения второй прямой была найдена проекция SK” точки на оси вращения тора, в которой сходятся все касательные прямые к поверхности тора во всех точках, находящихся на той же параллели, что и точка T(T”,T’).
Структуризация материала двенадцатой лекции в рассмотренном объеме схематически представлена на рис. 12.7 (лист 1). На последующем листе 2 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 12.8).
Пересечение линии с поверхностью:
Касательные плоскости и нормаль к поверхности
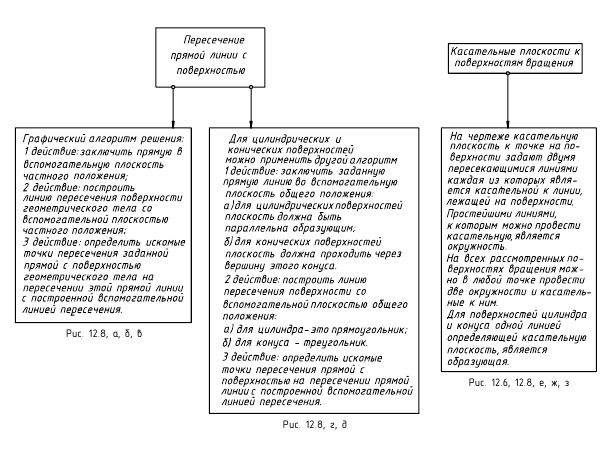
Касательная плоскость к кривой поверхности в некоторой точке – это плоскость, в которой лежат все касательные прямые ко всем кривым, которые можно провести на поверхности через ту же точку.
Нормалью к поверхности в данной точке называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.
12.1. Пересечение прямой с поверхностью
12.2. Касательные плоскости
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Проецирование прямой
- Взаимное положение плоскостей, прямой линии и плоскости
- Взаимное расположение точки, прямых и плоскостей
- Перпендикулярность геометрических объектов
- Прямая в пространстве и ее изображение на чертеже
- Многогранники
- Поверхности вращения
- Пересечение прямой линии с поверхностью
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Линия пересечения плоскостей онлайн
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Линия пересечения плоскостей − теория, примеры и решения
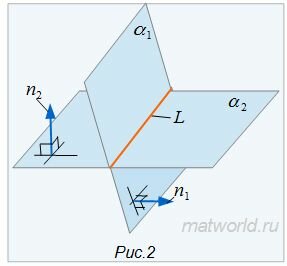
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
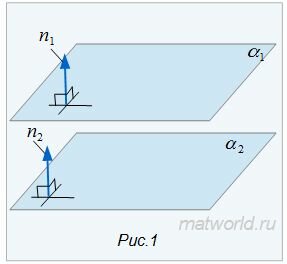
Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
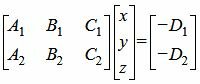 |
(4) |
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1=<A1, B1, C1> и n2=<A2, B2, C2> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
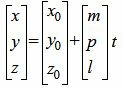 , , |
(5) |
Равенство (5) можно записать в следующем виде:
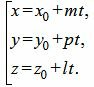 . . |
(6) |
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2. Полученное уравнение прямой можно записать в каноническом виде:
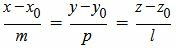 .
.
Пример 1. Найти линию пересечения плоскостей α1 и α2:
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
 . . |
(9) |
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 . . |
(10) |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
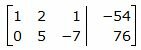 .
.
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
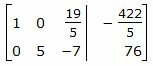 .
.
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 .
.
 . . |
(11) |
где t− произвольное действительное число.
Запишем (11) в следующем виде:
 . . |
(12) |
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
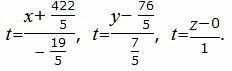 |
(13) |
Из равентсв выше получим каноническое уравнение прямой:

Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:

Пример 2. Найти линию пересечения плоскостей α1 и α2:
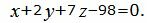 |
(14) |
 |
(15) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
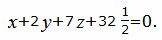 |
(16) |
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей α1 и α2:
 |
(17) |
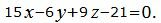 |
(18) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
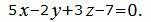 |
(19) |
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.
[spoiler title=”источники:”]
http://www.evkova.org/postroenie-linii-peresecheniya-poverhnostej
http://matworld.ru/analytic-geometry/linija-peresechenija-ploskostej.php
[/spoiler]

