Преподаватель который помогает студентам и школьникам в учёбе.
Определение видимости в начертательной геометрии с примерами
Определение видимости:
Точки, расположенные на одной проецирующей прямой, называются конкурирующими.
Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).
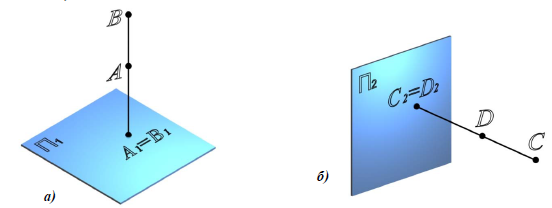
Рис. 7.1. Конкурирующие точки:
а – относительно горизонтальной плоскости проекций;
б – относительно фронтальной плоскости проекций
Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D – невидима).
Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).
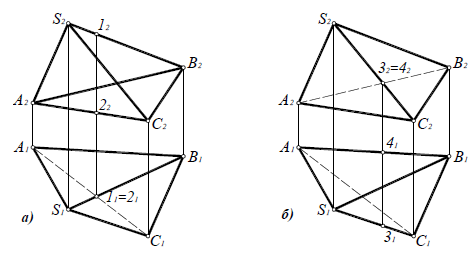
Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже:
а – относительно горизонтальной плоскости проекций;
б – относительно фронтальной плоскости проекций
Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П1, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П1.
- Заказать чертежи
Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П2.
- Конструктивное отображение пространства
- Чертежи точки, отрезка прямой
- Чертежи плоскости
- Взаимное положение двух плоскостей, прямой линии и плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Геометрические тела
- Комплексный чертеж
Определение видимости точек, прямых и плоских фигур.
Видимость
— это изображение на чертеже только
тех точек, прямых и поверхностей
(плоскостей) предметов, которые расположены
ближе к наблюдателю. Изображение
предметов с учетом видимости улучшает
восприятие их формы и размещения в
пространстве.
Определение
видимости — это определение точек
предмета, лежащих на одном луче
проецирования (называемых конкурирующими),
и обозначение на чертеже только тех из
них, которые расположены по этому лучу
ближе к наблюдателю.
в
F’
С’
Г
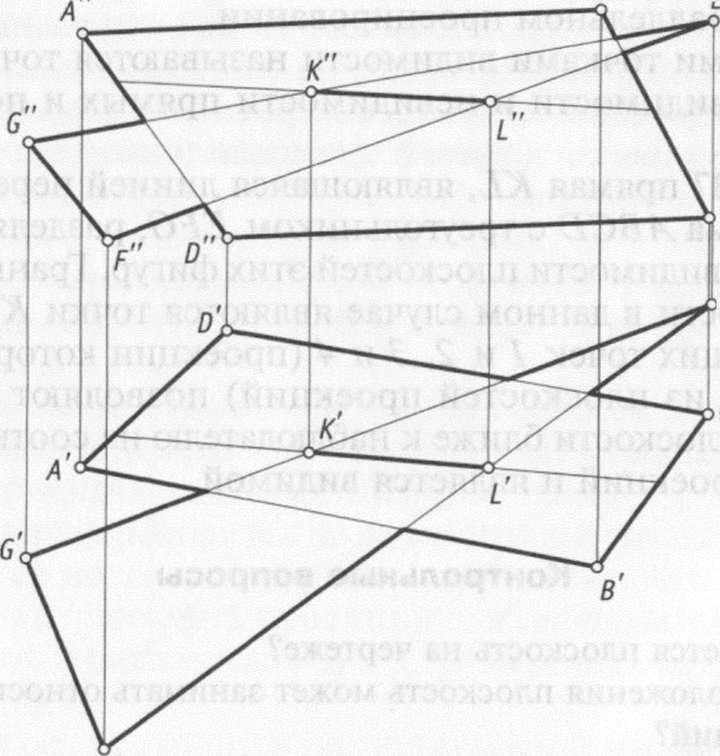
Рис. 3.16

Если
необходимо указать невидимые точки, их
обозначения на плоскости проекций, где
проекции точек совпадают, заключают в
круглые скобки. Невидимые линии
изображаются на чертеже штриховыми
линиями.
Определение
видимости осуществляется как при
центральном, так и при параллельном
проецировании.
Граничными точками
видимости называются точки, разделяющие
зоны видимости и невидимости прямых и
поверхностей (плоскостей).
На
рис. 3.17 прямая АХ, являющаяся линией
пересечения параллелограмма ABCD с
треугольником EFG, разделяет зоны видимости
и невидимости плоскостей этих фигур.
Граничными точками видимости в данном
случае являются точки К и L, а пары
конкурирующих точек 1 и 2, 3 и 4 (проекции
которых совпадают на одной из
плоскостей проекций) позволяют определить,
какая часть плоскости ближе к наблюдателю
на соответствующей плоскости проекций
и является видимой.
Контрольные
вопросы
-
Как задается
плоскость на чертеже? -
Какие
положения плоскость может занимать
относительно плоскостей проекций? -
Как определить
на чертеже восходящую и нисходящую
плоскости общего положения? -
Какие положения
занимают горизонтально-проецирующая,
фрон- тально-проецирующая и
профильно-проецирующая плоскости? -
Как определить
углы между проецирующими плоскостями
и плоскостями проекций? -
Где располагается
проекция любой точки, находящейся в
проецирующих плоскостях? -
Какие положения
занимают плоскости уровня? -
Как определяются
углы наклона плоскости уровня к
плоскостям проекций? -
Каково условие
принадлежности точки плоскости? -
Дайте определения
горизонтали, фронтали и профильной
прямой плоскости. -
Каковы условия
параллельности прямой и плоскости? -
Как могут
располагаться две плоскости относительно
друг друга?
Глава 4. Способы преобразования чертежа
Использование
частных положений прямых линий и плоских
фигур относительно плоскостей проекций
значительно упрощает построение чертежа
и позволяет отобразить натуральные
размеры прямых линий, плоских фигур,
расположенных на одной плоскости
проекций, и расстояний между ними. Для
такого преобразования чертежа используют:
-
введение
дополнительных плоскостей проекций
таким образом, чтобы прямая линия или
плоская фигура, не изменяя своего
положения в пространстве, оказалась в
каком-либо частном положении в новой
системе плоскостей проекций — способ
перемены плоскостей проекций; -
изменение
положения прямой линии или плоской
фигуры посредством поворота вокруг
некоторой оси таким образом, чтобы
прямая или плоская фигура оказалась в
частном положении относительно
неизменной системы плоскостей проекций
— способ вращения.
Преобразование
чертежа (для достижения необходимого
результата) при определении натуральных
размеров отрезков и углов может
осуществляться многократно одним или
разными способами.
Способ
перемены плоскостей проекций.
При использовании способа перемены
плоскостей проекций (рис. 4.1) положение
точек, линий, плоских фигур, поверхностей
в пространстве остается неизменным, а
система щ, п2 дополняется плоскостями,
образующими с щ или п2, или между собой
системы двух взаимно-перпендикулярных
плоскостей, принимаемых за плоскости
проекций.
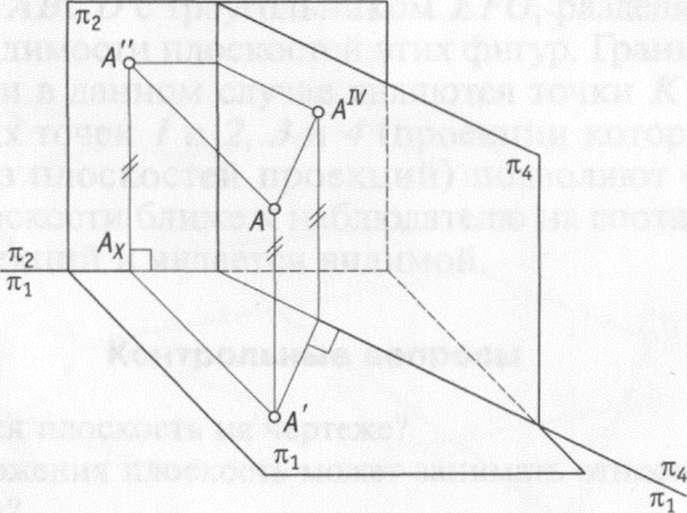
Рис. 4.1

При введении
дополнительной плоскости проекций
проводят новую ось системы проекций
(рис. 4.2), разделяющую две плоскости
проекций в новой системе проекций. При
этом новую ось проводят либо параллельно,
либо перпендикулярно проекциям прямых,
чтобы получить частное положение этих
прямых в новой системе проекций.
При построении в
новой системе плоскостей следует
соблюдать те же условия положения
наблюдателя, которые были установлены
в первоначальной системе проекций.
Если новая ось
проводится на горизонтальной плоскости,
значит, изменяется положение фронтальной
плоскости проекций и дополнительная
плоскость проекций для наблюдателя
становится фронтальной. Наблюдатель
при этом перемещается в горизонтальной
плоскости.
Если
новая ось проводится на фронтальной
плоскости, значит, изменяется положение
горизонтальной плоскости проекций и
дополнительная плоскость проекций для
наблюдателя становится горизонтальной.
Наблюдатель при этом перемещается в
фронтальной плоскости.
Таким образом,
наблюдатель может рассматривать предметы
с любой стороны.
Дополнительные
плоскости по мере построения обозначают
тг4, 7с5и т.д. Обозначения дополнительных
плоскостей представляют собой как бы
числитель и знаменатель дроби,
разделительной чертой которой является
ось проекций, причем их обозначения
располагаются по ту сторону оси, где
должны размещаться соответствующие
проекции.
На
рис. 4.2 показано определение угла наклона
плоскости треугольника к фронтальной
(введением дополнительной плоскости
я6) и горизонтальной (введением
дополнительной плоскости я4) плоскостям
проекций посредством одной их перемены
и определение натурального размера
треугольника ЛВС выполнением двух
перемен плоскостей проекций (введением
дополнительных плоскостей я4, тс5).
Способ
вращения.
При вращении вокруг некоторой неподвижной
прямой — оси вращения — каждая точка
вращаемой фигуры перемещается в
плоскости, перпендикулярной этой оси
(т.е. плоскости вращения).
Точка
вращаемой фигуры перемещается по
окружности, центр которой находится в
точке пересечения оси вращения этой
фигуры с плоскостью вращения, называемой
центром вращения, а радиус этой окружности
равен расстоянию от вращаемой точки до
центра вращения и называется радиусом
вращения.
Если какая-либо
из точек данной системы находится на
оси вращения, то при ее вращении эта
точка считается неподвижной.
Ось
вращения может быть задана или выбрана.
В последнем случае ее выгодно располагать
перпендикулярно одной из плоскостей
проекций, так как при этом упрощаются
построения.
Действительно,
если ось вращения перпендикулярна,
например, плоскости тс2, то плоскость,
в которой происходит вращение точки,
параллельна плоскости п2. Следовательно,
траектория этой точки на плоскость п2
проецируется в виде окружности без
искажения, а на плоскость 7Cj — в виде
отрезка прямой линии (рис. 4.3).
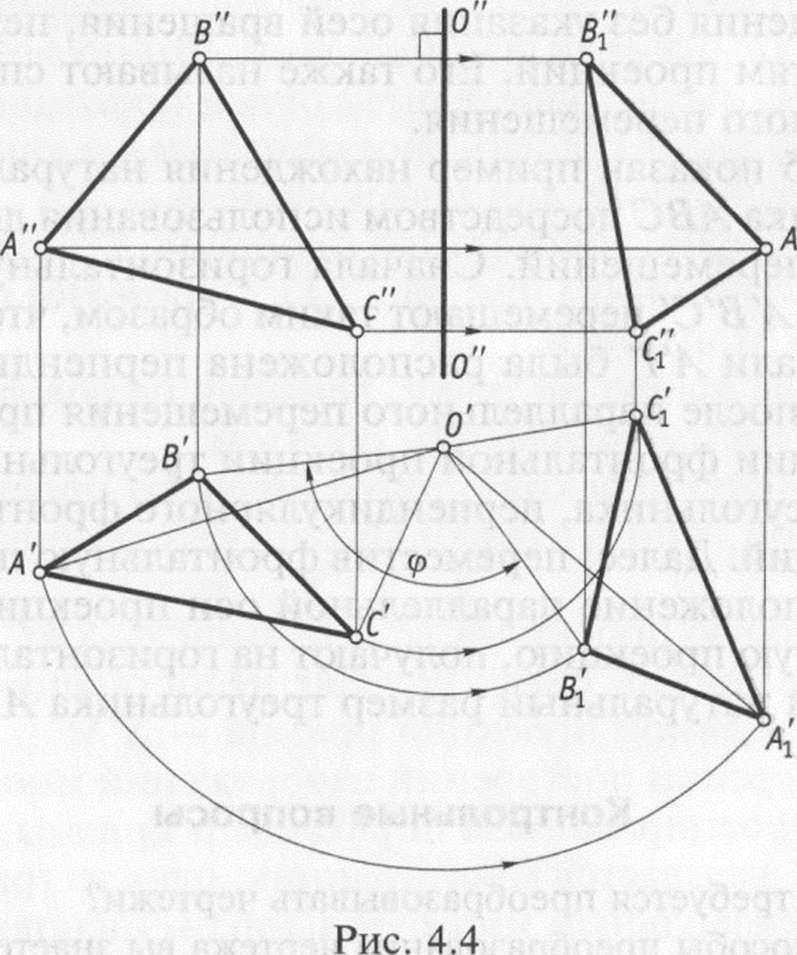
На
рис. 4.4 показан поворот треугольника
ABC вокруг выбранной оси О на угол ср.
Если
вращать отрезок прямой линии или плоскую
фигуру вокруг оси, перпендикулярной
плоскости проекций, то проекция на эту
плоскость не изменится ни по виду, ни
по размеру, изменится лишь положение
этой проекции относительно оси проекций.
Что же касается проекции на плоскость,
параллельную оси вращения, все ее точки
(за исключением, конечно, точек, проекции
которых расположены на оси вращения)
перемещаются по прямым, параллельным
оси проекций, и, следовательно, изменяются
ее форма и размер. В этом случае можно
не указывать проек цию оси вращения, не
устанавливать радиус вращения, а, не
изменяя вид и размер одной из проекций
заданной плоской фигуры, переместить
ее в требуемое положение и построить
другую проекцию с помощью линий,
параллельных оси проекций.
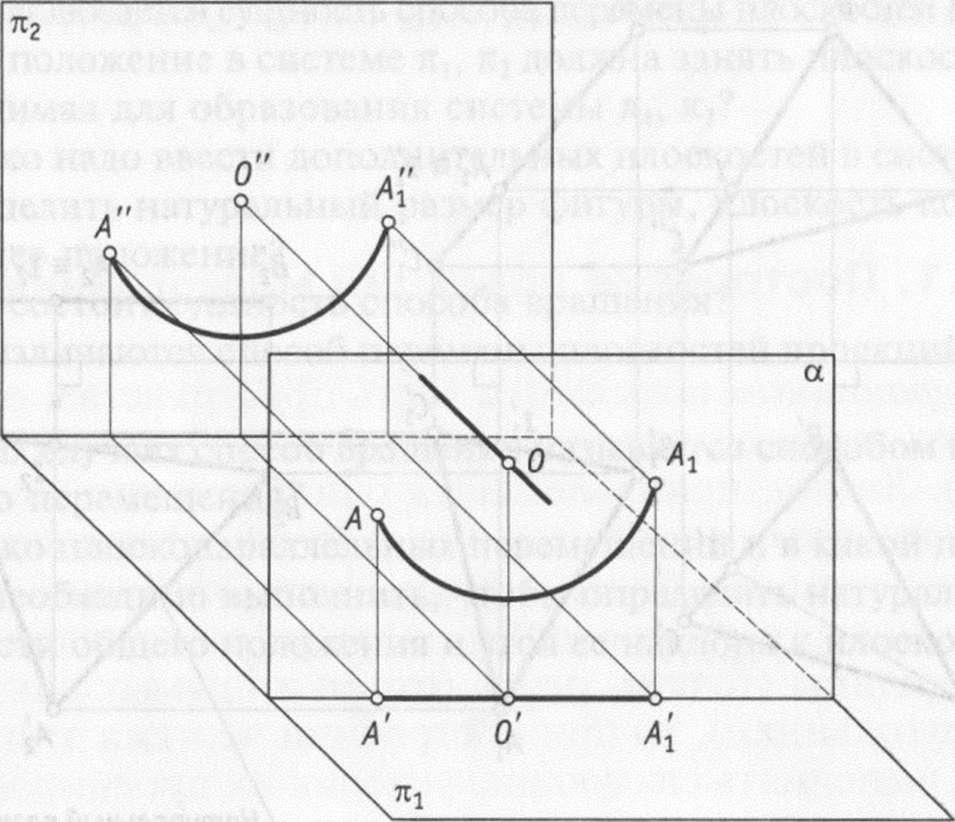
Рис. 4.3
33
Натуральный размер
Рис. 4.5
Данный
способ преобразования чертежа получил
название способа вращения без указания
осей вращения, перпендикулярных
плоскостям проекций. Его также называют
способом плоскопараллельного перемещения.
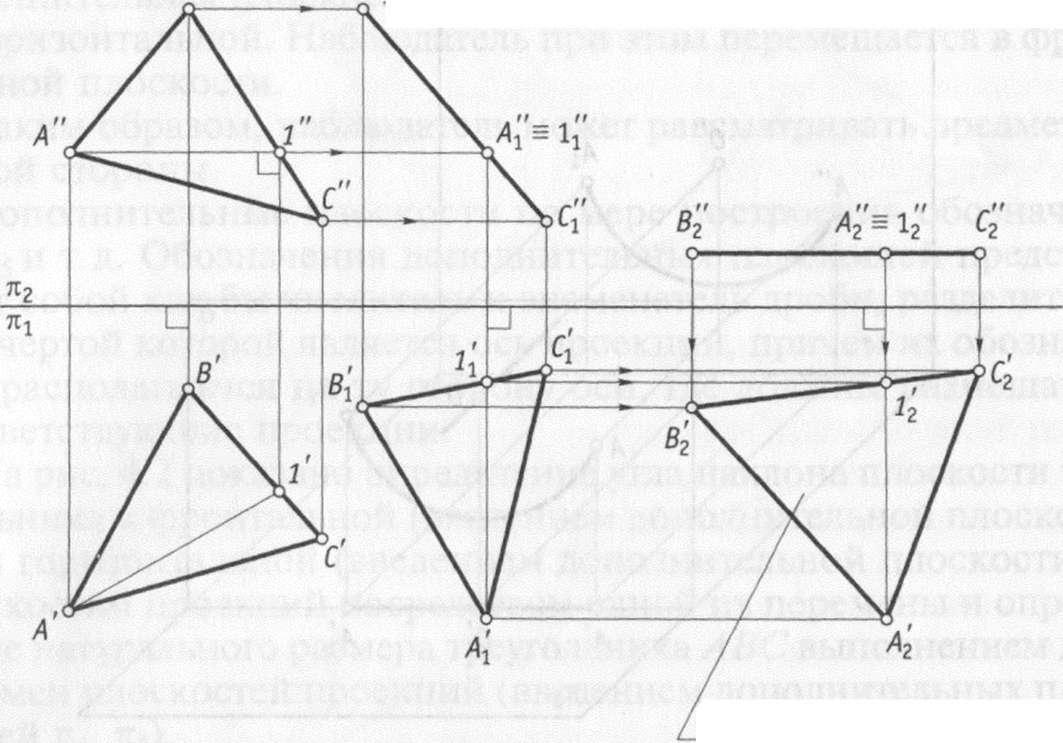
На
рис. 4.5 показан пример нахождения
натурального размера треугольника ABC
посредством использования двух
плоскопараллельных перемещений. Сначала
горизонтальную проекцию треугольника
А’В’С’ перемещают таким образом, чтобы
проекция его горизонтали AT была
расположена перпендикулярно оси
проекций, и после параллельного
перемещения проекций точек при построении
фронтальной проекции треугольника
получают плоскость треугольника,
перпендикулярного фронтальной плоскости
проекций. Далее, переместив фронтальную
проекцию треугольника в положение
параллельной оси проекций и построив
горизонтальную проекцию, получают на
горизонтальной плоскости проекций
натуральный размер треугольника ЛВС.
Контрольные
вопросы
-
Для чего требуется
преобразовывать чертежи? -
Какие способы
преобразования чертежа вы знаете? -
В чем заключается
сущность способа перемены плоскостей
проекции? -
Какое
положение в системе щ9 к2 должна занять
плоскость я3 проекций, вводимая для
образования системы я4, Я|? -
Сколько
надо ввести дополнительных плоскостей
в систему яь тс2, чтобы определить
натуральный размер фигуры, плоскость
которой занимает общее положение? -
В чем состоит
сущность способа вращения? -
Чем различаются
способ перемены плоскостей проекций
и способ вращения? -
В каких случаях
способ вращения называется способом
плоскопараллельного перемещения? -
Сколько
плоскопараллельных перемещений и в
какой последовательности необходимо
выполнить, чтобы определить натуральный
размер плоскости общего положения и
угол ее наклона к плоскостям проекций?

Чертеж — важный конструкторский документ. Это проекционное изображения предмета. При создании чертежей в начертательной геометрии нужно следовать особым правилам. Все элементы должны находиться в строгой зависимости от положения в пространстве. Простым геометрическим образом пространства является точка. Что такое точки на чертеже? Как их использовать при создании чертежа? Разбираемся в нашем материале.
Что такое точка на чертеже?
Изображение предмета на чертеже состоит из двух или более геометрических фигур, только так можно передать форму изделия. В инженерной графике используются разные элементы графического языка. Одним из них является точка.
Точка — геометрический элемент, не имеющий размеров. Другими словами, все параметры точки равны нулю.
Чтобы изобразить изделие на чертеже, его необходимо перенести на плоскость. В построении любого изображения в инженерной графике применяется метод прямоугольного проецирования, который определяет расположение предмета на области за счет точек.
Проекция точки
Это точка пересечения прямой линии с плоскостью (рисунок 1).
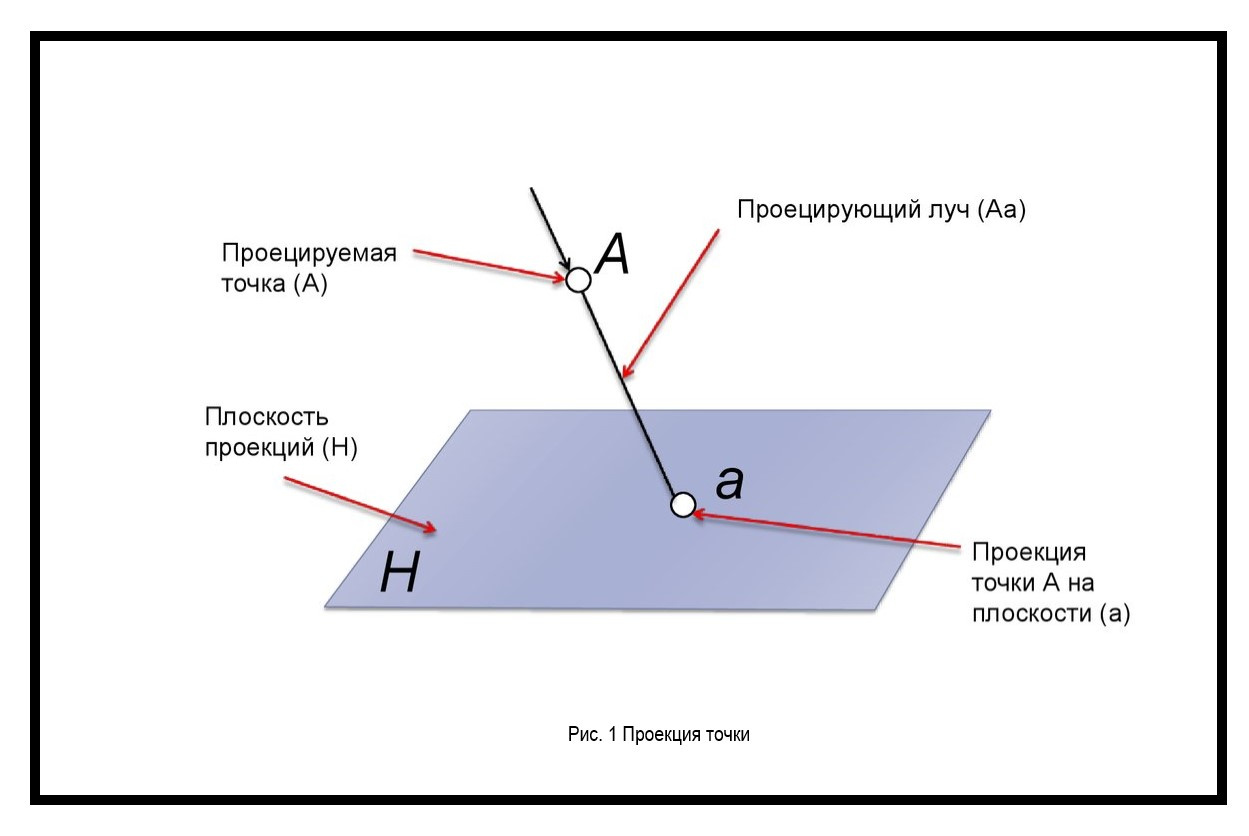
Проецируемая точка на плоскости обозначается как точка проекции. Это позволяет определить ее местоположение на плоскости. Каждая точка на чертеже имеет определенные координаты. Их используют для определения положения других элементов на комплексном чертеже (рисунок 2).
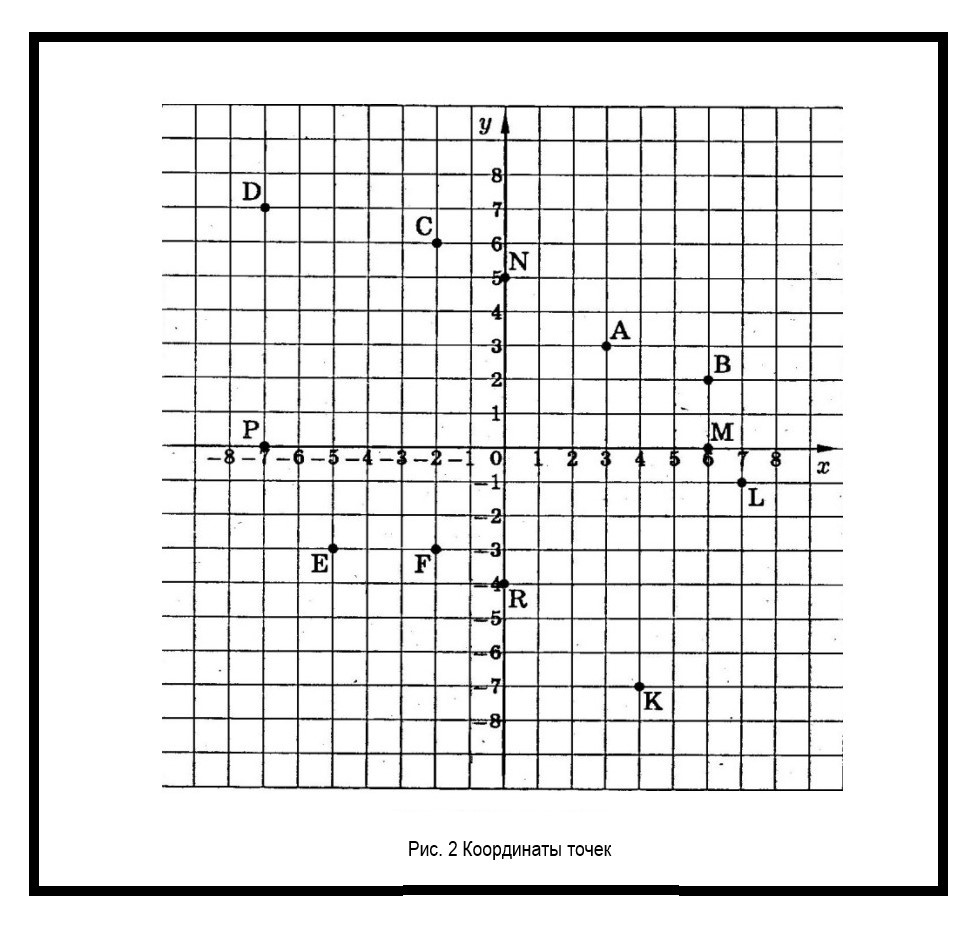
Как определить координаты по проекциям точки?
Для определения координат по проекциям точки используются две ортогональные проекции. Например, фронтальная и профильная. Они позволяют узнать конкретное значение координат точки, а также определить ее октант.
Как определить положение точки в пространстве?
Положение точки в пространстве определяется тремя координатами. Они показывают расстояние точки от плоскостей проекции. Пример представлен на рисунке рисунок 2.1.
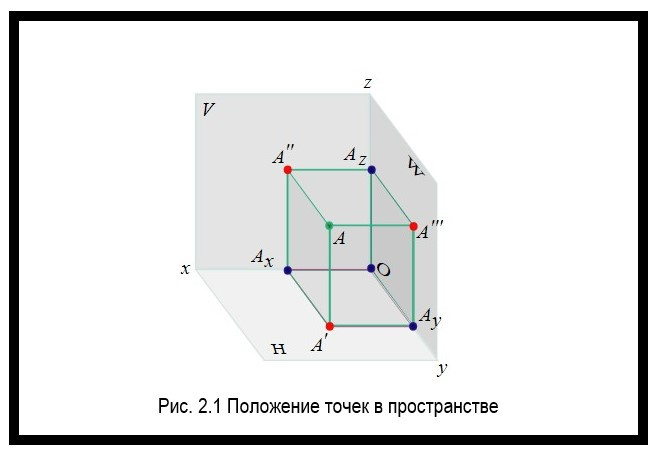
Комплексный чертеж точки
Чтобы изображение предмета было понятным, отражающим форму, размер и положение изделия в пространстве, необходимо использовать комплексный чертеж. Он представляет собой изображение предмета на совмещенных плоскостях проекции (рисунок 3).
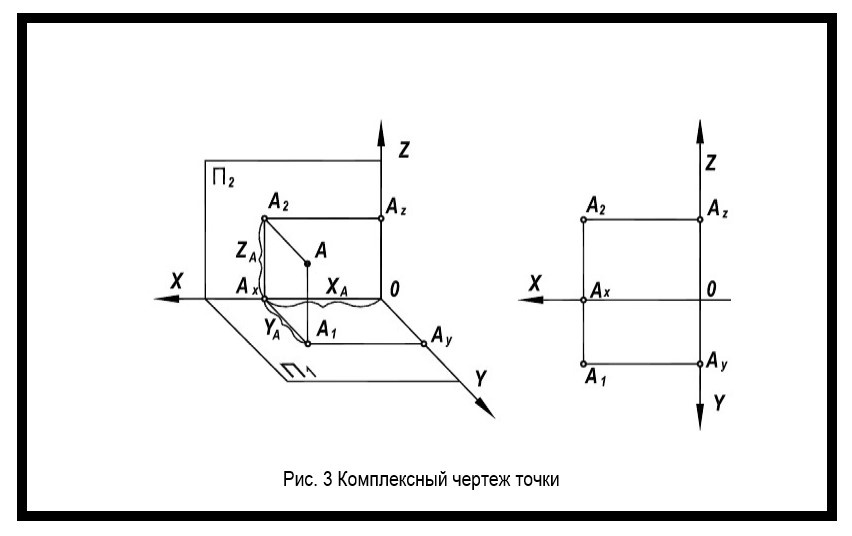
Построение комплексного чертежа состоит из нескольких этапов (рисунок 4).
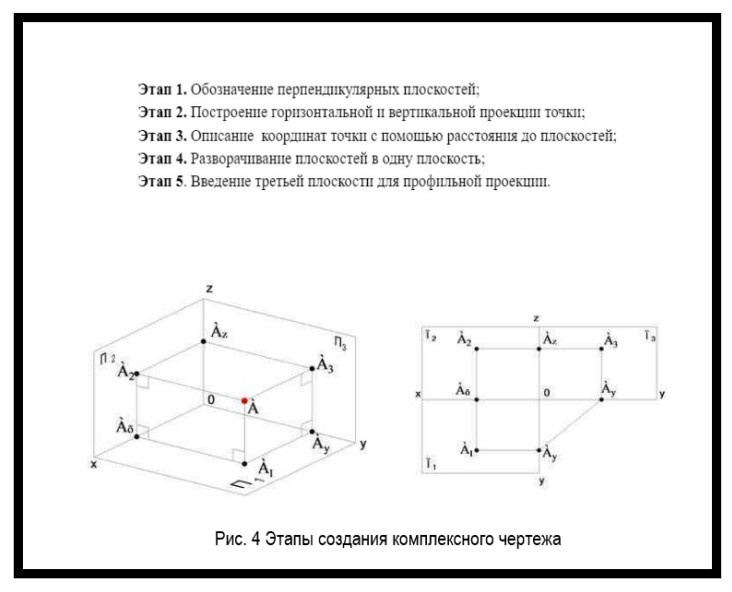
На таких чертежах объемный предмет проецируется ортогонально на две взаимно перпендикулярные плоскости. Одна из них — вертикальная, другая — горизонтальная. Прямая пересечения этих плоскостей называется осью проекции
.
Изображение точки на комплексном чертеже
На комплексном чертеже точка — пара координат. Для изображения точки на чертеже нужно провести две перпендикулярные оси: горизонтальную и вертикальную ось. В зависимости от положения точки относительно плоскостей проекции, точки пространства могут быть нескольких видов (рисунок 4.1).
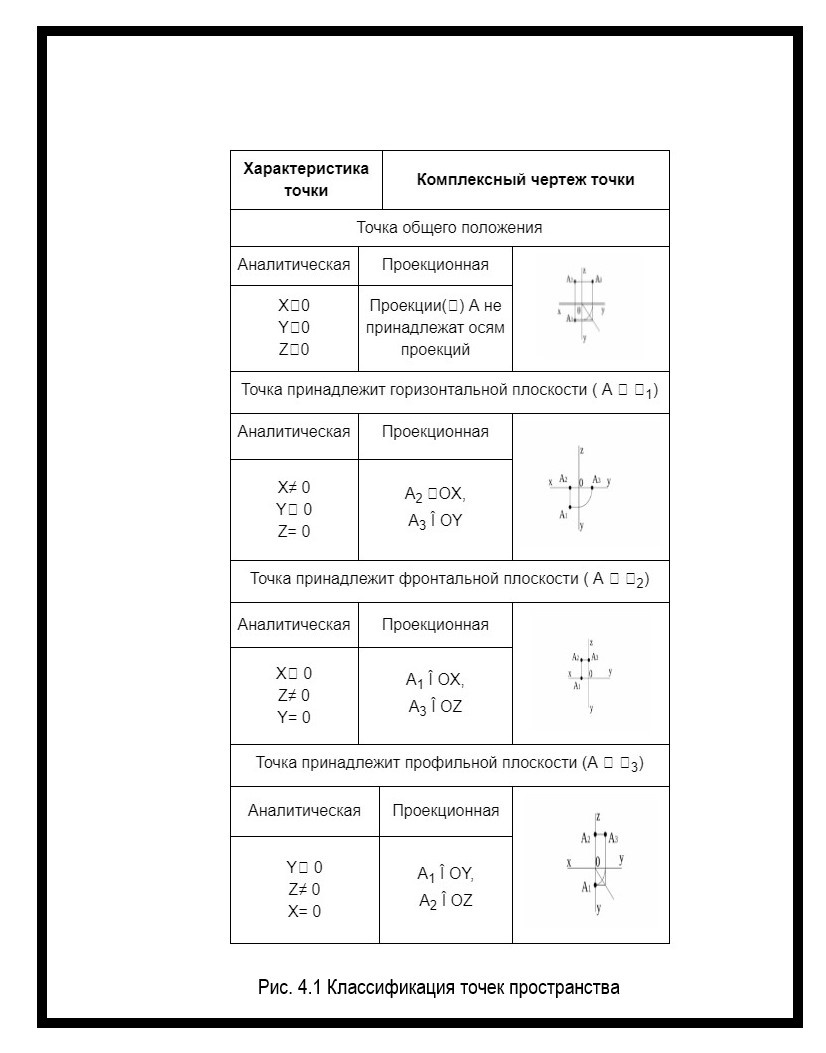
Обозначение точек на чертеже
Обозначение точек на чертеже осуществляется разными способами. Все параметры точек равны нулю, поэтому для их изображения используют условные обозначения (рис. 3.1).
Точка обозначаются буквами (например, точка A, B, C) или цифрами (например, точка 1, 2, 3). Кроме того, она может быть обозначена геометрическими символами кружочком или пересечением двух линий (рисунок 3).

Конкурирующие точки на чертеже
Точки на чертеже с двумя одинаковыми координатами называются конкурирующими (рисунок 4). Это точки, которые лежат на одном проецирующем луче.
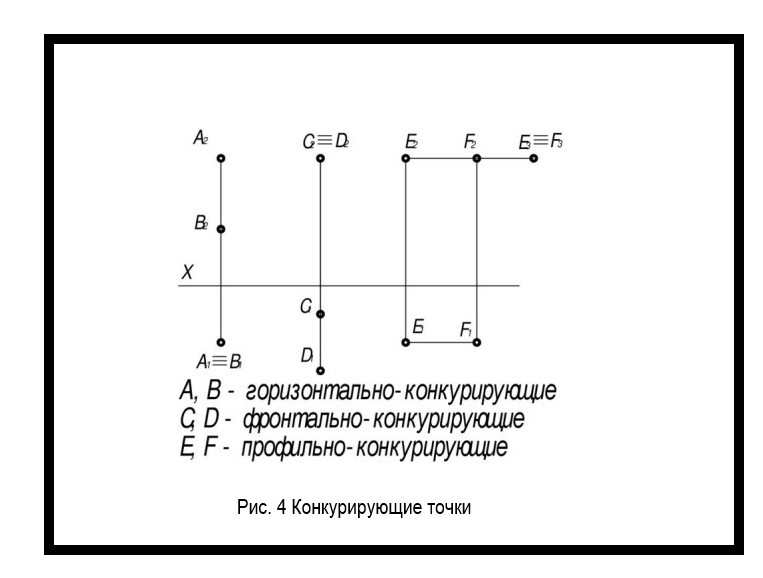
Они могут быть нескольких видов, название которых определяет плоскость совпадающих проекций:
- Горизонтально конкурирующие — лежат на одном перпендикуляре к горизонтальной плоскости;
- Фронтально конкурирующие — лежат на одном луче к фронтальной плоскости;
- Профильно конкурирующие — лежат на одном перпендикуляре к профильной плоскости.
Видимые и невидимые конкурирующие точки на чертеже
Видимостью называют изображение близких к наблюдателю точек. Этот параметр помогает улучшить понимание геометрической формы и расположения предмета в пространстве.
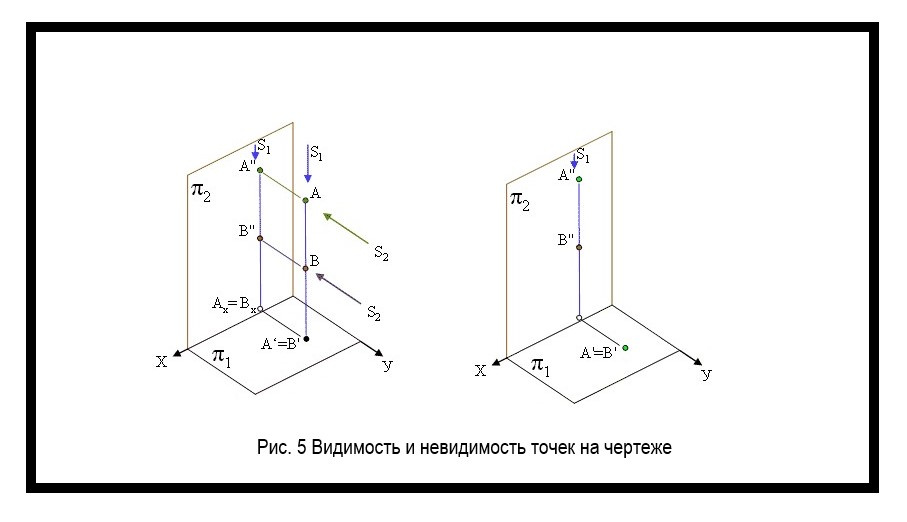
Для определения видимости, нужно найти точки предмета на одном луче и обозначить только те, которые расположены ближе к вам (рисунок 5). Без видимости определить положение объекта сложно.
Как обозначить видимость точек на чертеже
Видимость точек обозначается буквами (например, точка C”), невидимость — буквами с круглыми скобками (например, точка (С”)).
Типы точек на чертеже
Точки на чертеже по ГОСТу могут быть следующих типов:
Не хотите тратить время на чертежи? Вы можете заказать готовый чертеж у экспертов Студворк!
Определение видимостиОпределение видимости геометрических фигур на плоскости проекций выполняют с использованием конкурирующих точек.
Определение видимости рассмотрим на примерах:
Определение видимости
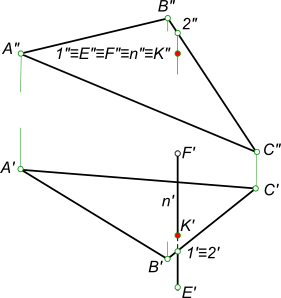
Конкурирующие точки находим в пересечении проекций прямой с проекциями треугольника ABC – это точки 1 и 2 их проекции 1` и 2` на плоскость H совпадают. – имеется готовый эпюр пересечения прямой с плоскостью заданной следами
Определение видимости
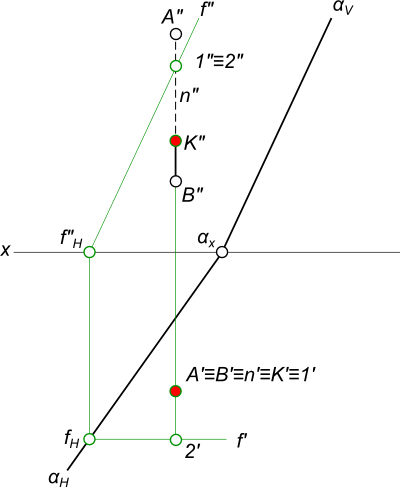
Конкурирующие точки находим в пересечении проекций прямой с проекциями плоскости α – для этого проводим в плоскости произвольную прямую f, чтобы имело место пересечение фронтальных проекций заданной прямой n и прямой f. + |
3.1. Способы задания плоскости на ортогональных чертежах
Положение плоскости в пространстве определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, взятой вне прямой;
- двумя пересекающимися прямыми;
- двумя параллельными прямыми;
- плоской фигурой.
В соответствии с этим на эпюре плоскость может быть задана:
- проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
- проекциями точки и прямой (Рисунок 3.1,б);
- проекциями двух пересекающихся прямых (Рисунок 3.1,в);
- проекциями двух параллельных прямых (Рисунок 3.1,г);
- плоской фигурой (Рисунок 3.1,д);
- следами плоскости;
- линией наибольшего ската плоскости.
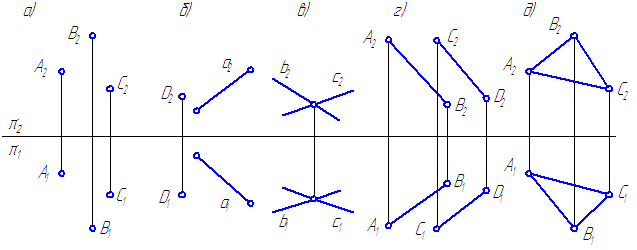
Рисунок 3.1 – Способы задания плоскостей
Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
Плоскость общего положения может иметь три следа: горизонтальный – απ1, фронтальный – απ2 и профильный – απ3, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π1, фронтальной π2 и профильной π3 (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения
3.2. Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости: все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения
3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости
α = m // n D ∈ n ⇒ D ∈ α

Рисунок 3.6 – Принадлежность прямой плоскости
left.begin{array}{l}alpha=mparallel n,\Dinalpha\Cinalpha\end{array}right} Longrightarrow CDinalpha
Упражнение
Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С.

Рисунок 3.7 – Решение задачи
Решение:
- ABCD – плоский четырехугольник, задающий плоскость.
- Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
- Согласно признаку пересекающихся прямых, построим фронтальную проекцию точки пересечения этих прямых — K: A2C2 ∩ B2D2=K2.
- Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD: на проекции диагонали B1D1 строим К1.
- Через А1К1 проводим проекцию диагонали А1С1.
- Точку С1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А1К1.
3.4. Главные линии плоскости
В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).
Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1) (Рисунок 3.8, а; 3.9).
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2) (Рисунок 3.8, б; 3.10).
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π3) (Рисунок 3.8, в; 3.11).
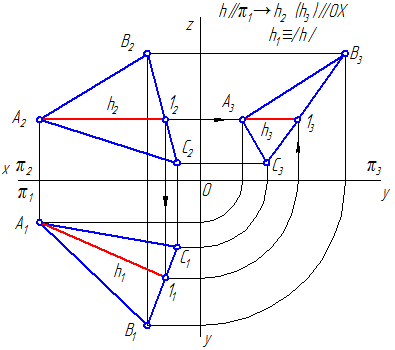
Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником
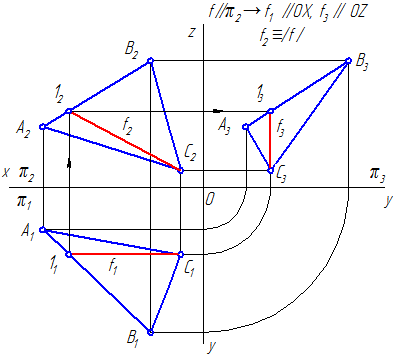
Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником
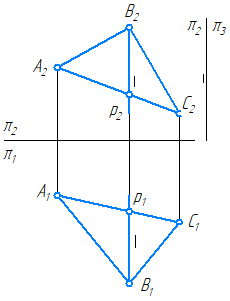
Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости: прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).
alpha=mcap n\left.begin{array}{l}a_2parallel m_2\a_1parallel m_1\end{array}right} Rightarrow aparallelalpha

Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
- Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
- Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
- Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.
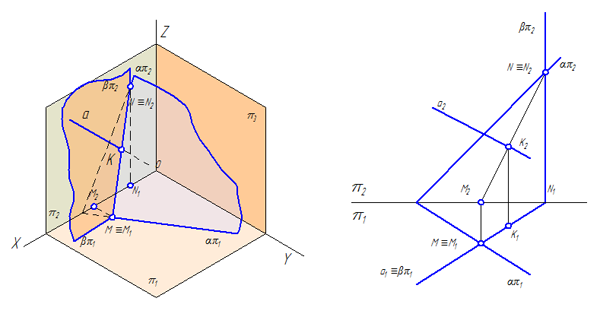
Рисунок 3.13 – Построение точки встречи прямой с плоскостью
Упражнение
Заданы: прямая АВ общего положения, плоскость σ⊥π1. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.
Решение:
-
- Точка К должна принадлежать прямой АВ ⇒ К1∈А1В и заданной плоскости σ ⇒ К1∈σ, следовательно, К1 находится в точке пересечения проекций А1В1 и σ1;
- Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ1 (горизонтальный след плоскости);
- Фронтальную проекцию точки К находим посредством линии проекционной связи: К2∈А2В2.
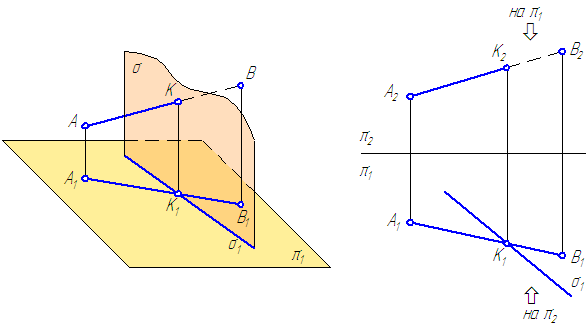
Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения
Упражнение
Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).
Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью
Решение:
- Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
- Если α⊥π1, то на плоскость проекций π1 плоскость α проецируется в прямую (горизонтальный след плоскости απ1 или α1), совпадающую с E1F1;
- Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
- Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.
Алгоритм решения задачи (Рисунок 3.15, б): Через EF проведем вспомогательную плоскость α:
- left.begin{array}{l}alpha perp pi_1\alphain EF\end{array}right} Longrightarrow alpha_1in E_1F_1
- alphacapsigma=(1-2)left.begin{array}{l}|alpha_1cap A_1C_1=1_1longrightarrow 1_2\|alpha_1cap A_1B_1=2_1longrightarrow 2_2\end{array}right.
- (1_2-2_2)cap E_2F_2=K_2\left.begin{array}{l}Kin EF\Kin (1-2)Rightarrow Kinsigma\end{array}right}Longrightarrow K=EFcap (sigma =triangle ABC)
3.6. Определение видимости методом конкурирующих точек
При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π1 или π2.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π2 (рис. 3.15)
Выберем точки, конкурирующие на π2 – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π2.
Направление взгляда на π2 показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π2, видно, что точка 41 располагается ближе к наблюдателю, чем 31.
41∈E1F1 ⇒ 4∈EF ⇒ на π2 будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π1.
Для определения видимости выберем точки, конкурирующие на π1 – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π1.
Направление взгляда на π1 показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π1, видно, что точка 22 располагается ближе к наблюдателю, чем 52.
22∈А2В2 ⇒ 2∈АВ ⇒ на π1 будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.
3.7. Перпендикулярность прямой плоскости
Признак перпендикулярности прямой плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости
Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)
Теорема доказывается через теорему о проецировании прямого угла в частном случае.
Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).
Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.
- Построим горизонталь и фронталь в плоскости σ=ΔАВС : σ=ΔАВС : A-1∈σ; A-1//π1; С-2∈σ; С-2//π2.
- Восстановим из точки K перпендикуляр к заданной плоскости: p1⊥h1 и p2⊥f2, или p1⊥απ1 и p2⊥απ2.
3.8. Взаимное положение двух плоскостей
3.8.1. Параллельность плоскостей
Две плоскости могут быть параллельными и пересекающимися между собой.
Признак параллельности двух плоскостей: две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Упражнение
Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).
Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной
Решение: В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.
- Через точку F проводим прямую m, параллельную, например, АВ.
- Через точку F, или же через любую точку, принадлежащую m, проводим прямую n, параллельную, например, ВС, причём m∩n=F.
- β = m∩n и β//α по определению.
3.8.2. Пересечение плоскостей
Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.
Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.
Упражнение
Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей. 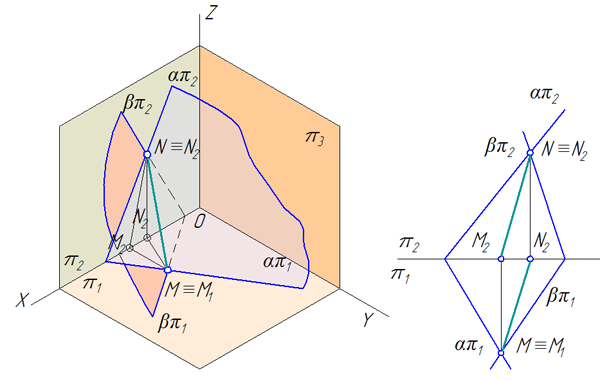
Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами
Порядок построения линии пересечения плоскостей:
- Найти точку пересечения горизонтальных следов — это точка М (её проекции М1 и М2, при этом М1=М, т.к. М – точка частного положения, принадлежащая плоскости π1).
- Найти точку пересечения фронтальных следов — это точка N (её проекции N1 и N2, при этом N2=N, т.к. N – точка частного положения, принадлежащая плоскости π2).
- Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М1N1 и М2N2.
МN – линия пересечения плоскостей.
Упражнение
Задана плоскость σ = ΔАВС, плоскость α – горизонтально- проецирующая (α⊥π1) ⇒α1 – горизонтальный след плоскости (Рисунок 3.19). Построить линию пересечения этих плоскостей.
Решение:
Так как плоскость α пересекает стороны АВ и АС треугольника АВС, то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L, то есть K1 и L1 , на пересечении горизонтального следа (α1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС: А1В1 и A1C1. После чего посредством линий проекционной связи находим фронтальные проекции этих точек K2 и L2 на фронтальных проекциях прямых АВ и АС. Соединим одноимённые проекции: K1 и L1; K2 и L2. Линия пересечения заданных плоскостей построена.
Алгоритм решения задачи:
left.begin{array}{l}ABcapsigma=K\ACcapsigma=L\end{array}right} left.begin{array}{l}Rightarrow A_1B_1capsigma_1=K_1 rightarrow K_2\Rightarrow A_1C_1cap sigma_1=L_1 rightarrow L_2\end{array}right.
KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения
Упражнение
Заданы плоскости α = m//n и плоскость σ = ΔАВС (Рисунок 3.20). Построить линию пересечения заданных плоскостей. Решение:
- Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
- В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π2; τ⊥π2.
- Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:
— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7); — результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).
- Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях σ и β, то есть на прямой пересечения этих плоскостей;
- Аналогично находим точку N, общую для плоскостей σ и β.
- Соединив точки M и N, построим прямую пересечения плоскостей σ и β.
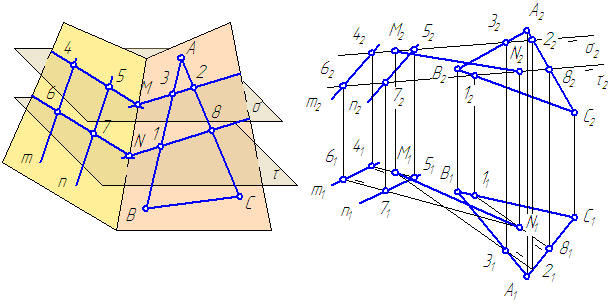
Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)
Алгоритм решения задачи:
left.begin{array}{l}alphacapsigma=(4-5)\betacapsigma=(3-2)\end{array}right}\left.begin{array}{l}alphacaptau=(6-7)\betacaptau=(1-8)\end{array}right}left.begin{array}{l}(4_1-5_1)cap(3_1-2_1)=M_1rightarrow M_2\(6_1-7_1)cap(1_1-8_1)=N_1rightarrow N_2\end{array}right}rightarrow\left.begin{array}{l}M_1N_1\M_2N_2\end{array}right}Rightarrowalphacapbeta=MN
Упражнение
Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей
Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π2, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π2 (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Упражнение
Задана плоскость σ⊥π2 и прямая общего положения – DE (Рисунок 3.22)
Требуется построить через DE плоскость τ⊥σ.
Решение.
Проведём перпендикуляр CD к плоскости σ – C2D2⊥σ2 (на основании теоремы о проецировании прямого угла).

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости
По теореме о проецировании прямого угла C1D1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.
Упражнение
Задана плоскость α = ΔАВС и точка K вне плоскости α. Требуется построить плоскость β⊥α, проходящую через точку K. Алгоритм решения (Рисунок 3.23):
- Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС;
- Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости: если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b2⊥f2; b1⊥h1;
- Задаём плоскость β любым способом, например, β = a∩b, таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.
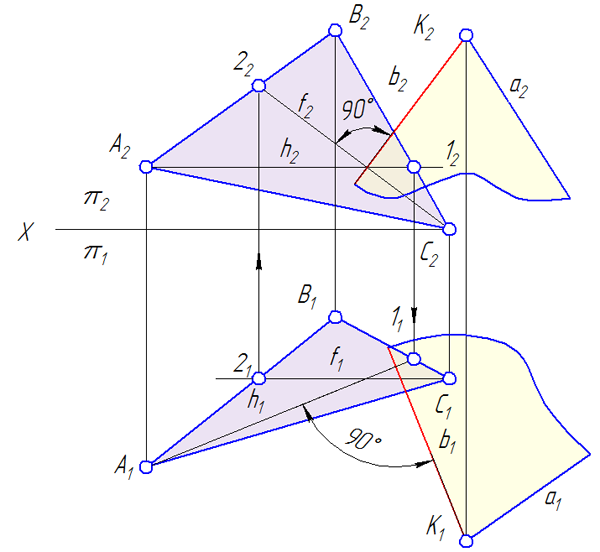
Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.
Постройте фронтальную проекцию точки К.

Рисунок 3.24
2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

Рисунок 3.25
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π2, если его диагональ MN //π2 (Рисунок 3.26).

Рисунок 3.26
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

Рисунок 3.27
5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

Рисунок 3.28
6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π1.
7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π1.