Астероид (65) Кибела и две звезды с указанными для них видимыми звёздными величинами
Ви́димая звёздная величина́ (обозначается m) — мера яркости небесного тела (точнее, освещённости, создаваемой этим телом) с точки зрения земного наблюдателя. Обычно используют величину, скорректированную до значения, которое она имела бы при отсутствии атмосферы. Чем ярче объект, тем меньше его звёздная величина.
Уточнение «видимая» указывает только на то, что эта звёздная величина наблюдается с Земли; это уточнение нужно, чтобы отличить её от абсолютной звёздной величины (которая является характеристикой самого́ источника, а не условий его наблюдения). Оно не указывает на видимый диапазон: видимыми называют и величины, измеренные в инфракрасном или каком-либо другом диапазоне. Величина, измеренная в видимом диапазоне, называется визуальной[1].
В видимой части спектра самая яркая звезда на ночном небе вне Солнечной системы, Сириус, имеет видимую звёздную величину −1,46m
Самая близкая к нам звезда, Солнце, имеет видимую величину −26,74m
Источник, излучающий в видимом диапазоне и создающий освещённость в 1 люкс (например, источник с силой света в 1 канделу, находящийся на расстоянии 1 м), имеет видимую звёздную величину −14,20m[2][3].
История[править | править код]
| Видны невооружённым глазом[4] |
Видимая величина |
Яркость относительно Веги |
Число звёзд ярче этой видимой величины[5] |
|---|---|---|---|
| Да | −1,0 | 250 % | 1 |
| 0,0 | 100 % | 4 | |
| 1,0 | 40 % | 15 | |
| 2,0 | 16 % | 48 | |
| 3,0 | 6,3 % | 171 | |
| 4,0 | 2,5 % | 513 | |
| 5,0 | 1,0 % | 1 602 | |
| 6,0 | 0,40 % | 4 800 | |
| 6,5 | 0,25 % | 9 096[6] | |
| Нет | 7,0 | 0,16 % | 14 000 |
| 8,0 | 0,063 % | 42 000 | |
| 9,0 | 0,025 % | 121 000 | |
| 10,0 | 0,010 % | 340 000 |
Шкала, используемая для обозначения звёздной величины, возникла в эллинистической Греции и использовалась для разделения видимых невооружённым глазом звёзд на шесть величин. Самые яркие звезды на ночном небе имеют первую звездную величину (m = 1), а самые тусклые соответствуют шестой звёздной величине (m = 6), что является пределом человеческого зрительного восприятия (без помощи оптических инструментов). Каждая целая величина считалась обладающей вдвое большей яркости по сравнению с последующей величиной (то есть использовалась логарифмическая шкала), хотя это соотношение было субъективным из-за отсутствия фотодетекторов. Эта довольно грубая шкала яркости звёзд была популяризирована Птолемеем в его труде Альмагесте и, как принято считать, придумана Гиппархом. Это невозможно ни доказать, ни опровергнуть, поскольку исходный звёздный каталог Гиппарха был утерян. Единственный сохранившийся текст самого Гиппарха (комментарий к Арату) свидетельствует о том, что у него не было системы для численного описания яркости: он всегда использует такие термины, как «большой» или «маленький», «яркий» или «слабый» или даже такие описания, как «видны в полнолуние»[7].
В 1856 году Норман Роберт Погсон дал более формальное определение, определив звезду первой величины как звезду, которая в 100 раз ярче звезды шестой звёздной величины, тем самым постулировав логарифмическую шкалу, используемую до сих пор. Это означает, что звезда со звёздной величиной m примерно в 2,512 раза ярче звезды со звёздной величиной m + 1. Эта цифра соответствует корню пятой степени из 100 и известна как коэффициент Погсона[8]. Нулевую точку шкалы Погсона первоначально определяли, принимая видимую звёздную величину Полярной звезды равной в точности 2,00m. Позже астрономы обнаружили, что Полярная является переменной звездой и немного изменяет свою яркость, поэтому они переключились на Вегу в качестве стандартной точки отсчёта, постулировав яркость Веги как определение нулевой звёздной величины для любой заданной длины волны.
Помимо небольших поправок, яркость Веги по-прежнему служит определением нулевой величины для видимой и ближней инфракрасной частей спектра, где её спектральное распределение энергии близко к излучению чёрного тела при температуре 11 000 K. Однако с появлением инфракрасной астрономии было обнаружено, что излучение Веги включает в себя избыток инфракрасного излучения, предположительно из-за околозвёздного диска, состоящего из пыли при высоких температурах (но намного более холодной, чем поверхность звезды). На более коротких (например, видимых) длинах волн при этих температурах наблюдается незначительное излучение пыли. Для того, чтобы правильно расширить шкалу звёздных величин на инфракрасный диапазон спектра, эта особенность Веги не должна влиять на определение шкалы звёздных величин. Поэтому шкала звёздных величин была экстраполирована на все длины волн на основе кривой излучения чёрного тела для идеальной поверхности звезды при температуре 11 000 K, не загрязнённой излучением из её окрестностей. На основе этой модели можно вычислить спектральную энергетическую освещённость (обычно выражаемую в янских) для точки, соответствующей нулевой звёздной величине, как функцию длины волны[9]. Небольшие отклонения указываются между системами, использующими измерительные приборы, разработанные независимо, чтобы можно было должным образом сравнивать данные, полученные разными астрономами, но большее практическое значение имеет определение звёздной величины не на одной длине волны, а применительно к отклику стандартных спектральных фильтров, используемых в фотометрии, в различных диапазонах длин волн.
| Диаметр телескопа (мм) |
Ограничение на звёздную величину |
|---|---|
| 35 | 11,3 |
| 60 | 12,3 |
| 102 | 13,3 |
| 152 | 14.1 |
| 203 | 14,7 |
| 305 | 15.4 |
| 406 | 15,7 |
| 508 | 16,4 |
В современных системах звёздных величин яркость в очень широком диапазоне определяется в соответствии с логарифмическим определением, подробно описанным ниже, с использованием заданного эталона. На практике такие видимые звёздные величины не превышают 30 (для возможных наблюдаемых значений). Яркость Веги превосходят четыре звезды на ночном небе в видимом диапазоне длин волн (и больше в инфракрасном диапазоне), а также яркие планеты Венера, Марс и Юпитер, и их следует описывать отрицательными величинами. Например, Сириус, самая яркая звезда небесной сферы, имеет звёздную величину −1,4m в видимом диапазоне. Отрицательные величины для других очень ярких астрономических объектов можно найти в таблице справа.
Астрономы разработали и другие фотометрические системы точки отсчета в качестве альтернативы системы основанной на яркости Веги. Наиболее широко используется система звёздных величин AB[11], в которой фотометрические нулевые точки основаны на гипотетическом эталонном спектре, имеющем постоянный поток на единичный частотный интервал, а не на использовании звёздного спектра или кривой чёрного тела в качестве эталона. Нулевая точка величины AB определяется таким образом, чтобы величины объекта на основе AB и Веги были приблизительно равны в полосе фильтра V.
Разность звёздных величин[править | править код]
Если видимые звёздные величины объектов 1 и 2 равны m1 и m2, то их разность определяется как
где L1, L2 — освещённости от этих объектов. Это соотношение известно как уравнение Погсона. Его можно записать также в другом виде[2]:
или
Таким образом, разница в 5 звёздных величин соответствует отношению освещённостей в 100 раз, а разница в одну звёздную величину — в 1001/5 ≈ 2,512 раза.
Из уравнения Погсона можно получить освещённость в люксах, создаваемую источником с известной видимой звёздной величиной m1 в видимом диапазоне. Поскольку освещённость L2 = 1 люкс создаёт источник с видимой звёздной величиной m2 = −14,20m, то[2]
люкс.
Обратив формулу, получаем видимую звёздную величину объекта, создающего освещённость L1, выраженную в люксах:
Примеры[править | править код]
Видимая звёздная величина полной Луны равна −12,7m; яркость Солнца составляет −26,7m.
Разница звёздных величин Луны (

Отношение освещённостей от Солнца и Луны:
Таким образом, Солнце примерно в 400 000 раз ярче полной Луны.
Освещённость, создаваемая звёздами с видимой звёздной величиной 1,0m и 6,0m в видимом диапазоне, равна соответственно 8,3×10−7 люкс и 8,3×10−9 люкс[2].
Суммарная звёздная величина[править | править код]
Общая видимая звёздная величина (ms) двух близко расположенных небесных светил с видимыми звёздными величинами m1 и m2 вычисляется путём преобразования величин m1 и m2 к освещённостям, сложению освещённостей и последующему обратному преобразованию к логарифмическому виду:[12]
По тому же принципу может быть вычислена общая звёздная величина систем, которые обладают бо́льшими уровнями кратности.
Примечания[править | править код]
- ↑ Сурдин В. Г.. Звёздная величина. Глоссарий Astronet.ru. Астронет. Дата обращения: 28 февраля 2015. Архивировано 28 ноября 2010 года.
- ↑ 1 2 3 4 Dufay J. Introduction to Astrophysics: The Stars (англ.). — Dover Publications, 2012. — P. 3. — ISBN 9780486607719.
- ↑ McLean I. S. Electronic Imaging in Astronomy: Detectors and Instrumentation (англ.). — Springer, 2008. — P. 529. — ISBN 978-3-540-76582-0.
- ↑ Vmag<6.5. SIMBAD Astronomical Database. Дата обращения: 25 июня 2010. Архивировано 12 марта 2020 года.
- ↑ Magnitude. National Solar Observatory—Sacramento Peak. Дата обращения: 23 августа 2006. Архивировано 6 февраля 2008 года.
- ↑ «Каталог ярких звёзд»
- ↑ Hoffmann, S., Hipparchs Himmelsglobus, Springer, Wiesbaden/ New York, 2017
- ↑ Pogson, N. (1856). “Magnitudes of Thirty-six of the Minor Planets for the first day of each month of the year 1857”. MNRAS. 17. Bibcode:1856MNRAS..17…12P. DOI:10.1093/mnras/17.1.12. Архивировано из оригинала 2007-07-03. Дата обращения 2006-06-16.
- ↑ www.astro.utoronto.ca.
- ↑ North, Gerald. Observing Variable Stars, Novae and Supernovae / Gerald North, Nick James. — Cambridge University Press, 2014. — P. 24. — ISBN 9781107636125. Архивная копия от 24 августа 2021 на Wayback Machine
- ↑ Oke, J. B. (15 March 1983). “Secondary standard stars for absolute spectrophotometry”. The Astrophysical Journal. 266: 713—717. Bibcode:1983ApJ…266..713O. DOI:10.1086/160817.
- ↑ Magnitude Arithmetic (англ.). Weekly Topic. Caglow. Дата обращения: 30 января 2012. Архивировано 11 декабря 2018 года.
Ссылки[править | править код]
- The astronomical magnitude scale Архивная копия от 29 августа 2019 на Wayback Machine // International Comet Quarterly (англ.)
|
ВС, 01/09/2011 – 13:16 — mav Звёздная величина(из Википедии)Звёздная величина – числовая характеристика объекта на небе, чаще всего звезды, показывающая, сколько света приходит от него в точку, где находится наблюдатель. Видимая (визуальная) Современное понятие видимой звёздной величины сделано таким, чтобы оно соответствовало величинам, приписанным звёздам древнегреческим астрономом Гиппархом во II веке до н. э. Гиппарх разделил все звёзды на шесть величин. Самые яркие он назвал звёздами первой величины, самые тусклые — звёздами шестой величины. Промежуточные величины он распределил равномерно между оставшимися звёздами. Видимая звёздная величина зависит не только от того, сколько света излучает объект, но и от того, на каком расстоянии от наблюдателя он находится. Видимая звёздная величина считается единицей измерения блеска звезды, причём чем блеск больше, тем величина меньше, и наоборот. В 1856 году Н. Погсон предложил формализацию шкалы звёздных величин. Видимая звёздная величина определяется по формуле:
Поскольку данная шкала относительная, то её нуль-пункт (0m) определяют как яркость такой звезды, у которой световой поток равен 10³ квантов /(см²·с·Å) в зелёном свете (шкала UBV) или 106 квантов /(см²·с·Å) во всём видимом диапазоне света. Звезда 0m за пределами земной атмосферы создаёт освещённость в 2,54·10−6 люкс. Шкала звёздных величин является логарифмической, поскольку изменение яркости в одинаковое число раз воспринимается как одинаковое (закон Вебера — Фехнера). Кроме того, поскольку Гиппарх решил, что величина тем меньше, чем звезда ярче, то в формуле присутствует знак минус. Следующие два свойства помогают пользоваться видимыми звёздными величинами на практике:
В наши дни видимая звёздная величина используется не только для звёзд, но и для других объектов, например, для Луны и Солнца и планет. Поскольку они могут быть ярче самой яркой звезды, то у них может быть отрицательная видимая звёздная величина. Видимая звёздная величина зависит от спектральной чувствительности приёмника излучения (глаза, фотоэлектрического детектора, фотопластинки и т. п.)
Разности звёздных величин одного объекта в разных диапазонах U−B и B−V являются интегральными показателями цвета объекта, чем они больше, тем более красным является объект.
абсолютнаяАбсолютная звёздная величина (M) определяется как видимая звёздная величина объекта, если бы он был расположен на расстоянии 10 парсек от наблюдателя. Абсолютная болометрическая звёздная величина Солнца +4,7. Если известна видимая звёздная величина и расстояние до объекта, можно вычислить абсолютную звёздную величину по формуле:
Соответственно, если известны видимая и абсолютная звёздные величины, можно вычислить расстояние по формуле Абсолютная звёздная величина связана со светимостью следующим соотношением: Звёздные величины некоторых объектов
Самые яркие звёзды
Солнце с разных расстояний
|
Наше Солнце справедливо называют типичной звездой. Но среди
большого и разнообразного числа звёзд есть немало таких, которые значительно
отличаются от него по своим физическим характеристикам и химическому составу.
Поэтому полное представление о звёздах даст такое определение:
Звезда — это массивный газовый шар, излучающий свет и
удерживаемый в состоянии равновесия силами собственной гравитации и внутренним
давлением, в недрах которого происходят (или происходили ранее) реакции
термоядерного синтеза.
Мысли о том, что звёзды — это далёкие солнца, высказывались
ещё в глубокой древности. Но из-за колоссальных расстояний до них диски звёзд
не видны даже в самые мощные телескопы. Поэтому, чтобы найти возможность
сравнивать звёзды между собой и с Солнцем, необходимо было придумать способы
определения расстояний до них.
Ещё Аристотель предполагал, что если Земля движется вокруг
Солнца, то, наблюдая за звездой из двух диаметрально противоположных точек
земной орбиты, можно заметить изменение направления на звезду — её параллактическое
(то есть кажущееся) смещение.
Такая же идея измерения расстояний была предложена и Николаем
Коперником после опубликования им гелиоцентрической системы мироустройства.
Однако ни Копернику, ни тем более Аристотелю не удалось обнаружить это
смещение.
Лишь к середине XIX века, когда на телескопы стали ставить оборудование для
точного измерения углов, удалось измерить такое смещение у ближайших звёзд. Как
удалось установить, кажущееся перемещение более близкой звезды на фоне очень
далёких звёзд происходит по эллипсу с периодом в один год и отражает движение
наблюдателя вместе с Землёй вокруг Солнца. Этот небольшой эллипс, который
описывает звезда, называется параллактическим эллипсом.
В угловой мере его большая полуось равна величине угла, под
которым со звезды видна большая полуось земной орбиты, перпендикулярная
направлению на звезду. Этот угол называется годичным параллаксом и
обозначается греческой буквой π или латинской буквой р.
Зная годичное параллактическое смещение звезды, можно легко
определить расстояние до неё:
В записанной формуле а — это
средний радиус земной орбиты.
Если учесть, что годичные параллаксы звёзд измеряются десятитысячными
долями секунды, а большая полуось земной орбиты равна одной астрономической
единице, то можно получить формулу для вычисления расстояния до звезды в
астрономических единицах:
Первые надёжные измерения годичного параллакса были
осуществлены почти одновременно в Германии, России и Англии в 1837 году.
В России первые измерения годичного параллакса были проведены
Василием Яковлевичем Струве для яркой звезды Северного полушария Веги. Давайте
по его данным определим расстояние до этой звезды.
Согласитесь, что для измерения расстояний до звёзд
астрономическая единица слишком мала. Даже ближайшая к нам звезда —
альфа-Центавра — расположена более чем в 273,5 тысячах а. е. Поэтому для
удобства определения расстояний до звёзд в астрономии применяется специальная
единица длины — парсек (сокращённо пк), название
которой происходит от двух слов — «параллакс» и «секунда».
Парсек — это расстояние, с которого средний радиус
земной орбиты, перпендикулярный лучу зрения, виден под углом в одну угловую
секунду:
1 пк
= 206 265 а. е. =30,8586 трлн км.
Исходя из определения, расстояние в парсеках равно обратной
величине годичного параллакса:
Вернёмся к нашей задаче и определим расстояние до Веги в
парсеках, воспользовавшись полученным нами уравнением.
Также, помимо парсека, в астрономии используется ещё одна
внесистемная единица измерения расстояний — световой год.
Световой год — это расстояние, которое свет,
распространяясь в вакууме, проходит за один год:
1 пк
= 3,26 св. г. = 206 265 а. е. = 3 ∙ 1013 км.
В 1989 году Европейским космическим агентством был запущен
спутник «Гиппаркос». За 37 месяцев своей работы ему удалось
измерить годичные параллаксы более чем миллиона звёзд. При этом точность
измерений для более ста тысяч из них составила одну угловую миллисекунду.
Однако после того, как астрономы научились определять
расстояния до звёзд, возникла ещё одна проблема. Оказалось, что звёзды,
находящиеся примерно на одинаковом расстоянии от Земли, могут отличаться друг
от друга по видимой яркости (блеску). При этом видимый блеск не характеризует
реального излучения звезды. Например, Солнце нам кажется самым ярким объектом
на небе лишь потому, что оно находится гораздо ближе к Земле, чем остальные
звёзды. Поэтому для сравнения истинного блеска звёзд необходимо было определять
их звёздную величину на определённом одинаковом расстоянии от Земли. За такое
одинаковое (или стандартное) расстояние принято 10 пк. Видимая звёздная величина, которую
имела бы звезда, если бы находилась от нас на расстоянии 10 пк,
называется абсолютной звёздной величиной.
Почему в качестве эталонного расстояния было выбрано 10
парсек? Да для простоты расчётов. Итак, предположим, что видимая звёздная
величина звезды на некотором расстоянии D равна т а её блеск — I.
Напомним, что блеск двух источников, звёздные величины
которых отличаются на единицу, отличаются в 2,512 раза. То есть для двух звёзд,
звёздные величины которых равны т1 и т2
соответственно, отношение их блесков выражается соотношением:
Тогда по определению видимая звёздная величина звезды с
расстояния в 10 пк будет равна абсолютной звёздной
величине М. Если обозначить блеск звезды на этом расстоянии через I0, то для
видимой и абсолютной звёздных величин одной и той же звезды предыдущее
уравнение будет выглядеть так:
В тоже время из физики известно, что блеск меняется обратно
пропорционально квадрату расстояния:
Подставим данное выражение в предыдущее уравнение, при этом
учтём, что :
Теперь прологарифмируем полученное выражение:
И упростим его:
Если учесть, что расстояние до звезды обратно пропорционально
её годичному параллаксу, то получим формулу, по которой можно вычислить
абсолютную звёздную величину близко расположенных к нам звёзд
Теперь давайте по полученной формуле рассчитаем абсолютную
звёздную величину нашего Солнца. Для этого учтём, что его видимая звёздная
величина равна–26,8т, а среднее расстояние до него составляет
одну астрономическую единицу
То есть наше Солнце выглядит слабой звёздочкой почти пятой
звёздной величины.
Зная абсолютную звёздную величину звезды, можно вычислить её
действительное общее излучение или светимость.
Светимостью называют полную энергию, излучаемую
звездой за единицу времени. Светимость звезды можно выразить в ваттах, но чаще
её выражают в светимостях Солнца.
Используя формулу Погсона, можно записать соотношение между светимостями
и абсолютными звёздными величинами какой-либо звезды и Солнца:
Данную формулу можно переписать, если учесть, что светимость
Солнца принята за единицу, а его абсолютна звёздная величина равна 4,8m:
По светимости (то есть мощности излучения) звёзды значительно
отличаются друг от друга. Так мощность излучения некоторых звёзд-сверхгигантов
больше мощности излучения Солнца в 330 тыс. А некоторые звёзды-карлики,
обладающие наименьшей светимостью, излучают свет в 480 тыс. раз слабее нашего
Солнца.
Звездная величина или блеск – это безразмерная величина, характеризующая видимость космического объекта на ночном небе. Обозначается буквой m, что пошло от латинского magnitude – величина, размер. Звездная величина зависит как от физических свойств объекта, так и от расстояния до него.
Оглавление
- 1 История
- 2 Классификация звездных величин
- 2.1 Видимая звездная величина
- 2.2
- 2.3 Абсолютная звездная величина
- 3
- 4 Применение звездных величин
История
Считается, что понятие звездой величины ввел Гиппарх Никейский. Однако, письменных подтверждений этому нет. Гиппарх составил первый каталог звезд, где разделили их на шесть величин – по яркости на небе, где первая – самые яркие, шестая – самые тусклые – предел человеческого восприятия невооруженным глазом.
Птолемей описал данную систему в Альмогесте, тем самым дав ей широкую огласку.
Норман Погсон в 1856 году ввел ясность в определение звездных величин, обозначив звезды первой величины в 100 раз ярче чем звезды шестой величин. Тем самым введя логарифмическую шкалу. Такой ее вид используется и по ныне.
В качестве эталонной звезды изначально была принятая Полярная, ее видимая звездная величина была определена как 2,00m. Но с развитием телескопов, стало понятно, что Полярная – переменная звезда, ее видимая величина меняется со временем. Тогда, в качестве эталона взяли Вегу, приняв ее звездную величину равную 0,00m.
В современной шкале используется и отрицательные звездные величины, так как под их описание попадают и планеты, и Луна, и Солнце.
Классификация звездных величин
В зависимости от спектральной чувствительности приемника (глаза, фотопластины, фотодетектора и т.п.) можно выделить 5 звездных величин:
- болометрическая – распространяется на весь спектр излучения, на все длины волн. Удобна, когда основная часть излучения звезды находится не в видимом спектре;
- визуальная – распространяется только на видимую часть спектра, максимум восприятия приходится на 555 нм (зеленый цвет);
- синяя – распространяется только на синюю часть спектра, как следует из названия, максимум восприятия приходится на 445 нм;
- ультрафиолетовая – распространяется на ультрафиолетовый спектр излучения с максимумом на 350 нм;
- фотографическая – показывает видимую звездную величину, если бы чувствительность человеческого глаза совпадала с чувствительностью фотоприбора. Максиму приходится на 425 нм.
Видимая звездная величина
Тем самым, исторически, видимая звездная величина – это сугубо человеческая характеристика яркости космического объекта на звездном небе и опирается она на чувствительность человеческого глаза.
Но в настоящее время, для определения видимой звездой величины используется логарифмические зависимости, основываясь на освещенности (отношение светового потока к площади на которую он падает) от этих объектов.
Абсолютная звездная величина
Абсолютная звездная величина уравнивает все объекты на одно расстояние, то есть, абсолютная звездная величина звезды – это видимая величина светила, если бы оно находилось на расстоянии 10 персек (32, 616 световых лет), без учета атмосферного или межзвездного поглощения.
Абсолютная звездная величина планет Солнечной системы – видимая величина на расстоянии 1 астрономической единицы от наблюдателя.
Для метеоров – видимая звездная величина, если бы метеор находился на расстоянии 100 км в зените.
Если же космический объект по своим размерам больше 10 парсек (галактика, туманность, звездное скопление), то тогда этот объект считают, как точечный объект, со суммарной светимостью.
Применение звездных величин
В астрономии используются все виды звездных величин, в зависимости от характера объекта и тех данных, которые надо сравнить. Особых предпочтений ученые не делают. Зная видимую и абсолютные звездные величины можно рассчитать расстояние до объекта.
For a more detailed discussion of the history of the magnitude system, see Magnitude (astronomy).
Asteroid 65 Cybele and two stars, with their magnitudes labeled
Apparent magnitude (m) is a measure of the brightness of a star or other astronomical object observed from Earth. An object’s apparent magnitude depends on its intrinsic luminosity, its distance from Earth, and any extinction of the object’s light caused by interstellar dust along the line of sight to the observer.
The word magnitude in astronomy, unless stated otherwise, usually refers to a celestial object’s apparent magnitude. The magnitude scale dates back to the ancient Roman astronomer Claudius Ptolemy, whose star catalog listed stars from 1st magnitude (brightest) to 6th magnitude (dimmest). The modern scale was mathematically defined in a way to closely match this historical system.
The scale is reverse logarithmic: the brighter an object is, the lower its magnitude number. A difference of 1.0 in magnitude corresponds to a brightness ratio of ![{displaystyle {sqrt[{5}]{100}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d26eff2c044a521107db3cf827e04c2b8415691d)
Differences in astronomical magnitudes can also be related to another logarithmic ratio scale, the decibel: an increase of one astronomical magnitude is exactly equal to a decrease of 4 decibels (dB).
The brightest astronomical objects have negative apparent magnitudes: for example, Venus at −4.2 or Sirius at −1.46. The faintest stars visible with the naked eye on the darkest night have apparent magnitudes of about +6.5, though this varies depending on a person’s eyesight and with altitude and atmospheric conditions.[1] The apparent magnitudes of known objects range from the Sun at −26.832 to objects in deep Hubble Space Telescope images of magnitude +31.5.[2]
The measurement of apparent magnitude is called photometry. Photometric measurements are made in the ultraviolet, visible, or infrared wavelength bands using standard passband filters belonging to photometric systems such as the UBV system or the Strömgren uvbyβ system.
Absolute magnitude is a measure of the intrinsic luminosity of a celestial object, rather than its apparent brightness, and is expressed on the same reverse logarithmic scale. Absolute magnitude is defined as the apparent magnitude that a star or object would have if it were observed from a distance of 10 parsecs (33 light-years; 3.1×1014 kilometres; 1.9×1014 miles). Therefore, it is of greater use in stellar astrophysics since it refers to a property of a star regardless of how close it is to Earth. But in observational astronomy and popular stargazing, unqualified references to “magnitude” are understood to mean apparent magnitude.
Amateur astronomers commonly express the darkness of the sky in terms of limiting magnitude, i.e. the apparent magnitude of the faintest star they can see with the naked eye. This can be useful as a way of monitoring the spread of light pollution.
Apparent magnitude is really a measure of illuminance, which can also be measured in photometric units such as lux.[3]
History[edit]
| Visible to typical human eye[4] |
Apparent magnitude |
Bright- ness relative to Vega |
Number of stars (other than the Sun) brighter than apparent magnitude[5] in the night sky |
|---|---|---|---|
| Yes | −1.0 | 251% | 1 (Sirius) |
| 00.0 | 100% | 4
(Sirius, Canopus, Alpha Centauri, |
|
| 01.0 | 40% | 15 | |
| 02.0 | 16% | 48 | |
| 03.0 | 6.3% | 171 | |
| 04.0 | 2.5% | 513 | |
| 05.0 | 1.0% | 1602 | |
| 06.0 | 0.4% | 4800 | |
| 06.5 | 0.25% | 9100[6] | |
| No | 07.0 | 0.16% | 14000 |
| 08.0 | 0.063% | 42000 | |
| 09.0 | 0.025% | 121000 | |
| 10.0 | 0.010% | 340000 |
The scale used to indicate magnitude originates in the Hellenistic practice of dividing stars visible to the naked eye into six magnitudes. The brightest stars in the night sky were said to be of first magnitude (m = 1), whereas the faintest were of sixth magnitude (m = 6), which is the limit of human visual perception (without the aid of a telescope). Each grade of magnitude was considered twice the brightness of the following grade (a logarithmic scale), although that ratio was subjective as no photodetectors existed. This rather crude scale for the brightness of stars was popularized by Ptolemy in his Almagest and is generally believed to have originated with Hipparchus. This cannot be proved or disproved because Hipparchus’s original star catalogue is lost. The only preserved text by Hipparchus himself (a commentary to Aratus) clearly documents that he did not have a system to describe brightness with numbers: He always uses terms like “big” or “small”, “bright” or “faint” or even descriptions such as “visible at full moon”.[7]
In 1856, Norman Robert Pogson formalized the system by defining a first magnitude star as a star that is 100 times as bright as a sixth-magnitude star, thereby establishing the logarithmic scale still in use today. This implies that a star of magnitude m is about 2.512 times as bright as a star of magnitude m + 1. This figure, the fifth root of 100, became known as Pogson’s Ratio.[8] The zero point of Pogson’s scale was originally defined by assigning Polaris a magnitude of exactly 2. Astronomers later discovered that Polaris is slightly variable, so they switched to Vega as the standard reference star, assigning the brightness of Vega as the definition of zero magnitude at any specified wavelength.
Apart from small corrections, the brightness of Vega still serves as the definition of zero magnitude for visible and near infrared wavelengths, where its spectral energy distribution (SED) closely approximates that of a black body for a temperature of 11000 K. However, with the advent of infrared astronomy it was revealed that Vega’s radiation includes an infrared excess presumably due to a circumstellar disk consisting of dust at warm temperatures (but much cooler than the star’s surface). At shorter (e.g. visible) wavelengths, there is negligible emission from dust at these temperatures. However, in order to properly extend the magnitude scale further into the infrared, this peculiarity of Vega should not affect the definition of the magnitude scale. Therefore, the magnitude scale was extrapolated to all wavelengths on the basis of the black-body radiation curve for an ideal stellar surface at 11000 K uncontaminated by circumstellar radiation. On this basis the spectral irradiance (usually expressed in janskys) for the zero magnitude point, as a function of wavelength, can be computed.[9] Small deviations are specified between systems using measurement apparatuses developed independently so that data obtained by different astronomers can be properly compared, but of greater practical importance is the definition of magnitude not at a single wavelength but applying to the response of standard spectral filters used in photometry over various wavelength bands.
| Telescope aperture (mm) |
Limiting Magnitude |
|---|---|
| 35 | 11.3 |
| 60 | 12.3 |
| 102 | 13.3 |
| 152 | 14.1 |
| 203 | 14.7 |
| 305 | 15.4 |
| 406 | 15.7 |
| 508 | 16.4 |
With the modern magnitude systems, brightness over a very wide range is specified according to the logarithmic definition detailed below, using this zero reference. In practice such apparent magnitudes do not exceed 30 (for detectable measurements). The brightness of Vega is exceeded by four stars in the night sky at visible wavelengths (and more at infrared wavelengths) as well as the bright planets Venus, Mars, and Jupiter, and these must be described by negative magnitudes. For example, Sirius, the brightest star of the celestial sphere, has a magnitude of −1.4 in the visible. Negative magnitudes for other very bright astronomical objects can be found in the table below.
Astronomers have developed other photometric zero point systems as alternatives to the Vega system. The most widely used is the AB magnitude system,[11] in which photometric zero points are based on a hypothetical reference spectrum having constant flux per unit frequency interval, rather than using a stellar spectrum or blackbody curve as the reference. The AB magnitude zero point is defined such that an object’s AB and Vega-based magnitudes will be approximately equal in the V filter band.
Measurement[edit]
Precision measurement of magnitude (photometry) requires calibration of the photographic or (usually) electronic detection apparatus. This generally involves contemporaneous observation, under identical conditions, of standard stars whose magnitude using that spectral filter is accurately known. Moreover, as the amount of light actually received by a telescope is reduced due to transmission through the Earth’s atmosphere, the airmasses of the target and calibration stars must be taken into account. Typically one would observe a few different stars of known magnitude which are sufficiently similar. Calibrator stars close in the sky to the target are favoured (to avoid large differences in the atmospheric paths). If those stars have somewhat different zenith angles (altitudes) then a correction factor as a function of airmass can be derived and applied to the airmass at the target’s position. Such calibration obtains the brightness as would be observed from above the atmosphere, where apparent magnitude is defined.
For those new to astronomy, Apparent Magnitude scales with the received power (as opposed to amplitude), so for astrophotography you can use the relative brightness measure to scale the exposure times between stars. Apparent magnitude also adds up (integrates) over the entire object, so it is focus independent. This needs to be taken into account when scaling exposure times for objects with significant apparent size, like the Sun, Moon and planets. For example, directly scaling the exposure time from the Moon to the Sun works, because they are approximately the same size in the sky, but scaling the exposure from the Moon to Saturn would result in an overexposure, if the image of Saturn takes up a smaller area on your sensor than the Moon did (at the same magnification or more generally f/#).
Calculations[edit]
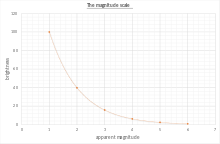
Graph of relative brightness versus magnitude
The dimmer an object appears, the higher the numerical value given to its magnitude, with a difference of 5 magnitudes corresponding to a brightness factor of exactly 100. Therefore, the magnitude m, in the spectral band x, would be given by
which is more commonly expressed in terms of common (base-10) logarithms as
where Fx is the observed irradiance using spectral filter x, and Fx,0 is the reference flux (zero-point) for that photometric filter. Since an increase of 5 magnitudes corresponds to a decrease in brightness by a factor of exactly 100, each magnitude increase implies a decrease in brightness by the factor ![{sqrt[{5}]{100}}approx 2.512](https://wikimedia.org/api/rest_v1/media/math/render/svg/fed184113e02b2f8b9edcedca0920c0d14661ead)
Example: Sun and Moon[edit]
What is the ratio in brightness between the Sun and the full Moon?
The apparent magnitude of the Sun is −26.832[12] (brighter), and the mean magnitude of the full moon is −12.74[13] (dimmer).
Difference in magnitude:
Brightness factor:
The Sun appears about 400000 times as bright as the full Moon.
Magnitude addition[edit]
Sometimes one might wish to add brightness. For example, photometry on closely separated double stars may only be able to produce a measurement of their combined light output. To find the combined magnitude of that double star knowing only the magnitudes of the individual components, this can be done by adding the brightness (in linear units) corresponding to each magnitude.[14]
Solving for 
where mf is the resulting magnitude after adding the brightnesses referred to by m1 and m2.
Apparent bolometric magnitude[edit]
While magnitude generally refers to a measurement in a particular filter band corresponding to some range of wavelengths, the apparent or absolute bolometric magnitude (mbol) is a measure of an object’s apparent or absolute brightness integrated over all wavelengths of the electromagnetic spectrum (also known as the object’s irradiance or power, respectively). The zero point of the apparent bolometric magnitude scale is based on the definition that an apparent bolometric magnitude of 0 mag is equivalent to a received irradiance of 2.518×10−8 watts per square metre (W·m−2).[12]
Absolute magnitude[edit]
While apparent magnitude is a measure of the brightness of an object as seen by a particular observer, absolute magnitude is a measure of the intrinsic brightness of an object. Flux decreases with distance according to an inverse-square law, so the apparent magnitude of a star depends on both its absolute brightness and its distance (and any extinction). For example, a star at one distance will have the same apparent magnitude as a star four times as bright at twice that distance. In contrast, the intrinsic brightness of an astronomical object, does not depend on the distance of the observer or any extinction.
The absolute magnitude M, of a star or astronomical object is defined as the apparent magnitude it would have as seen from a distance of 10 parsecs (33 ly). The absolute magnitude of the Sun is 4.83 in the V band (visual), 4.68 in the Gaia satellite’s G band (green) and 5.48 in the B band (blue).[15][16][17]
In the case of a planet or asteroid, the absolute magnitude H rather means the apparent magnitude it would have if it were 1 astronomical unit (150,000,000 km) from both the observer and the Sun, and fully illuminated at maximum opposition (a configuration that is only theoretically achievable, with the observer situated on the surface of the Sun).[18]
Standard reference values[edit]
| Band | λ (μm) |
Δλ/λ (FWHM) |
Flux at m = 0, Fx,0 | |
|---|---|---|---|---|
| Jy | 10−20 erg/(s·cm2·Hz) | |||
| U | 0.36 | 0.15 | 1810 | 1.81 |
| B | 0.44 | 0.22 | 4260 | 4.26 |
| V | 0.55 | 0.16 | 3640 | 3.64 |
| R | 0.64 | 0.23 | 3080 | 3.08 |
| I | 0.79 | 0.19 | 2550 | 2.55 |
| J | 1.26 | 0.16 | 1600 | 1.60 |
| H | 1.60 | 0.23 | 1080 | 1.08 |
| K | 2.22 | 0.23 | 0670 | 0.67 |
| L | 3.50 | |||
| g | 0.52 | 0.14 | 3730 | 3.73 |
| r | 0.67 | 0.14 | 4490 | 4.49 |
| i | 0.79 | 0.16 | 4760 | 4.76 |
| z | 0.91 | 0.13 | 4810 | 4.81 |
The magnitude scale is a reverse logarithmic scale. A common misconception is that the logarithmic nature of the scale is because the human eye itself has a logarithmic response. In Pogson’s time this was thought to be true (see Weber–Fechner law), but it is now believed that the response is a power law (see Stevens’ power law).[20]
Magnitude is complicated by the fact that light is not monochromatic. The sensitivity of a light detector varies according to the wavelength of the light, and the way it varies depends on the type of light detector. For this reason, it is necessary to specify how the magnitude is measured for the value to be meaningful. For this purpose the UBV system is widely used, in which the magnitude is measured in three different wavelength bands: U (centred at about 350 nm, in the near ultraviolet), B (about 435 nm, in the blue region) and V (about 555 nm, in the middle of the human visual range in daylight). The V band was chosen for spectral purposes and gives magnitudes closely corresponding to those seen by the human eye. When an apparent magnitude is discussed without further qualification, the V magnitude is generally understood.[citation needed]
Because cooler stars, such as red giants and red dwarfs, emit little energy in the blue and UV regions of the spectrum, their power is often under-represented by the UBV scale. Indeed, some L and T class stars have an estimated magnitude of well over 100, because they emit extremely little visible light, but are strongest in infrared.[citation needed]
Measures of magnitude need cautious treatment and it is extremely important to measure like with like. On early 20th century and older orthochromatic (blue-sensitive) photographic film, the relative brightnesses of the blue supergiant Rigel and the red supergiant Betelgeuse irregular variable star (at maximum) are reversed compared to what human eyes perceive, because this archaic film is more sensitive to blue light than it is to red light. Magnitudes obtained from this method are known as photographic magnitudes, and are now considered obsolete.[citation needed]
For objects within the Milky Way with a given absolute magnitude, 5 is added to the apparent magnitude for every tenfold increase in the distance to the object. For objects at very great distances (far beyond the Milky Way), this relationship must be adjusted for redshifts and for non-Euclidean distance measures due to general relativity.[21][22]
For planets and other Solar System bodies, the apparent magnitude is derived from its phase curve and the distances to the Sun and observer.[citation needed]
List of apparent magnitudes[edit]
Some of the listed magnitudes are approximate. Telescope sensitivity depends on observing time, optical bandpass, and interfering light from scattering and airglow.
| Apparent magnitude (V) |
Object | Seen from… | Notes |
|---|---|---|---|
| −67.57 | gamma-ray burst GRB 080319B | seen from 1 AU away | would be over 2×1016 (20 quadrillion) times as bright as the Sun when seen from the Earth |
| −41.39 | star Cygnus OB2-12 | seen from 1 AU away | |
| −40.67 | star M33-013406.63 | seen from 1 AU away | |
| –40.17 | star Eta Carinae A | seen from 1 AU away | |
| −40.07 | star Zeta1 Scorpii | seen from 1 AU away | |
| −39.66 | star R136a1 | seen from 1 AU away | |
| –39.47 | star P Cygni | seen from 1 AU away | |
| −38.00 | star Rigel | seen from 1 AU away | would be seen as a large, very bright bluish disk of 35° apparent diameter |
| −30.30 | star Sirius A | seen from 1 AU away | |
| −29.30 | star Sun | seen from Mercury at perihelion | |
| −27.40 | star Sun | seen from Venus at perihelion | |
| −26.832 | star Sun | seen from Earth[12] | about 400,000 times as bright as mean full Moon |
| −25.60 | star Sun | seen from Mars at aphelion | |
| −25.00 | Minimum brightness that causes the typical eye slight pain to look at | ||
| −23.00 | star Sun | seen from Jupiter at aphelion | |
| −21.70 | star Sun | seen from Saturn at aphelion | |
| −20.20 | star Sun | seen from Uranus at aphelion | |
| −19.30 | star Sun | seen from Neptune | |
| −18.20 | star Sun | seen from Pluto at aphelion | |
| −17.70 | planet Earth | seen as earthlight from Moon[23] | |
| −16.70 | star Sun | seen from Eris at aphelion | |
| −14.20 | An illumination level of 1 lux[24][25] | ||
| −12.90 | full moon | seen from Earth at perihelion | maximum brightness of perigee + perihelion + full Moon (mean distance value is −12.74,[13] though values are about 0.18 magnitude brighter when including the opposition effect) |
| −12.40 | Betelgeuse (when supernova) | seen from Earth when it goes supernova[26] | |
| −11.20 | star Sun | seen from Sedna at aphelion | |
| −10.00 | Comet Ikeya–Seki (1965) | seen from Earth | which was the brightest Kreutz Sungrazer of modern times[27] |
| −9.50 | Iridium (satellite) flare | seen from Earth | maximum brightness |
| −9 to −10 | Phobos (moon) | seen from Mars | maximum brightness |
| −7.50 | supernova of 1006 | seen from Earth | the brightest stellar event in recorded history (7200 light-years away)[28] |
| −6.80 | Alpha Centauri A | seen from Proxima Centauri b | [29] |
| −6.50 | The total integrated magnitude of the night sky | seen from Earth | |
| −6.00 | Crab Supernova of 1054 | seen from Earth | (6500 light-years away)[30] |
| −5.90 | International Space Station | seen from Earth | when the ISS is at its perigee and fully lit by the Sun[31] |
| −4.92 | planet Venus | seen from Earth | maximum brightness[32] when illuminated as a crescent |
| −4.14 | planet Venus | seen from Earth | mean brightness[32] |
| −4 | Faintest objects observable during the day with naked eye when Sun is high. An astronomical object casts human-visible shadows when its apparent magnitude is equal to or lower than -4 [33] | ||
| −3.99 | star Epsilon Canis Majoris | seen from Earth | maximum brightness of 4.7 million years ago, the historical brightest star of the last and next five million years.[34] |
| −3.69 | Moon | lit by earthlight, reflecting earthshine seen from Earth (maximum)[23] | |
| −2.98 | planet Venus | seen from Earth | minimum brightness when it is on the far side of the Sun[32] |
| −2.94 | planet Jupiter | seen from Earth | maximum brightness[32] |
| −2.94 | planet Mars | seen from Earth | maximum brightness[32] |
| −2.5 | Faintest objects visible during the day with naked eye when Sun is less than 10° above the horizon | ||
| −2.50 | new moon | seen from Earth | minimum brightness |
| −2.50 | planet Earth | seen from Mars | maximum brightness |
| −2.48 | planet Mercury | seen from Earth | maximum brightness at superior conjunction (unlike Venus, Mercury is at its brightest when on the far side of the Sun, the reason being their different phase curves)[32] |
| −2.20 | planet Jupiter | seen from Earth | mean brightness[32] |
| −1.66 | planet Jupiter | seen from Earth | minimum brightness[32] |
| −1.47 | star system Sirius | seen from Earth | Brightest star except for the Sun at visible wavelengths[35] |
| −0.83 | star Eta Carinae | seen from Earth | apparent brightness as a supernova impostor in April 1843 |
| −0.72 | star Canopus | seen from Earth | 2nd brightest star in night sky[36] |
| −0.55 | planet Saturn | seen from Earth | maximum brightness near opposition and perihelion when the rings are angled toward Earth[32] |
| −0.3 | Halley’s comet | seen from Earth | Expected apparent magnitude at 2061 passage |
| −0.27 | star system Alpha Centauri AB | seen from Earth | Combined magnitude (3rd brightest star in night sky) |
| −0.04 | star Arcturus | seen from Earth | 4th brightest star to the naked eye[37] |
| −0.01 | star Alpha Centauri A | seen from Earth | 4th brightest individual star visible telescopically in the night sky |
| +0.03 | star Vega | seen from Earth | which was originally chosen as a definition of the zero point[38] |
| +0.23 | planet Mercury | seen from Earth | mean brightness[32] |
| +0.46 | star Sun | seen from Alpha Centauri | |
| +0.46 | planet Saturn | seen from Earth | mean brightness[32] |
| +0.71 | planet Mars | seen from Earth | mean brightness[32] |
| +0.90 | Moon | seen from Mars | maximum brightness |
| +1.17 | planet Saturn | seen from Earth | minimum brightness[32] |
| +1.33 | star Alpha Centauri B | seen from Earth | |
| +1.86 | planet Mars | seen from Earth | minimum brightness[32] |
| +1.98 | star Polaris | seen from Earth | mean brightness[39] |
| +3.03 | supernova SN 1987A | seen from Earth | in the Large Magellanic Cloud (160,000 light-years away) |
| +3 to +4 | Faintest stars visible in an urban neighborhood with naked eye | ||
| +3.44 | Andromeda Galaxy | seen from Earth | M31[40] |
| +4 | Orion Nebula | seen from Earth | M42 |
| +4.38 | moon Ganymede | seen from Earth | maximum brightness[41] (moon of Jupiter and the largest moon in the Solar System) |
| +4.50 | open cluster M41 | seen from Earth | an open cluster that may have been seen by Aristotle[42] |
| +4.5 | Sagittarius Dwarf Spheroidal Galaxy | seen from Earth | |
| +5.20 | asteroid Vesta | seen from Earth | maximum brightness |
| +5.38[43] | planet Uranus | seen from Earth | maximum brightness[32] (Uranus comes to perihelion in 2050) |
| +5.68 | planet Uranus | seen from Earth | mean brightness[32] |
| +5.72 | spiral galaxy M33 | seen from Earth | which is used as a test for naked eye seeing under dark skies[44][45] |
| +5.8 | gamma-ray burst GRB 080319B | seen from Earth | Peak visual magnitude (the “Clarke Event”) seen on Earth on 19 March 2008 from a distance of 7.5 billion light-years. |
| +6.03 | planet Uranus | seen from Earth | minimum brightness[32] |
| +6.49 | asteroid Pallas | seen from Earth | maximum brightness |
| +6.5 | Approximate limit of stars observed by a mean naked eye observer under very good conditions. There are about 9,500 stars visible to mag 6.5.[4] | ||
| +6.64 | dwarf planet Ceres | seen from Earth | maximum brightness |
| +6.75 | asteroid Iris | seen from Earth | maximum brightness |
| +6.90 | spiral galaxy M81 | seen from Earth | This is an extreme naked-eye target that pushes human eyesight and the Bortle scale to the limit[46] |
| +7.25 | planet Mercury | seen from Earth | minimum brightness[32] |
| +7.67[47] | planet Neptune | seen from Earth | maximum brightness[32] (Neptune comes to perihelion in 2042) |
| +7.78 | planet Neptune | seen from Earth | mean brightness[32] |
| +8.00 | planet Neptune | seen from Earth | minimum brightness[32] |
| +8 | Extreme naked-eye limit, Class 1 on Bortle scale, the darkest skies available on Earth.[48] | ||
| +8.10 | moon Titan | seen from Earth | maximum brightness; largest moon of Saturn;[49][50] mean opposition magnitude 8.4[51] |
| +8.29 | star UY Scuti | seen from Earth | Maximum brightness; one of largest known stars by radius |
| +8.94 | asteroid 10 Hygiea | seen from Earth | maximum brightness[52] |
| +9.50 | Faintest objects visible using common 7×50 binoculars under typical conditions[53] | ||
| +10.20 | moon Iapetus | seen from Earth | maximum brightness,[50] brightest when west of Saturn and takes 40 days to switch sides |
| +11.05 | star Proxima Centauri | seen from Earth | closest star |
| +11.8 | moon Phobos | seen from Earth | Maximum brightness; brighter moon of Mars |
| +12.23 | star R136a1 | seen from Earth | Most luminous and massive star known[54] |
| +12.89 | moon Deimos | seen from Earth | Maximum brightness |
| +12.91 | quasar 3C 273 | seen from Earth | brightest (luminosity distance of 2.4 billion light-years) |
| +13.42 | moon Triton | seen from Earth | Maximum brightness[51] |
| +13.65 | dwarf planet Pluto | seen from Earth | maximum brightness,[55] 725 times fainter than magnitude 6.5 naked eye skies |
| +13.9 | moon Titania | seen from Earth | Maximum brightness; brightest moon of Uranus |
| +14.1 | star WR 102 | seen from Earth | Hottest known star |
| +15.4 | centaur Chiron | seen from Earth | maximum brightness[56] |
| +15.55 | moon Charon | seen from Earth | maximum brightness (the largest moon of Pluto) |
| +16.8 | dwarf planet Makemake | seen from Earth | Current opposition brightness[57] |
| +17.27 | dwarf planet Haumea | seen from Earth | Current opposition brightness[58] |
| +18.7 | dwarf planet Eris | seen from Earth | Current opposition brightness |
| +19.5 | Faintest objects observable with the Catalina Sky Survey 0.7-meter telescope using a 30-second exposure[59] and also the approximate limiting magnitude of Asteroid Terrestrial-impact Last Alert System (ATLAS) | ||
| +20.7 | moon Callirrhoe | seen from Earth | (small ≈8 km satellite of Jupiter)[51] |
| +22 | Faintest objects observable in visible light with a 600 mm (24″) Ritchey-Chrétien telescope with 30 minutes of stacked images (6 subframes at 5 minutes each) using a CCD detector[60] | ||
| +22.8 | Luhman 16 | seen from Earth | Closest brown dwarfs (Luhman 16A=23.25, Luhman 16B=24.07)[61] |
| +22.91 | moon Hydra | seen from Earth | maximum brightness of Pluto’s moon |
| +23.38 | moon Nix | seen from Earth | maximum brightness of Pluto’s moon |
| +24 | Faintest objects observable with the Pan-STARRS 1.8-meter telescope using a 60-second exposure[62] This is currently the limiting magnitude of automated allsky astronomical surveys. | ||
| +25.0 | moon Fenrir | seen from Earth | (small ≈4 km satellite of Saturn)[63] |
| +25.3 | Trans-Neptunian object 2018 AG37 | seen from Earth | Furthest known observable object in the Solar System about 132 AU (19.7 billion km) from the Sun |
| +26.2 | Trans-Neptunian object 2015 TH367 | seen from Earth | 200 km sized object about 90 AU (13 billion km) from the Sun and about 75 million times fainter than what can be seen with the naked eye. |
| +27.7 | Faintest objects observable with a single 8-meter class ground-based telescope such as the Subaru Telescope in a 10-hour image[64] | ||
| +28.2 | Halley’s Comet | seen from Earth (2003) | in 2003 when it was 28 AU (4.2 billion km) from the Sun, imaged using 3 of 4 synchronised individual scopes in the ESO’s Very Large Telescope array using a total exposure time of about 9 hours[65] |
| +28.4 | asteroid 2003 BH91 | seen from Earth orbit | observed magnitude of ≈15-kilometer Kuiper belt object seen by the Hubble Space Telescope (HST) in 2003, dimmest known directly observed asteroid. |
| +29.4 | JADES-GS-z13-0 | seen from Earth | Discovered by the James Webb Space Telescope. One of the furthest objects discovered. [66] |
| +31.5 | Faintest objects observable in visible light with Hubble Space Telescope via the EXtreme Deep Field with ≈23 days of exposure time collected over 10 years[67] | ||
| +34 | Faintest objects observable in visible light with James Webb Space Telescope[68] | ||
| +35 | unnamed asteroid | seen from Earth orbit | expected magnitude of dimmest known asteroid, a 950-meter Kuiper belt object discovered (by the HST) passing in front of a star in 2009.[69] |
| +35 | star LBV 1806-20 | seen from Earth | a luminous blue variable star, expected magnitude at visible wavelengths due to interstellar extinction |
See also[edit]
- Distance modulus
- List of nearest bright stars
- List of nearest stars
- Luminosity in astronomy
- Surface brightness
References[edit]
- ^ Curtis, Heber Doust (1903) [1901-03-27]. “On the Limits of Unaided Vision”. Lick Observatory Bulletin. University of California. 2 (38): 67–69. Bibcode:1903LicOB…2…67C. doi:10.5479/ADS/bib/1903LicOB.2.67C.
- ^ Matthew, Templeton (21 October 2011). “Magnitudes: Measuring the Brightness of Stars”. American Association of Variable Stars (AAVSO). Archived from the original on 18 May 2019. Retrieved 19 May 2019.
- ^ Crumey, A. (October 2006). “Human Contrast Threshold and Astronomical Visibility”. Monthly Notices of the Royal Astronomical Society. 442 (3): 2600–2619. doi:10.1093/mnras/stu992. Retrieved 7 April 2023.
- ^ a b “Vmag<6.5”. SIMBAD Astronomical Database. Archived from the original on 22 February 2015. Retrieved 25 June 2010.
- ^ “Magnitude”. National Solar Observatory—Sacramento Peak. Archived from the original on 6 February 2008. Retrieved 23 August 2006.
- ^ Bright Star Catalogue
- ^ Hoffmann, S., Hipparchs Himmelsglobus, Springer, Wiesbaden/ New York, 2017
- ^ Pogson, N. (1856). “Magnitudes of Thirty-six of the Minor Planets for the first day of each month of the year 1857”. MNRAS. 17: 12. Bibcode:1856MNRAS..17…12P. doi:10.1093/mnras/17.1.12.
- ^ See [1].
- ^ North, Gerald; James, Nick (2014). Observing Variable Stars, Novae and Supernovae. Cambridge University Press. p. 24. ISBN 9781107636125.
- ^ Oke, J. B.; Gunn, J. E. (15 March 1983). “Secondary standard stars for absolute spectrophotometry”. The Astrophysical Journal. 266: 713–717. Bibcode:1983ApJ…266..713O. doi:10.1086/160817.
- ^ a b c IAU Inter-Division A-G Working Group on Nominal Units for Stellar & Planetary Astronomy (13 August 2015). “IAU 2015 Resolution B2 on Recommended Zero Points for the Absolute and Apparent Bolometric Magnitude Scales” (PDF). Resolutions Adopted at the General Assemblies. arXiv:1510.06262. Bibcode:2015arXiv151006262M. Archived (PDF) from the original on 28 January 2016. Retrieved 19 May 2019.
- ^ a b Williams, David R. (2 February 2010). “Moon Fact Sheet”. NASA (National Space Science Data Center). Archived from the original on 23 March 2010. Retrieved 9 April 2010.
- ^ “Magnitude Arithmetic”. Weekly Topic. Caglow. Archived from the original on 1 February 2012. Retrieved 30 January 2012.
- ^ Evans, Aaron. “Some Useful Astronomical Definitions” (PDF). Stony Brook Astronomy Program. Archived (PDF) from the original on 20 July 2011. Retrieved 12 July 2009.
- ^ Čotar, Klemen; Zwitter, Tomaž; et al. (21 May 2019). “The GALAH survey: unresolved triple Sun-like stars discovered by the Gaia mission”. Monthly Notices of the Royal Astronomical Society. Oxford University Press (OUP). 487 (2): 2474–2490. arXiv:1904.04841. doi:10.1093/mnras/stz1397. ISSN 0035-8711.
- ^ Bessell, Michael S. (September 2005). “Standard Photometric Systems” (PDF). Annual Review of Astronomy and Astrophysics. 43 (1): 293–336. Bibcode:2005ARA&A..43..293B. doi:10.1146/annurev.astro.41.082801.100251. ISSN 0066-4146. Archived (PDF) from the original on 9 October 2022.
- ^ Luciuk, M. “Astronomical Magnitudes” (PDF). p. 8. Retrieved 11 January 2019.
- ^ Huchra, John. “Astronomical Magnitude Systems”. Harvard-Smithsonian Center for Astrophysics. Archived from the original on 21 July 2018. Retrieved 18 July 2017.
- ^ Schulman, E.; Cox, C. V. (1997). “Misconceptions About Astronomical Magnitudes”. American Journal of Physics. 65 (10): 1003. Bibcode:1997AmJPh..65.1003S. doi:10.1119/1.18714.
- ^ Umeh, Obinna; Clarkson, Chris; Maartens, Roy (2014). “Nonlinear relativistic corrections to cosmological distances, redshift and gravitational lensing magnification: II. Derivation”. Classical and Quantum Gravity. 31 (20): 205001. arXiv:1402.1933. Bibcode:2014CQGra..31t5001U. doi:10.1088/0264-9381/31/20/205001. S2CID 54527784.
- ^ Hogg, David W.; Baldry, Ivan K.; Blanton, Michael R.; Eisenstein, Daniel J. (2002). “The K correction”. arXiv:astro-ph/0210394.
- ^ a b Agrawal, Dulli Chandra (30 March 2016). “Apparent magnitude of earthshine: a simple calculation”. European Journal of Physics. IOP Publishing. 37 (3): 035601. Bibcode:2016EJPh…37c5601A. doi:10.1088/0143-0807/37/3/035601. ISSN 0143-0807. S2CID 124231299.
- ^ Dufay, Jean (17 October 2012). Introduction to Astrophysics: The Stars. p. 3. ISBN 9780486607719. Archived from the original on 24 March 2017. Retrieved 28 February 2016.
- ^ McLean, Ian S. (2008). Electronic Imaging in Astronomy: Detectors and Instrumentation. Springer. p. 529. ISBN 978-3-540-76582-0.
- ^ Dolan, Michelle M.; Mathews, Grant J.; Lam, Doan Duc; Lan, Nguyen Quynh; Herczeg, Gregory J.; Dearborn, David S. P. (2017). “Evolutionary Tracks for Betelgeuse”. The Astrophysical Journal. 819 (1): 7. arXiv:1406.3143. Bibcode:2016ApJ…819….7D. doi:10.3847/0004-637X/819/1/7. S2CID 37913442.
- ^ “Brightest comets seen since 1935”. International Comet Quarterly. Archived from the original on 28 December 2011. Retrieved 18 December 2011.
- ^ Winkler, P. Frank; Gupta, Gaurav; Long, Knox S. (2003). “The SN 1006 Remnant: Optical Proper Motions, Deep Imaging, Distance, and Brightness at Maximum”. The Astrophysical Journal. 585 (1): 324–335. arXiv:astro-ph/0208415. Bibcode:2003ApJ…585..324W. doi:10.1086/345985. S2CID 1626564.
- ^ Siegel, Ethan (6 September 2016). “Ten Ways ‘Proxima b’ Is Different From Earth”. Forbes. Retrieved 19 February 2023.
- ^ “Supernova 1054 – Creation of the Crab Nebula”. SEDS. Archived from the original on 28 May 2014. Retrieved 29 July 2014.
- ^ “Heavens-above.com”. Heavens-above. Archived from the original on 5 July 2009. Retrieved 22 December 2007.
- ^ a b c d e f g h i j k l m n o p q r s t u Mallama, A.; Hilton, J.L. (2018). “Computing Apparent Planetary Magnitudes for The Astronomical Almanac”. Astronomy and Computing. 25: 10–24. arXiv:1808.01973. Bibcode:2018A&C….25…10M. doi:10.1016/j.ascom.2018.08.002. S2CID 69912809.
- ^ NASA Science Question of the Week. Gsfc.nasa.gov (April 7, 2006). Retrieved on 2013-04-26.
- ^ Tomkin, Jocelyn (April 1998). “Once and Future Celestial Kings”. Sky and Telescope. 95 (4): 59–63. Bibcode:1998S&T….95d..59T. – based on computations from HIPPARCOS data. (The calculations exclude stars whose distance or proper motion is uncertain.) PDF[permanent dead link]
- ^ “Sirius”. SIMBAD Astronomical Database. Archived from the original on 11 January 2014. Retrieved 26 June 2010.
- ^ “Canopus”. SIMBAD Astronomical Database. Archived from the original on 14 July 2014. Retrieved 26 June 2010.
- ^ “Arcturus”. SIMBAD Astronomical Database. Archived from the original on 14 January 2014. Retrieved 26 June 2010.
- ^ “Vega”. SIMBAD Astronomical Database. Archived from the original on 7 July 2015. Retrieved 14 April 2010.
- ^ Evans, N. R.; Schaefer, G. H.; Bond, H. E.; Bono, G.; Karovska, M.; Nelan, E.; Sasselov, D.; Mason, B. D. (2008). “Direct Detection of the Close Companion of Polaris with The Hubble Space Telescope”. The Astronomical Journal. 136 (3): 1137. arXiv:0806.4904. Bibcode:2008AJ….136.1137E. doi:10.1088/0004-6256/136/3/1137. S2CID 16966094.
- ^ “SIMBAD-M31”. SIMBAD Astronomical Database. Archived from the original on 19 May 2014. Retrieved 29 November 2009.
- ^ Yeomans; Chamberlin. “Horizon Online Ephemeris System for Ganymede (Major Body 503)”. California Institute of Technology, Jet Propulsion Laboratory. Archived from the original on 2 February 2014. Retrieved 14 April 2010. (4.38 on 1951-Oct-03)
- ^ “M41 possibly recorded by Aristotle”. SEDS (Students for the Exploration and Development of Space). 28 July 2006. Archived from the original on 18 April 2017. Retrieved 29 November 2009.
- ^ “Uranus Fact Sheet”. nssdc.gsfc.nasa.gov. Archived from the original on 22 January 2019. Retrieved 8 November 2018.
- ^ “SIMBAD-M33”. SIMBAD Astronomical Database. Archived from the original on 13 September 2014. Retrieved 28 November 2009.
- ^ Lodriguss, Jerry (1993). “M33 (Triangulum Galaxy)”. Archived from the original on 15 January 2010. Retrieved 27 November 2009. (Shows bolometric magnitude not visual magnitude.)
- ^ “Messier 81”. SEDS (Students for the Exploration and Development of Space). 2 September 2007. Archived from the original on 14 July 2017. Retrieved 28 November 2009.
- ^ “Neptune Fact Sheet”. nssdc.gsfc.nasa.gov. Archived from the original on 10 January 2019. Retrieved 8 November 2018.
- ^ John E. Bortle (February 2001). “The Bortle Dark-Sky Scale”. Sky & Telescope. Archived from the original on 23 March 2009. Retrieved 18 November 2009.
- ^ Yeomans; Chamberlin. “Horizon Online Ephemeris System for Titan (Major Body 606)”. California Institute of Technology, Jet Propulsion Laboratory. Archived from the original on 13 November 2012. Retrieved 28 June 2010. (8.10 on 2003-Dec-30)
- ^ a b “Classic Satellites of the Solar System”. Observatorio ARVAL. Archived from the original on 31 July 2010. Retrieved 25 June 2010.
- ^ a b c “Planetary Satellite Physical Parameters”. JPL (Solar System Dynamics). 3 April 2009. Archived from the original on 23 July 2009. Retrieved 25 July 2009.
- ^ “AstDys (10) Hygiea Ephemerides”. Department of Mathematics, University of Pisa, Italy. Archived from the original on 12 May 2014. Retrieved 26 June 2010.
- ^ Zarenski, Ed (2004). “Limiting Magnitude in Binoculars” (PDF). Cloudy Nights. Archived (PDF) from the original on 21 July 2011. Retrieved 6 May 2011.
- ^ “What Is the Most Massive Star?”. Space.com. Archived from the original on 11 January 2019. Retrieved 5 November 2018.
- ^ Williams, David R. (7 September 2006). “Pluto Fact Sheet”. National Space Science Data Center. NASA. Archived from the original on 1 July 2010. Retrieved 26 June 2010.
- ^ “AstDys (2060) Chiron Ephemerides”. Department of Mathematics, University of Pisa, Italy. Archived from the original on 29 June 2011. Retrieved 26 June 2010.
- ^ “AstDys (136472) Makemake Ephemerides”. Department of Mathematics, University of Pisa, Italy. Archived from the original on 29 June 2011. Retrieved 26 June 2010.
- ^ “AstDys (136108) Haumea Ephemerides”. Department of Mathematics, University of Pisa, Italy. Archived from the original on 29 June 2011. Retrieved 26 June 2010.
- ^ “Catalina Sky Survey (CSS) Facilities”. Archived from the original on 3 November 2019. Retrieved 3 November 2019.
- ^ Steve Cullen (sgcullen) (5 October 2009). “17 New Asteroids Found by LightBuckets”. LightBuckets. Archived from the original on 31 January 2010. Retrieved 15 November 2009.
- ^ Boffin, H.M.J.; Pourbaix, D. (2014). “Possible astrometric discovery of a substellar companion to the closest binary brown dwarf system WISE J104915.57–531906.1”. Astronomy and Astrophysics. 561: 5. arXiv:1312.1303. Bibcode:2014A&A…561L…4B. doi:10.1051/0004-6361/201322975. S2CID 33043358.
- ^ “Pan-STARRS limiting magnitude”.
- ^ Sheppard, Scott S. “Saturn’s Known Satellites”. Carnegie Institution (Department of Terrestrial Magnetism). Archived from the original on 15 May 2011. Retrieved 28 June 2010.
- ^ What is the faintest object imaged by ground-based telescopes? Archived 2016-02-02 at the Wayback Machine, by: The Editors of Sky Telescope, 24 July 2006
- ^ “New Image of Comet Halley in the Cold”. ESO. 1 September 2003. Archived from the original on 1 March 2009. Retrieved 22 February 2009.
- ^ Robertson, B. E.; et al. (2023). “Identification and properties of intense star-forming galaxies at redshifts z > 10”. Nature Astronomy. arXiv:2212.04480. Bibcode:2023NatAs.tmp…67R. doi:10.1038/s41550-023-01921-1. S2CID 257968812.
- ^ Illingworth, G. D.; Magee, D.; Oesch, P. A.; Bouwens, R. J.; Labbé, I.; Stiavelli, M.; van Dokkum, P. G.; Franx, M.; Trenti, M.; Carollo, C. M.; Gonzalez, V. (21 October 2013). “The HST eXtreme Deep Field XDF: Combining all ACS and WFC3/IR Data on the HUDF Region into the Deepest Field Ever”. The Astrophysical Journal Supplement Series. 209 (1): 6. arXiv:1305.1931. Bibcode:2013ApJS..209….6I. doi:10.1088/0067-0049/209/1/6. S2CID 55052332.
- ^ http://www.jaymaron.com/telescopes/telescopes.html Archived 2017-08-01 at the Wayback Machine (retrieved Sep 14 2017)
- ^ “Hubble Finds Smallest Kuiper Belt Object Ever Seen”. NASA. Archived from the original on 9 June 2017. Retrieved 16 March 2018.
External links[edit]
- “The astronomical magnitude scale”. International Comet Quarterly.