У этого термина существуют и другие значения, см. Объём (значения).
| Объём | |
|---|---|
 |
|
| Размерность | L3 |
| Единицы измерения | |
| СИ | м3 |
| СГС | см3 |
Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела определяется его формой и линейными размерами. Основное свойство объёма — аддитивность , то есть объём любого тела равен сумме объёмов его (непересекающихся) частей[1].
Единица объёма в СИ — кубический метр; от неё образуются производные единицы — кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель и др.
В формулах для обозначения объёма традиционно используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».
Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.
Вычисление объёма[править | править код]
На практике приблизительный объём тела, в том числе сложной формы, можно вычислить по закону Архимеда, погрузив это тело в жидкость: объём вытесненной жидкости будет равен объёму измеряемого тела.
Математически[править | править код]
Для объёмов тел простой формы имеются специальные формулы. Например, объём куба с ребром 

Объём тела сложной формы вычисляется разбиением этого тела на отдельные части простой формы и суммированием объёмов этих частей. В интегральном исчислении объёмы частей, из которых складывается объём всего тела, рассматриваются как бесконечно малые величины.
Сводка формул[править | править код]
| Форма тела | Формула для вычисления объёма | Обозначения |
|---|---|---|
| Куб | 
|

|
| Прямоугольный параллелепипед | 
|

|
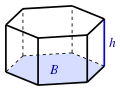
| Призма
(B: площадь основания) |

|
|
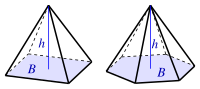
| Пирамида
(B: площадь основания) |

|
|
| Параллелепипед | 
|

|
| Тетраэдр | 
|

|
| Шар | 
|

|
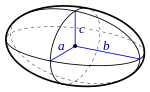
| Эллипсоид | 
|
|
| Прямой круговой цилиндр | 
|

|
| Конус | 
|

|
| Тело вращения | 
|

|
Через плотность[править | править код]
Зная массу (m) и среднюю плотность (ρ) тела, его объём рассчитывают по формуле: 
Единицы объёма жидкости[править | править код]
- 1 литр = 1 кубический дециметр = 1,76 пинты = 0,23 галлона
Русские[2][править | править код]
- Ведро = 12,3 литра
- Бочка = 40 вёдер = 492 литра
Английские[править | править код]
- 1 пинта = 0,568 литра
- 1 кварта (жидкостная) = 2 пинтам = 1,136 литра
- 1 галлон = 8 пинтам = 4,55 литра
- 1 галлон (амер.) = 3,785 литра
Античные[править | править код]
- Котила = 0,275 литра
Немецкие[править | править код]
- Шоппен
Древнееврейские[3][править | править код]
- Эйфа = 24,883 литра
- Гин = 1/6 эйфы = 4,147 литра
- Омер = 1/10 эйфы = 2,4883 литра
- Кав = 1/3 гина = 1,382 литра
Единицы объёма сыпучих веществ[править | править код]
Русские[править | править код]
- Четверик = 26,24 литра (1 пуд зерна)
- Гарнец = 3,28 литра
- Четверть = 1/4 ведра = 3,075 литра
- Штоф = 1/8 ведра = 1,54 литра
- Кружка = 1/10 ведра = 1,23 литра
- Бутылка (винная) = 1/16 ведра = 0,77 литра
- Бутылка (пивная) = 1/20 ведра = 0,61 литра
- Чарка = 1/10 кружки = 0,123 литра
- Шкалик (косушка) = 1/2 чарки = 0,0615 литра
Английские[править | править код]
- 1 бушель = 8 галлонов = 36,36872 литра
- 1 баррель = 163,65 литра
Прочие единицы[править | править код]
- 1 унция (англ.) = 2,841⋅10−5 м³
- 1 унция (амер.) = 2,957⋅10−5 м³
- 1 кубический дюйм = 1,63871⋅10−5 м³
- 1 кубический фут = 2,83168⋅10−2 м³
- 1 кубический ярд = 0,76455 м³
- 1 кубическая астрономическая единица =3,348⋅1024 км³
- 1 кубический световой год = 8,466⋅1038 км³
- 1 кубический парсек = 2,938⋅1040 км³
- 1 кубический килопарсек = 1 000 000 000 пк³ = 2,938⋅1049 км³
Примечания[править | править код]
- ↑ Математическая энциклопедия, 1982, с. 1149.
- ↑ Меры объёма в Древней Руси. Дата обращения: 17 ноября 2013. Архивировано 14 июля 2014 года.
- ↑ «ТЕГИЛАТ ГАШЕМ» — ISBN 965-310-008-4
Литература[править | править код]
- Объём // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- Объём // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Ссылки[править | править код]
- Формулы объёма и программы для расчета объёма. Дата обращения: 26 ноября 2020. Архивировано 24 ноября 2020 года.
Измерение объёма тела по формуле — возможные способы, единицы измерения
Содержание:
- Понятие объема тела
- Свойства объема тела
- Как вычислить объем тела: все формулы
- Примеры решения задач
- Задания для самостоятельной работы
Понятие объема тела
Объем является количественным параметром пространства, занятого телом или веществом.
Термин объема можно рассматривать совместно с понятием вместимости. Это обозначение для объема какого-то внутреннего пространства сосуда, коробки и тому подобного. Объем тела, как и вместимость некой емкости, зависит от таких характеристик, как:
- форма;
- линейные размеры.
Главным свойством объема принято считать аддитивность.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Аддитивность означает равенство объема какого-либо тела сумме объемов частей этого тела, которые не пересекаются между собой.
Согласно СИ, единицей измерения объема является метр кубический (м³). В процессе решения задач можно встретить единицы измерения объемов тел в виде см³, дм³, или литров. В иностранной литературе также используются указания объемов веществ, находящихся в жидком или сыпучем состоянии, в таких единицах измерения, как, например, галлон, баррель и другие.
Величина объема используется при составлении различных уравнений и неравенств. При этом данный параметр обозначают с помощью буквы V. Это сокращение от латинского слова volume, которое в переводе означает объем или наполнение.
Свойства объема тела
В процессе решения разнообразных задач по физике, алгебре и геометрии целесообразно использовать свойства, которыми обладает объем тела. Перечислим основные из них:
- Объем тела не может быть отрицательной величиной.
- В том случае, когда некое геометрическое тело состоит из определенного количества геометрических тел, не обладающих едиными внутренними точками, объем такого тела складывается из объемов составляющих его тел.
- Объем фигуры в виде куба с ребром, значение которого равно единице измерения длины, равен единице.
- Аналогичные друг другу геометрические тела обладают одинаковыми объемами.
- В том случае, когда тело имеет объем V1 и расположено в другом теле с объемом V2, справедливо следующее соотношение: (V1<V2
).
Как вычислить объем тела: все формулы
Существует практический способ определения объема тела, включая тела, обладающие сложной формой и геометрией. Данная методика основана на законе Архимеда и предполагает погружение рассматриваемого тела в некую жидкость. По результатам следует измерить объем вытесненной телом жидкости. Данная величина равна объему измеряемого тела.
Формула расчета объема тела, исходя из известных величин массы и плотности:
(V={frac {m}{rho }})
Здесь m определяется, как масса, а rho является средней плотностью тела.
В том случае, когда тела обладают простыми геометрическими формами, в решении задач допустимо использовать специальные формулы. К примеру, для того чтобы найти объем куба, ребро которого равно а, следует применить такую формулу: (V=a^{3}).
Вычислить объем некого прямоугольного параллелепипеда можно путем умножения длины, ширины и высоты. Запишем другие распространенные формулы для расчета объемов геометрических фигур:
- куб, формула объема: (V=a^{3}):
- прямоугольный параллелепипед, формула объема: (V=abc) (произведение длин трех сторон):
- призма, формула объема: ( V=Bh) (произведение площади основания и высоты):
- пирамида, формула объема: (V={frac {1}{3}}Bh:)
- параллелепипед, формула объема: (V=abc{sqrt {K}}, {begin{aligned}K=1&+2cos(alpha )cos(beta )cos(gamma )\&-cos ^{2}(alpha )-cos ^{2}(beta )-cos ^{2}(gamma )end{aligned}}:
) -
- тетраэдр, формула объема: (V={{sqrt {2}} over 12}a^{3}:)
- шар, формула объема: (V={frac {4}{3}}pi r^{3}):
- эллипсоид, формула объема: (V={frac {4}{3}}pi abc):
- прямой круговой цилиндр, формула объема: (V=pi r^{2}h):
- конус, формула объема: (V={frac {1}{3}}pi r^{2}h):
- тело вращения, формула объема: (V=pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x):
В том случае, когда необходимо определить объем, которым обладает некое тело, имеющее сложную форму, нужно разбить мысленно данное тело на отдельные части. Такие части целого должны иметь простую форму. Далее следует сложить вычисленные объемы простых тел. Результат будет являться значением объема начального тела.
Примеры решения задач
Задача 1
Задача
Имеется пара шаров. Радиус первого шара в 5 раз превышает радиус второго шара.
Требуется определить, во сколько раз площадь поверхности второго шара меньше по сравнению с площадью поверхности первого шара
Решение
Рассчитать площадь поверхности можно по формуле:
(S=4pi R^2)
Тогда запишем отношения площадей пары шаров:
(dfrac{S_1}{S_2}=dfrac{4pi , R_1^2}{4pi , R_2^2})
Сравним радиусы геометрических фигур:
(R_1=5R_2)
В результате:
(dfrac{S_1}{S_2}=dfrac{(5R_2)^2}{R_2^2}=25)
Таким образом, первый шар имеет площадь поверхности, которая в 25 раз больше по сравнению с аналогичной характеристикой второго шара.
Ответ: 25.
Задача 2
На рисунке изображены конусы. Назовем их (K_1) и (K_2).
Полная поверхность (K_1) по площади относится к площади полной поверхности (K_2) как 4:1.
Фигура (K_1) обладает радиусом, который в 4 раза больше образующей (K_1) и в 2 раза больше радиуса (K_2).
Требуется вычислить, как относится образующая (K_2) к образующей (K_1.)
Решение
Представим, что образующая конуса равна 1, а радиус основания обозначим, как R. Тогда можно записать следующее соотношение:
(S=pi R (R+l))
Запишем отношения площадей полной поверхности заданных конусов:
(dfrac41=dfrac{pi ,R_1cdot (R_1+l_1)}{pi , R_2cdot (R_2+l_2)})
Согласно условию задачи, имеем:
(R_1=4l_1, R_2=frac12R_1=2l_1)
В результате:
(dfrac41=dfrac{4l_1cdot (4l_1+l_1)}{2l_1cdot (2l_1+l_2)} quadRightarrowquad dfrac{l_2}{l_1}=dfrac12=0,5)
Ответ: 0,5.
Задача 3
Даны два прямоугольных параллелепипеда. Объем первой фигуры равен 105. Известно, что первый параллелепипед по высоте превышает второй в 7 раз. Ширина второй фигуры в 2 раза больше по сравнению с аналогичным параметром первой фигуры. Первый параллелепипед длиннее в три раза, чем второй. Необходимо вычислить объем, который имеет второй параллелепипед.
Решение
Обозначим высоту, ширину и длину геометрических фигур с помощью букв а, b, с соответственно. Вспомним формулу, по которой можно найти объем прямоугольного параллелепипеда:
V=abc
Применительно к нашей задаче, запишем:
(dfrac{105}{V_2}=dfrac{V_1}{V_2}=dfrac{a_1b_1c_1}{a_2b_2c_2})
Известно, что:
(a_1=7a_2, b_2=2b_1, c_1=3c_2)
В результате:
(dfrac{105}{V_2}=dfrac{7a_2cdot b_1cdot 3c_2}{a_2cdot 2b_1cdot c_2}= dfrac{7cdot 3}2 quadRightarrowquad V_2=dfrac{105cdot 2}{21}=10)
Ответ: 10.
Задача 4
Даны два конуса. Площадь боковой поверхности первой геометрической фигуры относится к площади боковой поверхности второй фигуры как 3:7. Первый конус обладает радиусом, который относится к радиусу второго конуса, как 15:7. Необходимо определить, как относится образующая первого конуса к образующей второго конуса.
Решение
Составим формулу для расчета площади боковой поверхности конуса:
(S=pi Rl)
Запишем отношения площадей боковых поверхностей для первого и второго конусов:
(dfrac 37=dfrac{S_1}{S_2}=dfrac{pi R_1,l_1}{pi R_2,l_2})
Зная, что отношение радиусов двух геометрических фигур равно 15:7, получим:
(frac{R_1}{R_2}=frac{15}7, то dfrac37=dfrac {15}7cdot dfrac{l_1}{l_2} quadRightarrowquad dfrac{l_1}{l_2}=dfrac37cdot dfrac7{15}=dfrac15=0,2)
Ответ: 0,2.
Задача 5
Имеется пара шаров. Объем первой фигуры составляет 54. Радиус второй фигуры в 3 раза меньше по сравнению с радиусом первой. Нужно определить объем второго шара.
Решение
Запишем формулу, согласно которой можно определить объем шара:
(V=dfrac43 pi R^3)
Составим отношение объемов двух фигур:
(dfrac{54}{V_2}=dfrac{V_1}{V_2}= dfrac{frac43 pi ,R_1^3}{frac43 pi ,R_2^3}=left(dfrac{R_1}{R_2}right)^3)
По условиям задачи:
(R_1=3R_2)
В результате:
(dfrac{54}{V_2}=left(dfrac{3R_2}{R_2}right)^3=27 quadRightarrowquad V_2=dfrac{54}{27}=2)
Ответ: 2.
Задача 6
Имеется некая емкость конусообразной формы. Ее заполнили до половины с помощью 75 гр жидкости. Необходимо вычислить вес жидкости, которую нужно добавить в емкость, чтобы заполнить ее до верхнего края.
Решение
Вспомним формулу объема из курса физики:
(V=frac{m}{rho})
Предположим, что O является центром основания большего конуса. Пусть Q — центр основания меньшего конуса, а S обозначает общую вершину данных фигур. В одной плоскости построим радиусы OA и QB:
В таком случае:
(QBparallel OA)
(triangle SQBsim triangle SOA)
В результате:
(dfrac{OA}{QB}=dfrac{OS}{QS}=dfrac21)
Получим, что:
(m_{small{text{ж}}}=V_{small{text{ж}}}cdot rho= dfrac13cdot picdot QScdot QB^2 cdot rho)
Можно сделать вывод, что:
(m=Vrho=dfrac13cdot picdot OScdot OA^2cdot rho= dfrac 13cdot picdot 2QScdot (2QB)^2cdot rho= 8cdot left(dfrac13cdot picdot QScdot QB^2cdot rhoright)=8cdot 75=600 {small{text{грамм}}})
Таким образом, потребуется долить в емкость:
(600-75=525 {small{text{грамм}}})
Ответ: 525.
Задача 7
Изображена четырехугольная пирамида. Ее высота равна h. Отметим точку сбоку на ребре геометрической фигуры так, чтобы она была удалена на frac13h от плоскости основания. Данную точку пересекает плоскость, которая параллельна плоскости основания и отделяет от пирамиды аналогичную фигуру меньшего размера. Объем начальной пирамиды равен 54. Требуется вычислить объем меньшей пирамиды, которая получилась в результате.
Решение
Назовем точку, через которую проведена плоскость, A’ на ребре AS. Параллельность плоскости и основания является причиной пересечения боковых граней по прямым A’B’, B’C’, C’D’, D’A’, параллельным соответственно AB, BC, CD, DA. В этом случае SA’B’C’D’ является правильной четырехугольной пирамидой.
Исследуем плоскость ASO. Построим (A’Hparallel SO), где SO представляет собой высоту начальной фигуры. В таком случае:
(A’Hperp ABC)
В результате получилось расстояние, которое равно (frac13SO:)
(triangle AA’Hsim triangle ASO)
(dfrac{SA}{AA’}=dfrac{SO}{A’H}=3 quadRightarrowquad SA=3AA’ quadRightarrowquad SA’=dfrac23SA)
Таким образом:
(SQ=frac23SO)
(triangle ASBsim triangle A’SB’)
Получим, что:
(dfrac23=dfrac{SA’}{SA}=dfrac{A’B’}{AB} quadRightarrowquad A’B’=dfrac23AB)
Запишем отношения объемов пирамид:
(dfrac{V_{{small{text{м}}}}}{V_{small{text{б}}}}= dfrac{frac13cdot SQcdot A’B’^2}{frac13cdot SOcdot AB^2}=dfrac{SQ}{SO}cdot left(dfrac{A’B’}{AB}right)^2=dfrac23cdot left(dfrac23right)^2=dfrac8{27})
В результате объем малой фигуры составит:
(V_{{small{text{м}}}}=dfrac8{27}cdot 54=16)
Ответ: 16.
Задания для самостоятельной работы
Задание 1
Имеется пара конусов. Вторая фигура обладает радиусом, который в три раза больше по сравнению с радиусом первой фигуры. Второй конус выше первого в шесть раз. Объем второй фигуры равен 18. Требуется вычислить, чему равен объем первого конуса.
Решение
Формула определения объема конуса:
(V=frac13pi R^2h)
Запишем отношения объемов двух фигур:
(dfrac{V_1}{18}=dfrac{V_1}{V_2}= dfrac{frac13pi ,R_1^2,h_1}{frac13 pi ,R_2^2,h_2}=left(dfrac{R_1}{R_2}right)^2cdot dfrac{h_1}{h_2})
Исходя из условий задачи:
(R_2=3R_1)
(h_1=6h_2)
В результате:
(dfrac{V_1}{18}=left(dfrac{R_1}{3R_1}right)^2cdot dfrac{6h_2}{h_2}= dfrac19cdot 6=dfrac23 quadRightarrowquad V_1=dfrac23cdot 18=12)
Ответ: 12
Задание 2
Дано два шара. Объем первого шара в 343 раза больше по сравнению с объемом второго шара. Нужно вычислить, во сколько раз радиус первой фигуры больше, чем радиус второй фигуры.
Решение
Запишем формулу для нахождения объема шара:
(V=dfrac43 pi R^3)
Составим отношения объемов данных шаров:
(dfrac{343}1=dfrac{V_1}{V_2}=dfrac{frac43 pi , R_1^3}{frac43 pi , R_2^3}= left(dfrac{R_1}{R_2}right)^3 quadRightarrowquad dfrac{R_1}{R_2}=sqrt[3]{343}=7)
Сделаем вывод, что радиус первого шара в 7 раз больше по сравнению с радиусом второго шара.
Ответ: 7.
Задание 3
На рисунке изображены два цилиндра. Первый из них обладает площадью боковой поверхности, равной 16. Радиус второй фигуры больше в 4 раза по сравнению с радиусом первой фигуры. Второй цилиндр ниже, чем первый цилиндр, в 5 раз. Требуется вычислить площадь боковой поверхности второго цилиндра.
Решение
Запишем формулу для вычисления площади боковой поверхности цилиндра, которую уже проходили ранее:
(S=2pi RH)
Составим отношение площадей боковых поверхностей двух фигур:
(dfrac{16}{S_2}=dfrac{S_1}{S_2}=dfrac{2pi ,R_1,H_1}{2pi ,R_2,H_2}= dfrac{R_1}{R_2}cdot dfrac{H_1}{H_2})
В результате:
(R_2=4R_1, H_1=5H_2)
Таким образом:
(dfrac{16}{S_2}=dfrac{R_1}{4R_1}cdot dfrac{5H_2}{H_2}= dfrac14cdot 5=dfrac54)
Получим, что:
(S_2=dfrac{16cdot 4}5=12,8)
Ответ: 12,8.
Задание 4
Имеется некая емкость конусообразной формы. Объем этой емкости составляет 2700 мл. Требуется рассчитать количество жидкости, налитой в емкость, если ее уровень в 3 раза меньше по сравнению с высотой емкости.
Решение
Введем обозначения, как на рисунке:
В таком случае:
(QBparallel OA и triangle SQBsim triangle SOA)
Таким образом:
(dfrac{QB}{OA}=dfrac{QS}{OS}=dfrac13)
Соотношение объемов жидкости до определенной линии и емкости:
(dfrac{V_{small{text{ж}}}}{2700}=dfrac{V_{small{text{ж}}}}{V}= dfrac{frac13cdot picdot QB^2cdot QS}{frac13cdot pi cdot OA^2cdot OS}= left(dfrac{QB}{OA}right)^2cdot dfrac{QS}{OS}=dfrac19cdot dfrac13=dfrac1{27})
В результате:
(V_{small{text{ж}}}=dfrac1{27}V=100)
Ответ: 100.
Задача 5
На рисунке изображены фигуры в виде шаров. Первый шар имеет радиус 6. Второй шар имеет радиус 2. Нужно вычислить, во сколько раз объем первой фигуры превышает объем второй фигуры.
Решение
Запишем формулу для расчета объема шара, который не может изменяться:
(V=dfrac43 pi R^3)
Составим отношение объемов двух шаров:
(dfrac{V_1}{V_2}=dfrac{frac43 pi cdot 6^3}{frac43 pi cdot 2^3}= left(dfrac62right)^3=27)
В результате объем первого шара в 27 раз больше по сравнению с объемом второго шара.
Ответ: 27.
Содержание:
- § 1 Расчет массы и объема вещества по его плотности
- § 2 Решение задач
- § 3 Важно запомнить
§ 1 Расчет массы и объема вещества по его плотности
В этом уроке мы изучим, как можно определить массу и объем тела, если известна плотность вещества.
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Из формулы плотности следует, что масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: v = m : p.
Для правильного решения задач нужно уметь верно переводить единицы измерения величин в Международную систему единиц: 1 г = 0,001 кг, 1 л = 1 дм3 = 0,001 м3, 1 см3 = 0,000 001 м3, 1 г/см3 = 1000 кг/м3.
§ 2 Решение задач
Какова масса подсолнечного масла в бутылке объемом 3 л, если плотность масла равна 930 кг/м3?
Запишем условие задачи. Нам известны объем бутылки (обозначается буквой V) 3 л, и плотность подсолнечного масла (обозначается буквой ρ) 930 кг/м3. Выразим объем бутылки в Международной системе единиц. 1 л = 0,001 м3, следовательно, 3 л составляют 0,003 м3.
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.

Сколько штук строительного кирпича размером 250 мм х 120 мм х 65 мм допускается перевозить на автомашине грузоподъемностью 4 т? Плотность кирпича 1800 кг/м3.
Запишем условие задачи и выразим данные в Международной системе единиц. Известны размеры кирпича: длина а = 250 мм = 0,25 м, ширина b= 120 мм = 0,12 м, высота с = 60 мм = 0,06 м, плотность кирпича ρ = 1800 кг/м3, грузоподъемность – наибольшая масса груза, которую может перевезти автомобиль – m = 4 т = 4000 кг. Найти количество кирпичей – обозначим латинской буквой N.
Решение: Количество кирпичей можно найти, поделив общую массу всех кирпичей на массу одного кирпича: N = m/m1. Чтобы найти массу одного кирпича, нужно плотность умножить на его объем: m1 = ρ · V. Кирпич имеет форму прямоугольного параллелепипеда, следовательно, его объем равен произведению длины, ширины и высоты кирпича. Подставим числовые значения известных величин и вычислим. Объем кирпича равен 0,0018 м3. Масса одного кирпича m1 равна 1800 кг/м3 , умножим на 0,0018 м3 , равно 3,24 кг. Тогда число кирпичей равно N 4000 кг, разделим на 3,24 кг и получим 1234, 567 штук или число целых кирпичей 1234 штуки.

Медный шар имеет массу 840 г при объеме 120 см3. Сплошной этот шар или полый? Плотность меди 8900 кг/м3.
Запишем условие задачи. Известна масса шара m 840 г, что в системе СИ составляет 0,84 кг, объем шара V=120 см3, в СИ 0,00 012 м3, плотность меди ρ = 8900 кг/м3. Определить, сплошной шар или содержит внутри пустое пространство?
Решение. Представим, что на рычажных весах лежат два медных шара, один сплошной, второй содержит внутри пустое пространство, то есть полый шар. Если у них массы одинаковы, то объем полого шара должен быть больше, чем объем сплошного шара (рис 1).
Определим, каков объем шара, состоящего полностью из меди. Если объем окажется равным 120 см3, то шар сплошной и пустот не содержит. Если же вычисленный объем окажется меньше 120 см3, значит, внутри есть полость.
Чтобы найти объем сплошного медного шара, массу шара разделим на его плотность. Для упрощения проведем вычисления в граммах и кубических сантиметрах.

§ 3 Важно запомнить
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: V = m : p.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. – М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
Использованные изображения:
Обновлено: 18.05.2023
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: v = m : p. Для правильного решения задач нужно уметь верно переводить единицы измерения величин в Международную систему единиц: 1 г = 0,001 кг, 1 л = 1 дм3 = 0,001 м3, 1 см3 = 0,000 001 м3, 1 г/см3 = 1000 кг/м3.
Что такое объем в физике 7 класс?
Объём — количественная характеристика пространства, занимаемого телом или веществом. С понятием объёма тесно связано понятие вместимости — объёма внутреннего пространства сосуда, упаковочного ящика и т. п. Объём тела (как и вместимость сосуда) определяется его формой и линейными размерами.
Чему равен объем 7 класс?
Объём тела вычисляют по формулам: Для прямоугольного параллелепипеда: объём = длина ⋅ ширина ⋅ высота . Если длина равна l 1 , ширина l 2 , высота l 3 , тогда объём будет V = l 1 ⋅ l 2 ⋅ l 3 .
Как найти n в физике 7 класс?
Измерение физических величин
- из значения верхней границы (ВГ) шкалы вычесть значение нижней границы (НГ) шкалы и результат разделить на количество делений (N);
- найти разницу между значениями двух соседних числовых меток (А и Б) шкалы и разделить на количество делений между ними (n).
Что такое МЮ в физике 7 класс?
Масса (m) — мера инертности тела, определяемая при его взвешивании как отношение силы тяжести (P) к коэффициенту (g). Плотность (ρ) — масса единицы объёма вещества, численно равная отношению массы (m) вещества к его объёму (V).
Как найти объем в физике через массу?
Отсюда видно, что для определения объема тела надо массу этого тела разделить на его плотность. Чтобы определить массу тела, надо плотность тела умножить на его объем. 1.
Как измеряется объем в физике?
Единицей объема в СИ считается кубический метр, его производные – кубический сантиметр, кубический дециметр и т. д. Жидкость измеряется в литрах. Для жидких и сыпучих веществ в разных странах используют различные внесистемные единицы – галлон, баррель.
Как вычислить массу?
Вес можно рассчитать по формуле: m=V*p, где р – плотность, V – объем материала. Например, 10 м3 речного песка весят 13 тонн. Если известна масса материала, то объем можно узнать по формуле: V = m/ p.
Как найти объем по формуле?
По какой формуле можно найти объем?
- Зная массу и плотность V = m/ρ, где m — масса, а ρ — плотность
- Для геометрических фигур, например куб V = a^3 перемножить три стороны, а для цилиндра V = S*H площадь основания помножить на высоту
Как можно найти массу вещества?
И наоборот, массу вещества определяют как произведение молярной массы на количество вещества: m = n . M. Так, масса 0,1 моля Na составляет 0,1 моль×23 г/моль = 2,3 Молярная масса численно всегда совпадает с молекулярной массой (или атомной массой — если вещество состоит не из молекул, а из атомов).
Что такое сила в физике 7 класс?
Си́ла — физическая векторная величина, являющаяся мерой воздействия на данное тело со стороны других тел или полей. Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений.
Как найти F в физике 7 класс?
A = Fs, где А — работа, F — сила и s — пройденный путь.
Как найти P в физике 7 класс?
Если высоту столба жидкости, находящейся в сосуде, обозначить буквой h, а площадь дна сосуда S, то V = S·h. Масса жидкости m = ρ·V, или m = ρ·S·h . Вес этой жидкости P = g·m, или P = g·ρ·S·h. p = g·ρ·h.

В повседневной жизни встречается единица объёма литр л . Она названа именем французского винодела Литра.
Литр является кубическим дециметром 1 л = 1 дм 3 .
Деления мензурки обычно выражаются в миллилитрах (мл) 1 мл = 1 см 3 .
1 м 3 = 10 дм ⋅ 10 дм ⋅ 10 дм = 1000 дм 3 1 м 3 = 100 см ⋅ 100 см ⋅ 100 см = 1000 000 см 3 1 м 3 = 1000 мм ⋅ 1000 мм ⋅ 1000 мм = 1000 000 000 мм 3
1 см 3 = 1 100 м ⋅ 1 100 м ⋅ 1 100 м = 1 1000 000 м 3 = 0,000 001 м 3
1 мм 3 = 1 1000 м ⋅ 1 1000 м ⋅ 1 1000 м = 1 1000 000 000 м 3 = 0,000 000 001 м 3

- В мензурку наливают воду и определяют её объём.
- В воду погружают тело и определяют общий объём тела и воды.
- Объём тела определяют, вычитая из общего объёма начальный объём.
Рис. 1. Кубический метр. © ЯКласс.
Рис. 2. Прямоугольный параллелепипед. © ЯКласс.
Рис. 3. Погружение в жидкость тела неправильной формы. © ЯКласс.
Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. Синонимом вместимости частично является ёмкость, но словом ёмкость обозначают также сосуды и качественную характеристику конденсаторов.
Принятые единицы измерения — в СИ и производных от неё — кубический метр, кубический сантиметр, литр (кубический дециметр) и т. д. Внесистемные — галлон, баррель.
Содержание
Вычисление объёма
Математически
В общем случае математически объём тела вычисляется по следующей интегральной формуле:

,

где — характеристическая функция геометрического образа тела.

Для ряда тел с простой формой более удобным является использование специальных формул. Например, объём куба с длиной стороны, равной a, равен .
Через плотность

Единицы объёма жидкости
Английские внесистемные
- 1 пинта = 0,57 л
- 1 Кварта = 2 пинты = 1,23 л
- 1 галлон = 8 пинтам = 4,55 л (Имперский галлон)
Американские внесистемные
- 1 американский галлон = 3,785 л (Распространён в США)
Античные внесистемные
Древнееврейские
-
= 24 883 см³ (Эйфа́)
- Омер = 1 /10 эйфы
- Гин = 4147 см³ [1]
- Кав = 1382 см³
Русские внесистемные
-
= 40 вёдер = 492 л = 4 четверти = 8 штофов = 12,3 л = 10 чарок = 20 шкаликов = 1,23 л
- Бутылка (винная) = 1/16 Ведра = 0,77 л
- Бутылка (пивная) = 1/20 Ведра = 0,61 л = 4,7 ведра = 2 шкалика = 0,123 л = 4 бутылки = 3,075 л (косушка) = пол чарки = 0,0615 л = 1,54 л
Единицы сыпучих веществ
Английские внесистемные
- 1 бушель = 36,36872 литров = 8 галлонов = 3,63687·10 −2 м³
- 1 баррель = 0,16365 м³. (для сыпучих веществ)
Русские внесистемные
Молярный объём
Vm — величина, равная отношению объёма V системы (тела) к её количеству вещества n:
Молярный объем для газов при нормальных условиях: Vm = 22,4 л/моль
Прочие единицы измерения
- 1 дюйм кубический = 1,63871·10 −5 м³
- 1 литр = 1·10 −3 м³
- Лямбда 1 λ = 1·10 −9 м³
- 1 унция = 2,841·10 −5 м³ (анг.)
- 1 унция = 2,957·10 −5 м³ (амер.)
- 1 фут кубический = 2,83168·10 −2 м³
- 1 ярд кубический = 0,76455 м³
- 1 стер = 1 м³
- 1 ае кубическая =3,348071936e+40 км³
- 1 км кубический = 1 000 000 000 м³
- 1 световой год кубический = 8,46590536e+38 км³
- 1 пк кубический = 2,9379989989648103256576e+40 км³
- 1 мпк кубический =1 000 000 000 пк³=2,9379989989648103256576e+49 км³
Примечания
Литература
- Проставив сноски, внести более точные указания на источники.
- Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.
- Добавить иллюстрации.
- Физические величины по алфавиту
- Единицы измерения объёма
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое “Объём” в других словарях:
объём — объём, а … Русский орфографический словарь
объём — объём … Словарь употребления буквы Ё
объём — объём/ … Морфемно-орфографический словарь
объём — сущ., м., употр. сравн. часто Морфология: (нет) чего? объёма, чему? объёму, (вижу) что? объём, чем? объёмом, о чём? об объёме; мн. что? объёмы, (нет) чего? объёмов, чему? объёмам, (вижу) что? объёмы, чем? объёмами, о чём? об объёмах 1. В… … Толковый словарь Дмитриева
объём — а; м. 1. Величина чего л. в длину, высоту и ширину, измеряемая в кубических единицах. О. геометрического тела. О. куба, цилиндра. О. здания. О. полтора кубометра. В объёме (в трёх измерениях; объёмно). 2. Содержание чего л. с точки зрения… … Энциклопедический словарь
ОБЪЁМ — ОБЪЁМ, а, муж. 1. Величина чего н. в длину, высоту и ширину, измеряемая в кубических единицах. О. пирамиды. О. здания. 2. Вообще величина, количество. Большой о. работ. О. информации. О. знаний. | прил. объёмный, ая, ое (к 1 знач.). Объёмное… … Толковый словарь Ожегова
объём — ОБЪЁМ1, а, м Величина или вместимость предмета, определяемая произведением длины, высоты и ширины и измеряемая в кубических единицах. Объем бассейна в новой школе составляет 300 кубических метров. ОБЪЁМ2, а, м Количество или величина чего л.… … Толковый словарь русских существительных
ОБЪЁМ — ОБЪЁМ, мера части пространства, занимаемого телом. Единицей измерения служит объём единичного куба … Современная энциклопедия
объ — объ. Пишется вм. (об) перед е, ю, я, напр. объехать, объявить.Примечание. Вм. этой приставки и следующей за ней буквы и пишется обы, напр. обыграть. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
объ… — Пишется вместо об… перед е, ю, я, напр. объехать, объявить. Примечание. вместо этой приставки и следующей за ней буквы и пишется обы, напр. обыграть. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
Физика. Наука, изучающая явления природы, свойства и строение материи.
Материя . Всё, что есть во Вселенной.
Молекула . Мельчайшая частица данного вещества.
Диффузия . Взаимное перемешивание молекул одного вещества с молекулами другого.
Механическое движение . Изменение положения тела относительно других тел с течением времени.
Путь . Длина траектории.
Траектория . Линия, по которой движется тело.
Равномерное движение. Движение, при котором тело за любые равные промежутки времени проходит одинаковые пути.
Скорость . Величина, равная отношению пути ко времени, за которое этот путь пройден.
Инерция . Явление сохранения скорости тела при отсутствии действия на него других тел.
Тормозной путь . Путь, который проходит автомобиль после выключения двигателя до полной остановки.
Плотность . Физическая величина, равная отношению массы тела к его объёму.
Сила. Мера механического воздействия на тело со стороны других тел.
Масса. Мера инертности.
Вес. Сила, с которой тело вследствие притяжения к Земле действует на горизонтальную опору или подвес.
Равнодействующая сила . Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Сила трения . Сила, возникающая при движении одного тела по поверхности другого и направленная против движения.
Давление . Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности.
Атмосфера . Воздушная оболочка Земли.
Архимедова сила . Сила, выталкивающая тело из жидкости или газа.
Работа. Величина, равная произведению приложенной силы на пройденный путь.
Мощность. Величина, равная отношению работы ко времени, за которое она была совершена.
Рычаг. Твёрдое тело, которое может вращаться вокруг неподвижной опоры.
КПД. Отношение полезной работы к полной работе.
Потенциальная энергия . Энергия взаимодействия.
Кинетическая энергия . Энергия движения.
Определения и формулы
Измерение физических величин
Измерение физических величин
- из значения верхней границы (ВГ) шкалы вычесть значение нижней границы (НГ) шкалы и результат разделить на количество делений (N);
- найти разницу между значениями двух соседних числовых меток (А и Б) шкалы и разделить на количество делений между ними (n).
ЦД = (ВГ — НГ) / N
ЦД = (Б — А) / n
Механическое движение
Скорость (ʋ) — физическая величина, численно равна пути (S), пройденного телом за единицу времени (t).
Путь (S) — длина траектории, по которой двигалось тело, численно равен произведению скорости (ʋ) тела на время (t) движения.
Время движения (t) — равно отношению пути (S), пройденного телом, к скорости (ʋ) движения.
Средняя скорость (ʋ ср ) — равна отношению суммы участков пути (S1, S2, S3, …), пройденного телом, к промежутку времени (t1 + t2+ t3+ …), за который этот путь пройден.
ʋср = (S1 + S2 + S3 + …) / (t1 + t2 + t3 + …)
Сила тяжести, вес, масса, плотность
Сила тяжести — сила (FТ), с которой Земля притягивает к себе тело, равная произведению массы (т) тела на коэффициент пропорциональности (g) — постоянную величину для Земли. (g = 9,8 H/кг)
FТ = m*g
Вес (Р) — сила, с которой тело действует на горизонтальную опору или вертикальный подвес, равная произведению массы (т) тела на коэффициент (g).
Масса (т) — мера инертности тела, определяемая при его взвешивании как отношение силы тяжести (Р) к коэффициенту (g).
т = Р / g
Плотность (ρ) — масса единицы объёма вещества, численно равная отношению массы (т) вещества к его объёму (V).
Механический рычаг, момент силы
Момент силы (М) равен произведению силы (F) на сё плечо (l)
М = F*l
Условие равновесия рычага — рычаг находится в равновесии, если плечи (l1, l2)действующих на него двух сил (F1, F2) обратно пропорциональны значениям сил.
a) F1 / F2 = l1 / l2
Давление, сила давления
Давление (р) — величина, численно равная отношению силы (F), действующей перпендикулярно поверхности, к площади (S) этой поверхности
Сила давления (F) — сила, действующая перпендикулярно поверхности тела, равная произведению давления (р) на площадь этой поверхности (S)
Давление газов и жидкостей
Давление однородной жидкости (р) — на дно сосуда зависит только от её плотности (ρ) и высоты столба жидкости (h).
Закон Архимеда — на тело, погруженное в жидкость (или газ), действует выталкивающая сила — архимедова сила (FВ). равная весу жидкости (или газа), в объёме (VТ) этого тела.
FВ = ρ*g*Vт
Условие плавания тел — если архимедова сила (FВ) больше силы тяжести (FТ)тела, то тело всплывает.
FВ > FТ
Закон гидравлической машины — силы (F1, F2), действующие на уравновешенные поршни гидравлической машины, пропорциональны площадям (S1, S2) этих поршней.
F1 / F2 = S1 / S2
Закон сообщающихся сосудов — однородная жидкость в сообщающихся сосудах находится на одном уровне (h)
Работа, энергия, мощность
Механическая работа — Работа (A) — величина, равная произведению перемещения тела (S) на силу (F), под действием которой это перемещение произошло.
Формула:
А = F*S
Коэффициент полезного действия механизма (КПД) — коэффициент полезного действия (КПД) механизма — число, показывающее, какую часть от всей выполненной работы (АВ) составляет полезная работа (АП).
ɳ = АП / АВ *100%
Потенциальная энергия (Е П ) тела, поднятого над Землей, пропорциональна его массе (т) и высоте (h) над Землей.
Формула:
ЕП = m*g*h
Кинетическая энергия (Е К ) движущегося тела пропорциональна его массе (m) и квадрату скорости (ʋ 2 ).
ЕК = m*ʋ 2 / 2
Сохранение и превращение механической энергии — Сумма потенциальной (ЕП) и кинетической (ЕК) энергии в любой момент времени остается постоянной.
EП + EК = const
Мощность (N) — величина, показывающая скорость выполнения работы и равная:
а) отношению работы (А) ко времени (t), за которое она выполнена;
б) произведению силы (F), под действием которой перемещается тело, на среднюю скорость (ʋ) его перемещения.
Формулы меры длины и веса и соотношения между единицами

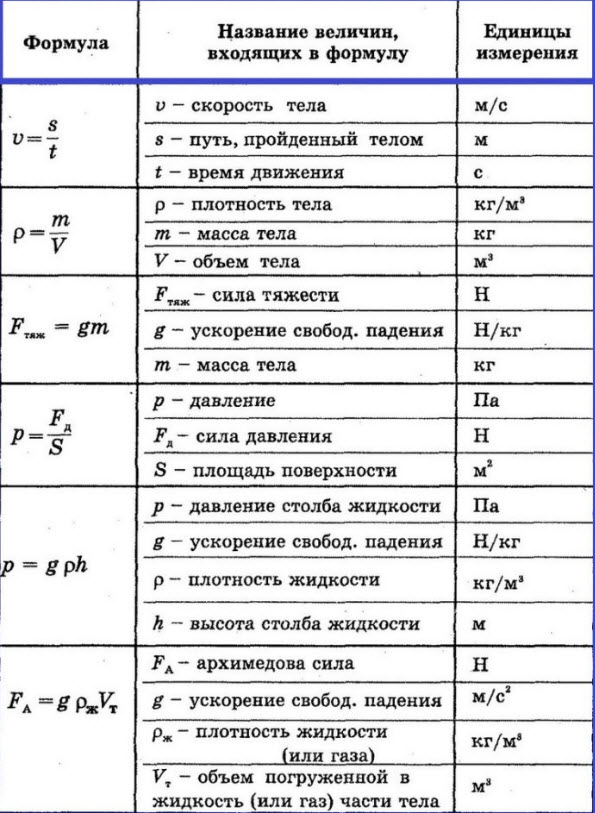
12 самых востребованных формул по физике в 7 классе

Тест для закрепления материала
- Сколько в теле молекул
- Чему равна масса тела из данного вещества
- Что массы разных тел неодинаковы
- Отношение массы тела к его объему
2 Вычислите скорость (в м/с) равномерного полёта воздушного шара в течение 1,5 мин., за которые он пролетел 540 м
Объем – мера в трехмерном пространстве, занимаемом объектом (длина, ширина и высота).
Задача обучения
- Понять, как геометрически можно измерить объем.
Основные пункты
- В качестве единицы чаще всего используют м 3 . Но для жидкостей – литр (0.001 м 3 ).
- Можно воспринимать как количество жидкости, вытесненной погруженным телом.
- Объем можно вычислить у геометрических объектов по формулам. В случае со сложными объектами следует измерить вытесненную жидкость.
Термины
- Поперечное сечение – срез, образованный плоскостью, прорезающей предмет под прямым углом.
- Измерение – мера пространственной протяженности в конкретном направлении (высота, ширина и глубина).
Объем в физике – мера трехмерного пространства, ограниченного чертой. В нем может вмещаться определенное вещество или отображает форму. В чем измеряется объем в физике? В качестве единицы используют м 3 , но для жидкостей – литр (0.001 м 3 ).
Геометрически определяется через умножение трех измерений объекта (длина, ширина и высота). Как провести измерение объема? Некоторые объемы вычисляются как:
- объем куба: две ширины, одна высота.
- объем цилиндра: площадь поперечного сечения превосходит высоту цилиндра.
- объем сферы: в 4/3 раза больше радиуса куба.
Объем твердого тела вычисляется через объем жидкости, которую вытесняет при погружении.
Объем сосуда можно определить как его емкость, то есть количество вмещаемой жидкости. Таким же образом работают и измерительные чаши: площадь поперечного сечения умножается на переменную высоту. Жидкость всегда будет покрывать поперечное сечение, а добавление увеличит высоту внутри контейнера.

Мерную чашу используют для определения объемов жидкостей. Единицами служат унции, чаши и миллилитры
Жидкость расплывается по форме контейнера, заполняя минимально требуемую высоту. Газы же стараются заполнить собою все максимально. Поэтому измерить объем жидкости очень просто, ведь газ всегда равномерно распространяется по пространству.
Читайте также:
- Какие черты характера раскрывают поведение бирюка в грозовую ночь кратко
- Презентация отчет по проекту пдд в детском саду
- Исследовательская деятельность в средней школе
- Как жизнедеятельность живых организмов повлияла на изменение геологических оболочек земли кратко
- Какие события связаны с правлением князя игоря княгини ольги князя святослава кратко
Как найти объем тела?
Объем (V) физического тела любой формы можно определить, если знать его массу (m) и среднюю плотность материала (p) — эти две величины надо перемножить: V=m∗p.
Как найти объем с помощью воды?
V = πr2h, где π ≈ 3,14; r – радиус цилиндра; h – расстояние между двумя метками. Посредством этой формулы вы вычислите объем вытесненной воды, а значит и объем тела.
Как найти объем по весу?
Вес можно рассчитать по формуле: m=V*p, где р – плотность, V – объем материала. Например, 10 м3 речного песка весят 13 тонн. Если известна масса материала, то объем можно узнать по формуле: V = m/ p.
Чему равен объем погруженной части тела?
= m ⋅ g = ρ тела ⋅ V всего тела ⏟ ∥ m ⋅ g . Отношение объёма погруженной части тела к полному объёму тела равно отношению плотности тела к плотности жидкости.
Как найти объем в физике 7 класс?
Объём тела вычисляют по формулам: Для прямоугольного параллелепипеда: объём = длина ⋅ ширина ⋅ высота . Если длина равна l 1 , ширина l 2 , высота l 3 , тогда объём будет V = l 1 ⋅ l 2 ⋅ l 3 .
Как найти массу тела по его весу?
Получится m = P/g. Подставьте известные значения: m = 549/9,8 = 56 кг. Вы решили задачу. Ответ: масса тела, которое весит 549 Н (на поверхности Земли) равна 56 кг, или m = 56 кг.
Как определить объем погруженного тела?
Согласно закону Архимеда, объем тела, погруженного в воду равен объему вытесненной им воды. Чтобы определить таким образом объем цилиндра, нужно взять мерный стакан с водой со шкалой объема. Определить по шкале первоначальный объем воды — V1. Затем погружаем цилиндр в воду и отмечаем объем воды после погружения — V2.
Как найти вес и массу?
1 Часть 1 из 4: Вычисление веса
- Так как вес является силой, X Источник информации эту формулу можно записать и как F = mg.
- P или F — соответственно, вес или сила (измеряется в ньютонах, Н).
- m — масса тела (измеряется в килограммах, кг).
- g — ускорение свободного падения (измеряется в метрах на секунду в квадрате, м/с2).
Как найти вес жидкости формула?
Вес тела направлен вниз. Архимедова сила: F А = m ж ⋅ g . Сила направлена вверх. Вес тела в жидкости: P 1 = P − F А = mg − m ж g .
Что такое выталкивающая сила 4 класс?
На тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа в объёме погружённой части тела. Эта выталкивающая сила и называется силой Архимеда. У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.
Чему равна выталкивающая сила?
Закон Архимеда: Выталкивающая сила равна силе тяжести жидкости (или газа) вытесненной телом.
Как определить объем 7 класс?
Объём тела вычисляют по формулам: Для прямоугольного параллелепипеда: объём = длина ⋅ ширина ⋅ высота . Если длина равна l 1 , ширина l 2 , высота l 3 , тогда объём будет V = l 1 ⋅ l 2 ⋅ l 3 .
Как найти объем по формуле?
Для вычисления объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу: объем = L × W × H (длину умножить на ширину умножить на высоту). Эту формулу можно рассматривать как произведение площади поверхности одной из граней фигуры на ребро, перпендикулярное этой грани. = 30.
Как найти вес подвижного тела?
P=m(g-a) — вес тела в случае, когда вектор ускорения совпадает по направлению с вектором ускорения свободного падения. В этом случае сила веса по модулю меньше силы тяжести.
Как найти массу зная вес и объём?
Исходя из определения, d=m/V, гдеm – масса предмета (кг),V — его объем (м3). Как видно из формулы, плотность вещества – это масса единицы его объема. 3.
Как найти объем цилиндра?
Чтобы определить объем цилиндра по радиусу, необходимо произвести расчет по формуле:
- V = π·r²·h.
- π — константа равная (3.14);
В чем измеряется объем?
| Объём | |
|---|---|
| Размерность | L3 |
| Единицы измерения | |
| СИ | м3 |
| СГС | см3 |

