Внешний угол треугольника
- Сумма внешних углов
Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:
∠1 + ∠4 = 180°.
Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:
∠2 + ∠3 + ∠4 = 180°.
Из этого следует, что
∠1 + ∠4 = ∠2 + ∠3 + ∠4.
Сократив обе части полученного равенства на одно и тоже число (∠4), получим:
∠1 = ∠2 + ∠3.
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°
Рассмотрим треугольник ABC:
Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:
(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
∠1 + ∠2 + ∠3 = 540° – (∠4 + ∠5 + ∠6) = 540° – 180° = 360°.
Внешний угол треугольника
Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
Сколько внешних углов у треугольника?
При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.
Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):
Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.
Чему равен внешний угол?
Теорема (о внешнем угле треугольника)
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Дано : ∆АВС, ∠1 — внешний угол при вершине С.
∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.
Теорема о внешнем угле треугольника: формулировка и задачи
В данной публикации мы рассмотрим одну из основных теорем в геометрии 7 класса – о внешнем угле треугольника. Также разберем примеры решения задач, чтобы закрепить представленный материал.
Определение внешнего угла
Для начала вспомним, что такое внешний угол. Допустим у нас есть треугольник:
Смежный с внутренним углом ( λ ) треугольника угол при той же вершине является внешним. На нашем рисунке он обозначен буквой γ .
-
сумма данных углов равна 180 градусам, т.е. γ + λ = 180° (свойство внешнего угла);
Формулировка теоремы
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.
Примеры задач
Задание 1
Дан треугольник, в котором известны значения двух углов – 45° и 58°. Найдите внешний угол, смежный с неизвестным углом треугольника.
Решение
Воспользовавшись формулой теоремы получаем: 45° + 58° = 103°.
Задание 1
Внешний угол треугольника равен 115°, а один из несмежных с ним внутренних углов – 28°. Вычислите значения оставшихся углов треугольника.
Решение
Для удобства будем использовать обозначения, указанные на рисунках выше. Известный внутренний угол примем за α .
Исходя из теоремы: β = γ – α = 115° – 28° = 87° .
Угол λ является смежным с внешним, а значит вычисляется по следующей формуле (следует из свойства внешнего угла): λ = 180° – γ = 180° – 115° = 65° .
Внешний угол треугольника. Синус и косинус внешнего угла
В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом . Если угол острый, то смежный с ним угол — тупой, и наоборот.
Обратите внимание, что:
Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Ты нашел то, что искал? Поделись с друзьями!
1. В треугольнике угол равен , . Найдите тангенс внешнего угла при вершине .
Пусть — внешний угол при вершине .
Зная , найдем по формуле
2. В треугольнике угол равен , . Найдите синус внешнего угла при вершине .
Задача решается за четыре секунды. Поскольку сумма углов и равна , . Тогда и синус внешнего угла при вершине также равен .
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vneshnij-ugol-treugolnika/
[/spoiler]
Содержание:
- Определение внешнего угла треугольника
- Свойства внешних углов треугольника
- Примеры решения задач
Определение внешнего угла треугольника
Определение
Углы, смежные с углами треугольника, называются внешними.
Например, для $angle A$, внешними будут углы $angle 1$ и $angle 2$ (см. рис.)
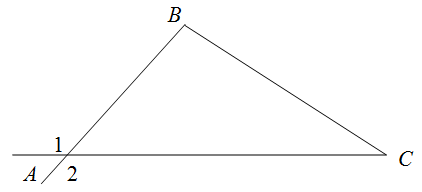
Свойства внешних углов треугольника
- Сумма внешних углов треугольника, взятых по одному при каждой вершине, равна $360^{circ}$.
- Сумма внешнего и внутреннего угла при одной вершине равна $180^{circ}$.
-
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
$$angle 1=angle B+angle C$$
Примеры решения задач
Пример
Задание. В треугольнике $Delta M N K$, внешний угол $angle M$ равен $120^{circ}$,
а угол $angle N=65^{circ}$. Найти угол $angle K$.
Решение. По теореме о внешнем угле
$angle M=angle N+angle K$. Подставляя в это равенство исходные данные, получим
$$120^{circ}=65^{circ}+angle K$$
Выразим $angle K : angle K=120^{circ}-65^{circ} Rightarrow angle K=55^{circ}$
Ответ. $angle K=55^{circ}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Внешние углы при двух вершинах треугольник равны $70^{circ}$ и $150^{circ}$.
Найти внутренний угол при третьей вершине.
Решение. Обозначим внешние углы $angle 1, angle 2, angle 3$, а соответствующие им
внутренние – $alpha, beta, gamma$.
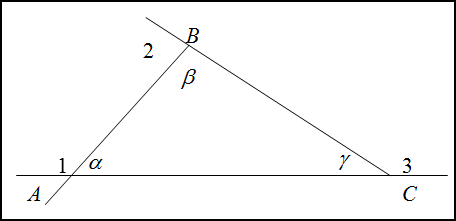
По условию $angle 1=150^{circ}$ и $angle 2=70^{circ}$. По свойству внешних углов, их сумма,
взятых по одному при каждой вершине, равна $360^{circ}$. То есть
$$angle 1+angle 2+angle 3=360^{circ}$$
Выразим из этого равенства неизвестный угол $angle 3$
$$angle 3=360^{circ}-angle 1-angle 2$$
$$angle 3=360^{circ}-150^{circ}-70^{circ}$$
$$angle 3=140^{circ}$$
Тогда искомый внутренний угол можно найти из условия, что сумма внутреннего и внешнего углов равна
$180^{circ}$, то есть $gamma+angle 3=180^{circ}$, тогда:
$$gamma=180^{circ}-angle 3$$
$$gamma=180^{circ}-140^{circ}=40^{circ}$$
Ответ. $gamma=40^{circ}$
Читать дальше: что такое медиана треугольника.
Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?
Определение.
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
На рисунке:
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
Сколько внешних углов у треугольника?
При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.
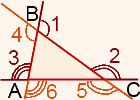Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):
∠1=∠4, ∠2=∠5, ∠3=∠6.
Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.
Чему равен внешний угол?
Теорема (о внешнем угле треугольника)
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Дано: ∆АВС, ∠1 — внешний угол при вершине С.
Доказать: ∠1=∠А+∠В.
Доказательство:
Так как сумма углов треугольника равна 180º, ∠А+∠В+∠С=180º.
Следовательно, ∠С=180º-(∠А+∠В).
∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.
Что и требовалось доказать.
1
Анатолий-тдр5
[15.3K]
3 года назад
Из известного отношения внутренних углов легко найти сами эти углы.
2x+3x+4x=180°, 9x=180°, x=20°. Тогда внутренние углы: 40°, 60°, 80°.
Дополнительные им внешние углы: 140°, 120°, 100°.
Их соотношение будет равно 140:120:100=7:6:5.
Ответ: 7:6:5
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное
ссылка
отблагодарить
