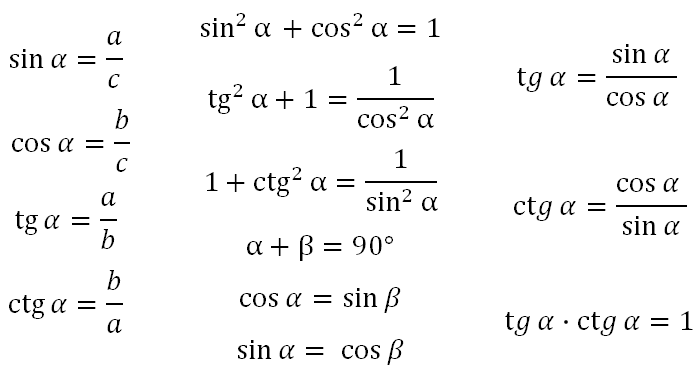Внешний угол треугольника
Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
Сколько внешних углов у треугольника?
При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.
Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):
Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.
Чему равен внешний угол?
Теорема (о внешнем угле треугольника)
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Дано : ∆АВС, ∠1 — внешний угол при вершине С.
∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.
Внешний угол треугольника. Синус и косинус внешнего угла
В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом . Если угол острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:
Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Ты нашел то, что искал? Поделись с друзьями!
1. В треугольнике угол равен , . Найдите тангенс внешнего угла при вершине .
Пусть — внешний угол при вершине .
Зная , найдем по формуле
2. В треугольнике угол равен , . Найдите синус внешнего угла при вершине .
Задача решается за четыре секунды. Поскольку сумма углов и равна , . Тогда и синус внешнего угла при вершине также равен .
Внешний угол треугольника
Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:
Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:
Из этого следует, что
Сократив обе части полученного равенства на одно и тоже число (∠4), получим:
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°
Рассмотрим треугольник ABC:
Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:
(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
∠1 + ∠2 + ∠3 = 540° – (∠4 + ∠5 + ∠6) = 540° – 180° = 360°.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vneshnij-ugol-treugolnika/
http://izamorfix.ru/matematika/planimetriya/vneshnie_ugly_treug.html
[/spoiler]
Внешний угол треугольника. Синус и косинус внешнего угла
В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом
. Если угол
острый, то смежный с ним угол — тупой, и наоборот.
Обратите внимание, что:
Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
1. В треугольнике угол
равен
,
. Найдите тангенс внешнего угла при вершине
.
Пусть — внешний угол при вершине
.
Зная , найдем
по формуле:
Получим:
2. В треугольнике угол
равен
,
. Найдите синус внешнего угла при вершине
.
Задача решается за четыре секунды. Поскольку сумма углов и
равна
,
. Тогда и синус внешнего угла при вершине
также равен
.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Внешний угол треугольника. Синус и косинус внешнего угла» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
07.05.2023
Внешний угол треугольника
- Сумма внешних углов
Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:
∠1 + ∠4 = 180°.
Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:
∠2 + ∠3 + ∠4 = 180°.
Из этого следует, что
∠1 + ∠4 = ∠2 + ∠3 + ∠4.
Сократив обе части полученного равенства на одно и тоже число (∠4), получим:
∠1 = ∠2 + ∠3.
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°
Рассмотрим треугольник ABC:
Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:
(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
∠1 + ∠2 + ∠3 = 540° – (∠4 + ∠5 + ∠6) = 540° – 180° = 360°.
Внешний угол треугольника. Продолжаем рассматривать задачи на решение прямоугольного треугольника. Такие типы заданий имеются в прототипах открытого банка заданий по математике. Некоторые примеры мы уже рассмотрели в статьях «Прямоугольный треугольник. Часть 1» и «Прямоугольный треугольник. Часть 2». В этой статье разберём задачи, в которых необходимо определить значения тригонометрических функций внешнего угла треугольника (или внутреннего, когда дано значение внешнего).
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине
Угол DAB является внешним.
Стоит повторить определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике, также основные тригонометрические формулы для решения прямоугольного треугольника. Вспомним основные из них:
А также формулы приведения (не все). Отмечу одну типичную ошибку, которую допускают (из-за невнимательности). При решении подобных задач часто используется формула основного тригонометрического тождества:
Из неё мы получаем:
*Запись с ошибкой (её часто допускают — теряют квадрат):
Будьте внимательны!
Рассмотрим задачи:
В треугольнике ABC угол C равен 900, sin A = 0,27. Найдите синус внешнего угла при вершине А.
Углы ВАС и BAD смежные, значит:
По свойству синуса:
А лучше раз и навсегда запомнить сам факт того, что синусы смежных углов равны, и вам даже не будет необходимости что-то записывать при решении такой задачи, ответ вы озвучите сразу.
Ответ: 0,27
Решите самостоятельно:
Посмотреть решение
В треугольнике ABC угол C равен 900, 
Углы ВАС и BAD смежные, значит:
Значит по свойству тангенса (используем формулу приведения):
То есть необходимо найти тангенс угла ВАС. Известно, что:
Синус угла ВАС нам известен. Найдём его косинус.
Из основного тригонометрического тождества:
Вычисляем тангенс:
Таким образом tg BAD = – tg BAC = – 0,3
Ответ: – 0,3
Решите самостоятельно:
Посмотреть решение
Посмотреть решение
В треугольнике ABC угол C равен 900, АВ = 6, 
Углы ВАС и BAD смежные, значит:
По свойству косинуса:
Найдём cos BAC Для этого необходимо найти сторону АС. По теореме Пифагора:
Значит АС = 3.
По определению косинуса:
Таким образом, cos DAB = – cos BAC = – 0,5.
Ответ: – 0,5
Решите самостоятельно:
Посмотреть решение
Посмотреть решение
В треугольнике ABC угол C равен 900, косинус внешнего угла при вершине A равен 
Углы ВАС и BAD смежные, значит:
В данной задаче можем найти косинус угла ВАС, а затем используя основное тригонометрическое тождество синус этого угла.
По свойству косинуса (используем формулу приведения):
Значит
Найдём sin BAC. Из основного тригонометрического тождества получим:
Ответ: 0,9
В треугольнике ABC угол C равен 900, тангенс внешнего угла при вершине A равен –2/9. Найдите tg = B.
Из свойств прямоугольного треугольника мы знаем, что tg ABC = ctg BAC.
Найдём ctg BAC. Известно, что tg BAC ∙ ctg BAC = 1, значит
Тангенс угла ВАС найти не сложно. Углы BAC и BAD смежные. Это значит, что
По свойству тангенса:
Значит
Таким образом:
Ответ: 4,5
В треугольнике ABC угол C равен 900, косинус внешнего угла при вершине A равен – 0,7; АВ = 20. Найдите AC.
Найти АС мы сможем, если нам будет известен косинус угла ВАС. Так как по определению косинуса в прямоугольном треугольнике:
Найдём косинус. По его свойству:
*Использовали формулу приведения.
Значит
Таким образом:
Ответ: 14
Решите самостоятельно:
Посмотреть решение
Посмотреть решение
Посмотреть решение
Посмотреть решение
В треугольнике ABC АС = ВС, АВ = 12, тангенс внешнего угла при вершине A равен 
Построим высоту CH.
Найдём тангенс внутреннего угла. По свойству тангенса:
Сторона АС является гипотенузой в прямоугольном треугольнике АСН. В этом треугольнике зная тангенс острого угла и один катет мы без труда можем найти второй катет.
Высота проведённая к основанию равнобедренного треугольника является медианой, то есть АН = ВН, a АВ = 2АН:
Рассмотрим прямоугольный треугольник ACH: по определению тангенса в прямоугольном треугольнике:
Следовательно:
В прямоугольном треугольнике нам известны катеты АН и СН.
По теореме Пифагора мы можем найти гипотенузу АС:
Таким образом, АС = 9.
Ответ: 9
Решите самостоятельно:
Посмотреть решение
В будущем будем рассматривать другие задачи, не пропустите! Успехов Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?
Определение.
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
На рисунке:
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
Сколько внешних углов у треугольника?
При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.
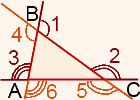
∠1=∠4, ∠2=∠5, ∠3=∠6.
Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.
Чему равен внешний угол?
Теорема (о внешнем угле треугольника)
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Дано: ∆АВС, ∠1 — внешний угол при вершине С.
Доказать: ∠1=∠А+∠В.
Доказательство:
Так как сумма углов треугольника равна 180º, ∠А+∠В+∠С=180º.
Следовательно, ∠С=180º-(∠А+∠В).
∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.
Что и требовалось доказать.