Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами
Доказательства теорем об углах, связанных с окружностью
Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).
Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.
Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).
В этом случае справедливы равенства
и теорема 1 в этом случае доказана.
Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).
В этом случае справедливы равенства
что и завершает доказательство теоремы 1.
Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.
Доказательство . Рассмотрим рисунок 8.
Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство . Рассмотрим рисунок 9.
Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.
Доказательство . Рассмотрим рисунок 10.
Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства
что и требовалось доказать
Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство . Рассмотрим рисунок 11.
Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства
что и требовалось доказать.
Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.
Доказательство . Рассмотрим рисунок 12.
Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство
Центральные и вписанные углы
О чем эта статья:
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°
Треугольник вписанный в окружность
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac<1><2>ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/centralnye-i-vpisannye-ugly
http://colibrus.ru/treugolnik-vpisannyy-v-okruzhnost/
[/spoiler]
Свойства внешнего угла
- Внешний угол треугольника равен сумме внутренних углов не смежных с ним:
- Сумма внешнего и внутреннего углов при одной вершине равна :
- Сумма внешних углов треугольник взятых по одному при каждой вершине равна .
- Внешние углы при одной вершине треугольника равны между собой (как вертикальные):
:
.
Видео
Диагонали n угольника
Число диагоналей n – угольника равно
| Фигура | Рисунок | Описание |
| Диагональмногоугольника |  |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |  |
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |  |
| Диагональ многоугольника |
 |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника
Диагонали n – угольника, выходящие из одной вершины 
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника
Все диагонали n – угольника 
Число диагоналей n – угольника равно
Внешний угол многоугольника
Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).
Рис.1
Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
Рис.2
Замечание. Мы рассматриваем только выпуклые многоугольникивыпуклые многоугольники.
Чему равен, как найти при вершине
Определение
Для того, чтобы найти ВУТ при вершине, необходимо сложить значения не соседних с ним частей плоскости, которые ограничены двумя лучами, рассматриваемой геометрической фигуры.
Продемонстрируем это положение на примерах.
Задача №1
В треугольнике DEF угол D = 50°, а F = 45°. Найти: ВУ при каждой вершине фигуры.
Решение
Сумма углов треугольника всегда равна 180°. Из этого следует, что angle E=180˚-angle D-angle F=85^circ. ВУ при точке соединения сторон DE и DF будет равняться сложенным внутренним углам при вершинах E и F, а это 130°. Соответственно, ВУ при E составляет 95°, а при F — 135°.
Ответ: ∠ D = 130°, ∠ E = 95°, ∠ F = 135°.
Задача №2
В треугольнике ABC ВУ при вершине A = 68°, а при вершине C = 55°. Найти: Внутренний угол при B. На иллюстрации отображены пронумерованные названия углов.
Решение
Если сложить смежные углы, то в любом случае получится 180°. Из этого составляем равенства: ∠ A = 180° – ∠ 3 = ∠ 180° – 112° = 68°; ∠ С = 180° – ∠ 2 = ∠ 180° – 125° = 55°. Далее из сложенного вычитаем уже известное: ∠ A = 180° – ∠ A – ∠ C = ∠ 180° – 68° – 55° = 57°.
Ответ: ∠ B = 57°.
Формулировка теоремы
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
γ = α + β
Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.
Свойства углов правильного n –угольника
Теги
В данной публикации мы рассмотрим одну из основных теорем в геометрии 7 класса – о внешнем угле треугольника. Также разберем примеры решения задач, чтобы закрепить представленный материал.
Определение внешнего угла
Для начала вспомним, что такое внешний угол. Допустим у нас есть треугольник:
Смежный с внутренним углом (λ) треугольника угол при той же вершине является внешним. На нашем рисунке он обозначен буквой γ.
При этом:
- сумма данных углов равна 180 градусам, т.е. γ + λ = 180° (свойство внешнего угла);
- 0 и 0.
Формулировка теоремы
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
γ = α + β
Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.
Примеры задач
Задание 1
Дан треугольник, в котором известны значения двух углов – 45° и 58°. Найдите внешний угол, смежный с неизвестным углом треугольника.
Решение
Воспользовавшись формулой теоремы получаем: 45° + 58° = 103°.
Задание 1
Внешний угол треугольника равен 115°, а один из несмежных с ним внутренних углов – 28°. Вычислите значения оставшихся углов треугольника.
Решение
Для удобства будем использовать обозначения, указанные на рисунках выше. Известный внутренний угол примем за α.
Исходя из теоремы: β = γ – α = 115° – 28° = 87°.
Угол λ является смежным с внешним, а значит вычисляется по следующей формуле (следует из свойства внешнего угла): λ = 180° – γ = 180° – 115° = 65°.
Мы привыкли рассматривать треугольники, в особенности их углы, только «изнутри». Однако, знаете ли, «снаружи» треугольника тоже кипит жизнь. В этом уроке предлагаем узнать, что в геометрии треугольников имеется также внешний угол. А что же такое внешний угол? Какие свойства внешнего угла треугольника существуют? Может, есть какая-нибудь теорема о внешнем угле треугольника? Вот, сейчас будем все выяснять.
Что такое внешний угол?
Начертим треугольник $bigtriangleup{ABC}$ и построим при вершине $B$ угол, смежный с $angle{B}$. Теперь в $bigtriangleup{ABC}$ при вершине $B$ появилось два угла — один «внутри», другой «снаружи». Угол «снаружи» называется внешним углом при вершине $B$. Дадим ему определение.
Внешний угол при данной вершине — угол, смежный с углом треугольника при этой вершине.
Как обозначается внешний угол?
Углы в треугольнике обозначаются согласно вершинам, где они располагаются, либо по трем точкам.
Например, в треугольнике $bigtriangleup{ABC}$ угол при вершине $B$ обозначается как $angle{B}$, либо как $angle{ABC}$. А если при вершине $B$ в том числе имеется внешний угол? Его тоже обозначать как $angle{B}$?
Или лучше указать дополнительную точку на продолжении стороны? Вопрос отличный. Для того, чтобы подобной путаницы не возникало, в геометрии принят термин «внутренний угол».
К примеру, в ходе задачи или доказательства вы пользуетесь внешним углом при некоторой вершине. Скажем, вновь при вершине $B$ в треугольнике $bigtriangleup{ABC}$. Когда вы ссылаетесь к углу треугольника внутри, можно уточнить: «Внутренний угол $angle{B}$».
Когда ссылаетесь к углу снаружи, уточняйте: «Внешний угол $angle{B}$».
Способ с уточнениями «внутренний угол», «внешний угол» проще и не требует дополнительных точек. К тому же, такое обозначение облегчает понимание, где в треугольнике располагается угол. Ведь вы акцентируете внимание только на вершине.
Такое особенно полезно, когда решения или чертежи к задачам громоздкие. Бывает, что при одной вершине нужно рассматривать два внешних угла. Они все равно равны как вертикальные, но все же… Мало ли. Тут удобнее дать углам обозначение в стиле «$angle{1}$» или, например, «$angle{x}$».
Теорема о внешнем угле треугольника
Применим наши знания теоремы о сумме углов треугольника к внешним углам. Рассмотрим внешний угол $angle{B}$ в треугольнике $bigtriangleup{ABC}$. Сумма $angle{B}$ внешнего и $angle{B}$ внутреннего равняется $180^circ$, как смежных.
По теореме о сумме углов треугольника: $$angle{A}+angle{B}+angle{C}=180^circ$$
Если:
- внутр. $angle{B}+$ внеш. $angle{B}=180^circ$
- $angle{A}+$ внутр. $angle{B}+angle{C}=180^circ$
То:
- внеш. $angle{B}=180^circ-$ внутр. $angle{B}$
- внутр. $angle{B}=180^circ-angle{A}-angle{C}$
- внеш. $angle{B}=180^circ-180^circ+angle{A}+angle{C}$
Методом подстановки переменных из одного уравнения в другое мы обнаружили, что внешний угол равняется сумме двух других углов, с ним не смежных. Так, величина внешнего $angle{B}$ равна сумме $angle{A}+angle{C}$ внутренних.
Теорема о внешнем угле треугольника. Внешний угол треугольника равен сумме двух внутренних углов, с ним не смежных.
Обратим ваше внимание вот еще на что.
Раз внешний угол по величине — это сумма двух внутренних углов, внешний угол всегда будет по величине больше любого внутреннего угла, не смежного с ним. Полезное следствие, особенно если вдруг придется, скажем, доказывать возможность или невозможность существования некоторого треугольника. Или еще для чего-нибудь.
Теорема о внешнем угле треугольника: доказательство Евклида
Официально теорему о внешнем угле треугольника впервые доказал Евклид — древнегреческий математик, считающийся «отцом геометрии». Примечательно, что его доказательство не имеет ничего общего с теоремой о сумме углов треугольника — математик воспользовался свойствами углов при параллельных и секущей. Оно в принципе и понятно: Евклид огромное количество времени посвятил изучению параллельных прямых.
В качестве практики и повторения материала по параллельным прямым и секущим мы приводим евклидовое доказательство. Оно очень даже достойно внимания. Итак, посмотрим, как внешний угол треугольника «общается» с параллельными прямыми.
Доказательство
Рассмотрим $bigtriangleup{ABC}$ с внешним углом при вершине $B$. Проведем через эту вершину луч, параллельный стороне $AC$. Отметим на полученном луче точку $B_1$. На продолжении стороны $AB$ отметим точку $B_2$.
Теперь рассмотрим параллельные отрезки $BB_1$ и $AC$ при секущей $AB$. Внутренний угол $angle{A}$ и угол $angle{B_{1}BB_2}$ равны как соответственные. Далее рассмотрим отрезки $BB_1$ и $AC$ при секущей $CB$. Углы $angle{B_{1}BC}$ и $angle{ACB}$ равны как накрест лежащие.
Видим, что внешний $angle{B}$ состоит из суммы внутренних углов $angle{A}$ и $angle{C}$. Что и требовалось доказать.
Свойства внешнего угла
Не сказать, что свойства внешнего угла многочисленные. В основном, когда затрагивается внешний угол, для решения задач или доказательства чего-либо хватает теоремы о внешнем угле треугольника. Ну, и смежности внутреннего и внешнего углов.
То есть базового определения.
Правда если к делу подключается биссектриса, свойства внешнего угла, помимо «классических», таки обнаруживаются. Разберем одно наиболее полезное.
Свойство биссектрис внешнего и внутреннего углов треугольника. Биссектрисы внутреннего и внешнего углов являются перпендикулярными друг к другу.
Доказательство
Проведем в треугольнике $bigtriangleup{ABC}$ биссектрисы при внешнем $angle{B}$ и при внутреннем $angle{B}$. Для удобства разметим все полученные углы следующим образом: $x$ и $y$ — значения внутренних углов при вершинах $A$ и $C$ соответственно; $z$ — половина внутреннего $angle{B}$; $f$ — половина внешнего $angle{B}$.
Нам требуется установить, чему равняется $z+f$. Если сумма будет равна $90^circ$ — свойство доказано. Воспользуемся теоремой о внешнем угле и теоремой о сумме углов треугольника.
$$2f=x+y\2z+x+y=180^circ$$
Так как нам нужно найти сумму $z+f$, сложим уравнения выше:
$$2f+2z+x+y=x+y+180^circ$$
Видим, что после сокращения $2(f+z)=180^circ$.
Следовательно сумма $f$ и $z$ равняется $90^circ$. Биссектрисы перпендикулярны друг к другу. Свойство доказано.
Задача для самостоятельного решения
Свойства внешнего угла треугольника — нет. Теорема о внешнем угле треугольника — однозначное да. Решите данную задачу, не используя свойство смежности внешнего и внутреннего углов.
Условие. В треугольнике $bigtriangleup{ABH}$ величина внешних углов $angle{1}$ и $angle{2}$ равняется $97^circ$ и $125^circ$ соответственно. Найдите, чему равняется внутренний $angle{A}$.
Показать решение
Спрятать решение
Дано:
$bigtriangleup{ABH}$
$angle{1}=97^circ$
$angle{2}=125^circ$
Найти:
внутр. $angle{A}$ — ?
Решение. Воспользуемся теоремой о внешнем угле треугольника. Так как рассматривать мы будем только два внешних угла — $angle{1}$ и $angle{2}$, договоримся, что $angle{A}$, $angle{B}$ и $angle{H}$ далее в решении относятся к обозначению только внутренних углов треугольника $bigtriangleup{ABH}$.
Имеем следующие равенства:
$$angle{1}=angle{A}+angle{B}\angle{2}=angle{A}+angle{H}$$
Сложим между собой данные равенства и подставим имеющиеся по условию значения внешних углов $angle{1}$ и $angle{2}$:
$$2angle{A}+angle{B}+angle{H}=angle{1}+angle{2}=222^circ$$
Сумма углов $angle{A}$, $angle{B}$ и $angle{H}$ составляет $180^circ$. Вычтем из полученного выше равенства равенство $angle{A}+angle{B}+angle{H}=180^circ$.
Получаем следующее:
$$2angle{A}+angle{B}+angle{H}=222^circ\angle{A}+angle{B}+angle{H}=180^circ\angle{A}=222^circ-180^circ$$
Откуда получаем, что значение внутреннего угла $angle{A}$ равняется $42^circ$.
Ответ: $42^circ$.
Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?
Определение.
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
На рисунке:
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
Сколько внешних углов у треугольника?
При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.
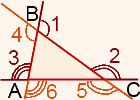Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):
∠1=∠4, ∠2=∠5, ∠3=∠6.
Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.
Чему равен внешний угол?
Теорема (о внешнем угле треугольника)
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Дано: ∆АВС, ∠1 — внешний угол при вершине С.
Доказать: ∠1=∠А+∠В.
Доказательство:
Так как сумма углов треугольника равна 180º, ∠А+∠В+∠С=180º.
Следовательно, ∠С=180º-(∠А+∠В).
∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.
Что и требовалось доказать.
