2.2 Работа внешних сил. Потенциальная энергия
Определим работу силы F, статически приложенной к некоторой упругой системе (рис.20, а), материал которой следует закону Гука.

Рис. 20
При малых деформациях к этой системе применим принцип независимости действия сил, следовательно, перемещения отдельных точек и сечений конструкции прямо пропорциональны вызывающей их нагрузке:
 , (2.2)
, (2.2)
где  – перемещение по направлению силы F;
– перемещение по направлению силы F;  – некоторый коэффициент, зависящий от материала, схемы и размеров сооружения. Увеличение силы F на бесконечно малую величину dF вызовет увеличение перемещения на
– некоторый коэффициент, зависящий от материала, схемы и размеров сооружения. Увеличение силы F на бесконечно малую величину dF вызовет увеличение перемещения на  .
.
Составим выражение элементарной работы внешней силы на перемещении  , отбрасывая при этом бесконечно малые величины второго порядка малости:
, отбрасывая при этом бесконечно малые величины второго порядка малости:  .
.
Заменим  , используя (2.2):
, используя (2.2):
Рекомендуемые материалы
 .
.
Интегрируя это выражение в пределах полного изменения силы от нуля до ее конечного значения, получим формулу для определения работы, совершаемой статически приложенной внешней силой F:

или, с учетом(2.2):
 , (2.3)
, (2.3)
то есть работа внешней силы при статическом действии ее на любое упругое сооружение равна половине произведения значения этой силы на величину соответствующего ей перемещения.
Для обобщения полученного вывода под силой понимают любое воздействие, приложенное к упругой системе, то есть не только сосредоточенную силу, но и момент или равномерно распределенную нагрузку; под перемещением понимают тот его вид, на котором данная сила производит работу: сосредоточенной силе соответствует линейное перемещение, сосредоточенному моменту – угловое, равномерно распределенной нагрузке – площадь эпюры перемещений на участке действия нагрузки.
При статическим действии на конструкцию группы внешних сил работа этих сил равна половине суммы произведений каждой силы на величину соответствующего ей перемещения, вызванного действием всей группы сил. Например, при действии на балку (рис.20,б) сосредоточенных сил F1, F2 и сосредоточенных моментов М1 и М2 работа внешних сил:
 (2.4)
(2.4)
Работу внешних сил на вызванных ими перемещения можно выразить и иначе – через внутренние силовые факторы (изгибающие моменты, продольные и поперечные силы), возникающие в поперечных сечениях системы.
Выделим из прямолинейного стержня двумя сечениями, перпендикулярными его оси (рис.21, а), бесконечно малый элемент dz.
Стержень состоит из бесконечно большого числа таких элементов. К каждому элементу dz в общем случае плоской задачи приложены продольная сила Nz, изгибающий момент Мх и поперечная сила Qy.
Для выделенного элемента dz усилия N, M, Q являются внешними силами, поэтому работу  можно получить как сумму работ, совершенных статически возрастающими усилиями N, M, Q на соответствующих деформациях элементов dz.
можно получить как сумму работ, совершенных статически возрастающими усилиями N, M, Q на соответствующих деформациях элементов dz.
Рассмотрим элемент dz, находящийся только под действием продольных сил N (рис.21,б). Если его левое сечение считать неподвижным, то правое сечение под влиянием продольной силы переместится вправо на величину  . На этом перемещении сила N совершит работу:
. На этом перемещении сила N совершит работу:
 (2.5)
(2.5)

Рис. 21
Если неподвижно закрепить левое сечение элемента dz, находящегося под действием только изгибающих моментов М (рис.22,а), то взаимный угол поворота торцевых сечений элемента будет равен углу поворота  его правого сечения:
его правого сечения:
 .
.
На этом перемещении момент М совершит работу:
 (2.6)
(2.6)

Рис. 22
Закрепим левое сечение элемента dz, находящегося под действием только поперечных сил Q (рис.22,б,в), а к правому приложим касательные усилия  , равнодействующей которых является поперечная сила Q. Предположим, что касательные напряжения
, равнодействующей которых является поперечная сила Q. Предположим, что касательные напряжения  равномерно распределены по всей площади А поперечного сечения, то есть
равномерно распределены по всей площади А поперечного сечения, то есть  , тогда перемещение
, тогда перемещение  определяется в виде:
определяется в виде:
 ,
,
а работа силы Q на этом перемещении будет:
 (2.7)
(2.7)
В действительности касательные напряжения  распределены по площади поперечного сечения неравномерно, что учитывается введением в (2.7) поправочного коэффициента
распределены по площади поперечного сечения неравномерно, что учитывается введением в (2.7) поправочного коэффициента  .
.
Обратите внимание на лекцию “15 лекция”.
Суммируя (2.5) – (2.7), получим полное значение работы:
 (2.8)
(2.8)
Интегрируя выражение  в пределах длины L каждого участка всех стержней и суммируя результаты, получим:
в пределах длины L каждого участка всех стержней и суммируя результаты, получим:
 (2.9)
(2.9)
Из формулы (2.9) следует, что работа внешних сил на вызванных ими перемещениях всегда положительна.
На основании закона сохранения энергии работа  внешних сил переходит в потенциальную энергию деформации, то есть
внешних сил переходит в потенциальную энергию деформации, то есть  .
.
Загрузить PDF
Загрузить PDF
Сила — это толчок или усилие, приложенное к объекту, которое заставляет его сдвинуться с места или ускориться. Второй закон Ньютона описывает связь силы с массой и ускорением, позволяя вычислить силу. Как правило, чем больше масса объекта, тем бóльшая сила требуется для того, чтобы сдвинуть его с места.[1]
-

1
Умножьте массу на ускорение. Сила F, необходимая для того, чтобы придать объекту массой m ускорение a, определяется по следующей формуле: F = m x a. То есть сила равна массе, умноженной на ускорение.[2]
-

2
Переведите единицы измерения в систему СИ. В Международной системе единиц (СИ) основной единицей измерения массы служит килограмм, а ускорения — м/с2 (метр на секунду в квадрате). Выразив массу и ускорение в единицах СИ, мы получим значение силы в ньютонах (Н).[3]
- Например, если масса объекта составляет 3 фунта, необходимо перевести ее в килограммы. 3 фунта равны 1,36 кг, то есть масса объекта равна 1,36 кг.
-

3
Помните о том, что в физике вес и масса — это разные понятия. Если вес объекта дан в ньютонах, для нахождения массы его следует разделить на 9,8. Например, 10 Н эквивалентны 10/9,8 = 1,02 кг.[4]
Реклама
-

1
Найдите силу, необходимую для того, чтобы разогнать автомобиль массой 1000 кг до 5 м/с2.[5]
- Сначала проверим, все ли величины приведены в единицах измерения системы СИ.
- Умножив массу (1000 кг) на ускорение (5 м/с2), получим силу (5000 Н).
-

2
Вычислите силу, необходимую для того, чтобы разогнать тележку массой 8 фунтов до ускорения 7 м/с2.
- Сначала выразим все величины в единицах измерения СИ. Один фунт равен 0,453 кг, поэтому, умножив 8 фунтов на этот коэффициент, находим, что масса тележки составляет 3,62 кг.
- Умножив массу (3,62 кг) на заданное ускорение (7 м/с2), находим необходимую силу (25,34 Н).
-

3
Найдите силу, действующую на тележку весом 100 Н, которая движется с ускорением 2,5 м/с2.
- Как мы помним, вес в ньютонах следует перевести в массу в килограммах, поделив на 9,8. Разделив 100 Н на 9,8, получаем массу 10,2 кг.
- Умножив найденную массу тележки (10,2 кг) на заданное ускорение (2,5 м/с2), получаем силу (25,5 Н).
Реклама
Советы
- Всегда внимательно читайте условие задачи, чтобы определить, что дано: масса или вес.
- Проверьте единицы измерения и при необходимости выразите массу в килограммах, а ускорение — в м/с2.
- Согласно определению основной единицы измерения силы в системе СИ, Н = кг * м/с2.[6]
Реклама
Об этой статье
Эту страницу просматривали 64 601 раз.
Была ли эта статья полезной?
Содержание:
Сила:
При изучения природных явлений используют разные физические величины. Для того чтобы описать качественно и количественно взаимодействие тел, вводят физическую величину, которую называют силой.
Определение силы
Сила – это физическая величина, которая служит мерой взаимодействия тел и является причиной изменения скоростей тел или их частей.
Наблюдение. Если мы рассматриваем, например, взаимодействие руки с волейбольным мячом, то мы говорим: «Мяч действует с силой на руку или рука действует с силой на мяч».
Опыт. Подвесим на пружину яблоко (рис. 66).

Пружина удлинится. Если на неё подвесить два яблока, то она удлинится больше. Итак, два яблока действуют на пружину с большей силой, чем одно.
Результат действия одного тела на другое зависит от значения приложенной силы.
Чем плотнее закрыта дверь, тем с большей силой мы должны её толкать или тянуть на себя, чтобы отворить.
Для того чтобы легче открывать дверь, её ручку прикрепляют как можно дальше от петель. Попробуйте открыть дверь, толкая её в точке, размещённой вблизи петель. Вы убедитесь, что это сделать намного труднее, чем с помощью ручки. Результат действия одного тела на другое зависит от точки приложения силы.
Для достижения определённого результата действия, например, растяжения или сжатия пружины, закрытия или открытия двери, нужно прикладывать силы в разных направлениях.
Действие одного тела на другое зависит от направления действия силы.
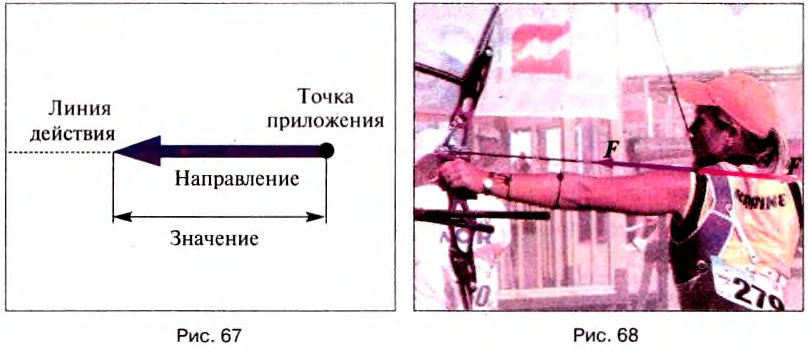
Графически силу изображают в виде отрезка прямой со стрелкой на конце (рис. 67).
Начало отрезка совмещают с точкой приложения силы. Длина отрезка в определённом масштабе равна значению силы. Стрелка показывает направление силы. Величины, характеризующиеся кроме числового значения еще и направлением в пространстве, называют векторными, или векторами (от латинского слова вектор — ведущий, несущий).
Почему тела изменяют свое состояние в пространстве
Любые изменения в природе происходят в результате взаимодействия между телами. Чтобы изменить положение вагона на рельсах, железнодорожники направляют к нему локомотив, который смещает вагон с места и приводит его в состояние движения (рис. 32). 
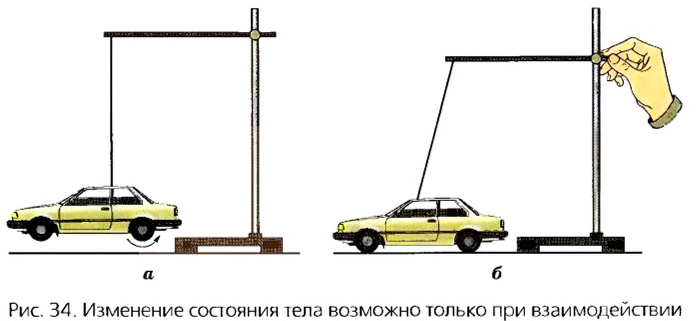
Парусник может длительное время стоять возле берега до тех пор, пока не подует попутный ветер и подействует на его паруса (рис. 33). Колеса игрушечного автомобиля могут вращаться с любой скоростью, но игрушка не изменит своего положения, если под игрушку не положить дощечку или линейку (рис.34). Форму или размер пружины можно изменить, лишь подвесив к ней груз или потянув рукой за один из его концов.
Все тела в природе так или иначе связаны между собой и действуют друг на друга или непосредственно, или через физические поля. Такое действие всегда является взаимным. Если тепловоз действует на вагон и изменяет его скорость, то скорость тепловоза при этом также изменяется благодаря обратному действию вагона. Солнце действует на все тела на Земле и на саму Землю, удерживая ее на орбите. Но и Земля притягивает Солнце и, в свою очередь, изменяет его траекторию. Таким образом, во всех случаях можно говорить только о взаимном действии тел – взаимодействии.
При взаимодействии могут изменяться скорости тел или их частей.
Однако, взаимодействуя с различными телами, данное тело будет изменять свою скорость по-разному. Так, парусник может приобрести скорость вследствие действия на него ветра. Но такой же результат можно получить, включив двигатель, который находится на паруснике. Парусник может сдвинуть с места и катер, действуя на него через трос. Чтобы каждый раз не называть все взаимодействующие тела, все эти действия объединяют одним понятием силы.
Что такое сила
Сила как физическое понятие может быть большей или меньшей, как и вызванные ею изменения в состоянии тела или его частей.
Сила – это физическое понятие, которое обобщает все взаимодействия, вследствие чего тело или его части изменяют свое состояние.
Действие тепловоза на вагон будет значительно интенсивнее, чем действие нескольких грузчиков. Под действием тепловоза вагон быстрее сдвинется с места и начнет двигаться с большей скоростью, чем тогда, когда вагон будут толкать грузчики, которые еле сдвинут его на небольшое расстояние или совсем его не сдвинут.
Сила как физическая величина количественно характеризует действие одного тела на другое.
Для того чтобы можно было производить математические расчеты, силу обозначают определенной буквой. Как правило, это латинская буква F.
Как и все другие физические величины, сила имеет единицы измерения. Современная наука пользуется единицей, которая называется ньютоном (Н). Единица получила такое название в честь английского ученого Исаака Ньютона, который внес значительную лепту в развитие физической и математической наук.
 Исаак Ньютон (1643-1727) – выдающийся английский ученый, основоположник классической физики. Научные труды касаются механики, оптики, астрономии и математики. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, дисперсию света, развил корпускулярную теорию света, разработал дифференциальное и интегральное исчисление.
Исаак Ньютон (1643-1727) – выдающийся английский ученый, основоположник классической физики. Научные труды касаются механики, оптики, астрономии и математики. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, дисперсию света, развил корпускулярную теорию света, разработал дифференциальное и интегральное исчисление.
Силы могут иметь различные значения. Так, на стакан с водой действует сила со стороны Земли, которая равна примерно 2 Н. А трактор, когда тянет плуг, действует на него с силой в несколько тысяч ньютонов.
Чем измеряют силу
Для измерения силы используют специальные приборы, называющиеся динамометрами (dina – сила; metro – меряю). Как правило, каждый такой прибор имеет измерительный элемент в виде пружины определенной формы (рис. 35).

Сила характеризуется направлением.
Указать числовое значение силы не всегда достаточно для определения результата ее действия. Важно знать точку ее приложения и направление действия.
Если высокий брусок, стоящий на столе, толкать в нижней части, то он будет скользить по поверхности стола. Если же к бруску приложить силу в верхней его части, то он просто перевернется (рис. 36).

Понятно, что направление падения бруска зависит от того, в каком направлении будем его толкать. Следовательно, сила имеет направление. От направления силы зависит изменение скорости тела, на которое эта сила действует.
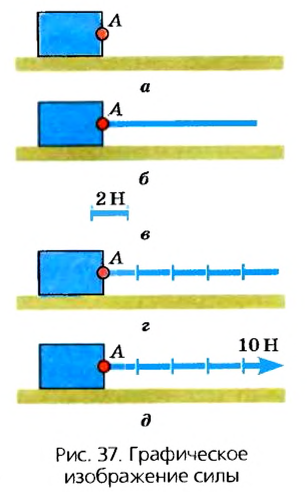
Учитывая, что сила имеет направление и числовое значение, ее изображают в виде стрелки определенной длины и направления (вектора). Такая стрелка начинается в точке на теле, которая называется точкой приложения силы. На рисунке 37 изображена сила, значение которой равно 10 Н, направлена она слева направо и приложена в точке А.
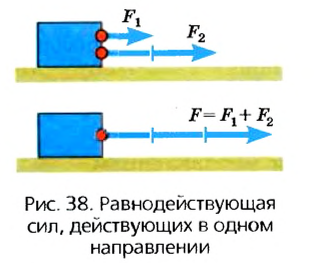
Пользуясь графическим методом, можно производить различные математические операции с силами. Так, если к одной точке на теле приложены силы 2 Н и 3 Н, которые действуют в одном направлении, то их можно заменить одной силой, которая будет приложена в той же точке и действовать в том же направлении, а ее значение будет равно сумме значений каждой из сил (рис. 38). Вектор этой силы будет иметь длину, равную сумме длин двух векторов.
Возможен и другой случай, когда силы, приложенные в одной точке тела, действуют в противоположных направлениях. Тогда их можно заменить одной силой, направленной в направлении большей силы, а ее значение будет равняться разности значений каждой силы (рис. 39). Длина вектора этой силы будет равна разности длин векторов приложенных сил.
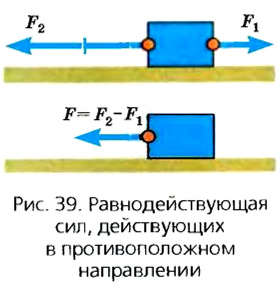
Сила, которой можно заменить действие нескольких сил, приложенных в определенной точке тела, называется равнодействующей.
Равнодействующая – это сила, действие которой равнозначно действию нескольких сил, приложенных к телу в определенной его точке.
Силу обозначают большой латинской буквой 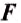 .
.
На рис. 68 спортсменка приготовилась стрелять из лука. В этом случае её рука действует на тетиву с силой направленной вправо, а тетива действует на руку с такой же по значению силой, направленной влево. Итак, значения сил одинаковы, но их направления противоположны.
- Заказать решение задач по физике
Сложение сил
Главная задача динамики – по действующей силе определить движение тела или по характеру движения тела установить, какая сила на него действует. Понятие о силе является основным в механике. И. Ньютон утверждал то, что мы называем силой, есть действие одного тела на другое, или их взаимодействие.
Действие одних тел на другие сообщает ускорение их движению. Полученное телом ускорение является внешним проявлением того, что оно взаимодействовало с другим телом. Когда мы говорим «сила», то подразумеваем, что на данное тело действуют другие тела.
Сила, являющаяся причиной изменения состояния движения тел или их деформации, характеризует взаимодействие тел, которое происходит при их непосредственном контакте (например столкновении) или через поля (рис. 2.2).
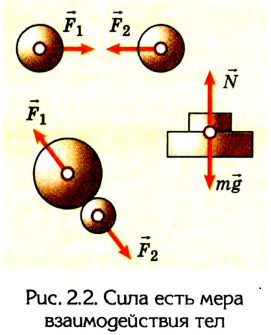
Сила – векторная величина, характеризующая действие, которое является причиной изменения состояния движения или покоя.
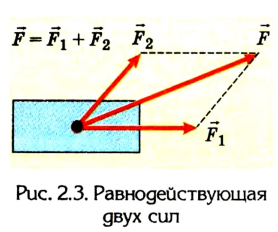
Действие на тело нескольких сил может быть заменено их равнодействующей (рис. 2.3), которую определяют геометрическим сложением этих сил как векторов:
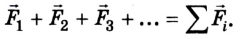
Не скорость тела, а ее изменение есть следствием действия силы (действия других тел).
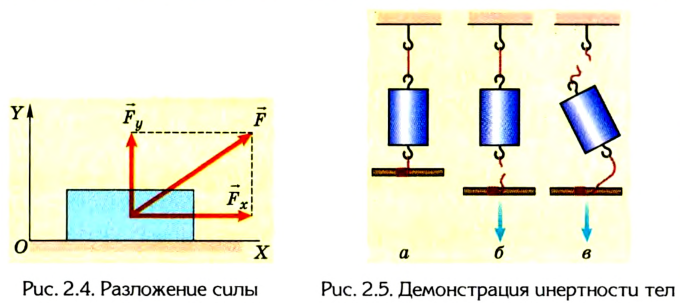
Помимо значения и направления сила характеризуется еще и точкой приложения, которую можно перемещать вдоль линии действия силы, если тело абсолютно твердое (не деформируется). Поскольку действия сил независимы, то сила может быть разложена на составляющие 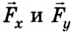 (рис. 2.4) как проекции на оси координат.
(рис. 2.4) как проекции на оси координат.
Для того чтобы выявить инертность тел и увидеть, как на нее влияет время их взаимодействия, проведем такой опыт. На тонкой нитке подвесим груз (рис. 2.5, а). Снизу к грузу прикрепим точно такую же нитку. Если резко дернуть за нижнюю нитку, то она оборвется, а груз останется висеть на верхней нитке (рис. 2.5, б). Если нижнюю нитку натягивать медленно, то оборвется верхняя нитка (рис. 2.5, в).
Когда мы резко дергаем за нижнюю нитку, взаимодействие руки и нитки кратковременно, груз не успевает изменить свою скорость – верхняя нитка не обрывается, т. к. груз имеет значительную инертность.
Если же за нижнюю нитку тянуть медленно (рука действует на груз продолжительное время), то груз набирает такую скорость, что его перемещение достаточно для разрыва и без того натянутой верхней нитки.
Как вы уже знаете, инертность тел определяется их массой, т. е. масса тела характеризует его инертность.
Во время тщательных исследований взаимодействия двух тел, например столкновения двух абсолютно упругих шаров, установлено, что отношение модулей ускорений взаимодействующих тел равно обратному отношению их масс: 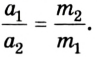
Следствием этого соотношения является один из методов измерения массы тел. Сначала выбирают тело, массу которого условно берут за единицу, – эталон массы. Между эталоном массы и телом, массу которого нужно измерить, можно поместить сжатую при помощи нитки пружину. Потом нитку поджечь и определить ускорение эталона 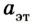 и исследуемого тела
и исследуемого тела 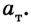 Из соотношения
Из соотношения 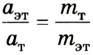 находим массу исследуемого тела:
находим массу исследуемого тела: 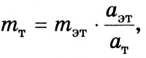
где 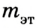 и
и 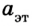 – масса и ускорение эталона (1 единица массы). Отсюда
– масса и ускорение эталона (1 единица массы). Отсюда 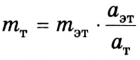 единиц массы.
единиц массы.
По международному соглашению за единицу массы принята масса эталона килограмма (рис. 2.6).

Килограмм (кг) – основная единица массы в Международной системе единиц (СИ). Килограмм равен массе международного прототипа килограмма – гире из платино-иридиевого сплава (90 % Pt, 10 % lr) в виде цилиндра диаметром и высотой 39 мм, хранящейся в Международном бюро мер и весов (г. Севр, предместье Парижа).
С достаточной точностью можно сказать, что массу 1 кг имеет 1  чистой воды
чистой воды 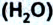 при 15 °C.
при 15 °C.
Для измерения массы тела часто используют способ сравнения масс тел с помощью весов. При этом учитывают способность тел взаимодействовать с Землей. Как подтверждают опыты, тела, имеющие одинаковую массу, одинаково притягиваются к Земле в данном месте.
Равнодействующая сила
При изучении физики в 7-м классе вы познакомились с понятием «сила», которое используется для описания взаимодействия тел.
Чтобы вспомнить основные характеристики силы, проведем опыт, например, с куском поролона, покоящимся на неподвижном столе, так как притяжение Земли уравновешено воздействием стола.
Используя пинцет, можно действовать на поролон в различных точках и видеть его поступательное, вращательное или более сложное движение в зависимости от направления, места и величины воздействия.
При этом легко наблюдать не только изменение скорости поролона, но и его деформацию (изменение формы и размеров) (рис. 34) в местах контакта поролона с пинцетом.

Рис. 34
Изменение скорости и деформация тел проявляются в любых опытах при самых разнообразных взаимодействиях, и поэтому принято следующее определение силы:
- сила — физическая векторная величина, являющаяся количественной мерой действия одного тела на другое, в результате которого изменяется скорость тела и происходит его деформация.
Опыт показывает, что результат воздействия силы определяется не только ее направлением и модулем, но и точкой приложения.
Единицей измерения силы в СИ является 1 ньютон (сокращенно 1 Н).
Вспомним исторически сложившиеся названия сил и их обозначения.
Силой тяжести 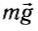 называется сила, с которой тело притягивается к Земле. Силой давления
называется сила, с которой тело притягивается к Земле. Силой давления 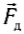 называется сила, с которой тело действует на опору или жидкость и газ действуют на стенки сосуда. Силой упругости
называется сила, с которой тело действует на опору или жидкость и газ действуют на стенки сосуда. Силой упругости 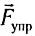 называется сила, возникающая при деформации тела. Силой реакции
называется сила, возникающая при деформации тела. Силой реакции 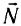 называется сила, действующая на тело со стороны опоры или подвеса. Силой сопротивления
называется сила, действующая на тело со стороны опоры или подвеса. Силой сопротивления 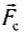 и силой трения
и силой трения 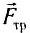 называются силы, препятствующие механическому движению тела.
называются силы, препятствующие механическому движению тела.
Силы могут действовать на поверхность тела (например, сила давления воздуха) (рис. 35) или быть приложены в некоторой условной точке (например, сила упругости нити в точке ее крепления к телу) (рис. 36).
Для упрощения математического описания механического движения тело рассматривается как материальная точка, если не указаны его размеры и форма. На рисунке тело чаще всего изображают прямоугольником.
Можно изображать силы, действующие на тело, приложенными в центре прямоугольника. Но обычно в центре прямоугольника изображают приложенной силу тяжести, а силу трения и силу реакции опоры рисуют приложенными в точке на нижней грани тела под его центром (рис. 37). Если на тело действуют другие тела, то необходимо учесть одновременно действие нескольких сил.
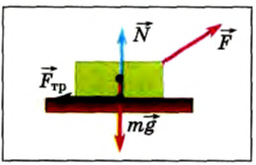
Рис. 37
При изучении физики в 7-м классе вы познакомились со сложением сил и научились складывать силы, действующие на тело вдоль одной прямой.
В этом случае действие, например, двух сил можно заменить одной силой. Модуль равнодействующей силы равен сумме или разности модулей двух слагаемых сил в зависимости от того, совпадают их направления (рис. 38, а, б) или противоположны (рис. 39. а, б). Направление равнодействующей двух сил совпадает с направлением большей силы.
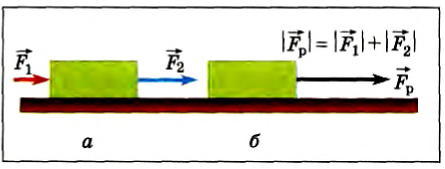
Рис. 38
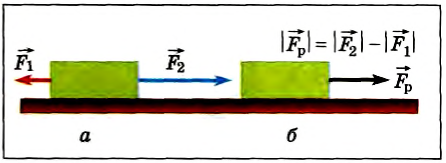
Рис. 39
А как складываются силы, если они направлены под некоторым углом друг к другу? Покажем на опыте, что они складываются также векторно. Подвесим груз массой 0,2 кг на динамометре, закрепленном на неподвижном штативе. Если груз покоится, то сила упругости пружины динамометра уравновешивает силу тяжести груза (рис. 40), а показания прибора равны: Fупр = mg = 2H (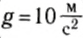 )
)
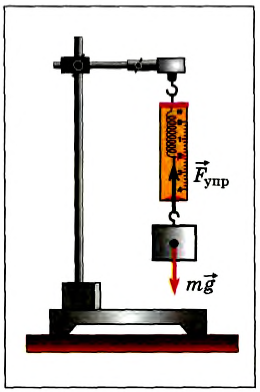
Рис. 40
Теперь подвесим этот же груз с помощью двух одинаковых динамометров (рис. 41, а), закрепленных на одной высоте. Меняя положения динамометров, а следовательно, угол между силами 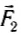 и
и 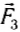 , действующими на груз со стороны динамометров, можно убедиться, что их показания зависят от этого угла и лишь при угле, равном нулю, в сумме равны 2 Н.
, действующими на груз со стороны динамометров, можно убедиться, что их показания зависят от этого угла и лишь при угле, равном нулю, в сумме равны 2 Н.
Следовательно, совместное действие сил 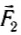 и
и 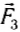 уравновешивает действие силы тяжести груза, но сумма модулей этих сил не равна 2 Н, т. е. силы нельзя складывать как скалярные величины.
уравновешивает действие силы тяжести груза, но сумма модулей этих сил не равна 2 Н, т. е. силы нельзя складывать как скалярные величины.
Когда угол между силами 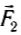 и
и 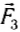 равен 120° (рис. 41,6), то сумма показаний динамометров — 4 Н, а сила тяжести груза все та же — 2 H. Но если найти в этом случае векторную сумму
равен 120° (рис. 41,6), то сумма показаний динамометров — 4 Н, а сила тяжести груза все та же — 2 H. Но если найти в этом случае векторную сумму 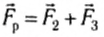 по правилу сложения векторов, то она по модулю равна Fp= 2 Н.
по правилу сложения векторов, то она по модулю равна Fp= 2 Н.
Следовательно, силы нужно складывать по правилам сложения векторов.
Модуль векторной суммы сил 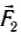 и
и 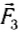 равен 2 H при любом значении угла между направлениями этих сил, а также и во всех случаях, когда модули сил не равны друг другу (рис. 41, в).
равен 2 H при любом значении угла между направлениями этих сил, а также и во всех случаях, когда модули сил не равны друг другу (рис. 41, в).
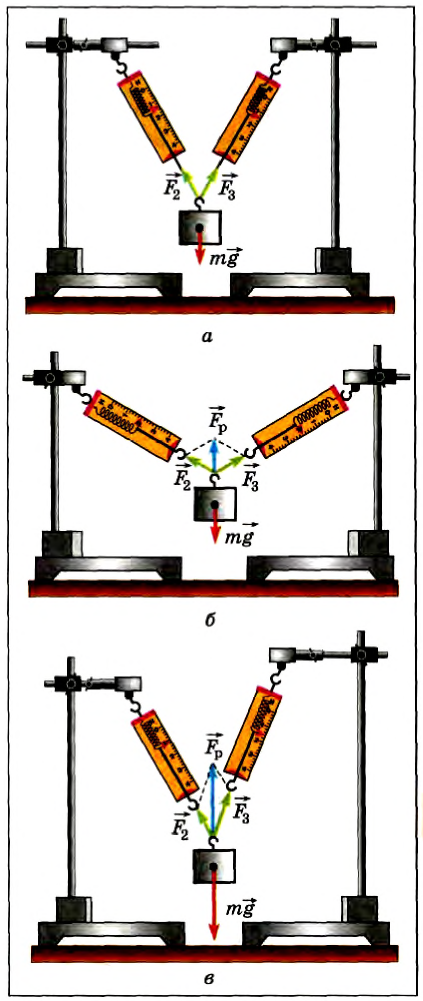
Рис. 41
Какие бы более сложные опыты не проводились (и при действии на тело нескольких сил), всегда результаты измерений показывают, что действие нескольких сил можно заменить их векторной суммой, т. е. силы складываются, как векторы, — геометрически.
Векторная сумма сил, действующих на тело, называется равнодействующей и определяется по формуле:
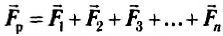
Если размерами тела нельзя пренебречь и силы приложены в разных его точках, то векторы сил можно перенести в одну точку, сохраняя модуль и направление, и векторно сложить (рис. 42).
Необходимо понимать, что равнодействующая сила заменяет действие нескольких сил только по отношению к движению тела в целом, но не заменяет действие каждой слагаемой силы в других отношениях.
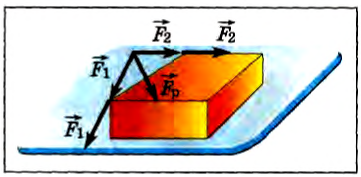
Рис. 42
Например, растянутая двумя руками пружина покоится (рис. 43), а значит, равнодействующая сил 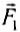 и
и 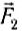 равна нулю, но каждая из этих сил деформирует соответственно подвес динамометра и пружину.
равна нулю, но каждая из этих сил деформирует соответственно подвес динамометра и пружину.
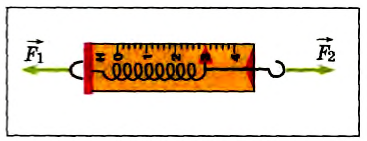
Рис. 43
Если тело движется с постоянной скоростью, то согласно первому закону Ньютона все воздействия на тело скомпенсированы, т. е. равнодействующая всех сил также должна быть равна нулю.
Главные выводы:
- Сила — физическая векторная величина, являющаяся количественной мерой действия одного тела на другое, в результате которого изменяется скорость тела и происходит его деформация.
- Сила характеризуется модулем, направлением, а также точкой приложения.
- Заменить действие нескольких сил можно равнодействующей силой, которая определяется как векторная сумма этих сил.
- При движении тела с постоянной скоростью (или в состоянии покоя) равнодействующая всех сил, действующих на него, равна нулю.
Что означает понятие “Сила” в физике
Вам хорошо известно слово «сила». Обычно смысл слова «сила» и образованных от него слов «силач», «сильный» и т. д. связан с возможностями человека, животного, механизма, с интенсивностью проявления природных явлений. Мы говорим «самый сильный человек», «сила воли», «сильные чувства», «сильный мороз», «сильный двигатель». А какое содержание вкладывают в слово «сила» физики?
Мы уже говорили о том, что причина изменения скорости движения тела — его взаимодействие с другими телами.
Чтобы теннисный мяч вернулся на сторону соперника, вы бьете по мячу ракеткой, но и мяч «бьет» по ракетке. Чтобы остановить велосипед, вы нажимаете на ручки тормоза и в то же время ощущаете, как они давят на ваши ладони. Обратите внимание: в любом случае результат зависит от того, насколько «сильным» будет взаимодействие: сильнее ударите по мячу — мяч наберет большую скорость (рис. 18.1); сильнее нажмете на тормоз — быстрее остановится велосипед. Мерой действия одного тела на другое служит физическая величина сила.
Сила — это физическая величина, которая является мерой действия одного тела на другое (мерой взаимодействия тел).
Силу обычно обозначают символом F. Единица силы в СИ — ньютон (названа в честь Исаака Ньютона): [F]=Н. 1 Н — это сила, которая, действуя на тело массой 1 кг в течение 1 с, изменяет скорость его движения на 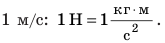 Чем больше сила и чем дольше она действует на тело, тем заметнее изменяется скорость движения тела (см. рис. 18.1). Чтобы тела разной массы за одинаковое время изменяли скорости своего движения одинаково, на них должны действовать разные силы (рис. 18.2).
Чем больше сила и чем дольше она действует на тело, тем заметнее изменяется скорость движения тела (см. рис. 18.1). Чтобы тела разной массы за одинаковое время изменяли скорости своего движения одинаково, на них должны действовать разные силы (рис. 18.2).


Графическое изображение сил
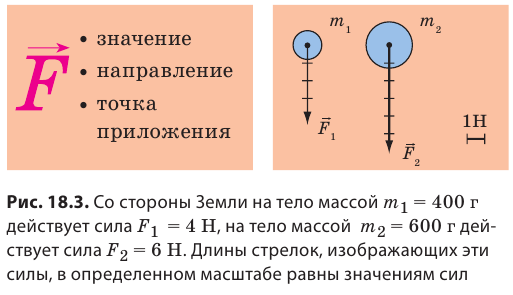
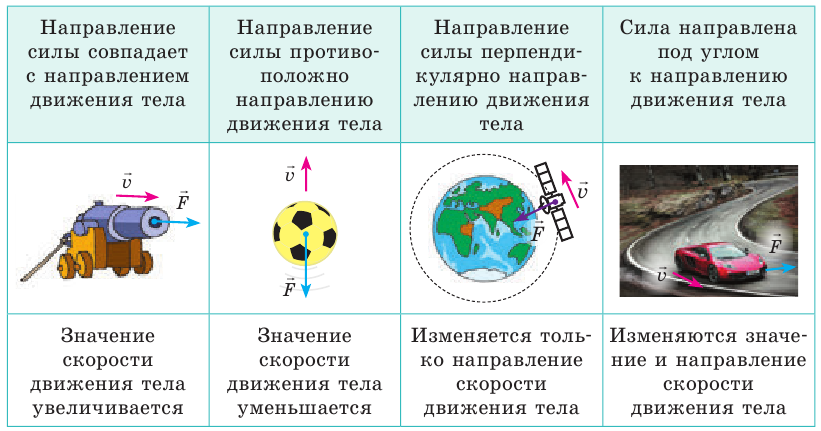
Сила, действуя на тело, может изменить скорость его движения как по значению, так и по направлению, поэтому сила определяется и значением, и направлением. Уже говорилось о том, что физические величины, имеющие значение и направление, называют векторными. Итак, сила — векторная величина. На рисунках вектор силы начинают в точке, к которой приложена сила (эту точку так и называют — точка приложения силы), и направляют в сторону действия силы. Длину стрелки иногда выбирают так, чтобы она в определенном масштабе соответствовала значению силы (рис. 18.3). Изменение скорости движения тела (по значению, по направлению) зависит от направления силы (см. таблицу на с. 123).
Сложение сил, действующие вдоль одной прямой
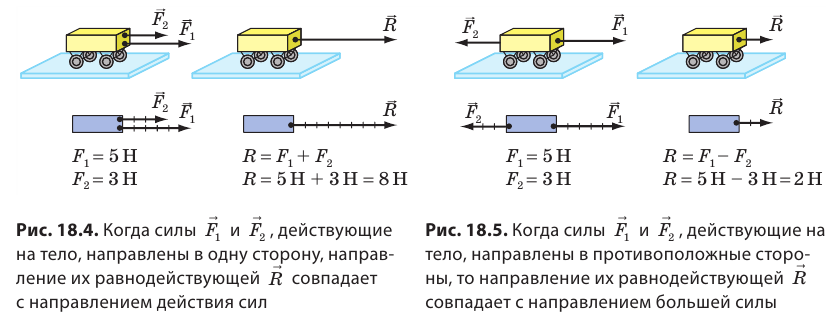
Обычно на тело действует не одна сила, а две, три или больше. Проведем опыт. Поставим на стол тележку и привяжем к ней две нити. Потянем за одну нить с силой 5 Н, а за другую — в том же направлении — с силой 3 Н (рис. 18.4). Тележка придет в движение, увеличивая свою скорость так, как если бы на нее действовала одна сила 8 Н. Силу 8 Н, которой в данном случае можно заменить две силы 5 и 3 Н, называют равнодействующей двух сил и обозначают символом R (или F). Силу, которая производит на тело такое же действие, как несколько одновременно действующих сил, называют равнодействующей этих сил. Если тележку одновременно тянуть за две нити в противоположные стороны (рис. 18.5), то силы не будут «помогать» друг другу разгонять тележку, а наоборот — будут «мешать». В этом случае тележка будет двигаться так, будто на нее действует одна сила 2 Н в направлении, в котором действует сила 5 Н, то есть равнодействующей сил 5 и 3 Н будет сила 2 Н.
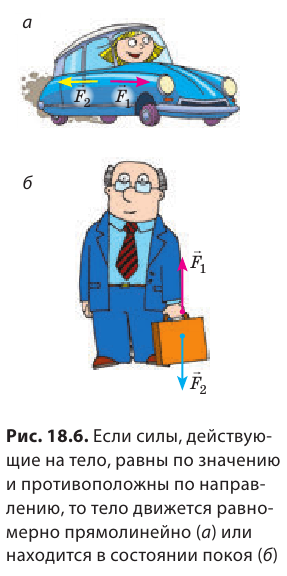
Как вы считаете, какой будет равнодействующая, если нити, привязанные к тележке с противоположных сторон, потянуть с силами, одинаковыми по значению, например 5 Н? Изменится ли в этом случае скорость движения тележки? 4 Выясняем, когда силы компенсируют друг друга Надеемся, вы правильно ответили на вопрос в п. 3 и самостоятельно пришли к выводу: если две силы равны по значению, противоположны по направлению и приложены к одному телу, то равнодействующая этих сил равна нулю. Силы уравновешивают (компенсируют) друг друга, поэтому причины для изменения скорости движения тела нет. Так, по горизонтальному прямолинейному отрезку шоссе автомобиль движется равномерно (рис. 18.6, а), если сила тяги его двигателя компенсирует силу сопротивления движению (сила сопротивления движению достаточно быстро остановит автомобиль, если двигатель не будет работать). Портфель в руке находится в состоянии покоя, если сила притяжения Земли, действующая на портфель, компенсируется силой, которую прикладывает к портфелю человек (рис. 18.6, б).
Итоги:
Сила F — физическая величина, являющаяся мерой действия одного тела на другое (мерой взаимодействия тел). Сила — причина изменения скорости движения тела. Единица силы в СИ — ньютон (Н). 1 Н равен силе, которая, действуя на тело массой 1 кг в течение 1 с, изменяет скорость его движения на 1 м/с.
Сила — векторная величина. Чтобы охарактеризовать силу, необходимо указать значение, направление и точку приложения силы. Если на тело действуют несколько сил, то их общее действие всегда можно заменить действием одной силы — равнодействующей. Равнодействующей сил, которые действуют на тело в одном направлении, является сила, значение которой равно сумме значений сил, а направление совпадает с направлением этих сил. Если две силы, действующие на тело, направлены в противоположные стороны, то направление равнодействующей совпадает с направлением большей силы, а для нахождения значения равнодействующей нужно из значения большей силы вычесть значение меньшей. Две силы компенсируют (уравновешивают) друг друга, если они равны по значению, противоположны по направлению и приложены к одному телу.
- Силы в механике
- Сила тяжести в физике
- Сила упругости в физике и закон Гука
- Деформация в физике
- Звук в физике и его характеристики
- Звуковые и ультразвуковые колебания
- Инерция в физике
- Масса тела в физике

Все внешние силы (нагрузки), действующие на изучаемое тело, следует рассматривать как проявление взаимодействия его с окружающими телами, которое представляется в виде сил или пар сил (моментов).
Все внешние силы (нагрузки) могут рассматриваться как сосредоточенные или распределённые.
В природе сосредоточенных сил не бывает. Все реальные тела практически контактируют через небольшие площадки. Однако принцип Сен-Венана позволяет распределенную нагрузку заменить равнодействующей силой, что упрощает расчёт.
Сосредоточенные нагрузки выражаются в ньютонах [H] и обозначается буквой F.
Распределённые нагрузки обозначаются буквой q и они бывают:
- поверхностными (например, давление ветра, воды на стенку). Размерность [FL-2].
- объёмными. Их размерность [FL-3].
- распределенными по длине (например, силу тяжести стержня, учитывая небольшие размеры его поперечного сечения, рассматривают как распределённую нагрузку по длине). Размерность [FL-1].
Сосредоточенные и распределённые нагрузки могут быть как статическими, так и динамическими.
Статическими называются нагрузки, которые изменяют свою величину или точку приложения с очень небольшой скоростью, так что возникающими при этом ускорениями можно пренебречь.
Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью. Возникшие при этом силы инерции могут многократно превосходить те же нагрузки, приложенные статически.
Законы изменения нагрузок во времени могут иметь весьма сложный характер.
В сопротивлении материалов основным изучаемым элементом конструкции является брус – тело, у которого один из линейных размеров (длина) значительно превышает два других, определяющих поперечное сечение. При работе конструкции ее элементы воспринимают внешние силы и действие их передают друг другу.
Классификация внешних нагрузок
Внешние силы делятся на активные и реактивные (реакции связей). Активные связи принято называть нагрузками.
По способу приложения нагрузки бывают объемные и поверхностные, распределенные и сосредоточенные, по характеру изменения в процессе приложения – статические, динамические и повторно-переменные, по продолжительности действия – постоянные и временные.
Примеры решения задач >
Внутренние силовые факторы >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Содержание:
- Определение и формула силы
- Второй закон Ньютона
- Единицы измерения силы
- Примеры решения задач
Определение и формула силы
Определение
Силой называют векторную величину, которая характеризует взаимодействия тел. Ее модуль определяет «степень»
(интенсивность) воздействия. Направление силы совпадает с направлением ускорения, которое приобретает тело при взаимодействии с другими телами.
Силы способны изменять скорости тел и вызывать их деформации. Примером деформированного тела служит сжатая (растянутая) пружина.
Две силы считают равными по модулю и противоположными по направлению, если они приложены к одному телу, но ускорение такого тела равно нулю.
Второй закон Ньютона
Равнодействующая всех сил приложенных к телу (векторная сумма всех сил)
($bar{F}$) равна производной от импульса тела по времени:
$$bar{F}=sum_{i=1}^{n} bar{F}_{i}=frac{d bar{p}}{d t}(1)$$
где $bar{p}=m bar{v}$ – импульс тела, m–масса рассматриваемого тела,
$bar{v}$ – скорость. Надо отметить, что уравнение (1) строго применимо только относительно
материальной точки. Если рассматривается протяженное тело, то под скоростью понимают скорость движения центра масс тела.
Если масса материальной точки (m)не изменяется во времени, то формула, определяющая результирующую силу, приложенную к ней
(второй закон Ньютона) можно представить в виде:
$$bar{F}=m frac{d bar{v}}{d t}=m bar{a}(2)$$
где $bar{a}$ – ускорение, которое материальная точка приобретает в результате
воздействия на нее силы. Выражение (2) показывает то, что если
$bar{F}$=0, то тело (материальная точка) движется равномерно и прямолинейно или покоится.
Если сила, приложенная к телу, является постоянной (по модулю и направлению), то формулу для нее можно представить в виде:
$$F=frac{Delta p}{Delta t}=frac{mleft(v_{2}-v_{1}right)}{t_{2}-t_{1}}$$
Единицы измерения силы
Основной единицей измерения момента силы в системе СИ является: [F]=Н=(кг•м)/с2
В СГС: [F]=дин
1Н=105 дин
Примеры решения задач
Пример
Задание. Уравнения $x=alpha t^{3}, y=beta t$ ($alpha$ и
$beta$ – постоянные коэффициенты) задают движение материальной точки массы m=const.
Как изменяется по модулю сила, которая действует на точку?
Решение. В качестве основы для решения задачи используем второй закон Ньютона в виде:
$bar{F} = mbar{a} (1.1)$
Зная законы изменения координат точки в зависимости от времени определим уравнения изменения составляющих ускорения.
Для этого найдем производные по времени от соответствующих координат:
$$
begin{array}{c}
a_{x}=frac{d^{2} x}{d t^{2}}=6 alpha t(1.2) \
a_{y}=frac{d^{2} y}{d t^{2}}=0(1.3)
end{array}
$$
Так как модуль ускорения равен:
$$a=sqrt{a_{x}^{2}+a_{y}^{2}}(1.4)$$
то, учитывая выражения (1.2) и (1.3), получаем:
$a = 6 alpha t (1.5)$
Так как ay=0, то получаем, что сила, которая действует на нашу точку, направлена по оси X, так как направление ускорение
и силы совпадают, а мы получили:
$$bar{a}=6 alpha t cdot bar{i}(1.6)$$
где $bar{i}$ – единичный вектор, направленный по оси X.
Исходя из второго закона Ньютона, имеем:
$$F=m cdot 6 alpha t, bar{F}=m 6 alpha t cdot bar{i}$$
Ответ. Так как $F=m cdot 6 alpha t$, то с течением времени сила увеличивается по модулю.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два параллелепипеда лежат на горизонтальной поверхности. Они соприкасаются. Данные тела могут
скользить по поверхности опоры без трения. Масса одного тела равна m1, второго – m2. Первое тело толкнули с силой F0.
Какова сила давления тел друг на друга (F)?
Решение. Сделаем рисунок.
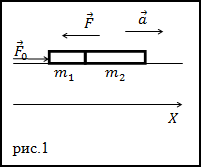
Рассмотрим, какие силы приложены к первому телув момент толчка, запишем для него второй закон Ньютона:
$$bar{F}_{0}+bar{F}+m_{1} bar{g}+bar{N}=m_{1} bar{a}(2.1)$$
где $m_{1} bar{g}$ – сила тяжести,
$bar{N}$ – реакция опоры,
$bar{a}$ – ускорение тела.
В проекции на ось Xуравнение (2.1) примет вид:
$$F_{0}-F=m_{1} a rightarrow F=F_{0}-m_{1} a(2.2)$$
Рассмотрим силы, приложенные к двум параллелепипедам как системе:
$$bar{F}_{0}+left(m_{1}+m_{2}right) bar{g}+overline{N^{prime}}=left(m_{1}+m_{2}right) bar{a}(2.3)$$
В проекции на ось X уравнение (2.3) примет вид:
$$F_{0}=left(m_{1}+m_{2}right) a(2.4)$$
Из уравнения (2.4) выразим ускорение:
$$a=frac{F_{0}}{m_{1}+m_{2}}$$
Подставим правую часть выражения (2.5) в (2.2) вместо ускорения:
$$F=F_{0}-m_{1} cdot frac{F_{0}}{m_{1}+m_{2}}$$
Ответ. $F=F_{0}-m_{1} cdot frac{F_{0}}{m_{1}+m_{2}}$
Читать дальше: Формула сопротивления.
