Как определить мощность источника тока
Содержание
- 1 Виды мощности
- 2 Активная и реактивная мощность
- 3 Как определяется мощность
- 4 Мощность источника питания
- 5 Видео по теме
Источники питания используются повсеместно. Их основная задача — преобразование параметров электроэнергии, поступающей из сети, в такие, которые необходимы для конкретного электротехнического устройства. Способность ИП выполнять данную задачу зависит от его мощности. Она является главной характеристикой любого блока питания. Чтобы оценить эффективность устройства, необходимо понимать, как найти мощность, если известны различные характеристики электрической цепи.

Виды мощности
При вычислении мощности возможны следующие ситуации:
- Мгновенная мощность вычисляется для очень малого промежутка времени. Это значение важно знать в тех случаях, когда в разные моменты времени эта величина меняется. Проведение замеров позволит мастеру получить целостное представление об используемой мощности. Для постоянного тока данная характеристика постоянна.
- Активное значение мощности применяется для определения постоянной величины, которая фактически является средним значением при наличии переменного тока. При этом мгновенные значения будут изменяться, а активная мощность будет в среднем характеризовать происходящие процессы. Активная мощность — это показатель выполнения полезной работы электрическим оборудованием.
- Реактивная мощность относится к работе индуктивных и емкостных элементов электрических приборов. Она циклически переходит из одной формы в другую. При этом происходит перемещение зарядов, то есть, осуществляется электрическая работа, которая обычно не является полезной.

Активная и реактивная мощность
При работе электрического оборудования следует рассматривать полную мощность. Она показывает работу, которая проводится в единицу времени (в СИ в этом качестве рассматривается 1 секунда). При этом нужно помнить, что полная мощность складывается из активной и реактивной мощности.
Это разделение связано с используемым сопротивлением. Если электрические заряды преодолевают активное сопротивление, мощность также является активной. Она, как правило, относится к выполнению полезной работы.
При наличии переменного тока в электрической цепи присутствует реактивное сопротивление. Оно связано с работой электромагнитного поля и фактически сводится к периодическим изменениям, при которых энергия регулярно перетекает из одной формы в другую, практически не расходуясь.
В бытовых приборах и промышленном оборудовании в большинстве случаев присутствуют оба вида мощности. Активная играет основную роль при использовании постоянного тока или в тех случаях, когда её доля в общей мощности относительно высока.
Обычно в технической документации указывается параметр cosφ. Он может принимать значения от 0 до 1 включительно. Его величина показывает долю активной мощности в полной. Она будет высокой, например, в электронагревательных приборах, где значительная часть энергии тратится на выполнение полезной работы по обогреву помещения.
Надо учитывать, что наличие реактивной мощности оказывает разрушительное действие на прибор. Это может быть, например, связано с разрушением изоляции проводов и кабелей, с повышением риска возникновения короткого замыкания или с порчей оболочек электроприводов или трансформаторов.
Для получения полной мощности применяется векторное сложение активной и реактивной мощности. Её величину вычисляют по теореме Пифагора как длину гипотенузы прямоугольного треугольника, в котором катетами являются активная и реактивная мощности.

Как определяется мощность
Эта величина определяется на основе работы, выполненной при перемещении заряда. Мощность равна частному от деления её величины на потраченное для этого время. Из курса физики известно, что работу можно выразить как произведение разности потенциалов на перемещаемый заряд. Для вычисления заряда можно применить следующую формулу:

На основе сказанного можно привести такое равенство:

Из формулы видно, что мощность можно выразить как произведение напряжения и силы тока. Её можно преобразовать с использованием закона Ома:

Подставив это выражение в формулу мощности, выводят эквивалентные формы, которые могут быть более удобными в некоторых ситуациях.

Например, при рассмотрении последовательного соединения удобной будет формула с использованием силы тока и напряжения. Это связано с тем, что сила электротока на рассматриваемом участке является одинаковой.
При параллельном соединении одинаковым на различных участках будет электронапряжение. В данном случае производить вычисления проще с использованием формулы, которая выражает мощность через разницу потенциалов и сопротивление.
В международной системе измерений для мощности используется ватт. Иногда применяют эквивалентную единицу вольт*ампер. Широко используются значения, которые выражаются в единицах, кратных ваттам. В качестве примера можно привести киловатт и мегаватт, которые соответствуют тысяче и миллиону ватт соответственно.
У большинства электроприборов, используемых в быту, мощность находится в определённых пределах, которые примерно соответствуют значениям, указанным в следующей таблице:

В прошлом в качестве единицы измерения мощности активно использовалась лошадиная сила. Для ее выражения через ватты нужно применять следующую формулу:

Хотя классической единицей измерения энергии или выполненной работы является джоуль, для электрических приборов чаще используется ватт*час.
При описании электрических устройств или деталей часто указывают предельную мощность. В технической документации также может быть указана номинальная мощность оборудования. Режим работы устройства в этом случае считается оптимальным. Если реальная мощность будет выше, то это означает, что прибор эксплуатируется очень интенсивно.
Сказанное можно пояснить на следующем примере. Допустим, речь идёт о резисторе на 500 Ом. Пусть в технической документации сказано, что предельно допустимая мощность при его использовании составляет 10 Вт. В этом случае предельно допустимое напряжение определяется по формуле:

Из этого выражения можно найти напряжение. Для него будет правильным следующее равенство:

Подставляя конкретные значения, получаем, что квадратный корень нужно извлечь из произведения 500 * 10 = 5000. Он будет примерно равен 70.7. Таким образом, предельно допустимым напряжением для этого резистора будет 70.7 В.
Иногда возникает необходимость практически измерить мощность. Это можно сделать с помощью ваттметра.

Для определения мощности также используют амперметр и вольтметр. Первый присоединяют последовательно, второй — параллельно. Получив значения силы тока и напряжения, на их основе производят вычисления для определения мощности.

Мощность источника питания
В предыдущем разделе было рассмотрено понятие мощности и относящиеся к ней характеристики в применении к различным электрическим узлам или приборам. При рассмотрении источника элетротока потребуется учитывать имеющиеся в этом случае особенности.
Используемый ИП должен соответствовать параметрам электрической цепи, которую он питает. При этом необходимо обратить внимание на следующее:
- Значение полной мощности электрической цепи.
- ЭДС источника.
- Внутренне сопротивление ИП.
- Потери энергии внутри источника питания.
- Значение полезной мощности.
Мощность источника тока должна превосходить мощность электроприбора не меньше, чем на 5-10%. Это позволит обеспечить электропитание даже в условиях интенсивного использования прибора. Энергия источника питания будет расходоваться на совершение полезной работы, а также на потери.
Для понимания особенностей работы источника питания важно знать разницу между электронапряжением на клеммах и электродвижущей силой. Практически в работающей цепи электроны перемещаются по замкнутому пути. Они переходят от отрицательной клеммы через электрическую цепь к положительной. Попадая внутрь батареи под воздействием электродвижущей силы, электроны будут вновь перемещаться на отрицательную клемму.

Нужно учитывать, что величина ЭДС не является независимой от нагрузки. Её точное значение можно узнать при измерении на холостом ходу. Чтобы вычислить мощность источника питания, можно воспользоваться формулой, которая выражает её через ЭДС и сопротивление. Для этого потребуется выполнить следующие действия:
- Нужно определить величину электродвижущей силы (E) источника питания. Для этого замеряют разность потенциалов на клеммах на холостом ходу.
- Далее требуется подключить нагрузку, которая имеет известное сопротивление (R).
- Затем в электрической цепи измеряют силу тока (I), а также напряжение (U).
- Теперь есть возможность узнать падение напряжения (U0) внутри источника тока. Оно представляет собой разность между электродвижущей силой и напряжением в цепи.
- Внутреннее сопротивление (R0) вычисляется по формуле R0 = U0 / I.
Подставив полученные значения в формулу, выраженную через напряжение и сопротивление, можно определить мощность источника тока.

Полную мощность ИП можно представить как Рполн = Рполезн + Рпотерь.
Для определения полезной мощности используется одна из трех формул:

Мощность потерь, возникающая во внутренней цепи, то есть, в источнике тока, расходуется лишь на процессы, происходящие в самом ИТ и не может использоваться для каких-либо других целей. Ее вычисляют по формуле:

Для определения полной мощности можно воспользоваться одной из трех формул:

Используя приведённый здесь алгоритм, можно определить полезную мощность, которая создаётся рассматриваемым источником тока. Чтобы составить представление о зависимости полезной мощности и той, которая расходуется на нагрев ИТ, можно воспользоваться графиком. Из него видно, что полезная мощность сначала возрастает, а затем начинает убывать. Максимума она достигает в точке, в которой сопротивление нагрузки равно внутреннему сопротивлению источника электротока, то есть, R = r.

КПД при таком условии будет равен 50%. В общем случае коэффициент полезного действия находят по формуле:

Максимальная полезная мощность равняется половине полной. Следовательно

Из сказанного видно, что при подборе наиболее подходящего источника питания для электрического устройства нужно стремиться к тому, чтобы внутреннее сопротивление источника питания было равно сопротивлению нагрузки. Если оно значительно меньше, то существенная часть мощности в процессе эксплуатации будет рассеиваться в виде тепла. Приведённое требование соответствия величин называют условием согласования.
Важно отметить, что в качестве устройства питания не обязательно может использоваться батарея или аккумулятор. Отмеченная здесь закономерность будет действовать и в том случае, если речь идёт об использовании усилителя.
В качестве примера использования указанного правила можно привести подключение акустической системы к усилителю. В этом случае выходной импеданс последнего должен подбираться таким образом, чтобы быть примерно равным входному импедансу подключённых динамиков. На практике в технической документации усилителя указывают границы, в которых должна находиться соответствующая характеристика подключённых устройств.
Видео по теме
Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!
Идеальный источник ЭДС
Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Или проще:
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.
Выглядит все это в аккумуляторе примерно вот так:
Цепляем лампочку
Итак, что у нас получается в чистом виде?
Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Далее



Закон Ома для полной цепи
Итак, последнее выражение носит название «закон Ома для полной цепи»

где
Е — ЭДС источника питания, В
R — сопротивление всех внешних элементов в цепи, Ом
I — сила ток в цепи, А
r — внутреннее сопротивление источника питания, Ом
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r


Вывод
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
На этой странице вы узнаете
- Где самое большое сопротивление в теле человека?
- Какой ученый променял бильярд на физику?
- К чему может привести авария среди электронов?
Весь современный мир держится на электричестве. Наряду с глобальной интернет-сетью, наш мир «опутан» сетью электрических проводов. Что такого происходит в этих тоненьких проводах, что от них зависит жизнь целого города? Давайте поближе познакомимся с электрическим током и узнаем, откуда он появляется.
Мы с вами уже познакомились с электрическими схемами в теме «Законы постоянного тока», где выяснили, какие приборы существуют и как используются в схемах. В этой статье мы поговорим о том, как в элементарных электрических цепях появляется ток. Начало положено, сопротивление бесполезно.
Источник тока

Как мы уже выяснили, электрические схемы не могут работать просто так. Представим, что вы хотите поехать на машине, в которой нет бензина. Конечно, машина не заведется, так как ее нужно заправить. Электрические схемы работают по такому же принципу. Если их не подпитывать током, то они не будут работать.
Электрический ток — это направленное, упорядоченное движение электрических зарядов. Поэтому, чтобы поддерживать в цепи ток длительное время, в нем должен быть участок, на котором будет происходить перенос зарядов против сил электростатического поля (поля, создаваемого неподвижными зарядами). То есть, то место, где электроны будут принудительно приходить в движение.
Источник тока — элемент электрической цепи, в котором на заряды действует сторонняя сила, задающая направление движения зарядов (тока).
Перемещение зарядов на этом участке возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними силами. Эти силы приводят заряды в движение. Благодаря этому поддерживается ток в цепи. Действие сторонних сил характеризуется величиной, называемой электродвижущей силой источника тока (ЭДС), о которой поговорим чуть позднее.

Примером источника тока может служить обычная батарейка. Вы наверняка замечали, что на пальчиковых батарейках с одной стороны пишется «плюс», а с другой — «минус». Это означает, что электрический ток пойдет от положительной части батарейки к отрицательной. А почему ток выходит из одной части, но заходит в другую?
Для объяснения этого явления рассмотрим картинку ниже. Главным критерием рабочей электрической цепи является ее замкнутость, то есть вся цепь неразрывно связана. Подключим нашу батарейку (источник тока) к электрической цепи, которую также называют внешней электрической цепью.
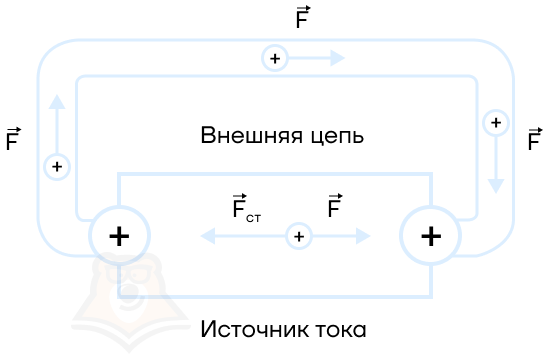
Как мы видим на этом рисунке, на заряды внутри источника тока действует сторонняя сила ((F_{ст})), от плюса к плюсу) и сила электростатического поля ((F)), которая направлена от плюса к минусу. Без действия сторонних сил внутри источника положительный заряд будет двигаться от «+» к «-» (по направлению силы (F)).
Мы действуем сторонними силами так, чтобы он стал двигаться к «+» (по направлению (F_{ст})), то есть против сил электростатического поля. Тогда заряды вылетают из источника тока и далее по внешней цепи, уже под действием обычного электростатического поля, движутся по стандартным законам от «+» к «-». Это и есть наш долгожданный электрический ток – движущиеся заряды. Если бы мы не действовали сторонними силами, все заряды бы просто сидели на месте («+» окружили бы «-», и наоборот). То есть, сама сторонняя сила задает направление движения заряда.
После того как заряд выходит из источника тока, на него действует только одна сила F. Поэтому он обходит всю цепь и возвращается в этот же источник тока. Там на него вновь действует сторонняя сила, ну а дальше вы уже знаете.
Если бы в источнике тока не было сторонних сил, то все положительные заряды застряли бы у минуса.
Основные параметры источника тока
Как и любой другой элемент электрической цепи, источник тока обладает своими характеристиками, которые могут меняться в зависимости от условий использования. Главными характеристиками являются ЭДС источника тока (электродвижущая сила) и его внутреннее сопротивление.
ЭДС источника тока (ε) — это физический параметр, который характеризует работу сторонних сил ((А_{ст})), затраченную на перемещение зарядов (q) внутри источника.
(ε) – ЭДС источника тока (В);
(А_{ст})– работа сторонних сил (Дж);
(q) – заряд, помещенный внутри источника (Кл).
Внутреннее сопротивление определяет количество потерь энергии при прохождении тока через источник тока.
Стоит понимать, что внутреннее сопротивление появляется из-за неидеальности реальных предметов. Только у идеальных источников тока отсутствует внутреннее сопротивление.

Однако при расчете характеристик электрических схем никакой сложности не возникает, так как мы просто представляем, что в цепи появляется дополнительный резистор (на схемах обозначается прямоугольником и буквой R), сопротивление которого будет равняться внутреннему сопротивлению источника тока.
Раз уж мы затронули расчеты электрических схем, то пора вплотную к ним приблизиться.
Закон Ома для участка цепи
Георг Ом рос в небогатой семье. Также он был довольно азартным человеком, любил играть в бильярд в компании друзей. В университетские годы Ом был лучшим игроком в бильярд среди студенческой молодежи, показывал прекрасные результаты в конькобежном спорте.
Но его очень манили точные науки: физика и математика. Однажды он смог собрать всю свою волю «в кулак» и начать проводить опыты в лаборатории обычной школы, где работал учителем. И так он окончательно вжился в статус ученого-физика. После этого он играл в бильярд только для получения удовольствия, а не использовал его как способ заработка.
Дальше мы с вами поговорим о напряжении на элементах электрической цепи, и, в частности, на источнике тока. Поэтому вспомним, что такое напряжение из темы «Законы постоянного тока». Напряжение – физическая величина, которая показывает, какую работу сторонние силы должны приложить, чтобы перенести заряд от одной точки до другой.
Так как у источника тока имеется внутреннее сопротивление, значит, внутри него также будет и напряжение. Чтобы найти его, воспользуемся законом Ома — умножим внутреннее сопротивление источника тока r на сам ток I и получим:
Ur = Ir.
Также мы можем найти напряжение, которое будет выделяться на внешней цепи. Для этого снова умножим ток I на общее сопротивление цепи R:
UR = IR.
Оказывается, что не вся энергия источника тока уходит в цепь. Как раз таки та часть энергии, которая уходит на преодоление внутреннего сопротивления, и будет характеризовать потери. Тогда мы можем записать еще одну формулу для нахождения ЭДС источника тока:
ε – ЭДС источника тока (В);
UR – напряжение на самой электрической цепи (В);
Ur – напряжение внутри источника тока (В).
Теперь давайте подставим вместо напряжений полученные формулы через токи и сопротивления и выразим силу тока. Так мы получим закон Ома для полной цепи:
I – ток в цепи (А);
ε – ЭДС источника тока (В);
R – сопротивление в цепи (Ом);
r – внутреннее сопротивление источника (Ом).
Сила тока в цепи с заданным источником тока (при неизменной ЭДС и с постоянным внутренним сопротивлением) зависит только от сопротивления внешней цепи R.
Самое большое электрическое сопротивление на теле человека — поверхность верхнего рогового слоя кожи человека. Оно может достигать 40000–100000 Ом. Но это не значит, что можно хвататься за оголенные провода голыми руками! Этого сопротивления далеко не достаточно, чтобы защитить человека от опасного электрического тока.
Резко уменьшают сопротивление человека потливость кожного покрова, переутомление, нервное возбуждение. Значение снижается до 800–1000 Ом. Поэтому даже самое небольшое напряжение может вызвать ожог кожи.
Задачи на данную тему встречаются в №12 ЕГЭ. Давайте рассмотрим один пример.
Задача. Найдите внутреннее сопротивление источника ЭДС, если сопротивление в цепи R = 4 Ом, а ЭДС ε=10 В. Сила тока в цепи 2 А.
Решение.Воспользуемся законом Ома для полной цепи и выразим из него внутреннее сопротивление источника ЭДС:
(I=frac{ε}{R + r}),
(r=frac{ε}{I}-R=frac{10}{2}-4=1) (Ом).
Ответ: 1 Ом
Короткозамкнутая цепь
Рассмотрим частный случай электрической цепи, в котором источник тока будет подключен сам на себя. Иначе говоря, он будет короткозамкнутым.
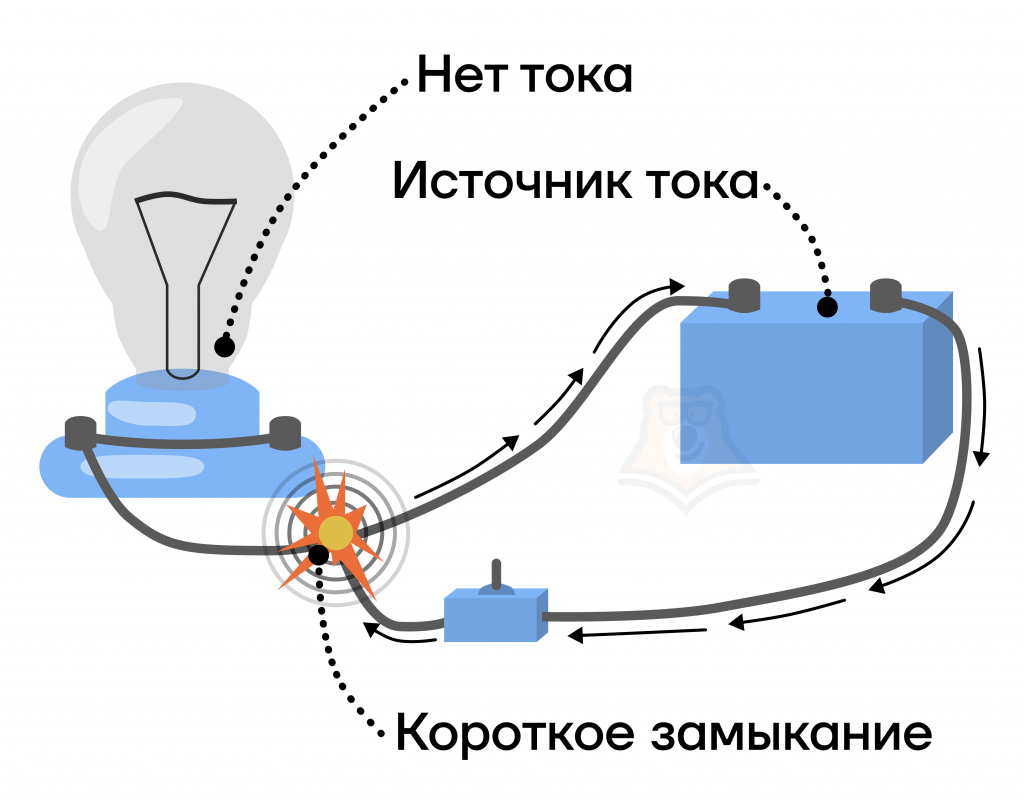
В этом случае отсутствует сопротивление внешней цепи и закон Ома для цепи будет выглядеть так:
(I_{кз}) – ток короткого замыкания (А);
(ε) – ЭДС источника тока (В);
(r) – сопротивление источника ЭДС (Ом).
Короткое замыкание — это такой случай соединения проводов, при котором практически весь ток проходит по пустому проводу и возвращается в источник тока.
Короткое замыкание приводит к сильному нагреву, расплавлению металлов, а иногда и к пожарам.
Если сравнить поток электронов с потоком машин, то ток короткого замыкания – это авария на автодороге. Один поток машин решил влезть в другой. В результате на дороге образовалась авария. Но машины продолжают налетать одна на другую (как в метель в Норильске).
При коротком замыкании сила тока будет увеличиваться до тех пор, пока отключающие механизмы не прекратят поступление силы тока.
Теперь, когда мы уже рассмотрели основные характеристики источника тока, можем перейти к мощности и КПД источника тока.
Мощность и КПД источника тока
Мы уже не раз говорили о том, что при протекании тока выделяется энергия. Источники тока не исключение. При подключении их к цепи на них выделяется энергия. При этом энергия выделяется и в самой цепи.
Чтобы найти мощность передачи энергии (P), выделяемой источником тока, необходимо умножить силу тока на ЭДС этого источника тока. Тогда получим:
(P_{ист}) – мощность источника тока (Вт);
(ε) – ЭДС источника тока (В);
(I) – сила тока (А).
При этом часть этой мощности уходит на элементы внешней цепи, а другая часть – на преодоление внутреннего сопротивления источника тока:
(εI = I^2R + I^2r).
Тогда мощность, выделяемая на внешней цепи:
(P_R=I^2R).
А мощность, которая теряется на внутреннее сопротивление источника тока:
(P_r=I^2r).
Теперь давайте рассмотрим коэффициент полезного действия (КПД, ) источника тока. Как мы уже говорили ранее, часть ЭДС источника тока уходит на внутреннее сопротивление, а часть – на внешнюю цепь. При этом вспомним, что КПД – это отношение полезной мощности к затраченной.
Запишем формулы для мощности:
(P_{ист}=εI=I^2(R+r)),
(P_R=IU =I^2R).
Тогда КПД:
(eta) – КПД источника тока;
(ε) – ЭДС источника тока (В);
(U) – напряжение на внешней цепи (В);
(I) – сила тока (А):
(R) – сопротивление на внешней цепи (Ом);
(r) – сопротивление источника тока (Ом).
Также задачи на тему ЭДС встречаются и в №16 ЕГЭ. Сложность данных задач заключается в установлении правильной зависимости величин друг от друга.
Задача.Определите, как изменятся сила тока (А) в цепи и сопротивление резистора (Б), если ЭДС источника тока заменить на такую же ЭДС, но с большим внутренним сопротивлением.
1) увеличится
2) уменьшится
3) не изменится
Решение.
Б) Внешнее сопротивление никак не зависит от источника тока. Поэтому оно не изменится — выбираем ответ 3.
А) Запишем закон Ома для полной цепи:
(I=frac{ε}{R + r})
При увеличении внутреннего сопротивления знаменатель увеличится. Следовательно, сила тока уменьшится, так что вариант 2 тоже нам подходит.
Ответ: 23
Мы с вами выяснили, что источники тока – элементы электрической цепи, без которых самой цепи не существовало бы. Хотя, конечно, она бы существовала, но была бы бесполезной. Однако и они «не без греха», так как существует опасное внутреннее сопротивление, которое является головной болью для многих инженеров. А все потому, что оно снижает КПД источников тока. Дальше вы можете ознакомиться с полноценными электрическими схемами и посмотреть, как ток ведет себя за пределами источника тока.
Термины
Напряжение – произведение сопротивления элемента и протекающего через него тока.
Резистор (или резистивный элемент) – элемент электрической цепи, который может только потреблять энергию и не может ее создавать.
Сторонние силы — это все внешние силы, воздействующие на заряд.
Электростатическое поле — невидимое поле, создаваемое постоянными электрическими зарядами.
Фактчек
- ЭДС источника тока (ε) — это физический параметр, который характеризует работу, затраченную на перемещение зарядов внутри источника сторонними силами: (ε =frac{А_{cт}}{q}).
- Внутреннее сопротивление (r) — определяет количество потерь энергии при прохождении тока через источник тока.
- Закон Ома для полной цепи: Сила тока в замкнутой цепи равна отношению ЭДС цепи к ее полному сопротивлению: (I =frac{ε}{R + r}).
- Предельное значение силы тока для данного источника тока называется током короткого замыкания: (I_{кз} =frac{ε}{r}).
- Полная мощность цепи — это есть мощность источника тока: (P_ист=εI).
Проверь себя
Задание 1.
Как рассчитывается ЭДС источника тока?
- (ε =frac{А_{ст}}{q})
- (ε =frac{U}{q})
- (ε =frac{А_{ст}}{I})
- (ε =frac{А_{ст}}{qt})
Задание 2.
Короткое замыкание — это:
- Соединение концов участка цепи проводником, сопротивление которого очень мало по сравнению с сопротивлением участка цепи.
- Соединение концов участка цепи проводником, сопротивление которого очень велико по сравнению с сопротивлением участка цепи.
- Соединение концов участка цепи проводником, сопротивление которого не зависит от сопротивления участка цепи.
- Отсутствие электрического тока в цепи.
Задание 3.
Чему равно ЭДС источника тока?
- (ε = U_R- U_r)
- (ε = U_R+ U_r)
- (ε = U_R U_r)
- (ε = U_R)
Задание 4.
От чего зависит сила тока в цепи с заданным источником тока?
- от внутреннего сопротивления цепи
- от внутреннего сопротивления источника тока
- от внешнего сопротивления цепи
- не зависит ни от каких величин
Задание 5.
Где самое большое сопротивление в человеке?
- в сердце
- в пищеварительной системе
- на коже
- в голове
Ответы: 1. — 1; 2. — 1; 3. — 2; 4. — 3; 5. — 3.
Что означает внутреннее сопротивление?
Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет. В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r.
Внутреннее сопротивление источника тока .
Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R. Ток в замкнутой цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r.
В генераторе r — это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов.
Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до сотни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше). Это позволяет с их помощью получать токи, измеряемые амперами.
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.
Выглядит все это в аккумуляторе примерно вот так:


Цепляем лампочку


Итак, что у нас получается в чистом виде?
Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.


На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что


Далее






Закон Ома для полной цепи
Итак, последнее выражение носит название «закон Ома для полной цепи»


где
Е — ЭДС источника питания, В
R — сопротивление всех внешних элементов в цепи, Ом
I — сила ток в цепи, А
r — внутреннее сопротивление источника питания, Ом
Как измеряется внутреннее сопротивление
Для определения значения рассматриваемой характеристики применяются измерения во время прямого замыкания клемм, которое называют коротким замыканием. Как известно, если закоротить клеммы источника, между ними протечёт значительный ток. Часто это является следствием неосторожности и приводит к обгоранию изоляции и расплавлению провода.
При коротком замыкании сопротивление цепи становится минимальным. Точно измерив силу тока в этой ситуации и зная величину напряжения на клеммах при отсутствии нагрузки, можно определить внутреннее сопротивление источника питания. Для этого понадобится следующая формула:
r = U / I(зам), где
- буквой r обозначено внутреннее сопротивление источника тока;
- U — разность потенциалов на клеммах батареи без подсоединения к электрической цепи;
- I(зам) — ток, который проходит при непосредственном замыкании клемм друг на друга.
Находить значение нагрузки таким образом не всегда возможно или целесообразно, поскольку короткое замыкание может стать причиной серьезной аварии.
Поэтому используются другие решения вопроса, как найти внутреннее сопротивление источника. Например, с помощью специальных измерительных приборов. Функцией измерения данного параметра снабжены оригинальные зарядные устройства iMax B6, ToolkinRC M8, M6, M600.
Зачем нужно знать внутреннее сопротивление
На первый взгляд может показаться, что наличие внутреннего сопротивления интересно только с теоретической точки зрения. На самом деле в некоторых ситуациях знать чему оно равно бывает жизненно важным.
Одна из таких ситуаций — определение работоспособности автомобильного аккумулятора. Его внутреннее сопротивление не является постоянным. Оно изменяется под воздействием различных факторов и влияет на напряжение на клеммах. Чтобы быть уверенным в работоспособности оборудования, нужно не только уметь найти его внутреннее сопротивление, но и знать, какая его величина соответствует норме.

На внутреннее сопротивление источника питания могут оказывать влияние такие факторы:
- Температурные условия. Чем холоднее, тем с меньшей скоростью в аккумуляторе протекают химические процессы. Это приводит к увеличению внутреннего сопротивления и постепенному уменьшению напряжения на клеммах.
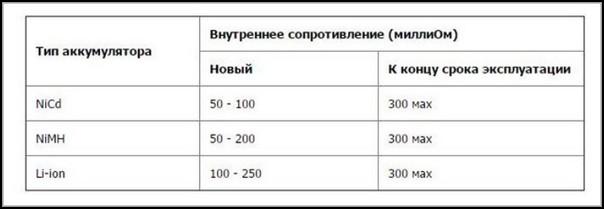
- Срок службы аккумулятора. У новых устройств внутреннее сопротивление имеет минимальную величину. Постепенно оно начинает расти. Это связано с тем, что в аккумуляторе происходит необратимый химический процесс. В некоторых случаях он относительно медленный, а в других может быть довольно заметным. Последнее, например, относится к свинцово-кислотным аккумуляторам.
- Емкость аккумулятора.
- Иногда на устройство может оказываться механическое воздействие, из-за которого появляются внутренние обрывы.
- Количество используемого электролита.
- Ток, который создаётся батареей, зависит от нагрузки цепи. В зависимости от него меняется сопротивление.
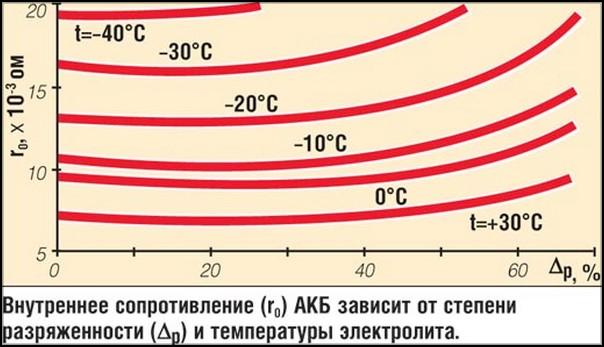
Влияние большого количества факторов приводит к тому, что в качестве нормального можно рассматривать различные значения внутреннего сопротивления. Однако его стандартным увеличением за год принято считать 5%. Если эта норма превышена, значит, на исправность аккумулятора нужно обратить особое внимание.
При анализе стоит принимать во внимание не только те значения, которые указаны в технической документации. Необходимо учитывать и то, насколько интенсивно происходят изменения сопротивления со временем. Это даст более точную информацию об исправности батареи и поможет понять, чего нужно добиваться, чтобы обеспечить работоспособность оборудования.
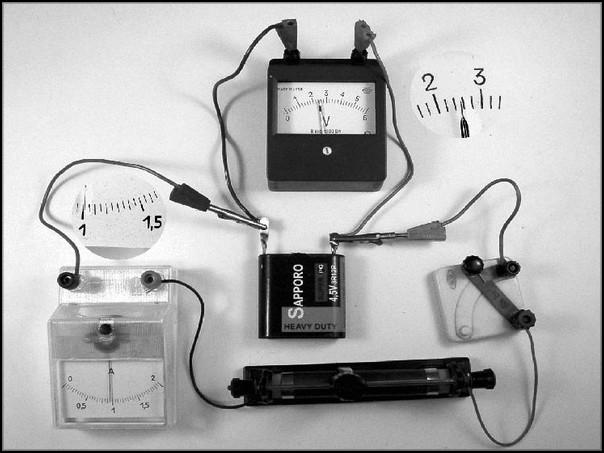
Один из наиболее простых способов измерения внутреннего сопротивления можно продемонстрировать на следующем примере. Его применение возможно при условии, что ЭДС аккумулятора известна.
ЭДС (ℰ, единица измерения — вольты, В) — это электродвижущая сила источника питания, равная отношению работы сторонних сил по перемещению заряда от отрицательного полюса источника к положительному к величине этого заряда: ℰ=A/q. Если к источнику питания не подключена нагрузка, то ЭДС по своему значению равно напряжению на его клеммах.
Будет рассмотрена ситуация, когда ЭДС равна 1.5 В. Составляется электрическая цепь, в которой выходы аккумулятора присоединяются к электрической лампочке. Измеряется падение напряжения на ней и ток, проходящий через цепь. Они, соответственно, равны 1.2 В и 0.3 А.
Цифры, которые здесь приводятся, являются условными. При измерении мастер может выбрать другой тип электрической нагрузки, если сочтёт это необходимым.
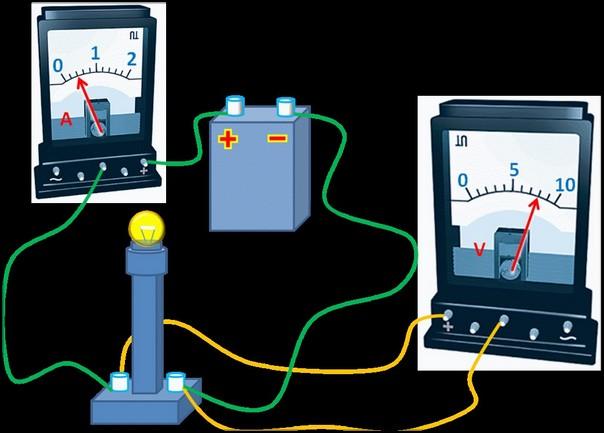
По закону Ома можно определить сопротивление лампочки:
R = U / I = 1.2 / 0.3 = 4 Ом.
В этой формуле буквой R обозначается полное сопротивление цепи. Его можно выразить, как сумму r + R, где r — внутреннее и R — обычное сопротивление.
Тогда: R + r = ℰ / I
Из этой формулы определяется r = ℰ / I − R = 1.5 / 0.3 − 4 = 1 Ом.
Важным условием нахождения значения r является знание величины электродвижущей силы. Эта характеристика имеет максимальное значение у новых и хорошо заряженных батарей. Те, что уже долго были в использовании, могут иметь значительно меньшую ЭДС вследствие разряда, износа, который часто связан с необратимыми химическими процессами в аккумуляторе.
Для определения ℰ необходимо отключить любую нагрузку от клемм источника питания и подключить вольтметр или мультиметр в режиме измерения напряжения. Прибор покажет значение ЭДС. Почему — это легко понять. По закону Ома для полной цепи:
I = ℰ / (R + r),
так как вольтметр имеет сопротивление R→∞, то ток I≈0. Следовательно напряжение на клеммах равно ЭДС:
U = I·R = ℰ – I·r = ℰ.
Также следует упомянуть, что нулевым внутренним сопротивлением «r» обладает только идеальный генератор напряжения. Также существуют элементы с большим внутренним сопротивлением — это разные датчики, источники сигналов, а r=∞ обладает только идеальный источник тока. Помимо этого, существуют двухполюсники с отрицательным значением r, его можно получить в схемах с обратной связью и в элементах с отрицательным дифференциальным сопротивлением. Расчеты применимы не только для аккумулятора, но и для любого другого источника тока, например, гальванической батареи, двухполюсника, петли фаза-нуль. Использовать эти знания можно для согласования источника и нагрузки, понижения высоких напряжений и минимизации шума.
Расчет внутреннего сопротивления источника напряжения
Реальные источники напряжения обладают собственным электрическим сопротивлением, которое называется «внутреннее сопротивление». Присоединенная на выводы источника нагрузка обозначается под названием «внешнее сопротивление» – R.
Батарея аккумуляторов генерирует ЭДС:
ε = E/Q, где:
- Е – энергия (Дж);
- Q – заряд (Кл).
Суммарная ЭДС аккумуляторного элемента является напряжением его разомкнутой цепи при отсутствии нагрузки. Его можно проконтролировать с хорошей точностью цифровым мультиметром. Разность потенциалов, измеренная на выходных контактах батареи, когда она включена на нагрузочный резистор, составит меньшую величину, чем ее напряжение при незамкнутой цепи, по причине протекания тока через нагрузочное внешнее и через внутреннее сопротивление источника, это приводит к рассеиванию энергии в нем как теплового излучения.
Внутреннее сопротивление аккумулятора с химическим принципом действия находится между долей ома и несколькими омами и в основном связано с сопротивлением электролитических материалов, используемых при изготовлении батареи.
Если резистор сопротивлением R подсоединить к батарее, ток в цепи I = ε/(R + r).
Внутреннее сопротивление – не постоянная величина. На него влияет род батареи (щелочная, свинцово-кислотная и т. д.), оно изменяется в зависимости от нагрузочного значения, температуры и срока использования аккумулятора. К примеру, у разовых батареек внутреннее сопротивление возрастает во время использования, а напряжение в связи с этим падает до прихода в состояние, непригодное для дальнейшей эксплуатации.
Если ЭДС источника – заранее данная величина, внутреннее сопротивление источника определяется, измеряя ток, протекающий через нагрузочное сопротивление.
- Так как внутреннее и внешнее сопротивление в приближённой схеме включены последовательно, можно использовать законы Ома и Кирхгофа для применения формулы:
- Из этого выражения r = ε/I — R.
Пример.
Аккумулятор с известной ЭДС ε = 1.5 В и соединен последовательно с лампочкой. Падение напряжения на лампочке составляет 1,2 В. Следовательно, внутреннее сопротивление элемента создает падение напряжения: 1,5 — 1,2 = 0,3 В. Сопротивление проводов в цепи считается пренебрежимо малым, сопротивление лампы не известно. Измеренный ток, проходящий через цепь: I = 0,3 А. Нужно определить внутреннее сопротивление аккумулятора.
- По закону Ома сопротивление лампочки R = U/I = 1,2/0,3 = 4 Ом;
- Теперь по формуле для расчета внутреннего сопротивления r = ε/I — R = 1,5/0,3 — 4 = 1 Ом.
В случае короткого замыкания внешнее сопротивление падает почти до нуля. Ток может ограничивать свое значение только маленьким сопротивлением источника. Сила тока, возникающая в такой ситуации, настолько велика, что источник напряжения может быть поврежден тепловым воздействием тока, существует опасность возгорания. Риск пожара предотвращается установкой предохранителей, например, в цепях автомобильных аккумуляторов.
Внутреннее сопротивление источника напряжения – важный фактор, когда решается вопрос, как передать наиболее эффективную мощность подсоединенному электроприбору.
Важно!
Максимальная передача мощности происходит, когда внутреннее сопротивление источника равно сопротивлению нагрузки.
Однако при этом условии, помня формулу Р = I² x R, идентичное количество энергии отдается нагрузке и рассеивается в самом источнике, а его КПД составляет всего 50%.
Требования нагрузки должны быть тщательно рассмотрены для принятия решения о наилучшем использовании источника. Например, свинцово-кислотная автомобильная батарея должна обеспечивать высокие токи при сравнительно низком напряжении 12 В. Ее низкое внутреннее сопротивление позволяет ей это делать.
В некоторых случаях источники питания высокого напряжения должны иметь чрезвычайно большое внутреннее сопротивление, чтобы ограничить ток к. з.
Нахождение внутреннего сопротивления
Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.
Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:
Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.
Выразив отсюда r, получают формулу для его вычисления:
где:
- r – внутреннее сопротивление источника;
- ε – ЭДС источника;
- I – сила тока в полной цепи;
- R – сопротивление в полной цепи.
Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.
Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.
В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.
Таблица удельных сопротивлений различных материалов
| Удельное сопротивление
ρ, Ом*мм2/м |
Удельное сопротивление
ρ, Ом*мм2/м |
| Алюминий | 0,028 |
| Бронза | 0,095 – 0,1 |
| Висмут | 1,2 |
| Вольфрам | 0,05 |
| Железо | 0,1 |
| Золото | 0,023 |
| Иридий | 0,0474 |
| Константан ( сплав Ni-Cu + Mn) | 0,5 |
| Латунь | 0,025 – 0,108 |
| Магний | 0,045 |
| Манганин (сплав меди марганца и никеля – приборный) | 0,43 – 0,51 |
| Медь | 0,0175 |
| Молибден | 0,059 |
| Нейзильбер (сплав меди цинка и никеля) | 0,2 |
| Натрий | 0,047 |
| Никелин ( сплав меди и никеля) | 0,42 |
| Никель | 0,087 |
| Нихром ( сплав никеля хрома железы и марганца) | 1,05 – 1,4 |
| Олово | 0,12 |
| Платина | 0.107 |
| Ртуть | 0,94 |
| Свинец | 0,22 |
| Серебро | 0,015 |
| Сталь | 0,103 – 0,137 |
| Титан | 0,6 |
| Хромаль | 1,3 – 1,5 |
| Цинк | 0,054 |
| Чугун | 0,5-1,0 |
Ответ: нить накаливания сделана из константана.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
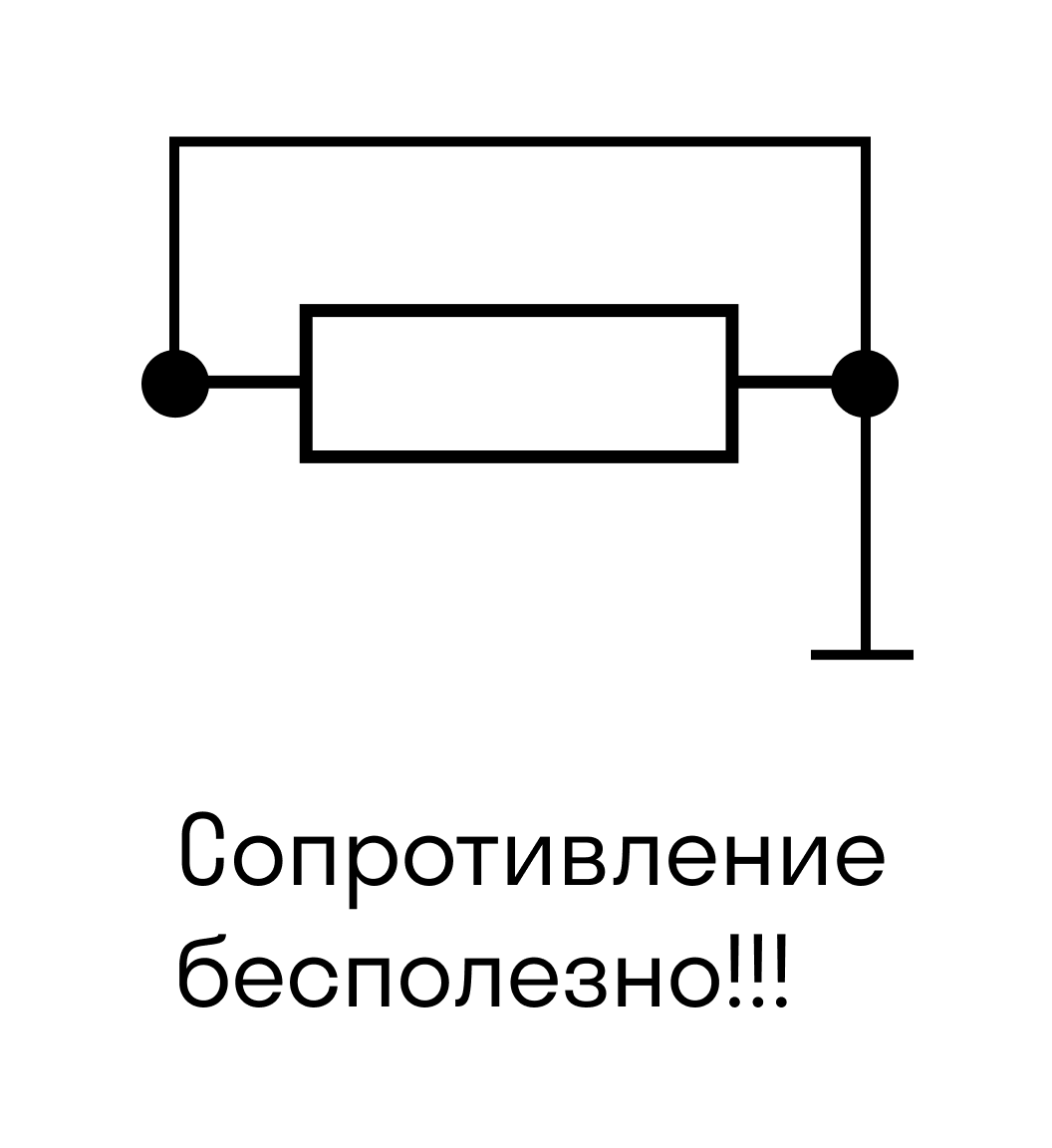
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
I = U/R
I — сила тока [A]
U — напряжение [В]
R — сопротивление [Ом]
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Измерение внутреннего сопротивления.
Существует несколько методик измерения внутреннего сопротивления. Две из них прописаны в ГОСТ Р МЭК 61960-2007. Перед замером любым из приведенных ниже методов аккумулятор должен быть полностью заряжен. Испытания проводятся при температуре 20±5ºC.
Измерение внутреннего сопротивления методом переменного тока (а.с.)
С помощью этого метода измеряется импеданс, который на частоте 1000 Гц приблизительно равен сопротивлению.
Электрический импеданс (комплексное электрическое сопротивление) (англ. impedance от лат. impedio «препятствовать») — комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала.
Описание методики из ГОСТ
В течение одной – пяти секунд измеряем среднеквадратичное значение переменного напряжения Urms, возникающего при прохождении через аккумулятор переменного тока со среднеквадратичным значением Irms , следующего с частотой 1000 Гц. Внутреннее сопротивление Ra.c., Ом рассчитываем по формуле Ra.c.= Urms / Irms .
Irms (rms – Root Mean Square – среднеквадратичное значение).
Переменный ток должен иметь такое значение, чтобы пиковое напряжение не превышало 20 мВ.
Этот метод сложно воплотить в домашних условиях без специального оборудования. Популярный прибор YR1035 отлично справляется с измерениями с точностью 0,01 мОм. Зарядные устройства SKYRC MC3000 ,Opus BT-C3100V2.2, Liitokala Lii-500 также измеряют методом АС, но весьма с посредственной точностью.
Измерение внутреннего сопротивления методом постоянного тока (d.c.)
Этот метод возможно выполнить в домашних условиях с помощью обычных вольтметра и амперметра и пары подходящих нагрузочных сопротивлений. В качестве сопротивлений вполне можно использовать несколько автомобильных ламп накаливания или импровизированный резистор из нихромовой проволоки.
Описание метода из ГОСТ
- Разряжаем аккумулятор постоянным током I1= 0,2 Iн. На десятой секунде измеряем значение напряжения U1 на клеммах аккумулятора.
- Увеличиваем разрядный ток до значения I2=Iн. На следующей секунде измеряем значение напряжения U2 на клеммах аккумулятора.
Внутреннее сопротивление Rd.c., Ом рассчитываем по формуле Rd.c. = (U1-U2)/(I2-I1)
- Iн – номинальный ток разряда аккумулятора.
Схема для измерения внутреннего сопротивления по методике постоянного тока (d.c.)
Сопротивление R1 и R2 подбирается таким образом, чтобы протекали токи I1 и I2 нужной величины. Ориентироваться нужно на номинальный разрядный ток аккумулятора.
Вольтметр необходимо подключать непосредственно на полюса источника, чтобы исключить влияние от падения напряжения на проводах .
Идеальный источник тока
Идеальный источник тока представляет собой активный элемент, ток которого не зависит от напряжения на его зажимах. Предполагается, что внутреннее сопротивление идеального источника тока бесконечно велико , и поэтому параметры внешней электрической цепи, от которых зависит напряжение на зажимах источника, не влияют на ток источника. Условные обозначения идеального источника тока приведены на рис. 1
Стрелка в источнике тока или знаки «+» и «—» указывают положительное направление тока i(t)
или полярность источника, т. е. направление перемещения положительных зарядов.
Сейчас принято обозначать источники тока буквой J, и чаще всего применяется нижнее условно графическое изображение.
Идеальный источник тока
По мере неограниченного увеличения сопротивления внешней электрической цепи, присоединенной к идеальном
у источнику тока, напряжение на его зажимах и соответственно мощность, развиваемая им, неограниченно возрастают.Поэтому идеальный источник тока, так же как и идеальный источник напряжения, рассматривается как источник бесконечной мощности.
Источник тока конечной мощности изображается в виде идеального источника тока с параллельно подключенным к его зажимам пассивным элементом который характеризует внутренние параметры источника и
Представляя собой теоретическое понятие, источник тока применяется в ряде случаев для расчета электрических цепей.
Некоторым подобием источника тока может служить устройство, состоящее из аккумулятора, соединенного последовательно с дополнительным большим сопротивлением Другим примером источника тока может являться пяти электродная усилительная электронная лампа (пентод). Имея внутреннее сопротивление несоизмеримо большее, чем сопротивление внешней электрической цепи, эти устройства отдают ток, почти не зависящий от изменения внешней нагрузки в широких пределах, и именно в этом отношении они аналогичны источнику тока.
Чему равно внутреннее сопротивление источника тока?
Внутреннее сопротивление источника тока r будет определяться формулой: r = ЭДС / I — R. Подставим данные из условия задачи: r = 10 В / 2 А — 4 Ом = 1 Ом. Ответ: источник тока имеет внутреннее сопротивление r = 1 Ом.
Как правильно пользоваться мультиметром: инструкция для чайников
Рассмотрим, как измерить несколько электрических характеристик.
Потенциал
Алгоритм для определения напряжения:
- Установить режим в позицию ACV или DCV в предполагаемом интервале.
- Черный провод подключить к коннектору СОМ, красный — к разъему VΩmA.
- Наконечники щупов соединить с контактами цепи. Например, ввести в отверстия розетки или на полюса батарейки.
- Провести измерение.
Высветившееся на дисплее число — величина напряжения в вольтах. Знак «минус» говорит о том, что полярность была нарушена. Если мультиметр поддерживает функцию удержания, значение можно зафиксировать кнопкой HOLD. Это удобно для большой цепочки измерений.
Сила тока
Эта характеристика измеряется только при последовательном подключении тестера в цепь и включенном питании. Большинство приборов дают возможность определить силу тока до 10 А, поскольку в быту большие значения используются редко.
Для проведения измерений в цепи устраивается разрыв. Дальнейшие действия по следующей схеме:
- Черный щуп — в гнездо СОМ.
- Красный — в разъем до 200 мА или 10А.
- Наконечниками осторожно прикоснуться к контактам.
- Считать с дисплея значение напряжения.
При работе с оголенными проводами необходимо соблюдать технику безопасности, чтобы не допустить удара током.
Сопротивление
Эту характеристику можно измерить без подачи питания. Исследуемый элемент просто замыкается между двумя щупами. Если проводимости нет, на экране высвечивается единица.
Последовательность действий:
- Установить режим Ω, выбрав максимальный диапазон.
- Щупы вставить в соответствующие коннекторы.
- Проверить состояние — замкнуть щупы друг на друга. Должен появиться 0 или небольшое число, которое нужно учитывать при измерении сопротивления цепи.
- Концы проводников набросить на контакты исследуемого объекта.
- На экране появится сопротивление элемента или участка цепи.
Для точных измерений рекомендуется провести 2-3 попытки.
Измерение транзисторов
Для проверки исправности pn-переходов и определения коэффициента усиления:
- Установить режим
- Вставить ножки транзистора в разъем в соответствии с цоколевкой, соблюдая зоны PNP и NPN.
- Отображением на дисплее будет значение усиления сигнала.
Диоды и простейшие транзисторы также измеряются при установленном режиме «диод». К базе подключается красный щуп (плюс), на эмиттер или коллектор черный (минус). При правильной полярности на экране высветится коэффициент передачи.
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними
Электрическая мощность и закон Ома
Для анализа и расчета параметров нагревателей, как правило, мы используем различные методы, в частности закон Ома. Этот закон используется в основном для определения неизвестных величин, таких как напряжение, ток, сопротивление и мощность, которые связаны с одним или несколькими элементами электронной схемы. Закон Ома – основной закон теории электрических цепей, который определяет линейную зависимость между напряжением, током и сопротивлением. В данной статье мы постараемся подробно рассказать о законе Ома и его практическом применении.

Закон Ома
Закон Ома – это основной, главный и важный закон теории электрических цепей, который исследует взаимосвязь между напряжением, током и сопротивлением. В нем говорится, что при постоянной температуре ток, протекающий по цепи, прямо пропорционален напряжению или разности потенциалов в этой цепи.
В алгебраической форме, V∝ I
V = IR
Где
I – ток, протекающий по цепи, измеряется в амперах.
V — напряжение, приложенное к цепи, измеряется в вольтах.
А R — это константа пропорциональности, называемая сопротивлением, которое измеряется в омах.
Это сопротивление также указывается в килоомах, мегаомах и т. д.
Следовательно, закон Ома гласит, что ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению в этой цепи. Закон Ома можно применить как к отдельным частям, так и ко всей цепи.
Математически ток, I = V/R
Напряжение, V = IR
Сопротивление, R = V/I
Треугольник закона Ома
Ниже показано, что отношение между различными величинами в законе Ома называется треугольником закона Ома. Это простой метод описания, а также простой для запоминания соотношения между напряжением, током и сопротивлением.

На приведенном выше рисунке показан треугольник закона Ома, где отдельные термины, такие как напряжение, ток и сопротивление, и их формулы представлены из основного уравнения закона Ома. На приведенном выше рисунке один параметр вычисляется из оставшихся двух параметров. Таким образом, можно сделать вывод, что при высоком сопротивлении ток будет низким, а ток будет высоким, когда сопротивление низкое, при любом приложенном напряжении.
Электрическая мощность
Электрическая мощность дает скорость, с которой энергия передается по цепи. Электрическая мощность измеряется в ваттах. Эта мощность потребляется, когда напряжение вызывает протекание тока в цепи.
Следовательно, электрическая мощность есть произведение напряжения и силы тока.
Математически P = VI
По закону Ома V = IR и I = V/R
Подставляя в уравнение мощности
P = I2 R
P = V2/ R
Следовательно, электрическая мощность, P =VI или I 2 R или V 2 / R
Это три основные формулы для нахождения электрической мощности в цепи. Таким образом, мощность может быть рассчитана, когда известна любая из двух величин.
Треугольник мощности
Подобно треугольнику закона Ома, на рисунке ниже показан треугольник мощности, чтобы показать соотношение между мощностью, напряжением и током. Уравнения отдельных параметров легко запоминаются по этому рисунку. Округлите и скройте параметр, который необходимо измерить, а положение оставшихся двух параметров дает уравнение для поиска скрытого или округленного параметра, как показано на рисунке ниже.

Круговая диаграмма закона Ома
В дополнение к двум вышеупомянутым концепциям существует еще один метод определения параметров схемы с использованием закона Ома, который представляет собой круговую диаграмму закона Ома. Используя круговую диаграмму закона Ома, можно легко запомнить все уравнения для нахождения напряжения, тока, сопротивления и мощности, которые необходимы для упрощения электрических цепей, которые могут быть простыми или сложными.

На приведенном выше рисунке показана круговая диаграмма, которая показывает взаимосвязь между мощностью, напряжением, током и сопротивлением. Эта диаграмма разделена на четыре блока для мощности, напряжения, сопротивления и тока. Каждый блок состоит из трех формул с двумя известными значениями для каждой формулы. Из диаграммы для нахождения каждого параметра в цепи мы можем использовать любую из трех доступных формул.
Графическое представление закона Ома
Для лучшего понимания этой концепции ниже приведена экспериментальная установка, в которой регулируемый источник напряжения с шестью ячейками (по 2 В каждая) подключен к нагрузочному резистору через переключатель выбора напряжения. Измерительные приборы, такие как вольтметр и амперметр, также подключены к цепи для измерения напряжения и тока в цепи.

Регулируемый источник напряжения с нагрузочным резистором
Сначала подключите резистор 10 Ом и установите переключатель в положение «1». Тогда амперметр показывает 0,2 А, а вольтметр показывает 2 В, потому что I = V/R, т. е. I = 2/10 = 0,2 А. Затем измените положение селекторного переключателя на вторую ячейку, чтобы подать 4 В на нагрузку и запишите показания амперметра. По мере того, как селектор будет постепенно изменяться от первого положения к последнему, мы получим текущие значения, такие как 0,2, 0,4, 0,6, 0,8, 1, 1,2 для значений напряжения 2, 4, 6, 8, 10 и 12 соответственно.
Точно так же поместите резистор 20 Ом вместо резистора 10 Ом и выполните ту же процедуру, что и выше. Мы получим значения тока 0,1, 0,2, 0,3, 0,4, 0,5, 0,6 для значений напряжения 2, 4, 6, 8, 10 и 12В соответственно. Постройте график этих значений, как показано ниже.

Графическое представление закона Ома
На приведенном выше графике для данного напряжения ток меньше, когда сопротивление больше. Рассмотрим случай приложенного напряжения 12 В, когда значение тока составляет 1,2 А при сопротивлении 10 Ом и 0,6 Ом при сопротивлении 20 Ом. Точно так же при одном и том же токе напряжение тем больше, чем больше сопротивление. Из приведенных выше результатов следует, что отношение напряжения к току постоянно, когда сопротивление постоянно. Следовательно, зависимость между напряжением и током является линейной, и наклон этой линейной кривой становится тем круче, чем больше сопротивление.
Пример применения закона Ома
Рассмотрим приведенную ниже схему, в которой батарея на 6 В подключена к нагрузке 6 Ом. Амперметр и вольтметры подключены к цепи для измерения тока и напряжения практически. Но используя закон Ома мы можем найти силу тока и мощность следующим образом.

Из закона Ома
V = IR
I = V/R
I = 6/6
I = 1 А
Мощность, P = VI
P = 6×1
P = 6 Вт
Но практически амперметр не показывает точное значение из-за внутреннего сопротивления батареи. Включив внутреннее сопротивление батареи (предположим, что батарея имеет внутреннее сопротивление 1 Ом), текущее значение рассчитывается следующим образом.

Общее сопротивление цепи 6+1=7 Ом.
Ток, I = V/R
I = 6/7
I = 0,85 Ампер
Цепь фар в автомобиле
На приведенном ниже рисунке показана схема фар легкового автомобиля без схемы управления. С применением закона Ома мы можем узнать ток, протекающий через каждую лампу. Как правило, каждая лампочка подключается параллельно к аккумулятору, что позволяет другим элементам светиться, даже если какой-то из них поврежден. К этим параллельным лампам подводится батарея 12 В, где лампы имеют сопротивление 2,4 каждая (считается в данном случае).

Общее сопротивление цепи равно R = R1x R2/(R1 + R2), так как они соединены параллельно.
R = 5,76/4,8 = 1,2
Тогда ток, протекающий по цепи, равен I = V/R.
I = 12/1,2
I = 10А.
Ток, протекающий через отдельную лампу, равен I1 = I2 = 5 А (из-за одинаковых сопротивлений).
Закон Ома для цепей переменного тока
В общем, закон Ома можно применить и к цепям переменного тока . Если нагрузка индуктивная или емкостная, то также учитывается реактивное сопротивление нагрузки. Следовательно, с некоторыми изменениями закона Ома, учитывающими влияние реактивного сопротивления, его можно применять к цепям переменного тока. Из-за индуктивности и емкости в переменном токе будет значительный фазовый угол между напряжением и током. А также сопротивление переменному току называется импедансом и обозначается как Z.
Таким образом, закон Ома для цепей переменного тока задается как
E = IZ
I = E/Z
Z = E/I
Где E – напряжение в цепи переменного тока,
I – текущий ток,
Z — импеданс.
Все параметры в приведенном выше уравнении представлены в комплексной форме, которая включает фазовый угол. Подобно круговой диаграмме цепи постоянного тока, круговая диаграмма закона Ома для цепи переменного тока приведена ниже.

Пример закона Ома (цепи переменного тока)
Рассмотрим приведенную ниже схему, в которой нагрузка переменного тока (сочетание резистивной и индуктивной) подключена к источнику переменного тока 10 В, 60 Гц. Нагрузка имеет сопротивление 5 Ом и индуктивность 10 мГн.

Тогда значение импеданса нагрузки Z = R + jX L
Z = 5 + j (2∏ × f × L)
Z = 5+ j (2×3,14×60×10×10-3)
Z = 5 + j3,76 Ом или 6,26 Ом при фазовом угле -37,016
Ток, протекающий по цепи, равен
I = V/Z = 10/(5+ j3,76) = 1,597 А при фазовом угле -37,016
Для расчета параметров сети для подключения нагревателей вы можете воспользоваться данными в данной статье основными формулами, или же просто позвоните нашим специалистам компании Термоэлемент по телефону и получите полную бесплатную консультацию и помощь с выбором нужных параметров нагревателей для вашей задачи по нагреву.


