Как найти внутреннее сопротивление для полной цепи – Сайт, где вы сможете решить свои вопросы

Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!

Идеальный источник ЭДС

Имеем источник ЭДС

источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

идеальный источник ЭДС

Или проще:

Закон Ома для полной цепи

Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.

Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?

Внутреннее сопротивление источника ЭДС

Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.

Выглядит все это в аккумуляторе примерно вот так:

закон Ома для полной цепи

Цепляем лампочку

замкнутная цепь закон Ома для полной цепи

Итак, что у нас получается в чистом виде?

Закон Ома для полной цепи

Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:

Закон Ома для полной цепи

Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.

падение напряжения закон Ома для полной цепи

На резисторе R падает напряжение U_R , а на внутреннем резисторе r падает напряжение U_r .

Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.

Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Закон Ома для полной цепи

формула закон Ома для полной цепи

Закон Ома для полной цепи

Итак, последнее выражение носит название «закон Ома для полной цепи»

закон Ома для полной цепи формула

где

Е — ЭДС источника питания, В

R — сопротивление всех внешних элементов в цепи, Ом

I — сила ток в цепи, А

r — внутреннее сопротивление источника питания, Ом

Просадка напряжения

Итак, знакомьтесь, автомобильный аккумулятор!

автомобильный аккумулятор

Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус

Закон Ома для полной цепи

Наш подопечный готов к бою.

Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.

галогенная лампочка

Первым делом давайте замеряем напряжение на клеммах аккумулятора

Закон Ома для полной цепи

12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.

Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:

закон Ома для полной цепи на практике

Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!

А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:

схема закон Ома для полной цепи

Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.

Смотрим на показания приборов:

закон Ома для полной цепи

Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.

Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла

Закон Ома для полной цепи

Смотрим показания:

Закон Ома для полной цепи

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.

Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.

Как найти внутреннее сопротивление источника ЭДС

Давайте снова вернемся к этой фотографии

ЭДС аккумулятора закон Ома для полной цепи

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:

закон Ома для полной цепи

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r

как найти внутреннее сопротивление

Закон Ома для полной цепи

Вывод

Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.

Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.

Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.

Источник

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
Сторонняя сила
Закон Ома для полной цепи
КПД электрической цепи
Закон Ома для неоднородного участка

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд $q$ :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду $q$ нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила $vec{F_E}$ , направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила $vec{F_{CT}}$ не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через $A_{CT}$ работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы $A_{CT}$ называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда $q$ вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, $A_{CT}$ — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа $A_{CT}$ прямо пропорциональна перемещаемому заряду $q$ . Поэтому отношение $A_{CT}/q$ уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается $mathcal E$ :

$mathcal E = frac{displaystyle A_{CT}}{displaystyle q vphantom{1^a}}.$ (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением $r$ , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной $mathcal E$ , и внутренним сопротивлением $r$ подключён к резистору $R$ (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока $I$ в цепи и напряжение $U$ на резисторе $R$ .

За время $t$ по цепи проходит заряд $q = It$ . Согласно формуле (1) источник тока совершает при этом работу:

$A_{CT} = Eq = EIt.$ (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях $R$ и $r$ . Данное количество теплоты определяется законом Джоуля–Ленца:

$Q = I^2Rt + I^2rt = I^2(R + r)t.$ (3)

Итак, $A_{CT} = Q$ , и мы приравниваем правые части формул (2) и (3):

$mathcal E It = I^2(R + r)t.$

После сокращения на $It$ получаем:

$mathcal E = I(R + r).$

Вот мы и нашли ток в цепи:

$I = frac{displaystyle mathcal E}{displaystyle R + r vphantom{1^a}}.$ (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления $(R = 0)$ , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

$I_{K3} = frac{displaystyle mathcal E}{displaystyle r vphantom{1^a}}.$

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе $R$ с помощью закона Ома для участка цепи:

$U = IR = frac{displaystyle mathcal E R}{displaystyle R + r vphantom{1^a}}.$ (5)

Это напряжение является разностью потенциалов между точками $a$ и $b$ (рис. 2). Потенциал точки $a$ равен потенциалу положительной клеммы источника; потенциал точки $b$ равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет $Utextless mathcal E$ — ведь $mathcal E$ умножается на дробь, меньшую единицы. Но есть два случая, когда $U = mathcal E$ .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При $r = 0$ формула (5) даёт $U = mathcal E$ .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: $R = infty$ . Тогда величина $R + r$ неотличима от $R$ , и формула (5) снова даёт нам $U = mathcal E$ .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор $R$ называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке $R$ за время $t$ , обозначим $Q_{polezn}$ .

Если сила тока в цепи равна $I$ , то

$Q_{polezn} = I^2Rt.$

Некоторое количество теплоты выделяется также на источнике тока:

$Q_{ist} = I^2rt.$

Полное количество теплоты, которое выделяется в цепи, равно:

$Q_{poln} = Q_{polezn} + Q_{ist} = I^2Rt + I^2rt = I^2(R + r)t.$

КПД электрической цепи — это отношение полезного тепла к полному:

$eta = frac{displaystyle Q_{polezn}}{displaystyle Q_{poln} vphantom{1^a}} = frac{displaystyle I^2Rt}{displaystyle I^2(R+r)t vphantom{1^a}} = frac{displaystyle R}{displaystyle R+r vphantom{1^a}}.$

КПД цепи равен единице лишь в том случае, если источник тока идеальный $(r = 0)$ .

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома $U = IR$ справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3 показан неоднородный участок, содержащий резистор $R$ и источник тока. ЭДС источника равна $mathcal E$ , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно $r$ , можно просто заменить резистор $R$ на резистор $R + r$ ).

Рис. 3. ЭДС «помогает» току: $varphi_a - varphi_b + mathcal E = IR$

Сила тока на участке равна $I$ , ток течёт от точки $a$ к точке $b$ . Этот ток не обязательно вызван одним лишь источником $mathcal E$ . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток $I$ является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек $a$ и $b$ равны соответственно $varphi_a$ и $varphi_b$ . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: $U = varphi_a - varphi_b$ . За время $t$ через участок проходит заряд $q = It$ , при этом стационарное электрическое поле совершает работу:

$A_{POL} = Uq = UIt.$

Кроме того, положительную работу совершает источник тока (ведь заряд $q$ прошёл сквозь него!):

$A_{CT} = mathcal Eq = mathcal EIt.$

Сила тока постоянна, поэтому суммарная работа по продвижению заряда $q$ , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: $A_{POL} + A_{CT} = Q$ .

Подставляем сюда выражения для $A_{POL}$ , $A_{CT}$ и закон Джоуля–Ленца:

$UIt + mathcal EIt = I^2Rt.$

Сокращая на $It$ , получаем закон Ома для неоднородного участка цепи:

$U + mathcal E = IR,$ (6)

или, что то же самое:

$varphi a - varphi b + mathcal E = IR.$ (7)

Обратите внимание: перед $mathcal E$ стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд $q$ от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки $a$ к точке $b$ .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то $mathcal E = 0$ . Тогда из формулы (6) получаем $U = IR$ — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением $r$ . Это, как мы уже упоминали, равносильно замене $R$ на $R + r$ :

$varphi_a - varphi_b + mathcal E = I(R + r).$

Теперь замкнём наш участок, соединив точки $a$ и $b$ . Получим рассмотренную выше полную цепь. При этом окажется, что $varphi_a = varphi_b,$ и предыдущая формула превратится в закон Ома для полной цепи:

$mathcal E = I(R + r).$

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник $mathcal E$ «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от $a$ к $b$ , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току: $varphi_a - varphi_b - mathcal E = IR$

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против $mathcal E$ . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

$A_{CT} = mathcal E q = mathcal EIt.$

Тогда закон Ома для неоднородного участка примет вид:

$varphi_a - varphi_b - mathcal E = IR,$ (8)

или:

$U - mathcal E = IR,$

где по-прежнему $U = varphi_a - varphi_b$ — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

$varphi_a - varphi_b pm mathcal E = IR.$

Ток при этом течёт от точки $a$ к точке $b$ . Если направление тока совпадает с направлением сторонних сил, то перед $mathcal E$ ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

Сопротивление проводника тем больше, чем больше его длина.
Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм²/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм² от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм²/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

$displaystyle I=frac{U}{R};$

$displaystyle R=frac{U}{I}.$

По графику: при $U=60 B, I=3 B.$

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через поперечное сечение проводников за 8 с прошло 10²⁰ электронов. Какова сила тока в проводнике? Ответ дайте в амперах.

Решение:

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Заряд всех электронов: $q=Ncdot e,$ где е — модуль заряда электрона, $e=1,6cdot 10^{-19}$ Кл.

Тогда $displaystyle I=frac{Ncdot e}{t}=frac{10^{20}cdot 1,6cdot 10^{-19}}{8}=2 A.$

Ответ: 2.

Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда $displaystyle I=frac{5}{66+4}=0,07 A.$

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Отсюда $q=Icdot t=2,5cdot 600=1500$ Кл.

Ответ: 1500.

Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.

В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.

Закон Ома

Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:

U = I × R

или

I = V/R

или

R = V/I

Где:

V – напряжение в вольтах (В);
I – сила тока в амперах (А);
R – сопротивление в омах (Ом);

Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.

Видоизменения закона Ома.

Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».

Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление: I = V/R .
Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .

Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.

Закон Ома для цепи

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R, где

I – ток, протекающий по участку цепи.
R – сопротивление этого участка.
φ1-φ2 – разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

U1=I*R1
U2=I*R2
Un=I*Rn
U=I*(R1+R2+…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.

Закон Ома для участка цепи.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:

Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

Для полной цепи

Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.

Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

Все о законе Ома: простыми словами с примерами для “чайников”

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Для переменного тока

Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).

Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.

Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.

Для замкнутой цепи

На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.

Следствия закона Ома.

Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.

Формула для расчета падения напряжения на индуктивном сопротивлении:

U = I ⋅ ωL

Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).

Формула для расчета падения напряжения на емкостном сопротивлении:

U = I / ω ⋅ С

С – емкость реактивного сопротивления.

Эти две формулы – частные случаи закона Ома для переменных цепей.

Полный же будет выглядеть следующем образом:

I = U / Z

Здесь Z – полное сопротивление переменной цепи известное как импеданс.

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
В сверхпроводниках;
Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
В вакуумных и газовых радиолампах;
В диодах и транзисторах.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

I = I1= I2 ;
U = U1+ U2 ;
R = R1+ R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

I = I1+ I2 … ;
U = U1= U2 … ;
1 / R = 1 / R1+ 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.

Источник

На этой странице вы узнаете

Где самое большое сопротивление в теле человека?
Какой ученый променял бильярд на физику?
К чему может привести авария среди электронов?

Весь современный мир держится на электричестве. Наряду с глобальной интернет-сетью, наш мир «опутан» сетью электрических проводов. Что такого происходит в этих тоненьких проводах, что от них зависит жизнь целого города? Давайте поближе познакомимся с электрическим током и узнаем, откуда он появляется.

Мы с вами уже познакомились с электрическими схемами в теме «Законы постоянного тока», где выяснили, какие приборы существуют и как используются в схемах. В этой статье мы поговорим о том, как в элементарных электрических цепях появляется ток. Начало положено, сопротивление бесполезно.

Источник тока

Как мы уже выяснили, электрические схемы не могут работать просто так. Представим, что вы хотите поехать на машине, в которой нет бензина. Конечно, машина не заведется, так как ее нужно заправить. Электрические схемы работают по такому же принципу. Если их не подпитывать током, то они не будут работать.

Электрический ток — это направленное, упорядоченное движение электрических зарядов. Поэтому, чтобы поддерживать в цепи ток длительное время, в нем должен быть участок, на котором будет происходить перенос зарядов против сил электростатического поля (поля, создаваемого неподвижными зарядами). То есть, то место, где электроны будут принудительно приходить в движение.

Источник тока — элемент электрической цепи, в котором на заряды действует сторонняя сила, задающая направление движения зарядов (тока).

Перемещение зарядов на этом участке возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними силами. Эти силы приводят заряды в движение. Благодаря этому поддерживается ток в цепи. Действие сторонних сил характеризуется величиной, называемой электродвижущей силой источника тока (ЭДС), о которой поговорим чуть позднее.

Примером источника тока может служить обычная батарейка. Вы наверняка замечали, что на пальчиковых батарейках с одной стороны пишется «плюс», а с другой — «минус». Это означает, что электрический ток пойдет от положительной части батарейки к отрицательной. А почему ток выходит из одной части, но заходит в другую?

Для объяснения этого явления рассмотрим картинку ниже. Главным критерием рабочей электрической цепи является ее замкнутость, то есть вся цепь неразрывно связана. Подключим нашу батарейку (источник тока) к электрической цепи, которую также называют внешней электрической цепью.

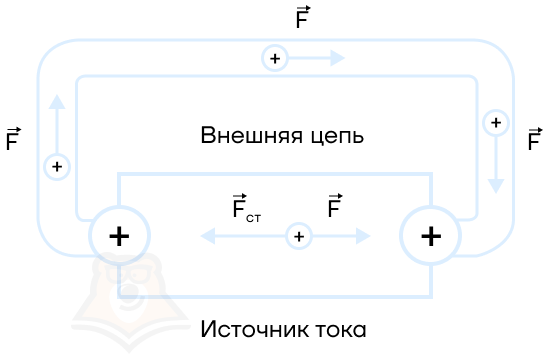
Как мы видим на этом рисунке, на заряды внутри источника тока действует сторонняя сила ((F_{ст})), от плюса к плюсу) и сила электростатического поля ((F)), которая направлена от плюса к минусу. Без действия сторонних сил внутри источника положительный заряд будет двигаться от «+» к «-» (по направлению силы (F)).

Мы действуем сторонними силами так, чтобы он стал двигаться к «+» (по направлению (F_{ст})), то есть против сил электростатического поля. Тогда заряды вылетают из источника тока и далее по внешней цепи, уже под действием обычного электростатического поля, движутся по стандартным законам от «+» к «-». Это и есть наш долгожданный электрический ток – движущиеся заряды. Если бы мы не действовали сторонними силами, все заряды бы просто сидели на месте («+» окружили бы «-», и наоборот). То есть, сама сторонняя сила задает направление движения заряда.

После того как заряд выходит из источника тока, на него действует только одна сила F. Поэтому он обходит всю цепь и возвращается в этот же источник тока. Там на него вновь действует сторонняя сила, ну а дальше вы уже знаете.

Если бы в источнике тока не было сторонних сил, то все положительные заряды застряли бы у минуса.

Основные параметры источника тока

Как и любой другой элемент электрической цепи, источник тока обладает своими характеристиками, которые могут меняться в зависимости от условий использования. Главными характеристиками являются ЭДС источника тока (электродвижущая сила) и его внутреннее сопротивление.

ЭДС источника тока (ε) — это физический параметр, который характеризует работу сторонних сил ((А_{ст})), затраченную на перемещение зарядов (q) внутри источника.

(ε =frac{А_{ст}}{q}), где

(ε) – ЭДС источника тока (В);
(А_{ст})– работа сторонних сил (Дж);
(q) – заряд, помещенный внутри источника (Кл).

Внутреннее сопротивление определяет количество потерь энергии при прохождении тока через источник тока.

Стоит понимать, что внутреннее сопротивление появляется из-за неидеальности реальных предметов. Только у идеальных источников тока отсутствует внутреннее сопротивление.

Однако при расчете характеристик электрических схем никакой сложности не возникает, так как мы просто представляем, что в цепи появляется дополнительный резистор (на схемах обозначается прямоугольником и буквой R), сопротивление которого будет равняться внутреннему сопротивлению источника тока.

Раз уж мы затронули расчеты электрических схем, то пора вплотную к ним приблизиться.

Закон Ома для участка цепи

Какой ученый променял бильярд на физику?

Георг Ом рос в небогатой семье. Также он был довольно азартным человеком, любил играть в бильярд в компании друзей. В университетские годы Ом был лучшим игроком в бильярд среди студенческой молодежи, показывал прекрасные результаты в конькобежном спорте.

Но его очень манили точные науки: физика и математика. Однажды он смог собрать всю свою волю «в кулак» и начать проводить опыты в лаборатории обычной школы, где работал учителем. И так он окончательно вжился в статус ученого-физика. После этого он играл в бильярд только для получения удовольствия, а не использовал его как способ заработка.

Дальше мы с вами поговорим о напряжении на элементах электрической цепи, и, в частности, на источнике тока. Поэтому вспомним, что такое напряжение из темы «Законы постоянного тока». Напряжение – физическая величина, которая показывает, какую работу сторонние силы должны приложить, чтобы перенести заряд от одной точки до другой.

Так как у источника тока имеется внутреннее сопротивление, значит, внутри него также будет и напряжение. Чтобы найти его, воспользуемся законом Ома — умножим внутреннее сопротивление источника тока r на сам ток I и получим:

U_r = Ir.

Также мы можем найти напряжение, которое будет выделяться на внешней цепи. Для этого снова умножим ток I на общее сопротивление цепи R:

U_R = IR.

Оказывается, что не вся энергия источника тока уходит в цепь. Как раз таки та часть энергии, которая уходит на преодоление внутреннего сопротивления, и будет характеризовать потери. Тогда мы можем записать еще одну формулу для нахождения ЭДС источника тока:

ε = U_R+ U_r , где

ε – ЭДС источника тока (В);
U_R – напряжение на самой электрической цепи (В);
U_r – напряжение внутри источника тока (В).

Теперь давайте подставим вместо напряжений полученные формулы через токи и сопротивления и выразим силу тока. Так мы получим закон Ома для полной цепи:

(I=frac{ε}{R + r}) , где

I – ток в цепи (А);
ε – ЭДС источника тока (В);
R – сопротивление в цепи (Ом);
r – внутреннее сопротивление источника (Ом).

Сила тока в цепи с заданным источником тока (при неизменной ЭДС и с постоянным внутренним сопротивлением) зависит только от сопротивления внешней цепи R.

Где самое большое сопротивление в теле человека?

Самое большое электрическое сопротивление на теле человека — поверхность верхнего рогового слоя кожи человека. Оно может достигать 40000–100000 Ом. Но это не значит, что можно хвататься за оголенные провода голыми руками! Этого сопротивления далеко не достаточно, чтобы защитить человека от опасного электрического тока.

Резко уменьшают сопротивление человека потливость кожного покрова, переутомление, нервное возбуждение. Значение снижается до 800–1000 Ом. Поэтому даже самое небольшое напряжение может вызвать ожог кожи.

Задачи на данную тему встречаются в №12 ЕГЭ. Давайте рассмотрим один пример.

Задача. Найдите внутреннее сопротивление источника ЭДС, если сопротивление в цепи R = 4 Ом, а ЭДС ε=10 В. Сила тока в цепи 2 А.

Решение.Воспользуемся законом Ома для полной цепи и выразим из него внутреннее сопротивление источника ЭДС:

(I=frac{ε}{R + r}),
(r=frac{ε}{I}-R=frac{10}{2}-4=1) (Ом).

Ответ: 1 Ом

Короткозамкнутая цепь

Рассмотрим частный случай электрической цепи, в котором источник тока будет подключен сам на себя. Иначе говоря, он будет короткозамкнутым.

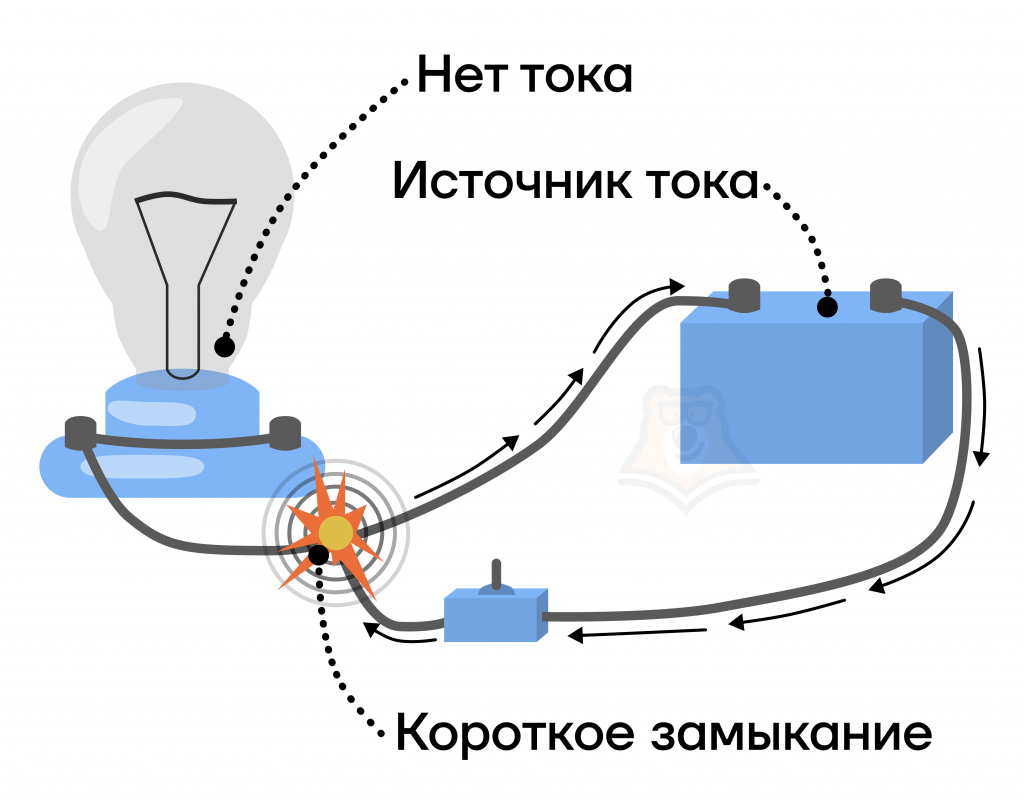
В этом случае отсутствует сопротивление внешней цепи и закон Ома для цепи будет выглядеть так:

(I_{кз}=frac{ε}{r}) , где

(I_{кз}) – ток короткого замыкания (А);
(ε) – ЭДС источника тока (В);
(r) – сопротивление источника ЭДС (Ом).

Короткое замыкание — это такой случай соединения проводов, при котором практически весь ток проходит по пустому проводу и возвращается в источник тока.

Короткое замыкание приводит к сильному нагреву, расплавлению металлов, а иногда и к пожарам.

К чему может привести авария среди электронов?

Если сравнить поток электронов с потоком машин, то ток короткого замыкания – это авария на автодороге. Один поток машин решил влезть в другой. В результате на дороге образовалась авария. Но машины продолжают налетать одна на другую (как в метель в Норильске).

При коротком замыкании сила тока будет увеличиваться до тех пор, пока отключающие механизмы не прекратят поступление силы тока.

Теперь, когда мы уже рассмотрели основные характеристики источника тока, можем перейти к мощности и КПД источника тока.

Мощность и КПД источника тока

Мы уже не раз говорили о том, что при протекании тока выделяется энергия. Источники тока не исключение. При подключении их к цепи на них выделяется энергия. При этом энергия выделяется и в самой цепи.

Чтобы найти мощность передачи энергии (P), выделяемой источником тока, необходимо умножить силу тока на ЭДС этого источника тока. Тогда получим:

(P_{ист}=εI), где

(P_{ист}) – мощность источника тока (Вт);
(ε) – ЭДС источника тока (В);
(I) – сила тока (А).

При этом часть этой мощности уходит на элементы внешней цепи, а другая часть – на преодоление внутреннего сопротивления источника тока:

(εI = I^2R + I^2r).

Тогда мощность, выделяемая на внешней цепи:

(P_R=I^2R).

А мощность, которая теряется на внутреннее сопротивление источника тока:

(P_r=I^2r).

Теперь давайте рассмотрим коэффициент полезного действия (КПД, ) источника тока. Как мы уже говорили ранее, часть ЭДС источника тока уходит на внутреннее сопротивление, а часть – на внешнюю цепь. При этом вспомним, что КПД – это отношение полезной мощности к затраченной.

Запишем формулы для мощности:

(P_{ист}=εI=I^2(R+r)),
(P_R=IU =I^2R).

Тогда КПД:

(eta=frac{IU}{εI}*100%=frac{U}{ε}*100%=frac{R}{R+r}*100%), где

(eta) – КПД источника тока;
(ε) – ЭДС источника тока (В);
(U) – напряжение на внешней цепи (В);
(I) – сила тока (А):
(R) – сопротивление на внешней цепи (Ом);
(r) – сопротивление источника тока (Ом).

Также задачи на тему ЭДС встречаются и в №16 ЕГЭ. Сложность данных задач заключается в установлении правильной зависимости величин друг от друга.

Задача.Определите, как изменятся сила тока (А) в цепи и сопротивление резистора (Б), если ЭДС источника тока заменить на такую же ЭДС, но с большим внутренним сопротивлением.
1) увеличится
2) уменьшится
3) не изменится

Решение.
Б) Внешнее сопротивление никак не зависит от источника тока. Поэтому оно не изменится — выбираем ответ 3.

А) Запишем закон Ома для полной цепи:
(I=frac{ε}{R + r})
При увеличении внутреннего сопротивления знаменатель увеличится. Следовательно, сила тока уменьшится, так что вариант 2 тоже нам подходит.

Ответ: 23

Мы с вами выяснили, что источники тока – элементы электрической цепи, без которых самой цепи не существовало бы. Хотя, конечно, она бы существовала, но была бы бесполезной. Однако и они «не без греха», так как существует опасное внутреннее сопротивление, которое является головной болью для многих инженеров. А все потому, что оно снижает КПД источников тока. Дальше вы можете ознакомиться с полноценными электрическими схемами и посмотреть, как ток ведет себя за пределами источника тока.

Термины

Напряжение – произведение сопротивления элемента и протекающего через него тока.

Резистор (или резистивный элемент) – элемент электрической цепи, который может только потреблять энергию и не может ее создавать.

Сторонние силы — это все внешние силы, воздействующие на заряд.

Электростатическое поле — невидимое поле, создаваемое постоянными электрическими зарядами.

Фактчек

ЭДС источника тока (ε) — это физический параметр, который характеризует работу, затраченную на перемещение зарядов внутри источника сторонними силами: (ε =frac{А_{cт}}{q}).
Внутреннее сопротивление (r) — определяет количество потерь энергии при прохождении тока через источник тока.
Закон Ома для полной цепи: Сила тока в замкнутой цепи равна отношению ЭДС цепи к ее полному сопротивлению: (I =frac{ε}{R + r}).
Предельное значение силы тока для данного источника тока называется током короткого замыкания: (I_{кз} =frac{ε}{r}).
Полная мощность цепи — это есть мощность источника тока: (P_ист=εI).

Проверь себя

Задание 1.
Как рассчитывается ЭДС источника тока?

(ε =frac{А_{ст}}{q})
(ε =frac{U}{q})
(ε =frac{А_{ст}}{I})
(ε =frac{А_{ст}}{qt})

Задание 2.
Короткое замыкание — это:

Соединение концов участка цепи проводником, сопротивление которого очень мало по сравнению с сопротивлением участка цепи.
Соединение концов участка цепи проводником, сопротивление которого очень велико по сравнению с сопротивлением участка цепи.
Соединение концов участка цепи проводником, сопротивление которого не зависит от сопротивления участка цепи.
Отсутствие электрического тока в цепи.

Задание 3.
Чему равно ЭДС источника тока?

(ε = U_R- U_r)
(ε = U_R+ U_r)
(ε = U_R U_r)
(ε = U_R)

Задание 4.
От чего зависит сила тока в цепи с заданным источником тока?

от внутреннего сопротивления цепи
от внутреннего сопротивления источника тока
от внешнего сопротивления цепи
не зависит ни от каких величин

Задание 5.
Где самое большое сопротивление в человеке?

в сердце
в пищеварительной системе
на коже
в голове

Ответы: 1. — 1; 2. — 1; 3. — 2; 4. — 3; 5. — 3.

Источник

Закон Ома для полной цепи:

Работа тока на участке цепи равна произведению силы тока, напряжения па этом участке и промежутка времени, в течение которого совершалась работа:
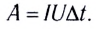
Закон Ома для полной цепи - формулы и определение с примерами

Закон Джоуля — Ленца:

количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени прохождения тока по проводнику:

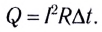
Закон Ома для полной цепи - формулы и определение с примерами

Для однородного участка цепи количество выделившейся теплоты можно вычислить по любой из трех эквивалентных формул: 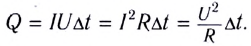Закон Ома для полной цепи - формулы и определение с примерами

Мощность, идущая на нагревание проводника, равна работе, которая совершается током за единицу времени:
Закон Ома для полной цепи - формулы и определение с примерами

Единицей мощности электрического тока, так же как и механической мощности, является ватт (1 Вт):
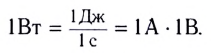
Закон Ома для полной цепи - формулы и определение с примерами

Коэффициент полезного действия (КПД) 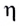Закон Ома для полной цепи - формулы и определение с примерами определяется отношением полезно использованной энергии 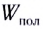к полной энергии 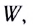полученной системой: 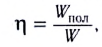и является характеристикой эффективности работы системы.

Рассмотрим полную электрическую цепь, содержащую источник ЭДС 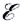Закон Ома для полной цепи - формулы и определение с примерами с внутренним сопротивлением r и подключенный к ним резистор сопротивлением R (рис. 121).

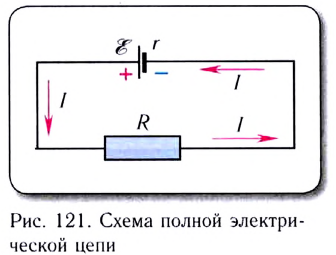
Закон Ома для полной цепи - формулы и определение с примерами

Из определения ЭДС источника тока следует, что совершаемая источником работа
Закон Ома для полной цепи - формулы и определение с примерами

Из закона сохранения энергии следует, что в такой цепи происходит превращение энергии, запасенной источником тока, только в теплоту. При этом работа сторонних сил за промежуток времени 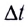Закон Ома для полной цепи - формулы и определение с примерами равна выделившемуся в цепи количеству теплоты:

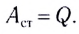
По закону Джоуля — Ленца

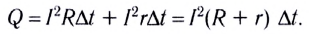
Закон Ома для полной цепи - формулы и определение с примерами
Таким образом,

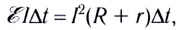
откуда

Полученное выражение представляет собой закон Ома для полной цепи:
сила тока в полной цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна полному сопротивлению цепи.
Заметим, что максимально возможный ток в цепи с данным источником тока возникает в том случае, если сопротивление внешней части цепи стремится к нулю.

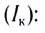
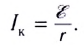
Максимально возможный ток через источник называют также током короткого замыкания Закон Ома для полной цепи - формулы и определение с примерами

Закон Ома для полной цепи - формулы и определение с примерами
Короткое замыкание представляет серьезную опасность для мощных источников тока, поскольку может вывести их из строя.

У гальванических элементов (батареек) сила тока короткого замыкания небольшая, поэтому оно для них не очень опасно.

Внутреннее сопротивление свинцовых аккумуляторов имеет значение от r = 0,1 Ом до r = 0,01 Ом, и сила тока короткого замыкания в них может быть от 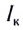Закон Ома для полной цепи - формулы и определение с примерами = 20 А до 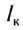= 200 А. А поскольку при этом возможно разрушение пластин аккумуляторов, то следует соблюдать меры безопасности при работе с ними.
В быту, в осветительных сетях, на распределительных станциях ЭДС имеет величины свыше 100 В, а внутреннее сопротивление цепи очень мало, и согласно закону Ома для замкнутой цепи сила тока короткого замыкания может доходить до 1000 А. Вследствие этого короткое замыкание может привести к пожару. Для зашиты от пожаров в электрические цепи включаются плавкие предохранители, которые плавятся при определенной силе тока и размыкают цепь.

Короткое замыкание может возникнуть из-за плохой изоляции, когда два токоведущих провода соединяются между собой (закорачиваются). Внешнее сопротивление цепи в этом случае стремится к нулю, и сила тока резко возрастает.

Короткое замыкание электропроводки в быту может стать причиной пожара, поэтому ни в коем случае не занимайтесь ремонтом электрических сетей самостоятельно!

Закон Ома для полной цепи можно записать в следующем виде:
Закон Ома для полной цепи - формулы и определение с примерами

Таким образом, ЭДС источника равна сумме падений напряжений на внешнем и внутреннем участках замкнутой цепи.

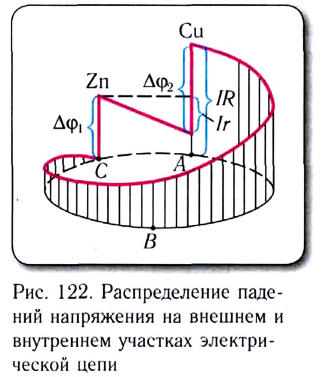
Закон Ома для полной цепи - формулы и определение с примерами

Закон Ома для полной цепи наглядно можно показать с помощью рисунка 122, где в качестве источника тока взят гальванический элемент Вольта (Сu—Zn).
Потенциал клеммы у цинковой пластины условно принят за нуль. Длина перпендикуляра к проводнику АВС в данной точке цепи пропорциональна ее потенциалу.

Падение напряжения на внешнем участке цепи равно IR, внутри источника — Ir.
Скачки потенциалов на цинковой и медной пластинах 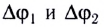Закон Ома для полной цепи - формулы и определение с примерами соответственно обусловлены химическими процессами.
Для лучшего понимания процессов, происходящих в замкнутой электрической цепи рассмотрим аналогичную механическую модель (рис. 123).

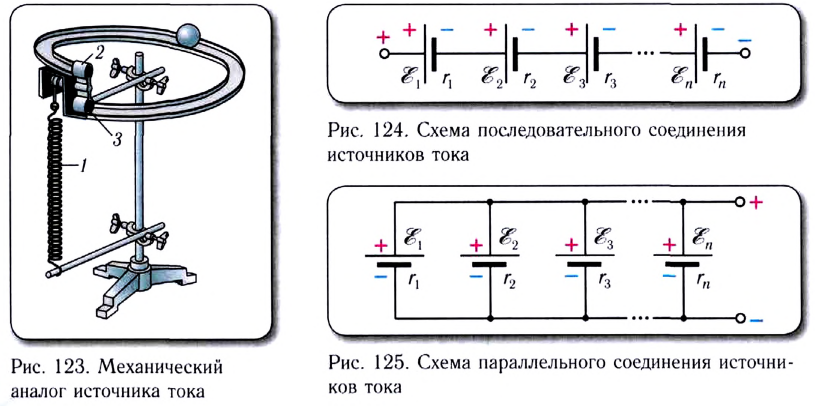
Закон Ома для полной цепи - формулы и определение с примерами

Подобно тому как шарик скатывается по винтовой наклонной плоскости под действием силы тяжести из положения 2 в положение 3, так электроны движутся на внешнем участке цепи под действием сил электрического поля.
Для того чтобы поднять шарик в исходное положение 2, необходимо совершить работу против силы тяжести, которая в случае электрической цепи аналогична работе сторонних сил внутри источника тока.

В данном случае пружинное устройство 1, совершающее работу за счет энергии упругой деформации, является механическим аналогом источника ЭДС в замкнутой цепи.

Для работы различных устройств мы используем батарейки (гальванические элементы), которые включаем последовательно с соблюдением полярности.
При последовательном соединении n источников тока, когда «минус» первого источника соединяется с «плюсом» второго и т. д. (рис. 124), их ЭДС и внутренние сопротивления суммируются:
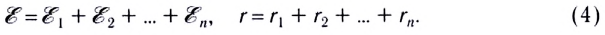
Закон Ома для полной цепи - формулы и определение с примерами
В частном случае, если 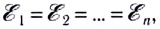то

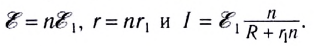
Параллельное соединение источников тока, когда «плюсы» всех источников соединяются в один узел, а «минусы» — в другой (рис. 125), используется значительно реже для повышения надежности электропитания. Можно показать, что при параллельном соединении п одинаковых источников тока суммарная ЭДС батареи равна ЭДС одного источника, а внутреннее сопротивление рассчитывается по законам параллельного соединения:
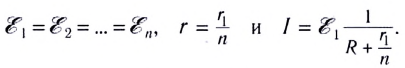
Закон Ома для полной цепи - формулы и определение с примерами

Работа по перемещению зарядов на неоднородном участке цепи равна сумме работ, совершаемых сторонними силами источника тока и силами электрического поля.

Поскольку напряжение на участке цепи равно отношению работы к перенесенному заряду 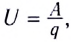Закон Ома для полной цепи - формулы и определение с примерами то

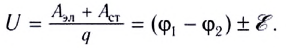
Знак перед 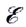Закон Ома для полной цепи - формулы и определение с примерами берется положительный, если ЭДС увеличивает потенциал в цепи в направлении прохождения тока, и отрицательный — если уменьшает.

С учетом того, что U = IR (R — полное сопротивление резисторов и источников ЭДС на участке цепи), находим силу тока на участке цепи:
Закон Ома для полной цепи - формулы и определение с примерами

Эта формула выражает закон Ома для неоднородного участка цепи: падение напряжения на неоднородном участке цепи — произведение силы тока I и сопротивления участка цепи R:
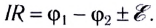
Закон Ома для полной цепи - формулы и определение с примерами

Отметим, что падение напряжения пропорционально суммарной работе всех сил, в то время как напряжение U пропорционально работе только электростатических сил.

Мощность, выделяемая на внешнем участке цепи, в которую включены тепловые потребители энергии, называется полезной мощностью. Для ее вычисления используются формулы:
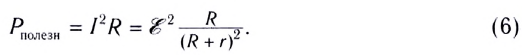
Закон Ома для полной цепи - формулы и определение с примерами

Мощность, выделяемая на внутреннем сопротивлении источника тока, называется теряемой мощностью и вычисляется по формулам:
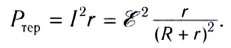
Закон Ома для полной цепи - формулы и определение с примерами

Сумма полезной и теряемой мощностей равна полной мощности источника тока, которая учитывает выделение энергии как на внешнем, так и на внутреннем участках цепи:
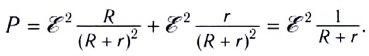
Закон Ома для полной цепи - формулы и определение с примерами

Коэффициент полезного действия источника тока, определяемый как отношение полезной мощности к полной, зависит от сопротивления нагрузки и внутреннего сопротивления источника тока:
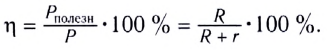
Закон Ома для полной цепи - формулы и определение с примерами

Наибольшую полезную мощность от данного источника можно получить тогда, когда внешнее сопротивление равно внутреннему (R = r), и в этом случае максимальный КПД 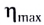Закон Ома для полной цепи - формулы и определение с примерами = 50 % (докажите это).

Заказать решение задач по физике

Закон Ома для полной цепи

Открытый Г. Омом закон для участка цени в общем случае справедлив и для полной цепи, если принимать во внимание как внешнюю, так и внутреннюю части цепи. Математическую запись закона Ома для этого случая можно получить на основании закона сохранения энергии, универсального для всех процессов в природе.

Пусть электрическая цепь состоит из источника тока, имеющего ЭДС и внутреннее сопротивление г, и проводника сопротивлением R (рис. 1.51).

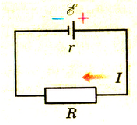
Закон Ома для полной цепи - формулы и определение с примерами
Pиc. 151. Замкнутая электрическая цепь

Согласно закону сохранения энергии работа сторонних сил равна сумме работ электрического тока во внешней и внутренней частях цепи:

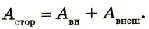
Закон Ома для полной цепи - формулы и определение с примерами

По определению
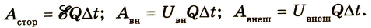
Закон Ома для полной цепи - формулы и определение с примерами

Отсюда

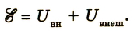
Закон Ома для полной цепи - формулы и определение с примерами

Если учесть, что по закону Ома для участка цепи U =IR, то получим формулу этого закона для полной цепи:

Закон Ома для полной цепи - формулы и определение с примерами

Таким образом, сила тока в полной цепи пропорциональна электроднижущей силе источника и обратно пропорциональна полному сопротивлению цепи.

Сила тока в полной цепи пропорциональна электродвижущей силе источника и обратно пропорциональна полному сопротивлению цепи:
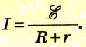
Закон Ома для полной цепи - формулы и определение с примерами

Пользуясь законом Ома для полной цепи, можно рассчитать два экстремальных случая н электрической цепи – короткое замыкание и разомкнутую цепь. Если сопротивление внешней цепи стремится к нулю (короткое замыкание), то сила тока в цепи
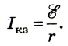
Закон Ома для полной цепи - формулы и определение с примерами

Это будет максимальное значение силы тока для данной цепи.
Если цепь разорвана (R→∞ ), то ток в цени прекращается при любых значениях ЭДС и внутреннего сопротивления. В последнем случае напряжение нм полюсах источника тока будет равно электродвижущей силе. Поэтому иногда дают упрощенное определение ЭДС: это величина, равная напряжению на клеммах источника при разомкнутой цепи.

Источники тока могут соединяться в батареи. Существуют несколько способов соединения источников тока.

Последовательным называют соединение, при котором соединяются друг с другом разноименные полюса источников: положительный предыдущего с отрицательным следующего и т. д. (рис. 1.52). Чаще всего соединяют источники с одинаковыми характеристиками, поэтому при последовательном соединении N источников ЭДС батареи будет в N раз больше, чем ЭДС одного источника:

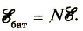
Закон Ома для полной цепи - формулы и определение с примерами

Внутреннее сопротивление такой батареи будет также в N раз больше:
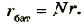
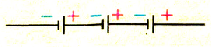
Закон Ома для полной цепи - формулы и определение с примерами

Закон Ома для полной цепи - формулы и определение с примерами
Рис. 152. Схема последовательного соединения источников тока

Для последовательного соединения источников тока закон Ома для полной цепи будет записываться:

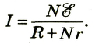
Закон Ома для полной цепи - формулы и определение с примерами

Последовательное соединение источников τoιca удобно в том случае, когда сопротивление потребителя значительно больше внутреннего сопротивления одного источника тока.
Параллельным является соединение, при котором все одноименные полюса соединяется в один узел (рис. 1.53).

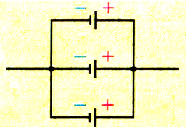
Закон Ома для полной цепи - формулы и определение с примерами

Pиc. 153. Схема параллельного соединения источников тока

Параллельное соединение применяют тогда, когда в цепи необходимо получить большое значение силы тока при небольшом напряжении.

Электродвижущая сила батареи параллельно соединенных одинаковых источников равна ЭДС одного источника:

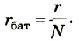
Закон Ома для полной цепи - формулы и определение с примерами

Формула закона Ома для параллельного соединения источников имеет вид:

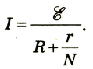
Закон Ома для полной цепи - формулы и определение с примерами

Параллельное соединения удобно тогда» когда сопротивление внешней части цепи значительно меньше внутреннего сопротивления одного источника.

При смешанном соединении батареи источников тока (параллельно или последовательно) в свою очередь соединяют последовательно или параллельно (рис. 1.54).

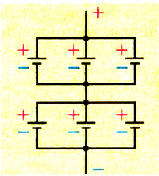
Закон Ома для полной цепи - формулы и определение с примерами
Pиc. 1.54. Смешанное соединение источников тoκa

Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
Сила и закон Ампера
Закон взаимодействия прямолинейных параллельных проводников с током
Сила Лоренца
Звуковые волны в физике
Электрическое поле в физике
Работа по перемещению заряда в электростатическом поле
Закон Ома для однородного участка электрической цепи

Источник

Идеальный источник ЭДС

Внутреннее сопротивление источника ЭДС

Закон Ома для полной цепи

Просадка напряжения

Как найти внутреннее сопротивление источника ЭДС

Вывод

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

Сторонняя сила

Закон Ома для полной цепи

КПД электрической цепи

Закон Ома для неоднородного участка

Закон Ома

Закон Ома для цепи

Для ЭДС

Для полной цепи

Для переменного тока

Для замкнутой цепи

Сфера применения

Последовательное и параллельное включение элементов

Цепь последовательно включенных резистивных элементов

Цепь параллельно включенных резистивных элементов

Интегральная и дифференциальная формы закона

На этой странице вы узнаете

Источник тока

Основные параметры источника тока

Закон Ома для участка цепи

Короткозамкнутая цепь

Мощность и КПД источника тока

Термины

Фактчек

Проверь себя

Закон Ома для полной цепи

Вам также может понравиться

Как найти вдохновение зимой

Как найти номер на айфоне если удалил

Как исправить папку которая не открывается

Добавить комментарий Отменить ответ