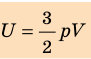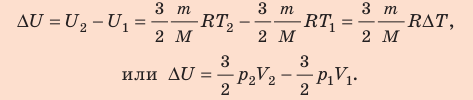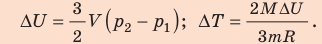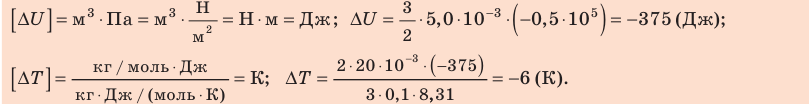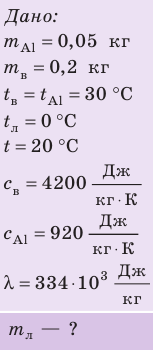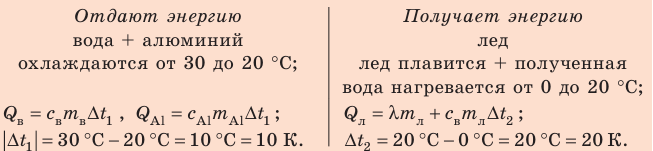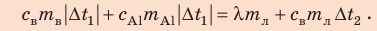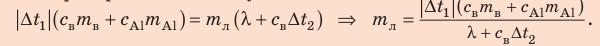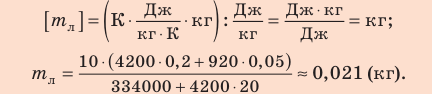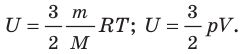Содержание:
- Определение и формула внутренней энергии
- Внутренняя энергия идеального газа
- Первое начало термодинамики
- Единицы измерения внутренней энергии
- Примеры решения задач
Определение и формула внутренней энергии
Определение
Внутренней энергией тела (системы) называют энергию, которая связана со всеми видами движения и взаимодействия частиц,
составляющих тело (систему), включая энергию взаимодействия и движения сложных частиц.
Из выше сказанного следует, что к внутренней энергии не относят кинетическую энергию движения центра масс системы и потенциальную энергию системы, вызванную действием внешних сил. Это энергия, которая зависит только от термодинамического состояния системы.
Внутреннюю энергию чаще всего обозначают буквой U. При этом бесконечно малое ее изменение станет обозначаться dU. Считается, что dU является положительной величиной, если внутренняя энергия системы растет, соответственно, внутренняя энергия отрицательна, если внутренняя энергия уменьшается.
Внутренняя энергия системы тел равна сумме внутренних энергий каждого отдельного тела плюс энергия взаимодействия между телами внутри системы.
Внутренняя энергия – функция состояния системы. Это означает, что изменение внутренней энергии системы при переходе системы из одного состояния в другое не зависит от способа перехода (вида термодинамического процесса при переходе) системы и равно разности внутренних энергий конечного и начального состояний:
$$Delta U=U_{2}-U_{1}(1)$$
Для кругового процесса полное изменение внутренней энергии системы равно нулю:
$$oint d U=0(2)$$
Для системы, на которую не действуют внешние силы и находящуюся в состоянии макроскопического покоя, внутренняя энергия – полная энергия системы.
Внутренняя энергия может быть определена только с точностью до некоторого постоянного слагаемого (U0), которое не определимо
методами термодинамики. Однако, данный факт не существенен, так как при использовании термодинамического анализа, имеют дело с изменениями
внутренней энергии, а не абсолютными ее величинами. Часто U_0 полагают равным нулю. При этом в качестве внутренней энергии рассматривают ее
составляющие, которые изменяются в предлагаемых обстоятельствах.
Внутреннюю энергию считают ограниченной и ее граница (нижняя) соответствует T=0K.
Внутренняя энергия идеального газа
Внутренняя энергия идеального газа зависит только от его абсолютной температуры (T) и пропорциональна массе:
$$U=int_{0}^{T} C_{V} d T+U_{0}=mleft(int_{0}^{T} c_{V} d T+u_{0}right)$$
где CV – теплоемкость газа в изохорном процессе; cV – удельная теплоемкость газа в изохорном процессе;
$u_{0}=frac{U_{0}}{m}$ – внутренняя энергия, приходящаяся на единицу массы газа
при абсолютном нуле температур. Или:
$$d U=frac{i}{2} nu R d T(4)$$
i – число степеней свободы молекулы идеального газа, v – число молей газа, R=8,31 Дж/(моль•К) – универсальная газовая постоянная.
Первое начало термодинамики
Как известно первое начало термодинамики имеет несколько формулировок. Одна из формулировок, которую предложил К.
Каратеодори говорит о существовании внутренней энергии как составляющей полной энергии системы.Она является функцией состояния,
в простых системах зависящей от объема (V), давления (p), масс веществ (mi), которые составляют данную систему:
$U=Uleft(p, V, sum m_{i}right)$ . В формулировке, которую дал Каратеодори внутренняя
энергия не является характеристической функцией своих независимых переменных.
В более привычных формулировках первого начала термодинамики, например, формулировке Гельмгольца внутренняя энергия системы вводится как физическая характеристика системы. При этом поведение системы определено законом сохранения энергии. Гельмгольц не определяет внутреннюю энергию как функцию конкретных параметров состояния системы:
$$Delta U=Q-A(5)$$
$Delta U$ – изменение внутренней энергии в равновесном процессе,
Q – количество теплоты, которое получила система в рассматриваемом процессе, A – работа, которую система совершила.
Единицы измерения внутренней энергии
Основной единицей измерения внутренней энергии в системе СИ является: [U]=Дж
Примеры решения задач
Пример
Задание. Вычислите, на какую величину изменится внутренняя энергия гелия имеющего массу 0,1 кг, если его температура увеличилась на 20С.
Решение. При решении задачи считаем гелий одноатомным идеальным газом, тогда для расчетов можно применить формулу:
$$d U=frac{i}{2} nu R d T(1.1)$$
Так как мы имеем с одноатомным газом, то $i=3 ; nu=frac{m}{mu}$, молярную массу
($mu$) возьмем из таблицы Менделеева
($mu_{H e}=4 cdot 10^{-3}$ кг/моль). Масса газа в представленном процессе
не изменяется, следовательно, изменение внутренней энергии равно:
$$Delta U=int_{T_{1}}^{T_{2}} d U=frac{i}{2} frac{m}{mu} R int_{T_{1}}^{T_{2}} d T=frac{i}{2} frac{m}{mu} Rleft(T_{2}-T_{1}right)$$
где $T_{2}-T_{1}=Delta T=Delta t$
Все величины необходимые для вычислений имеются:
$Delta U=frac{3}{2} cdot frac{0,1}{4 cdot 10^{-3}} cdot 20 cdot 8,31=6,2 cdot 10^{3}$ (Дж)
Ответ. $Delta U=6,2 cdot 10^{3}$ (Дж)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
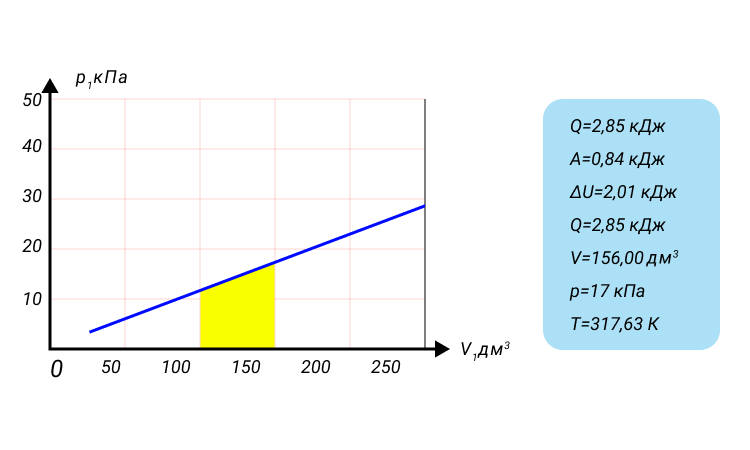
Задание. Идеальный газ расширили в соответствии с законом, который изображен графиком на рис.1. от начального объема
V0. При расширении объем сал равен $V=tau V_{0}$ .
Каково приращение внутренней энергии газа в заданном процессе? Коэффициент адиабаты равен $gamma$.
Решение. Исходя из рисунка, уравнение процесса можно представить аналитически как:
$$p=alpha V(2.1)$$
Показатель адиабаты связан с числом степеней свободы газа выражением:
$$gamma=frac{i+2}{i}(2.2)$$
Выразим число степеней свободы из (2.2):
$$i=frac{2}{gamma-1}$$
Приращение внутренней энергии для постоянной массы газа (см. Пример 1) найдем в соответствии с формулой:
$$Delta U=frac{i}{2} nu R Delta T(2.4)$$
Запишем уравнения состояний идеального газа для точек (1) и (2) рис.1:
$$
begin{aligned}
p V &=nu R T(2.5) \
p_{0} V_{0} &=nu R T_{0}
end{aligned}
$$
Тогда приращение температуры, учитывая уравнение процесса и выражения (2.5), (2.6) найдем как:
$$
begin{aligned}
Delta T &=T-T_{0}=frac{1}{nu R}left(p V-p_{0} V_{0}right)=frac{1}{nu R}left(alpha V cdot V-alpha V_{0} V_{0}right)=\
&=frac{1}{nu R}left(alpha tau V_{0} cdot tau V_{0}-alpha V_{0} V_{0}right)=frac{1}{nu R} V_{0}^{2} alphaleft(tau^{2}-1right)(2.7)
end{aligned}
$$
Подставим $Delta T$ в выражение для
$Delta U$ (2.4), получим:
$Delta U=frac{i}{2} v R frac{1}{v R} V_{0}^{2} alphaleft(tau^{2}-1right)=frac{1}{gamma-1} V_{0}^{2} alphaleft(tau^{2}-1right)$
Ответ. $Delta U=frac{1}{gamma-1} V_{0}^{2} alphaleft(tau^{2}-1right)$
Читать дальше: Формула времени.
Термодинамика – раздел физики, изучающий превращения энергии в макроскопических системах и основные свойства этих систем.
Термодинамика опирается на общие закономерности тепловых процессов и свойств макроскопических систем. Выводы термодинамики эмпирические, то есть опираются на факты, проверенные опытным путем с использованием молекулярно-кинетической модели.
Для описания термодинамических процессов в системах, состоящих из большого числа частиц, используются величины, не применимые к отдельным молекулам и атомам: температура, давление, концентрация, объем, энтропия)
Термодинамическое равновесие – состояние макросопической системы, когда описывающие ее макроскопические величины остаются неизменными.
В термодинамике рассматриваются изолированные системы тел, находящиеся в термодинамическом равновесии. То есть в системах с прекращением всех наблюдаемых макроскопических процессов. Особую важность представляет свойство, которое получило название выравнивания температуры всех ее частей.
При внешнем воздействии на термодинамическую систему наблюдается переход в другое равновесное состояние. Он получил название термодинамического процесса. Когда время его протекания достаточно медленное, система приближена к состоянию равновесия. Процессы, состоящие из последовательности равновесных состояний, называют квазистатическими.
Внутренняя энергия. Формулы
Внутренняя энергия считается важнейшим понятием термодинамики. Макроскопические тела (системы) имеют внутреннюю энергию, состящую из энергии каждой молекулы. Исходя из молекулярно-кинетической теории, внутренняя энергия состоит из кинетической энергии атомов и молекул, а также потенциальной энергии их взаимодействия.
Например, внутренняя энергия идеального газа равняется сумме кинетических энергий частиц газа, которые находятся в непрерывном беспорядочном тепловом движении. После подтверждений большим количеством экспериментов, был получен закон Джоуля:
Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема.
Применение молекулярно-кинетической теории говорит о том, что выражение для определения внутренней энергии 1 моля одноатомного газа, с поступательными движениями молекул записывается как:
U=32NАkT=32RT.
Зависимость от расстояния между молекулами у потенциальной энергии очевидна, поэтому внутренняя U и температура Т обусловлены изменениями V:
U=U(T, V).
Определение внутренней энергии U производится с помощью наличия макроскопических параметров, характеризующих состояние тела. Изменение внутренней энергии происходит по причине действия на тело внешних сил, совершающих работу. Внутренняя энергия является функцией состояния системы.
Когда газ в цилиндре сжимается под поршнем, то внешние силы совершают положительную работу A’. Силы давления газа на поршень также совершают работу, но равную A=-A’. При изменении объема газа на величину ∆V, говорят, что он совершает работу pS∆x=p∆V, где p – давление газа, S – площадь поршня, ∆x – его перемещение. Подробно показано в примере на рисунке 1.
Наличие знака перед работой говорит о работе газа в разных состояниях: положительная при расширении и отрицательная при сжатии. Переход из начального в конечное состояние работы газа может быть описан с помощью формулы:
A=∑pidVi или в пределе при ∆Vi→0:
A=∫V1V2pdV.
Рисунок 1. Работа газа при расширении.
Обратимые и необратимые процессы
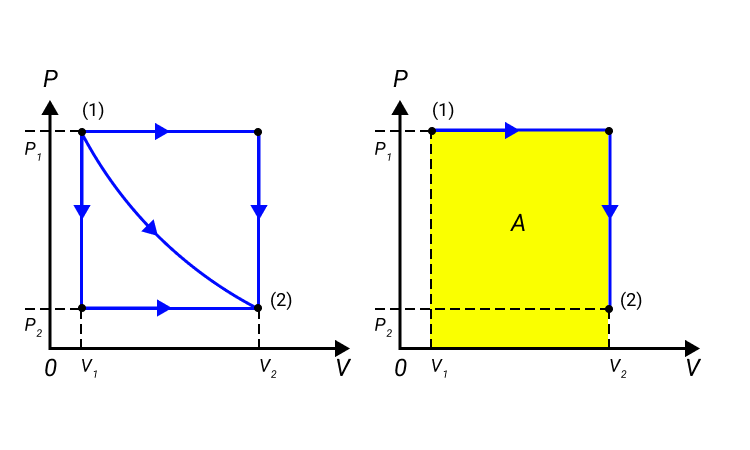
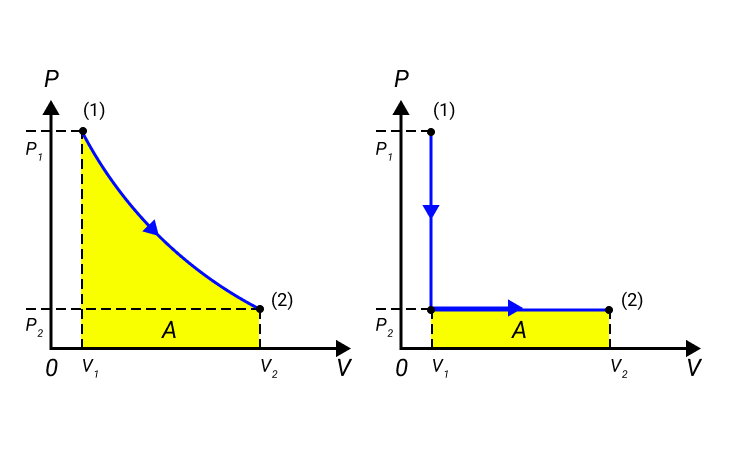
Работа численно равняется площади процесса, изображенного на диаграмме p, V. Величина А зависит от метода перехода от начального состояния в конечное. Рисунок 2 показывает 3 процесса, которые переводят газ из состояние (1) в состояние (2). Во всех случаях газ совершает работу.
Рисунок 2. Три различных пути перехода из состояния (1) в состояние (2). Во всех трех случаях газ совершает разную работу, равную площади под графиком процесса.
Процессы из рисунка 2 возможно провести в обратном направлении. Тогда произойдет изменение знака А на противоположный.
Процессы, которые возможно проводить в обоих направлениях, получили название обратимых.
Жидкости и твердые тела могут незначительно изменять свой объем, поэтому при совершении работы разрешено им пренебречь. Но их внутренняя энергия подвергается изменениям посредствам совершения работы.
Механическая обработка деталей нагревает их. Это способствует изменению внутренней энергии. Имеется еще один пример опыта Джоуля 1843 года, служащий для определения механического эквивалента теплоты, изображенного на рисунке 3. Во время вращения катушки, находящейся в воде, внешние силы совершают положительную работу A’>0, тогда жидкость повышает температуру из-за наличия силы трения, то есть происходит увеличение внутренней энергии.
Процессы примеров не могут проводиться в противоположных направлениях, поэтому они получили название необратимых.
Рисунок 3. Упрощенная схема опыта Джоуля по определению механического эквивалента теплоты.
Изменение внутренней энергии возможно при наличии совершаемой работы и при теплообмене. Тепловой контакт тел позволяет увеличиваться энергии одного тела с уменьшением энергии другого. Иначе это называется тепловым потоком.
Количество теплоты
Количество теплоты Q, полученное телом, называется его внутренней энергией, получаемой в результате теплообмена.
Рисунок 4. Модель работы газа.
Процесс передачи тепла тел возможен только при разности их температур.
Направление теплового потока всегда идет к холодному телу.
Количество теплоты Q считается энергетической величиной и измеряется в джоулях (Дж).
| Виды энергии: | ||
|---|---|---|
| Механическая | Потенциальная Кинетическая |
|
| ‹♦› | Внутренняя | |
| Электромагнитная | Электрическая Магнитная |
|
| Химическая | ||
| Ядерная | ||
 |
Гравитационная | |
 |
Вакуума | |
| Гипотетические: | ||
 |
Тёмная | |
| См. также: Закон сохранения энергии |
| Внутренняя энергия | |
|---|---|
 |
|
| Размерность | L2MT−2 |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
Вну́тренняя эне́ргия — принятое в физике сплошных сред, термодинамике и статистической физике название для той части полной энергии термодинамической системы, которая не зависит от выбора системы отсчета[1] и которая в рамках рассматриваемой задачи может изменяться[2]. То есть для равновесных процессов в системе отсчета, относительно которой центр масс рассматриваемого макроскопического объекта покоится, изменения полной и внутренней энергии всегда совпадают. Перечень составных частей полной энергии, входящих во внутреннюю энергию, непостоянен и зависит от решаемой задачи. Иначе говоря, внутренняя энергия — это не специфический вид энергии[3], а совокупность тех изменяемых составных частей полной энергии системы, которые следует учитывать в конкретной ситуации.
Внутренняя энергия как специфическое для термических систем понятие, а не просто как термин для обозначения изменяемой части полной энергии, нужна постольку, поскольку с её помощью в физику вводят новые величины: термические (температура и энтропия) и химические (химические потенциалы и массы составляющих систему веществ)[4].
Деление полной энергии системы на потенциальную, кинетическую, внутреннюю и т. д. зависит от формальных определений этих понятий и поэтому достаточно условно[5][K 1][K 2]. Так, иногда во внутреннюю энергию не включают потенциальную энергию, связанную с полями внешних сил[2][9][10]. Важно, что правильность получаемых при решении конкретной задачи результатов зависит от корректности составления уравнения энергетического баланса, а не от терминологических нюансов.
Воспринимаемые органами чувств человека нагрев или охлаждение макроскопического объекта при прочих равных условиях (например, при постоянстве давления) есть проявления изменения внутренней энергии этого объекта: при повышении температуры внутренняя энергия системы увеличивается, а при понижении температуры — уменьшается[11]. Обратное неверно: постоянство температуры объекта не означает неизменность его внутренней энергии (например, температура системы неизменна при фазовых переходах первого рода — плавлении, кипении и др.).
Свойства внутренней энергии[править | править код]
Непосредственно из определения внутренней энергии как части полной энергии вытекает, что
- внутренняя энергия есть индифферентный[12] скаляр, то есть во внутреннюю энергию не входит кинетическая энергия системы как единого целого и кинетическая энергия среды внутри системы (энергия смещения элементарных областей[13] при деформации твёрдых тел и энергия потоков жидкостей и газов в среде);
- внутренняя энергия есть величина аддитивная[5][14], то есть внутренняя энергия системы равна сумме внутренних энергий её подсистем;
- внутренняя энергия задаётся с точностью до постоянного слагаемого, зависящего от выбранного нуля отсчёта и не сказывающегося на экспериментальных замерах изменения внутренней энергии[15].
Составные части внутренней энергии[править | править код]
Термодинамика вопрос о природе внутренней энергии не рассматривает и энергетические превращения (подчас весьма сложные), происходящие внутри системы на микроуровне, не детализирует[16]. В статистической физике во внутреннюю энергию системы включают энергию разных видов движения и взаимодействия входящих в систему частиц: энергию поступательного, вращательного и колебательного движений атомов и молекул, энергию внутри- и межмолекулярного взаимодействия, энергию электронных оболочек атомов и др.[15]
Во внутреннюю энергию не включают те составные части полной энергии, которые не меняются при изменении макроскопического состояния системы. Так, при обычных температурах в состав внутренней энергии не включают энергию атомных ядер, ибо она в этих условиях не меняется[17]. Но если речь идёт о температурах, при которых начинается термический распад атомных ядер, то эту энергию необходимо учитывать.
Энергию системы в поле внешних сил в состав её внутренней энергии не включают при условии, что термодинамическое состояние системы при перемещении в поле этих сил не изменяется[15][18]. При изменении состояния системы под действием внешних полей во внутреннюю энергию системы включают потенциальную энергию системы в этих полях (гравитационном, электромагнитном)[19][20].
Влияние поля тяготения на внутреннюю энергию термодинамической системы учитывают тогда, когда высота рассматриваемого столба газа (жидкости) значительна, например, при анализе состояния атмосферы[20].
Так как поверхность тела растет пропорционально квадрату размеров этого тела, а объём — пропорционально кубу этих размеров, то для больших тел поверхностными эффектами по сравнению с объёмными можно пренебречь[21]. Однако для дисперсных систем с развитыми поверхностями раздела между жидкими, твердыми и газообразными фазами (адсорбенты и микрогетерогенные системы: коллоидные растворы, эмульсии, туманы, дымы) пренебрежение поверхностными эффектами недопустимо, более того, они определяют многие своеобразные свойства таких систем и для них энергию поверхностных слоёв на границах раздела фаз (поверхностную энергию) учитывают как часть внутренней энергии[22].
При решении задач, требующих учёта кинетической энергии (физика сплошных сред, техническая и релятивистская термодинамика), оперируют полной энергией, совместно рассматривая законы сохранения массы, энергии, заряда, законы механики и законы термодинамики[23].
Внутренняя энергия в равновесной термодинамике[править | править код]
Историческая справка[править | править код]
В термодинамику внутреннюю энергию ввёл Р. Клаузиус (1850), не озаботившийся присвоением специального наименования «функции 
[K 3]; впоследствии Клаузиус называл функцию 
Первое начало термодинамики[править | править код]
Первое начало (закон) термодинамики представляет собой конкретизацию общефизического закона сохранения энергии для термодинамических систем. В рамках традиционного подхода первое начало формулируют как соотношение, устанавливающее связь между внутренней энергией, работой и теплотой: одна из этих физических величин задаётся с помощью двух других, которые, будучи исходными объектами теории, в рамках самой этой теории определены быть не могут просто потому, что не существует понятий более общих, под которые можно было бы подвести подлежащие определению термины[41]. В соответствии с интерпретацией У. Томсона первое начало трактуют как дефиницию внутренней энергии для закрытых систем[33][42][2]. А именно, изменение внутренней энергии термодинамической системы 



|
(Первое начало в формулировке Томсона) |
В этом выражении использовано «термодинамическое правило знаков для теплоты и работы».
Термодинамика заимствует понятия энергии и работы из других разделов физики, тогда как определение количеству теплоты, наоборот, даётся только и именно в термодинамике. По этой причине логичнее сразу трактовать первое начало так, как это делали Клаузиус[31] и его последователи, а именно, как определение теплоты через внутреннюю энергию и работу[43][44]. С использованием «теплотехнического правила знаков для теплоты и работы» математическое выражение для первого начала в формулировке Клаузиуса имеет вид:

|
(Первое начало в формулировке Клаузиуса) |
При использовании термодинамического правила знаков для теплоты и работы знак у 

Первое начало в формулировке Томсона вводит внутреннюю энергию как физическую характеристику системы, поведение которой определяется законом сохранения энергии, но не определяет эту величину как математический объект, то есть функцию конкретных параметров состояния[45]. Альтернативное определение внутренней энергии предложено К. Каратеодори (1909), который сформулировал первое начало термодинамики в виде аксиомы о существовании внутренней энергии — составной части полной энергии системы — как функции состояния, зависящей для простых систем[46] от объёма системы 





|
(Первое начало в формулировке Каратеодори) |
Важно, что данное определение внутренней энергии справедливо для открытых систем[48]. В формулировке Каратеодори внутренняя энергия не представляет собой характеристическую функцию своих независимых переменных.
Постулат Тиссы[править | править код]
В аксиоматической системе Л. Тиссы набор постулатов термодинамики дополнен утверждением о том, что внутренняя энергия ограничена снизу, и что эта граница соответствует абсолютному нулю температуры[49].
Калорические уравнения состояния[править | править код]
Внутренняя энергия системы есть однозначная, непрерывная и ограниченная функция состояния системы[3]. Для определённости полагают внутреннюю энергию ограниченной снизу. За начало отсчёта внутренней энергии принимают её значения при абсолютном нуле температуры[50]. Уравнение, выражающее функциональную зависимость внутренней энергии от параметров состояния, носит название калорического уравнения состояния[51][52]. Для простых однокомпонентных систем калорическое уравнение связывает внутреннюю энергию с любыми двумя из трёх параметров 



|
(Калорическое уравнение состояния с независимыми переменными T и V) |

|
(Калорическое уравнение состояния с независимыми переменными T и p) |

|
(Калорическое уравнение состояния с независимыми переменными V и p) |
Выбор независимых переменных для калорического уравнения состояния, теоретически не имеющий принципиального значения, важен с практической точки зрения: удобнее иметь дело с непосредственно измеримыми величинами типа температуры и давления.
Применение термодинамики для решения практических задач часто требует знания параметров, конкретизирующих свойства изучаемого объекта, то есть требуется математическая модель системы, с необходимой точностью описывающая её свойства. К таким моделям, называемым в термодинамике уравнениями состояния, относятся термическое и калорическое уравнения состояния. Для каждой конкретной термодинамической системы её уравнения состояния устанавливают по экспериментальным данным или находят методами статистической физики, и в рамках термодинамики они считаются заданными при определении системы[53]. Если для системы известны её термическое и калорическое уравнения состояния, то тем самым задано полное термодинамическое описание системы и можно вычислить все её термодинамические свойства[52].
Внутренняя энергия как характеристическая функция[править | править код]
Условия равновесия и стабильности термодинамических систем, выраженные через внутреннюю энергию[править | править код]
Экспериментальное определение внутренней энергии[править | править код]
В рамках термодинамики абсолютное значение внутренней энергии найдено быть не может, поскольку она задаётся с точностью до аддитивной постоянной. Экспериментально можно определить изменение внутренней энергии, а неопределённость, обусловленную аддитивной постоянной, устранить выбором стандартного состояния в качестве состояния отсчёта[54]. С приближением температуры к абсолютному нулю внутренняя энергия становится независимой от температуры и приближается к определённому постоянному значению, которое может быть принято за начало отсчёта внутренней энергии[50].
С метрологической точки зрения нахождение изменения внутренней энергии есть косвенное измерение, поскольку это изменение определяют по результатам прямых измерений других физических величин, функционально связанных с изменением внутренней энергии. Основная роль при этом отводится определению температурной зависимости теплоёмкости системы. Действительно, дифференцируя калорическое уравнение состояния, получаем[55]:
![dU=left({frac {partial U}{partial T}}right)_{V}dT+left({frac {partial U}{partial V}}right)_{T}dV=C_{V}dT+left[Tleft({frac {partial p}{partial T}}right)_{V}-pright]dV=C_{V}dT+left({frac {alpha }{chi }}T-pright)dV.](https://wikimedia.org/api/rest_v1/media/math/render/svg/46c9830c246e58fdc14f3f977ffe63d614213d25)
|
Здесь 



|
где индексы 1 и 2 относятся к начальному и конечному состоянию системы. Для вычисления изменения внутренней энергии в изохорных процессах 


|
(Изменение внутренней энергии в изохорном процессе) |
Внутренняя энергия классического идеального газа[править | править код]
Из уравнения Клапейрона — Менделеева следует, что внутренняя энергия идеального газа зависит от его температуры и массы и не зависит от объёма[56] (закон Джоуля)[57][58]:

|
(Закон Джоуля) |
Для классического (неквантового) идеального газа статистическая физика даёт следующее калорическое уравнение состояния[53]:

|
(Внутренняя энергия идеального газа) |
где 



Каноническое уравнение состояния для внутренней энергии, рассматриваемой как характеристическая функция энтропии 


|
(Каноническое уравнение состояния для внутренней энергии) |
где 









Внутренняя энергия фотонного газа[править | править код]
В термодинамике равновесное тепловое излучение рассматривают как фотонный газ, заполняющий объём 

|
(Внутренняя энергия фотонного газа) |
где 

Каноническое уравнение состояния для внутренней энергии фотонного газа имеет вид[61]:

|
(Каноническое уравнение состояния для внутренней энергии фотонного газа) |
Внутренняя энергия в физике сплошных сред[править | править код]
В физике сплошных сред, составной частью которой является неравновесная термодинамика, оперируют полной энергией среды, рассматривая её как сумму кинетической и внутренней энергии среды . Кинетическая энергия сплошной среды зависит от выбора системы отсчета, а внутренняя энергия — нет [1]. Образно говоря, внутренняя энергия элементарного тела[13] среды как бы «вморожена» в элементарный объём и перемещается вместе с ним, а кинетическая энергия связана с движением внутри непрерывной среды. Для внутренней энергии принимают справедливость всех соотношений, даваемых для неё равновесной термодинамикой в локальной формулировке[62].
Комментарии[править | править код]
- ↑ …закон сохранения энергии, несмотря на кажущуюся ясность и простоту, в действительности нельзя считать ни простым, ни ясным. Этот закон выражает постоянство суммы трёх слагаемых: 1) кинетической энергии, 2) потенциальной энергии, зависящей от положения тела, и 3) внутренней молекулярной энергии в формах тепловой, химической или электрической. При этом, как указывает Пуанкаре[6], такое выражение закона не представляло бы затруднений, если бы между указанными слагаемыми можно было провести строгое различие, т. е. первое слагаемое зависело бы только от скоростей, второе не зависело бы от скоростей и внутреннего состояния тел, а третье зависело бы только от внутреннего состояния тел. На самом же деле это не так, ибо, например, в случае наэлектризованных тел их электростатическая энергия зависит и от состояния тел, и от их положения в пространстве: если же тела ещё и движутся, то их электродинамическая энергия зависит уже не только от состояния тел и их положения в пространстве, но и от их скоростей. Пуанкаре показывает, что в этих условиях выбор функции, которую мы называем «энергией», оказывается условным, и, следовательно, единственная возможная формулировка закона сохранения энергии гласит: «существует нечто, остающееся постоянным»[7].
- ↑ Важно понимать, что физике сегодняшнего дня неизвестно, что такое энергия. <…> Просто имеются формулы для расчёта определённых численных величин, сложив которые, мы получаем <…> всегда одно и то же число. Это нечто отвлечённое, ничего не говорящее нам ни о механизме, ни о причинах появления в формуле различных членов[8].
- ↑ Статью Р. Клаузиуса «О движущей силе теплоты и о законах, которые можно отсюда получить для теории теплоты (Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen)», опубликованную в 1850 году, принято ныне рассматривать в качестве работы, положившей начало термодинамике как научной дисциплине[28][29]. Использованное в статье Клаузиуса не слишком удачное[30] — по меркам сегодняшнего дня — понятие «Gesammtwärme (полное количество теплоты)» относится к трактовке смысла функции
, но не к названию этой функции.
- ↑ В некоторых изданиях указывают, что понятие «внутренняя энергия» введено У. Томсоном[34][2][35]. Ему же иногда приписывают авторство термина «внутренняя энергия»[26]. Говоря о механической энергии, Томсон в статье «О динамической теории теплоты»[33] не упоминает первую часть работы Клаузиуса «О движущей силе теплоты…»[36], в которой Клаузиус ввёл в рассмотрение свою — пока ещё безымянную — функцию
, но даёт ссылку[37] на вторую часть указанной статьи Клаузиуса[38], опубликованную в следующем номере журнала «Annalen der Physik». Иными словами, на момент сдачи в печать статьи «О динамической теории теплоты» Томсон знал об опередившей эту статью работе Клаузиуса. С точки зрения научного приоритета не имеет значения, представляет ли трактат Томсона опоздавшее с публикацией независимое исследование, либо же статья Клаузиуса послужила для Томсона отправной точкой для развития идей немецкого учёного.
- ↑ Применение в одном разделе разных правил знаков для теплоты и работы призвано приблизить написание приводимых в разделе формул к их написанию в источниках, из которых эти формулы заимствованы.
Примечания[править | править код]
- ↑ 1 2 Жилин, 2012, с. 84.
- ↑ 1 2 3 4 5 6 Физика. Большой энциклопедический словарь, 1998, с. 80.
- ↑ 1 2 Герасимов и др., 1970, с. 31.
- ↑ Более того, П. А. Жилин считает единственно правильным такой подход к построению/изложению физики сплошных сред, когда «…понятия энергии, температуры, энтропии и химического потенциала вводятся одновременно…» (Жилин П. А. Рациональная механика сплошных сред, 2012, с. 48). «…Нельзя сначала определить внутреннюю энергию, а затем химический потенциал и энтропию. Все эти понятия могут быть введены только одновременно» (Жилин П. А. Рациональная механика сплошных сред, 2012, с. 140)”.
- ↑ 1 2 Жилин, 2012, с. 111.
- ↑ Пуанкаре А., О науке, 1990, с. 105—106.
- ↑ Шамбадаль П., Развитие и приложение понятия энтропии, 1967, с. 13.
- ↑ Фейнман Р. Ф. и др., Фейнмановские лекции по физике, вып. 1—2, 2011, с. 74.
- ↑ Дырдин В. В. и др., Термодинамика, 2005, с. 14.
- ↑ Глаголев, Морозов, 2007, с. 13–14.
- ↑ Булер П., Физико-химическая термодинамика вещества, 2001, с. 21.
- ↑ Не зависящий от системы отсчёта.
- ↑ 1 2 Элементарная область (она же элементарный объём, она же частица, она же элементарное тело) сплошной среды есть мысленно выделяемый объём сплошной среды (континуума), который бесконечно мал по сравнению с неоднородностями среды и бесконечно велик по отношению к размерам частиц (атомов, ионов, молекул и т. п.) сплошной среды.
- ↑ 1 2 3 В физике сплошных сред различают аддитивность по геометрическим параметрам (длине растягиваемой пружины, площади поверхности раздела фаз, объёму), аддитивность по массе (экстенсивность) и аддитивность по элементарным телам сплошной среды. Различие в типах аддитивности имеет значение, когда, например, плотность по массе и плотность по телам не выражаются одна через другую, то есть являются независимыми величинами (например, не все рассматриваемые элементарные тела обладают массой или имеет значение распад или агрегация элементарных тел сплошной среды). Так, при образовании трещин на линии разрыва происходит удвоение числа элементарных тел, хотя массовая плотность при этом не меняется. Кинетическая энергия аддитивна по массе, тогда как внутренняя энергия аддитивна по элементарным телам, составляющим систему, но не всегда может рассматриваться как аддитивная функция массы. Для фотонного газа имеет место аддитивность внутренней энергии по объёму.
- ↑ 1 2 3 Базаров, 2010, с. 25.
- ↑ Герасимов и др., 1970, с. 26.
- ↑ Путилов К. А., Термодинамика, 1971, с. 59.
- ↑ Путилов К. А., Термодинамика, 1971, с. 54.
- ↑ Физическая энциклопедия, т. 1, 1988, с. 292.
- ↑ 1 2 Сычев, 2009.
- ↑ Базаров, 2010, с. 223.
- ↑ Герасимов и др., 1970, с. 19.
- ↑ Пальмов, 2008, с. 141.
- ↑ Clausius R., Ueber die bewegende Kraft der Wärme (1), 1850, S. 384.
- ↑ 1 2 Кричевский И. Р., Понятия и основы термодинамики, 1970, с. 126.
- ↑ 1 2 3 Гельфер, 1981, с. 162.
- ↑ Крутов В.И. и др., Техническая термодинамика, 1991, с. 7.
- ↑ Мюнстер А., Химическая термодинамика, 2002, с. 12.
- ↑ Гельфер, 1981, с. 159.
- ↑ Гельфер, 1981, с. 161—162.
- ↑ 1 2 Clausius, 1887, S. 33.
- ↑ 1 2 Второе начало термодинамики, 2012, с. 98.
- ↑ 1 2 3 4 Thomson W., Mathematical and Physical Papers, vol. 1, 1882, Article «On the dynamical theory of heat» (1851), pp. 174—232.
- ↑ Башкиров А. Г., Внутренняя энергия, 2006.
- ↑ Лопаткин А. А., Внутренняя энергия, 1971.
- ↑ Clausius R., Ueber die bewegende Kraft der Wärme (1), 1850.
- ↑ Thomson W., Mathematical and Physical Papers, vol. 1, 1882, Article «On the dynamical theory of heat» (1851), p. 195.
- ↑ Clausius R., Ueber die bewegende Kraft der Wärme (2), 1850.
- ↑ Rankine, 1872, p. 508.
- ↑ Гельфер, 1981, с. 164.
- ↑ Хазен, 2000.
- ↑ Kirchhoff G., Vorlesungen über die Theorie der Wärme, 1894, S. 63.
- ↑ Березин, 2008, с. 34.
- ↑ Борн, 1964, с. 230–231.
- ↑ Жилин, 2012, с. 140.
- ↑ Состояние простой термодинамической системы (газы и изотропные жидкости в ситуации, когда поверхностными эффектами и наличием внешних силовых полей можно пренебречь) полностью задано её объёмом, давлением в системе и массами составляющих систему веществ.
- ↑ Каратеодори К., Об основах термодинамики, 1964, с. 196.
- ↑ Дж. У. Гиббс в своей работе «О равновесии гетерогенных веществ» (1875—1876) рассматривает внутреннюю энергию как функцию энтропии, объёма и масс компонентов.
- ↑ Tisza, 1966, p. 125.
- ↑ 1 2 Внутренняя энергия // БСЭ (3-е изд.). Дата обращения: 10 марта 2016. Архивировано 11 марта 2016 года.
- ↑ Физическая энциклопедия, т. 5, 1998, с. 236.
- ↑ 1 2 Базаров, 2010, с. 30.
- ↑ 1 2 Кубо Р., Термодинамика, 1970, с. 25.
- ↑ Химическая энциклопедия, т. 4, 1995, с. 413.
- ↑ Полторак, 1991, с. 61.
- ↑ Герасимов и др., 1970, с. 51.
- ↑ Глазов В. М., Основы физической химии, 1981, с. 146.
- ↑ Базаров, 2010, с. 65.
- ↑ Базаров, 2010, с. 111.
- ↑ Гуггенгейм, Современная термодинамика, 1941, с. 165.
- ↑ Базаров, 2010, с. 157.
- ↑ Дьярмати И., Неравновесная термодинамика, 1974, с. 111.
Литература[править | править код]
- Clausius R. Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen (Anfang des Artikels) (нем.) // Annalen der Physik und Chemie. — 1850. — Bd. 79, Nr. 3. — S. 368—397.
- Clausius R. Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen (Ende des Artikels) (нем.) // Annalen der Physik und Chemie. — 1850. — Bd. 79, Nr. 4. — S. 500—524.
- Clausius R. Abhandlungen über die mechanische Wärmetheorie. Erste Abtheilung. — Braunschweig: Druck und Verlag von Friedrich Vieweg und Sohn, 1864. — xviii + 351 S.
- Clausius R. Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie (нем.) // Annalen der Physik und Chemie. — 1865. — Bd. 125, Nr. 7. — S. 353—400.
- Clausius R. Die mechanische Wärmetheorie. Band 1. — 3 Auflage. — Braunschweig: Druck und Verlag von Friedrich Vieweg und Sohn, 1887. — xvi + 403 S.
- Kirchhoff Gustav. Vorlesungen über mathematische Physik. Band IV. Theorie der Wärme (нем.). — Leipzig: Verlag von B. J. Teubner, 1894. — x + 210 S.
- Rankine W.J.M. A manual applied mechanics. — 6 ed. — London: Charles Griffin and company, 1872. — XVI + 648 с.
- Thomson William. Mathematical and Physical Papers. Volume 1. — Cambridge: The Cambridge University Press, 1882. — xii + 558 p.
- Tisza Laszlo. Generalized Thermodynamics. — Cambridge (Massachusetts) — London (England): The M.I.T. Press, 1966. — 384 с.
- Базаров И. П. Термодинамика. — 5-е изд. — СПб. — М. — Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Башкиров А. Г. Внутренняя энергия // Большая российская энциклопедия. — Большая Российская энциклопедия, 2006. — Т. 5. — С. 476.
- Березин Ф. А. Лекции по статистической физике / Под ред. Д. А. Лейтеса. — М.: МЦНМО, 2008. — 197 с. — ISBN 978-5-94057-352-4.
- Борн М. Критические замечания по поводу традиционного изложения термодинамики // Развитие современной физики / Отв. ред. Б. Г. Кузнецов. — М.: Наука, 1964. — С. 223—256.
- Булер П. Физико-химическая термодинамика вещества. — СПб.: Янус, 2001. — 192 с. — ISBN 5-9276-0011-5.
- Гельфер Я. М. История и методология термодинамики и статистической физики. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1981. — 536 с.
- Герасимов Я. И., Древинг В. П., Еремин Е. Н. и др. Курс физической химии / Под общ. ред. Я. И. Герасимова. — 2-е изд. — М.: Химия, 1970. — Т. I. — 592 с.
- Гиббс Дж. В. Термодинамика. Статистическая механика / Отв. ред. Д. Н. Зубарев. — М.: Наука, 1982. — 584 с. — (Классики науки).
- Глаголев К. В., Морозов А. Н. Физическая термодинамика. — 2-е изд., испр. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2007. — 270 с. — (Физика в техническом университете). — ISBN 978-5-7038-3026-0.
- Глазов В. М. Основы физической химии. — М.: Высшая школа, 1981. — 456 с.
- Гуггенгейм. Современная термодинамика, изложенная по методу У. Гиббса / Пер. под ред. проф. С. А. Щукарева. — Л. — М.: Госхимиздат, 1941. — 188 с.
- Дырдин В. В., Мальшин А. А., Янина Т. И., Ёлкин И. С. Термодинамика: Учебное пособие. — Кемерово: Изд-во КузГТУ, 2005. — 148 с. — ISBN 5-89070-482-6.
- Дьярмати И. Неравновесная термодинамика. Теория поля и вариационные принципы. — М.: Мир, 1974. — 304 с.
- Жилин П. А. Рациональная механика сплошных сред. — 2-е изд. — СПб.: Изд-во Политехн. ун-та, 2012. — 584 с. — ISBN 978-5-7422-3248-3.
- Зубарев Д. Н. Внутренняя энергия // Физическая энциклопедия. — Советская энциклопедия, 1988. — Т. 1. — С. 292.
- Каратеодори К. Об основах термодинамики // Развитие современной физики. — Наука, 1964.
- Карно С., Клаузиус, Р., Томсон У. (лорд Кельвин) и др. Второе начало термодинамики / Под ред. А. К. Тимирязева. — 4-е изд. — М.: Либроком, 2012. — 312 с. — (Физико-математическое наследие: физика (термодинамика и статистическая механика)). — ISBN 978-5-397-02688-8.
- Квасников И. А. Термодинамика и статистическая физика. Т. 1: Теория равновесных систем: Термодинамика. — 2-е изд., сущ. перераб. и доп. — М.: Едиториал УРСС, 2002. — 240 с. — ISBN 5-354-00077-7.
- Кричевский И. Р. Понятия и основы термодинамики. — 2-е изд., пересмотр. и доп. — М.: Химия, 1970. — 440 с.
- В. И. Крутов, Исаев С. И., Кожинов И. А. и др. Техническая термодинамика / Под. ред. В. И. Крутова. — 3-е изд., перераб. и доп. — М.: Высшая школа, 1991. — 384 с. — ISBN 5-06-002045-2.
- Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
- Лопаткин А. А. Внутренняя энергия // Большая советская энциклопедия, 3-е изд. — Советская энциклопедия, 1971. — Т. 5. — С. 167.
- Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — 2-е изд., стер. — М.: УРСС, 2002. — 296 с. — ISBN 5-354-00217-6.
- Пальмов В. А. Фундаментальные законы природы в нелинейной термомеханике деформируемых тел. — СПб.: Изд-во СПбГПУ, 2008. — 143 с.
- Полторак О. М. Термодинамика в физической химии. — М.: Высшая школа, 1991. — 320 с. — ISBN 5-06-002041-X.
- Пуанкаре А. О науке / Пер. с фр. Под ред. Л. С. Понтрягина. — 2-е изд., стер. — М.: Наука, 1990. — 736 с. — ISBN 5-02-014328-6.
- Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с.
- Сивухин Д. В. Общий курс физики. Т. II. Термодинамика и молекулярная физика. — 5-е изд., испр. — М.: ФИЗМАТЛИТ, 2005. — 544 с. — ISBN 5-9221-0601-5.
- Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп.. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
- Фейнман Р. Ф., Лейтон Р. Б., Сэндс М. Фейнмановские лекции по физике. Вып. 1, 2. Современная наука о природе. Законы механики. Пространство. Время. Движение / Пер. с англ. под ред. Я. А. Смородинского. — 8-е изд., сущ. испр. — М.: УРСС; Либроком, 2011. — 439 с. — ISBN 978-5-453-00021-0 (УРСС), 978-5-397-02133-3 (Либроком).
- Физика. Большой энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — 944 с. — ISBN 5-85270-306-0.
- Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Длинные. — 704 с.
- Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5: Стробоскопические приборы — Яркость. — 760 с. — ISBN 5-85270-101-7.
- Хазен А. М. Разум природы и разум человека. — М.: РИО «Мособлполиграфиздата»; НТЦ «Университетский», 2000. — 600 с. — ISBN 5-7953-0044-6.
- Хачкурузов Г. А. Основы общей и химической термодинамики. — М.: Высшая школа, 1979. — 268 с.
- Химическая энциклопедия / Гл. ред. Н. С. Зефиров. — М.: Большая Российская энциклопедия, 1995. — Т. 4: Пол — Три. — 640 с. — ISBN 5-85270-092-4.
- Шамбадаль П. Развитие и приложение понятия энтропии / Пер. с франц. — М.: Наука, 1967. — 279 с.
Содержание:
Внутренняя энергия:
Вы знаете, что движущееся тело обладает кинетической энергией. А если оно еще и взаимодействует с другим телом, то обладает потенциальной энергией. Оба вида энергии представляют собой механическую энергию. Они взаимно превращаемы: кинетическая энергия может переходить в потенциальную и наоборот. Кроме того, вы знаете, что любое тело имеет дискретную структуру, т. е. состоит из частиц (атомов, молекул). Частицы находятся в непрерывном хаотическом движении. А частицы жидкости и твердого тела еще и взаимодействуют между собой. Следовательно, частицы обладают кинетической, а частицы жидкости и твердых тел — еще и потенциальной энергией. Сумма кинетической и потенциальной энергий всех частиц тела называется внутренней энергией. Внутренняя энергия измеряется в джоулях. Чем отличается внутренняя энергия от механической? В чем ее особенности? Может ли механическая энергия переходить во внутреннюю?
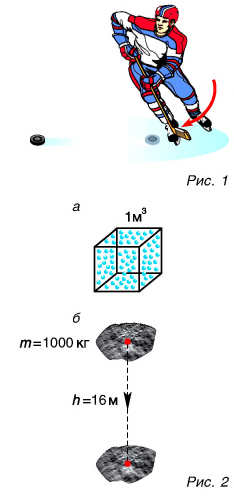
Для ответа на эти вопросы рассмотрим пример. Шайба, двигавшаяся горизонтально по льду (рис. 1), остановилась. Как изменилась ее механическая энергия относительно льда?
Кинетическая энергия шайбы уменьшилась до нуля. Положение шайбы над уровнем льда не изменилось, шайба не деформировалась. Значит, изменение потенциальной энергии равно нулю. Означает ли это, что се механическая (кинетическая) энергия исчезла бесследно? Нет. Механическая энергия шайбы перешла во внутреннюю энергию шайбы и льда.
А может ли внутренняя энергия тела, как механическая, быть равной нулю? Движение частиц, из которых состоит тело, не прекращается даже при самых низких температурах. Значит, тело всегда (подчеркиваем, всегда) обладает некоторым запасом внутренней энергии. Его можно либо увеличить, либо уменьшить — и только!
Велико ли значение внутренней энергии тела? Энергия одной частицы, например кинетическая, в силу незначительности ее массы чрезвычайно мала. Расчеты для средней энергии поступательного движения молекулы кислорода показывают, что ее значение при комнатной температуре
Главные выводы:
- Независимо от того, есть у тела механическая энергия или нет, оно обладает внутренней энергией.
- Внутренняя энергия тела равна сумме кинетической и потенциальной энергий частиц, из которых оно состоит.
- Внутренняя энергия тела всегда не равна нулю.
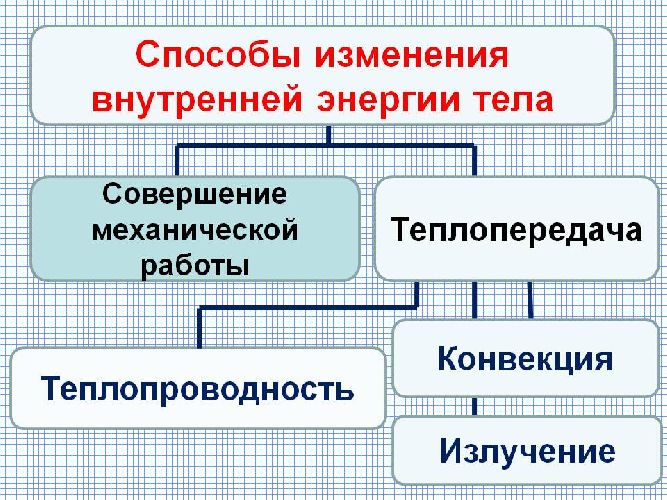
Способы изменения внутренней энергии
Чтобы изменить механическую энергию тела, надо изменить скорость его движения, взаимодействие с другими телами или взаимодействие частей тела. Вы уже знаете, что это достигается совершением работы.
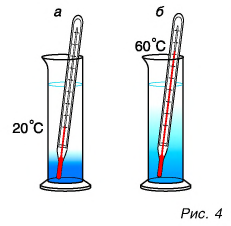
Как можно изменить (увеличить или уменьшить) внутреннюю энергию тела? Рассуждаем логически. Внутренняя энергия определяется как сумма кинетической и потенциальной энергий частиц. Значит, нужно изменить либо скорость движения частиц, либо их взаимодействие (изменить расстояния между ними). Очевидно, можно изменить и скорость, и расстояния между частицами одновременно. Изменить скорость частиц тела можно, увеличив или уменьшив его температуру. Действительно, наблюдения за диффузией показывают, что быстрота ее протекания увеличивается при нагревании (рис. 4, а, б).
Значит, увеличивается средняя скорость движения частиц, а следовательно, их средняя кинетическая энергия. Отсюда следует важный вывод: температура является мерой средней кинетической энергии частиц.
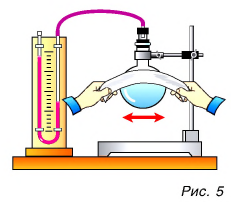
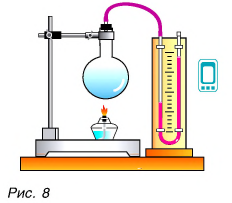
Как изменить кинетическую энергию частиц тела? Существуют два способа. Рассмотрим их на опытах. Будем натирать колбу с воздухом полоской сукна (рис. 5).
Через некоторое время уровень жидкости в правом колене манометра (см. рис. 5) опустится, т. е. давление воздуха в колбе увеличится. Это говорит о нагревании воздуха. Значит, увеличилась скорость движения и кинетическая энергия его молекул, а следовательно, и внутренняя энергия. Но за счет чего? Очевидно, за счет совершения механической работы при трении сукна о колбу. Нагрелась колба, а от нее — газ.
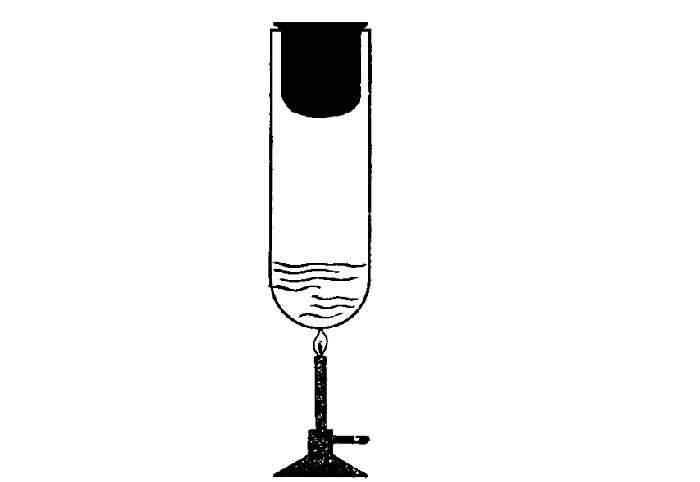
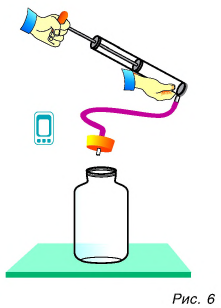
Проведем еще один опыт. В толстостенный стеклянный сосуд нальем немного воды (чайную ложку для увлажнения воздуха в нем. Насосом (рис. 6) будем накачивать в сосуд воздух. Через несколько качков пробка вылетит, а в сосуде образуется туман. Из наблюдений за окружающей средой мы знаем, что туман появляется тогда, когда после теплого дня наступает холодная ночь. Образование тумана в сосуде свидетельствует об охлаждении воздуха, т. е. об уменьшении его внутренней энергии. Но почему уменьшилась энергия? Потому что за ее счет совершена работа по выталкиванию пробки из сосуда.
Сравним результаты опытов. В обоих случаях изменилась внутренняя энергия газа, но в первом опыте она увеличилась, так как работа совершалась внешней силой (над колбой с газом), а во втором — уменьшилась, ибо работу совершала сила давления самого газа.
А можно ли, совершая работу, изменить потенциальную энергию взаимодействия молекул?
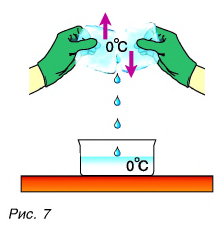
Опять обратимся к опыту. Два куска льда при О °C будем тереть друг о друга (рис. 7).
Лед превращается в воду, при этом температура воды и льда остается постоянной, равной О °C (см. рис. 7). На что тратится механическая работа силы трения?
Конечно же, на изменение внутренней энергии!
Но кинетическая энергия молекул не изменилась, так как температура не изменилась. Лед превратился в воду. При этом изменились силы взаимодействия молекул 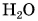
Совершение механической работы — один из способов изменения внутренней энергии тела.
А есть ли возможность изменить внутреннюю энергию тела, не совершая механическую работу?
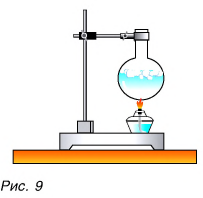
Да, есть. Нагреть воздух в колбе (рис. 8), расплавить лед (рис. 9) можно с помощью спиртовки, передав и воздуху, и льду теплоту. В обоих случаях внутренняя энергия увеличивается.
При охлаждении тел (если колбы со льдом и воздухом поместить в морозильник) их внутренняя энергия уменьшается. Теплота от тел передается окружающей среде.
Процесс изменения внутренней энергии тела, происходящий без совершения работы, называется теплопередачей (теплообменом).
Таким образом, совершение механической работы и теплопередача — два способа изменения внутренней энергии тела.
Величину, равную изменению внутренней энергии при теплопередаче, называют количеством теплоты (обозначается Q). Единицей количества теплоты, как работы и энергии, в СИ является 1 джоуль.
Для любознательных:
Физики XVIII в. и первой половины XIX в. рассматривали теплоту не как изменение энергии, а как особое вещество — теплород — жидкость (флюид), которая может перетекать от одного тела к другому. Если тело нагревалось, то считалось, что в него вливался теплород, а если охлаждалось — то выливался. При нагревании тела расширяются. Это объяснялось тем, что теплород имеет объем. Но если теплород — вещество, то тела при нагревании должны увеличивать свою массу. Однако взвешивания показывали, что масса тела не менялась. Поэтому теплород считали невесомым. Теорию теплорода поддерживали многие ученые, в том числе и такой гениальный ученый, как Г. Галилей. Позже Дж. Джоуль на основании проведенных им опытов пришел к выводу, что теплород не существует и что теплота есть мера изменения кинетической и потенциальной энергий движущихся частиц тела.
В дальнейшем выражение «сообщить телу количество теплоты» мы будем понимать как «изменить внутреннюю энергию тела без совершения механической работы, т. е. путем теплообмена». А выражение «нагреть тело» будем понимать как «повысить его температуру» любым из двух способов.
Главные выводы:
- Внутреннюю энергию тела можно изменить путем совершения механической работы или теплопередачи (теплообмена).
- Изменение внутренней энергии при нагревании или охлаждении тела при постоянном объеме связано с изменением средней кинетической энергии его частиц.
- Изменение внутренней энергии тела при неизменной температуре связано с изменением потенциальной энергии его частиц.
Основы термодинамики
МКТ стала общепризнанной на рубеже XIX и XX веков. Задолго до ее создания исследованием тепловых процессов занималась термодинамика — раздел физики, изучающий превращение внутренней (тепловой) энергии в другие виды энергии и наоборот, а также количественные соотношения при таких превращениях.
- Заказать решение задач по физике
Внутренняя энергия и ее особенности
Внутренняя энергия макроскопического тела определяется характером движения и взаимодействия всех микрочастиц, из которых состоит тело (система тел). Таким образом, к внутренней энергии следует отнести:
- кинетическую энергию хаотического (теплового) движения частиц вещества (атомов, молекул, ионов);
- потенциальную энергию взаимодействия частиц вещества;
- энергию взаимодействия атомов в молекулах (химическую энергию);
- энергию взаимодействия электронов и ядра в атоме и энергию взаимодействия нуклонов в ядре (внутриатомную и внутриядерную энергии).
Однако для описания тепловых процессов важно не столько значение внутренней энергии, как ее изменение. При тепловых процессах химическая, внутриатомная и внутриядерная энергии практически не изменяются. Именно поэтому внутренняя энергия в термодинамике определяется как сумма кинетических энергий хаотического (теплового) движения частиц вещества (атомов, молекул, ионов), из которых состоит тело, и потенциальных энергий их взаимодействия.
Внутреннюю энергию обозначают символом U.
Единица внутренней энергии в СИ — джоуль: [U]=1 Дж (J).
Особенности внутренней энергии идеального газа
- Атомы и молекулы идеального газа практически не взаимодействуют друг с другом, поэтому внутренняя энергия идеального газа равна кинетической энергии поступательного и вращательного движений его частиц.
- Внутренняя энергия данной массы идеального газа прямо пропорциональна его абсолютной температуре. Докажем данное утверждение для одноатомного газа. Атомы такого газа движутся только поступательно, поэтому, чтобы определить его внутреннюю энергию, следует среднюю кинетическую энергию поступательного движения атомов умножить на количество атомов:
Итак, для одноатомного идеального газа:
. Используя уравнение состояния
, выражение для внутренней энергии идеального одноатомного газа можно представить так:
- Внутренняя энергия — функция состояния системы, то есть она однозначно определяется основными макроскопическими параметрами (p, V, T), характеризующими систему. Независимо от того, каким образом система переведена из одного состояния в другое, изменение внутренней энергии будет одинаковым.
- Внутреннюю энергию можно изменить двумя способами: совершением работы и теплопередачей.
Какие существуют виды теплопередачи
Теплопередача (теплообмен) — процесс изменения внутренней энергии тела или частей тела без совершения работы. Процесс теплопередачи возможен только при наличии разности температур. Самопроизвольно тепло всегда передается от более нагретого тела к менее нагретому. Чем больше разность температур, тем быстрее — при прочих равных условиях — протекает процесс передачи тепла.
| Виды теплопередачи | ||
|---|---|---|
| Теплопроводность | Конвекция | Излучение |
|
Вид теплопередачи, который обусловлен хаотическим движением частиц вещества и не сопровождается переносом этого вещества. Лучшие проводники тепла — металлы, плохо проводят тепло дерево, стекло, кожа, жидкости (за исключением жидких металлов); самые плохие проводники тепла — газы. Передача энергии от горячей воды к батарее отопления, от поверхности воды до ее нижних слоев и т. д. происходит благодаря теплопроводности. |
Вид теплопередачи, при котором тепло переносится потоками жидкости или газа. Теплые потоки жидкости или газа имеют меньшую плотность, поэтому под действием архимедовой силы поднимаются, а холодные потоки — опускаются. Благодаря конвекции происходит циркуляция воздуха в помещении, нагревается жидкость в стоящей на плите кастрюле, существуют ветры и морские течения и т. д. В твердых телах конвекция невозможна. | Вид теплопередачи, при котором энергия передается посредством электромагнитных волн. Излучение — универсальный вид теплопередачи: тела всегда излучают и поглощают инфракрасное (тепловое) излучение. Это единственный вид теплообмена, возможный в вакууме (энергия от Солнца передается только излучением). Лучше излучают и поглощают энергию тела с темной поверхностью. |
Как определить количество теплоты
Количество теплоты Q — это физическая величина, равная энергии, которую тело получает (или отдает) в ходе теплопередачи.
Единица количества теплоты в СИ — джоуль: [П] =1 Дж (J).
Из курса физики 8 класса вы знаете, что количество теплоты, которое поглощается при нагревании вещества (или выделяется при его охлаждении), вычисляют по формуле: Q=cm∆Т=cm∆t , где c — удельная теплоемкость вещества; m — масса вещества; 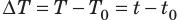
Обратите внимание! Произведение удельной теплоемкости на массу вещества, из которого изготовлено тело, называют теплоемкостью тела: C=cm . Если известна теплоемкость C тела, то количество теплоты, которое получает тело при изменении температуры на ∆T, вычисляют по формуле: Q=C∆T .
| Расчет количества теплоты при фазовых переходах | |
|---|---|
| Кристаллическое состояние ↔ Жидкое состояние | Жидкое состояние ↔ Газообразное состояние |
|
Температуру, при которой происходят фазовые переходы «кристалл → жидкость» и «жидкость → кристалл», называют температурой плавления. Температура плавления зависит от рода вещества и внешнего давления. Количество теплоты Q, которое поглощается при плавлении кристаллического вещества (или выделяется при кристаллизации жидкости), вычисляют по формуле: Q = λm, где m — масса вещества; λ — удельная теплота плавления. |
Фазовые переходы «жидкость → пар» и «пар → жидкость» происходят при любой температуре. Количество теплоты Q, которая поглощается при парообразовании (или выделяется при конденсации), вычисляют по формуле: Q=rm (Q=Lm), где m — масса вещества; r (L) — удельная теплота парообразования при данной температуре (обычно в таблицах представлена удельная теплота парообразования при температуре кипения жидкости). |
| Напомним: и при плавлении, и при кипении температура вещества не изменяется. |
Пример решения задачи №1
Неон массой 100 г находится в колбе объемом 5,0 л. В процессе изохорного охлаждения давление неона уменьшилось с 100 до 50 кПа. На сколько при этом изменились внутренняя энергия и температура неона?
Решение:
Неон — одноатомный газ; для таких газов изменение внутренней энергии равно:
Поскольку охлаждение изохорное, объем неона не изменяется: 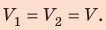
Проверим единицы, найдем значения искомых величин:
Анализ результатов. Знак «–» свидетельствует о том, что внутренняя энергия и температура неона уменьшились, — это соответствует изохорному охлаждению. Ответ: ∆U = –375 Дж; ∆T = –6 К.
Пример решения задачи №2
Внутренний алюминиевый сосуд калориметра имеет массу 50 г и содержит 200 г воды при температуре 30 °С. В сосуд бросили кубики льда при температуре 0 °С, в результате чего температура воды в калориметре снизилась до 20 °С. Определите массу льда. Удельные теплоемкости воды и алюминия: 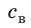
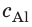
Анализ физической проблемы.
Калориметр имеет такое устройство, что теплообмен с окружающей средой практически отсутствует, поэтому для решения задачи воспользуемся уравнением теплового баланса. В теплообмене участвуют три тела: вода, внутренний сосуд калориметра, лед.
Решение:
Запишем уравнение теплового баланса:
После преобразований получим:
Проверим единицу, найдем значение искомой величины:
Ответ: 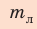
Выводы:
- В термодинамике под внутренней энергией U тела понимают сумму кинетических энергий хаотического движения частиц вещества, из которых состоит тело, и потенциальных энергий их взаимодействия. Внутренняя энергия однозначно определяется основными макроскопическими параметрами (p, V, T), характеризующими термодинамическую систему. Внутреннюю энергию идеального одноатомного газа определяют по формулам:
- Внутреннюю энергию можно изменить двумя способами: совершением работы и теплопередачей. Существует три вида теплопередачи: теплопроводность, конвекция, излучение.
- Физическую величину, равную энергии, которую тело получает или отдает при теплопередаче, называют количеством теплоты (Q): Q=cm∆T = С∆T — количество теплоты, которое поглощается при нагревании тела (или выделяется при его охлаждении); Q = λm — количество теплоты, которое поглощается при плавлении вещества (или выделяется при кристаллизации); Q=rm (Q=Lm) — количество теплоты, которое поглощается при парообразовании вещества (или выделяется при конденсации).
- Теплопроводность в физике
- Конвекция в физике
- Излучение тепла в физике
- Виды излучений в физике
- Машины и механизмы в физике
- Коэффициент полезного действия (КПД) механизмов
- Тепловые явления в физике
- Тепловое движение в физике и его измерение
Внутренняя энергия

4.6
Средняя оценка: 4.6
Всего получено оценок: 294.
4.6
Средняя оценка: 4.6
Всего получено оценок: 294.
Энергия как физическая величина характеризует способность физических объектов совершать работу. Механическая энергия является суммой потенциальной и кинетической энергий, которые зависят от взаимного расположения тел и скорости их движения. С помощью характеристики внутренней энергии в физике объясняются процессы, когда работа может совершаться покоящимся телом за счет энергии отдельных частиц, из которых состоит это тело.
Примеры внутренней энергии
Если в лабораторную колбу налить немного воды, закрыть ее пробкой и поставить нагреваться на плитке, то через некоторое время пробка выскочит под давлением пара, который образуется в результате кипения воды. То есть будет произведена работа по выталкиванию (перемещению) пробки, хотя весь объем пара (как целое) находился в состоянии покоя. Электрическая энергия перешла в тепло, которое довело воду до точки кипения, и образовавшийся пар (газообразное состояние воды) вытолкнул пробку. На совершение работа была затрачена внутренняя энергия пара.
.
Откуда берется эта энергия?
Все физические объекты (твердые, жидкие и газообразные) состоят из атомов и молекул, которые находятся в постоянном движении. В газах атомы и молекулы перемещаются внутри всего объема хаотично. В жидкостях длина пробега намного меньше, а в твердом теле молекулы колеблются в узлах кристаллической решетки. При повышении температуры возрастают скорость перемещения частиц, то есть увеличивается их кинетическая энергия, которая равняется:
$$Ek={mv^2 over 2}$$
где:
Ek — кинетическая энергия;
m — масса;
v — скорость.
Все частицы взаимодействуют друг с другом (притягиваются, отталкиваются), а значит обладают еще и потенциальной энергией Eп. Сумма этих двух энергий является внутренней энергией системы, которую обозначают U:
$$U=Ek + Eп $$
Скорости молекул в газах сильно зависят от массы молекул и температуры. Например, при комнатной температуре средняя скорость молекул в водороде составляет 1930 м/сек, а в кислороде — 480 м/сек.
Как измерить внутреннюю энергию?
Внутренняя энергия тела может изменяться под воздействием внешней средой либо получая или отдавая тепло Q, либо совершая работу А. Экспериментально можно измерить только изменение внутренней энергии U. Первый закон термодинамики устанавливает формулу нахождения U:
$∆U ={ Q – A }$
Величину совершенной работы и полученное (или отданное) тепло можно измерить, а значит можно определить изменение внутренней энергии.
Молекулярная внутренняя энергия идеального газа
Идеальным газом называют такую среду, в которой расстояния между молекулами настолько велики, что друг с другом они не взаимодействуют, а значит внутренняя энергия газа представляет собой только сумму кинетических энергий всех молекул. Для такой модели удается получить формулу для вычисления внутренней энергии U:
$$U={3mRTover 2}$$
где:
m — масса газа, кг;
M — молярная масса газа, кг/моль;
T — температура газа;
R — универсальная газовая постоянная, R = 8,3144598 Дж/(моль*К).
Из этой формулы следует, что внутренняя энергия идеального газа U зависит только от температуры.
Реальные физические объекты (газов, жидкостей, твердых тел) такая модель не описывает, так как необходимо учитывать энергию взаимодействия между частицами. Значит появится зависимость от объема тела.
Что мы узнали?
Итак, мы узнали, что внутренняя энергия тела — это сумма кинетической и потенциальной энергий всех частиц тела. В идеальном газе внутренняя энергия зависит только от температуры. Изменить внутреннюю энергию можно только либо с помощью совершения работы, либо подведения (или отбора) тепла к телу.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-
Айана Капсаргина
9/10
-
Мария Кшевач
8/10
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 294.
А какая ваша оценка?
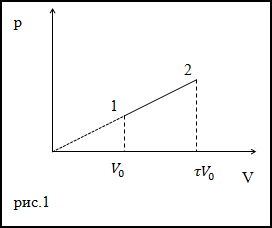

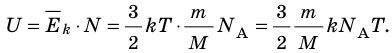 Итак, для одноатомного идеального газа:
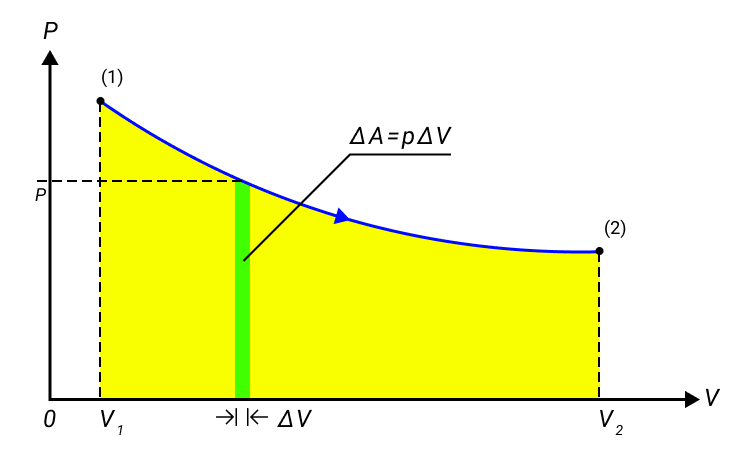
Итак, для одноатомного идеального газа: 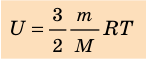 . Используя уравнение состояния
. Используя уравнение состояния 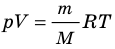 , выражение для внутренней энергии идеального одноатомного газа можно представить так:
, выражение для внутренней энергии идеального одноатомного газа можно представить так: