Внутренние
силовые факторы
В процессе
деформации бруса, под нагрузкой происходит
изменение взаимного расположения
элементарных частиц тела, в результате
чего в нем возникают внутренние силы.
По своей природе внутренние силы
представляют собой взаимодействие
частиц тела, обеспечивающее его
целостность и совместность деформаций.
Для определения этих сил применяют
метод сечений: надо мысленно рассечь
брус, находящийся в равновесии, на две
части и рассмотреть равновесие одной
из них.
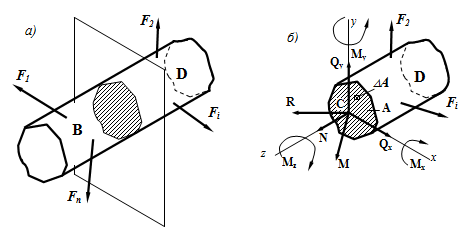
Под действием
внешних нагрузок в поперечном сечении
бруса возникают следующие внутренние
силовые факторы (рис. 2.1):
Nz = N –
продольная растягивающая (сжимающая)
сила
Mz = T – крутящий
(скручивающий) момент
Qx (Qy) = Q –
поперечные силы
Mx (My) = M –
изгибающие моменты
Каждый
внутренний силовой фактор определяется
из соответствующего уравнения равновесия
оставшейся после рассечения бруса части
(уравнения статики):
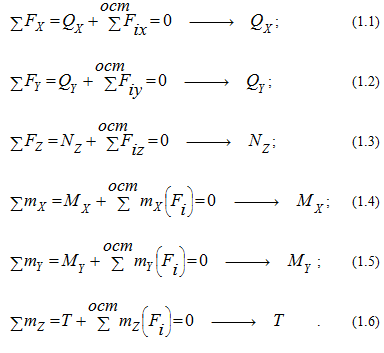
5. Виды нагружений. Понятие напряжения
Основные
виды нагружения
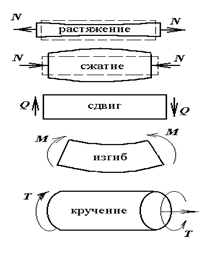
При простейших
случаях нагружения бруса в его поперечных
сечениях возникает один внутренний
силовой фактор (Рис. 2.2).
Если в
поперечном сечении бруса имеет место
только внутренняя продольная сила N,
такая деформация называется
растяжением/сжатием;
Если в
сечении бруса возникает только внутренний
крутящий момент T, то такая деформация
называется кручением (скручиванием);
Изгиб – вид
нагружения, при котором в поперечных
сечениях бруса действует изгибающий
момент M.
Случай,
когда в поперечных сечениях бруса есть
только поперечная сила Q называется
сдвиг.
Понятие о
напряжениях в точке
На основании
допущения о сплошности тела можно
считать, что внутренние силы непрерывно
распределены по всему сечению. Выделим
в произвольной точке малую площадку
ΔA, а равнодействующую внутренних сил
на этой площадке обозначим ΔR.
![]() Отношение
Отношение
представляет
собой среднее напряжение на данной
площадке. Если площадку ΔA уменьшить,
то в пределе получим полное напряжение
в точке
![]()
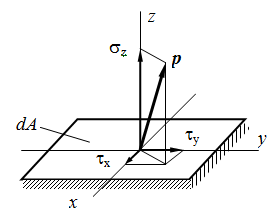
Полное
напряжение р может быть разложено на
три составляющие: по нормали к плоскости
сечения и по двум осям в плоскости
сечения. Проекция вектора полного
напряжения р на нормаль обозначается
через σ и называется нормальным
напряжением. Составляющие в плоскости
сечения называются касательными
напряжениями и обозначаются τ . В
зависимости от расположения и наименования
осей обозначения σ и τ снабжаются
системой индексов.
6, Закон Гука.
Зако́н
Гу́ка — уравнение теории упругости,
связывающее напряжение и деформацию
упругой среды
Для тонкого
растяжимого стержня закон Гука имеет
вид:
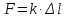
Здесь F— сила, которой растягивают (сжимают)
стержень,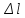 — абсолютное удлинение (сжатие) стержня,
— абсолютное удлинение (сжатие) стержня,
аk— коэффициент упругости
(или жёсткости).
Можно
выделить зависимость от размеров стержня
(площади поперечного сечения и длины
L) явно, записав коэффициент
упругости как
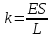
Величина
Eназывается модулем
упругости первого рода или модулем Юнга
и является механической характеристикой
материала.
Если
ввести относительное удлинение e
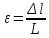
и нормальное
напряжение в поперечном сечении
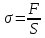
то закон
Гука в относительных единицах запишется
как
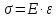
В такой
форме он справедлив для любых малых
объёмов материала.
Также при
расчёте прямых стержней применяют
запись закона Гука в относительной
форме
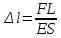
Следует
иметь в виду, что закон Гука выполняется
только при малых деформациях. При
превышении предела пропорциональности
связь между напряжениями и деформациями
становится нелинейной. Для многих сред
закон Гука неприменим даже при малых
деформациях.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
28.03.201514.85 Mб19История. Методичка.pdf
- #
- #
- #
- #
- #
- #
- #
- #

Внутренние силовые факторы (усилия) возникают в результате деформации бруса, когда под действием внешних нагрузок происходит изменение взаимного расположения элементарных частиц тела.
По своей природе внутренние силовые факторы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих усилий применяют метод сечений:
надо мысленно рассечь брус, находящийся в равновесии, на две части
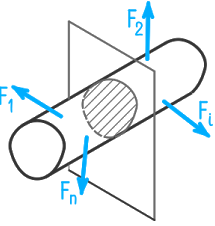
и рассмотреть равновесие одной из них.
Действие усилий отброшенной части бруса заменим уравновешивающими рассматриваемую часть внутренней силой R и внутренним моментом M.
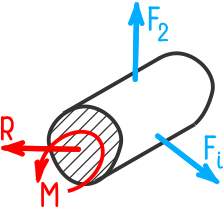
Для упрощения расчетов силу R и момент M принято раскладывать на составляющие усилия относительно осей координат x, y и z.
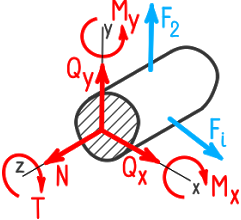
Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут возникать следующие внутренние силовые факторы:
- Nz = N — продольная растягивающая (сжимающая) сила;
- Mz = T — крутящий (скручивающий) момент;
- Qx (Qy) = Q — поперечные силы;
- Mx (My) = M — изгибающие моменты.
Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):
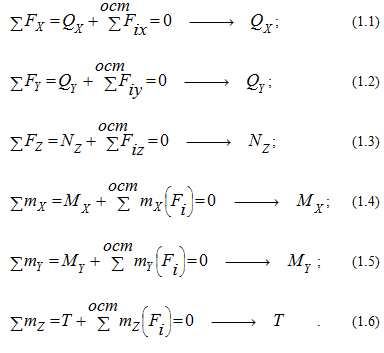
Наш видеоурок построения эпюр внутренних силовых факторов для балки:
Другие видео
Правила знаков для внутренних силовых факторов
Для определения знаков внутренних усилий, возникающих в брусе при различных способах его нагружения, приняты следующие правила:
- при растяжении/сжатии — положительными являются растягивающие усилия;
- при кручении — положительны моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки;
- при изгибе — положительны моменты сжимающие верхний слой балки.
Эпюры внутренних силовых факторов
В инженерной практике особое место занимает умение ясно представить взаимодействие усилий в конструкции, а также связь между внешними и внутренними силами в элементах конструкции, для этого графически изображают внутренние силовые факторы в функции осевой координаты и называют эти графики — эпюрами.
Примеры решения задач >
Основные виды нагружения и деформаций >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Техническая механика
Сопротивление материалов
Метод сечений. Напряжения
Сущность метода сечений
Для расчетов элементов конструкции на прочность необходимо знать внутренние силы упругости, возникающие в результате приложения внешних сил в разных точках и частях конструкции.
Но как заглянуть внутрь материального тела, чтобы выяснить, какие же силы возникают между его частицами или отдельными частями, при приложении нагрузок? Представление о внутренних усилиях, возникающих в теле или элементе конструкции можно получить лишь с помощью воображения и аксиом статики, поясняющих условия равновесного состояния материальных тел.
Способы определения этих внутренних сил с помощью науки сопротивление материалов включают такой прием, как метод сечений .
Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается и взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие на нее до разреза со стороны отброшенной части. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием приложенных к сечению внешних и внутренних сил (третий закон Ньютона – действие равно противодействию).
При применении этого метода выгоднее отбрасывать ту часть элемента конструкции (тела), для которой проще составить уравнение равновесия. Таким образом, появляется возможность определить внутренние силовые факторы в сечении, благодаря которым оставшаяся часть тела находится в равновесии (прием, часто применяемый в Статике).
Применяя к оставленной части тела условия равновесия, невозможно найти закон распределения внутренних сил по сечению, но можно определить статические эквиваленты этих сил (равнодействующие силовые факторы).
Так как основным расчетным объектом в сопротивлении материалов является брус, рассмотрим, какие статические эквиваленты внутренних сил проявляются в поперечном сечении бруса.
Рассечем брус (рис. 1) поперечным сечением а-а и рассмотрим равновесие его левой части.
Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а-а , будут главный вектор Fгл , приложенный в центре тяжести сечения, и главный момент Мгл = Ми , уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.
Разложим главный вектор на составляющую N , направленную вдоль оси бруса, и составляющую Q , перпендикулярную этой оси и лежащую в плоскости сечения. Эти составляющие главного вектора и главный момент называют внутренними силовыми факторами , действующими в сечении бруса. Составляющую N называют продольной силой , составляющую Q – поперечной силой , пару сил с моментом Ми – изгибающим моментом .
Для определения указанных трех внутренних силовых факторов применим известные из Статики уравнения равновесия оставленной части бруса:
Σ Z = 0; Σ Y = 0; Σ M = 0; (ось z всегда направляем по оси бруса).
Если внешние силы, действующие на брус, не лежат в одной плоскости, т. е. представляют собой пространственную систему сил, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (рис. 2) , для определения которых применяют известные из Статики шесть уравнений равновесия оставленной части бруса:
Σ X = 0; Σ Y = 0; Σ Z = 0;
Σ Mx = 0; Σ My = 0; Σ Mz = 0 .
Эти силовые факторы в общем случае носят следующие названия: N – продольная сила, Qx , Qy – поперечные силы, Мкр – крутящий момент, Мих и Миу – изгибающие моменты.
При разных деформациях в поперечном сечении бруса возникают различные силовые факторы.
Рассмотрим частные случаи:
1. В сечении возникает только продольная сила N . Это деформация растяжения (если N направлена от сечения) или сжатия (если N направлена к сечению).
2. В сечении возникает только поперечная сила Q . Это деформация сдвига .
3. В сечении возникает только крутящий момент Мкр . Это деформация кручения .
4. В сечении возникает только изгибающий момент Ми . Это деформация чистого изгиба . Если в сечении одновременно возникает изгибающий момент Ми и поперечная сила Q , то изгиб называют поперечным .
5. Если в сечении одновременно возникает несколько внутренних силовых факторов (например, изгибающий момент и продольная сила), то имеет место сочетание основных деформаций (сложное сопротивление).
Напряжение
Наряду с понятием деформации одним из основных понятий сопротивления материалов является напряжение (обозначается р ).
Напряжение характеризует интенсивность внутренних сил, действующих в сечении, и определяется, как отношение величины внутренней силы к площади сечения.
Напряжение является величиной векторной.
Вектор напряжения можно разложить на две составляющие (рис. 3) – одну вдоль оси сечения, вторую – в плоскости сечения (перпендикулярно оси). Эти составляющие носят название нормальное напряжение (обозначается σ) и касательное напряжение (обозначается τ ).
Поскольку нормальные и касательные напряжения расположены под прямым углом друг к другу, модуль полного напряжения p можно определить по теореме Пифагора:
Единица измерения напряжения – паскаль (Па).
1 Па = Н / м 2 . Поскольку эта единица очень мала, в расчетах часто применяют более крупную кратную единицу – мегапаскаль (МПа), который равен миллиону паскалей (10 6 Па).
Объяснить сущность напряжения можно на таком простом примере.
В соответствии с гипотезой об отсутствии первоначальных внутренних усилий, считается, что когда к телу не приложены внешние нагрузки его частицы не взаимодействуют друг с другом, т. е. абсолютно равнодушны к “соседкам” справа, слева и т. п. Но стоит приложить к телу внешнюю нагрузку, его частицы начинают лихорадочно цепляться друг за друга, пытаясь удержаться в “кучке”. Если нагрузка растягивает тело, его частицы держатся друг за дружку, не давая разорвать тело, если нагрузка сжимающая – частицы тела стараются удержать “соседок” на прежнем расстоянии.
Совокупность всех этих усилий внутренних частиц, противостоящих внешним раздражителям-нагрузкам, и является напряжением.
Задачи сопромата чаще всего сводятся к тому, чтобы определить предельные величины нагрузок, способных разорвать связи между частицами, из которых состоит тело или, по известным предельным напряжениям определить, какие нагрузки способно выдержать тело не разрушаясь, не деформируясь и т. д.
Нетрудно заметить, что напряжение измеряется в тех же единицах, что и давление, поэтому можно провести некоторую аналогию между этими физическими понятиями. Принципиальная разница заключается в том, что давление – внешний силовой фактор (т. е. воздействующий на тело или его части извне), а напряжение – внутренний силовой фактор, характеризующий степень взаимодействия (взаимосвязи) частиц тела между собой.
Метод сечений и внутренние силовые факторы (ВСФ)
Прочность твердого тела обусловлена силами сцепления между отдельными его частицами (атомами, молекулами и т. п.). В случае нагружения твердого тела внешней нагрузкой (активными и реактивными силами) внутренние силы сцепления изменяются. При этом появляются дополнительные внутренние силы, сопровождающие деформацию тела. Именно эти дополнительные внутренние силы и являются предметом изучения в курсе сопротивления материалов. По мере возрастания внешней нагрузки увеличиваются и внутренние силы, но лишь до определенного предела, при превышении которого наступает разрушение.
Для решения задач сопротивления материалов очень важно уметь определять внутренние силы и деформации стержня. При определении внутренних сил в каком-либо сечении стержня используют метод сечений.
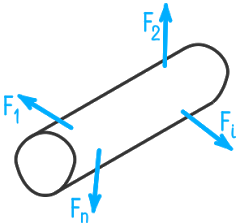
Рассмотрим на конкретном примере сущность метода сечений. Возьмем стержень, находящийся в состоянии равновесия под действием сил Ft, F2, F> и F4 (рис. 3,а). Для определения внутренних сил, действующих в произвольном сечении А, мысленно рассечем стержень и отбросим одну из двух полученных частей, например, правую. Тогда на оставшуюся левую часть стержня будут действовать внешние силы F и F2.
Рис. 3. Метод сечений: а) стержень, рассеченный плоскостью;
б) левая отсеченная часть стержня
Для того чтобы эта часть стержня оставалась в равновесии, следует действие отброшенной правой части стержня на оставшуюся левую часть заменить внутренними силами, приложенными по всему сечению (рис. 3, б).
Являясь внутренними силами для целого стержня, эти силы играют роль внешних сил для его левой части.
NB: в дальнейшем силы, возникающие в сечении, будем называть внутренними и в то же время на рисунках изображать их в виде внешних сил.
Распределенные по сечению внутренние силы образуют пространственную систему сил и приводятся к статически эквивалентным им обобщенным усилиям – главному вектору и главному моменту Мгл (рис. 4, а).
В сопротивлении материалов, характеризуя усилия в стержне, обычно рассматривают поперечные сечения, а обобщенные усилия представляют в главной координатной системе (при этом ось z направляют по нормали к сечению, а оси х и у располагают в плоскости сечения).
Проецируя главный вектор /?г, на оси координат, получаем три его составляющие: Ny Qy и Qx. Проекциями главного момента на координатные оси являются его составляющие: моменты Мх, Му и Г, каждый из которых стремится повернуть отсеченную часть стержня вокруг одной из координатных осей. Эти составляющие главного вектора и главного момента на координатные оси называют внутренними силовыми факторами (рис. 4, б).
Рис. 4. Метод сечений: а) приведение системы внутренних сил в сечении к главному вектору и главному моменту; б) разложение главного вектора и главного момента на координатные оси
Внутренними силовыми факторами называются проекции главного вектора и главного момента всех внутренних сил, возникающих в поперечном сечении стержня, на главные координаты оси, помещаемые обычно в центр тяжести сечения.
В общем случае нагружения стержня в его поперечном сечении могут возникать шесть внутренних силовых факторов, которые имеют следующие названия:
S N – продольная (нормальная) сила;
S Т – крутящий момент.
При известных внешних силах все шесть внутренних силовых факторов могут быть определены из шести уравнений статики (уравнений равновесия), которые составляются для отсеченной части стержня (правой или левой):
NB: в приведенных условиях равновесия отсеченной части стержня символами Fx omc , Fy omc и Fz ome обозначены проекции внешних сил на соответствующие координатные оси; а символом F° mc – внешние силы.
Рассмотренный метод сечений позволяет перевести внутренние силовые факторы в категорию внешних сил и, подчинив условиям равновесия, определить их величины и направления.
Сущность метода сечений заключается в следующих четырех действиях:
- 1. Рассечь мысленно стержень плоскостью, перпендикулярной его оси в том месте, где требуется найти внутренние силовые факторы (см. рис. 3, а).
- 2. Отбросить одну из частей стержня (правую или левую).
- 3. Заменить действие отброшенной части стержня на оставленную часть искомыми внутренними силовыми факторами (см. рис. 4, б). Равновесие оставленной части не нарушится лишь в том случае, если к ней приложить ВСФ, заменяющие действие отброшенной части. Для оставленной части они будут играть роль внешних сил (см. рис. 3, б).
- 4. Уравновесить оставленную часть стержня и из условий равновесия оставленной части стержня найти величины и направления внутренних силовых факторов.
От степени усвоения метода сечений зависит успешное изучение и понимание основных вопросов сопротивления материалов. Добиться этого несложно, если при применении метода сечений каждый раз последовательно использовать все четыре указанные операции. При этом следует помнить, что пропуск какой-либо из этих операций неизбежно приведет к ошибкам и недопониманию изучаемого вопроса.
При применении метода сечений должны быть предварительно определены все внешние силы и моменты, приложенные к отсеченной части стержня, в том числе и опорные реакции. Оставленная часть стержня должна рассматриваться как свободное тело, находящееся под действием приложенных к нему внешних сил, моментов и внутренних силовых факторов, не изменяющее своего положения в пространстве (опоры отсутствуют, так как их действия заменены опорными реакциями).
iSopromat.ru
Внутренние силовые факторы (усилия) возникают в результате деформации бруса, когда под действием внешних нагрузок происходит изменение взаимного расположения элементарных частиц тела.
По своей природе внутренние силовые факторы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих усилий применяют метод сечений:
надо мысленно рассечь брус, находящийся в равновесии, на две части
и рассмотреть равновесие одной из них.
Действие усилий отброшенной части бруса заменим уравновешивающими рассматриваемую часть внутренней силой R и внутренним моментом M.
Для упрощения расчетов силу R и момент M принято раскладывать на составляющие усилия относительно осей координат x, y и z.
Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут возникать следующие внутренние силовые факторы:
- Nz = N — продольная растягивающая (сжимающая) сила;
- Mz = T — крутящий (скручивающий) момент;
- Qx (Qy) = Q — поперечные силы;
- Mx (My) = M — изгибающие моменты.
Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):
Наш видеоурок построения эпюр внутренних силовых факторов для балки:
Правила знаков для внутренних силовых факторов
Для определения знаков внутренних усилий, возникающих в брусе при различных способах его нагружения, приняты следующие правила:
- при растяжении/сжатии — положительными являются растягивающие усилия;
- при кручении — положительны моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки;
- при изгибе — положительны моменты сжимающие верхний слой балки.
Эпюры внутренних силовых факторов
В инженерной практике особое место занимает умение ясно представить взаимодействие усилий в конструкции, а также связь между внешними и внутренними силами в элементах конструкции, для этого графически изображают внутренние силовые факторы в функции осевой координаты и называют эти графики — эпюрами.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
[spoiler title=”источники:”]
http://studme.org/230316/tehnika/metod_secheniy_vnutrennie_silovye_faktory
[/spoiler]
1. Метод сечений. Внутренние силовые факторы
Внешние силы стремятся разрушить конструкции или узлы, а внутренние силы противодействуют этому.
Рассмотрим произвольный брус, нагруженный самоуравновешенной системой сил (рис. 1.1):

Рис. 1.1 Приведение внешних нагрузок
Чтобы найти внутренние силы воспользуемся методом сечений РОЗУ (рис. 1.2).
Р – разрезаем произвольной плоскостью на А и В.
О – отбрасываем одну из этих частей, например, В (рис. 1.2а). Рассмотрим оставшуюся часть(рис. 1.2б).
З – заменяем. Внутренние силы мы заменяем главным вектором и главным моментом.
Рекомендуемые материалы

Рис. 1.2 Метод сечений РОЗУ
Раскладываем главный вектор и главный момент в плоскости на оси (рис. 1.2в).
Внутренние силовые факторы:
Qx, Qy – вызывают сдвиг – перерезывающие поперечные силы;
N – нормальная продольная шина, растяжение, сжатие бруса;
Мz – крутящий момент;
Мx, Мy – изгибающий момент (рис. 1.2в).
В общем случае нагружения в сечении действуют 6 внутренних факторов. График изменения внутреннего фактора при передвижении вдоль оси стержня называется – эпюрой.
У – уравновешиваем.
1.1 Построение эпюр внутренних факторов для стержней
Построение эпюр нормальных сил N
Правило знаков для N имеет физический смысл: нормальная сила является положительной, если вызывает растяжение бруса, отрицательной – если сжатие.
Пример 1 (рис. 1.3).
Если на стержень действуют силы, приложенные вдоль его оси, то он находится в условиях растяжения и остается только один внутренний фактор N.

Рис. 1.3 Стержень
Порядок построения эпюр:
1. Определяем реакции опор.
2. Разбиваем стержень на участки.
Участок – часть стержня между точками приложения сосредоточенных сил, включая опорные реакции.
3. Записываем аналитические выражения для внутренних силовых факторов.
4. Строим график (эпюру) (рис. 1.4).

Рис. 1.4 Построение эпюры нормальных сил
Эпюра – график, заштрихованный линиями, перпендикулярными оси.
Используя метод РОЗУ, отбрасывают ту часть, где больше нагрузки.
Внутренний фактор – равнодействующая внутренних сил.
Nz2 = P-3P = -2P
Nz2 = P-3P = -2P
Пример 2 (рис. 1.5).
Построить эпюру нормальных сил N.
q – интенсивность равномерно – распределенной нагрузки.
Опасное сечение в заделке, т.к. там самое большое значение N.

Рис. 1.5 Построение эпюры нормальных сил

Построим эпюру нормальных сил

1.2 Построение эпюр крутящих моментов
Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент, а прочие силовые факторы равны нулю. Для крутящего момента, независимо от формы сечения, принято следующее правило знаков.

Рис. 1.6 Правило знаков для крутящего момента
Если со стороны внешней нормали к сечению вращение осуществляется против часовой стрелки, то крутящий момент положительный (рис.1.6).
Правило знаков носит формальный характер (можно установить произвольно).
Стержень, в основном работающий на кручение, называется валом.

Рис.1.7 Схематичное изображение крутящего момента (против часовой стрелки).
Пример (К – 1)
Построить эпюру крутящих моментов (рис 1.9).

Рис.1.9 Построение эпюры крутящих моментов







Пример на построение эпюры крутящих моментов (рис 1.10).

Рис.1.10 Построение эпюры крутящих моментов




1.3 Построение эпюр поперечных сил Q и изгибающих моментов M для балок
Балка – стержень, в основном работающий на изгиб. При расчете балку принято заменять ее осью, все нагрузки приводятся к этой оси, а силовая плоскость будет совпадать с плоскостью чертежа.
Вал – стержень в основном работающий на кручение.
Виды опор:
Шарнирно-подвижная опора – опора, в которой может возникать только одна составляющая реакции, направленная вдоль опорного стержня (рис.1.11).

Рис.1.11 Шарнирно-подвижная опора
Шарнирно-неподвижная опора – опора, в которой могут возникать две составляющие реакции: вертикальная и горизонтальная (рис.1.12).

Рис.1.12 Шарнирно-неподвижная опора
Заделка (жесткое защемление) – опора, в которой могут быть: вертикальная и горизонтальная реакции и опорный момент (рис.1.13).

Рис.1.13 Заделка
1.3.1 Правило знаков для Q

1.3.2 Правило знаков для М
Эпюру для М строят на сжатых волокнах.

Пример (Э-3)
Построить эпюры внутренних усилий Q и M для однопролетной балки (рис. 1.14).

Рис. 1.14 Расчетная схема
Дано:
Р=0,5qa
M=0,5qa2
Решение:
Вычислим реакции опор.
Освободим балку от связей и заменим их действие реакциями.
Y: RA-P-q·2a+RB=0
Составим уравнения равновесия:
Сумма моментов всех сил относительно точки А равна


откуда



Сумма моментов всех сил относительно точки В равна


Разделим балку на четыре участка. Применим метод сечений на каждом из участков и запишем выражения для внутренних усилий


Внутренние усилия на втором участке равны


На третьем участке



Внутренние усилия на четвертом участке равны


Строим эпюры для M и Q (рис 1.15). Для проверки правильности полученных эпюр могут быть использованы следствия из дифференциальных зависимостей между Q и M.
Ещё посмотрите лекцию “Содержание и литература” по этой теме.

Рис. 1.15 Построение эпюр Q и M
