Треугольник вписанный в окружность

Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.

Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac<1><2>ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов



По числу равных сторон



Вершины углы и стороны треугольника
Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 – 2 bc · cos α
b 2 = a 2 + c 2 – 2 ac · cos β
c 2 = a 2 + b 2 – 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника

Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 – a 2
mb = 1 2 √ 2 a 2 +2 c 2 – b 2
mc = 1 2 √ 2 a 2 +2 b 2 – c 2
Биссектрисы треугольника

Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p – a ) b + c
lb = 2√ acp ( p – b ) a + c
lc = 2√ abp ( p – c ) a + b
где p = a + b + c 2 – полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника

Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b – c )( b + c – a )( c + a – b ) 4( a + b + c )
Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника

Формула Герона
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников

∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k – коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры – треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
Определение треугольника
Треугольник – это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом – △, после которго пишут названия вершин треугольника напр. △ABC.

Треугольник ABC (△ABC)
- Точки A, B и C – вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА – стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b – β, с – γ.
Углы треугольника, также, можно обозначать специальным символом – ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.

2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β

3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°

5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).

Свойства треугольника
1.Свойства углов и сторон треугольника.

- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника
Формулы медиан треугольника через стороны:
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/formula/triangle/
http://binary2hex.ru/triangle.html
[/spoiler]
Как найти внутренний угол треугольника
Содержание
- Ответ
- Проверено экспертом
- Внешние и внутренние углы треугольника.
- Особенности наружных и внутренних углов для сайдинга
- Назначение и характеристики угловых элементов
- Особенности стыковки
- Монтаж угловых профилей
- Рекомендации
- Как правильно вырезать внешний и внутренний угол на потолочном плинтусе своими руками
- Выбираем галтели на потолок
- Правильное решение — вырезать внешний и внутренний угол с помощью стусла
- Как правильно обрезать потолочный плинтус без стусла
- Другие способы ровно состыковать углы

- Как найти внутренний угол
- Как найти углы треугольника по трем его сторонам
- Как найти угол треугольника по его координатам
Для нахождения внутреннего угла треугольника вспомните теорему о сумме углов треугольника.
Теорема: сумма углов треугольника равна 180°.
Из этой теоремы выделите пять следствий, которые могут помочь в расчете внутреннего угла.
1. Сумма острых углов прямоугольного треугольника равна 90°.
2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
3. В равностороннем треугольнике каждый угол равен 60°.
4. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
5. Внешний угол треугольника равен сумме двух внутренних углов.
Пример 1:
Найти углы треугольника АВС, зная, что угол С на 15° больше, а угол И на 30° меньше угла А.
Решение:
Обозначьте градусную меру угла А через Х, тогда градусная мера угла С равна Х+15°, а угол В равен Х-30°. Так как сумма внутренних углов треугольника равна 180°, то вы получите уравнение:
Х+(Х+15)+(Х-30)=180
Решая его, вы найдете Х=65°. Таким образом угол А равен 65°, угол В равен 35°, угол С равен 80°.
Еще для нахождения внутреннего угла вы можете использовать равенство треугольников:
Теорема 1: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
На основе Теоремы 1 устанавливается Теорема 2.
Теорема 2: Сумма любых двух внутренних углов треугольника меньше 180°.
Из предыдущей теоремы вытекает Теорема 3.
Теорема 3: Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Также для вычисления внутреннего угла треугольника можно использовать теорему косинусов, но только в том случае, если известны все три стороны.
Ответ
Проверено экспертом
Длина сторон треугольника
Найдем угол между векторами AB(-3;3) и AC(1;-3)
Найдем угол между векторами BA(3;-3) и BC(4;-6)
Тогда третий угол, если А=153°, В=11°, С=180°-(153°+11°)=16°
Внешние и внутренние углы треугольника.
Данная геометрическая задача рассчитана на применение свойств произвольного треугольника, проверку знаний теоремы о сумме внутренних углов треугольника, понятии внешнего угла треугольника и его свойств.
По условию задачи, внешние углы треугольника пропорциональны числам 3,5 и7.
Требуется найти внутренние и внешние углы треугольника.
Возьмем произвольный треугольник ?АВС (см.рис.).
Обозначим внутренние углы треугольника ?, ? и ?, а смежные с ними внешние соответственно a,b,c
Введем неизвестную величину, равную x.Выразим через x внешние углы треугольника, исходя из условия задачи:
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.
По теореме, сумма смежных углов равна 180?.
Выразим внешние углы треугольника через смежные внутренние углы:
c =180? – ? , получим
180? – ? = 3x уравнение (1)
180? – ? = 5x уравнение (2)
180? – ? = 7x уравнение (3)
По теореме, сумма внутренних углов треугольника всегда равна 180 градусов.
? + ? + ? = 180? уравнение (4),
Решим систему 4х уравнений:
180? – ? = 3x уравнение (1)
180? – ? = 5x уравнение (2)
180? – ? = 7x уравнение (3)
? + ? + ? = 180? уравнение (4)
Для этого выразим из уравнения (4) угол ?:
? = 180? – ? – ? уравнение (5)
Подставим уравнение ( 5) в уравнение (1),
180? – (180? – ? – ?) = 3x (1)
Раскроем скобки, преобразуем
180? – 180? + ? + ? = 3x => ? + ? = 3x (1)
получим систему 3х уравнений:
Выразим угол ? из уравнения (2):
и преобразуем с учетом этого уравнение (1):
180? – 5x + ? = 3x (1) => 180? + ? = 3x + 5x => 180? + ? = 8 x
получим систему 2х уравнений с двумя неизвестными:
Выразим угол ? из уравнения (2):
Подставим полученное выражение для угла ? в уравнение (1):
180?+ 180? – 7x = 8x
360? = 15 х, отсюда:
Зная величину х, найдем углы треугольника.
Внешние углы треугольника :
a = 3x = 24? *3 = 72? ,
b = 5x = 24? *5 = 120? ,
c = 7x = 24? *7 =168?
Найдем внутренние углы треугольника, зная, что сумма смежных углов равна 180?:
? = 180? – a = 180? – 72? = 108?
? = 180? – b = 180? – 120? = 60?
? = 180? – c = 180? – 168? = 12?
108? + 60? + 12? = 180?, что соответствует теореме о сумме углов треугольника.
Угол a = 72? – пропорционален (кратен) 3
Угол b = 120? – пропорционален (кратен) 5
Угол c = 168 – пропорционален (кратен) 7, что удовлетворяет условиям задачи.
Также, можно было решить данную задачу, применив теорему о внешних углах треугольника ( внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним). Однако, в таком варианте получается более громоздкая система уравнений.
Особенности наружных и внутренних углов для сайдинга
При облицовке дома большое значение имеет правильный выбор комплектующих. Упростить работу и придать строению законченность позволят внутренний и наружный угол для сайдинга. Такие детали разбиваются на нескольких основных категорий, используемых в зависимости от ситуации. Монтаж доборов не составит особого труда при условии соблюдения простых правил.
Назначение и характеристики угловых элементов
Применение изделий обуславливается выбранной разновидностью. Вся продукция делится на группы, различающиеся выполняемыми функциями.
Основное назначение – создание нужного декоративного вида. Также детали играют защитную роль, препятствуя проникновению атмосферных осадков и ветра. Имеют обычную форму с углом 90 градусов. Выставляются после завершения основных работ.
Благодаря своей конструкции планка полностью закрывает стыковые соединения, образуя плавный переход. Хотя цветовая гамма элементов может быть весьма разнообразна, чаще всего в продаже встречаются варианты в светлом и темном исполнении.
Размерный ряд зависит от производителя, наиболее популярные параметры: ширина – 50*50 мм и 65*65, длина – от 2 до 4 м.
На заметку! В качестве альтернативы могут применяться комплектующие других отделочных материалов соответствующей формы.
Наиболее предпочтительная разновидность, выполняющая несколько функций:
Габариты сложных элементов также зависят от изготовителя. Наиболее распространенные параметры:
Эту продукцию часто относят к отдельной группе, но она может использоваться и для отделки фасадных участков. Элементы считаются сложными, хотя имеют внешний вид, имитирующий кирпичную или каменную облицовку. Длина деталей составляет 42–47 см, ширина бока 9–16 см.
Особенности стыковки
Поскольку при установке фрагментов не всегда есть возможность использовать целую деталь, возникает потребность соединения по длине (высоте). Для этого существует несколько методов:
Довольно распространенный способ, заключающийся в наложении верхнего элемента на нижний. Инструкция по монтажу:
Переход также можно сформировать, если нарастить участок при помощи накладки. Для этих целей используется обрезок применяемого элемента. Технология следующая:
Существенным недостатком метода является возможность проникновения влаги, поэтому дополнительно нужно использовать эластичный герметик.
Другие способы имеют намного больше минусов и не рекомендуются к применению.
На заметку! При монтировании фрагментов цокольной серии в качестве дополнительной детали можно использовать стартовую угловую планку.
Монтаж угловых профилей
Крепление фурнитуры происходит на определенном этапе отделочных работ и включает ряд обязательных действий.
Прикрепить его можно по следующему алгоритму:
- Изделие выставляется после фиксации стартовой планки. Существует два варианта подгонки: первый заключается в формировании зазора между доборами, второй – в подрезке нижней части углового элемента, что позволяет располагать начальный сегмент заподлицо. Ввиду того что внутренний участок каркаса не всегда расположена под углом 90 градусов, в случае необходимости деталь можно слегка выгнуть. Это обеспечит плотное и ровное прилегание.
- Сверху и снизу оставляются зазоры для компенсации расширения.
- Крепить элемент следует на саморезы. Если имеющиеся отверстия не подходят, то дополнительные прорезаются своими руками. Шуруп вкручивается по центру под прямым углом с зазором 1 мм.
Такой угол также используется при обшивке свеса фронтона и крыши.
Внешняя деталь сложной формы наиболее предпочтительна для работ снаружи. Монтаж производится по схеме:
- Элемент прикладывается к углу, отмечается месторасположение. При необходимости определяется участок для наращивания.
- С учетом зазора выставляется стартовая планка.
- Наружный сегмент опускается на 4–5 мм от начального фрагмента, но с обязательным промежутком сверху и снизу.
- Если требуется, угол можно немного согнуть в нужную сторону. Это особенно актуально при работе без обрешетки.
- Фиксация осуществляется на саморезы по тому же принципу, что и предыдущий вариант.
Наружный угловой сегмент применяется для отделки оконных и дверных проемов, выступая в роли наличника.
Следует знать! Простые элементы крепятся поверх созданной обшивки, для этого в них просверливаются отверстия.
Рекомендации
Чтобы сделать работу правильно, можно воспользоваться простыми советами:
- Подбор комплектующих той же марки, что и выбранный сайдинг, избавит от проблем с подгонкой.
- Обрезка производится при помощи болгарки, ножниц по металлу или электрического лобзика.
- Обязательно формировать зазоры между установочными профилями и крепежами.
- Лучше отказаться от слишком дешевой продукции. Из-за теплового расширения она может деформироваться и потянет за собой всю облицовку стен.
Если выбрать подходящий материал и выполнить работы правильно, то отделка дома прослужит долгие годы.
Как правильно вырезать внешний и внутренний угол на потолочном плинтусе своими руками
Угол между потолком и стеной в домах и квартирах редко бывает идеальным. В этом случае установка потолочного плинтуса — наиболее практичный способ закрыть неровную границу и украсить пространство над головой. Закрепить отделочные элементы на потолке — сравнительно несложно, например, с помощью «жидких гвоздей». При этом выполнить аккуратное сочленение своими руками вовсе непросто, и лучше предварительно ознакомиться, как правильно вырезать угол на потолочном плинтусе.
Выбираем галтели на потолок
Потолочный плинтус, другое название галтель или потолочный уголок, может быть изготовлен из различных материалов, а также иметь самую разную форму и размеры. Начиная с внешнего вида, следует выбирать высоту профиля элементов отделки пропорционально размерам комнаты. Так, для помещения высотой 2,7м подойдет плинтус высотой 50мм. В комнатах высотой от 2,5 до 3м будут уместны отделочные элементы соответственно от 40 до 80мм.
Замечательный выбор – долговечные и влагоустойчивые галтели из полиуретана. При этом их не рекомендуется использовать на кухне, где под воздействием меняющихся температур отделка может деформироваться.
Галтели из дерева выделяются экологической чистотой и проверены временем. Однако древесина может коробиться и менять свои размеры под воздействием колебаний температуры и влаги в определенных помещениях. Относительно большой вес таких изделий усложняет их монтаж наверху. Стыковать деревянные галтели сложнее, чем перечисленные выше. При отсутствии опыта установки плинтуса лучше его приобрести с определенным запасом, так как ошибки неизбежны.
Правильное решение — вырезать внешний и внутренний угол с помощью стусла
Может возникнуть впечатление, что галтель нужно просто подрезать под углом 45? и приклеить на место. Однако, действуя таким образом, можно совершить до трех ошибок:
При наличии даже одного упущения место стыка двух галтелей будет иметь недопустимые зазоры и щели. При этом применение простого и недорогого инструмента под названием стусло решает все проблемы. Кстати, его несложно сделать самому в соответствии с рекомендациями «Как правильно сделать своими руками стусло, фото самодельных конструкций».
В стандартном исполнении стусло позволяет резать заготовки под углами 30, 45, 60 и 90?, что обеспечивает возможность ровно зарезать как внутренние, так и внешние углы, а также ровно состыковать отрезки галтелей. Для резки таких материалов, как пенополистирол, можно воспользоваться пистолетным ножом с лезвием шириной 18мм, для работы с деревянным плинтусом и прочими материалами подойдет ножовка по металлу.
Внутренний угол в помещениях встречается заметно чаще, так что с него и начнем действовать по следующему плану:
- Сначала необходимо разметить галтель по длине, приложив к стене в соответствующем месте. Если это невозможно, придется воспользоваться рулеткой. Метку наносят карандашом, причем так, чтобы она не оставалась на галтели после обрезки.
- Заготовку укладывают в стусло таким образом, чтобы она находилась в рабочем положении. Ребро плинтуса, которое будет на стене, должно быть вверху, а та сторона, которой положено быть на потолке, попадает на дно стусла.
- Теперь вставляем ножовку в направляющие под углом 45? так, чтобы после обрезки ребро на потолке было короче ребра на стене. Левой рукой прижимаем заготовку к стуслу и аккуратно режем галтель, стараясь не допускать сколов материала.
- Так же вырезаем вторую деталь угла по направляющей, расположенной под 90? к предыдущему резу. Для этого заготовку размещаем на противоположной стороне стусла.
- Пробуем соединить детали на месте. При наличии зазора выполняем коррекцию напильником или ножом.
- Если плинтус имеет цветное покрытие, место реза необходимо подкрасить тем же цветом, иначе стык будет виден. Галтели можно клеить на место.
Наружный угол режется примерно так же, но если одна и та же деталь имеет оба вида углов, сначала вырезают внутренний. Действуем по следующему плану:
- При разметке внешнего стыка следует учесть, что деталь будет длиннее на величину ширины плинтуса.
- Заготовку укладывают в стусло таким образом, чтобы она находилась в рабочем положении. Ребро плинтуса, которое будет на стене, должно быть вверху, а та сторона, которой положено быть на потолке, попадает на дно стусла.
- Теперь вставляем ножовку в направляющие под углом 45? так, чтобы после обрезки ребро на потолке было длиннее ребра на стене. Левой рукой прижимаем заготовку к стуслу и аккуратно режем галтель, стараясь не допускать сколов материала.
В этом случае проблему решает профессиональная пила со стуслом, которая позволяет правильно отрезать деталь под любым углом. При ее отсутствии угол реза можно скорректировать, устанавливая прокладки между галтелью и стуслом. Пр этом толщина прокладки должна быть больше компенсируемого зазора во столько раз, во сколько расстояние от прокладки до места реза больше ширины плинтуса.
Как правильно обрезать потолочный плинтус без стусла
Разметку углов стыковки плинтуса можно сделать «по месту» на потолке, и тогда вопроса, под каким углом отрезать плинтус, не возникает. Более того, правильно обрезать галтель возможно без стусла, однако для получения углов без зазоров нужно работать очень аккуратно и точно.
В данном случае оформления внутреннего угла последовательность действий следующая:
Разметка внешнего угла производится по-другому. Плинтус прикладывается на место монтажа, и на его нижней кромке делается отметка линии угла на стене. Затем на вторую грань угла прикладывается обрезок галтели, и наносится отметка на верхней кромке заготовки в месте соприкосновения двух профилей. Разметка переносится с внутренней стороны плинтуса на внешнюю, и выполняется резка.
Заметим, что в данном случае остаются следы карандаша на потолке, которые не всегда просто удалить. Кроме того, вырезая каждый угол, операцию разметки нужно делать на месте. Вероятно, работать будет удобнее, если на подставке для резки нанести шаблон с пересечением линий под углом в 45?.
Теперь заготовку можно уложить на основание и отрезать, ориентируясь по шаблону. Кстати, разметку шаблона можно сделать с учетом отклонений углов в комнате и получить стыки без зазоров.
Другие способы ровно состыковать углы
Очень просто стыковку профиля в углах можно сделать с помощью специальных декоративных угловых элементов. К сожалению, не ко всякому плинтусу можно подобрать необходимые комплектующие.
Более того, дизайн подобных элементов далеко не всегда согласуется с общим интерьером комнаты. Напротив, в определенной ситуации специальные уголки послужат украшением помещения.
Как найти внутренний угол
Строительные работы, а также перепланировка квартиры и подготовка к ее ремонту требуют не только строительных навыков, но и познаний в математике, геометрии и пр. Так, часто бывает нужно найти внутренний угол треугольника.

Инструкция
Для нахождения внутреннего угла треугольника вспомните теорему о сумме углов треугольника.
Теорема: сумма углов треугольника равна 180°.
Из этой теоремы выделите пять следствий, которые могут помочь в расчете внутреннего угла.
1. Сумма острых углов прямоугольного треугольника равна 90°.
2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
3. В равностороннем треугольнике каждый угол равен 60°.
4. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
5. Внешний угол треугольника равен сумме двух внутренних углов.
Пример 1:
Найти углы треугольника АВС, зная, что угол С на 15° больше, а угол И на 30° меньше угла А.
Решение:
Обозначьте градусную меру угла А через Х, тогда градусная мера угла С равна Х+15°, а угол В равен Х-30°. Так как сумма внутренних углов треугольника равна 180°, то вы получите уравнение:
Х+(Х+15)+(Х-30)=180
Решая его, вы найдете Х=65°. Таким образом угол А равен 65°, угол В равен 35°, угол С равен 80°.
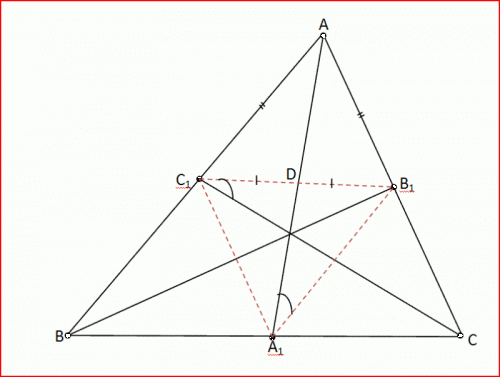
Поработайте с биссектрисой угла. В треугольнике АВС угол А равен 60°, угол В равен 80°. Биссектриса АD этого треугольника отсекает от него треугольник АСD. Попробуйте найти углы этого треугольника. Постройте график для наглядности.
Угол DAB равен 30°, так как AD – биссектриса угла А, угол ADC равен 30°+80°=110° как внешний угол треугольника ABD (следствие 5), угол С равен 180°-(110°+30°)=40° по теореме о сумме углов треугольника ACD.

Еще для нахождения внутреннего угла вы можете использовать равенство треугольников:
Теорема 1: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
На основе Теоремы 1 устанавливается Теорема 2.
Теорема 2: Сумма любых двух внутренних углов треугольника меньше 180°.
Из предыдущей теоремы вытекает Теорема 3.
Теорема 3: Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Также для вычисления внутреннего угла треугольника можно использовать теорему косинусов, но только в том случае, если известны все три стороны.
Вспомните теорему косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
a2=b2+c2-2bc cos A
или
b2=a2+c2- 2ac cos B
или
с2=a2+b2-2ab cos C
Источники:
- вычислить внутренние углы треугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Углы треугольника
Треугольники делятся на остроугольные (у которых все углы острые), тупоугольные (один угол тупой) и прямоугольные (один угол равен ![]() ).
).
Угол смежный с внутренним углом треугольника называется внешним углом.
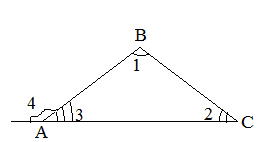
![]()
Примеры решения задач
![]()
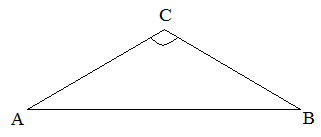
т.е. каждый из углов А и В заведомо меньше угла С. Это значит, что против угла С лежит большая сторона треугольника. Используя условие задачи, можно записать следующее неравенство:
![]()
т.е. сторона ![]() имеет наименьшую длину.
имеет наименьшую длину.
![]()
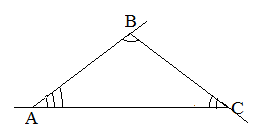
Внешний угол при вершине ![]() равен сумме внутренних углов при вершинах
равен сумме внутренних углов при вершинах ![]() и
и ![]() , т.е. равен
, т.е. равен ![]() . Аналогично получаем, что внешний угол при вершине
. Аналогично получаем, что внешний угол при вершине ![]() равен
равен ![]() , а внешний угол при вершине
, а внешний угол при вершине ![]() равен
равен ![]() .
.
Внешний угол треугольника
Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.

При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:

Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:
Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:
Из этого следует, что
Сократив обе части полученного равенства на одно и тоже число (∠4), получим:
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°
Рассмотрим треугольник ABC:

Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
Как найти внутренний угол

Для нахождения внутреннего угла треугольника вспомните теорему о сумме углов треугольника.
Теорема: сумма углов треугольника равна 180°.
Из этой теоремы выделите пять следствий, которые могут помочь в расчете внутреннего угла.
1. Сумма острых углов прямоугольного треугольника равна 90°.
2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
3. В равностороннем треугольнике каждый угол равен 60°.
4. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
5. Внешний угол треугольника равен сумме двух внутренних углов.
Пример 1:
Найти углы треугольника АВС, зная, что угол С на 15° больше, а угол И на 30° меньше угла А.
Решение:
Обозначьте градусную меру угла А через Х, тогда градусная мера угла С равна Х+15°, а угол В равен Х-30°. Так как сумма внутренних углов треугольника равна 180°, то вы получите уравнение:
Х+(Х+15)+(Х-30)=180
Решая его, вы найдете Х=65°. Таким образом угол А равен 65°, угол В равен 35°, угол С равен 80°.
Еще для нахождения внутреннего угла вы можете использовать равенство треугольников:
Теорема 1: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
На основе Теоремы 1 устанавливается Теорема 2.
Теорема 2: Сумма любых двух внутренних углов треугольника меньше 180°.
Из предыдущей теоремы вытекает Теорема 3.
Теорема 3: Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Также для вычисления внутреннего угла треугольника можно использовать теорему косинусов, но только в том случае, если известны все три стороны.
- вычислить внутренние углы треугольника
- Как по сторонам треугольника узнать угол
- Как найти углы треугольника по сторонам
- Как вычислить угол в треугольнике
Информация по назначению калькулятора
Треугольник – это одна из основных геометрических фигур: многоугольник с тремя углами (или вершинами) и тремя сторонами (или ребрами), которые являются прямыми отрезками.
В евклидовой геометрии любые три неколлинеарные точки определяют треугольник и единственную плоскость, то есть двумерное декартово пространство.
Сумма длин любых двух сторон треугольника всегда превышает длину третьей стороны. Это и есть неравенство треугольника.
Треугольники могут быть классифицированы в соответствии с относительной длиной их сторон:
⇒ В равностороннем треугольнике все стороны имеют одинаковую длину. Равносторонний треугольник также является равноугольным многоугольником, т.е. все его внутренние углы равны, а именно 60° – это правильный многоугольник.
⇒ В равнобедренном треугольнике две стороны имеют одинаковую длину. Равнобедренный треугольник также имеет два совпадающих угла (а именно, углы, противоположные совпадающим сторонам). Равносторонний треугольник – это равнобедренный треугольник, но не все равнобедренные треугольники являются равносторонними треугольниками.
⇒ В скалярном треугольнике все стороны имеют разную длину. Внутренние углы в скалярном треугольнике все разные.
Треугольники также могут быть классифицированы в соответствии с их внутренними углами:
⇒ Прямоугольный треугольник имеет один внутренний угол 90° (прямой угол). Сторона, противоположная прямому углу, является гипотенузой; это самая длинная сторона в прямоугольном треугольнике. Две другие стороны – катеты треугольника.
⇒ Тупой треугольник имеет один внутренний угол, больший 90° (тупой угол).
⇒ Острый треугольник имеет внутренние углы, которые все меньше 90° (три острых угла). Равносторонний треугольник – это острый треугольник, но не все острые треугольники являются равносторонними треугольниками.
⇒ Наклонный треугольник имеет только углы, которые меньше или больше 90°. Следовательно, это любой треугольник, который не является прямоугольным треугольником.
Онлайн калькулятор поможет найти параметры треугольника, такие как:
- Длины сторон
- Углы
- Высота
- Периметр
- Площадь
- Медианы
- Биссектрисы
- Радиус Вписанной и Описанной окружностей
- Диаметр Вписанной и Описанной окружностей
- Длина Вписанной и Описанной окружностей
- Площадь Вписанной и Описанной окружностей
– равны в равностороннем треугольнике
– также равны в равностороннем треугольнике
– это прямая линия, проходящая через вершину и перпендикулярная противоположной стороне (т. е. образующая прямой угол с ней)
– равен сумме всех 3х сторон (P=AB+BC+AC)
– равна половине произведения высоты и стороны к которой построена высота (S=1/2 * H * AC)
