На этой странице вы можете рассчитать внутреннюю энергию идеального газа с помощью калькулятора онлайн или самостоятельно по формулам.
Содержание:
- калькулятор внутренней энергии идеального газа
- внутренняя энергия идеального газа через массу, молярную массу и температуру
- внутренняя энергия идеального газа через давление и объем
- внутренняя энергия идеального газа через количество вещества и температуру
- внутренняя энергия идеального газа через степени свободы
- степени свободы идеальных газов
Формула внутренней энергии идеального газа через массу, молярную массу и температуру
{U = dfrac{3}{2} cdot dfrac{m}{M} cdot R T}
U – внутренняя энергия газа
m – масса газа
M – молярная масса газа
R – универсальная газовая постоянная R = 8,314 462 618 153 24 Дж/(моль∙К)
T – абсолютная температура газа
Формула внутренней энергии идеального газа через давление и объем
{U = dfrac{3}{2} cdot p V}
U – внутренняя энергия газа
p – давление газа
V – объем газа
Формула внутренней энергии идеального газа через количество вещества и температуру
{U = dfrac{3}{2} cdot nu RT}
U – внутренняя энергия газа
ν – количество вещества (в молях)
R – универсальная газовая постоянная R = 8,314 462 618 153 24 Дж/(моль∙К)
T – абсолютная температура газа
Формула внутренней энергии идеального газа через степени свободы
{U = dfrac{i}{2} cdot nu RT}
U – внутренняя энергия газа
i – количество степеней свободы
ν – количество вещества (в молях)
R – универсальная газовая постоянная R = 8,314 462 618 153 24 Дж/(моль∙К)
T – абсолютная температура газа
Количество степеней свободы молекулы идеального газа
Число степеней свободы (i) – наименьшее число независимых координат, которое необходимо ввести, чтобы определить положение тела в пространстве.
- для одноатомного газа (гелий, неон, аргон, криптон, ксенон, радон, оганесон и т. д.) i=3;
- для двухатомного газа (водород, азот, кислород, фтор, хлор и т. д.) i=5;
- для трехатомного газа i=6;
- для многоатомного (>3) газа i=6;
1. Внутренняя энергия газа
Из курса физики основной школы вы знаете, что сумму кинетической энергии хаотического движения частиц и потенциальной энергии их взаимодействия называют внутренней энергией.
Внутренняя энергия U данной массы одноатомного идеального газа равна произведению средней кинетической энергии 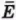 одной молекулы на число молекул N:
одной молекулы на число молекул N:
U = 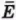 N.
N.
? 1. Объясните, почему внутренняя энергия U данной массы одноатомного идеального газа выражается формулой

Итак, внутренняя энергия идеального газа определяется только его абсолютной температурой и числом молекул в нем.
? 2. Объем одного моля газа при температуре 20 ºС и нормальном атмосферном давлении составляет 24 л.
а) Чему равна внутренняя энергия этого газа, если он одноатомный и его можно считать идеальным?
б) На какую высоту можно было бы забросить мяч массой 365 г, если бы можно было сообщить ему такую кинетическую энергию и пренебречь сопротивлением воздуха?
Выполнив это задание, вы сможете представить, как велика внутренняя энергия тела. Объясняется это тем, что скорость хаотического движения молекул в десятки и сотни раз превышает скорости движения окружающих нас тел. А кинетическая энергия пропорциональна квадрату скорости. Поэтому при увеличении скорости в 10 раз кинетическая энергия увеличивается в 100 раз, а при увеличении скорости в 100 раз кинетическая энергия увеличивается в 10 000 раз.
Внутреннюю энергию идеального одноатомного газа можно выразить также через его давление p и объем V.
? 3. Объясните, почему внутренняя энергия U данной массы одноатомного идеального газа выражается формулой
U = (3/2)pV. (2)
Подсказка. Воспользуйтесь формулой (1) и уравнением состояния идеального газа.
? 4. Из формулы (1) следует, что внутренняя энергия одного моля газа зависит только от его абсолютной температуры и количества вещества (числа молекул). А из формулы (2) следует, что она зависит от давления и объема, но зато не зависит от количества вещества. Объясните, почему тут нет противоречия.
? 5. Ширина класса 5 м, длина 10 м, а высота – 4 м. Температура воздуха 20 ºС, давление равно нормальному атмосферному давлению.
а) Чему была бы равна внутренняя энергия газа, заполняющего класс, если бы он был одноатомным? (Воздух состоит в основном из двухатомных молекул. Как показывает расчет, выходящий за рамки нашего курса, внутренняя энергия двухатомного газа при тех же макроскопических параметрах в 5/3 раза больше, чем внутренняя энергия одноатомного газа.)
б) На какую высоту можно было бы поднять автомобиль массой 1 т, затратив такую энергию?
в) Есть ли в условии лишние данные?
Результаты выполнения этого задания раскроют, какая огромная энергия «окружает» каждого из нас! А ведь мы ее практически не замечаем, считая воздух «пустотой».
Большую внутреннюю энергию имеют, конечно, и другие тела. Например, внутренняя энергия литра кипятка больше внутренней энергии того же литра воды при комнатной температуре на величину, равную работе, которую надо совершить для того, чтобы поднять легковой автомобиль на двенадцать этажей!
При изучении тепловых явлений мы учитываем только кинетическую энергию хаотического движения молекул и потенциальную энергию их взаимодействия. А ведь есть еще и во много раз большая энергия взаимодействия частиц в атомных ядрах. Вы знаете о ней из курса физики основной школы. К ядерной физике мы вернемся в 11-м классе.
Соотношение между различными видами энергии, которыми обладает данное тело, схематически представлено на рисунке 42.1. Мы видим, что непосредственно наблюдаемая механическая энергия составляет лишь очень малую долю всей энергии тела. Соблюсти масштаб на этом рисунке невозможно, потому что тепловая внутренняя энергия в тысячи раз больше механической, а ядерная – в миллионы раз больше тепловой.

Два способа изменения внутренней энергии
Из курса физики основной школы вы знаете, что внутреннюю энергию тела можно изменить двумя способами:
- совершая работу над телом – например, сжимая газ (рис. 42.2, а);
- посредством теплопередачи, то есть без совершения работы, – например, при контакте с более горячим телом (рис. 42.2, б). (Теплопередачу называют иногда также теплообменом.)

Напомним, что меру изменения внутренней энергии при теплопередаче называют количеством теплоты и обозначают Q. Количество теплоты измеряют в джоулях.
Как мы знаем, внутренняя энергия данной массы идеального газа определяется только его температурой и числом молекул. Поэтому при постоянном числе молекул изменить внутреннюю энергию идеального газа можно только изменив его температуру.
Например, при сжатии газа в теплоизолированном сосуде газ нагревается вследствие того, что над ним производят работу. Нагревание газа может быть при атом весьма заметным.
Поставим опыт
Поместим кусочек сухой ваты в толстостенный прозрачный цилиндр и быстро (резким толчком) вдвинем в цилиндр поршень (рис. 42.3).

Воздух в цилиндре нагреется так сильно, что вата воспламенится.
Нагревание газа при сжатии используют в дизельных двигателях: при сжатии горючая смесь в цилиндре нагревается настолько, что воспламеняется без искры.
Газовый процесс, который происходит в теплоизолированном сосуде, то есть без теплопередачи, называют адиабатным. Адиабатным можно считать также процесс, когда тепло- передачей можно пренебречь: например, если процесс происходит за время, в течение которого не успевает произойти теплообмен с окружающей средой.
При адиабатном расширении газ охлаждается. По этой причине, например, образуются облака. Поднимающийся влажный воздух попадает в более разреженные слои атмосферы, расширяется и вследствие этого охлаждается. Как мы увидим далее, при охлаждении ниже определенной температуры (точки росы) содержащийся в воздухе водяной пар конденсируется: образуются капельки тумана, из которого и состоят облака.
Увеличить или уменьшить температуру газа можно, конечно, и посредством теплопередачи. Например, сосуд с газом можно поместить над огнем, в кипящую воду или в морозильную камеру.
? 6. Изменяется ли, н если да, то как внутренняя энергия данной массы идеального газа:
а) при изотермическом расширении? сжатии?
б) при изобарном расширении? сжатии?
в) при изохорном охлаждении? нагревании?
г) при адиабатном сжатии? расширении?
2. Первый закон термодинамики
Итак, внутренняя энергия газа U может изменяться как вследствие того, что ему сообщают количество теплоты Q, так и потому, что внешние силы совершают работу A над газом.
Согласно закону сохранения энергии
изменение внутренней энергии газа ∆U равно сумме количества теплоты Q, переданного газу, и работы A, совершенной над газом:
∆U = Q + A. (3)
Закон сохранения энергии применительно к тепловым явлениям называют первым законом термодинамики. (Термодинамикой называют раздел физики, изучающий общие законы тепловых явлений.)
Как Q, так и A могут быть положительными, отрицательными или равными нулю. Если газ сжимают, то A > 0, а если он расширяется, то A < 0. Если объем газа не изменяется, то A = 0. Если газу передают некоторое количество теплоты, то Q > 0, а если газ отдает некоторое количество теплоты, то Q < 0.
В практических расчетах и при решении многих задач часто используют другую формулировку первого закона термодинамики. Дело в том, что при рассмотрении тепловых двигателей главный интерес представляет работа, совершенная самим газом (то есть силой давления, действующей со стороны газа на поршень; при расширении газа работа газа положительна).
Обозначим работу газа Aг. Она связана с работой A, совершенной внешними силами над газом, соотношением
Aг = –A.
При сжатии газа A > 0, Aг < 0; а при расширении газа A < 0, Aг > 0.
Используя понятие работы газа, первый закон термодинамики формулируют так:
количество теплоты, переданное газу, равно сумме изменения внутренней энергии газа и работы, совершенной газом:
Q = ∆U + Aг. (4)
Чтобы использовать соотношения (3) и (4) на практике, надо уметь находить выражения для изменения внутренней энергии газа и работы газа (или работы внешних сил).
Как найти изменение внутренней энергии газа?
Для одноатомного идеального газа внутренняя энергия выражается формулой (1), поэтому для изменения ∆U внутренней энергии получаем:
∆U = (3/2)νR∆T. (5)
Здесь ∆T = T2 – T1, ∆U = U2 – U1, а индексами 1 и 2 обозначены соответственно начальное и конечное состояния газа.
? 7. Начальная температура пяти молей гелия 100 ºС. Газ нагрели на 50 ºС.
а) Насколько увеличилась внутренняя энергия газа?
б) Есть ли в условии лишние данные?
Изменение внутренней энергии одноатомного идеального газа можно найти и с помощью формулы (2):
∆U = (3/2)∆(pV). (6)
Здесь ∆(pV) – изменение произведения давления на объем. Например, при переходе газа из состояния 1 в состояние 2
∆(pV) = p2V2 – p1V1. (7)
? 8. Чему равно изменение внутренней энергии одного моля одноатомного идеального газа:
а) при изобарном расширении, если давление газа равно p0, а объем газа увеличился от V0 до 3V0?
б) при изохорном охлаждении, если объем газа равен V0, а давление газа уменьшилось от p0 до 0,5p0?
в) в процессе, в котором начальные давление и объем газа равны p0 и V0, а конечные равны 2p0 и 3V0?
Есть ли в условии лишние данные?
Важным достоинством формулы (6) является то, что в нее не входят ни количество вещества в газе, ни его масса. Поэтому, например, если давление и объем газа остались неизменными, то не изменилась и внутренняя энергия газа, хотя при этом могла измениться его масса. Рассмотрим пример, в котором речь идет о воздухе, который состоит в основном из двух- атомных молекул. Их средняя кинетическая энергия при заданной температуре больше, чем у одноатомных молекул (двухатомные молекулы обладают еще кинетической энергией вращательного движения). Однако для выполнения следующего задания то, что воздух состоит из двухатомных молекул, несущественно.
? 9. До включения отопления температура воздуха в комнате объемом 60 м3 была равна 15 ºС. После включения отопления воздух нагрелся до 20 ºС. Давление воздуха постоянно и равно 105 Па.
а) На сколько процентов увеличилась средняя кинетическая энергия молекул в воздухе?
б) Как изменилась внутренняя энергия воздуха в комнате?
в) На сколько процентов изменилась концентрация молекул воздуха?
г) Насколько изменилась масса воздуха в комнате?
Как найти совершенную газом работу?
Рассмотрим сначала изобарное расширение газа в цилиндре под поршнем (рис. 42.4). Газ давит на поршень с силой F = pS, где p – давление газа, S – площадь поршня.

Если поршень переместился на ∆x, то совершенная газом работа Aг = F * ∆x = pS * ∆x. Так как S * ∆x = ∆V, получаем, что при изобарном расшинерии работа газа выражается формулой
Aг = p * ∆V. (8)
? 10. Используя рисунок 42.5, объясните, почему работа газа численно равна площади фигуры под графиком зависимости p(V).

Это свойство графика зависимости p(V) сохраняется и тогда, когда давление газа изменяется.
Пусть, например, график зависимости p(V) имеет вид, изображенный на рисунке 42.6. Процесс расширения газа мысленно разобьем на большое число этапов, в каждом из которых объем газа изменяется настолько мало, что его давление можно считать практически постоянным. Поскольку для каждого этапа работа газа численно равна площади под соответствующим участком графика, то и вся работа, совершенная газом при расширении, равна площади под всем графиком p(V).

? 11. Один моль идеального газа можно перевести из состояния 1 в состояние 2 многими способами. Рассмотрим процессы, которым соответствуют графики а и б (рис. 42.7).
а) В каком случае совершенная газом работа больше? Во сколько раз больше?
б) В каком случае изменение внутренней энергии газа больше? Во сколько раз больше?
в) В каком случае переданное газу количество теплоты больше? Во сколько раз больше?

На примере этого задания вы могли заметить, что изменение ∆U внутренней энергии данной массы идеального газа определяется только начальным и конечным состоянием газа.
Обусловлено это тем, что каждому состоянию данной массы газа (с определенными значениями p, V и T) соответствует одно определенное значение внутренней энергии, которое можно найти либо по формуле (1), либо по формуле (2).
А вот работа, совершенная газом при переходе из начального состояния в конечное, зависит от характера процесса, которым газ был переведен из начального состояния в конечное.
Действительно, работа газа численно равна площади под графиком зависимости p(V). А эта площадь зависит от того, какой вид имела функция p(V).
Если газ не расширяется, а сжимается (рис. 42.8), то внешние силы производят работу над газом. В таком случае говорят также, что газ производит отрицательную работу. Она численно равна взятой со знаком минус площади S под графиком зависимости p(V).

На том, что работа газа зависит от вида зависимости p(V), а не только от начального и конечного состояния, основан принцип действия тепловых двигателей (в следующем параграфе мы рассмотрим их подробнее).
В тепловых двигателях газ расширяется при высокой температуре. При атом давление газа велико, поэтому он совершает большую работу. А сжимают газ при более низкой температуре, когда давление газа меньше. Поэтому для того, чтобы вернуть газ в начальное состояние, внешние силы должны совершить меньшую работу.
Рассмотрим пример.
? 12. Газ совершает циклический процесс: переходит из состояния 1 в состояние 2 (рис. 42.9), а потом возвращается в состояние 1. При этом объем газа не должен быть меньше начального и больше конечного.

а) Какую максимально возможную работу может совершить газ при переходе 1–2, если давление газа не должно превышать 3p0?
б) Какую минимально возможную работу должны совершить внешние силы при переходе 2–1, если давление газа не должно быть меньше p0?
в) Насколько в этом случае работа газа при циклическом процессе больше работы внешних сил?
Применение первого закона термодинамики к изопроцессам и адиабатному процессу
? 13. Используя первый закон термодинамики, а также выражения для внутренней энергии и работы газа, объясните, почему:
а) при изохорном процессе Aг = 0, Q = ∆U, то есть сообщенное газу количество теплоты (напомним, что оно может быть как положительным, так и отрицательным) равно изменению внутренней энергии газа;
б) при изотермическом процессе ∆U = 0, Q = Aг, то есть сообщенное газу количество теплоты равно работе газа;
в) при изобарном процессе Aг ≠ 0, ∆U ≠ 0;
г) при адиабатном процессе Q = 0, Aг = –∆U, то есть при расширении газ совершает работу за счет уменьшения внутренней энергии, а при сжатии газа его внутренняя энергия увеличивается за счет работы внешних сил.
Подсказка. Если давление не изменяется, то ∆(pV) = p∆V.

Дополнительные вопросы и задания
14. На рисунках 42.10, а, б, в изображены графики трех процессов с данной массой одноатомного идеального газа. Чему равно изменение внутренней энергии газа для каждого из этих процессов при переходе 1–2?

15. При изобарном расширении данной массы одноатомного идеального газа его температура возросла от 0 ºС до 100 ºС. При этом газу было передано количество теплоты, равное 5 кДж.
а) Насколько изменилась внутренняя энергия газа?
б) Чему равно количество вещества в сосуде с газом?
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?

Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.

Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.

Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505
 Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?
Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?
Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A

pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
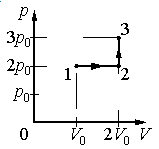 Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления газа от объёма. Работа, совершённая при этом газом, равна
Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления газа от объёма. Работа, совершённая при этом газом, равна
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15k
При
изучении тепловых явлений наряду с
механической энергией тел вводится
новый вид энергии —
внутренняя
энергия. Вычислить внутреннюю энергию
идеального газа не составляет большого
труда.
Наиболее
прост по своим свойствам одноатомный
газ, т. е. газ, состоящий из отдельных
атомов, а не молекул. Одноатомными
являются инертные газы — гелий, неон,
аргон и др. Можно получить одноатомный
(атомарный) водород, кислород и т. д.
Однако такие газы будут неустойчивыми,
так как при столкновениях атомов
образуются молекулы Н2,
О2
и др.
Молекулы
идеального газа не взаимодействуют
друг с другом, кроме моментов
непосредственного столкновения. Поэтому
их средняя потенциальная энергия очень
мала и вся
энергия представляет собой кинетическую
энергию хаотического движения молекул.
Это,
конечно, справедливо, если сосуд с газом
покоится, т. е. газ как целое не движется
(его центр масс находится в покое). В
этом случае упорядоченное движение
отсутствует и механическая энергия
газа равна нулю. Газ обладает энергией,
которую называют внутренней.
Для
вычисления внутренней энергии идеального
одноатомного газа массой т
нужно
умножить среднюю энергию одного атома,
выражаемую формулой (4.5.5), на число
атомов. Это число равно произведению
количества вещества
![]()
на
постоянную Авогадро NA.
Умножая
выражение (4.5.5) на
![]() ,
,
получим
внутреннюю энергию идеального одноатомного
газа:
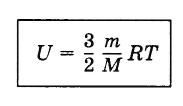
(4.8.1)
Внутренняя
энергия идеального газа прямо
пропорциональна его абсолютной
температуре. От
объема газа она не зависит. Внутренняя
энергия газа представляет собой среднюю
кинетическую энергию всех его атомов.
Если
центр масс газа движется со скоростью
v0,
то
полная энергия газа равна сумме
механической (кинетической) энергии
![]() и внутренней энергииU:
и внутренней энергииU:
![]()
(4.8.2)
Внутренняя энергия молекулярных газов
Внутренняя энергия
одноатомного газа (4.8.1) — это по существу
средняя кинетическая энергия
поступательного движения молекул. В
отличие от атомов молекулы, лишенные
сферической симметрии, могут еще
вращаться. Поэтому наряду с кинетической
энергией поступательного движения
молекулы обладают и кинетической
энергией вращательного движения.
В
классической молекулярно-кинетической
теории атомы и молекулы рассматриваются
как очень маленькие абсолютно твердые
тела. Любое тело в классической механике
характеризуется определенным числом
степеней свободы
f
— числом независимых переменных
(координат), однозначно определяющих
положение тела в пространстве.
Соответственно число независимых
движений, которые тело может совершать,
также равно f.
Атом
можно рассматривать как однородный
шарик с числом степеней свободы f
=
3 (рис. 4.16, а). Атом может совершать только
поступательное движение по трем
независимым взаимно перпендикулярным
направлениям. Двухатомная молекула
обладает осевой симметрией (рис. 4.16, б)
и
имеет пять степеней свободы. Три степени
свободы соответствуют ее поступательному
движению и две — вращательному вокруг
двух осей, перпендикулярных друг другу
и оси симметрии (линии, соединяющей
центры атомов в молекуле). Многоатомная
молекула, подобно, твердому телу
произвольной формы, характеризуется
шестью степенями свободы (рис. 4.16, в);
наряду
с поступательным движением молекула
может совершать вращения вокруг трех
взаимно перпендикулярных осей.
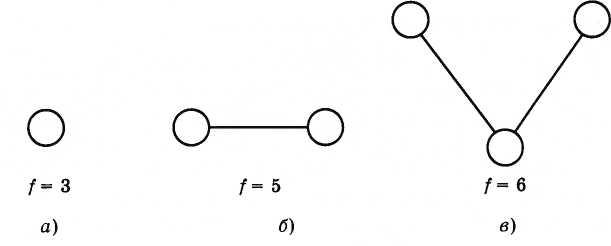
Рис. 4.16
От числа степеней
свободы молекул зависит внутренняя
энергия газа. Вследствие полной
беспорядочности теплового движения ни
один из видов движения молекулы не имеет
преимущества перед другим. На каждую
степень свободы, соответствующую
поступательному или вращательному
движению молекул, приходится одна и та
же средняя кинетическая энергия. В этом
состоит теорема о равномерном распределении
кинетической энергии по степеням свободы
(она строго доказывается в статистической
механике).
Средняя
кинетическая энергия поступательного
движения молекул равна
![]() .
.
Поступательному
движению соответствуют три степени
свободы. Следовательно, средняя
кинетическая энергия
![]() ,
,
приходящаяся на одну степень свободы,
равна:
![]()
(4.8.3)
Если
эту величину умножить на число степеней
свободы и число молекул газа массой т,
то
получится внутренняя энергия произвольного
идеального газа:
![]()
(4.8.4)
Эта
формула отличается от формулы (4.8.1) для
одноатомного газа заменой множителя 3
на множитель f.
Внутренняя
энергия идеального газа прямо
пропорциональна абсолютной температуре
и не зависит от объема газа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти внутреннюю энергию газа
Поскольку внутренняя энергия газа является суммой всех кинетических энергий его молекул, то измерить ее непосредственно, не представляется возможным. Поэтому для ее расчета воспользуйтесь специальными формулами, которые выражают эту величину через такие макроскопические параметры как температура, объем и давление.

Вам понадобится
- Термометр, манометр, герметичный баллон, весы
Инструкция
Рассчитать внутреннюю энергию газа достоверно можно только тогда, когда его состояние близко к идеальному. Тогда можно пренебречь потенциальной энергией взаимодействия его молекул. Практически все газы при комнатной температуре имеют свойства, схожие с идеальным газом.
Сначала определите химическую формулу газа, внутренняя энергия которого вычисляется. Измерьте массу газа с помощью весов в граммах. Для этого взвесьте сначала пустой баллон, а затем заполненный газом, разность их масс будет равна массе газа. С помощью таблицы Менделеева найдите его молярную массу в граммах на моль.
С помощью термометра измерьте температуру газа. Если шкала термометра проградуирована в градусах Цельсия, переведите ее в Кельвины. Для этого к полученному значению прибавьте 273.
Рассчитайте внутреннюю энергию газа. Для этого массу газа поделите на молярную массу. Получившийся результат умножьте на значение температуры и число 8,31 (универсальную газовую постоянную), затем умножьте на число степеней вольности молекулы газа и поделите на 2 (U=m/M•(R•T)•i/2). Количество степеней вольности для одноатомного газа составляет 3, для двухатомной молекулы 5, а для многоатомной молекулы 6. Это связанно с особенностями движения каждой из молекул.
Если нет возможности измерить температуру газа, но и известны его объем и давление, рассчитайте его внутреннюю энергию через эти величины. Для этого измерьте массу газа, его молярную массу и узнайте химическую формулу. Выразите объем в м³, а давление в Паскалях. Рассчитайте внутреннюю энергию газа, перемножив число степеней вольности молекулы газа, значения его массы, давления и объема, а результат поделите на 2 и значение молярной массы газа (U = i•m•P•V/(2•M)).
В общем случае изменение внутренней энергии газа равно разности полученной им извне теплоты и выполненной работы ΔU=Q-A.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
