Решение задач – занятие, которое любит далеко не каждый. Здесь мы стараемся сделать так, чтобы оно занимало у вас поменьше времени без ущерба для качества самого решения. Тема этой статьи — задачи на внутреннюю энергию.
Подписывайтесь на наш телеграм и читайте полезные материалы для студентов каждый день!
Решение задач: внутренняя энергия
Прежде чем приступать к задачам на внутреннюю энергию тела, посмотрите общую памятку по решению физических задач. И пусть под рукой на всякий случай всегда будут основные физические формулы.
Задача №1. Изменение внутренней энергии
Условие
Воздушный шар объёмом 500 м3 наполнен гелием под давлением 105 Па. В результате нагрева температура газа в аэростате поднялась от 10 °С до 25 °С. Как увеличилась внутренняя энергия газа?
Решение
Для решения будем использовать формулу внутренней энергии идеального газа:
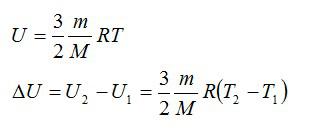
Массу гелия выразим из уравнения Клапейрона-Менделеева:
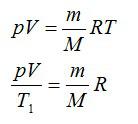
Тогда можно записать:
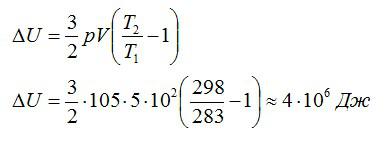
Ответ: 4 МДж.
Задача №2. Внутренняя энергия и работа
Условие
Азот массой 200 г расширяется изотермически при температуре 280 К, причем объём газа увеличивается в 2 раза. Найти:
- Изменение ∆U внутренней энергии газа.
- Совершенную при расширении газа работу А.
- Количество теплоты Q, полученное газом.
Решение
Так как процесс изотермический, то изменение внутренней энергии равно нулю, а работа равна количеству теплоты, полученному газом:
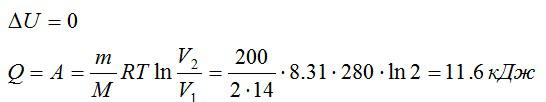
Ответ: 0; 11,6 кДж; 11,6 кДж.
Задача №3. Изменение внутренней энергии при изобарном и изохорном процессе
Условие
Кислород занимает объём V1= 3 л при давлении p1= 820 кПа. В результате изохорного нагревания и изобарного расширения газ переведён в состояние с объёмом V2= 4,5 л и давлением p2= 600 кПа. Найти количество теплоты, полученное газом; изменение внутренней энергии газа.
Решение
Теплота, подведенная к газу, идет на совершение работы и изменение внутренней энергии:
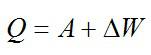
В изохорном и изобарном процессе соответственно:
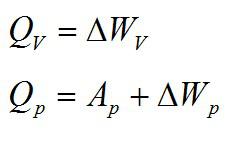
Изохорное нагревание:
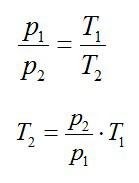
Изменение внутренней энергии при изохорном процессе:
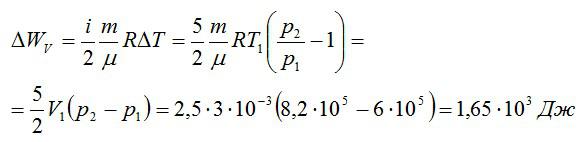
Изменение внутренней энергии при изобарном процессе:
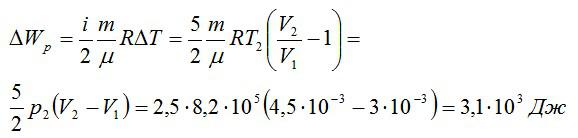
Общее изменение внутренней энергии:
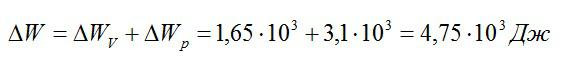
Ответ: 4,75 кДж.
Задача №4. Изменение внутренней энергии двухатомного газа
Условие
Кислород массой 2 кг занимает объём 6 м3 и находится под давлением 1 атм. Газ был нагрет сначала при постоянном давлении до объёма 13 м3, а затем при постоянном объёме – до давления 23 атм. Найти изменение внутренней энергии газа.
Решение
Изменение внутренней энергии находим по формуле:
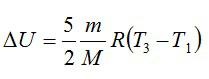
Эту форму можно преобразовать, используя уравнение Клапейрона-Менделеева:
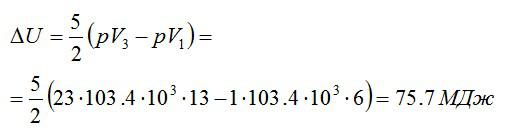
Ответ: 75,7 МДж.
Задача №5. Внутренняя энергия смеси газов
Условие
В закрытом сосуде находится масса m1 = 20 г азота и масса m2 = 32 г кислорода. Определить изменение ΔU внутренней энергии смеси газов при охлаждении ее на ΔТ = 28 К.
Решение
Определим количество молей азота и кислорода, а затем общее количество вещества в смеси соответственно:
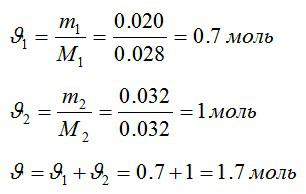
Изменение внутренней энергии:
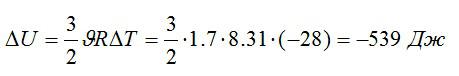
Знак «минус» означает, что внутренняя энергия уменьшается.
Ответ: -539 Дж.
Вопросы на тему «Внутренняя энергия тела»
Вопрос 1. Что такое внутренняя энергия?
Ответ. Для начала, внутренняя энергия чего? Бутылки с пивом, воздуха в шарике, тазика с водой? Все макроскопические тела обладают энергией, заключенной внутри них: атомы твердого тела колеблются в кристаллической решетке около положений равновесия, молекулы газа находятся в постоянном хаотическом движении и т.д.
По определению:
Внутренняя энергия вещества – это энергия, которая складывается из кинетической энергии всех атомов и молекул, и потенциальной энергии их взаимодействия друг с другом.
Для идеального газа с числом степеней свободы i внутренняя энергия вычисляется по формуле:
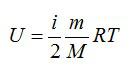
Вопрос 2. От чего зависит внутренняя энергия идеального газа?
Ответ. Эта величина не зависит от объёма и определяется только температурой.
Вопрос 3. Как изменяется внутренняя энергия тела?
Ответ. Если тело совершает работу, его внутренняя энергия уменьшается. Например, газ передвигает поршень. Если же работа совершается над телом, то внутренняя энергия увеличивается.
Вопрос 4. Что такое функция состояния?
Ответ. Функция состояния – это один из параметров, которым можно описать термодинамическую систему. Функция состояния не зависит от того, как система пришла в то или иное состояние, а определяется несколькими переменными состояния.
Внутренняя энергия – это функция состояния термодинамической системы. В общем случае она зависит от температуры и объёма.
Вопрос 5. Можно ли изменить внутреннюю энергию тела, не совершая над ним работы?
Ответ. Да, еще один способ изменения внутренней энергии – теплопередача. В процессе теплопередачи внутренняя энергия тел изменяется.
Нужна помощь в решении задач по любой теме и других студенческих заданий? Профессиональный студенческий сервис поспособствует в выполнении работы вне зависимости от ее сложности.
Уравнение
Клапейрона-Менделеева описывает
равновесные состояния идеального газа,
а, следовательно, и любые обратимые
процессы, которые в нем могут протекать.
При наложении на систему дополнительных
условий, можно получить уравнения
термодинамических процессов, и
соответствующие им законы, которые
имеют ограниченное применение и являются
частными случаями допускаемых уравнением
термодинамических процессов.
Согласно закону
Бойля-Мариотта для неизменной массы
газа при постоянной температуре давление
газа меняется обратно пропорционально
объёму, занимаемому газом. Процесс,
описываемый этим законом, называется
изотермическим (T=const),
и его уравнение имеет вид:
Жозеф Луи
Гей-Люссак (1778 – 1850) провёл серию опытов
для различных газов и установил, что
при постоянном давлении и одинаковом
количестве вещества расширение газов
происходит одинаково при повышении
температуры на одну и ту же величину.
Этот закон носит название закона
Гей-Люссака. Ранее, в конце ХVIII
века, этот закон был установлен Жаком
Александром Цезарем Шарлем (1746 – 1823), но
не был опубликован им.
Установленный
ими закон описывает изобарический
(P=const)
процесс:
или
.
где:Vo
– объем газа при температуре равной нулю
градусов по шкале Цельсия,
– температурный коэффициент расширения
газа, который для идеального газа должен
быть равен 1/273,15. Для реальных газов при
нормальных условиях он близок к этому
значению.
Если оставлять
неизменным объем газа, что, например,
имеет место в газовых термометрах
постоянного объема, то происходящий
при этом процесс будет называться
изохорическим (V=const)
и описываться уравнением:
Этот закон называется
законом Шарля.
Процессы в идеальном
газе, происходящие при постоянстве
одного из параметров состояния:
температуры, давления или объема,
называются изопроцессами.
ВНУТРЕННЯЯ ЭНЕРГИЯ:
Внутреннюю энергию
тела нельзя измерить напрямую. Можно
определить только изменение внутренней
энергии:
В изохорном
процессе (V
= const) газ работы не совершает, A = 0.
Следовательно,
Q = ΔU = U(T2) – U(T1).
Здесь U(T1) и U(T2) –
внутренние энергии газа в начальном и
конечном состояниях. Внутренняя энергия
идеального газа зависит только от
температуры (закон Джоуля). При изохорном
нагревании тепло поглощается газом (Q
> 0), и его внутренняя энергия увеличивается.
При охлаждении тепло отдается внешним
телам (Q < 0).
В изобарном
процессе (p
= const) работа, совершаемая газом, выражается
соотношением
A = p(V2 – V1) = pΔV.
Первый закон
термодинамики для изобарного процесса
дает:
Q = U(T2) – U(T1) + p(V2 –
V1) = ΔU + pΔV.
При изобарном
расширении Q > 0 – тепло поглощается
газом, и газ совершает положительную
работу. При изобарном сжатии Q < 0 –
тепло отдается внешним телам. В этом
случае A < 0. Температура газа при
изобарном сжатии уменьшается, T2 <
T1; внутренняя
энергия убывает, ΔU < 0.
В изотермическом
процессе
температура газа не изменяется,
следовательно, не изменяется и внутренняя
энергия газа, ΔU = 0.
Первый закон
термодинамики для изотермического
процесса выражается соотношением Q =
A.
Количество теплоты
Q, полученной газом в процессе
изотермического расширения, превращается
в работу над внешними телами. При
изотермическом сжатии работа внешних
сил, произведенная над газом, превращается
в тепло, которое передается окружающим
телам.
Наряду с изохорным,
изобарным и изотермическим процессами
в термодинамике часто рассматриваются
процессы, протекающие в отсутствие
теплообмена с окружающими телами. Сосуды
с теплонепроницаемыми стенками называются
адиабатическими оболочками, а процессы
расширения или сжатия газа в таких
сосудах называются адиабатическими.
В адиабатическом
процессе Q
= 0; поэтому первый закон термодинамики
принимает вид
A = –ΔU,
то есть газ совершает
работу за счет убыли его внутренней
энергии.
Соседние файлы в папке Физика. Общая физика
- #
- #
Изобарический процесс — процесс, протекающий в идеальном газе, при котором p=const.
Процесс протекания описывается законом Гей-Люссака: при постоянном давлении отношение объема газа к его температуре постоянно ((frac VT=const))
Внутренняя энергия и количество теплоты изобарического процесса
Системе передается определенное количество теплоты. Оно идет на изменение внутренней энергии и совершение работы над веществом:
(Q=A’+triangle U)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
где Q — количество теплоты, Дж
(А) — работа, совершаемая при расширении или сжатии газа, Дж
(triangle U) — внутренняя энергия, Дж
Работа над газом определяется по формулам:
(А’=p(V_2-V_1)=ptriangle V)
где (А) — работа, Дж
(p) — давление, (Н/м^2)
(V_1) — начальный объем газа, (м^3)
(V_2) — конечный объем газа, (м^3)
(А=frac mMR(Т_2-Т_1))
(m) — масса, г
(M) — молярная масса, г/моль
(R) — универсальная газовая постоянная, ≈ 8,314 Дж/(моль⋅К)
T — температура газа, К
Примечание
Условие протекания изобарического процесса: неизменное значение давления ((triangle p=0))
График изобарного процесса в идеальном газе
Изопроцессы очень часто изображают на термодинамических диаграммах. Так, линия, изображающая на такой диаграмме изобарический процесс, называется изобарой.
Зависимости параметров:
Каким законом описывается изобарный процесс, уравнение
Согласно закону Гей-Люссака объем пропорционален температуре. Выполняется соотношение:
(frac{V_1}{T_1}=frac{V_2}{T_2})
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505
Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?
Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
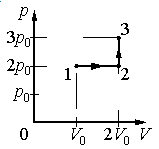Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления газа от объёма. Работа, совершённая при этом газом, равна
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15k
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,657 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,952 -
разное
16,904
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
