Как найти внутреннюю точку области

Как найти внутреннюю точку области

Макеты страниц

Точка называется внутренней точкой множества если существует круг с центром в точке и настолько малым радиусом, что все точки круга принадлежат множеству

Точка есть внешняя точка множества если существует круг с центром в точке такой, что ни одна точка этого круга не принадлежит множеству

Точка есть граничная точка множества есть сколь угодно малый круг с центром в точке содержит внутри точки множества и точки, не принадлежащие

Всякая точка плоскости будет либо внешней точкой либо внутренней точкой либо граничной точкой множества

Областью называется множество, все точки которого — внутренние точки. Например, множество точек, принадлежащих кругу и не принадлежащих самой окружности, есть область.

Область называется ограниченной в том случае, когда множество ее точек есть множество ограниченное.

Если множество не содержит всех точек плоскости, то оно имеет граничные точки Чтобы в этом убедиться, достаточно соединить прямолинейным отрезком точку области с точкой, не принадлежащей области: легко видеть, что на этом отрезке найдется не менее одной граничной точчи. Граничные точки области образуют множество которое называется границей этой области.

Множество называется более точно открытой областью; жество, образованное присоединением к множеству точек множества есть множество замкнутое, это множество называется замкнутой областью. Всякий раз, когда мы говорим область, не прибавляя, что она замкнута, речь идет об открытой области.

Область заключена полностью внутри другой области если все точки области и все точки ее границы суть внутренние точки области

Область называется связной, когда две любые точки этой области могут быть соединены непрерывной линией, все точки которой суть внутренние точки области.

Область будет односвязной, если любые два пути, расположенные внутри области и соединяющие точки можно, все время оставаясь полностью внутри, превратить один в другой непрерывной деформацией. Всякая замкнутая кривая, взятая внутри такой области, может быть непрерывной деформацией стячута в точку. Эта деформация в плоскости комплексного переменного может приводить к бесконечно удаленной точке: например, точки внешние какому-нибудь кругу образуют односвязную область. Можно уничтожить всякое различие между бесконечно удаленной точкой и любой другой точкой плоскости помощью сферы

Римана: применив инверсию плоскости по отношению полюса вне плоскости, можно получить, таким образом, сферу, на которой точка или северный полюс, соответствует бесконечно удаленной точке плоскости. Множество точек, внешних кругу, переходят тогда в сферический сегмент, содержащий точку

Если точка А границы области есть изолированная по отношению к то все точки, близкие к суть внутренние точки.

В самом деле, предположим, что внутри круга, не содержащего ни одной точки границы отличной от с центром в точке Лис произвольно малым радиусом, можно найти точку В, внешнюю области В том же самом круге в силу определения границы существует точка С, внутренняя для Мы можем в случае необходимости заменить точку С близкой так, чтобы отрезок прямой не проходил через точку Этот отрезок содержит точку границы отличную от и лежащую внутри круга, что противоречит условию.

Из предыдущего замечания получаем, что если граница односвязной области содержит более одной точки, то она не имеет ни одной изолированной точки и, следовательно, граница содержйт бесконечное множество точек.

В самом деле, пусть есть изолированная граничная точка, тогда существует маленький круг с центром в точке покрывающий эту единственную граничную точку, окружность которого находится полностью внутри эту линию нельзя превратить в точку непрерывным преобразованием, не выходя из области, потому что внутри имеется точка границы, а вне имеется другая точка границы: итак, эта область не будет односвязной; это свойство мы используем в дальнейшем.

Для любой точки, внутренней к ограниченной области можно найти область содержащую точку О, заключенную полностью внутри и ограниченную конечным числом спрямляемых дуг, все точки которых удалены от границы области на расстояния, меньшие любого заданного числа

В самом деле, разобьем плоскости на квадраты со сторонами, меньшими и настолько малыми, что квадрат, содержащий О, заключен полностью внутри Покроем штриховкой этот квадрат, а также все смежные с ним квадраты, которые заключены полностью внутри области Продолжаем так шаг за шагом штриховать все квадраты, которые содержатся строго внутри и имеют стороны, общие с квадратами, уже заштрихованными. Все заштрихованные таким образом квадраты, число которых, конечно, образуют связную область содержащую точку О и ограниченную конечным числом ломаных, образованных из сторон квадратов. Пусть одна из этих сторон. Один из квадратов, прилежащих к содержит граничные точки области в противном случае оба квадрата должны быть заштрихованы, и тогда не будет частью границы Итак, все точки находятся от точек границы области на расстоянии, меньшем

Доказательство приложимо и в том случае, когда не ограничена, но в этом случае ломаных линий не будет обязательно конечное число.

1

Оглавление

  • ПРЕДИСЛОВИЕ
  • ГЛАВА 1. МНОЖЕСТВА ТОЧЕК. СЕМЕЙСТВА ФУНКЦИЙ. МНОЖЕСТВА ТОЧЕК ОБЛАСТИ
  • § 1. Множество. Предельная точка.
  • § 2. Производное множество.
  • § 3. Внутренние и внешние точки. Границы. Области.
  • § 4. Непрерывные множества.
  • § 5. Кривые Жордана. Достижимые точки границы.
  • § 6. Множества точек в произвольном пространстве.
  • § 7. Множества точек в функциональном пространстве.
  • СЕМЕЙСТВА ФУНКЦИЙ
  • § 8. Теорема Вейерштрасса.
  • § 9. Сгущение значений.
  • § 10. Функции, ограниченные в своей совокупности
  • § 11. Равностепенная непрерывность.
  • § 12. Существование предельных функций.
  • § 13. Случай открытой области.
  • § 14. Случай неаналитических функций.
  • § 15. Теорема Стилтьеса.
  • § 16. Теорема Витали.
  • § 17. Функции, допускающие исключительные области.
  • § 18. Определение нормального семейства.
  • § 19. Семейство нормальное в точке.
  • § 20. Нормальные и ограниченные семейства.
  • § 21. Число нулей функций нормального семейства.
  • § 22. Иррегулярные точки.
  • § 23. Семейство гармонических функций. Теорема Харнака.
  • § 24. Частные ограниченных функций.
  • § 25. Нормальное семейство функций N.
  • ГЛАВА II. ГОЛОМОРФНЫЕ ФУНКЦИИ С ИСКЛЮЧИТЕЛЬНЫМИ ЗНАЧЕНИЯМИ. КВАЗИ-НОРМАЛЬНЫЕ СЕМЕЙСТВА. ФУНКЦИИ ШВАРЦА
  • § 26. Теорема Пэнлеве.
  • § 27. Метод симметрии.
  • § 28. Функции Шварца.
  • § 23. Замощение фундаментального круга.
  • § 30. Фундаментальные подстановки.
  • § 31. Построение функции Шварца.
  • СЕМЕЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ С ИСКЛЮЧИТЕЛЬНЫМИ ЗНАЧЕНИЯМИ
  • § 32. Основной признак.
  • § 33. Обобщение.
  • КВАЗИ-НОРМАЛЬНЫЕ СЕМЕЙСТВА
  • § 34. Определение квазинормального семейства.
  • § 35. Иррегулярные точки.
  • § 36. Основной признак.
  • § 37. Случай, когда квазинормальное семейство будет нормальным.
  • § 38. Расширение признаков нормальности и квазинормальности.
  • ГЛАВА III. ИЗУЧЕНИЕ ОДНОЗНАЧНЫХ ФУНКЦИЙ В ОКРЕСТНОСТИ ИЗОЛИРОВАННОЙ СУЩЕСТВЕННО ОСОБОЙ ТОЧКИ
  • § 40. Первая теорема Пикара.
  • § 41. Обобщения.
  • § 42. Вторая теорема Пикара.
  • § 43. Обобщения.
  • § 44. Теорема Жюлиа.
  • § 45. Случай целых функций.
  • § 46. Теорема Шоттки (Schottky).
  • § 47. Теорема Ландау.
  • § 48. Обобщения.
  • ГЛАВА IV. КОНФОРМНОЕ ОТОБРАЖЕНИЕ. КОНФОРМНОЕ ОТОБРАЖЕНИЕ ОТКРЫТОЙ ОБЛАСТИ
  • § 50. Отображение внутренности области на круг.
  • § 51. Теорема Пуанкаре.
  • § 52. Теорема Каратеодори.
  • СООТВЕТСТВИЕ ГРАНИЦ
  • § 53. Достижимые точки границы.
  • § 54. Точки, достижимые единственным способом.
  • § 55. Множество достижимых точек.
  • § 56. Трансверсали области.
  • § 57. Прерывное приближение к точкам границы.
  • § 58. Простые концы.
  • § 59. Области, ограниченные кривой Жордана.
  • § 60. Теорема Фейера (Fejer).
  • ГЛАВА V. СЕМЕЙСТВО МЕРОМОРФНЫХ ФУНКЦИЙ
  • § 62. Нормальное семейство.
  • § 63. Иррегулярные точки. Исключительные последовательности.
  • § 64. Равностепенная непрерывность на сфере Римана.
  • § 65. Число нулей функций нормального семейства.
  • § 66. Количественные свойства.
  • § 67. Функции с асимптотическими значениями.
  • § 68. Тождества Бореля (Borel)
  • КВАЗИНОРМАЛЬНЫЕ СЕМЕЙСТВА
  • § 69. Определение. Свойства иррегулярных точек.
  • § 70. Порядок иррегулярной точки. Полный порядок.
  • § 71. Квазинормальные семейства функций, число нулей которых ограничено.
  • § 72. Случай, когда предельные функции конечны.
  • ГЛАВА VI. ЧАСТНЫЕ КВАЗИ-НОРМАЛЬНЫЕ СЕМЕЙСТВА
  • СЕМЕЙСТВА ФУНКЦИЙ С КВАЗИ-ИСКЛЮЧИТЕЛЬНЫМИ ЗНАЧЕНИЯМИ
  • § 74. Распространение теоремы Шоттки.
  • § 75. Обобщения.
  • § 76. Распространение теоремы Ландау.
  • § 77. Частные случаи.
  • ИСКЛЮЧИТЕЛЬНЫЕ МЕРОМОРФНЫЕ ФУНКЦИИ
  • § 82. Условия Островского.
  • § 83. Обратное предложение.
  • § 84. Общая теорема.
  • ГЛАВА VII. ПОСЛЕДОВАТЕЛЬНОСТИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
  • ПОСЛЕДОВАТЕЛЬНОСТИ ГОЛОМОРФНЫХ ФУНКЦИЙ
  • § 86. Последовательности, сходящиеся на бесконечном множестве внутренних точек.
  • § 87. Теорема Бляшке.
  • § 88. Распространение на функции N.
  • § 89. Распространение на неограниченные функции.
  • § 90. Последовательности, сходящиеся на некоторой части границы.
  • § 91. Обобщения.
  • § 92. Теорема Адамара о трех кругах.
  • § 93. Быстрота сходимости. Распространения теоремы Стилтьеса.
  • § 94. Сходящиеся ряды голоморфных функций.
  • § 95. Теорема Ненча (Jentzsch).
  • § 96. Теорема Островского.
  • ПОСЛЕДОВАТЕЛЬНОСТИ МЕРОМОРФНЫХ ФУНКЦИЙ
  • § 97. Природа сходимости нормально или квази-нормальной последовательности.
  • § 98. Последовательности, которые сходятся на бесконечном множестве внутренних точек.
  • § 99. Сходящиеся последовательности мероморфных функций.
  • § 100. Множество иррегулярных точек.
  • ГЛАВА VIII. ИТЕРАЦИЯ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
  • § 102. Неподвижные точки. Циклы.
  • § 103. Множитель. Область притяжения.
  • § 104. Ограниченность числа притягивающих циклов.
  • § 105. Связь между итерацией и функциональными уравнениями.
  • § 106. Ограниченность числа индиферентных циклов.
  • § 107. Неподвижные отталкивающие точки.
  • § 108. Примеры итерации.
  • § 109. Множество иррегулярных точек
  • § 110. Инвариантность множества g.
  • § 111. Структура множества g.
  • § 112. Однородность множества g.
  • § 113. Примеры множества g.
  • § 114. Распределение областей притяжения.
  • ГЛАВА IX. СЕМЕЙСТВА ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
  • НОРМАЛЬНЫЕ СЕМЕЙСТВА ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
  • § 116. Нормальные семейства голоморфных функций.
  • § 117. Функции, ограниченные в своей совокупности.
  • § 118. Сгущение значений.
  • § 119. Функции, имеющие исключительные области.
  • § 120. Функции, имеющие два исключительных значения.
  • § 121. Нормальные последовательности, сходящиеся на бесконечном множестве точек.
  • § 122. Множество иррегулярных точек.
  • § 123. Структура множества (F).
  • СЕМЕЙСТВА УНИФОРМИЗИРУЮЩИХ ФУНКЦИЙ
  • § 124. Теорема Пикара.
  • § 125. Случай алгебраического соотношения жанра единица.
  • § 126. Случай алгебраического соотношения жанра нуль.
  • ГЛАВА X. СЛОЖНЫЕ СЕМЕЙСТВА И ПРИЛОЖЕНИЯ
  • СЛОЖНЫЕ НОРМАЛЬНЫЕ СЕМЕЙСТВА
  • § 128. Целые функции. Наибольшее число исключительных комбинаций.
  • § 129. Класс системы функций.
  • § 130. Треугольные таблицы комбинаций.
  • § 131. Определение сложного нормального семейства.
  • § 132. Признак нормальности для сложного семейства.
  • СПЕЦИАЛЬНЫЕ СЛОЖНЫЕ СЕМЕЙСТВА
  • § 133. Система трех голоморфных функций, никогда не равных.
  • § 134. Обобщения.
  • § 135. Случай, когда функции могут быть равными.
  • § 136. О некоторых нормальных семействах.
  • § 137. Системы из четырех мероморфных функций, никогда не равных.
  • § 138. Обобщения.
  • АЛГЕБРОИДНЫЕ ФУНКЦИИ, ДОПУСКАЮЩИЕ ИСКЛЮЧИТЕЛЬНЫЕ ИНВОЛЮЦИИ
  • § 140. Алгеброидные функции. Исключительная инволюция.
  • § 141. Класс алгеброидных функций.
  • § 142. Наибольшее число исключительных инволюций.
  • § 143. Порядок исключительного значения.
  • § 144. Нормальные семейства алгеброидных функций.
  • § 145. Случай неограниченных функций.
  • § 146. Признак нормальности семейства.
  • § 147. Распространение теоремы Шоттки.
  • § 148. Распространение теоремы Ландау.
  • § 149. Обобщения.
  • § 150. Алгеброидные функции, нецелые.
Источник

Внутренние, внешние и граничные точки

Пусть
(Х, Ф) – топологическое пространство.
Открытое множество U
называется окрестностью точки х если
х 
U
(х 
X
и U

Ф).

Определение
4. Точка


называется внутренней точкой некоторого
множества H
(H

X),
если существует такая окрестность U
точки


,что U

H.
Множество всех внутренних точек множества
H
обозначается через int
H
и называется внутренней областью H
или внутренностью H.

Определение
5. Точка

называется внешней точкой множества
H,
если существует такая окрестность V
точки

,
в которой нет точек из H,
т.е. V

Сх
H=Х
H.
Множество всех внешних точек множества
H
обозначается через ext
H
и называется внешней областью H.

Определение
6. Точка с
называется граничной для множеств H,
если в любой окрестности точки с имеются
как точки множества H,
так и точки не принадлежащие H.

Множество
всех граничных точек множества H
обозначается через

H
и называется границей H.

Очевидно:

int
H 
ext H 

H
= X

int
H 
ext H = ext H 

H
= int 

H
= 

int
H = ext Cx
H, ext H = int Cx
H

H
=

Cx
H

Теорема
3. Для любого
множества H
топологического пространства (Х, Ф)
имеем

int
H 
Ф
,ext H 
Ф.

H
– замкнутое множество.

Доказательство.
По определению для 


int
H
существует окрестность U
точки

такая, что U

H.

Поскольку
открытое множество является окрестностью
любой своей точки, то U

int
H
, то есть U
состоит только из внутренних точек H.

Тогда
int
H
=

U
 и в силу
аксиомы 2 топологического пространства
получим int
H

Ф.

Так
как ext
H
= int
(X
H),
то получаем ext
H

Ф.

Так
как

H
= X
(int
H

ext
H
), то

H
замкнуто в (Х, Ф).

Определение
7. Точка

называется точкой прикосновения
множества H,
если каждая окрестность точки

имеет с H
хотя бы одну общую точку.

Множество
всех точек прикосновения множества H
называется замыканием множества H
и обозначается

.
Ясно, что

= int
H

H
и является замкнутым множеством.

Определение
8. Точка


H
называется изолированной точкой
множества H,
если существует окрестность U
точки

,
такая, что

U

H
= 

Определение
9. Если

и не является изолированной для H,
то она называется предельной точкой
множества H.

Ясно,
что в каждой окрестности предельной
точки


H
существуют точки множества H,
отличные от

.

Поскольку
замыкание распадается на множество
изолированных и предельных точек, а
первое всегда содержится в H,
то приходим к следующему утверждению:

Теорема
4. Множество
H
замкнуто тогда и только тогда, когда
оно содержит все свои предельные точки,
то есть, если

H
=

Действительно,
если H
– замкнуто, то C
H
= X
H
открыто. Поэтому C
H
= ext
H.

Отсюда
получаем

H
= int
H

∂ H
=

.

Теорема
5. Если замкнутое
множество F
содержит множество H,
то F
содержит и

.

Доказательство.
Так как H

F,
то все предельные точки H
будут являться предельными и для F,
а поэтому они принадлежат F,
следовательно

 F.

Следствие.
Замыкание множеств H
есть пересечение всех замкнутых множеств,
содержащих H.

Действительно,
согласно теореме 5

принадлежит любому замкнутому множеству,
содержащему H
, а по теореме 3 из §3

–
замкнутое множество.

Пример
1. Если (Х, Ф)
– антидискретное топологическое
пространство, то внутренность любого
его подмножества, за исключением самого
Х, пустое множество.

Если
(Х, Ф) – дискретное пространство, то
любое его подмножество открыто и замкнуто
одновременно и, следовательно, совпадает
со своей внутренностью и со своим
замыканием.

Если
X
= R
с обычной топологией, то внутренность
множества всех целых чисел пустое
множество.

Внутренность
множества рациональных чисел

– пустое множество. Поэтому получаем,
что замыкание

= R,
а замыкание внутренности множества
рациональных чисел

= ,
при этом int

= R.

Таким
образом, замыкание внутренности
множества может сильно отличаться от
внутренности замыкания.

Таким
образом, оператор перехода к внутренности
и оператор замыкания, вообще говоря,
не коммутируют.

Если
Х – антидискретно и А 
Х, А 
,
то А
= Х.

Если
Х – дискретно и А 
Х, А 
,
то А
= .

Границей
множества рациональных чисел, так же
как и границей множества всех иррациональных
чисел, служит всё множество вещественных
чисел.

Пример
2. Пусть

,

,

Найти

и все замкнутые множества.

Решение.

Рассмотрим
точку

и выберем из списка открытых множеств

,
такое которое содержит точку

и входит в

.
Очевидно,

следовательно,

.
Для точки

такого открытого множества нет.
Следовательно,

.
Точка

и поэтому

.
Итак окончательно получаем

.


.


.
Найдем

.

Рассуждая
аналогично, получаем, что

.
Для точки

нет открытого множества содержащегося
в

.
Следовательно,

,

.
Для нахождения граничных точек

воспользуемся формулой

или

.


.

Напомним,
что множество называется замкнутым,
если его дополнение открыто, т.е.

– замкнуто

.
Возьмем список открытых множеств

и, используя дополнения, составим список
замкнутых множеств

.


.

Ответ:

,

,

,

.

Теорема
6. Пусть А –
подмножество топологического пространства
(Х, Ф). Тогда:

1)

А
=

=

int A.

2)
Х

A
= int A 
int (Х
A).

3)

= А 

А,
int
A
= А

А.

4)
А =


А

А.

А
= int
А 
А 
А
= 
.

Доказательство
непосредственно следует из определения

,
int
A,
ext
A
и

А.

Определение
10. Множество
H
называется всюду плотным в топологическом
пространстве (Х, Ф), если

= X.

Множество
А называется нигде не плотным в
пространстве(Х, Ф), если дополнение к
замыканию А всюду плотно в Х, то есть

=
Х

Теорема
7. Пусть H

X,
Ф = G

Тогда

= Х 
H



для любого



.

Доказательство.

1)

= Х. Тогда для произвольного открытого
множества

имеем

.

Если
х0

,
то х0

.
Но, согласно определению точки
прикосновения, имеем


H

2)
Пусть для любого


:


H

.

Покажем,
что Х 

.
Действительно, если х0

Х и х0

H,
то для любой окрестности

точки
х0
имеем:


H

,

а
это значит, что

х0

и Х 

.

Так
как всегда


Х, то Х =

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Алгоритм нахождения точек внутри выбранной области

Доброе время суток.

Подскажите пожалуйста алгоритм для построения условия нахождения всех точек внутри выбранной области.

image

Я только смог до думаться до следующей мысли.

1. Находим центр фигуры по координатам.
lat_center = сумма всех lat поделенная на количество lng_center = сумма всех lng поделенная на количество 2. В цикле строю условие для координат

  1.  
  2.                 $x_query        =       array();
  3.                 // строим условия для x
  4.                 foreach($x as $value){
  5.                         if (max($value,$x_center)==$value) {
  6.                                 $x_query[] = "`t3`.`lat_ya` <= ".$value;                               
  7.                         } else {
  8.                                 $x_query[] = "`t3`.`lat_ya` >= ".$value;
  9.                         }
  10.                 }              
  11.                
  12.                 $y_query        =       array();
  13.                 // строим условия для y
  14.                 foreach($y as $value){
  15.                         if (max($value,$y_center)==$value) {
  16.                                 $y_query[] = "`t3`.`lng_ya` <= ".$value;
  17.                         } else {
  18.                                 $y_query[] = "`t3`.`lng_ya` >= ".$value;
  19.                         }
  20.                 }
  21.  
  22.  

3. Далее строю запрос и получаю его 

  1.  
  2. SELECT *
  3. FROM `_perm_houses` as `t3`
  4. WHERE
  5. (
  6. `t3`.`lat_ya` >= 56.234189 AND
  7. `t3`.`lat_ya` >= 56.235627 AND
  8. `t3`.`lat_ya` <= 56.236925 AND
  9. `t3`.`lat_ya` <= 56.240583 AND
  10. `t3`.`lat_ya` <= 56.238459 AND
  11. `t3`.`lat_ya` >= 56.235348
  12. ) AND (
  13. `t3`.`lng_ya` <= 58.010264 AND
  14. `t3`.`lng_ya` >= 58.007918 AND
  15. `t3`.`lng_ya` >= 58.008186 AND
  16. `t3`.`lng_ya` >= 58.009228 AND
  17. `t3`.`lng_ya` <= 58.011346 AND
  18. `t3`.`lng_ya` <= 58.010509
  19. ) ;
  20.  
  21.  

Когда выделенная область прямоугольная и ее стороны параллельны осям координат, скажем так, он находит без проблем, а когда область более точно выделенная возникают проблемы.

Может есть какой алгоритм? Искал ни чего подобного не нашел.

За ранее благодарен.
______________________

Текст подготовлен в Редакторе Блогов от © SoftCoder.ru


  • Вопрос задан

    более трёх лет назад

  • 11799 просмотров

Пригласить эксперта

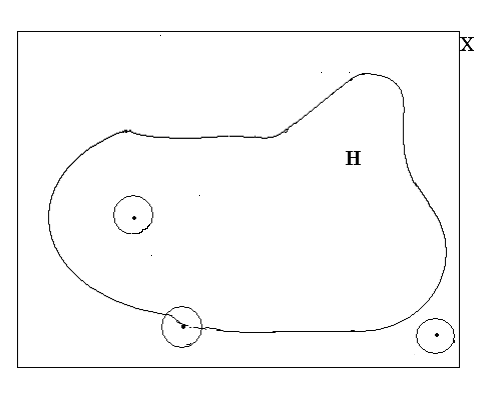
Точка x,y находится внутри многоугольника тогда и только тогда, когда луч (x,y) (x+m,y) пересекает многоугольник непарное количество раз. М — очень большое число.

В студенчестве, для случаев с выпуклыми многоугольниками я выяснял принадлежность точки с помощью равенства площадей самого многоугольника и суммы площадей треугольников, образованных точкой и всеми вершинами многоугольника. Если сумма больше площади (+некая погрешность вычислений), то точка лежит вне многоугольника.

ru.wikipedia.org/wiki/Алгоритм_точки_в_многоугольнике

Думаю, что подобный алгоритм через SQL не реализовать(Хотя можно попробовать определить функцию), поэтому:
1. «Рисуете» вокруг вашей области ограничивающий прямоугольник со сторонами параллельными координатной сетке. (Xmin, Ymin, Xmax, Ymax)
2. Выбираете все точки, принадлежащие этому прямоугольнику (простой, быстрый запрос)
3. Проверяете все эти точки скриптом.

Horse, Akr0n Дали два правильных варианта. Еще один.
Обходите вершины по порядку (по часовой стрелке или против) и проверяете с какой стороны от отрезка лежит искомая точка. В результате получите “+”, “-” или «0». «0» — точка лежит на отрезке, “+” с одной стороны (зависит как обходить), “-” — с другой. Если получили все плюсы или все минусы, то точка внутри полигона. Вот хорошие статьи на эту тему

суммируем углы между лучами (x,y)-(x1,y1) ….(x,y)-(xN,yN), где (x1,y1)… (xN,yN) координаты вершин, обходя их в том порядке в котором они связаны. (углы могут быть отрицательными)
если лежит внутри — то будет 2pi

Можно воспользоваться этим простым классом
https://github.com/xopbatgh/sb-polygon-pointer

Достаточно указать координаты полигона и координаты точки

Принцип работы заключается в том, что в самом начала создаётся такой квадрат, в который целиком помещается полигон. Далее из каждой стороны квадрата опускается перпендикуляр к искомой точке.
После этого считается число пересечений каждого перпендикуляра с рёбрами полигона. Если все перпендикуляры пересекают рёбра хотя бы один раз и ни разу нечётное число, то считается, что точка находится внутри полигона.

Это правило достаточно просто проверить с помощью листа бумаги и карандаша

5a6483d0315dd084509986.png


  • Показать ещё
    Загружается…

15 мая 2023, в 10:36

2000 руб./за проект

15 мая 2023, в 10:16

500 руб./за проект

15 мая 2023, в 10:14

4000 руб./за проект

Минуточку внимания

Источник

Исследование графика функции

На рисунке изображен график функции y=fleft( x right). Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:

  • область определения функции;
  • область значений функции;
  • нули функции;
  • промежутки возрастания и убывания;
  • точки максимума и минимума;
  • наибольшее и наименьшее значение функции на отрезке.

Уточним терминологию:

Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.

Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.

Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.
Обозначается: D(f) или D(y).

На нашем рисунке область определения функции y=fleft( x right) — это отрезок left[ -6; 6 right]. Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.

Область значений функции — это множество значений, которые принимает переменная y. На нашем рисунке это отрезок left[ -3; 7 right] — от самого нижнего до самого верхнего значения y.

Нули функции — точки, где значение функции равно нулю, то есть y=0. На нашем рисунке это точки x=-4 и x=1.

Значения функции положительны там, где y textgreater 0. На нашем рисунке это промежутки left[ -6; -4 right] и left[ 1; 6 right].
Значения функции отрицательны там, где y textless 0. У нас это промежуток (или интервал) от -4 до 1.

Важнейшие понятия — возрастание и убывание функции на некотором множестве M. В качестве множества M можно взять отрезок left[ a; b right], интервал left( a; b right), объединение промежутков или всю числовую прямую.

Функция y=fleft( x right) возрастает на множестве M, если для любых x_1 и x_2, принадлежащих множеству M, из неравенства x_2 textgreater x_1 следует неравенство fleft( x_2 right) textgreater fleft( x_1 right).

Иными словами, чем больше x, тем больше y, то есть график идет вправо и вверх.

Функция y=fleft( x right) убывает на множестве M, если для любых x_1 и x_2, принадлежащих множеству M, из неравенства x_2 textgreater x_1 следует неравенство fleft( x_2 right) textless fleft( x_1 right).

Для убывающей функции большему значению x соответствует меньшее значение y. График идет вправо и вниз.

На нашем рисунке функция fleft( x right) возрастает на промежутке left[ -2; 4 right] и убывает на промежутках left[ -6; -2 right] и left[ 4; 6 right].

Определим, что такое точки максимума и минимума функции.

Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.

На нашем рисунке x=4 — точка максимума.

Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».

На нашем рисунке x= -2 — точка минимума.

Точка x= -6 — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и x=6 на нашем графике не может быть точкой минимума.

Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это x=4 и x= -2.

А что делать, если нужно найти, например, минимум функции y=fleft ( x right ) на отрезке left[ -4; 0 right]? В данном случае ответ: y= -3. Потому что минимум функции — это ее значение в точке минимума.

Аналогично, максимум нашей функции равен 4. Он достигается в точке x=4.

Можно сказать, что экстремумы функции равны 4 и -3.

Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.

В нашем случае наименьшее значение функции на отрезке left[ -6; 6 right] равно -3 и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно 7. Оно достигается в левом конце отрезка.

В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Исследование графика функции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Определение принадлежности точки треугольнику

Дано: у нас есть треугольник, нам известны только координаты его вершин. У нас есть точка, нам известны её координаты.

Что нужно узнать: нужно установить принадлежность точки треугольнику.

В данной статье разбирается несколько разных методов определения принадлежности точки треугольнику.

Метод сравнения площадей

В данном методе сначала находятся площади 3-х треугольников, которые образует данная точка с каждой стороной треугольника. В нашем случае(рис. 1) это треугольники ABP, BCP, CAP и их площади s1, s2, s3 соответственно.

Затем находится площадь самого треугольника ABC.

Найденный площади сравниваются — если сумма 3-х площадей равна площади всего треугольника, то значит точка принадлежит треугольнику. При сравнении, как правило, задаётся погрешность.

Так как у нас известны только координаты точек, то все площади, находятся по формуле Герона, от обильности операций которой становится ясно, почему этот метод очень трудоёмкий.

Простейшая реализация алгоритма:

Атрибуты функции: aAx, aAy, aBx, aBy, aCx, aCy — координаты точек A, B, C треугольника; aPx, aPy — координаты точки, принадлежность которой надо определить.

Метод относительности

Данный метод заключается в следующем. Сначала выбирается ориентация движения по вершинам треугольника(по часовой или против часовой стрелке). Я выбираю по часовой. На рисунке 2 выбранная ориентация движения(по часовой) показана стрелками. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Не трудно догадаться, что если точка для всех прямых, при нашей ориентации, лежит с правой стороны, то значит точка принадлежит треугольнику, а если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.

На рисунке 2 продемонстрирована ситуация, когда точка только для одной прямой AB лежит по левую сторону, а значит не принадлежит треугольнику.

Всё относительно!

Тут надо кое что пояснить, весьма не маловажное, что может сыграть роль в оптимизации и выборе алгоритма. Обратите внимание, что в приведённом коде есть закомментированные блоки кода с комментариями «для строгой ориентации», в то время как рабочий код универсален — он предназначен для любой ориентации. Т.е. представленный код определит принадлежность точки для любого заданного треугольника. В моей тестирующей программе треугольники как раз таки строятся по random()-у координат вершин, а ориентация идёт по вершинам(A>B>C>A). Для рисунка 2 — это по часовой стрелки, но для рисунка 3 — это против часовой.

Так вот, в случае рисунка 3 точка должна лежать по левую сторону векторов, чтобы принадлежать треугольнику.

Вот тут и получается важный момент! Если вы уверены, что в вашем проекте все треугольники будут ориентированы по часовой стрелке(а т.е. вершина C будет всегда правее вектора AB), то вам можно закомментировать блок универсального решения и раскомментировать блок «для строгой ориентации по часовой» и данный алгоритм упрощается аж на 3 логических операции!

Векторный метод

Третий метод который я освещаю для меня самый интересный.

Идея его применения зарождается если взглянуть на треугольник как на половинку параллелограмма…

Данный метод я сначала проверил на бумаге. После всех оптимизаций формул, как всё сошлось, я реализовал его в коде, где он показал себя вполне успешным и результативным. Аж эффективнее 2-х предыдущих методов :]

1) одну вершину треугольника помещаем в координаты (0;0);

2) две стороны, выходящие из этой вершины, представляем как вектора.

Таким образом из всего этого появляется система простых условий нахождения точки P между векторами b и c.(рис. 4)

Рис. 4.

Как определить лежит ли точка внутри треугольника или снаружи.

Калькулятор поможет определить находится ли заданная точка внутри заданного треугольника. Точка и треугольник задаются декартовыми координатами на плоскости. Детально описан алгоритм вычисления.

Этот калькулятор определит где находится заданная точка внутри 2-мерного треугольника или вовне. Калькулятор использует простой алгоритм, основанный на свойствах векторного произведения. Описание этого алгоритма можно найти сразу за калькулятором.

Точка в треугольнике

Векторное произведение ( z – координата )

Точка внутри треугольника. Описание алгоритма.

Векторное произведение векторов a и b, заданного декартовыми координатами в пространстве для 3-х мерного правого ортонормального базиса можно выразить так:
[1].
Векторное произведение обладает свойством антикоммутативности:

Это важное свойство мы будем использовать для решения нашей задачи.

Попарное векторное произведение векторов-сторон треугольника и вектора из вершины в точку

Для того чтобы определить лежит ли точка P внутри треугольника ABC мы вычислим 3 векторных произведения: ABxAP, BCxBP and CAxCP. Так как наш треугольник и точка в 2-мерном пространстве на плоскости, третья координата z для трехмерного пространства равна нулю. Согласно формуле [1] мы можем не вычислять координаты x и y для векторного произведения, если координата z векторов-множителей равна нулю – координаты x и y результата в этом случае всегда равны нулю (результирующий псевдо-вектор перпендикулярен плоскости треугольника). Знак результата произведения для оставшейся координаты (z) зависит от относительного положения умножаемых векторов. Если первый вектор (в нашем случае это сторона треугольника) находится правее второго вектора (вектор из вершины в точку P), то координата z результата будет положительна, если первый вектор будет левее второго – отрицательна, и в противном случае, если оба вектора идут в одном и том же направлении, результат будет равен нулю.
Получив результаты по трем векторным произведениям, нам остается их проанализировать, чтобы понять лежит ли точка внутри треугольника:
Если мы имеем и положительные и отрицательные результаты, точка лежит вне треугольника, если результаты только положительные или только отрицательные, точка – внутри.
Таблица далее иллюстрирует все возможные варианты результатов векторного произведения:

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Источник

Добавить комментарий