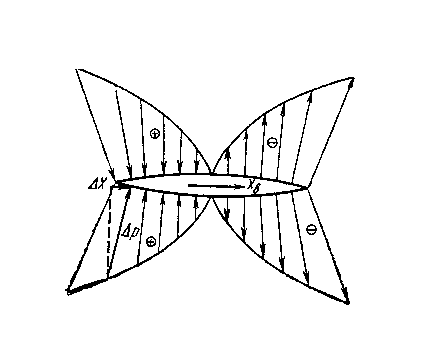
Как найти волновое сопротивление воздуха

Как найти волновое сопротивление воздуха

Волновое сопротивление

Причиной
необратимых потерь энергии потока в
скачке является так называемое волновое
сопротивление.

Образование
скачков уплотнения в сверхзвуковом
потоке вызывает перераспределение
давлений по профилю крыла (Рисунок5.4).
За головным скачком уплотнения давление
резко увеличивается. Далее из–за
увеличения скорости обтекания выпуклых
поверхностей давление убывает. На задних
скатах профиля уже создается подсос
(разрежение).

Образуется
аэродинамическая сила, направленная
по потоку (против движения крыла), которая
называется
волновым
сопротивлением

.

По
своей природе волновое
сопротивление является сопротивлением
давления и
определяется потерями кинетической
энергии потока. Оно зависит от формы
скачка уплотнения.

Рис 5.4. Волновое
сопротивление

Форма
скачка уплотнения
зависит от формы обтекаемого тела и
числа М сверхзвукового потока (Рисунок5.5).

-Прямой
скачок уплотнения
(Рисунок5.5,а). Направление потока при
прохождений через прямой скачок
уплотнения не изменяется. Скорость за
ним становится дозвуковой.

Прямой
скачок уплотнения является границей
между сверхзвуковой и дозвуковой частью
потока.

-При
небольшой
сверхзвуковой
скорости потока перед телом с тупой
передней кромкой образуется прямой
отсоединенный
скачок уплотнения (5.5,в).

Потери
энергии потока в таком скачке
максимальны.
С увеличением скорости сверхзвукового
потока прямой скачок уплотнения
приближается к передней кромке тела и
начинает “складываться”.

Рисунок5.5
Виды скачков уплотнения

-Косой
скачок (Рисунок5.5,б).
Это скачок уплотнения, поверхность
которого наклонна к потоку. В косом
скачке потери кинетической энергии
потока значительно
меньше, чем
в прямых, и зависят от угла наклона
скачка. Прохождение потока через косой
скачок вызывает изменение направления
потока. Скорость после косого скачка
может остаться сверхзвуковой.

Сопротивление,
создаваемое косыми скачками, значительно
меньше. Образуются косые скачки уплотнения
в потоке с большой сверхзвуковой
скоростью при обтекании тел с
острой
передней кромкой (Рисунок5.5,г).

Для
уменьшения сопротивления сверхзвуковых
самолетов предусматривают “дробление”
прямых скачков, т.е. замену их системой
косых скачков. Для этого делаются острыми
передние кромки крыла, оперения,
устанавливаются выдвижные
конусы на
входе в двигатель и профилированные
иглы
перед фюзеляжем (Рисунок5.5,е).

-По
расположению относительно обтекаемого
тела скачки уплотнения подразделяются
на головные
1, хвостовые 2, местные 3,
которые замыкают местные сверхзвуковые
зоны, возникающие при дозвуковых
скоростях полета (Рисунок5.5,д).

Критическое
число Маха.

Наименьшая
скорость дозвукового полета, при которой
где-либо в потоке, обтекающем самолет,
появляются скорости, равные скорости
звука, называ­ется критической
скоростью
полета
,
а соответствующее ей число Маха полета
–критическим
.
При
наступает очень опасное явление,
называемоеволновым
кризисом.

зависит
от геометрических характеристик профиля
крыла. Чем больше
ипрофиля, тем больше разрежение над
крылом, тем меньше.
Для каждого самолета критическое число
Маха имеет вполне определенное постоянное
значение. Так, например, для самолета
Ту-154Мкр
= 0,88, а для
АН-24 Мкр
= 0,7.

Чем
больше высота полета, тем раньше наступает
волновой кризис – критическое число М
уменьшается.

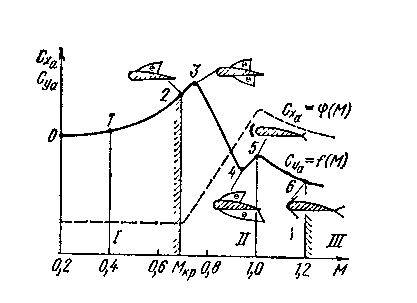
Рисунок5.6
Зависимость коэффициентов Сy
и
Cx
от
числа М

Для
измерения числа М полета на всех
скоростных самолетах в соответствии с
требо­ваниями ИКАО установлены
специальные приборы – указатели числа
М
(МС-1).
Критическое число М
для данного самолета отмечено на шкале
прибора красной чертой.

Занятие №11

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Dig



Ученик

(112),
закрыт



10 лет назад

Константин

Гуру

(4662)


12 лет назад

Если имеется в виду электрический импеданс (а не механическое сопротивление) , то он равен 377 Ом. Рассчитывается так же, как импеданс вакуума — корень из абсолютной мангитной проницаемости вакуума делённой на абсолютную диэелектрическую проницаемость вакуума (обозначаются как mu0 и epsilon0). Если воздух влажный, то импеданс меняется.

Источник

Волново́е сопротивле́ние — характеристика среды распространения волны.

В акустике[править | править код]

Волновое сопротивление в газе и жидкости — отношение звукового давления в бегущей плоской звуковой волне к колебательной скорости частиц среды. Также волновое сопротивление равно произведению плотности среды на скорость звука в ней.

Волновое сопротивление в твёрдых телах для продольных волн — отношение механического напряжения, взятого с обратным знаком, к колебательной скорости частиц среды.

См. также удельное акустическое сопротивление.

В гидромеханике[править | править код]

Волновое сопротивление в гидромеханике — часть гидро- и аэродинамического сопротивления, характеризующая затраты энергии на образование волн, например:

  • волн, образующихся на поверхности воды при движении корабля;
  • ударных волн, возникающих при сверхзвуковом полете самолёта;
  • и т. д.

В электродинамике[править | править код]

В электродинамике волновое сопротивление линии передачи (коротко — волновое сопротивление) — величина, определяемая отношением напряжения падающей волны к току этой волны в линии передачи (по закону Ома)[1].

При определении волнового сопротивления может использоваться также напряжение и ток отражённой или бегущей волн.

Единица измерения — Ом.

При расчёте волнового сопротивления по методу комплексных амплитуд используют амплитуды напряжения и силы тока. При наличии потерь в линии передачи значение становится комплексным.

Волновое сопротивление линии передачи зависит от её конструкции и электрофизических параметров применяемых материалов (ε, μ, σ), что совместно определяет погонные параметры линии передачи (ёмкость, индуктивность, сопротивление и проводимость на единицу длины), а также от типа волны, при наличии дисперсии — от частоты электромагнитных колебаний.

Волновое сопротивление часто путают с характеристическим сопротивлением волны — величиной, определяемой отношением поперечной составляющей напряженности электрического поля к поперечной составляющей напряженности магнитного поля бегущей волны[1].

В длинной линии волновое сопротивление равно (по закону Ома):

{displaystyle Z_{0}={U_{m} over I_{m}},}

где:

В бесконечно длинных линиях нагрузка имеет чисто активный характер, поэтому энергия, запасаемая в индуктивности и ёмкости, одинаковая.

{displaystyle {L_{1}XI_{m}^{2} over 2}={C_{1}XU_{m}^{2} over 2},}

где:

Поэтому волновое сопротивление в бесконечно длинных линиях определяется погонными индуктивностью и ёмкостью:

{displaystyle {sqrt {L_{1} over C_{1}}}={U_{m} over I_{m}}=Z_{0}.}

Волновое сопротивление среды — отношение амплитуд электрического и магнитного полей электромагнитных волн, распространяющихся в среде:

{displaystyle Z={E_{0}^{-}(x) over H_{0}^{-}(x)}.}

Если волновые сопротивления двух сред, имеющих границу раздела, одинаковы, то на этой границе не происходит отражения электромагнитных волн, даже если диэлектрическая и магнитная проницаемости в средах различны.

В радиотехнике[править | править код]

При распространении электромагнитной волны в среде с относительными диэлектрической varepsilon и магнитной mu проницаемостями амплитудные и мгновенные значения напряжённости электрического E и магнитного H полей связаны соотношением: {displaystyle {sqrt {varepsilon _{0}varepsilon }}E={sqrt {mu _{0}mu }}H}, где mu _{0} — магнитная постоянная, varepsilon _{0} — электрическая постоянная. Это выражение можно представить в виде:

{displaystyle {frac {E}{H}}={sqrt {frac {mu _{0}mu }{varepsilon _{0}varepsilon }}}}.

Отношение {displaystyle {frac {E}{H}}} принято называть волновым сопротивлением среды, поскольку существует формальная аналогия между уравнением {displaystyle {frac {E}{H}}={sqrt {frac {mu _{0}mu }{varepsilon _{0}varepsilon }}}} и законом Ома[2]. Для вакуума mu = varepsilon = 1, поэтому его волновое сопротивление {displaystyle rho _{v}={sqrt {frac {mu _{0}}{varepsilon _{0}}}}=376,73} Ом.

Примечания[править | править код]

  1. ↑ 1 2 ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
  2. ↑ Сена Л. А. Единицы физических величин и их размерности. — М., Наука, 1977. — С. 226—227
Источник

From Wikipedia, the free encyclopedia

In aeronautics, wave drag is a component of the aerodynamic drag on aircraft wings and fuselage, propeller blade tips and projectiles moving at transonic and supersonic speeds, due to the presence of shock waves.[1] Wave drag is independent of viscous effects,[2] and tends to present itself as a sudden and dramatic increase in drag as the vehicle increases speed to the critical Mach number. It is the sudden and dramatic rise of wave drag that leads to the concept of a sound barrier.

Overview[edit]

Wave drag is a component of pressure drag due to compressibility effects.[3] It is caused by the formation of shock waves around a body. Shock waves create a considerable amount of drag, which can result in extreme drag on the body. Although shock waves are typically associated with supersonic flow, they can form at subsonic aircraft speeds on areas of the body where local airflow accelerates to supersonic speed. The effect is typically seen on aircraft at transonic speeds (about Mach 0.8), but it is possible to notice the problem at any speed over that of the critical Mach of that aircraft. It is so pronounced that, prior to 1947, it was thought that aircraft engines would not be powerful enough to overcome the enhanced drag, or that the forces would be so great that aircraft would be at risk of breaking up in midflight. It led to the concept of a sound barrier.

Research[edit]

In 1947, studies into wave drag led to the development of perfect shapes to reduce wave drag as much as theoretically possible. For a fuselage the resulting shape was the Sears–Haack body, which suggested a perfect cross-sectional shape for any given internal volume. The von Kármán ogive was a similar shape for bodies with a blunt end, like a missile. Both were based on long narrow shapes with pointed ends, the main difference being that the ogive was pointed on only one end.

Reduction of drag[edit]

A number of new techniques developed during and just after World War II were able to dramatically reduce the magnitude of wave drag, and by the early 1950s the latest fighter aircraft could reach supersonic speeds.

These techniques were quickly put to use by aircraft designers. One common solution to the problem of wave drag was to use a swept wing, which had actually been developed before World War II and used on some German wartime designs. Sweeping the wing makes it appear thinner and longer in the direction of the airflow, making a conventional teardrop wing shape closer to that of the von Kármán ogive, while still remaining useful at lower speeds where curvature and thickness are important.

The wing need not be swept when it is possible to build a wing that is extremely thin. This solution was used on a number of designs, beginning with the Bell X-1, the first manned aircraft to fly at the speed of sound. The downside to this approach is that the wing is so thin it is no longer possible to use it for storage of fuel or landing gear. Such wings are very common on missiles, although, in that field, they are often referred to as “fins”.

Fuselage shaping was similarly changed with the introduction of the Whitcomb area rule. Whitcomb had been working on testing various airframe shapes for transonic drag when, after watching a presentation by Adolf Busemann in 1952, he realized that the Sears-Haack body had to apply to the entire aircraft, not just the fuselage. This meant that the fuselage needed to be made narrower where it joined the wings, so that the cross-section of the entire aircraft matched the Sears-Haack body.

Application of the area rule can also be seen in the use of anti-shock bodies on transonic aircraft, including some jet airliners. Anti-shock bodies, which are pods along the trailing edges of the wings, serve the same role as the narrow waist fuselage design of other transonic aircraft.

Other drag reduction methods[edit]

Several other attempts to reduce wave drag have been introduced over the years. The supercritical airfoil is a type that results in reasonable low speed lift like a normal airfoil, but has a profile considerably closer to that of the von Kármán ogive. All modern civil airliners use forms of supercritical aerofoil and have substantial supersonic flow over the wing upper surface.

Mathematical formula[edit]

For flat plate aerofoil[edit]

{displaystyle cd_{w}=4*{frac {alpha ^{2}}{sqrt {(M^{2}-1)}}}}[4]

For double-wedge aerofoil[edit]

{displaystyle cd_{w}=4*{frac {alpha ^{2}+(t/c)^{2}}{sqrt {(M^{2}-1)}}}}[4]

Where:

cd_w – Coefficient of drag from wave drag

α – Angle of attack

t/c – Thickness to Chord ratio

M – Freestream Mach number

These equations are applicable at low angles of attack (α < 5°)

References[edit]

  1. ^ Anderson, John D., Jr. (1991). Fundamentals of aerodynamics (2nd ed.). New York: McGraw-Hill. pp. 492, 573. ISBN 0-07-001679-8.
  2. ^ Clancy, L.J. (1975), Aerodynamics, Section 11.7
  3. ^ Anderson, John D., Jr. (1991). Fundamentals of aerodynamics (2nd ed.). New York: McGraw-Hill. p. 25. ISBN 0-07-001679-8.
  4. ^ a b “How can I calculate wave drag in supersonic airfoil?”. 2 February 2014. Retrieved 23 May 2019.
Источник

Волновое сопротивление

Волновое сопротивление
Волновое сопротивление

в аэродинамике — часть сопротивления аэродинамического, возникающая при достаточно большой скорости полёта, когда Маха число полета М превышает критическое М*. Его появление обусловлено тем, что при переходе от докритического обтекания (М* < М) к сверхкритическому (М* < М < 1) вблизи поверхности летательного аппарата (как правило, на крыле) формируются местные сверхзвуковые зоны (области со сверхзвуковыми скоростями газа), замыкающиеся скачками уплотнения, а при сверхзвуковом обтекании (М > l) образуется головной скачок уплотнения и, возможно, ряд внутренних скачков. Переход части кинетической энергии в тепловую энергию газа в таких скачках (ударных волнах) приводит к дополнительной силе, действующей противоположно направлению движения летательного аппарат. Это и есть сила В. с. Непосредственная связь В. с. со сверхкритическим (или сверхзвуковым) обтеканием и скачками уплотнения выражается также в том, что оно определяется суммарным приращением энтропии газа при переходе через скачок или систему скачков уплотнения.

Резкий рост сопротивления на сверхкритическом режиме и необходимое для перехода через скорость звука увеличение тяги двигателей летательного аппарата связаны с тем, что В. с. возрастает пропорционально (М — М*)/3. С целью уменьшения сопротивления и увеличения аэродинамического качества используются профили с возможно большим значением критического числа Маха (сверхкритические профили). Широкое распространение получили стреловидные и треугольные крылья, для которых вследствие скольжения принципа значение М* может быть существенно выше, чем для прямого крыла, а скачки уплотнения при сверхзвуковом обтекании значительно слабее.

Авиация: Энциклопедия. — М.: Большая Российская Энциклопедия.
.
1994.

.

Полезное

Смотреть что такое “Волновое сопротивление” в других словарях:

  • ВОЛНОВОЕ СОПРОТИВЛЕНИЕ — 1) в акустике: в газе и жидкости отношение звукового давления в бегущей плоской звуковой волне к колебательной скорости частиц среды, оно равно произведению плотности среды на скорость звука в ней; в твердых телах для продольных волн волновое с …   Большой Энциклопедический словарь

  • волновое сопротивление — импеданс Сопротивление среды передачи распространению электромагнитных волн. Определяется геометрией проводников и диэлектрическими свойствами изоляции. Измеряется в омах (ISO/IEC 11801). [http://www.iks… …   Справочник технического переводчика

  • Волновое сопротивление — (в гидромеханике) часть сопротивления воды движению судна, обусловленная затратами энергии на образование волн вблизи поверхности воды, возникающих при движении судна. Волновое сопротивление жидкости учитывается при проектировании подводных лодок …   Морской словарь

  • Волновое сопротивление — 24. Волновое сопротивление По ГОСТ 19880 74* Источник: ГОСТ 25903 83: Выключатели и переключатели вакуумные высокочастотные. Термины и определения …   Словарь-справочник терминов нормативно-технической документации

  • Волновое сопротивление — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете …   Википедия

  • волновое сопротивление — 1) в акустике: в газе и жидкости  отношение звукового давления в бегущей плоской звуковой волне к колебательной скорости частиц среды, оно равно произведению плотности среды на скорость звука в ней; в твердых телах для продольных волн волновое… …   Энциклопедический словарь

  • волновое сопротивление — būdingoji pilnutinė terpės varža statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, išreiškiamas terpėje sklindančios skersinės elektromagnetinės bangos elektrinių ir magnetinių stiprių dalmeniu. atitikmenys: angl. characteristic… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • волновое сопротивление — banginė varža statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. wave resistance vok. Wellenwiderstand, m rus. волновое сопротивление, n pranc. résistance d’onde, f; …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • волновое сопротивление — banginė varža statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, išreiškiamas elektrinės linijos, kai ja sklinda bėgančiosios elektromagnetinės bangos, bet kurio taško įtampos ir srovės stiprio dalmeniu. atitikmenys: angl. wave… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • волновое сопротивление — banginė varža statusas T sritis fizika atitikmenys: angl. wave impedance; wave resistance vok. Wellenwiderstand, m rus. волновое сопротивление, n pranc. résistance d’onde, f …   Fizikos terminų žodynas

Источник

Добавить комментарий