| Квантовая механика |
|---|
|
|
Основа
|
|
Фундаментальные понятия
|
|
Эксперименты
|
|
Формулировки
|
|
Уравнения
|
|
Интерпретации
|
|
Развитие теории
|
|
Сложные темы
|
|
Известные учёные
|
|
См. также
|
| См. также: Портал:Физика |

Сравнение концепций классического и квантового гармонического осциллятора для одиночной бесспиновой частицы. Эти два процесса сильно различаются. Классический процесс (A — B) представлен как движение частицы по траектории. В квантовом процессе (C — H) такой траектории нет. Движение квантового осциллятора похоже на волновое; здесь вертикальная ось показывает действительную часть (синий цвет) и мнимую часть (красный цвет) волновой функции. Панели (C — F) показывают четыре различных решения уравнения Шрëдингера для стоячей волны. На панелях (G — H) показаны две разные волновые функции, которые являются решениями уравнения Шрёдингера, но не являются стоячими волнами.
Волнова́я фу́нкция, или пси-фу́нкция 

где 

Согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.
Волновая функция — это функция степеней свободы, соответствующая некоторому максимальному набору коммутирующих наблюдаемых. Как только такое представление выбрано, волновая функция может быть получена из квантового состояния.
Для данной системы выбор коммутирующих степеней свободы не является уникальным, и, соответственно, область определения волновой функции также не уникальна. Например, её можно рассматривать как функцию всех координат положения частиц в координатном пространстве или импульсов всех частиц в пространстве импульсов; эти два описания связаны преобразованием Фурье. Некоторые частицы, такие как электроны и фотоны, имеют ненулевой спин, и волновая функция таких частиц включает спин как внутреннюю дискретную степень свободы; также для различных систем могут быть рассмотрены другие дискретные переменные, такие как изоспин. Когда система имеет внутренние степени свободы, волновая функция в каждой точке непрерывных степеней свободы (например, точка в координатном пространстве) присваивает комплексное число для каждого возможного значения дискретных степеней свободы (например, z-компонента спина) — эти значения часто отображаются в виде вектора-столбца (например, 2 × 1 для нерелятивистского электрона со спином.
Согласно принципу суперпозиции в квантовой механике, волновые функции можно складывать и умножать на комплексные числа, чтобы построить новые волновые функции и задать гильбертово пространство. Внутреннее произведение в гильбертовом пространстве между двумя волновыми функциями является мерой перекрытия между соответствующими физическими состояниями и используется в фундаментальной вероятностной интерпретации квантовой механики, правиле Борна, связывающем вероятности переходов со скалярным произведением состояний. Уравнение Шрёдингера определяет, как волновые функции эволюционируют с течением времени, а волновая функция качественно ведёт себя как другие волны, такие как волны на воде или волны в струне, потому что уравнение Шрёдингера математически является разновидностью волнового уравнения. Это объясняет название «волновая функция» и приводит к дуальности волна-частица. Однако волновая функция в квантовой механике описывает своего рода физическое явление, все ещё открытое для различных интерпретаций, которое принципиально отличается от такового для классических механических волн[1][2][3][4][5][6][7].
В статистической интерпретации Борна в нерелятивистской квантовой механике[8][9][10], квадрат модуля волновой функции — это вещественное число, интерпретируемым как плотность вероятности измерения частицы как находящейся в заданном месте или имеющей заданный импульс в заданное время и, возможно, имеющей определённые значения для дискретных степеней свободы. Интеграл этой величины по всем степеням свободы системы должен быть равен 1 в соответствии с вероятностной интерпретацией. Это общее требование, которому должна удовлетворять волновая функция, называется условием нормировки. Поскольку волновая функция имеет комплексные значения, можно измерить только её относительную фазу и относительную величину — её значение, по отдельности, ничего не говорит о величинах или направлениях измеряемых наблюдаемых; необходимо применить квантовые операторы, собственные значения которых соответствуют наборам возможных результатов измерений, к волновой функции ψ и вычислить статистические распределения для измеримых величин.
История[править | править код]
В 1905 году Альберт Эйнштейн постулировал пропорциональность между частотой 







В 1920-х и 1930-х годах квантовая механика развивалась с использованием математического анализа и линейной алгебры. Анализ в своих работах использовали Луи де Бройль, Эрвин Шредингер и другие, разработавшие «волновую механику». Среди тех, кто применял методы линейной алгебры, были Вернер Гейзенберг, Макс Борн и другие, разработавшие «матричную механику». Впоследствии Шрёдингер показал, что эти два подхода эквивалентны[14].
В 1926 году Шрёдингер опубликовал знаменитое волновое уравнение, теперь названное его именем, уравнением Шрёдингера. Это уравнение было основано на классическом законе сохранении энергии, но записано с использованием квантовых операторов и соотношений де Бройля, а его решения представлялись волновыми функциями квантовой системы[15]. Однако никто не знал, как это интерпретировать[16]. Сначала Шрёдингер и другие думали, что волновые функции представляют собой частицы, которые распределены по пространству, причём большая часть частицы находится там, где волновая функция велика[17]. Было показано, что это несовместимо с упругим рассеянием волнового пакета (представляющего собой частицу) от рассеивателя, потому что он распространяется во всех направлениях[8]. Хотя рассеянная частица может рассеяться в любом направлении, она не разбивается на части и не улетает во всех направлениях. В 1926 году Борн представил свою интерпретацию амплитуды вероятности[9][18]. Она связывает вычисления квантовой механики непосредственно с вероятностями наблюдаемыми в эксперименте. Сейчас эта картина принята как часть копенгагенской интерпретации квантовой механики. Существует много других интерпретаций квантовой механики. В 1927 году Хартри и Фок сделали первый шаг в попытке описать волновую функцию для N-частиц и разработали самосогласованую процедуру : итерационный алгоритм для аппроксимации решения многочастичной квантовомеханической задачи. Сейчас это метод известен как метод Хартри — Фока[19]. Определитель и перманент Слейтера (матрицы) были частью метода, предложенного Джоном К. Слейтером.
Шрёдингер действительно работал с уравнением для волновой функции, которое удовлетворяло релятивистскому закону сохранения энергии, прежде чем он опубликовал нерелятивистскую версию, но отбросил его, поскольку оно предсказывало отрицательные вероятности и отрицательные энергии. В 1927 году Клейн, Гордон и Фок также нашли его, но учли электромагнитное взаимодействие и доказали, что оно Лоренц-инвариантно. Де Бройль также пришёл к тому же уравнению в 1928 году. Это релятивистское волновое уравнение сейчас наиболее широко известно как уравнение Клейна — Гордона[20].
В 1927 году Паули феноменологически нашёл нерелятивистское уравнение для описания частиц со спином 1/2 в электромагнитных полях, которое теперь называется уравнением Паули[21]. Паули обнаружил, что волновая функция не описывалась одной комплексной функцией пространства и времени, а требовалось два комплексных числа, которые соответствуют состояниям фермиона со спином +1/2 и −1/2. Вскоре после этого, в 1928 году, Дирак нашёл уравнение из первого успешного объединения специальной теории относительности и квантовой механики в применении к электрону, которое теперь называется уравнением Дирака. В этом случае волновая функция представляет собой спинор, представленный четырьмя комплексными компонентами[19]: двумя для электрона и двумя для античастицы электрона — позитрона. В нерелятивистском пределе волновая функция Дирака напоминает волновую функцию Паули для электрона. Позже были найдены другие релятивистские волновые уравнения.
Волновые функции и волновые уравнения в современных теориях[править | править код]
Все эти волновые уравнения имеют непреходящее значение. Уравнение Шрёдингера и уравнение Паули во многих случаях являются превосходными приближениями для релятивистских задач. Их значительно легче решить в практических задачах, чем их релятивистские аналоги.
Уравнения Клейна — Гордона и Дирака, будучи релятивистскими, не полностью примиряют квантовую механику и специальную теорию относительности. Раздел квантовой механики, где эти уравнения изучаются так же, как уравнение Шрёдингера, часто называемый релятивистской квантовой механикой, хотя и очень успешен, имеет свои ограничения (см., например, Лэмбовский сдвиг) и концептуальные проблемы (см., например, море Дирака).
Относительность делает неизбежным то, что количество частиц в системе непостоянно. Для полного согласования нужна квантовая теория поля[22]. В этой теории волновые уравнения и волновые функции также используются, но в несколько ином виде. Основными объектами интереса являются не волновые функции, а скорее операторы, так называемые операторы поля (или просто поля, под которыми понимаются «операторы») в гильбертовом пространстве состояний. Оказывается, исходные релятивистские волновые уравнения и их решения всё ещё необходимы для построения гильбертова пространства. Более того, операторы свободных полей, то есть для невзаимодействующих частиц, во многих случаях формально удовлетворяют тому же уравнению, что и поля (волновые функции).
Таким образом, уравнение Клейна — Гордона (спин 0) и уравнение Дирака (спин 1⁄2) в таком виде остаются в теории. Аналоги высших спинов включают уравнение Прока (спин 1), уравнение Рариты — Швингера (спин 3⁄2) и, в более общем смысле, уравнения Баргмана — Вигнера. Для безмассовых свободных полей примерами являются уравнения Максвелла свободного поля (спин 1) и уравнение Эйнштейна свободного поля (спин 2) для операторов поля[23]. Все они по сути являются прямым следствием требования лоренц-инвариантности. Их решения должны преобразовываться при преобразовании Лоренца заданным образом, то есть в соответствии с определённым представлением группы Лоренца и, что вместе с некоторыми другими разумными требованиями, например принципом кластерной декомпозиции[24], с учётом причинности достаточно, для модификации уравнения.
Это относится к уравнениям свободного поля, когда взаимодействия не включены. Если доступна плотность лагранжиана (включая взаимодействия), то лагранжев формализм даст уравнение движения на классическом уровне. Это уравнение может быть очень сложным и не поддающимся решению. Любое решение будет относиться к фиксированному числу частиц и не будет учитывать термин «взаимодействие», как понимается в этих теориях, который включает в себя создание и уничтожение частиц, а не внешние потенциалы, как в обычной квантовой теории (первичного квантования).
В теории струн ситуация остаётся аналогичной. Например, волновая функция в импульсном пространстве играет роль коэффициента разложения Фурье в общем состоянии частицы (струны) с импульсом, который чётко не определён[25].
Физический смысл[править | править код]
В координатном представлении волновая функция 




-
.
Так, что в заданном квантовом состоянии системы, описываемом волновой функцией 


-
.
Возможно измерение и разницы фаз волновой функции, например, в опыте Ааронова — Бома.
Нормированность волновой функции[править | править код]
Поскольку суммарная вероятность обнаружения частицы во всём пространстве равна единице, то её волновая функция 
В общем случае интегрирование должно производиться по всем переменным, от которых волновая функция явно зависит в данном представлении (кроме времени).
Принцип суперпозиции квантовых состояний[править | править код]
Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями 




-
.
Очевидно, что можно говорить и о суперпозиции (сложении) любого числа квантовых состояний, то есть о существовании квантового состояния системы, которое описывается волновой функцией
-
.
В таком состоянии квадрат модуля коэффициента 

Поэтому для нормированных волновых функций 
Условия регулярности волновой функции[править | править код]
Вероятностный смысл волновой функции накладывает определённые ограничения, или условия, на волновые функции в задачах квантовой механики. Эти стандартные условия часто называют условиями регулярности волновой функции.
- Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений, таких, что интеграл
станет расходящимся. Следовательно, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией, т.е принадлежала гильбертовому пространству
. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.
- Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно. В задачах с использованием цилиндрической или сферической системы координат условие однозначности приводит к периодичности волновых функций по угловым переменным.
- Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции
,
,
. Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.
Волновая функция в различных представлениях[править | править код]
Набор координат, которые выступают в роли аргументов функции, представляет собой полную систему коммутирующих наблюдаемых. В квантовой механике возможно выбрать несколько полных наборов наблюдаемых, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор величин определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения, или представление Фока, и др.
Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.
Матричная и векторная формулировки[править | править код]
Волновая функция одного и того же состояния в различных представлениях будет соответствовать выражению одного и того же вектора в разных системах координат. Остальные операции с волновыми функциями также будут иметь аналоги на языке векторов.
В волновой механике используется представление, где аргументами пси-функции является полная система непрерывных коммутирующих наблюдаемых, а в матричной используется представление, где аргументами пси-функции является полная система дискретных коммутирующих наблюдаемых. Поэтому функциональная (волновая) и матричная формулировки, очевидно, математически эквивалентны.
Описание смешанных квантовых состояний[править | править код]
Волновая функция представляет собой метод описания чистого состояния квантовомеханической системы. Смешанные квантовые состояния (в квантовой статистике) следует описывать при помощи матрицы плотности.
Координатное и импульсное представления[править | править код]
Волновая функция, представленная в виде функции от координат 
Всякая волновая функция в координатном представлении может быть разложена по собственным функциям оператора её импульса:
В результате получаем обратное преобразование Фурье:
,
где 
Коэффициенты разложения 
Функция 


Волновые функции и функциональные пространства[править | править код]
Концепция функциональных пространств естественным образом используется в дискуссии о волновых функциях. Функциональное пространство — это набор функций, обычно с некоторыми определяющими требованиями к функциям (в данном случае они являются квадратично интегрируемыми), иногда с заданной алгебраической структурой на множестве (в данном случае структура векторного пространства со скалярным произведением) вместе с топологией на множестве. Последнее будет использоваться здесь редко, оно необходимо только для получения точного определения того, что означает замкнутое подмножества функционального пространства. Ниже будет сделан вывод, что функциональное пространство волновых функций является гильбертовым пространством. Это наблюдение является основой преобладающей математической формулировкой квантовой механики.
Структура векторного пространства[править | править код]
Волновая функция, как элемент функционального пространства, частично характеризуется следующими конкретными и абстрактными описаниями.
- Уравнение Шрёдингера линейно. Это означает, что его решения, волновые функции, можно складывать и умножать на скаляры, чтобы получить новое решение. Множество решений уравнения Шрёдингера представляет собой векторное пространство.
- Принцип суперпозиции квантовой механики. Если Ψ и Φ — два состояния в абстрактном пространстве состояний квантовой механической системы, а a и b — любые два комплексных числа, то aΨ + bΦ является допустимым состоянием. Считается ли нулевой вектор допустимым состоянием («система отсутствует») — вопрос определения. Нулевой вектор ни в коем случае не описывает состояние вакуума в квантовой теории поля. Множество допустимых состояний — векторное пространство.
Это сходство не случайно. Также следует помнить о различиях между пространствами.
Представления[править | править код]
Основные состояния характеризуются набором квантовых чисел. Это набор собственных значений максимального набора коммутирующих наблюдаемых. Физические наблюдаемые представлены линейными операторами, также называемыми наблюдаемыми, в пространстве векторов. Максимальность означает, что в такой набор нельзя добавить никакие другие алгебраически независимые наблюдаемые, которые коммутируют с уже имеющимися. Выбор такого множества можно назвать выбором представления.
- В квантовой механике постулируется, что физически наблюдаемая величина системы, такая как положение, импульс или спин, представлена линейным эрмитовым оператором в пространстве состояний. Возможными результатами измерения этой величины являются собственные значения оператора[17]. На более глубоком уровне большинство наблюдаемых, а возможно, и все, возникают как генераторы симметрий[17][28][nb 1].
- Физическая интерпретация состоит в том, что такой набор представляет то, что теоретически можно одновременно измерить с произвольной точностью. Соотношение неопределенностей Гейзенберга запрещает одновременные точные измерения двух некоммутирующих наблюдаемых.
- Набор неуникальный. Для одночастичной системы это может быть z проекция (x, Sz) y проекция (p, Sy). В этом случае оператор, соответствующий положению (оператор умножения в координатном представлении), и оператор, соответствующий импульсу (дифференциальный оператор в координатном представлении), не коммутируют.
- После того, как представление выбрано, неоднозначность остаётся. Осталось выбрать систему координат. Это может, например, соответствовать выбору осей x, y и z или выбору криволинейных координат, как показано на примере сферических координат, используемых для волновых функций атомов водорода. Этот окончательный выбор также фиксирует базис в абстрактном гильбертовом пространстве. Основные состояния помечены квантовыми числами, соответствующими максимальному набору коммутирующих наблюдаемых и соответствующей системе координат[nb 2].
Абстрактные состояния являются «абстрактными» только в том смысле, что не даётся произвольный выбор, необходимый для конкретного явного описания. Или другими словами, не было дано никакого выбора максимального набора коммутирующих наблюдаемых. Что аналогично векторному пространству без заданного базиса. Соответственно, волновые функции, соответствующие квантовому состоянию, не уникальны. Эта неоднозначность отражает неоднозначность в выборе максимального набора коммутирующих наблюдаемых. Для одной частицы со спином в одном измерении конкретному состоянию соответствуют две волновые функции Ψ(x, Sz) и Ψ(p, Sy), они обе описывают одно и то же состояние.
- Для каждого выбора максимального набора коммутирующих наблюдаемых для абстрактного пространства состояний существует соответствующее представление, которое связано с функциональным пространством волновых функций.
- Между всеми этими различными функциональными пространствами и абстрактным пространством состояний существуют взаимно однозначные соответствия (здесь не учитываются нормализация и ненаблюдаемые фазовые факторы), причём общим знаменателем здесь является конкретное абстрактное состояние. Связь между импульсными и координатными волновыми функциями, например, описывающими одно и то же состояние, даёт преобразование Фурье.
Каждый выбор представления следует рассматривать как определение уникального функционального пространства, в котором определены волновые функции, соответствующие этому выбору представления. Это различие лучше всего сохранить, даже если можно будет утверждать, что два таких функциональных пространства математически равны, например, являются набором квадратично интегрируемых функций. Тогда можно думать о функциональных пространствах как о двух различных копиях этого набора.
Внутреннее произведение[править | править код]
Имеется дополнительная алгебраическая структура векторных пространств волновых функций и абстрактного пространства состояний.
- Физически различные волновые функции интерпретируются как частично перекрывающиеся. Система в состоянии Ψ, которая не перекрывается с состоянием Φ не может быть найдена в состоянии Φ при измерении. Но если Φ1, Φ2, … перекрываются с Ψ в некоторой степени, существует вероятность того, что измерение системы, описываемой Ψ будет найдено в состояниях Φ1, Φ2, … Также соблюдаются правила отбора. Обычно их формулируют в терминах сохранения некоторых квантовых чисел. Это означает, что определённые процессы, допустимые с некоторых точек зрения (например, сохранение энергии и импульса), не происходят, потому что начальная и конечная полные волновые функции не перекрываются.
- Математически оказывается, что решения уравнения Шрёдингера для конкретных потенциалов каким-то образом ортогональны, это обычно описывается интегралом
-
- где m, n — (наборы) индексов (квантовых чисел), обозначающих различные решения, строго положительная функция w называется весовой функцией, а δmn — символом Кронекера. Интегрирование осуществляется по всему соответствующему пространству.
Это мотивирует введение внутреннего произведения на векторном пространстве абстрактных квантовых состояний, совместимого с математическими результатами приведёнными выше при переходе к представлению. Он обозначается (Ψ, Φ), или в обозначении бра и кет 
где Φ и Ψ предполагаются нормированными. Рассмотрим эксперимент по рассеянию. В квантовой теории поля, если Φout описывает состояние в «далёком будущем» («исходящая волна») после прекращения взаимодействий между рассеивающими частицами, и Ψin падающая волна в «далёком прошлом», то величины (Φout, Ψin), где Φout и Ψin изменяются по полному набору падающих и исходящих волн соответственно, называется S-матрицей или матрицей рассеяния. Знание этого, по сути, означает решение имеющейся задачи, по крайней мере, в том, что касается предсказаний. Измеримые величины, такие как скорость распада и сечения рассеяния, вычисляются с помощью S-матрицы[29].
Гильбертово пространство[править | править код]
Приведённые выше результаты отражают сущность функциональных пространств, элементами которых являются волновые функции. Однако описание ещё не полное. Существует ещё одно техническое требование к функциональному пространству, а именно требование полноты, которое позволяет брать пределы последовательностей в функциональном пространстве и гарантировать, что, если предел существует, то он является элементом функционального пространства. Полное предгильбертовое пространство называется гильбертовым пространством. Свойство полноты имеет решающее значение для передовых подходов и приложений квантовой механики. Например, существование проекционных операторов или зависит от полноты пространства[30]. Эти проекционные операторы, в свою очередь, необходимы для формулировки и доказательства многих полезных теорем, например, спектральной теоремы. Это не очень важно для вводной части квантовой механики, а технические детали и ссылки можно найти в сносках, подобных следующей[nb 3]. Пространство L2 — это гильбертово пространство, скалярное произведение которого будет представлено ниже. Функциональное пространство в примере на рисунке является подпространством L2. Подпространство гильбертова пространства называется гильбертовым пространством, если оно замкнуто.
Таким образом, набор всех возможных нормированных волновых функций для системы с определённым выбором базиса вместе с нулевым вектором составляют гильбертово пространство.
Не все интересующие функции являются элементами некоторого гильбертова пространства, скажем, L2. Самый яркий пример — набор функций e2πip · x⁄h . Эти плоские волны — решения уравнения Шрёдингера для свободной частицы, но они не нормируемые, следовательно, не принадлежат L2. Но, тем не менее, они являются основополагающими для описания квантовой механики. С их помощью можно выразить функции, которые можно нормализовать с помощью волновых пакетов. В каком-то смысле они являются базисом (но не базисом гильбертова пространства и не базисом Гамеля), в котором могут быть выражены интересующие волновые функции. Существует также другое описание: «нормализация на дельта-функцию», которое часто используется для удобства записи, см. ниже. Сами дельта-функции также не интегрируемы в квадрате.
Приведённое выше описание функционального пространства, содержащего волновые функции, в основном имеют математическую мотивацию. Функциональные пространства из-за полноты в определённом смысле очень велики. Не все функции являются реалистичным описанием какой-либо физической системы. Например, в функциональном пространстве L2 можно найти функцию, которая принимает значение 0 для всех рациональных чисел и –i для иррациональных [0, 1]. Это функция интегрируема с квадратом[nb 4], но вряд ли может представлять собой физическое состояние.
Общие гильбертовые пространства[править | править код]
Хотя пространство решений в целом является гильбертовым пространством, существует множество других гильбертовых пространств.
- Квадратно интегрируемые комплекснозначные функции на интервале [0, 2π]. Множество {eint/2π, n ∈ ℤ} является базисом гильбертова пространства, т.о есть максимальным ортонормированным множеством.
- Преобразование Фурье переводит функции из указанного выше пространства в элементы l2(ℤ), пространства суммируемых с квадратом функций ℤ → ℂ. Последнее пространство является гильбертовым пространством, а преобразование Фурье задаёт изоморфизмом гильбертовых пространств[nb 5]. Его базис — {ei, i ∈ ℤ} где ei(j) = δij, i, j ∈ ℤ .
- Самый простой пример ограниченных многочленов — это пространство квадратично интегрируемых функций на интервале [–1, 1] для которого многочлены Лежандра являются базисом гильбертова пространства (полным ортонормированным множеством).
- Квадратные интегрируемые функции на единичной сфере S2 образуют гильбертово пространство. Базисными функциями в этом случае являются сферические гармоники. Полиномы Лежандра входят в состав сферических гармоник. Большинство задач с вращательной симметрией будут иметь «то же самое» (известное) решение относительно этой симметрии, поэтому исходная задача сводится к задаче меньшей размерности.
- Соответствующие полиномы Лагерра появляются в задаче о водородных волновых функций после выделения сферических гармоник. Они покрывают гильбертово пространство квадратично интегрируемых функций на полубесконечном интервале [0, ∞) .
В более общем случае можно рассмотреть все полиномиальные решения уравнений Штурма — Лиувилля второго порядка в контексте гильбертова пространства. К ним относятся многочлены Лежандра и Лагерра, а также многочлены Чебышёва, многочлены Якоби и многочлены Эрмита. Они на самом деле возникают в физических задачах, последние — в гармоническом осцилляторе, и то, что в противном случае представляет собой запутанный лабиринт свойств специальных функций, представляется органичной картиной. Для этого см. Byron & Fuller (1992, Chapter 5) .
Встречаются также конечномерные гильбертовы пространства. Пространство ℂn является гильбертовым пространством размерности n. Внутреннее произведение является стандартным внутреннии произведением для этих пространств. В нём находится «спиновая часть» волновой функции одной частицы.
- При нерелятивистском описании электрона n = 2, а полная волновая функция является решением уравнения Паули.
- В соответствующей релятивистской трактовке n = 4 и волновая функция является решением уравнение Дирака.
С большим количеством частиц ситуация более сложная. Необходимо использовать тензорные произведения и теорию представлений задействованных групп симметрии (группы вращения и группы Лоренца соответственно). Дальнейшие трудности возникают в релятивистском случае, если частицы не являются свободными[31]. См. Уравнение Бете — Солпитера. Соответствующие замечания относятся к понятию изоспина, для которого группа симметрии — это SU (2). В моделях ядерных сил шестидесятых годов (которые всё ещё используются сегодня, см. ядерные силы) использовалась группа симметрии SU (3). В этом случае также часть волновых функций, соответствующая внутренним симметриям, находится в некоторых ℂn или подпространствах тензорных произведений таких пространств.
- В квантовой теории поля основным гильбертовым пространством является пространство Фока. Оно построено из свободных одночастичных состояний, то есть волновых функций, выбранного представления, и может вместить любое конечное, не обязательно постоянное во времени количество частиц. Интересная динамика скрыта не в волновых функциях, а в полевых операторах, действующих на пространстве Фока. Таким образом, картина Гейзенберга оказывается более удобной (постоянные состояния, изменяющиеся во времени операторы).
Из-за бесконечномерного характера системы соответствующие математические инструменты являются объектами изучения функционального анализа.
Онтология[править | править код]
Существует ли волновая функция на самом деле и что она представляет, — вот главные вопросы интерпретации квантовой механики. Многие известные физики предыдущего поколения ломали голову над этой проблемой, например, Шрёдингер, Эйнштейн и Бор. Некоторые выступают за формулировки или варианты копенгагенской интерпретации (например, Бор, Вигнер и фон Нейман), в то время как другие, такие как Уиллер или Джейнс, придерживаются более классического подхода[32] и рассматривают волновую функцию как представление информации в сознании наблюдателя, то есть меры нашего познания реальности. Некоторые, включая Шрёдингера, Бома, Эверетта и других, утверждали, что волновая функция должна иметь объективное физическое существование. Эйнштейн считал, что полное описание физической реальности должно относиться непосредственно к физическому пространству и времени, в отличие от волновой функции, которая относится к абстрактному математическому пространству[33].
См. также[править | править код]
- Собственное состояние
- Оператор (физика)
- Уравнение Шрёдингера
- Принцип неопределённости Гейзенберга
- Блоховская волна
- Редукция волновой функции
- Функция Вигнера
Примечания[править | править код]
- Комментарии
- ↑ Чтобы это утверждение имело смысл, наблюдаемые должны быть элементами максимального коммутирующего множества. Например, оператор импульса i-й частицы в системе из n частиц «не» является генератором какой-либо симметрии по своей природе. С другой стороны, «полный» импульс является генератором симметрии по своей природе; трансляционной симметрии.
- ↑ Результирующий базис может быть, а может и не быть в математическом смысле, базисом гильбертовых пространств. Например, состояния с определённым положением и определённым импульсом не интегрируемы с квадратом. Это можно преодолеть с помощью волновых пакетов или заключением системы в «коробку». См. Дальнейшие примечания ниже.
- ↑ Технически это формулируется следующим образом. Внутреннее произведение задаёт нормц. Эта норма, в свою очередь, индуцирует метрику. Если эта метрика полна, то вышеупомянутые пределы будут даны в функциональном пространстве. Тогда предгильбертово пространство называется полным. Полное внутреннее произведение — это гильбертово пространство. Абстрактное пространство состояний всегда рассматривается как гильбертово пространство. Требование согласуемости для функциональных пространств является естественным. Свойство гильбертова пространства абстрактного пространства состояний было первоначально определено из наблюдения, что функциональные пространства, образующие нормируемые решения уравнения Шредингера, являются гильбертовыми пространствами.
- ↑ Как поясняется в следующей сноске, интеграл следует рассматривать как интеграл Лебега, поскольку интеграл Римана недостаточно.
- ↑ Conway, 1990. Это означает, что скалярные произведения, а следовательно, и нормы, сохраняются и, что отображение является ограниченным, а значит, непрерывной линейной биекцией. Сохраняется и свойство полноты. Таким образом, это соответствует правильному понятию изоморфизма в категории гильбертовых пространств.
- Источники
- ↑ Born, 1927, pp. 354–357.
- ↑ Heisenberg, 1958, p. 143.
- ↑ Heisenberg, W. (1927/1985/2009). Heisenberg is translated by Camilleri, 2009, (from Bohr, 1985).
- ↑ Murdoch, 1987, p. 43.
- ↑ de Broglie, 1960, p. 48.
- ↑ Landau, Lifshitz, 1977, p. 6.
- ↑ Newton, 2002, pp. 19–21.
- ↑ 1 2 Born, 1926a, translated in Wheeler & Zurek, 1983 at pages 52-55.
- ↑ 1 2 Born, 1926b, translated in Ludwig, 1968. Also here Архивная копия от 1 декабря 2020 на Wayback Machine.
- ↑ Born, M. (1954).
- ↑ Einstein, 1905 (in German), Arons & Peppard, 1965 (in English)
- ↑ Einstein, 1916, and a nearly identical version Einstein, 1917 translated in ter Haar, 1967.
- ↑ de Broglie, 1923, pp. 507–510,548,630.
- ↑ Hanle, 1977, pp. 606–609.
- ↑ Schrödinger, 1926, pp. 1049–1070.
- ↑ Tipler, Mosca, Freeman, 2008.
- ↑ 1 2 3 Weinberg, 2013.
- ↑ Young, Freedman, 2008, p. 1333.
- ↑ 1 2 Atkins, 1974.
- ↑ Martin, Shaw, 2008.
- ↑ Pauli, 1927, pp. 601–623..
- ↑ Weinberg (2002) takes the standpoint that quantum field theory appears the way it does because it is the only way to reconcile quantum mechanics with special relativity.
- ↑ Weinberg (2002) See especially chapter 5, where some of these results are derived.
- ↑ Weinberg, 2002 Chapter 4.
- ↑ Zwiebach, 2009.
- ↑ Ландау Л. Д., Лившиц Е. М.
Квантовая механика. — М., Наука, 1972. — с. 29 - ↑ Ландау Л. Д., Лившиц Е. М. Квантовая механика. — М., Наука, 1972. — с. 49
- ↑ Weinberg, 2002.
- ↑ Weinberg, 2002, Chapter 3.
- ↑ Conway, 1990.
- ↑ Greiner, Reinhardt, 2008.
- ↑ Jaynes, 2003.
- ↑ Einstein, 1998, p. 682.
Литература[править | править код]
- Arons, A. B.; Peppard, M. B. (1965). “Einstein’s proposal of the photon concept: A translation of the Annalen der Physik paper of 1905” (PDF). American Journal of Physics. 33 (5): 367. Bibcode:1965AmJPh..33..367A. DOI:10.1119/1.1971542.
- Atkins, P. W. Quanta: A Handbook of Concepts. — 1974. — ISBN 978-0-19-855494-3.
- Bohr, N. Niels Bohr – Collected Works: Foundations of Quantum Physics I (1926 – 1932). — Amsterdam : North Holland, 1985. — Vol. Volume 6. — ISBN 978-044453289-3.
- Born, M. (1926). “Zur Quantenmechanik der Stoßvorgange”. Z. Phys. 37 (12): 863—867. Bibcode:1926ZPhy…37..863B. DOI:10.1007/bf01397477.
- Born, M. (1926). “Quantenmechanik der Stoßvorgange”. Z. Phys. 38 (11—12): 803—827. Bibcode:1926ZPhy…38..803B. DOI:10.1007/bf01397184.
- Born, M. (1927). “Physical aspects of quantum mechanics”. Nature. 119 (2992): 354—357. Bibcode:1927Natur.119..354B. DOI:10.1038/119354a0.
- Born, M. (11 December 1954). “The statistical interpretation of quantum mechanics”. Nobel Lecture. Nobel Foundation. 122 (3172): 675—9. DOI:10.1126/science.122.3172.675. PMID 17798674.
- de Broglie, L. (1923). “Radiations—Ondes et quanta” [Radiation—Waves and quanta]. Comptes Rendus [фр.]. 177: 507—510, 548, 630. Online copy (French) Online copy (English)
- de Broglie, L. Non-linear Wave Mechanics: a Causal Interpretation. — Amsterdam : Elsevier, 1960.
- Byron, F. W. Mathematics of Classical and Quantum Physics / F. W. Byron, R. W. Fuller. — revised. — Dover Publications, 1992. — ISBN 978-0-486-67164-2.
- Camilleri, K. Heisenberg and the Interpretation of Quantum Mechanics: the Physicist as Philosopher. — Cambridge UK : Cambridge University Press, 2009. — ISBN 978-0-521-88484-6.
- Conway, J. B. A Course in Functional Analysis. — Springer Verlag, 1990. — Vol. Volume 96. — ISBN 978-0-387-97245-9.
- Dirac, P. A. M. (1939). “A new notation for quantum mechanics”. Mathematical Proceedings of the Cambridge Philosophical Society. 35 (3): 416—418. Bibcode:1939PCPS…35..416D. DOI:10.1017/S0305004100021162.
- Dirac, P. A. M. The principles of quantum mechanics. — 4th. — Oxford University Press, 1982. — ISBN 0-19-852011-5.
- Einstein, A. (1905). “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt”. Annalen der Physik [нем.]. 17 (6): 132—148. Bibcode:1905AnP…322..132E. DOI:10.1002/andp.19053220607.
- Einstein, A. (1916). “Zur Quantentheorie der Strahlung”. Mitteilungen der Physikalischen Gesellschaft Zürich. 18: 47—62.
- Einstein, A. (1917). “Zur Quantentheorie der Strahlung”. Physikalische Zeitschrift [нем.]. 18: 121—128. Bibcode:1917PhyZ…18..121E.
- Einstein, A. Albert Einstein: Philosopher-Scientist. — 3rd. — La Salle Publishing Company, Illinois : Open Court, 1998. — Vol. VII. — ISBN 978-0-87548-133-3.
- Eisberg, R. Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles / R. Eisberg, R. Resnick. — 2nd. — John Wiley & Sons, 1985. — ISBN 978-0-471-87373-0.
- Greiner, W. Quantum Electrodynamics / W. Greiner, J. Reinhardt. — 4th. — springer, 2008. — ISBN 978-354087560-4.
- Griffiths, D. J. Introduction to Quantum Mechanics. — 2nd. — Essex England : Pearson Education, 2004. — ISBN 978-013111892-8.
- Griffiths, David. Introduction to elementary particles. — Wiley-VCH, 2008. — P. 162ff. — ISBN 978-3-527-40601-2.
- ter Haar, D. The Old Quantum Theory. — Pergamon Press, 1967. — P. 167–183.
- Hanle, P.A. (1977), Erwin Schrodinger’s Reaction to Louis de Broglie’s Thesis on the Quantum Theory, Isis Т. 68 (4): 606–609, DOI 10.1086/351880
- Heisenberg, W. Physics and Philosophy: the Revolution in Modern Science. — New York : Harper & Row, 1958.
- Jaynes, E. T. Probability Theory: The Logic of Science. — Cambridge University Press, 2003. — ISBN 978-0-521 59271-0.
- Landau, L.D. Quantum Mechanics: Non-Relativistic Theory / L.D. Landau, E. M. Lifshitz. — 3rd. — Pergamon Press, 1977. — Vol. Vol. 3. — ISBN 978-0-08-020940-1. Online copy
- Lerner, R.G. Encyclopaedia of Physics / R.G. Lerner, G.L. Trigg. — 2nd. — VHC Publishers, 1991. — ISBN 978-0-89573-752-6.
- Ludwig, G. Wave Mechanics. — Oxford UK : Pergamon Press, 1968. — ISBN 978-0-08-203204-5.
- Martin, B.R. Particle Physics / B.R. Martin, G. Shaw. — 3rd. — John Wiley & Sons, 2008. — ISBN 978-0-470-03294-7.
- Murdoch, D. Niels Bohr’s Philosophy of Physics. — Cambridge UK : Cambridge University Press, 1987. — ISBN 978-0-521-33320-7.
- Newton, R.G. Quantum Physics: a Text for Graduate Student. — New York : Springer, 2002. — ISBN 978-0-387-95473-8.
- Pauli, Wolfgang (1927). “Zur Quantenmechanik des magnetischen Elektrons”. Zeitschrift für Physik [нем.]. 43 (9—10): 601—623. Bibcode:1927ZPhy…43..601P. DOI:10.1007/bf01397326.
- Peleg, Y. Quantum mechanics / Y. Peleg, R. Pnini, E. Zaarur … []. — 2nd. — McGraw Hill, 2010. — ISBN 978-0-07-162358-2.
- Rae, A.I.M. Quantum Mechanics. — 5th. — Taylor & Francis Group, 2008. — Vol. Volume 2. — ISBN 978-1-5848-89700.
- Schrödinger, E. (1926). “An Undulatory Theory of the Mechanics of Atoms and Molecules” (PDF). Physical Review. 28 (6): 1049—1070. Bibcode:1926PhRv…28.1049S. DOI:10.1103/PhysRev.28.1049. Архивировано из оригинала (PDF) 17 December 2008.
- Shankar, R. Principles of Quantum Mechanics. — 2nd. — 1994. — ISBN 978-030644790-7.
- Tipler, P. A. Physics for Scientists and Engineers – with Modern Physics / P. A. Tipler, G. Mosca, Freeman. — 6th. — 2008. — ISBN 978-0-7167-8964-2.
- Weinberg, S. (2002), The Quantum Theory of Fields, vol. 1, Cambridge University Press, ISBN 978-0-521-55001-7, <https://archive.org/details/quantumtheoryoff00stev>
- Weinberg, S. (2013), Lectures in Quantum Mechanics, Cambridge University Press, ISBN 978-1-107-02872-2
- Wheeler, J.A. Quantum Theory and Measurement / J.A. Wheeler, W.H. Zurek. — Princeton NJ : Princeton University Press, 1983.
- Young, H. D. Sears’ and Zemansky’s University Physics / H. D. Young, R. A. Freedman. — 12th. — Addison-Wesley, 2008. — ISBN 978-0-321-50130-1.
- Zettili, N. Quantum Mechanics: Concepts and Applications. — 2nd. — 2009. — ISBN 978-0-470-02679-3.
- Zwiebach, Barton. A First Course in String Theory. — Cambridge University Press, 2009. — ISBN 978-0-521-88032-9.
- Физический энциклопедический словарь / Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др. — М.: Сов. Энциклопедия, 1984. — 944 с.
- Yong-Ki Kim. Practical Atomic Physics (неопр.) // National Institute of Standards and Technology. — 2000. — 2 September. — С. 1 (55 pages). Архивировано 22 июля 2011 года.
- Polkinghorne, John. Quantum Theory, A Very Short Introduction (англ.). — Oxford University Press, 2002. — ISBN 978-0-19-280252-1.
Ссылки[править | править код]
- Квантовая механика — статья из Большой советской энциклопедии.
- Физический энциклопедический словарь: Квантовая механика”
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
В соответствии с корпускулярно — волновым дуализмом в квантовой физике состояние частицы описывается при помощи волновой функции ($psi (overrightarrow{r},t)$- пси-функция).
Определение 1
Волновая функция — это функция, которая используется в квантовой механике. Она описывает состояние системы, которая имеет размеры в пространстве. Она является вектором состояния.
Данная функция является комплексной и формально имеет волновые свойства. Движение любой частицы микромира определено вероятностными законами. Распределение вероятности выявляется при проведении большого числа наблюдений (измерений) или большого количества частиц. Полученное распределение аналогично распределению интенсивности волны. То есть в местах с максимальной интенсивностью отмечено максимальное количество частиц.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Набор аргументов волновой функции определяет ее представление. Так, возможно координатное представление: $psi(overrightarrow{r},t)$, импульсное представление: $psi'(overrightarrow{p},t)$ и т.д.
В квантовой физике целью ставится не точность предсказания события, а оценка вероятности того или иного события. Зная величину вероятности, находят средние значения физических величин. Волновая функция позволяет находить подобные вероятности.
Так вероятность присутствия микрочастицы в объеме dV в момент времени t может быть определена как:
где $psi^*$- комплексно сопряженная функция к функции $psi.$ Плотность вероятности (вероятность в единице объёма) равна:
Вероятность является величиной, которую можно наблюдать в эксперименте. В это же время волновая функция не доступна для наблюдения, так как она является комплексной (в классической физике параметры, которые характеризуют состояние частицы, доступны для наблюдения).
Условие нормировки $psi$- функции
Волновая функция определена с точностью до произвольного постоянного множителя. Данный факт не оказывает влияния на состояние частицы, которую $psi$- функция описывает. Однако волновую функцию выбирают таким образом, что она удовлетворяет условию нормировки:
«Волновая функция» 👇
где интеграл берут по всему пространству или по области, в которой волновая функция не равна нулю. Условие нормировки (2) значит то, что во всей области, где $psine 0$ частица достоверно присутствует. Волновую функцию, которая подчинятся условию нормировки, называют нормированной. Если ${left|psiright|}^2=0$, то данное условие означает, что частицы в исследуемой области наверняка нет.
Нормировка вида (2) возможна при дискретном спектре собственных значений.
Условие нормировки может оказаться не осуществимым. Так, если $psi$ — функция является плоской волной де-Бройля и вероятность нахождения частицы является одинаковой для всех точек пространства. Данные случаи рассматривают как идеальную модель, в которой частица присутствует в большой, но имеющей ограничения области пространства.
Принцип суперпозиции волновой функции
Данный принцип является одним их основных постулатов квантовой теории. Его смысл в следующем: если для некоторой системы возможны состояния, описываемые волновыми функциями $psi_1 {rm и} $ $psi_2$, то для этой системы существует состояние:
где $C_{1 }и C_2$ — постоянные коэффициенты. Принцип суперпозиции подтверждается эмпирически.
Можно говорить о сложении любого количества квантовых состояний:
где ${left|C_nright|}^2$ — вероятность того, что система обнаруживается в состоянии, которое описывается волновой функцией $psi_n.$ Для волновых функций, подчиненных условию нормировки (2) выполняется условие:
Стационарные состояния
В квантовой теории особую роль имеют стационарные состояния (состояния в которых все наблюдаемые физические параметры не изменяются во времени). (Сама волновая функция принципиально не наблюдаема). В стационарном состоянии $psi$- функция имеет вид:
где $omega =frac{E}{hbar }$, $psileft(overrightarrow{r}right)$ не зависит от времени, $E$- энергия частицы. При виде (3) волновой функции плотность вероятности ($P$) является постоянной времени:
Из физических свойств стационарных состояний следуют математические требования к волновой функции $psileft(overrightarrow{r}right)to (psi(x,y,z))$.
Математические требования к волновой функции для стационарных состояний
$psileft(overrightarrow{r}right)$- функция должна быть во всех точках:
- непрерывна,
- однозначна,
- конечна.
Если потенциальная энергия имеет поверхность разрыва, то на подобных поверхностях функция $psileft(overrightarrow{r}right)$ и ее первая производная должны оставаться непрерывными. В области пространства, где потенциальная энергия становится бесконечной, $psileft(overrightarrow{r}right)$ должна быть равна нулю. Непрерывность функции $psileft(overrightarrow{r}right)$ требует, чтобы на любой границе этой области $psileft(overrightarrow{r}right)=0$. Условие непрерывности накладывается на частные производные от волновой функции ($frac{partial psi}{partial x}, frac{partial psi}{partial y},frac{partial psi}{partial z}$).
Пример 1
Задание: Для некоторой частицы задана волновая функция вида: $psi=frac{A}{r}e^{-{r}/{a}}$, где $r$ — расстояние от частицы до центра силы (рис.1), $a=const$. Примените условие нормировки, найдите нормировочный коэффициент A.
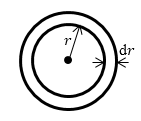
Рисунок 1.
Решение:
Запишем условие нормировки для нашего случая в виде:
[int{{left|psiright|}^2dV=int{psipsi^*dV=1left(1.1right),}}]
где $dV=4pi r^2dr$ (см.рис.1 Из условий понятно, что задача обладает сферической симметрией). Из условий задачи имеем:
[psi=frac{A}{r}e^{-{r}/{a}}to psi^*=frac{A}{r}e^{-{r}/{a}}left(1.2right).]
Подставим $dV$ и волновые функции (1.2) в условие нормировки:
[intlimits^{infty }_0{frac{A^2}{r^2}e^{-{2r}/{a}}4pi r^2dr=1left(1.3right).}]
Проведем интегрирование в левой части:
[intlimits^{infty }_0{frac{A^2}{r^2}e^{-{2r}/{a}}4pi r^2dr=2pi A^2a=1left(1.4right).}]
Из формулы (1.4) выразим искомый коэффициент:
[A=sqrt{frac{1}{2pi a}}.]
Ответ: $A=sqrt{frac{1}{2pi a}}.$
Пример 2
Задание: Каково наиболее вероятное расстояние ($r_B$) электрона от ядра, если волновая функция, которая описывает основное состояние электрона в атоме водорода может быть определена как: $psi=Ae^{-{r}/{a}}$, где $r$- расстояние от электрона до ядра, $a$ — первый Боровский радиус?
Решение:
Используем формулу, которая определяет вероятность присутствия микрочастицы в объеме $dV$ в момент времени $t$:
[dP={left|psiright|}^2dV=psipsi^*dVleft(2.1right),]
где $dV=4pi r^2dr. $Следователно, имеем:
[dP=4pi r^2A^2e^{-{2r}/{a}}drleft(2.2right).]
В таком случае, $p=frac{dP}{dr}$ запишем как:
[p=4pi r^2A^2e^{-{2r}/{a}}left(2.3right).]
Для определения наиболее вероятного расстояния производную $frac{dp}{dr}$ приравняетм к нулю:
[{left.frac{dp}{dr}right|}_{r=r_B}=8pi rA^2e^{-{2r}/{a}}+4pi r^2A^2e^{-{2r}/{a}}left(-frac{2}{a}right)=8pi rA^2e^{-{2r}/{a}}left(1-frac{r}{a}right)=0(2.4)]
Так как решение $8pi rA^2e^{-{2r_B}/{a}}=0 {rm при} r_Bto infty $, нам не подходит, то отсается:
[1-frac{r_B}{a}=0to r_B=a.]
Ответ: $r_B=a.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Векторы состояния атома водорода удобно
представлять в пространственном базисе:
|
= C1|
1
+ C2|
2
+ •
• • =
Ci|
i
,
где каждое базисное состояние
| i
отличается тем, что для него точно
известны положения обеих частиц в
пространстве относительно фиксированной
лабораторной системы координат, т.е.
известны 6 чисел-координат(x1,y1,z1,x2,y2,z2)i.Ясно, что с таким бесконечномерным
вектором состояния можно практически
работать только после его перевода в
функциональное представление —волновую
функцию. Эти волновые функции,
описывающие любые состояния атома,
допустимые законами квантовой механики,
должны, в общем случае, зависеть от шести
пространственных координат и от времени:Ф=Ф(x1,y1,z1,x2,y2,z2;t).
В дальнейшем ограничимся рассмотрением
только стационарных состояний
(нестационарные состояния не представляют
интереса для химической проблематики,
поскольку время их жизни, как правило,
не превышает 10–8с), для которых
волновую функцию можно представить в
виде произведения пространственного
и временного множителей:
Ф(x1,y1,z1,x2,y2,z2;t)
=Ф(x1,y1,z1,x2,y2,z2)exp(it),где=Е/
В результате задача сводится к установлению
вида пространственного множителя Ф(x1,y1,z1,x2,y2,z2) и значения энергииЕ,
которые можно найти из уравнения на
собственные значения:НФ=ЕФ. Оператор Гамильтона для
данной системы включает в себя три
слагаемых: два одночастичных оператора
кинетической энергии (Т1иТ2) и двухчастичный
оператор потенциальной энергии (U12):

Здесь символ 2
(иногда вместо него употребляется
эквивалентный символ)
обозначает одночастичный оператор
“набла-квадрат”, представляющий
собой сумму вторых частных производных
по декартовым координатам некоторой
частицы:
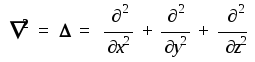
Таким образом, интересующее нас уравнение
на собственные значения (т.н.
“стационарное уравнение Шредингера”)
имеет вид:
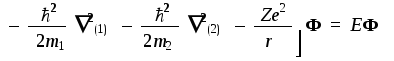
Решениями этого уравнения являются
волновые функции, описывающие все
возможные стационарные состояния атома
водорода, а также соответствующие им
энергии (в нерелятивистском приближении,
т.е. без учета магнитных эффектов). Если
атом изолирован от окружающих тел, то
движения частиц в нем можно разделить
на два типа:
1) глобальноедвижение атома как
материальной точки (центра масс) в
лабораторной системе координат (X,Y,Z).
2) локальныедвижения частиц во
внутренней системе координат (x,y,z), начало которой расположено в
центре масс.
Первый тип движения можно исследовать,
смотря на атом “издалека”, т.е.
полагая его просто материальной точкой
без внутренней структуры. Второй тип
движения можно исследовать, смотря на
атом “изнутри” и полагая, что атом
как целое является неподвижным. В этом
случае наблюдатель находится в центре
масс и видит лишь относительное движение
электрона и ядра. Независимость внешнего
и внутреннего движений позволяет
представить шестимерную волновую
функцию в виде произведения двух
трехмерных функций:
Ф (x1,y1,z1,x2,y2,z2) =Ф’(X,Y,Z)Ф” (x,y,z)
Первый сомножитель представляет собой
глобальную функцию, описывающую движение
атома как целого (т.е. как одной
бесструктурной частицы с массой M=m1+m2)
и удовлетворяет трехмерному уравнению:
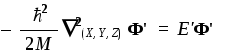
Это стандартное уравнение для свободной
частицы с массой М. Его решения
известны из модельных квантовомеханических
задач “свободная частица” и “частица
в трехмерном потенциальном ящике”
(см.[3]).
Второй сомножитель представляет собой
“внутреннюю” функцию, описывающую
движение электрона и ядра относительно
неподвижного центра масс. Согласованный
характер движения электрона и ядра дает
возможность заменить их единственной
“квазичастицей”, обладающей массой
и движущейся вокруг
неподвижного центра масс. Вследствие
большого различия в массах электрона
и ядра эта квазичастица по своим свойствам
практически совпадает с электроном.
Поэтому в дальнейшем будем рассматривать
ее как обычный электрон с незначительно
уменьшенной массой. Внутренняя функция,
описывающая движение электрона
(квазичастицы), удовлетворяет трехмерному
уравнению вида:
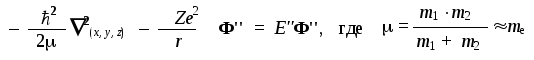
В декартовой системе координат это
уравнение невозможно сделать более
простым, так как входящая в него переменная
rзависит от всех трех
декартовых координат электрона:r2
= x2
+ y2
+ z2.
Поэтому целесообразно перейти к
сферической системе координат, в
которой переменнаяrявляется независимой координатой.
Замена производится по правилам:
x = r
sin
cos
; y =
r
sin
sin ;
z = r
cos
где угол отсчитывается
в вертикальной плоскости от осиzи
изменяется в интервале от 0 до,
а уголотсчитывается
в горизонтальной плоскости от осиxи изменяется в интервале от 0 до 2.
После замены переменных волновая функция
изменяет свой вид:Ф”(x,y,z)(r,,),
а стационарное уравнение Шредингера
приобретает такую форму:
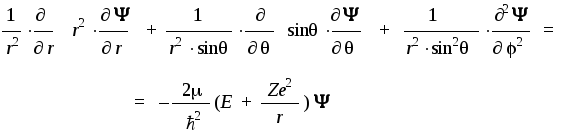
Сделанная замена переменных позволяет
представить трехмерную функцию в виде
произведения трех одномерных
функций-сомножителей:
(r,
, )
= R(r)
()
()
которые являются решениями системы из
трех одномерных уравнений:

Необходимо отметить, что в результате
процедуры разделения в уравнениях
появились две новые константы —
и, которые
учитывают существующие взаимосвязи
между уравнениями и их решениями. Эти
параметры должны иметь одни и те же
значения во всех уравнениях, куда они
входят. Данное условие выполняется
только для некоторых “разрешенных”
значений, образующих дискретный набор,
а именно:
= 0, 1, 4, 9, 16, 25, … и = 0, 2, 6, 12, 20,
30, 42, …
С целью упрощения этих рядов удобно
ввести два новых вспомогательных
параметра — иm, для которых выполняются
более простые условия:
= (
+ 1) , где= 0, 1, 2, . . .
=mm, гдеm= 0,1,2, . . .
Дискретность в решениях R-,– и-уравнений,
вызываемая приведенными ограничениями
для параметров
и, приводит, в
свою очередь, к дискретности допустимых
значений энергии атома (она входит вR‑уравнение),
связанной с внутренним движением:
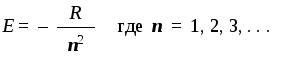
Целые числа, входящие в приведенные
формулы, называются квантовыми числами
атома водорода:n—главное,—орбитальное,m—магнитное. Они выступают
в роли параметров, нумерующих возможные
решения уравнения Шредингера, или, что
то же самое, волновые функции стационарных
состояний:
(r,,)
=R(r)•()•()
= (n,,m) =
= R(n,)
•(,m) •(m) =
R(n,
)
• Y(,
m)
Произведения (,m) •(m)=
Y(,
m)
называютсяшаровыми функциями.
Приведем явный вид –
и -функций
(в сферических координатах):


В этом уравнении символом Робозначен
т.н. “присоединенный полином Лежандра”
степении
порядка |m|, представляющий собой
некоторую степенную функцию от (cos).
Явный вид этих полиномов можно найти в
справочниках или вычислить по следующей
формуле:
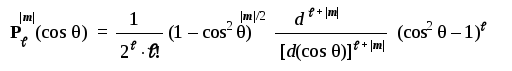
Для R-уравнения решения
имеют вид:
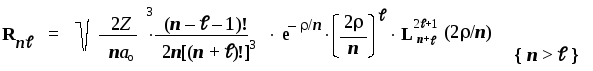
Здесь символом L обозначен т.н.
“присоединенный полином Лаггера”
степени (n+)
и порядка (2+
1) — степенная функция от новой переменной= (Z/ao)r,
которая представляет собой шкалу
расстояний: прокалиброванную с помощью
т.н. “атомных единиц длины”ао=4o2/e20,053 нм
(здесь константаo
= 8,8410–12
ф/м — диэлектрическая
постоянная).
Явный вид присоединенных полиномов
Лаггера можно найти в справочниках или
вычислить по формуле:

Стоящие впереди полиномов Лежандра и
Лаггера сложные выражения являются
нормировочными множителями, которые
при задании конкретных величин квантовых
чисел приобретают простой вид.
Следует обратить внимание на важное
обстоятельство. В формулы входят
некоторые величины, являющиеся
факториалами типа х!. Эта функция
определена только для целых неотрицательных
чиселх. В результате, на допустимые
совместные (т.е. относящиеся к одному
состоянию атома) значения квантовых
чисел накладываются ограничения,
указанные выше в фигурных скобках.
Для иллюстрации можно привести
конкретные выражения для волновых
функций с небольшими номерами.
R-функции(нормировочные множители
опущены):
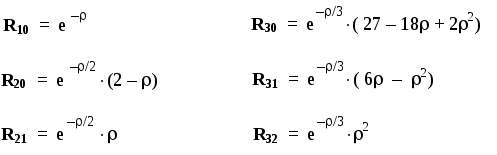
(В обозначениях функций первый числовой
индекс равен главному квантовому числу
n, а второй — орбитальному
квантовому числу.)
-функции (нормировочные множители
опущены):

(В обозначениях функций первый числовой
индекс равен орбитальному квантовому
числу , а второй
— модулю магнитного числа|m|.)
Ф-функции (нормировочные множители
опущены):
![]()
Располагая таблицами таких функций,
можно легко построить явный вид волновой
функции для любого стационарного
состояния атома водорода. Пусть, например,
состояние характеризуется набором
квантовых чисел {n,,m} = {2, 1, –1}. Тогда волновая функция
будет иметь вид (нормировочный множитель
опущен):
![]()
Полный вид волновой функции можно
получить при умножении этой пространственной
части на временной экспоненциальный
множитель:
(2, 1, –1), t
= (2,
1, –1)
exp[i(E2/)t]
,
где Е2— энергия, соответствующая
значениюn= 2.
Обозначаемые тремя индексами функции
n,,mчасто называют
водородными атомными орбиталямиили Н-АО. Заметим, что в большинстве
случаев они содержат комплексную
экспоненту и, следовательно, являются
комплекснозначными функциями. Это
обстоятельство часто отмечается и в
названии —комплексные атомные
орбитали(КАО).
Существует еще одна, более удобная,
номенклатура Н-АО. Каждый тип АО
обозначается определенным символом —
латинской буквой — указывающим на
значение орбитального квантового числа:
|
Значение |
0 |
1 |
2 |
3 |
4 |
5 |
… |
|
Символ |
s |
p |
d |
f |
g |
h |
… |
Впереди буквы-символа указывается
значение главного квантового числа, а
магнитное квантовое число обозначается
цифровым подстрочным индексом, следующим
за буквой-символом. Например:
100 =
1so
200 =
2so
210 = 2po
21–1 = 2p–1
211 = 2p1
300 =
3so
310 = 3po
31–1 = 3p–1
311 = 3p1
320 =
3do
321 = 3d1
32–1 = 3d–1. . . и т.д.
В ряде случаев бывает более удобным
использование не самих волновых функций,
а некоторых линейных комбинаций,
построенных из этих функций, с целью
получить чисто действительные функции.
Такие линейные комбинации строятся в
виде суммы или разности двух КАО, у
которых все квантовые числа одинаковы
по величине, но магнитные числа
противоположны по знаку. У таких пар
КАО R– и-сомножители
в точности одинаковы, поскольку они не
зависят от знака магнитного числа. В
результате получаются суммы и разности
комплексно сопряженных экспонент,
которые сводятся к действительным
тригонометрическим функциям (здесь
нормировочные множители опущены):
(n, ,
m) +(n,
,
–m) =R(
e im
e –im)
= R •
cos (m=+(
n, ,
|m|)
(n, ,
m) –(n,
,
–m) =R(
e im
–e –im)
= R •
sin (m= –(
n, ,
|m|)
Такие линейные комбинации называются
действительными атомными орбиталями(ДАО). В их обозначениях нижний индекс
заменяется на буквенный. Например, для
АОp-типа имеем:
(2р1+ 2р–1) ~
2px
(2р1– 2р–1)
~ 2py
2р0~2pz
или для АО d-типа:
(3d1+ 3d–1) ~
3dxz (3d1– 3d–1) ~ 3dyz
(3d2+ 3d–2) ~
3d(x2–
y2) (3d2– 3d–2) ~ 3dxy
3d0~ 3dz2
ДАО удобны в том отношении, что их можно
изображать графически, анализировать
различные пространственные характеристики
и симметрию. Подчеркнем, что наборы КАО
и ДАО полностью эквивалентны в
математическом отношении и представляют
собой два базисных набора в одном и том
же пространстве состояний (см. модель
“плоский ротатор” в [3]).
Состояния, описываемые волновыми
функциями типа n,,m,
обычно называютсячистыми. Кроме
них существует множество состоянийсмешанных(илисуперпозиционных),
для которых одно или несколько квантовых
чисел являются неопределенными:
n,=С1(2р–1) +С2(2р0) +С3(2р+1)
n=С1(2s)
+С2(2р+1)
= С1(1s) +С2(2р+1)
Все такие функции, составленные из
слагаемых с разными значениями квантовых
чисел nи/или,
описываютнестационарныесостояния,
которые в течение короткого времени
(порядка 10–8с) редуцируют к одному
из стационарных состояний типаn,,m,
в которых все три квантовые числа точно
определены. Исключением из этого общего
правила являются суперпозиционные
функции типаn,.
Редукция таких состояний может быть
вызвана только действием внешних причин
(например, магнитного поля).
Квантовомеханическая теория строения атома. Уравнение Шредингера. Волновая функция. Радиальная и угловая составляющие. Квантовые числа. атомные уровни, подуровни и орбитали. Формы s-. p-, d- атомных орбиталей.
Современные квантово-механические представления о строении электронной оболочки атома исходят из того, что движение электрона в атоме нельзя описать определенной траекторией. Можно рассматривать лишь некоторый объем пространства. В котором находится электрон. Поскольку электрон обладает одновременно свойствами частицы и волны, то подходом к объяснению строения электронной оболочки может быть как корпускулярная, так и волновая теория; обе они приводят к одинаковому наглядному представлению, сформулированному как орбитальная модель атома.
Атомная орбиталь – это геометрический образ, отвечающий объему пространства вокруг атомного ядра, который соответствует 90%-ой вероятности нахождения в этом объеме электрона (как частицы) и одновременно 90%-ой плотности заряда электрона (как волны).
Собственной характеристикой каждого электрона в атоме является спин. Два электрона, находящиеся в одной атомной орбитали, различаются по спину.
В квантовой механике каждая атомная орбиталь определяется тремя квантовыми числами.
Главное квантовое число n – может принимать целочисленные значения от 1 до ¥. В Периодической системе элементов максимальному значению главного квантового числа соответствует номер периода.
Орбитальное квантовое число l – определяем орбитальный момент количества движения (импульс) электрона, точное значение его энергии и форму орбитали. Может принимать значения 0,1,2,3,…(n-1). Орбитальное квантовое число определяет форму атомной орбитали. При l=0 это сфера, при l=1 – объемная восьмерка (гантель), при l =2 четырехлепестковая розетка.
Магнитное квантовое число ml определяет возможные значения проекции орбитального момента количества движения электрона на фиксированное направление в пространстве (например ось Z) движение электрона вокруг ядра можно сравнить с движением тока по замкнутому контуру. При этом возникает магнитное поле, вектор напряженности Н которого направлен перпендикулярно плоскости движения электрона. Если атом находится во внешнем магнитном поле, то, согласно квантово-механическим представлениям, его электроны должны располагаться так, чтобы проекции их магнитных моментов на направление этого поля были целочисленными. При этом они могут принимать как отрицательные, так и положительные значения, включая нулевое. В общем случае магнитное кантовое число характеризует ориентацию атомной орбитали в пространстве относительно внешней силы. Магнитное квантовое число определяет ориентацию орбитального углового момента относительно некоторого фиксированного направления. Орбитальному квантовому числу l =0 отвечает единственное значение магнитного квантового числа ml =0. Эти значения l и ml характеризуют все s –орбитали, которые имеют форму сферы. Так как в этом случае магнитное квантовое число принимает только одно значение, то каждый s подуровень состоит только из одной орбитали. Рассмотрим р-подуровень. При l =1 орбитали имеют форму гантелей, магнитное квантовое число принимает следующие значения ml = -1, 0, +1. Следовательно, р-подуровень состоит из трех атомных орбиталей, которые располагаются вдоль осей координат, их обозначают рx, рy, рz
Законы движения частиц в квантовой механике выражаются уравнением Шредингера, которое играет в ней ту же роль, что и законы Ньютона в классической механике. Уравнение Шредингера представляет собой дифференциальное уравнение в частных производных. Э. Шредингер в 1926 г. предложил использовать волновое уравнение в качестве модели для описания поведения электрона в атоме – уравнение, связывающее энергию системы с ее волновым движением. Стационарное уравнение Шредингера для одной частицы можно записать в следующей форме:
Рекомендуемые материалы
– h2__ (d2y + d2y + d2y) + Uy = Ey
В лекции “8.3. Культурные коды” также много полезной информации.
8p2m (dx2 dy2 dz2 )
где U – потенциальная энергия частицы; E – ее полная энергия; x, y, z – декартовы координаты; переменная величина y называется волновой функцией. Эта функция описывает все свойства системы в стационарном состоянии – состоянии, которое изменяется во времени. Функция y зависит от координат частиц и может зависеть от времени. Каждая частица (или набор частиц) характеризуется квантово-механической волновой функцией, которая описывает состояние данной системы. Функцию y можно рассматривать как амплитуду волнового процесса, следовательно, она может быть больше и меньше нуля, а также мнимой величиной. В соответствии с физическим смыслом волновая функция конечная, непрерывная и однозначная, а также обращается в ноль там, где частица не может находиться. Уравнение Шредингера можно решить точно только для очень простых систем (атом водорода).
Решая уравнение Шредингера в сферических координатах, получают
ynlml = R®rnlΘ(θ)lmlФ(φ)ml где R® – радиальная составляющая волновой функции;
Θ(θ) и Ф(φ) – угловые составляющие волновой функции. Следовательно, волновые функции зависят от трех целочисленных параметров n, l, ml – , которые называют квантовыми числами. Волновую функцию описывающую состояние электрона, называют атомной орбиталью.






