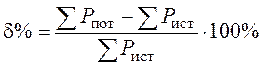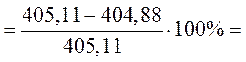Как найти вольтметр на схеме

Я в школе учился давно, поэтому не совсем уверен, что правильно понимаю термины “идеальный вольтметр” и ” идеальный источник тока”. Возможно это означает, что сопротивление вольтметра – бесконечно, а внутреннее сопротивление источника тока равно нулю. Если это так, то задачу можно решать так:

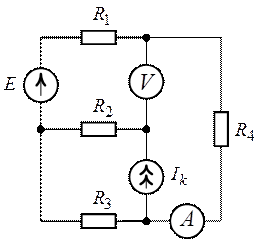
В приведённой схеме резистор R2 и сопротивление вольтметра (обозначим его R3, хотя оно и не очень нужно, просто для ясности) соединены параллельно. Их эквивалентное сопротивление (R) определяется по формуле 1/R=1/R2+1/R3, Получаем, что R=160 Ом. Ток в цепи равен 32/160=0,2 А. Полное сопротивление цепи 160+240=400 Ом, ЭДС источника*0,2=80 В.

Если сопротивление вольтметра R3 – бесконечное, то он не влияет на параметры цепи. Тогда полное сопротивление цепи равно 240+200=440 Ом, Ток в цепи равен 80/440=(2/11) А, Падение напряжения на резисторе R2 (именно это и покажет вольтметр) составит (2/11)*200=400/11 В, или приблизительно 36,(36) В. (36) обозначает 36 в периоде, т.е. 36,36363636… , или округлённо 36,37 В.

  

Рис. 2.3.                                          Рис.
2.4.

Решение.

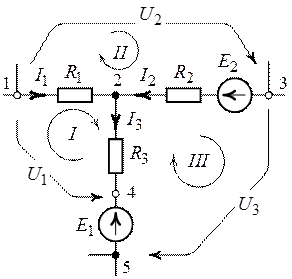
1. Цепь рис. 2.3 содержит шесть ветвей (), четыре узла (), один источник тока  ().

Выберем положительные направления токов в схеме, как
это указано на рис. 2.4.

2. Определим достаточное количество уравнений для
расчета цепи по первому закону Кирхгофа:

,

по второму закону Кирхгофа:  

.

Достаточное количество уравнений равно пяти, что
соответствует числу неизвестных токов  (рис.
2.4).

3. Составим систему уравнений по законам Кирхгофа.

Три уравнения по первому закону Кирхгофа, например,
для узлов 2, 3 и 4. Два уравнения по второму закону Кирхгофа.  Положительные направления
обхода независимых контуров выберем в соответствии с указанными на рис. 2.4.

для  узла 2:            ;

для узла  3:              ;

для узла  4:            ;

для контура  :      ;

для контура :   .

П р и м е ч а н и е: При выборе независимых контуров необходимо следить
за тем, чтобы контур не содержал ветви с источником тока.

4. После подстановки числовых значений параметров
элементов цепи получим:

5. Решение системы получим в матричной форме

.

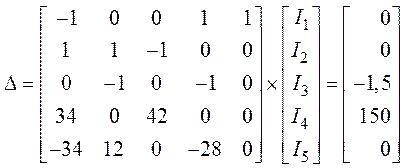
6. В результате решения матричной системы уравнений
находим токи:

,
 ,  ,  ,  .

Знак минус у тока  означает,
что действительное направление тока противоположно направлению, выбранному на
схеме рис.2.4.

П р и м е ч а н и е:  изменять знак тока на обратный не следует, так
как это может привести к ошибке в дальнейших расчетах.

7. Правильность расчета установим путем проверки
баланса мощностей.  Мощность, поступающая в цепь от источников энергии должна
равняться сумме мощностей потребителей электрической  энергии:

.

Предварительно найдем напряжение  на зажимах с источником тока  (рис. 2.4). На основании второго
закона Кирхгофа получим:

.

Полная  мощность, развиваемая источниками энергии

.

Полная мощность потерь в резистивных сопротивлениях

.

Следовательно

.

Погрешность расчета составляет:

.

Задача 2.3.

Для схемы электрической цепи (рис. 2.5) построить
график изменения потенциала во внешнем контуре. Параметры элементов цепи заданы
, , , ,
, ,
, .

     

Рис. 2.5.                                             
Рис. 2.6.

Решение.

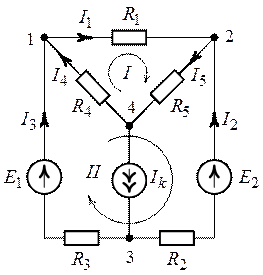
1. Предварительно выполним расчет токов внешнего
контура.  Цепь (рис. 2.5) содержит шесть ветвей  (),
четыре узла (), один источник тока   ().

Выберем положительные направления токов в схеме цепи в
соответствии с указанными на рис. 2.6.

2. Достаточное количество уравнений для расчета цепи
по первому закону Кирхгофа , по второму
закону Кирхгофа  .

Общее количество уравнений равно пяти.

3. Три уравнения по первому закону Кирхгофа составим
для узлов 1, 2 и 4. 

Два уравнения по второму закону Кирхгофа для контуров  и  обозначенных
в схеме на рис. 2.6.

4. Запишем систему в матричной форме

.

5. После подстановки числовых значений получим

.

6. Решение матричной системы позволяет определить токи

,  ,
 .

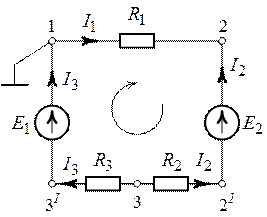
7. Выделим элемент внешнего контура (рис. 2.7). 
Примем потенциал точки 1 равным нулю ().
Рассчитаем потенциалы точек контура, обходя его по часовой стрелке:

;

;

;

;

.

Рис. 2.7.

8. Порядок построения потенциальной диаграммы
представлен на рис. 2.8. На диаграмме по оси абсцисс откладываем значения сопротивлений
участков в последовательности расположения их в контуре.

Рис. 2.8.

Задача 2.4.

Определить показания вольтметров в схеме цепи рис. 2.9,
если , , , , , ,
. Внутреннее сопротивление
вольтметров принять равным .

     

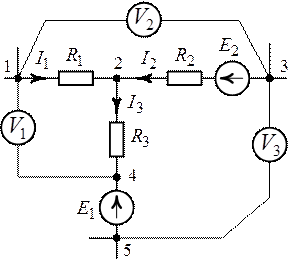
Рис. 2.9.                                              Рис.
2.10.

Решение.

1. Заменим вольтметры, изображенные на схеме (рис. 2.9),
векторами напряжений, указывающих на разность потенциалов между точками их
подключения (рис. 2.10). Направления действия векторов напряжений выбираем произвольно.

2. Определим недостающий ток  по
первому закону Кирхгофа

.

3. Показание вольтметра  определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура  (рис. 2.10).

,

откуда

.

4. Показание вольтметра  определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура , рис. 2.10:

,

откуда

.

5. Показание вольтметра  определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура , рис. 2.10:

,

откуда

.

Задача 2.5.

Определить показания приборов в схеме рис. 2.11, если , ,
, ,
. Внутренние сопротивления
вольтметров принять , амперметров .

   

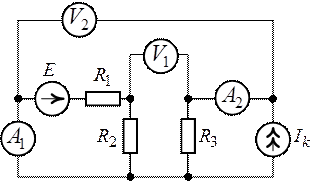
Рис. 2.11.                                             
Рис. 2.12.

Решение.

1. Выполним замену  приборов с учетом их внутренних
сопротивлений (рис. 2.12) и обозначим токи ветвей.

2. Показание амперметра   равно
значению тока (рис. 2.12)

.

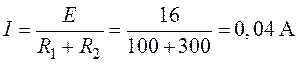
3. Показание амперметра  будет
определяться током источника , включенным
последовательно в цепь с амперметром, т.е.  .

4. Показание вольтметра  определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура  (рис. 2.12):

,

откуда

.

5. Показание вольтметра  определим
по выражению, записанному по второму закону Кирхгофа для замкнутого контура  (рис. 2.12):

,

откуда

.

Задачи для самостоятельного решения

Задача 2.6. В
цепи (рис. 2.13) , ,
, .
Определить показания приборов, если , .

О т в е т: ,

Задача 2.7. Определить
показание вольтметра в цепи рис. 2.14. Параметры цепи заданы: , , .

О т в е т: .

          

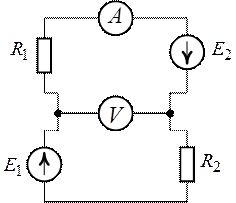
Рис. 2.13.                                           Рис.
2.14.

Задача 2.8. Для
схемы на рис. 2.15, пользуясь законами Кирхгофа, найти все токи, если , ,
,  ,
, ,
.

О т в е т: ,  ,  ,
,

 , .

Задача 2.9.
Для схемы рис. 2.16, пользуясь законами Кирхгофа определить токи в ветвях с резистивными
сопротивлениями, если  , , ,
.

О т в е т: , , , .

      

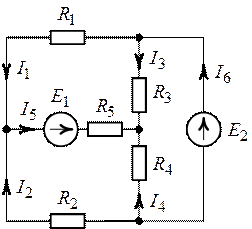
Рис. 2.15.                                          
Рис. 2.16.

Задача 2.10.
Для схемы рис. 2.17, пользуясь законами Кирхгофа определить все токи, если , , , ,
, ,
, ,
.

О т в е т: , , .

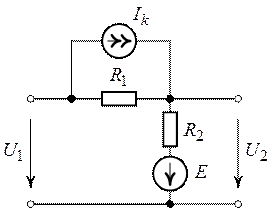
Задача 2.11. Напряжение
 на  входе цепи (рис. 2.18). составляет .
Определить напряжение  на выходе цепи, если , , ,
.

О т в е т: .

       

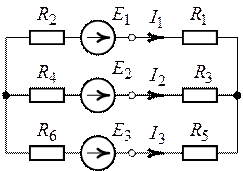
Рис. 2.17.                                          
Рис. 2.18.

Задача 2.12.
Определить токи в схеме  рис. 2.19, если ,
, , , ,
. Проверить баланс мощностей.

О т
в е т: ,  ,  .

Задача 2.13.
Для схемы рис. 2.20, пользуясь законами Кирхгофа определить показания приборов,
если , ,
, ,
, .
Принять внутренние сопротивления приборов: , .

О т
в е т: , .

   

Рис. 2.19.                                           Рис.
2.20.

Задача 2.14.
Для схемы рис. 2.21, пользуясь законами Кирхгофа определить все токи. Дано ,  , ,
, .

О т
в е т: , .

Задача 2.15.
Рассчитать с использованием законов Кирхгофа токи в схеме рис.2.22, если , ,
, ,
, ,
.

О т в е т: , , , .

Задача 2.16.
Для схемы рис. 2.23, пользуясь законами Кирхгофа определить все токи, если , , , , , .

О т в е т: , , , , .

     

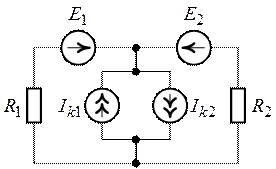
Рис. 2.21.                                          Рис.
2.22.

Задача 2.17.
Для схемы рис. 2.24, пользуясь законами Кирхгофа определить все токи. Дано , ,
, ,
, ,
, .

О т
в е т: , ,
, .

          

Рис. 2.23.                                         
Рис. 2.24.

Для характеристики электрического тока в цепи у нас есть уже две физические величины: сила тока ($I$) и напряжение ($U$).

Для измерения силы тока мы используем амперметр. Значит, существует прибор и для измерения электрического напряжения. 

Как называют прибор для измерения напряжения? Он называется вольтметром.
На данном уроке мы рассмотрим его применение, правила подключения в электрическую цепь и другие его характеристики.

Вольтметр

Вольтметр — это прибор для измерения напряжения на полюсах источника тока или на каком-либо другом участке цепи.

Вольтметры по внешнему виду очень похожи на амперметры. Как их различать тогда? Если на шкале амперметра стоит буква $A$, то на шкале вольтметра будет обязательно стоять буква $V$.

Вольтметры бывают разных видов. Это зависит от их назначения. Вы чаще всего будете встречать или демонстрационный вольтметр (рисунок 1, а) или лабораторный (рисунок 1, б).

Как можно догадаться из названий приборов, демонстрационный вольтметр используется для демонстрации опытов, а лабораторный вы будете использовать при выполнении лабораторных работ.

На шкале каждого вольтметра есть высшее (максимальное) значение напряжения, которое он способен измерить. Превышение этого предела может привести к выходу прибора из строя.

Вольтметр в электрической цепи

Вольтметр подключают в электрическую цепь на определенный ее участок, на котором необходимо измерить напряжение. 

Обратите внимание на то, что если амперметр, последовательно подключенный в электрическую цепь, будет показывать одинаковое значение силы тока на всех участках цепи, то с вольтметром у нас совершенно другая история. Он предназначен для измерения напряжения на определенном участке цепи.

Для обозначения на схемах электрических цепей у вольтметра имеется свой условный знак (рисунок 2). Выглядит он, как кружок с буквой $V$ посередине.

Правила подключения вольтметра в электрическую цепь

• Зажимы вольтметра нужно подсоединять к тем точкам цепи, между которыми надо измерить напряжение. Такое подключение называется параллельным (рисунок 3).

Подробнее об особенностях параллельного подключения приборов вы узнаете в следующих уроках.

• У одного из зажимов вольтметра стоит знак “+”. Провод, подключенный к этому зажиму, необходимо соединять с проводом, идущим от положительного полюса источника тока (рисунок 4). Если подключить прибор неправильно, то стрелка вольтметра просто начнет отклоняться в другую сторону.

Измерение напряжения вольтметром в электроприборе

Используя вышеприведенные правила, давайте попробуем на практическом опыте измерить напряжение. 

Допустим, его необходимо измерить на электрической лампе. Соберем электрическую цепь, состоящую из ключа, электрической лампы, источника тока. Подключим последовательно в эту цепь амперметр. Вольтметр подсоединяем параллельно к зажимам лампы (рисунок 5).

Схема такой электрической цепи будет выглядеть следующим образом (рисунок 6).

Обратите внимание, что амперметром здесь мы измеряем силу тока в электрической лампе. Вольтметром мы измеряем ее напряжение. 

Амперметр подключается последовательно, а вольтметр — параллельно.

А какой должна быть сила тока, проходящего через вольтметр, по сравнению с силой тока в цепи? Отличается ли она от силы тока во всей цепи?

Да, отличается. Вольтметр устроен таким образом, что сила тока, проходящего через него, крайне мала по сравнению с силой тока в самой электрической цепи. Это позволяет исключить изменение напряжения между теми точками, к которым подсоединен вольтметр. Это же и способствует получению более точных значений напряжения.

Измерение напряжения вольтметром на полюсах источника тока

Как с помощью вольтметра измерить напряжение на полюсах источника тока?

Чтобы узнать напряжение на полюсах источника тока, мы можем подключить вольтметр непосредственно к нему (рисунок 7). Не забывайте соблюдать полярность при подключении! Амперметр же включать в подобную цепь нельзя.

Это интересно: вольтамперметр

Упражнения

Определим цену деления такого вольтметра. Возьмем значения 0 и 3. От 0 до 3 у нас всего два деления. Получается, что $frac{3 space В — 0 space В}{2} = 1.5 space В$.
Цена деления этого вольтметра равна $1.5 space В$.

На рисунке 8 изображены показания этого вольтметра при:
$U_1 = 4.5 space В$ (рисунок 8, а);
$U_2 = 7.5 space В$ (рисунок 8, б);
$U_3 = 10.5 space В$ (рисунок 8, в).

Шкала вольтметра на рисунке 5 идентична шкале вольтметра на рисунке 1, а. Ее цену деления мы уже определили в предыдущем упражнении. Цена деления этого вольтметра равна $1.5 space В$.

На рисунке 5 вольтметр показывает значение напряжения, равное $1.5 space В$.

Схема такой цепи изображена на рисунке 9. Обратите внимание, что амперметр подключен в цепь последовательно, а вольтметр — параллельно.

Определение показаний вольтметров.

На рис.3 представлена схема с
вольтметрами и с соединением R6
и E6.

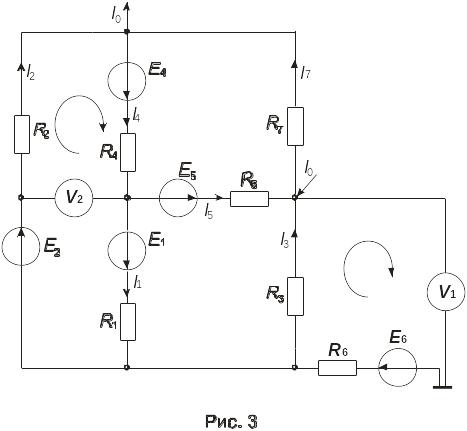
Рассмотрим контур a–R3-d–V1-o–E6-R6-a
и составим для него уравнение по второму
закону Кирхгофа:

E6
= I3R3
+ Udo,
здесь Udo
и есть показание вольтметра V1,

Udo
= E6
– I3R3.

Для нахождения показания второго
вольтметра, рассмотрим контур

f–R2-c–E4-R4-b–V2-f
и составим для него уравнение по второму
закону Кирхгофа:

E4
= I2R2
+ I4R4
+ Ubf,
здесь Ubf
и есть показание вольтметра V2,

Ubf
= E4
– I2R2
– I4R4.

Определение методом эквивалентного
генератора

величины дополнительной э.д.с.,

которую нужно включить во вторую
ветвь,

чтобы ток в ней увеличился в два раза

и сменил направление.

Составим схему, состоящую из
эквивалентного генератора и второй
ветви. Она представлена на рис.4:

Здесь Г – эквивалентный генератор,

Eг
и Rг
– э.д.с. и собственное сопротивление,
соответственно,

эквивалентного генератора,

E2
и R2
– э.д.с. и резистор второй ветви,

Ex
– искомая э.д.с.,

2I2
– ток во второй ветви, равный удвоенному
значению ранее

найденного тока I2,
и имеющий противоположное ему

направление.

Уравнение по второму закону Кирхгофа
для этой схемы будет иметь вид:

E2
+ EГ
– Ex
= -2I2(R2
+ RГ),

отсюда следует:

Ex
= E2
+ EГ
+ 2I2(R2
+ RГ).

Для того, чтобы найти Ex,
нужно найти э.д.с. эквивалентного
генератора EГ
и его собственное сопротивление RГ.

Определение э.Д.С. Эквивалентного генератора методом узловых потенциалов.

Рассмотрим схему эквивалентного
генератора. Она представлена на рис.5.

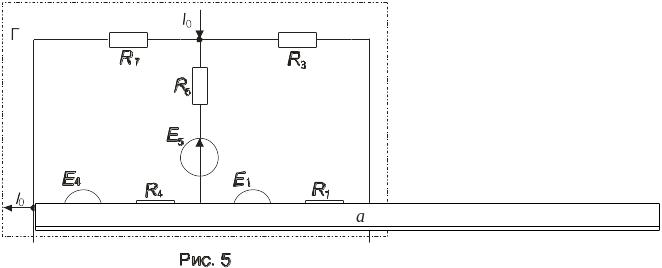
Э.д.с. эквивалентного генератора EГ,
которое равно падению напряжения Uac,
при отсоединённой второй ветви, т.е. при
режиме холостого хода эквивалентного
генератора. Для того, чтобы найти Uac,
достаточно знать потенциалы точек a
и c:

Uac
= φa
– φс, здесь
φa
и φс –
потенциалы точек a и
c.

При отсоединённой второй ветви a
и c не являются узлами,
но будем учитывать их узлами при
составлении уравнений по методу узловых
потенциалов. Источник тока I0
преобразуем в источник э.д.с. (рис.6) EI,
хотя в данной схеме это преобразование
не приведёт к уменьшению числа узлов:
EI
= I0R7.

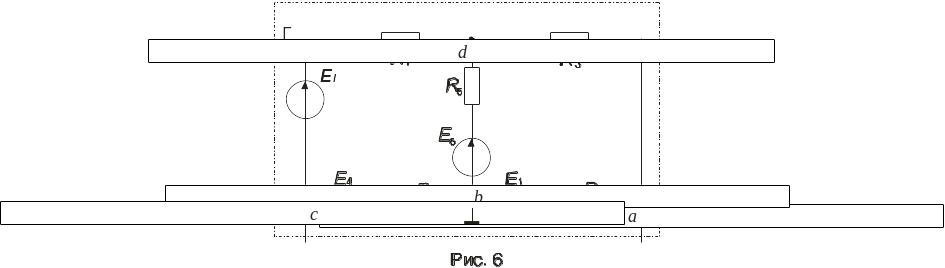
Примем потенциал узла b
за базовый (φb
= 0), а для определения потенциалов других
узлов, записываем уравнения:

a)
φa(G1
+ G3)
– φdG3
= E1G1,

1. φс(G4
   + G7)
   – φdG7
   = –E4G4
   – EIG7,

2. φd(G3
   + G5
   + G7)
   – φaG3
   – φсG7
   = E5G5
   + EIG7,

здесь G1,
G3,
G4,
G5,
G7,
проводимости соответствующих ветвей,

G1
= 1/R1,…,
G7
= 1/R7.
Подставим численные значения в уравнения:

a)
φa(0,2
+ 0,25) – φd0,25
= 130×0,2,

1. φс(0,2
   + 0,5) – φd0,5
   = -60×0,2 -8×0,5,

2. φd(0,25+
   0,33 +0,5) – φa0,25
   – φс0,5
   = 50×0,33+ 8×0,5,

сформируем матрицу из коэффициентов
при φa,
φс и φd
и столбец из правых частей:

0,45 0 -0,25 26

0 0,7 -0,5 -16

-0,25 -0,5 1,08 20,5.

В результате решения системы уравнений
получены значения:

φa
= 80,15 В, φb
= 0 В, φс =
5,906 В, φd
= 40,27 В,

Uac
= φa
– φс =
74,244 В, EГ
= 74,244 В.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

UR

Uliana Rusu

Вопрос по электротехнике. Как найти показания вольтметра на схеме? Желательно, по-подроней…

Кажется вы не поняли вопроса.. . Не экспериментально, теоретически, посчитав, как найти значение вольтметра?

ИМ

Ислом Муминов

Сначала нужно собрать схему, затем проверить правильно ли собрана схема, подключить вольтметр к источнику питания, сделать замер двумя клемами вольтметра. Соблюдать технику безопасности, нельзя касаться токопроводящих элементов схемы.

Марупчик Марупчик

Определяем сопротивления реактивных элементов цепи XL=534 Ом, Xс=15,9 Ом, Полное сопротивление цепи Z=519,7 Ом, Ток в цепи I=U/Z=0,423 А, Показание вольтметра – напряжение на конденсаторе :Uc=I*Xc=6,7 В .

ХУ

Хикмат Уринбаев

Собираете схему, проверяете, подключаете к питанию и делаете замер двумя щупами вольтметра параллельно конденсатору соблюдая технику безопасности (не касаться руками оголённых проводов), ОПАСНО ДЛЯ ЖИЗНИ !!!