Как найти вопрос задачи

Как быть, если ребенок не может правильно понять суть задачи и верно решить её? С чем связаны трудности в решении задач и как их преодолеть?

1. Задача и незадача.

2. Путаница.

3. Задачи-вопросы

Математика, 1 класс

Урок 21. Задача. Структура задачи.

Перечень вопросов, рассматриваемых на уроке:

1. Решение текстовых задач арифметическим способом.
2. Структура задачи: условие, вопрос, решение, ответ.
3. Решение задач в одно действие на увеличение (уменьшение) числа на несколько единиц.
4. Задачи, содержащие отношения «больше (меньше) на..», «больше (меньше) в…».
5. Дополнение условий задач недостающими данными или вопросом.

Глоссарий по теме

Компоненты задачи – условие, вопрос, решение, ответ.

Задачи на сложение и вычитание.

Взаимосвязь между условием и вопросом задачи.

Элементы задачи:

1. Условие (что известно в задаче).

2. Вопрос (что нужно узнать).

3. Решение (действие, нахождение неизвестного).

4. Ответ задачи (ответ на вопрос задачи).

Ключевые слова

Текстовая задача; условие задачи; вопрос задачи; решение задачи.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Волкова С. И., Степанова С. В. Математика. Учебник. 1 кл. В 2 ч. Ч. 1.– М.: Просвещение, 2017.– с. 88 – 89.

2. Моро М. И., Волкова С. И. Математика рабочая тетрадь. 1 кл. 1 ч.– М.: Просвещение, – с. 33 – 34.

На уроке мы узнаем, как построена задача и как называются структурные элементы задачи. Научимся решать задачи, записывать решение задачи и ответ. Сможем выделять задачи из предложенных текстов.

Основное содержание урока

Рассмотрите картинку.

Составьте задачу.

Послушайте два рассказа и сравните их:

1. В магазине мама купила 3 перца и 4 морковки. Сколько всего овощей купила мама?

2. В магазине мама купила 3 перца и 4 морковки. В овощах очень много витаминов, они очень полезные.

Какой из этих текстов мы будем изучать на уроке математики, а какой на уроке окружающего мира?

Первый текст на уроке математики, так как в нём есть вопрос, для ответа на который нужно выполнить вычисления, а второй на уроке окружающего мира.

Как называется текст с вопросом, для ответа на который нужны математические вычисления?

Такой текст называется «Задача».

Сегодня на уроке мы узнаем, какой текст называется задачей и из каких частей она состоит.

Тема нашего урока: «Задача. Структура задачи».

Посмотрите ещё раз на текст знакомой нам задачи и ответьте на вопрос.

Что в ней известно?

В магазине мама купила 3 перца и 4 морковки. Сколько всего овощей купила мама?

Что мама купила 3 перца и 4 морковки.

Это называется – условие задачи, другими словами, это то, что в задаче известно.

Что в задаче нужно узнать?

Сколько всего овощей купила мама.

Это вопрос задачи. Это о чём спрашивают в задаче, то, что нужно узнать.

Что нужно сделать, чтобы сосчитать, сколько мама купила овощей?

Нужно к трём прибавить четыре, получится семь овощей.

Это решение задачи.

Ещё раз прочитайте вопрос задачи и ответьте на него.

Мама купила семь овощей.

Это ответ задачи.

На уроке мы поймём, как построена задача – в ней есть условие и вопрос.

Будем учиться решать задачи, записывать решение задачи и ответ.

Составьте условие задачи по рисунку.

В корзинке четыре луковицы, ещё две луковицы лежат рядом.

Задайте вопрос.

Сколько всего луковиц?

Как решить такую задачу? Сложением или вычитанием?

Четыре да ещё две, задача решается сложением.

Запишем решение. К четырём прибавить два получится шесть.

Осталось записать ответ задачи. Ответим на вопрос задачи: всего шесть луковиц.

Ещё раз посмотрите внимательно на этот же рисунок:

Составьте другую задачу, которая будет решаться вычитанием:

В корзине было четыре луковицы, из неё взяли две луковицы.

Задайте вопрос.

Сколько луковиц осталось в корзине?

Как записать решение?

Из четырёх вычесть два, получится две луковицы.

Осталось записать ответ задачи.

Разбор тренировочных заданий.

Рассмотрите рисунок, дополните условие и решите задачу.

Ответ:

На огороде с одного куста сорвали 2 кабачка, а с другого куста 6 кабачков. Сколько кабачков собрали с двух кустов?

2 + 6 = 8 (к.)

Ответ: 8 кабачков.

Выберите только те тексты, которые являются математическими задачами.

Ответ:

Верные равенства обозначьте синим цветом, а неверные красным.

Ответ:

Прочитайте задачу и установите соответствия между её компонентами.

Ответ:

Попробуйте заменить овощи соответствующей цифрой.

Подсказка: у каждой цифры своя маска. На одинаковых цифрах – одинаковые маски.

Ответ:

Ответь на вопросы с помощью таблицы.

Ответ:

Покажите разным цветом, как можно получить число 6.

Ответ:

1. Целенаправленная работа с текстовой задачей.

   Текстовые задачи в курсе математики начальной школы занимают большое место. С одной стороны, они нужны для того, чтобы сформировать у учащихся умение решать задачи, с другой – они могут быть использованы для формирования математических понятий и их свойств, для мотивации введения новых знаний и т.п.

   Однако эффективное использование текстовых задач возможно лишь в том случае, когда учитель может  чётко определяет конкретную цель работы с каждой задачей на уроке, умеет организовать эту работу в строгом соответствии с поставленной целью.

   Часто работа с задачей на уроках строится однотипно и направлена главным образом на достижение практической цели: решить задачу, т. е. получить ответ на вопрос задачи.

    Включая задачу в урок, мы можем определить весьма разнообразные цели. Они либо являются конкретизацией общей обучающей цели – формирования умения решать задачи, либо вытекают из таких общих целей, как формирование какого-либо математического понятия и умения. И в зависимости от той или иной конкретной цели выбираются методические приёмы работы с задачей.

   Прежде всего необходимо остановиться на выборе конкретной цели включения той или иной задачи в урок. Этот выбор может осуществляться двумя взаимосвязанными путями:

1. От общей цели урока к выбору задачи и к конкретной цели работы с ней на уроке.
2. От конкретной задачи к цели, для достижения которой эту задачу можно включить в урок.

      Покажу на примере алгоритм действия по второму пути.

   Возьмём задачу: «В куске было 15 м ткани. Одному покупателю продали 5 м, а другому 4 м. сколько метров ткани осталось в куске?» необходимо проанализировать её и выяснить:

– какие математические понятия, отношения, связи, числовые данные содержатся в задаче;

– какие возможны в процессе её решения приёмы первичного анализа, в частности, какие виды моделей могут быть полезны;

– какие возможны приёмы поиска плана решения, виды записи решения;

– какие целесообразны виды проверки, варианты дополнительной работы с задачей;

– какое место в курсе математики занимает урок, в который предполагается включить данную задачу.

   Из текста задачи видно, что в ней имеется понятие длины. Ситуация задачи имеет структуру, определяемую словами было, продали, осталось, где неизвестно числовое значение последнего. Этими словами задаётся отношение между значениями длины, которое может быть названо отношениями «целого и части». Числовые данные невелики  (15, 4, 5), допускают решение задачи графически и даже практически.

   Ситуацию задачи легко представить и проиграть на уроке практически с помощью, например, бумажной ленты. Задача допускает следующие модели:

1. Рисунок;
2. Чертёж;
3. Краткую запись.

   Поиск плана решения задачи может быть проведён как от вопроса к данным, так и от данных к вопросу. Задача составная и легко решается арифметически в два действия. Решение может быть записано и по действиям, и в виде выражения. Возможны три арифметических способа решения:

15 – ( 5 + 4 ),

15 – 5 – 4,

15 – 4 – 5.

Запись решения в виде выражения позволяет применить правило вычитания суммы из числа. Разные способы решения задачи иллюстрируют это правило.

    Проверить задачу можно путём соотнесения полученного результата с условием; путём решения задачи другим способом, определения смысла каждого действия и проверки вычислений.

   К данной задаче легко можно составить обратные.

   После подробного анализа работа с задачей на уроке может проводиться с одной из следующих целей:

1. Закрепить умения измерять длину в метрах;
2. Научить составлять краткие записи к задачам данного вида;
3. Закреплять умения составлять краткую запись к задачам данного вида;
4. Учить использовать краткую запись для поиска плана решения задачи;
5. Учить строить чертёж к задаче;
6. Учить находить разные арифметические способы решения по чертежу;
7. Учить решать задачи практически;
8. Учить находить другие арифметические способы решения задачи с помощью представления жизненной ситуации;
9. Учить проводить разбор задачи от вопроса к данным или от данных к вопросу;
10. Учить записывать решение задачи в виде выражения;
11. Познакомить с правилом вычитания суммы из числа;
12. Научить применять правило вычитания суммы из числа при решении задач;
13. Учить проверять решение задачи одним из приёмов.

   Перечисленные способы можно ещё конкретизировать, определяя этап обучения: подготовка, введение, закрепление.

   В качестве примера можно показать методику работы с задачей в соответствии с поставленной на уроке целью.

   1. Закрепить умение измерять длину в метрах.

   Добиться поставленной цели можно только при практическом решении, причём не применяя масштаб. В качестве оборудования можно взять рулончики бумаги для оклейки окон или тесьму, или мерные ленты для швейных работ.

   Начать работу можно с мотивации предстоящей практической работы. Необходимо задать классу следующие вопросы:

– Какие единицы измерения длины вы знаете?

– Длину каких предметов удобнее измерять в сантиметрах? дециметрах? метрах?

– В каких единицах мы с вами уже учились измерять?

   После прослушивания задачи задаём вопрос о том, можно ли её решить выполняя арифметические действия, какие действия нужно выполнить. Затем предложить детям ответить на вопрос, как решить эту задачу, не прибегая к арифметическим действиям, если вместо куска ткани у них будет рулончик бумаги длиной 15 метров. Дети придут к выводу, что нужно отмерить 5 м, затем 4 м, а потом измерить длину оставшейся ленты. А так как целью является научиться измерять длину в метрах, то очень хорошо решается задача измерением. Заодно и проверяется, правильно ли дети ответили на вопрос задачи, выполняя действия.

   После измерения организуется обсуждение найденного решения. Вспоминается правило измерения в метрах (нужно взять метровую линейку и уложить её на измеряемой полоске столько раз, сколько нужно отмерить метров или необходимо отмерить на полоске один метр, потом сгибать ленту в «гармошку» так, чтобы каждый раз от сгиба до сгиба длина равнялась 1 м, а затем сосчитать число метров).

1. Познакомить с составлением краткой записи к задачам этого вида и научить составлять краткие записи.

   К данному виду задач удобна такая форма краткой записи:

Было…          

Продали…

Осталось…

   Вначале необходимо обеспечить понимание нужности, полезности предстоящей работы. Это можно сделать следующим образом.

   Предложить устно решить задачу, текст которой дети воспринимают на слух. Затем даётся другая задача такого же уровня сложности, которую учитель не только читает но и кратко записывает на доске. После этого задаётся вопрос: «Когда было легче решить задачу: без краткой записи или с записью?»  А далее ставится цель – научиться записывать кратко новый вид задач.

Но вначале составляется краткая запись к нашей задаче. Можно составить краткую запись при помощи карточек на наборном полотне. При составлении записи выясняем, какие слова необходимо использовать при составлении краткой записи и почему, какие числа нужно использовать и почему, куда поставить карточку с вопросом. Получается запись:

     Дети устно отвечают на вопрос задачи. Затем открывают учебник и читают похожую задачу. Выясняется, чем отличаются задачи, что нужно изменить в краткой записи предыдущей задачи. По составленной краткой записи дети самостоятельно решают задачу. Затем предлагается в сборнике задач или в карточке раздаточного материала найти задачу, к которой можно составить краткую запись по той же схеме и решить её.

1. Закреплять умения составлять краткую запись к задачам.

   Для детей готовится раздаточный материал с задачами:

1). В куске было 15 м ткани. Одному покупателю продали 4 м ткани, другому – 5 м . Сколько метров ткани осталось в куске?

2). У кормушки было 6 голубей. Сначала прилетели 2 голубя, потом ещё один. Сколько голубей стало у кормушки?

3). В магазине было 25 женских велосипедов и 16 мужских. За день купили 13 велосипедов. Сколько велосипедов осталось продать?

4). Сережа вырезал 5 красных флажков и 8 зелёных. После того, как он несколько флажков отдал сестре, у него осталось 2 красных и 4 зелёных флажка. Сколько флажков Серёжа отдал сестре?

    Даётся задание составить краткую запись к каждой задаче. Определяется, какие слова надо записать в кратких записях, заносятся числовые данные к каждому слову, выделяются неизвестные и определяются главные вопросы задач. Проверку выполненной работы можно провести по эталону. После проверки детям предлагается выбрать одну или несколько задач для решения (из предложенных). Акцентируется внимание на том, что последняя задача – самая сложная, было бы неплохо, если кто-нибудь с ней справится.

1. Учить использовать краткую запись для поиска решения.

   На доске записаны краткие записи задач. Задаётся вопрос для чего мы делаем краткую запись к задачам. Ставится цель – краткая запись часто помогает в решении задачи, поэтому мы поучимся находить решение задачи, опираясь на её краткую запись.

   Далее читается задача о ткани, а дети выбирают среди записей на доске краткую запись, соответствующую задаче и обосновывают свой выбор.

   Затем спрашивается, похожи ли другие краткие записи на эту. (Похожи, потому что в них есть слова было, взяли ( вышли, продали ), осталось.

Чтобы по этим записям можно было легко найти решение, необходимо определить, как связаны строки этих записей (было всегда состоит из того, что продали (взяли, вышли), осталось).

    Далее надо спросить у детей, что делается для того, чтобы узнать сколько осталось, если известно, сколько было и сколько продали. Т. е. по краткой записи намечается план решения. Полезно предложить детям составить выражения ко всем задачам, записанным кратко. Перед составлением выражения нужно по краткой записи прочитать задачи. Вместе с детьми проверяется правильность составления выражений, каждое выражение соотносится с краткой записью.

1. Учить строить чертёж к задаче.

  Детям предлагается сделать рисунок к задаче, чтобы её легче было представить и решить. Выслушиваются предложения детей относительно того, что должно быть на рисунке. Ткань можно изобразить в виде прямоугольника, но так как ширина ткани нам не важна, договариваемся изображать ткань в виде отрезка. Итак, чтобы построить чертёж к задаче, нужно вначале договориться, что будем изображать и в каком виде.

   Затем вместе с детьми выбирается длина отрезка, его расположение и т. д. до конца работы. В результате в тетрадях учеников появляется чертёж к задаче, а на доске записана памятка по построению чертежа.

   Затем детям предлагается, пользуясь памяткой, построить чертёж ещё к одной задаче. Полезно, чтобы дети проговаривали вслух, что нужно делать, а потом выполняли с комментированием соответствующий шаг в построении чертежа.

1. Учить находить разные арифметические способы решения задачи по чертежу.

Для достижения этой цели лучше вначале предложить учащимся решить задачу устно по готовой краткой записи. По записи дети легко находят один способ решения:

1). 4 + 5 = 9 (м)

2). 15 – 9 = 6 (м)

   Затем предлагаются детям чертежи к этой задаче или просим сделать чертёж к задаче в тетрадях, можно положить на парту каждому ученику листок с готовыми чертежами, чтобы внимание детей не рассеивалось, а полностью было сконцентрировано на поиске другого решения по чертежу.      

                                                 15 м

             ?                    4 м                5 м

                                                  15 м

             ?                    4 м                5 м

   Два чертежа нужны для того, чтобы дети вначале на первом чертеже показали, как отрезали ткань, и узнали, сколько осталось ткани, если решать задачу первым способом. А на втором чертеже показано, как можно узнать, сколько осталось ткани в куске после того, как ткань купил первый покупатель. Здесь очень важно, чтобы каждый ученик практически показал по чертежу, как он будет находить остаток.

   Далее делается вывод, что чертёж помогает найти другие способы решения, и детям предлагается ещё одна задача.

                                                  15 м

             ?                    4 м                5 м

                                                      ?                        

                                                  15 м

                         ?

             ?                    4 м                5 м

Лучше, если  будет дано решение этой задачи одним способом и чертёж, по которому детям нужно найти другие способы решения. Причём, полезнее взять вторую задачу другого типа, но допускающую разные способы решения.

   Такое понимание цели включения задачи в урок делает работу с задачами более интересной и повышает результативность использования задач в обучении детей математике.

1. Различные способы решения текстовых задач.

  Пользуясь различными приёмами решения текстовых задач, учитель при подготовке к уроку может самостоятельно найти несколько оригинальных способов решения задачи. Применяя эти приёмы в классе при руководстве коллективным решением задачи, учитель может подвести учащихся к отыскиванию другого способа решения, если это необходимо для достижения целей урока. Умелое использование различных способов решения задач на уроках математики в начальных классах оказывает положительное влияние на развитие мышления детей, на формирование их личности. Причём ценность имеют не только рациональные способы решения, но и все другие, во-первых, потому, что для учения более лёгким и понятным может оказаться как раз нерациональный с точки зрения математики способ, во-вторых, потому, что знание того, что большинство задач допускает много разных способов решения, предоставляет ученику значительные возможности для самостоятельного поиска решения. Ученик при этом не будет отказываться от решения задачи только потому, что он забыл, как такие задачи решаются.

   Рассмотрим суть каждого из приёмов, покажем на конкретных примерах возможности его применения для отыскания других способов решения.

1. Построение иной модели задачи, чем та, которая была использована при решении задачи первым способом.

Задача: « На одной машине увезли 28 мешков зерна, на другой – на 6 мешков больше, чем на первой машине, а на третьей – на 4 мешка меньше, чем на второй. Сколько мешков зерна увезли на третьей машине?»

Традиционная краткая запись выглядит так:

1 маш. – 28 меш.

2 маш. – ?, на 6 меш. больше

3 маш. – ?, на 4 меш. меньше  

   С помощью этой записи легко находится такое решение:

1). 28 + 6 = 34 (меш.) – привезли на второй машине.

2). 34 – 4 = 30 (меш.)

Ответ: на третьей машине привезли 30 мешков зерна.

Если же мы построим чертёж, то легко найдём другой способ решения:

                          28 меш.

1    

                     28 меш.                     6 меш.

2

                                                                4 меш.

                       28 меш.

    3 

                                    ?

1). 6 – 4 = 2 (меш.)  – больше привезли на третьей машине, чем на первой.

2). 28 + 2 = 30 (меш.)

Ответ: на третьей машине привезли 30 мешков зерна.

Рассмотрим ещё одну задачу: « В соревнованиях принимали участие 18 пловцов из нашей школы, а из соседней – в 2 раза больше. Сколько всего пловцов принимало участие в соревнованиях?»  традиционнее решение выглядит так:

1). 18 · 2 = 36 (плов.) – приняло участие из соседней школы.

2). 36 + 18 = 54 (плов.)

Ответ: в соревнованиях приняло участие всего 54 пловца.

   Но если к этой задаче построить чертёж, то решение может быть найдено с помощью выполнения одного действия, так как ещё одно действие выполняется устно или же его результат берётся для чертежа:

                         18 пл.              18 пл.           18 пл.

                              1 шк.                      2 шк.

                                                      ?

Решение: 18 · 3 = 54 (пл.)

 Ответ: в соревнованиях приняло участие всего 54 пловца.

Как видно из приведённых примеров, чертёж помогает найти другой способ решения задач, условия которых содержат отношения «больше на … (меньше на …)», « больше (меньше) в … раз».

   При решении задач, содержащих пропорциональную зависимость величин, другой способ решения зачастую помогает найти схематический рисунок. Рассмотрим это на примере: « В магазин привезли 12 ящиков с яблоками по 8 кг в каждом. До обеденного перерыва было продано 9 ящиков. Сколько килограммов яблок осталось продать после обеденного перерыва?»

   Задача имеет традиционную структуру: « Было 12 ящ. по 8 кг в каждом, продали – 9 ящ. по 8 кг в каждом; требуется узнать, сколько кг осталось продать». Путём рассуждения от вопроса к данным легко находится следующий способ решения:

1). 8 · 12 = 96 (кг) – привезли в магазин.

2). 8 · 9 = 72 (кг) – продали до обеденного перерыва.

3). 96 – 72 = 24 (кг)

Ответ: 24 кг яблок осталось продать после обеденного перерыва.

Если сделать схематический рисунок, то увидим, что после обеденного перерыва осталось продать 3 ящика яблок по 8 кг в каждом.

                                Было

Отсюда арифметическое решение данной задачи такое:

1). 12 – 9 = 3 (ящ.) – осталось продать после обеденного перерыва.

2). 8 · 3 = 24 (кг)

Ответ: 24 кг яблок осталось продать после обеденного перерыва.

   При решении некоторых задач хорошим подспорьем в отыскании других способов решения является табличная форма краткой записи и поиск плана решения по таблице.

  Задача: « Утром ушли в море 20 маленьких и 8 больших рыбачьих лодок. 6 лодок вернулись. Сколько лодок с рыбаками должно ещё вернуться?»

   В обычной форме краткая запись этой задачи выглядит так:

Ушли – 20 л. и 8 л.

Вернулись – 6 л.

Осталось вернуться – ?

По этой записи легко составляется выражение (20 + 8) – 6.

   Составим теперь таблицу и  занесём в неё содержание задачи. Для этого вначале определим, сколько строк и столбцов необходимо в этой таблице. Затем выясним, о каких лодках идёт речь в задаче. Из текста задачи видно, что речь идёт о больших лодках, маленьких лодках и обо всех лодках. Для занесения этих сведений в таблицу понадобится три строки. Теперь установим, о скольких ситуациях идёт речь в задаче: лодки ушли, лодки вернулись, лодки должны вернуться. Для занесения этих сведений в таблицу потребуется три столбца:

	Ушли	Вернулись	Должны вернуться
Большие лодки
Маленькие лодки
Всего

   Следующий шаг составления таблицы – внесение содержания задачи в неё. Для этого читаем задачу по частям, занося содержание каждой части в соответствующий столбец и строку. Однако при этом возникает вопрос: куда занести сведения о вернувшихся лодках? Так как в задаче ничего не сказано о том, какие лодки вернулись, то мы можем считать их: большими, тогда число 6 будет в первой строке; маленькими, тогда число 6 будет во второй строке; часть больших и часть маленьких лодок, тогда появится пять вариантов заполнения таблицы. Таким образом, таблицу можно заполнить семью различными способами, что определяет семь различных арифметических способов решения, не считая первого, который найден по краткой записи без таблицы.

	Ушли	Вернулись	Должны вернуться
Большие лодки	20	6	?
Маленькие лодки	8	—-	8
Всего	?	6	?

	Ушли	Вернулись	Должны вернуться
Большие лодки	20	—-	20
Маленькие лодки	8	6	?
Всего	?	6	?

	Ушли	Вернулись	Должны вернуться
Большие лодки	20	1 (2, 3, 4, 6)	?
Маленькие лодки	8	5 (4, 3, 2, 1)	?
Всего	?	6	?

2 способ:

20 – 6 + 8 = 22 (л.)

3 способ:

20 + ( 8 – 6 ) = 22 (л.)

4 способ:

( 20 – 1 ) + ( 8 – 5 ) = 22 (л.)

5 способ:

( 20 – 2 ) + ( 8 – 4 ) = 22 (л.)

6 способ:

( 20 – 3 ) + ( 8 – 3 ) = 22 (л.)

7 способ:

( 20 – 4 ) + ( 8 – 2 ) = 22 (л.)

8 способ:

( 20 – 5 ) + ( 8 – 1 ) = 22 (л.)

   Следует заметить, что, заполняя таблицу, мы вынуждены были дополнять условие задачи уточняющими сведениями о видах лодок, которые вернулись. Возможно также и представление практических ситуаций.

    Все приведённые способы решения могут быть также легко найдены, если построить предметную модель. Например, в классе можно поставить на планку у доски 20 больших треугольников – это большие лодки – и 8 маленьких – это маленькие лодки. По-разному беря 6 треугольников (лодок) и выполняя арифметические действия, мы получим все способы решения. Построение чертежа к этой задаче уже не даёт возможности найти столько способов решения, так как иное изображение 6 лодок требует построения другого чертежа:

                              20                                                8

•  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •  •

                                 ?                                                    6

( 20 + 8 ) – 6 = 22 (л.)

20 + ( 8 – 6 ) = 22 (л.)

1.  Использование другого способа разбора задачи при составлении плана решения.

   Приведём пример, когда выбор пары данных при разборе задачи от данных к вопросу неожиданно приводит к красивому и нестандартному решению.

Задача: « В зале 8 рядов по 12 стульев в каждом. В зал пришли учащиеся из трёх классов , в каждом из которых по 30 человек. Хватит ли стульев для всех учеников? Сколько свободных стульев останется?»

   Начнём рассуждение с первой пары данных: 8 рядов по 12 стульев в каждом. По этим данным можно узнать, сколько всего стульев в зале: 12 · 8 = 96  (с.) Возьмём теперь найденное число и количество учеников в одном классе: 96 стульев и 30 учеников. Что по этим данным можно найти? Т. к. в классе 30 учеников, то им понадобится 30 стульев. Зная это, можно узнать, на сколько классов хватит стульев в зале (сколько раз по 30 содержится в 96)

Разделим 96 на 30, получим 96 : 30 = 3 (ост. 6), т.е. стульев хватит на три класса и останутся незанятыми шесть стульев. Для ответа на вопрос задачи необходимо выполнить только два действия.

1. Дополнение условия задачи сведениями, не влияющими на результат решения.

Возьмём задачу: « В одном кувшине было 4 л молока, а в другом 3 литра. За обедом выпили 2 л молока. Сколько литров молока осталось?»

    Дополняя условие задачи сведениями о том, из какого кувшина выпили молоко за обедом, можно найти кроме основного (( 4 + 3 ) – 2 ) ещё три способа: ( 4 – 2 ) + 3, если за обедом пили молоко из первого кувшина; 4 + ( 3 – 2 ) , если за обедом пили молоко из второго кувшина; 4 – 1 = 3, 3 – 1 = 2, 3 + 2 = 5, если пили молоко поровну из каждого кувшина.

   Применение данного приёма может сочетаться с построением модели задачи и особенно тесно с приёмом представления практического разрешения ситуации, так как оно всегда сопровождается привнесением в содержание задачи дополнительной информации.

1. Представление практического разрешения ситуации, описанной в задаче.

Пусть нужно решить разными способами задачу: «На товарную станцию прибыло 2 состава с брёвнами. В одном из них было 39 платформ, а в другом на 4 больше. Разгрузили 60 платформ. Сколько ещё платформ осталось разгрузить?»

   Первый способ решения, основанный на традиционной структуре: «было», «разгрузили», «осталось разгрузить» находится довольно легко:

1). 39 + 4 = 43 (пл.) – во втором составе.

2). 39 + 43 = 82 (пл.) – всего в  двух составах.

3). 82 – 60 = 22 (пл.)

Ответ: осталось разгрузить 22 платформы.

   Другие способы не сразу находят даже учителя. Но стоит только предложить учащимся представить себе, что это они разгружают составы, представить, как они организуют разгрузку, как сразу же поступают предложения: нужно разгрузить вначале один состав, а потом другой; можно разгрузить вначале первый состав, а затем второй; можно разгрузить вначале второй состав, а потом начать разгружать первый. На основе этих рассуждений приходим к следующим способам решения.

2 способ.

  Узнаем, сколько платформ во втором составе: 39 + 4 = 43. пусть вначале разгрузили первый состав. Тогда из 60 разгруженных платформ 39 из первого состава, а остальные – из  второго. Узнаем сколько разгрузили платформ из второго состава: 60 –  39 = 21. знаем, что во втором составе было 43 платформы, а разгрузили из них 21. осталось разгрузить 43 – 21 = 22 платформы. Аналогичные рассуждения приводят к третьему способу решения.

3 способ.

1). 39 + 4 = 43 (пл.)  – во втором составе.

2). 60 – 43 = 17 (пл.) – разгрузили из первого состава.

3). 39 – 17 = 22 (пл.)

Ответ: осталось разгрузить 22 платформы.

   Если предложить рассуждения о практических способах разгрузки платформы, тогда появятся ещё несколько способов решения. Если представить, что разгрузили 30 платформ из первого состава, то получим ещё один способ решения:

1). 39 + 4 = 43 (пл.)  – во втором составе.

2). 39 – 30 = 9 (пл.) – остались неразгруженными из первого состава.

3). 43 – 30 = 13 (пл.) – остались неразгруженными из второго состава.

4) 9 + 13 = 22 (пл.)

 Ответ: осталось разгрузить 22 платформы.

   Существуют и другие аналогичные способы, которые также легко могут быть найдены при представлении практической ситуации. Использование рассматриваемого приёма позволяет привлечь к поиску решения задачи жизненный опыт детей, их практическую смекалку.

1. Замена данной задачи другой, по результату решения которой можно найти ответ на вопрос данной задачи.

Изменим условие предыдущей задачи: в обоих составах платформ было поровну – по 39. Нетрудно будет найти решение этой задачи:

1). 39 · 2 = 78 (пл.)  – в обоих составах.

2). 78 – 60 = 18 (пл.)

Ответ: осталось разгрузить 18 платформ.

   Сравним теперь содержание исходной задачи и изменённой. В исходной задаче платформ во втором составе на 4 больше, а значит, на 4 больше и общее число платформ которые осталось разгрузить. Тогда ответ на вопрос задачи  мы можем найти, увеличив результат решения изменённой задачи на 4, т. е. 18 + 4  = 22 (пл.)

   Нужно отметить, что показанный приём основан на свойствах отношений «больше», «меньше», «равно», что он служит средством отыскания нестандартных способов решения.

1. Явное выделение всех зависимостей в задаче.

В основе этого приёма лежит глубокий анализ математического содержания задачи.

   Рассмотрим задачу: « Ученики одной школы собрали 80 т металлолома, а другой –  5 ̸  8 этого количества. Из всего собранного лома на заводе изготовили рельсы. Сколько получили метров рельсов, если из каждых 10 т металлолома выходит 70 м рельсов?»

   В данной задаче две взаимосвязанные величины: масса и длина. Эти величины характеризуются металлоломом, собранным детьми первой школы, детьми второй школы и детьми обеих школ вместе. Учитывая эти зависимости можно найти несколько способов решения этой задачи.

1 способ.

1). 80 : 8 · 5 = 50 (т.)

2). 80 + 50 = 130 (т.)

3). 70 : 10 = 7 (м ̸ т)

4). 130 · 7 = 910 (м)

2 способ.

1).   80 : 8 · 5 = 50 (т.)

2). 70 : 10 = 7 (м ̸ т)

3). 7  · 80 = 560 (м)

4). 7 · 50 = 350 (м)

5) 350 + 560 = 910 (м)

3 способ.

1). 70 : 10 = 7 (м ̸ т)

2). 7  · 80 = 560 (м)

3). 560 : 8 · 5 = 350 (м)

4). 350 + 560 = 910 (м)

3. Развитие мышления детей при решении текстовых задач.

   Математику любят в основном те ученики, которые умеют решать задачи. Следовательно, научив детей владеть умением решать задачи, мы окажем существенное влияние на их интерес к предмету, на развитие мышления и речи.

  Остановимся на обучении решению задач на движение.

   В результате подготовительной работы к моменту обучения решению задач этого вида ученики владеют навыками устного счёта, умением самостоятельно решать простые задачи на зависимость между величинами «скорость», «время», «расстояние», применять алгоритм решения простой и составной задач.

   Текст задачи: « Расстояние между городом и зимовкой 150 км. Из города к зимовке выехали аэросани со скоростью 60 км ̸ ч. в это время навстречу им из зимовки выехал лыжник со скоростью 15 км ̸ ч. На каком расстоянии от зимовки он встретил аэросани?»

   Можно предложить ребятам в парах построить чертёж к этой задаче, либо предложить готовый, а ученики по чертежу повторяют задачу, показывая на нём своему соседу по парте, что известно в задаче и что необходимо найти. При этом дети учатся читать чертежи, контролируя друг друга.

   Далее можно спросить у детей, кто может самостоятельно решить задачу. Одному из поднявших руку предлагается решить задачу с обратной стороны доски. С остальными же ещё раз уточняется условие и вопрос задачи. Пока учащиеся решают задачу самостоятельно, учитель оказывает индивидуальную помощь тем детям, для кого задача оказалась трудна. К тому времени те, кто решил задачу, получают дополнительное задание на выбор: изменить вопрос задачи и решить её либо выбрать из сборника другую задачу на движение и решить её. Как только класс закончит работу, проверяется решение основной задачи:

 1). 60 + 15 = 75 ( км ̸ ч) – скорость сближения.

 2). 150 : 75 = 2 (ч) – время в пути.

 3). 15 · 2 = 30 (км)

Ответ: 30 км пройдёт лыжник до встречи.

  Затем проверяются дополнительные задания. Задаются новые вопросы к задаче и объясняется ход мыслей при решении. После проделанной работы можно задать дополнительные вопросы:

– Почему изменилось последнее действие в задаче?

– Как изменится условие в задаче, в которой нужно определить время? (условие не изменится, изменится только вопрос)

– Запишите выражение, с помощью которого можно найти время.

– Изменится ли текст задачи, если надо найти всё расстояние?

( да, т.к. должны быть даны скорость аэросаней, лыжника и время их движения)

   Также обнаруживается, что расстояние можно найти разными способами:

1 способ.

( 60 + 15) · 2  = 150 (км)

2 способ.

60 · 2 + 15 · 2 = 150 (км)

   Дети доказывают, что каждое из приведённых решений верно, определяют более рациональное из них.

– Какую ещё величину можно сделать неизвестной? (скорость)

– Найдите скорость аэросаней.

Дети предлагают два способа решения.

1 способ.

150 : 2 – 15 = 60 (км ̸ ч)

2 способ.

( 150 – 15 · 2 ) : 2 =  60 (км ̸ ч)

В результате такой работы большинство учащихся смогли решить шесть задач.

   Практика работы над составной задачей показывает, что одна из главных причин затруднения учащихся  – недостаточное понимание текста задачи. Чтобы задача стала понятней, можно применять следующие виды упражнений, которые используются не только при первичном знакомстве учащихся с задачей, но и при индивидуальной работе со слабыми учениками:

1. Преобразование условия задачи, например, из косвенной формы в прямую.
2. Решение задач, где вопрос стоит в начале условия в разных формулировках, например: «Найти скорость, если известно…», «Какова скорость, если известно…», «Вычисли скорость, если известно…»   Умение находить вопрос задачи – очень важный момент. Оно формируется при решении простых задач и совершенствуется при решении составных.

   Далее приведём некоторые приёмы, которыми пользуемся на уроках при решении составных задач.

1. Составление задач по выражению.    

540 : 4  – 60 = 70 (км ̸ ч)

Вначале можно предложить детям составить задачу на встречное движение, а затем придумать задачу с таким же решением на движение в противоположных направлениях.

1. Составление обратных задач в т.ч. с использованием готовых схем.

1. Составление задач на движение по чертежам.

1. Использование дидактического материала. Для этих целей можно сделать для каждого ребёнка в классе раздаточный материал по разным видам задач. При изучении того или иного вида задач у детей на уроках всегда должен быть этот раздаточный материал и в свободные минутки они самостоятельно решают задачи по выбору на дополнительную отметку.

1. Сравнение разных задач с одинаковым решением, например: « Из двух городов, находящихся на расстоянии 520 км, вышли навстречу друг другу два поезда в одно и то же время и встретились через 4 часа. Первый поезд шёл со скоростью 60 км ̸ ч С какой скоростью ехал второй поезд?»

Вторая задача: « Два поезда вышли из города одновременно в противоположных направлениях. Через 4 часа расстояние между ними было 520 км. Первый шёл со скоростью 60 км ̸ ч. С какой скоростью шёл второй поезд?»

                       Решение занимательных  задач.

                     – Два кирпича летели с одинаковой скоростью, хотя и были брошены      

                      разными мальчиками друг в друга. К счастью, оба кирпича  

                      промахнулись. Первый кирпич был в воздухе 8 секунд, а второй –  на 2

                     секунды меньше. Второй кирпич пролетел меньше первого на 6 метров.

                     Какое расстояние пролетел каждый кирпич?

6 : 2 = 3 ( м ̸ с) – скорость

3 · 8 = 24 (м) – пролетел первый кирпич.

24 – 6 = 18 (м)  или 3 · ( 8 – 2 ) = 18 (м) – пролетел второй кирпич

1. Фронтальная работа со схемами, вычерченными на доске.

–  Что происходит с движущимися объектам и при движении в одном направлении, в противоположных направлениях, навстречу друг другу. Ваша задача – определить вид движения, представленный на схеме, сказать, увеличится или уменьшится расстояние между объектами через 3 часа после начала движения и на сколько.

7 км ̸ ч       19 км ̸ ч

( движение с отставанием, расстояние увеличится,

Ȗ уд. = 19 – 7 = 12 км ̸ ч

Ś = 12 · 3 = 36 (км))

– Что произойдёт, если движущиеся объекты поменять местами?

( движение вдогонку, расстояние уменьшится,

Ȗсбл. = 19 – 7 = 12 км ̸ ч,        Ś = 12 · 3 = 36 км)

          60 км ̸ ч                             85 км ̸ ч

( движение в противоположных направлениях, расстояние увеличится,

Ȗуд. = 60 + 85 = 145 (км ̸ ч)

Ș = 145 · 3 = 435 (км))

– Что произойдёт, если объекты поменять местами?

( ничего не изменится)

1. Составление обратных задач к данной по выражениям, работа со схемами.

– Составьте обратные задачи, используя выражения.

( пока один из учеников составляет задачу, другой на доске работает со схемой)

   1320 : ( 75 + 35 )   ( ṭ встр. – ? )

   1320 : 12 – 35        ( Ȗ пасс. поезда)

   1320 : 12  – 75        ( Ȗтов. поезда )

1. Решение задачи разными способами.

                                                75 км ̸ ч                                      35 км ̸ ч

1. Блиц-турнир ( работа маркерами на альбомных листах).

18 км ̸ ч                                   13 км ̸ ч

                        ? км                            ṭ встр.= 4 ч.

         80 км ̸ ч                      60 км ̸ ч

                             45 км

                          ?                              ṭ = 6 ч.

                                                         ḍ 6 = ?

   18 км ̸ ч                                     8 км ̸ ч

                             78 км                                ṭ встр. = ?

             8 км ̸ ч                              ?

                                   15 км

                                   ?                                         ṭ = 3 ч

                                                                              ḍ 3 = 54 км

75 км ̸ ч                     68 км ̸ ч

            ?                                                         ṭ встр. = 3 ч

    67 км ̸ ч                    62 км ̸ ч

             25 км                                  ṭ встр. = ?

 15 км ̸ ч               24 км ̸ ч

          16 км                                         ṭ = 2 ч

                                                            ḍ 2 = ? км

1. + 18 ) • 4 = 128 (км)

45 + (( 80 + 60) • 6 ) = 885 (км)

78 : ( 18 + 8 ) = 3 (ч)

(54 – 15) : 3 – 8 = 5 ( км ̸ ч)

( 75 – 68 ) • 3 = 21 (км)

25 : ( 67 – 62 ) = 5 (ч)

16 + ( 24 – 15 ) • 2 = 34 (км))

  Было

 Продали

  Осталось

 Осталось

  15 м

4м, 5м

     ?

     Продали

?

?

ṭ встр. = 12 ч.

1 способ:

( 75 + 35 ) • 12 = 1320 (км)

– Как эту задачу можно было решить по-другому?

2 способ:

( 75 • 12) + ( 35 • 12) = 1320 (км)

– Какой способ более рациональный?

– Почему?

«СИСТЕМА РАБОТЫ НАД ТЕКСТОВОЙ АРИФМЕТИЧЕСКОЙ ЗАДАЧЕЙ

В НАЧАЛЬНОЙ ШКОЛЕ

ИЛИ КАК ЭФФЕКТИВНО НАУЧИТЬ УЧАЩИХСЯ РЕШАТЬ ЗАДАЧИ»

Схема т и чн о п л а н ре ш е н ия а р иф м е тиче с к о й з а д а чи мо ж но п р е дста в и т ь следующим образом:

I ЭТАП

ВОСПРИЯТИЕ И АНАЛИЗ ЗАДАЧИ

Цель этапа: понять задачу, представить, о чём эта задача; установить, что известно, что нужно найти, как связаны между собой данные и искомое.

Одной из главных причин, по которым школьники неверно решают ту или

иную задачу

является неспособность глубоко, осмысленно, внимательно проанализировать то, что дано

задаче (данные) и то, что нужно узнать (вопрос), и взаимосвязи между ними.

Мы постоянно

напоминаем детям: «Внимательно читайте условие и вопрос». Но ошибки продолжают

существовать. Чтобы решить эту проблему, я использую в работе следующие

приёмы:

Первый подэтап:

• Чтение текста задачи: сначала про себя, затем вслух одним из учеников.

• Пересказ задачи своими словами (этот приём способствует более глубокому осмыслению прочитанного).

• Представление жизненной ситуации, описанной в задаче, инсценировка этой ситуации.

Второй подэтап (графическая работа с цветом):

• Разбиение текста задачи на смысловые части, подчёркивание условия и вопроса синим и красным цветом, выделение числовых данных.

• Выделение наиболее важных слов в каждой смысловой части и в вопросе задачи.

Вот как должен выглядеть текст задачи после этого подэтапа:

«Лена нарисовала 10 шариков./ 3 шарика она раскрасила красным цветом/, синим – на 2 шарика больше /, остальные шарики – зелёным цветом. / Сколько

зелёных шариков на рисунке у Лены? красным – вопрос).

(Синим цветом выделяем условие,

Третий подэтап:

• Пере ф о р м ул и р о в к а т ек с т а з а д ачи ( о т б ра с ы ва н и е нес у ществе н н ы х деталей, зачёркивание).

Этот приём целесообразно использовать, если текст задачи объёмный и

содержит много несущественных деталей.

«В саду было 5 кустов облепихи. Когда посадили ещё несколько, то в саду стало 9 кустов облепихи. Сколько кустов посадили?»

«Было 5 кустов облепихи. Стало 9 кустов. Сколько кустов посадили?»

• Переконструирование текста задачи (У –В – У, В – У – У У – В )

В учебниках чаще всего используются задачи типичной конструкции У

– В, это способствует развитию у учащихся стереотипов, автоматизма при анализе текста задачи.

Важно как можно чаще использовать тексты нетипичных конструкций: текст задачи состоит из одного сложного вопросительного или повествовательного предложения, в котором стоит сначала вопрос, потом условие; часть условия представлена в начале текста, потом следует вопрос и другая часть условия; вместо слова «сколько» в вопросе используются слова

«найди», «узнай» и т. д.).

«Около школы росло 20 тополей. Сколько тополей посадили осенью, если стало 43 тополя?» (У – В – У)

«Сколько кроликов было в клетке, если после того, как отсадили 7 cерых

кроликов, осталось 5 белых кроликов?» (В – У – У)

«Узнай массу яйца кукушки, если оно на 1 грамм меньше яйца стрижа, которое весит 4 грамма»

Дополнительно для обучения учащихся анализировать текст задачи можно

использовать следующие упражнения:

• Анализ текстов задач с лишними и недостающими данными.

« На дереве сидело 8 птичек . Сначала улетели 3 птички, потом ещё 2. Сколько птичек улетело?»

«На одном проводе сидели ласточки , а на другом – 7 воробьёв. Сколько всего

сидело птиц на проводах?»

• Анализ текстов задач с противоречивым условием.

«На одной клумбе растёт 10 хризантем, а на другой – 15. Сколько тюльпанов на двух клумбах?»

• Анализ текстов задач с вопросом, в котором спрашивается о том, что уже известно.

«На клумбе росло 5 тюльпанов и 3 розы. Сколько тюльпанов росло на клумбе?»

• Анализ текстов задач с неопределённым условием.

« В вазе лежало 3 яблока, 5 апельсинов, а груш на 2 меньше. Сколько всего фруктов в вазе?» (не указано, с чем сравнивается количество груш).

• Сравнение текстов задач (сравниваются задачи, сходные по сюжету, но

раз н ые по ма т емати ч ес к ому с о д е рж а ни ю , л иб о с о д и на к о в ы м математическим содержанием, но совершенно разных по сюжету).

«В вазе лежало 3 яблока, а апельсинов на 2 больше. Сколько апельсинов лежало в вазе?»

«В вазе лежало 3 яблока, их на 2 больше, чем апельсинов. Сколько апельсинов лежало в вазе?»

• Составление условия к данному вопросу.

Составь условие к данному вопросу.

«Сколько марок в двух конвертах?»

«Сколько зебр привезли в зоопарк?»

• Постановка вопроса к данному условию.

Поставь вопрос к данному условию.

«В Тихом океане 9 морей, а в Атлантическом на 3 моря меньше».

«В Тихом океане 9 морей, а в Индийском океане 5 морей».

• Подбор условия к данному вопросу или вопроса к данному условию .

Подбери условие к данному вопросу.

«Сколько кленовых листьев засушила Таня?»

а) Осенью Таня засушила 4 кленовых и 5 дубовых листьев. б) Осенью Таня засушила 9 листьев. Из них 4 дубовых.

в ) Осенью Таня засушила 5 кленовых листьев, а дубовых на 4 больше.

г) Осенью Таня засушила 9 дубовых листьев, а кленовых на 4 меньше.

Подбери вопрос к данному условию.

«Дикие гуси живут 80 лет, а собаки 20 лет». а) Сколько всего лет живут гуси и собаки?

б) На сколько лет гуси живут больше, чем собаки?

в) На сколько лет гуси живут меньше, чем собаки? г) Сколько лет живут гуси?

I I этап – МОДЕЛИРОВАНИЕ

Моделирование – это замена действий с реальными предметами действиями с уменьшенными образцами, моделями, с их графическими заменителями: рисунками, схемами, чертежами, таблицами. Модель должна помочь ученику понять содержание задачи, выявить отношения между данными и искомым, найти разные способы решения задачи, увидеть новые,

не отражённые в задаче отношения.

Для того, чтобы самостоятельно решать задачи, школьнику нужно освоить различные виды моделей, научиться выбирать модель, соответствующую предложенной задаче и переходить от одной модели к другой. Наша задача – научить школьников применять тот способ моделирования, который наиболее подходит к той или иной задаче, помогает увидеть отношения между данными и искомым, найти разные способы решения задачи (если это возможно), увидеть скрытые взаимосвязи, не отражённые явно в тексте задачи.

На мой взгляд, самой удачной, с этой точки зрения, моделью, является схематический чертёж и менее удачной – краткая запись опорными словами.

Правильно выполненный чертёж наиболее точно отражает все взаимосвязи, о которых идёт речь в задаче. Но, к сожалению, не к каждой задаче подходит эта модель. Обычно, после анализа задачи, я предлагаю учащимся самим выбрать подходящую модель, учу находить их «плюсы» и «минусы» той или иной модели.

Для формирования умения моделировать задачу, я использую следующие приёмы:

• С о с т а в лен и е кр а т к ой за пи си зад а чи пр и п о мо щ и о п о р н ы х сл о в (рисунка, схемы, таблицы и т. д.). Этот приём чаще всего используется

на уроках в начальной школе.

• Выбор рисунка, схемы и т. д. к данной задаче.

Выбери схему, подходящую к данной задаче.

«В течение жизни человек спит 25 лет. 5 лет их них он видит сны. Сколько лет в течение жизни человек спит и не видит снов?»

3) Исправление ошибок в краткой записи задачи.

Соответствует ли данная схема задаче? Исправь ошибки в схеме, если они есть.

« В сосновом бору поселились 5 уссурийских тигров, их было на 2 меньше, чем в

кедровом лесу. Сколько тигров поселилось в кедровом лесу?»

4) Составление задачи по краткой записи (опорным словам, рисунку, схеме, чертежу, таблице).

Составь задачу по схеме.

5) Подбор к схеме подходящего текста из предложенных.

Подбери к схеме соответствующий текст задачи.

а) В конкурсе красоты приняли участие 5 бабочек махаонов, а бабочек адмиралов – на 4 больше. Сколько адмиралов участвовало в конкурсе?

б) В конкурсе красоты приняли участие 9 бабочек адмиралов, а махаонов на 4

меньше. Сколько махаонов участвовало в конкурсе?

в) В конкурсе красоты приняли участие 5 бабочек махаонов, а бабочек адмиралов на 4 больше. Сколько всего бабочек приняли участие в конкурсе?

г) В конкурсе красоты приняли участие 5 бабочек махаонов, это на 4 меньше,

чем бабочек адмиралов. Сколько адмиралов приняло участие в конкурсе?

д) В конкурсе красоты приняли участие 5 бабочек махаонов и 9 бабочек адмиралов. На сколько больше адмиралов приняли участие в конкурсе?

6 ) Установление взаимноодназначного соответствия – проведение

«дорожек» от слова к его изображению на схеме.

Объясни данную схематическую модель в соответствии с текстом задачи.

«В с о б а чь ю ш к о л у х о д ят 1 0 н е м е ц к их о в ча р о к и 4 шотл а ндск и х о в чар к и. На сколько больше немецких овчарок ходит в собачью школу?»

I I I

ЭТАП

ПОИСК И СОСТАВЛЕНИЕ ПЛАНА РЕШЕНИЯ ЗАДАЧИ

Самым важным на этом этапе является формирование умения рассуждать тем или иным способом. Поиск плана решения задачи можно проводить двумя путями:

• аналитическим способом, рассуждая от вопроса к данным ( «Чтобы ответить

на вопрос задачи, надо знать … и … );

• синтетическим, рассуждая от данных к вопросу.(«Мне известно … и …. По этим данным я могу узнать… и …).

Возможно использование их комбинации – аналитико-синтетического способа.

Чаще всего применяется аналитический способ рассуждения, но с точки зрения психологии в 1-2 классе ребёнку легче освоить синтетический способ разбора, так как в возрасте 6-8 лет формирование у ребёнка способности к синтезу несколько опережает формирование способности к анализу. На своих

уроках я стараюсь использовать и аналитический, и синтетический способы разбора. Поиск и составление плана решения учащимися начинается с самостоятельного обдумывания, обсуждения в парах, группах, составления цепочек рассуждений.

1) Разбор от вопроса к данным ( аналитический способ)

Поиск плана решения данным способом начинается с вопроса задачи. Выясняется, что нужно узнать, чтобы ответить на вопрос задачи. Для этого необходимо найти какую-то величину. А что нужно знать, чтобы её найти? и т. д.

Чтобы помочь учащимся вести рассуждения аналитическим способом, можно использовать приём « ДЕРЕВО РАССУЖДЕНИЙ». Суть его заключается в том, что по ходу рассуждений строится схема, которая помогает учащимся увидеть, какие простые задачи следует выделить (если это задача

составная), и каким будет план решения данной задачи.

• « В зоопарке было 2 зебры. Привезли ещё несколько зебр. Сколько зебр привезли, если их стало в зоопарке 7 ?»

• На какой вопрос нужно ответить?
• На какой вопрос нужно ответить?

• Что нужно знать, чтобы ответить на вопрос задачи? (нужно знать, сколько зебр было и сколько зебр стало).
• Что нужно знать, чтобы ответить на вопрос задачи? (нужно знать, сколько зебр было и сколько зебр стало).

• Известно ли в задаче, сколько зебр было? ( известно: было 2 зебры).
• Известно ли, сколько зебр стало? (известно: стало 7 зебр).
• Как узнать, сколько привезли зебр? На сколько больше стало зебр? ( на 5)
• Значит, сколько привезли зебр? (5)
• Каким действием решим задачу, почему?

?

бы л о ста л о 7 5

• «В зоопарке 5 обезьян, слонов на 3 меньше, а бизонов столько, сколько

слонов и обезьян вместе. Сколько бизонов в зоопарке?»

• На какой вопрос нужно ответить? Что сказано о бизонах в тексте задачи?
• На какой вопрос нужно ответить?
• Что сказано о бизонах в тексте задачи?

• Что нужно знать, чтобы ответить на вопрос задачи? ( сколько обезьян и слонов вместе) Можем ли мы узнать, сколько обезьян и слонов вместе? (нет, не знаем, сколько слонов).
• Что нужно знать, чтобы ответить на вопрос задачи? ( сколько обезьян и слонов вместе)
• Можем ли мы узнать, сколько обезьян и слонов вместе? (нет, не знаем, сколько слонов).

• Что сказано в тексте о слонах? ( слонов на 3 меньше, чем обезьян). Что

значит на 3 меньше?

• Как узнать, сколько слонов? Почему выбрали действие вычитания?

– Т епе р ь , можем от в етить на в о про с зада чи ? Ка к им д ейств и е м ? П о ч ему выбрали действие сложения?

?

обез ьян ы с л о н ы 5 + ?

обезьяны – 3

– Какие простые задачи можно выделить в данной составной?

«ДЕРЕВО РАССУЖДЕНИЙ» ОТ ВОПРОСА К ДАННЫМ

?

?

знаю не знаю

?

знаю не знаю

знаю знаю

Можно оформить рассуждения в таблице. Учитель выдаёт заготовки таблицы, в которые учащиеся записывают свои рассуждения. Такую работу целесообразно периодически проводить в 3, 4 классе.

Чтобы узнать

Надо знать

сколько обезьян (5)

сколько бизонов

сколько слонов (?)

сколько слонов

сколько обезьян (5)

на с к о ль к о сло н ов меньше, чем обезьян

(на 3)

2. Разбор

от данных к вопросу

(синтетический)

Синтетический способ характеризуется тем, что основным, направляющим вопросом при поиске плана решения задачи является вопрос о том, что можно найти по двум или нескольким известным в задаче числовым значениям (данным). По вновь полученным числовым данным и другим известным в задаче данным вновь ищется ответ на вопрос, что можно узнать по этим значениям. И так до ответа на вопрос задачи. Суть этого способа состоит в выделении учащимися простой задачи из составной и решении её.

« В зоопарке было 2 зебры. Привезли ещё несколько зебр. Сколько зебр привезли, если их стало 9».

• Что известно в задаче? ( сколько было зебр и сколько стало).
• Что можно узнать по этим данным? ( на сколько больше стало зебр)
• Как узнать, на сколько больше стало зебр? ( от 9 нужно отнять 2)
• Почему зебр стало больше? (привезли несколько зебр)
• Сколько зебр привезли?

2 9

было стало

привезли

?

«В зоопарке 5 обезьян, слонов на 3 меньше, чем обезьян, а бизонов столько, сколько обезьян и слонов вместе. Сколько бизонов в зоопарке?»

• Что известно в задаче? ( сколько обезьян;, на сколько слонов меньше, чем обезьян).

• Что можно узнать по этим данным? (сколько слонов). Какую задачу можно составить и решить?

• Как узнать, сколько слонов? ( от 5 отнять 3).
• Почему выбрали действие вычитания?
• Какие данные имеем теперь? (знаем, сколько обезьян и сколько слонов).

• Что можно узнать по этим данным? (сколько обезьян и слонов вместе). Какую задачу можно составить по этим данным?

• Как узнать, сколько слонов и обезьян вместе, каким действием? Почему сложением?

• Что сказано о бизонах? Сколько бизонов в зоопарке?

5 3

5 ? слонов

?

всего

Можно использовать таблицу.

Зная

сколько обезьян (5)

Узнаем

на с к о ль к о сло н ов меньше, чем обезьян (3)

сколько обезьян

сколько слонов ( -)

сколько слонов

сколько слонов и обезьян вместе ( +)

сколько бизонов

«ДЕРЕВО РАССУЖДЕНИЙ» ОТ ДАННЫХ К ВОПРОСУ

знаю знаю

?

м о г у з н аю узнать

?

могу уз н а т ь

Для формирования умения выделять простые задачи из составной, вести рассуждения от данных можно использовать следующие упражнения:

• Составь и реши простые задачи, используя эти данные.

« С одной пасеки собрали 12 кг мёда, а с другой 9 кг. Весь мёд разлили в бидоне по 7 кг в каждый»

• Поставь вопрос к данному условию. Выбери только те простые задачи, которые помогут ответить на главный вопрос.

«В школьный буфет привезли 5 ящиков яблок по 10 кг в каждом, и 4 ящика апельсинов, по 8 кг в каждом»

а) В школьный буфет привезли 5 ящиков яблок и 4 ящика апельсинов. Сколько всего ящиков фруктов привезли в буфет?

б) В школьный буфет привезли 5 ящиков яблок по 10 кг в каждом.. Сколько

кг яблок привезли?

в) В школьный буфет привезли 4 ящика апельсинов по 8 кг в каждом.

Сколько кг апельсинов привезли?

г) В школьн ы й б уфет п р и в ез л и 5 я щи к ов я б л ок и 4 я щ и ка ап е льси н о в . Н а сколько больше привезли ящиков с яблоками, чем ящиков с апельсинами?

д) В каждом ящике с яблоками 10 кг, а в ящике с апельсинами 8 кг. На

сколько

больше в каждом ящике кг яблок, чем апельсинов?

Материалом для таких упражнений могут служить любые составные задачи, представленные в учебнике, если использовать только условия этих задач.

3) Использование аналогии при поиске плана решения

В основе этого способа лежит сравнение задач, при котором выявляется полное или частичное сходство отношений между данными величинами в условии ранее решённой задачи и вновь предложенной и высказывается предположение, что для решения новой задачи можно воспользоваться планом ранее решённой задачи.

1) «Два мальчика выбежали одновременно навстречу друг другу по спортивной дорожке, длина которой 100 м. Они встретились через 10 с. Первый

мальчик бежал со скоростью 4 м /с. С какой скоростью бежал второй

мальчик?

План решения задачи:

І способ.

• Найти путь, который пробежал первый мальчик до встречи.

• Найти путь, который пробежал второй мальчик до встречи.

• Найти скорость, с которой бежал второй мальчик. II способ.

• Найти скорость сближения.
• Найти скорость, с которой бежал второй мальчик до встречи.

2) «Из города к зимовке, расстояние между которыми 150 км, выехали аэросани со скоростью 60 км /ч. В это же время навстречу им из зимовки

с ко рос т ь

вышел лыжник и встретил аэросани через 2 часа. Найти лыжника»

Сходства: 1. Движение двух предметов навстречу друг другу;

• Одновременное начало движения;

• Известно расстояние между пунктами, скорость одного и время до встречи;

• Требуется найти скорость второго предмета.

ВЫВОД: Можно использовать план решения первой задачи.

4) Поиск плана решения по модели

В некоторых случаях графическая модель подсказывает план задачи.

п р е дме т а

решения

« С одного поля собрали 370 т зерна, а с другого – в два раза больше.

Сколько тонн зерна собрали с двух полей?»

Данная модель показывает, для того, чтобы узнать общее количество зерна, нужно взять 3 раза по 370 тонн.

Решение задачи: 370 * 3 = 1110 (т)

5) Поиск плана решения путём составления уравнения

«С первого участка собрали 98 кг картофеля, со второго – 104 кг. Сколько кг картофеля собрали с третьего участка, если всего собрали 270 кг картофеля?»

• Что требуется узнать в задаче?

х кг – собрали картофеля с третьего участка

• Какие числовые данные известны в задаче? 98 кг – собрали с первого участка

104 кг – собрали со второго участка

270 кг – собрали всего с трёх участков

Схема уравнения: I + ІІ + III = всего 98 + 104 + х = 270

202 + х = 270

х = 68

IV ЭТАП

ЗАПИСЬ РЕШЕНИЯ И ОТВЕТА

Запись решения и ответа может производиться различными способами:

• класс – выражением в одно действие или по действиям с пояснениями (составная задача);

• класс – по действиям с пояснениями или вопросами;

• класс – по действиями с пояснениями или вопросами, а также в виде числового или буквенного выражения;

• класс – все способы + уравнением.

Мои ученики, начиная с 3-го класса, решают каждую задачу по действиям с пояснениями или вопросами и обязательно составляют выражение. Таким образом, формирование умения записывать решение задачи с помощью выражения является более эффективным.

V ЭТАП

ПРОВЕРКА РЕШЕНИЯ

Этот этап играет большую роль в развитии самоконтроля, формировании умения рассуждать, внимательно относиться к анализу задачи, активизирует познавательную деятельность. Зачастую, учащиеся получают ответ, который не может получиться с точки зрения здравого смысла. Но, если они не научены решение проверять, но такой результат их не удивляет.

После анализа задачи и составления плана решения, мы выполняем

прикидку ответа, то есть устанавливаем границы значений искомого с точки зрения здравого смысла.

После того, как задача решена, можно составить обратные задачи или

решить задачу другими способами, если это возможно, и сравнить полученные результаты.

Мой любимый приём – «подстановка данных», в текст задачи вставляются

полученные числа и устанавливается соответствие между ними и данными числами.

Для проверки решения задач используются следующие приёмы:

• Прикидка ответа или установление границ значений искомого с точки зрения здравого смысла (до решения).

В зоопарке было 2 зебры. Привезли ещё несколько зебр. Сколько зебр привезли, если их стало в зоопарке 7?»

• Если в зоопарке было 2 зебры, а стало 7 зебр, может получиться в ответе число большее 7? Обоснуйте свой ответ.
• Если в зоопарке было 2 зебры, а стало 7 зебр, может получиться в ответе число большее 7? Обоснуйте свой ответ.

• Установление соответствия между числами, полученными в результате решения задачи, и числами, данными в условии (приём подстановки).

В зоопарке было 2 зебры. Привезли ещё несколько зебр. Сколько зебр привезли, если их стало в зоопарке 7?»

7 – 2 = 5 (з.)

• Было 2 зебры, привезли 5 зебр. Стало 7 зебр. 2 + 5 = 7 (з.)
• Было 2 зебры, привезли 5 зебр. Стало 7 зебр. 2 + 5 = 7 (з.)

• Сравните число, полученное при проверке с данным в задаче.
• Сравните число, полученное при проверке с данным в задаче.

При проверке простой задачи этот способ совпадает со способом составления и решения обратной задачи. В 1 классе (1-4) используется данный способ, понятие «обратная задача» не вводится.

• Составление и решение обратных задач.

Этот способ вводится во 2 классе (1-4).

Составить обратную задачу – это значит преобразовать данную задачу так, чтобы искомое данной задачи стало данным числом, а одно из данных чисел – искомым.

Например:

« Портниха купила 10 м ткани на костюм и платье. На платье она израсходовала 2м. Сколько метров ткани пошло на костюм, если у неё осталось 3 м?»

Обратные задачи:

• «Портниха купила 10 м ткани на костюм и платье. На костюм она израсходовала 5 м. Сколько метров ткани пошло на платье, если у неё осталось 3 м?»

• «Портниха купила 10 м ткани на костюм и платье. Сколько метров

ткани у неё осталось, если на костюм она израсходовала 5 м ткани, а на платье 2 м?»

• «Портниха израсходовала на костюм 5 м ткани и на платье2 м

ткани. Сколько метров ткани купила портниха, если у неё осталось 3 м?»

• Решение задачи другим способом (если это возможно в составной задаче).

Сравнение полученных результатов при решении задачи разными

способами.

Например:

«На велогонках стартовало 70 спортсменов. На первом этапе с трассы сошли 4 велосипедиста, на втором -6. Сколько спортсменов пришло к финишу?»

I способ.

• 70 – 4 = 66 (с.)- осталось после первого этапа 2. 66 – 6 = 60 (с.)
• 70 – 4 = 66 (с.)- осталось после первого этапа 2. 66 – 6 = 60 (с.)

II способ.

1. 4 + 6 = 10 (с) – сошли с трассы на первом и втором этапах 2. 70 – 10 = 60 (с.)

VI ЭТАП

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА НАД ЗАДАЧЕЙ

На мой взгляд, этот этап является очень важным и интересным, хотя зачастую он опускается. Именно работа над задачей на данном этапе способствует развитию творческой активности и мышления учащихся, повышает интерес к математике, к решению задач, позволяет целенаправленнее формировать компоненты общего умения решать задачи.

Приёмы работы над задачей на данном этапе:

Эти приёмы также способствуют развитию умения производить анализ задачи, устанавливать взаимосвязи между величинами, осознанно выбирать действие при решении задач.

1) Решение задачи другим способом (если это возможно), сравнение разных способов решения;

«Длина пришкольного участка прямоугольной формы 120 м, а ширина 85 м.

3 часть площади занята цветами, а остальная часть – овощами и ягодами.

Чему равна площадь участка, занятая овощами и ягодами?»

1 способ

1) 120 * 85 = 10200 (кв.м ) – S участка

2) 10200 : 3 = 3400 (кв.м ) – занято цветами 3) 10200 – 3400 = 6800 (кв.м )

2 способ

1) 120 * 85 = 10200 (кв.м) – S участка

• 120 : 3 = 40 (м) – длина участка, занятого цветами

• 40 * 85 = 3400 (кв.м) – Sучастка, занятого цветами 4) 10200 – 3400 = 6800 (кв.м )

3 способ

• 120 : 3 = 40 (м) – длина участка, занятого цветами

• 120 – 40 = 80 (м) – длина участка, занятого овощами и ягодами 3) 85 * 80 = 6800 (кв. м)

4 способ

• 120 : 3 = 40 (м) – длина участка, занятого цветами

• 40 * 85 = 3400 (кв. м) – S участка, занятого цветами 3) 3400 * 2 = 6800 (кв. м)

5 способ

1) 120 * 85 = 10200 (кв.м) – S участка

2) 10200 : 3 = 3400 (кв.м) – S участка, занятого цветами 3) 3400 * 2 = 6800 (кв. м)

6 способ

• 120 : 3 = 40 (м) – длина участк5а, занятого цветами

• 40 * 2 = длина участка, занятого овощами и ягодами 3) 80 * 85 = 6800 (кв. м)

• Составление аналогичной задачи с новыми данными.

Этот приём помогает детям переносить известную схему решения на другие задачи этого вида, учит обобщать их в группы.

• Постановка дополнительных вопросов к решённой задаче.

Этот приём предполагает постановку дополнительных вопросов, замену известных величин неизвестными, поиск новых решений.

«Два лыжника вышли одновременно навстречу друг другу из двух пунктов,

расстояние между которыми 66 км. Скорость первого -12 км/ч, второго – 10 км/ч. Через какое время они встретятся?»

Что ещё можно узнать по имеющимся в тексте задачи и полученным данным? ( На сколько скорость первого лыжника больше скорости второго

лыжника? Сколько км прошёл до встречи первый лыжник? Сколько км прошёл

до встречи второй лыжник? На сколько км больше прошёл до встречи первый лыжник? На каком расстоянии друг от друга будут лыжники через 1 час после встречи, через 2 часа после встречи? и т. д. )

4) Изменение вопроса задачи.

• Измени вопрос так, чтобы задача решалась в одно действие, в два действия.
• Измени вопрос так, чтобы задача решалась вычитанием (делением, …).

Этот приём позволяет решить несколько задач по одному и тому же условию (при решении составных задач), тем самым экономя время, которое тратится на осмысление условия.

Например:

«В первый день улитка проползла 5 м, во второй на 2 м больше. Сколько метров проползла улитка во второй день?»

Измени вопрос задачи так, чтобы задача решалась в два действия.

• И з м е н ен и е у с ло в и я з ад а чи та к , ч т о бы з а д ача ре ш а л ась друг и м действием.

• Изменение числовых данных задачи так, чтобы появился новый способ

решения.

• Исследование решения.

Сколько способов решения имеет задача? При каких условиях она не имела бы решения? Какие приёмы целесообразны для поиска решения задачи?

• Сравнение задач и их решения. Этот приём позволяет глубже осознать

взаимосвязи между величинами, входящими в задачу, способствует лучшему усвоению идеи решения, формированию осознанного подхода к анализу задачи, выбору действий. Дети определяют, что одно и то же слово, один и тот же вопрос не определяют выбор действия и, что для этого нужно установить связи между величинами и на их основе выбрать, а затем выполнить действие.

Сравнение задач вырабатывает у учащихся привычку не начинать поиск решения задачи без глубокого, полного анализа задачи.

Кроме основного вида работы над задачей – её решения, можно использовать и другие виды работы, не включающие явное и полное решение задач , но способствующие формированию комплекса умений,

необходимых для плодотворного решения задач, развитию мышления, творческой активности, познавательного интереса.

ДОПОЛНИТЕЛЬНЫЕ ВИДЫ РАБОТЫ НАД ЗАДАЧЕЙ

• Блиц-турниры (в большом количестве представлены в учебниках Л. Г. Петерсон).

Блиц-турнир предполагает устное решение простых и составных задач с числами и с переменными (обобщённый вариант) за определённый отрезок времени, запись только решения задачи.

• Составление выражений, необходимых для решения задач с неопределёнными

данными.

« От двух пристаней, находящихся на расстоянии км, отплыли Одновременно навстречу друг другу катер и моторная лодка. Встреча произошла через часов. Катер шёл со скоростью км/ч. С какой скоростью шла моторная лодка?»

1 способ.

1)

• – расстояние, пройденное катером

2 )

– ∙ – расстояние, пройденное моторной лодкой

3 ) ( –

• ) : – скорость моторной лодки

2 способ.

• : – скорость сближения

• : – – скорость моторной лодки

• Составление устного плана решения ( «Дерево рассуждений») и его объяснение без последующих вычислений.

• Разъяснение готового плана решения задачи (вопросы, «Дерево

рассуждений»)

• Пояснение готовых способов решения задачи.

«Длина пришкольного участка прямоугольной формы 120 м, а ширина 85 м. 3 часть площади занята цветами, а остальная часть – овощами и ягодами. Чему равна площадь участка, занятая овощами и ягодами?»

1 способ:

4 способ:

1) 120 * 85 = 10200 (кв.м ) – ……

1) 120 : 3 = 40 (м) – …….

2) 40 * 86 = 3400 (кв.м ) – ……..

2) 10200 : 3 = 3400 (кв.м ) – …….

3) 3400 * 2 = 6800 (кв.м ) – ……..

3) 10200 – 3400 = 6800 (кв.м ) – …….

2 способ:

5 способ:

1) 120 * 85 = 10200 (кв.м ) -……

1) 120 * 85 = 10200 (кв.м ) – ……..

2) 10200 : 3 = 3400 (кв.м ) -…….

2) 120 : 3 = 40 (м) – ……….

3) 3400 * 2 = 6800 (кв.м ) – ………

3) 40 * 85 = 3400 (кв.м )- ………

4) 10200 – 3400 = 6800 (кв.м ) – ………

3 способ:

6 способ:

1) 120 : 3 = 40 (м) – ………

1) 120 : 3 = 40 (м) – ……..

2) 120 – 40 = 80 (м) – …….

2) 40 * 2 = 80 (м) – ……..

3) 85 * 80 = 6800 (кв.м ) – ……

3) 80 * 85 = 6800 (кв.м ) – ……..

• Составление решения задачи разными способами в соответствии с данными пояснениями.

« От двух пристаней, находящихся на расстоянии 510 км, отплыли

Одновременно навстречу друг другу катер и моторная лодка. Встреча произошла через 15 часов. Катер шёл со скоростью 19 км/ч. С какой скоростью шла моторная лодка?»

1способ.

• ………… . – прошёл катер до встречи
• ………… . – прошёл катер до встречи

• ………………… – проплыла моторная лодка до встречи
• ………………… – проплыла моторная лодка до встречи

• ………………… – скорость моторной лодки
• ………………… – скорость моторной лодки

2 способ.

• ………………… . – скорость сближения
• ………………… ..- скорость моторной лодки

7) Соотнесение пояснения с решением.

Усложнённый вариант – соотнесение групп пояснений с разными способами решений.

«Длина пришкольного участка прямоугольной формы 120 м, а ширина 85 м. 3 часть площади занята цветами, а остальная часть – овощами и ягодами. Чему равна площадь участка, занятая овощами и ягодами?»

1) 120 * 85 = 10200 (кв.м )

длина участка, занятого цветами площадь участка с цветами

площадь участка, занятого овощами и ягодами

2) 120 : 3 = 40 (м)

длина участка с цветами

3) 40 * 85 = 3400 (кв.м )

4) 10200 – 3400 = 6800 (кв.м )

8) Установление соответствия между содержанием задачи и её краткой записью (в виде чертежа, рисунка, таблицы и т. д.) и, наоборот, между краткой записью и содержанием.

• Соответствует ли схематический рисунок (чертёж, таблица,…) данной задаче? Обоснуйте свой ответ.

• Как нужно изменить рисунок (чертёж, таблицу,…), чтобы он

соответствовал данной задаче?

• Выбор среди нескольких схематических моделей (чертежей, таблиц, ….) той, которая соответствует данной задаче.

• Выбор равенства, являющегося решением задачи. Обоснование

выбора.

«В двух гнёздах скворцов 11 птенцов. Из одного гнезда уже вылетело 6 скворцов, из другого 4. Скольким скворчатам ещё предстоит вылететь?»

2) 11 + (6+4)= 21(ск.)

1) 11 – 6 – 4 = 1 (ск.)

4) 11 – (6+ 4)= 1 (ск.)

3) (11 – 6) + 4 =9 (ск.)

• Изменение текста задачи в соответствии с данным решением.
• Нахождение ложного способа решения.

«Нужно покрасить 150 рам. Один маляр может это сделать за 15 дней. Другой – за 10 дней. За сколько дней выполнят эту работу оба маляра, если будут работать вместе?»

1 способ

2 способ

1. 15 + 10 = 25 (д.)

1. 150 : 15 = 10 (р.)

2. 150 : 10 = 15 (р.)

2. 150 : 25 = 6 (д.)

3. 10 + 15 = 25 (р.)

4. 150 : 25 = 6 (д.)

• Продолжение решения задачи.

«Заяц за 3 прыжка преодолел расстояние в 13 м. Первый прыжок составил 3 м, второй 5 м. Сколько метров преодолел заяц в третьем прыжке?»

1. 3 + 5 = 8(м) -……..

2.

• Объяснение выражений, составленных по данному условию.

Например:

– О преде л и с м ыс л с о с та вленн ы х п о за д а ч е м а т е м а т и че с к их в ы р а же н и й, запиши пояснения

к каждому выражению.

– Выбери выражение, являющееся решением задачи.

«В вагоне поезда было 35 пассажиров. На станции вышли 7 пассажиров, а вошли 6.»

35 – 7

7 + 6

35 – ( 7+ 6)

35 + 6

7 – 6

35 – 7 + 6

• Составление выражений по вопросам к данному условию.

Запиши выражением ответ на каждый вопрос:

«На турбазе 8 маленьких палаток и 5 больших. Маленькие палатки вмещают 4 человека, а большие – 10. Сколько человек может разместиться во всех этих палатках?»

Сколько всего человек вмещают маленькие палатки?

Сколько всего больших и маленьких палаток на турбазе? На сколько больших палаток …, чем маленьких? Сколько человек вмещает маленькая палатка? Сколько всего человек вместят большие палатки? На сколько больше человек вмещают большие палатки, чем маленькие? Сколько всего человек вместят одна большая и маленькая палатки?

Одной из главных причин, по которым школьники неверно решают ту

или иную задачу, является неспособность глубоко, осмысленно, внимательно проанализировать то, что дано в задаче(данные) и то, что нужно узнать(вопрос), и взаимосвязи между ними. Учитель при этом постоянно напоминает детям: «Внимательно читайте условие и вопрос». Но ошибки продолжают существовать. Данный приём направлен на формирование у учащихся умения более глубоко, осмысленно подходить к анализу задачи, чётко выделять известные и неизвестные величины. При составлении вопросов используются вопросы с «подвохом» (неверно сформулированные). Для того, чтобы это заметить, учащимся нужно глубоко проанализировать взаимосвязи между данными задачи. Также используются вопросы, для ответа на которые не требуется составления выражения, так как нужно узнать то, что изначально известно

• Составление и определение смысла всевозможных выражений ( в том числе и не имеющих смысла в рамках данной задачи) из чисел, данных в условии задачи.

Этот приём трудоёмкий, но очень полезный. При его использовании учащиеся учатся глубокому анализу числовых данных задачи, взаимосвязей между ними.

• Составь как можно больше числовых выражений с данными задачи,
• Составь как можно больше числовых выражений с данными задачи,

объясни их смысл ;

• Из числовых данных задачи и значений ранее составленных выражений составь другие выражения и объясни их смысл;
• Из числовых данных задачи и значений ранее составленных выражений составь другие выражения и объясни их смысл;

• Выбери те выражения, значения которых помогают ответить на
• Выбери те выражения, значения которых помогают ответить на

вопрос задачи;

• Выпиши в отдельные столбцы выражения, которые имеют смысл и, которые смысла не имеют.
• Выпиши в отдельные столбцы выражения, которые имеют смысл и, которые смысла не имеют.

Например:

«На турбазе 8 маленьких палаток и 5 больших. Маленькие палатки вмещают 4 человека, а большие – 10. Сколько человек может разместиться во всех этих палатках?»

8 – 5 – на столько больше маленьких палаток, чем больших 8 + 5 – больших и маленьких палаток

8 * 5 – не имеет смысла

8 : 5 – не имеет смысла

4 + 10 – всего человек вмещает 1 большая и 1 маленькая палатка

10 – 4 – на столько человек больше вмещает большая палатка, чем маленькая

10 * 4 – не имеет смысла

10 : 4 – не имеет смысла 8 : 4 – не имеет смысла 8 + 4 – не имеет смысла 8 – 4 – не имеет смысла

8 * 4 – всего человек в маленьких палатках 4 * 8 – не имеет смысла

10 – 5 – не имеет смысла

10 + 5 – не имеет смысл 10 : 5 – не имеет смысла

10 * 5 – всего человек в больших палатках

5 * 10 – не имеет смысла

8 – 5 + 8 – не имеет смысла

8 – 5 + 5 – не имеет смысла

(8 – 5) + (8+ 5) – не имеет смысла

(8 – 5)+ (10 – 4) – не имеет смысла

( 8 * 4)+ (10 * 5)- всего человек в палатках

• Составление задач: – по иллюстрации;

– по краткой записи (рисунку, чертежу, таблице, опорным

словам);

• по данной записи решения;
• по данной записи решения;

• по пр е д л ож е н но й п ро г ра мм е де й ств и й, по
• по пр е д л ож е н но й п ро г ра мм е де й ств и й, по

«Дереву расс у ж д ен ий» ;

• по некоторым исходным данным: с числовыми данными 20,
• по некоторым исходным данным: с числовыми данными 20,

25, 3;

• с определёнными условиями: в 3 действия, в ответе – 120 кг; со
• с определёнными условиями: в 3 действия, в ответе – 120 кг; со

словами «больше на…» и т. д.

Для более эффективного обучения учащихся решать задачи, я использую в своей работе справочник «Учимся решать задачи» (20 памяток), составленный мною. Некоторые памятки представлены ниже.

СТРАНИЦЫ СПРАВОЧНИКА

ВАРИАНТ ПРОВЕДЕНИЯ УРОКА

ПО ОБУЧЕНИЮ УЧАЩИХСЯ РЕШЕНИЮ ЗАДАЧ

Те м а: Р Е Ш ЕНИЕ ЗА ДА Ч НА УВЕЛИЧЕ Н ИЕ И Л И УМ Е Н Ь Ш Е Н ИЕ ЧИСЛА НА НЕСКОЛЬКО ЕДИНИЦ ИЛИ В НЕСКОЛЬКО РАЗ (в

косвенной форме ) .

Первый урок по теме

Цель: научить учащихся решать задачи на увеличение или уменьшение числа на несколько единиц или в несколько раз в косвенной форме путём выполнения семантического анализа, осмысления отношений между искомым и данными, явно не отражённых в тексте задачи.

Задачи: 1) учить учащихся устанавливать взаимосвязи между условием (данными) и вопросом (искомыми) в задаче;

• совершенствовать умение составлять различные виды краткой записи (опорные слова, чертёж);
• формировать умение логически рассуждать и делать обоснованные умозаключения при выяснении хода решения задачи, используя синтетический и аналитический способы рассуждения;

• формировать умение обоснованно выбирать арифметические действия;

• развивать логическое мышление;

• производить вычисления с именованными числами, переводить одни единицы измерения в другие.

• развивать любознательность и познавательные интересы учащихся.

Раздаточный материал:

– таблица с названиями животных и величинами: длина, масса;

• карточка с задачами для блиц – турнира;
• картинки с изображениями животных;

План урока.

• П од г о т о вител ьны й этап . Выз о в име ю щ и х с я у учащ и хся з на н ий, необходимых для усвоения темы.
• Ознакомление с новым видом задач на увеличение и уменьшение числа на

несколько единиц или в несколько раз в косвенной форме.

• Первичное закрепление.

• Решение простой задачи на уменьшение числа в несколько раз в косвенной форме.
• Решение простой задачи на уменьшение числа в несколько раз в косвенной форме.

• Составление и решение составной задачи, включающей простую задачу
• Составление и решение составной задачи, включающей простую задачу

изученного вида.

• Обобщение.
• Домашнее задание.

Ход урока:

В ы з о в им е ю щ и хся з н а ни й уча щ и хся,

1. Под г о т о в и т е л ь ны й э т а п .

необходимых для усвоения темы ( понятие «задача», этапы работы над зад а чей, о т н о ш ен и я « б о л ь ш е » , « м е н ь ш е », « к о р о че » , «дли н н е е »,

«тяжелее», «легче», выбор арифметического действия при решении

задач на увеличение или уменьшение числа на несколько единиц или в несколько раз).

• Закрепление знаний учащихся об отношениях «короче», «длиннее»,
• Закрепление знаний учащихся об отношениях «короче», «длиннее»,

«тяжелее», «легче».

• Давайте познакомимся с животными, изображёнными на картинках. Кто готов правильно назвать этих животных.
• Давайте познакомимся с животными, изображёнными на картинках. Кто готов правильно назвать этих животных.
• Давайте познакомимся с животными, изображёнными на картинках. Кто готов правильно назвать этих животных.

На доске: картинки с изображениями моржа, лемминга, кита,

белого медведя, тюленя.

• Кто из них заблудился? Почему вы так думаете? Обоснуйте свою точку зрения.
• Кто из них заблудился? Почему вы так думаете? Обоснуйте свою точку зрения.
• Кто из них заблудился? Почему вы так думаете? Обоснуйте свою точку зрения.

• Сегодня нам предстоит узнать новую информацию об обитателях
• Сегодня нам предстоит узнать новую информацию об обитателях
• Сегодня нам предстоит узнать новую информацию об обитателях

Арктики и заполнить таблицу. Как вы думаете, кто из них самый тяжёлый?

• Попробуйте расположить этих животных в порядке возрастания по массе. Назовите животное, которое тяжелее медведя, но легче кита (морж). Если морж тяжелее медведя, что можно сказать о массе медведя
• Попробуйте расположить этих животных в порядке возрастания по массе. Назовите животное, которое тяжелее медведя, но легче кита (морж). Если морж тяжелее медведя, что можно сказать о массе медведя
• Попробуйте расположить этих животных в порядке возрастания по массе.
• Назовите животное, которое тяжелее медведя, но легче кита (морж).
• Если морж тяжелее медведя, что можно сказать о массе медведя

(он легче моржа).

• Если морж легче кита, что можно сказать о массе кита по отношению к массе медведя? ( кит тяжелее моржа)
• Если морж легче кита, что можно сказать о массе кита по отношению к массе медведя? ( кит тяжелее моржа)
• Если морж легче кита, что можно сказать о массе кита по отношению к массе медведя? ( кит тяжелее моржа)

• А кто из данных животных самый длинный? Расположите их по длине в
• А кто из данных животных самый длинный? Расположите их по длине в
• А кто из данных животных самый длинный? Расположите их по длине в

порядке убывания.

• Если медведь длиннее тюленя, что можно сказать о длине тюленя по отношению к длине медведя? (тюлень короче медведя)
• Если медведь длиннее тюленя, что можно сказать о длине тюленя по отношению к длине медведя? (тюлень короче медведя)
• Если медведь длиннее тюленя, что можно сказать о длине тюленя по отношению к длине медведя? (тюлень короче медведя)

• Положите перед собой таблицу № 1. С какими величинами нам предстоит
• Положите перед собой таблицу № 1. С какими величинами нам предстоит
• Положите перед собой таблицу № 1. С какими величинами нам предстоит

работать сегодня на уроке? (длина, масса)

• Верно, эти величины позволят нам реально представить обитателей ледяной зоны.
• Верно, эти величины позволят нам реально представить обитателей ледяной зоны.
• Верно, эти величины позволят нам реально представить обитателей ледяной зоны.

• Назовите единицы измерения длины, массы? С какими единицами будем
• Назовите единицы измерения длины, массы? С какими единицами будем
• Назовите единицы измерения длины, массы? С какими единицами будем

работать сегодня на уроке?

1.2 Формулировка темы и цели урока. Работа над простыми задачами на увеличение и уменьшение числа на несколько единиц и в несколько раз в прямой форме. Вызов знаний, связанных с понятием «задача» (этапы работы над задачей, виды задач).

– Возьмите карточку «Блиц – турнир». Сформулируйте задание, которое необходимо выполнить (нужно решить задачи)

На интерактивной доске:

А

Ч

А

Д

А

З

• Знаменитый математик Декарт сказал: « Жить – это значит ставить и решать задачи. Пока человек решает задачи, он живёт». Тема нашего сегодняшнего урока … ( Решение задач)
• Прочитайте тексты на карточке. Все ли тексты можно назвать задачами?

(3 и 4 тексты – не задачи, так как в них нет вопроса).

• Что необходимо сделать, чтобы эти тексты стали задачами?

( поставить вопрос)

• В чём особенность задач блиц – турнира? ( вместо чисел – буквы)
• Верно, в блиц – турнире даны задачи в обобщенном виде с переменными. В какой последовательности будете работать? (прочитать, поставить вопрос

( если нужно), выбрать арифметическое действие, записать решение ).

Время работы – 3 минуты.

• Самопроверка. Назовите выражение, которое является решением первой задачи.

Учащиеся предлагают свои варианты.

На интерактивной доске переворачивается карточка.

а +в

З

В

• Почему выбрали действие вычитания для решения задачи? Какие слова помогли выбрать действие? ( больше на….) .
• Что значит «больше на…» ? (нужно увеличить на несколько единиц, то есть прибавить).

На доске:

На … больше

Так же разбирается решение второй задачи блиц-турнира.

На интерактивной доске переворачивается карточка:

А

b – a

О

• Какой вопрос поставили к третьей задаче?
• Сверьте решение третьей задачи с соседом? У кого совпало решение?
• Назовите выражение, которое является решением третьей задачи.

Учащиеся предлагают свои варианты решения.

На доске переворачивается карточка:

Д

c ∙ d

П

• Какие слова помогли выбрать действие при решении задачи? (больше в…)
• Что значит “ больше в …”? ( это значит увеличить в несколько раз, то

есть умножить).

На интерактивной доске:

В …больше

Также разбирается решение третьей задачи. На доске переворачивается карточка:

c : d

А

О

На интерактивной доске :

в- a

а+в

с ∙d

d : c

О

Ч

П

А

В

О

На ….. больше

На ….. меньше

В ….. раз больше

В ….. раз меньше

• Что обозначают буквы на карточках? ( план решения задачи).

• Каких составляющих не хватает? (условие, решение) На интерактивной доске переворачивается карточ

У А Р

Ч

• Расставьте буквы в нужной последовательности. Перечислите этапы работы над задачей.

На доске У В О Р О П

• Что нужно знать и уметь, чтобы решить задачу?

• Чтобы верно решить задачу, нужно внимательно изучить условие задачи и проанализировать отношения между величинами, отражённые в этих задачах, а также явно не отражённые в ней. Учиться этому – основная цель нашего урока.

• Какие виды задач можно выделить? Можно использовать справочник

«Задачи».

на или числа на несколько единиц на ил и ч и сла

На ….. больше

На ….. меньше

В ….. раз больше

В ….. раз меньше

На доске:

в несколько раз

– С какими задачами будем работать на уроке?

2. Ознакомление с косвенной формой задач на увеличение или уменьшение числа на несколько единиц или в несколько раз. Создание проблемной ситуации.

• Прочитайте задачу № 1 блиц-турнира. Работаем с таблицей № 2. Вставьте в текст задачи значения переменных.
• Составьте краткую запись данной задачи . Какой вид краткой записи выберем?

Один ученик записывает краткую запись задачи на доске.

Т. – 3 м

М. – ? на 1 м 10 см б

• Как ещё можно выполнить модель задачи? (при помощи схематического чертеж

3 м

На доске: _1 м 10 см

?

• Как и м д е йст в ием ре ш им зад а ч у ? (сл о жением) . П о ч ем у ? За п и ш ите реше ни е задачи.
• Мы знаем, что морж длиннее тюленя. Что можно сказать о длине тюленя? (он короче моржа).

• На сколько длина моржа больше длины тюленя? ( на 1 м 10 см)
• На сколько длина тюленя будет меньше длины моржа? ( на 1 м 10 см)

• Мы выяснили, что длина тюленя на 1 м 10 см меньше длины моржа. Переформулируйте условие задачи так, чтобы вместо слов “ на …. больше” появились слова “ на …. меньше”. Факты изменять нельзя.

Учащиеся формулируют задачу: “Длина тюленя 3 м , это на 1 м 10 см меньше

длины моржа. Найти длину моржа».

• Сделайте прикидку результата. В ответе получится число, больше 3 или меньше? Почему?

• Каким действием будем решать задачу? Докажите свою точку зрения.

Мнения учащихся разделяются.

• Выполним чертёж к этой задаче.

• Прочитайте вопрос задачи. Если длина тюленя на 1 м 10 см меньше длины моржа, что можно сказать о длине моржа? Что значит на 1 м 10 см больше длины тюленя? Какое действие выбираем для решения?
• Можно ли при решении этой задачи ориентироваться на слова “ на меньше” при выборе действия?
• В этой задаче в отличие от первой отношение между величинами не отражено прямо, явно, оно отражено в косвенной форме. Сегодня мы знакомимся с задачами на увеличение и уменьшение числа в косвенной форме.

• Запишите решение этой задачи. Назовите длину моржа (4 м 10 см). Впишите в таблицу№ 1.

• С длиной каких предметов можно сравнить такую длину?

• Первичное закрепление.

• Решение простой задачи на уменьшение числа в несколько раз в косвенной форме.
• Решение простой задачи на уменьшение числа в несколько раз в косвенной форме.

• Прочитайте задачу № 3 блиц-турнира. Вставьте значения переменных из таблицы № 2.
• Е сли из в ест н о, ч т о масса м о ржа в 1 0 раз бо льш е м а с с ы т ю л еня, что м о ж н о сказать о массе тюленя? (масса тюленя в 10 раз меньше массы моржа).
• И зме н ите у словие т а к, ч т о б ы по л у ч и л ась за д ача в к о св е н н о й форм е . Запишите краткую запись и решение задачи.

Самостоятельная работа учащихся .

• Каким действием решили задачу? Почему выбрали деление, если сказано “ в 10 раз больше”? Можно ли опираться на данные слова при выборе действия?

• Какие графы в таблице мы не заполнили?
• Найдём массу кита и белого медведя. Как вы думаете, чья масса больше?

3.2 Составление и решение составной задачи, включающей простую задачу изученного вида.

• Работаем с таблицами № 1 и № 2. Что известно о массе кита? (она в 150 раз

больше массы медведя). Запишем кратко.

• Что известно о массе медведя? Что нужно знать, чтобы узнать массу медведя?

( надо знать массу моржа, так как масса моржа на 800 кг больше массы медведя)

Кит – ? в 150 раз б. Медведь – ? кг

Морж – 1800 кг, это на 800 кг б.

На доске краткая запись задачи:

• Что можно сказать о массе медведя по отношению к массе моржа?

• Что можем узнать по этим данным? На какие вопросы можем ответить, не выполняя арифметические действия?

• Сформулируйте главный вопрос задачи? Почему не может быть главным вопрос: какова масса медведя?

• Запишем схему решения задачи, размышляя от главного вопроса к данным.

Работа в группах. Одна из групп отвечает у доски.

• Что нужно знать, чтобы найти массу кита? (массу медведя).
• Зная массу медведя, можем ли ответить на главный вопрос задачи?

( масса кита в 150 раз больше, чем у медведя. Значит, чтобы найти массу кита, нужно массу медведя увеличить в 150 раз, то есть умножить на 150).

• Какие данные необходимы, чтобы найти массу медведя? (масса моржа).
• Что мы знаем о массе моржа? (масса моржа на 500 кг больше, чем у медведя).

• Что можем сказать о массе медведя по отношению к массе моржа? ( масса медведя на 500 кг меньше массы моржа)

• Известна ли масса моржа? (1800 кг)

• Каким действием узнаем, какова масса медведя? Почему вычитанием? На доске схема: ? масса кита

• 150

?

масса медведя

1800 – 800

масса моржа на … меньше

• Запишите решение задачи выражением.

Самостоятельная работа учащихся.

• Запишите полученные данные в таблице. Назовите их. ( масса кита 150000 кг, а масса медведя 1000 кг).

• Переведите кг в более крупные единицы измерения массы. С чем можно сравнить массу медведя? А массу кита?

• Пользуясь полученными данными в таблице № 1, попробуйте расположить животных по массе в порядке возрастания. Какое животное оказалось самым тяжёлым? А самым лёгким? Подтвердились ли ваши предположения, сделанные вначале урока?

4. Обобщение.

– С каким видом задач познакомились? В чём особенность данного вида задач? Какие умения необходимы для решения таких задач?

5. Домашнее задание.

• Какие строки таблицы остались пустыми? ( длина белого медведя и кита).

• Что известно о длине медведя из таблице № 2 ( на 60 см меньше длины моржа).

• Известна ли длина моржа? Можно найти длину медведя?

• Найдите данные в таблице, которые помогут найти длину кита (длина тюленя в 11 раз меньше, чем у кита).

• Известна ли длина тюленя? (3 м)
• Можем ли по этим данным найти длину кита?

• Дома вам предстоит составить задачи, пользуясь данными таблицы № 2 и узнать длину кита и медведя, а также выяснить, кто из них длиннее.

ПРИЛОЖЕНИЯ

Блиц – турнир.

• Длина тюленя a метров, а длина моржа на b

метров больше. Какова длина моржа?

• Длина моржа b метров, а длина белого медведя на a метров меньше. Какова длина медведя?

• Масса тюленя c кг, а масса моржа в d раз

больше.

• М ас с а ки т а c к г , а масс а т ю л еня в d р аз меньше.

Таблица № 1

Морж

Длина

Масса

Белый медведь

Кит

Тюлень

3 м

150 кг

Таблица № 2

Морж

Длина

Масса

? на 1 м 10 см больше, чем у тюленя

Белый медведь

Кит

? в 10 раз больше,

? н а 60 с м м ень ш е, чем у моржа

Тюлень

?

?

чем у тюленя

на 500 кг больше, чем у медведя

? в 150 раз больше, чем у медведя

3 м

150 кг

в 11 раз меньше, чем у кита

План урока:

Понятие «задача». Составные части задачи

Задачи на нахождение целого

Задачи на увеличение числа на несколько единиц

Задачи на нахождение части

Задачи на уменьшение числа на несколько единиц

Задачи на разностное сравнение

Привет! По пути на наше занятие я встретила свою очень хорошую подружку. Ее зовут Даша – следопыт.

Она очень любознательная и стремиться находить ответы на все вопросы, даже самые сложные. Ей стало очень интересно, чем мы будем заниматься на сегодняшнем уроке. Я рассказала Даше, что тема у нас довольно непростая, мы будем разбираться в типах задач, искать способы их решения.

Даша подумала, что это будет очень увлекательно и попросила разрешить ей поприсутствовать у нас на уроке. Конечно же, я с радостью согласилась. Итак, сегодня наше занятие мы проведем втроем.

Понятие «задача». Составные части задачи

Послушай, какую историю рассказала мне Даша. Ее друг бычок Борька попросил помочь и провести расследование.

Утром у него на столе в вазочке лежало 9 шоколадных конфет.

А когда бычок вернулся с прогулки, то увидел в вазочке всего 6 конфет.

Борька обратился к Даше с просьбой разобраться с исчезновением конфет и узнать, куда они делись.

Даша определила, что конфет стало меньше. Она задумалась, почему это могло случиться. Например, конфеты могли выпасть из вазочки. Но конфет ни на столе, ни под столом не оказалось.

Тогда Даша решила, что конфеты кто-то забрал. Она внимательно присмотрелась к друзьям бычка, которые собрались в комнате, и заметила, что у лисенка Жулика щеки испачканы шоколадом.

Даша все поняла и нашла правильный ответ: это лисенок съел конфеты. И Жулик сразу же в этом сознался, а затем попросил прощение за свой поступок. Все были очень рады, что проблема решилась.

Я тоже очень обрадовалась, ведь история Даши поможет объяснить новый материал на сегодняшнем уроке. Давай по порядку проанализируем последовательность расследования.

1. Бычок Борька рассказал, что произошло.
2. Он задал вопрос и попросил найти ответ.
3. Даша подумала, порассуждала и нашла правильное решение.
4. Она дала ответ на вопрос бычка.

Это же и есть порядок работы над задачей! Вот определение понятия задача – это проблемная ситуация, которую нужно решить путем логических рассуждений, математических вычислений. В результате решения задачи нужно найти правильный ответ на поставленный вопрос.

Вот составные части задачи.

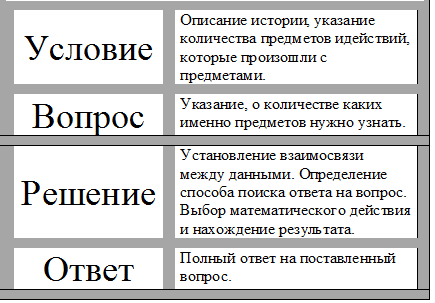
Давай мы Дашину историю превратим в задачу и решим ее.

Итак, приступим. Сначала разберемся с условием.Для математической задачи важно иметь необходимые числовые данные.

Чтобы лучше понять условие задачи, мы будем рисовать. Не обязательно рисовать именно конфеты. Можно их обозначить просто кружочками. Изобразим 9 кружочков–конфет.

Из этих конфет часть забрали и часть осталась. Мы знаем, что осталось 6 конфет. Отметим их.

Итак, мы проанализировали и изобразили условие нашей задачи. Идем дальше.

Теперь нам нужно определить вопрос задачи. Ее вопрос почти всегда включает слово «сколько».Даше нужно было узнать, куда исчезли конфеты. А мы узнаем, сколько исчезло конфет.

Для этого нам нужно определить количество конфет в той части, которую мы еще не выделили.

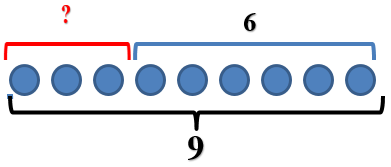
Пока все ясно? Тогда переходим к следующему этапу. Нам нужно понять, как найти решение задачи. Для этого давай подумаем. Нас интересуют конфеты в подмножестве, которое является частью множества из 9 конфет, лежавших в вазочке сначала. Мы с тобой выучили на прошлом уроке, что найти часть из целого можно с помощью действия вычитания. Осталось составить пример. Мы должны из общего количества конфет (число 9) вычесть количество конфет, которые остались (число 6). 9 минус 6 будет 3.

Ну вот, мы посчитали конфеты в подмножестве, которое забрали. Давай вспомним вопрос: «Сколько конфет исчезло?» Мы это только что установили, значит можно переходить к последнему этапу и дать ответ на вопрос.

Мы закончили работу над задачей.

1. Разобрались с ее условием.
2. Определили вопрос.
3. Подумали над решением.
4. И дали ответ.

Теперь ты сможешь решить любую задачу. Их очень много. Мы рассмотрим решение простых задач.

Задачи на нахождение целого

Вот наша первая задача. Ее составила для нас Даша.

У обезьянки Башмачок было 5 бананов. А Даша принесла ей еще 3 банана. 

Какой вопрос мы можем задать по условию этой задачи? Правильно, мы можем спросить, сколько всего бананов стало у обезьянки?

Итак, начнем работать. Сначала проанализируем первую составную часть задачи– условие.

О ком говорится в задаче? Правильно, об обезьянке. О том, что у нее было 5 бананов.

Что случилось потом? Верно, ей дали еще 3 банана. Запишем это в нашу таблицу

Теперь обозначим условие задачи схематически. Вместо бананов будем рисовать прямоугольники. Сначала нарисуем 5 бананов, которые были у обезьянки.

Поскольку обезьянке дали еще бананы, то нарисуем их рядом.

Вспомним вопрос задачи и запишем его в таблицу

Значит, нам нужно вместе посчитать бананы, которые были, и бананы, которые ей еще дали

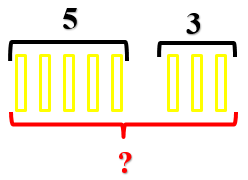
Теперь приступим к решению задачи.

Получается, что теперь у обезьянки все бананы лежат вместе, т.е. подмножество бананов, которые были у нее раньше, объединилось с подмножеством бананов, которые она получила потом.

Давай вспомним материал прошлого урока. Какое математическое действие мы используем при объединении подмножеств в одно общее?

Правильно, это действие сложение. Значит, для решения нашей задачи мы должны составить выражение на сложение. К 5 бананам, которые были у обезьянки, прибавим 3 банана, которые ей дала Даша. Что получится?

Сумма чисел 5 и 3 равна 8. Вот мы и посчитали все бананы. Теперь у обезьянки всего стало 8 бананов.

Обрати внимание, мы нашли ответ на вопрос нашей задачи! Можно заканчивать

Вот мы и разобрались с нашей задачей.

С помощью какого действия мы нашли ответ? Да, это было действие сложение.

Почему мы использовали именно это действие? Совершенно точно, потому что по условию предметы добавлялись. Два подмножества предметов объединяются в одно целое. Такой тип задач называется задачи на нахождение целого.

Один из главных вопросов в задачах на нахождение целого «Сколько всего?»  Потому что именно после объединения двух подмножеств надо пересчитать все предметы вместе.

В нашей задаче предметов прибавилось, потому что Даша дала еще бананы. Подумай, в каком еще случае предметов добавится?

Правильно, если:

• что-то подарят;
• что-то положат;
• сделают еще несколько предметов;
• кто-то придет или приедет;
• объединить две группы предметов (например, посчитать вместе мальчиков и девочек).

Во всех указанных случаях мы получим задачи на нахождение целого. Такие задачи нужно решать с помощью действия сложения.

Задачи на увеличение числа на несколько единиц

А вот другая задача. Она немного не похожа на предыдущие. Давай рассмотрим, в чем ее особенности.

У Даши было 4 воздушных шарика, а у игуаны Иса – на 5 шариков больше. Сколько шариков было у игуаны?

Сначала проанализируем условия задачи. Что нам известно?

Правильно, мы знаем о Даше. У нее 4 шарика.

Но мы не знаем, сколько шариков у игуаны! Однако у нас есть подсказка о их количестве. В задаче сказано, что у игуаны на 5 шариков больше.

Запишем это условие и вопрос.

Попробуем изобразить. Вот 4 шарика Даши

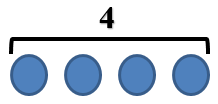
А как показать шарики игуаны? У нее их на 5 больше, чем у Даши. Значит их столько же (т.е. 4) и еще 5. Покажем это.

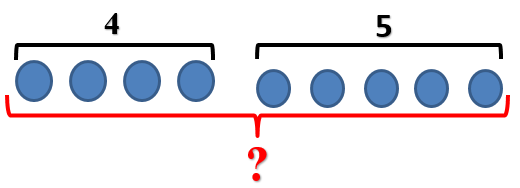
Давай подумаем над решением этой задачи. Выбор действия подсказан в самом условии. Помнишь, в результате какого действия становится больше?

Правильно, это действие сложения. Значит, для решения задачи нам нужно составить пример на сложение

Мы посчитали, сколько шариков у игуаны, а это и есть вопрос нашей задачи. Ура! Мы нашли нужный ответ! 

Задача решена!

Теперь давай разберемся, в чем ее особенность. В условии задачи содержалась подсказка, которая указала на выбор математического действия. Помнишь?

Было сказано, что у игуаны на несколько шариков больше. Больше становиться в результате действия сложения. Поэтому, чтобы посчитать шарики игуаны, нужно прибавлять.

Это задача на увеличение числа на несколько единиц. Их решать очень легко, если внимательно прочитать условие. Как только ты заметишь указание, что предметов, которые нужно посчитать, на несколько единиц больше, то сразу выбирай действие сложения. 

Задачи на нахождение части

А сейчас еще одна задача.

На кусте росло 8 ягод. Лис жулик сорвал 2 ягоды. Сколько ягод осталось?

Довольно простое и понятное условие. Попробуй сам записать все, что нам известно.

Давай проверим. Мы знаем, сколько было ягод, и знаем, сколько ягод сорвал Жулик. Поэтому запись такая

Что нужно узнать? Запиши вопрос

Кажется, все понятно. Теперь давай порассуждаем. Из тех ягод, что были на кусте, часть ягод сорвали. Изобразим это на схеме

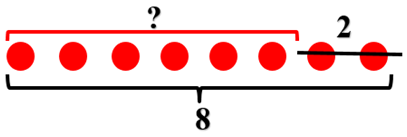
Подумай, что произойдет, если убрать часть предметов?

Правильно, их останется меньше.

А теперь вспомни, какое математическое действие используется при удалении из множества предметов одного его подмножества?

Конечно же, это действие вычитание. Значит нам нужно из числа 8, которое обозначает количество всех ягод вычесть число 2, которое обозначает количество сорванных ягод.

Запишем решение. 

Мы узнали, что на кусте осталось 6 ягод. Можем записать ответ.

Вот как просто! Когда мы что-то убираем, то остается только часть от всего, что было. Это задачи на нахождение части. Они решаются с помощью действия вычитания.

Давай подумаем, в каких еще ситуациях будет оставаться только часть предметов.

Например:

• что-то съели;
• забрали;
• продали;
• ушли;
• увезли;
• отрезали;
• прочитали.

Можно еще продолжать, но главное, ты должен запомнить, что в результате таких действий часть предметов убирается и их остается меньше. Поэтому в задачах на нахождение части всегда используется действие вычитания.

Задачи на уменьшение числа на несколько единиц

Давай разбираться со следующей задачей. Ее придумала Даша.

Даша собралась в поход. Она положила себе в рюкзак 5 пар носков, а футболок взяла на 3 меньше. 

Прочитай внимательно условие. Какие вещи взяла Даша? Что о них известно?

Правильно, мы знаем, что Даша взяла 5 пар носков.

А для каких вещей не указано точное количество?

Верно, мы не знаем точно, сколько Даша взяла футболок. Сказано, что их на 3 меньше, чем носков. Давай это запишем.

Можешь сказать, какой будет вопрос? Что нам нужно узнать?

Правильно, мы будем узнавать, сколько же футболок взяла с собой Даша

Это тоже задача с подсказкой. Мы можем даже не рисовать носки и футболки, чтобы понять, как ее решать. Ты уже догадался, что за подсказка?

Ну, конечно же, это указание, что футболок меньше! А мы уже знаем, какое математическое действие нужно применять, если предметов меньше. Это действие вычитание. 

Все очень просто. Нам нужно из числа 5, которое обозначает количество носков, вычесть число 3, которое показывает, на сколько футболок меньше

Вот и все! Теперь нам известно, что Даша взяла в поход 2 футболки. Можем писать ответ

И задача решена!

Это мой любимый тип задачи. Он называется задачи на уменьшение числа на несколько единиц. При их решении невозможно ошибиться. Раз сказано, что предметов на несколько единиц меньше, значит, будем вычитать, и получим правильный ответ.

Задачи на разностное сравнение

А вот еще одна задача от Даши и о ее друге Паровозике.

В первый день Паровозик перевез 9 пассажиров, а во второй день – 7 пассажиров. 

Очень простое и понятное условие. Все известно – и сколько в первый день перевез, и сколько во второй.

Можем это записать.

И нарисовать это можем. Пассажиров обозначим палочками. Сначала нарисуем пассажиров, которые ехал в первый день, а ниже тех, кто ехал во второй.

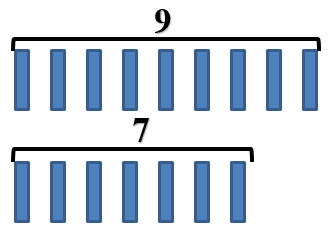
А вот вопрос Даша придумала очень необычный. Она решила, что мы слишком легко со всеми задачами справляемся и нужно немного усложнить. Вот вопрос.

Итак, нужно для начала определить в какой день он перевез пассажиров больше, а в какой меньше. Это довольно легко. Ты уже умеешь сравнивать числа. Скажи, что получиться?

Правильно, 9 > 7. Это можно прочитать, как «9 больше, чем 7» или «7 меньше, чем 9».

Но в задаче недостаточно только сравнить числа. Нужно узнать, какая между ними разница, т.е. выполнить разностное сравнение. Давай еще раз посмотрим на рисунок. Что ты заметил?

Видишь, в первый день изобразили палочек столько же, сколько и во второй день, и остались еще «лишние» палочки. Их можно отгородить. Для этого отделим одинаковое количество палочек. Во множестве с меньшим количеством элементов 7 палочек, значит, и во множестве с большим количеством элементов мы отсчитаем 7 палочек. 

Чтобы найти ответ на вопрос задачи, нужно узнать количество «лишних» палочек.

 То есть нам надо найти часть из множества, в котором 9 палочек.

А вот это уже просто! Вспомни, с помощью какого математического действия можно найти часть множества. Конечно же, это вычитание.

Получается, мы должны из большего числа вычесть меньшее число. 

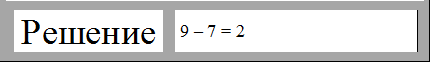
Мы провели не только сравнение чисел, но и нашли их разность. Это называется разностное сравнение чисел. Можно записывать ответ. 

Вот мы и познакомились еще с одним типом задач – задачи на разностное сравнение. Их главная особенность в том, что вопрос начинается со слов «На сколько …?». Для решения этих задач нужно следовать такому алгоритму.

1. Определить, какое число больше.
2. Из большего числа вычесть меньшее.

Ты еще не устал? Мы выучили 5 разных типов задач:

• задачи на нахождение целого;
• задачи на увеличение числа на несколько единиц;
• задачи на нахождение части;
• задачи на уменьшение числа на несколько единиц;
• задачи на разностное сравнение.

Каждая из них имеет один единственно правильный вариант решения. Поэтому нужно очень хорошо подумать и разобраться. Всегда будь внимательным к вопросу задачи. Поиск правильного решения зависит именно от того, количество каких предметов нужно узнать. 

Чтобы потренироваться в решении разных задач, попроси родителей приобрести сборник задач для 1 класса.

А сейчас давай проверим, как ты научился анализировать условие задачи и правильно определять ее тип. Выполни тестовые задания. 

Для материалов урока взяты кадры из обучающего м/с “Даша-путешественница”, 2004