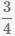Калькулятор дробей
- Главная
- /
- Математика
- /
- Арифметика
- /
- Калькулятор дробей
Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:
Просто заполните необходимые поля и получите ответ и подробное решение.
Данный калькулятор может работать как с положительными, так и с отрицательными дробями.
При этом нужно помнить, что:
− ac = a− c = − ac
Всегда нужно использовать только последний вариант.
Сложение дробей
С одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.
Формула
ac + bc = a + bc
Пример
Для примера сложим следующие дроби с равными знаменателями:
27 + 47 = 2 + 47 = 67
С разными знаменателями
При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю. А затем сложить числители.
Формула (универсальная)
ac + bd = a⋅d + b⋅cc⋅d
Пример №1
Для примера сложим следующие дроби с разными знаменателями:
12+13=1⋅32⋅3+1⋅23⋅2=36+26=3+26=56
Пример №2
Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:
12+14=1⋅22⋅2+14=24+14=2+14=34
Этот же пример можно решить и применяя вышеуказанную универсальную формулу:
12+14=1⋅42⋅4+1⋅24⋅2=48+28=4+28=68=34
Обратите внимание, что мы сократили дробь:
68=3 ⋅ 24 ⋅ 2=34
Сложение смешанных чисел
Смешанные числа – это такие числа, у которых есть как дробная часть, так и целая.
Преобразуя в неправильную дробь
Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.
Формула
a bc + d ef = b + a ⋅ cc + e + d ⋅ ff
Пример
Для примера сложим два смешанных числа:
312+123=1+3⋅22+2+1⋅33=72+53=7⋅32⋅3+5⋅23⋅2=216+106=21+106=316=5⋅6+16=5⋅66 + 16=516
Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:
316=5⋅6+16=5⋅66 + 16=516
Складывая целую и дробную части отдельно
Целую и дробную части смешанных чисел можно складывать по отдельности.
Формула
a bc + d ef = (a + d) + (bc + ef)
Пример
Решим предыдущий пример этим способом:
3 12 + 1 23 = (3+1)+(12+23) = 4+1⋅32⋅3+2⋅23⋅2=4+36+46=4+3+46=4+76=4+116 = 516
Вычитание дробей
Вычитание дробей происходит по тем же принципам, что и сложение.
С одинаковыми знаменателями
Формула
ac − bc = a − bc
Пример
Для примера вычтем одну дробь из другой с равными знаменателями:
35−25=3−25=15
С разными знаменателями
Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.
Формула
ac − bd = a⋅d − b⋅cc⋅d
Пример
Для примера вычтем одну дробь из другой, с разными знаменателями:
34−13=3⋅34⋅3−1⋅43⋅4=912−412=9−412=512
Вычитание смешанных чисел
Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.
Формула
a bc − d ef = b + a ⋅ cc − e + d ⋅ ff
Пример
312−123=1+3⋅22−2+1⋅33=72−53=7⋅32⋅3−5⋅23⋅2=216−106=21−106=116=1⋅6+56=1⋅66 + 56=156
Умножение дробей
При умножении дробей неважно одинаковые или разные у них знаменатели. Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.
Формула
ac ⋅ be = a ⋅ bc ⋅ e
Давайте рассмотрим несколько примеров:
Пример №1
Умножим дроби с одинаковыми знаменателями:
13⋅23=1⋅23⋅3=29
Пример №2
Умножим дроби с разными знаменателями:
13⋅24=1⋅23⋅4=212=1⋅26⋅2=16
Пример №3
Умножим смешанные числа:
112⋅223=1+1⋅22⋅2+2⋅33=32⋅83=3⋅82⋅3=246=4
Деление дробей
При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели. Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Формула
ac : be = a ⋅ ec ⋅ b
Давайте рассмотрим несколько примеров:
Пример №1
Разделим одну дробь на другую с таким же знаменателем:
23:13=23⋅31=2⋅33⋅1=63=2
Пример №2
Делим дроби с разными знаменателями:
12:23=12⋅32=1⋅32⋅2=34
Пример №3
Деление смешанных чисел:
412:223=1+4⋅22:2+2⋅33=92:83=92⋅38=9⋅32⋅8=2716=1⋅16+1116=1⋅1616 + 1116=11116
См. также
Калькулятор дробей выполнит основные арифметические действия с дробями и смешанными числами.
Если целая часть заполнена, калькулятор приведет смешанное число в неправильную дробь и выполнит операцию.
Заполните поля калькулятора чтобы найти сумму, разность, произведение и отношение дробей.
Основные операции с дробями
Сложение и вычитание
Чтобы сложить дроби с разными знаменателями необходимо: привести дробные части к наименьшему общему знаменателю;
затем сложить их числители. Рассмотрим на примере как сложить две дроби с разными знаменателями.
Пример Сложить дроби  и
и 
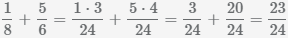
Наименьшее общее кратное знаменателей (8 и 6) равно 24.
Для нахождения разности дробей необходимо: привести дробные части к наименьшему общему знаменателю; затем выполнить вычитание числителей.
Пример Найти разность дробей  и
и 
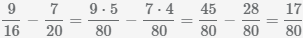
Общее кратное знаменателей НОК(16, 20)=80. Для вычисления наименьшего общего кратного можно воспользоваться калькулятором. Калькулятор вычислит НОК автоматически.
Умножение и деление
Для умножения двух дробей нужно: перемножить их числители и знаменатели 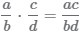
Чтобы разделить дробь на другую нужно: умножить первую дробь на дробь, обратную второй: 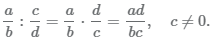
Приведение к общему знаменателю
Чтобы совершать операции с дробями часто требуется привести дроби к общему знаменателю.
Рассмотрим процесс приведения двух дробей 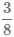
к наименьшему общему знаменателю :
Пример Сравнить дроби  и
и 
Для сравнения дробей приведем их к общему знаменателю и сравним их числители. Воспользуемся шагами описанными выше и найдем наименьшее общее кратное знаменателей дробей и далее преобразуем:
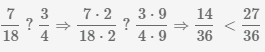
НОК(18, 4)=36, дополнительный множитель первой дроби 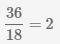
доп. множитель второй дроби 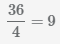
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Теория
- Дроби. Оглавление
- Сложение дробей
- Умножение дробей
- Деление дробей
Copyright calcs.su © 2021
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Выполнить сложение дробей путем сложения их числителей.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Данная задача не имеет решения в данной постановке. Докажем это и приведем возможное решение с добавочным условием.
Из условия: надо получить 8/5 из четырех чисел из набора {1; 1/2; 1/6; 1/5; 1/4; 1/3}
По контексту условия надо выбрать 4 числа сложить их и получить 8/5
Приведем эти числа к общему знаменателю. Для этого найдем НОК(2, 3, 4, 5, 6) = 2•2•3•5 = 60
Приведем все к знаменателю 60. Получим эквивалентную задачу:
8/5 = 96/60; 1 = 60/60; 1/2 = 30/60; 1/6 = 10/60; 1/5 = 12/60; 1/4 = 15/60; 1/3 = 20/60
Знаменатели одинаковые надо получить числитель сложением 4 чисел.
То есть надо 96 получить сложением 4 чисел из набора {60; 30; 10; 12; 15; 20}
Как видим 96 имеет 6 единиц (оканчивается на 6). В наборе чисел есть только 2 единицы и 5 единиц из них можно получить только 2; 5; и 7. Шесть получить нельзя. Таким образом никакие числа из набора в сумме не дадут 96.
Конечно, если каждую часть можно брать не один раз, То тут и не приводя к общему знаменателю видно. Берем 1/5 – 3 раза: получим 1/5+1/5+1/5 = 3/5 и к ним добавляем 1 =5/5 Получим: 5/5 + 3/5 =8/5
Но в задаче не упоминается про возможность брать части не один раз, а по графическому рисунку предполагается, что все же 1 раз каждую часть надо брать.
В этой задачи вам необходимо преобразить обыкновенную дробь 8/5 в десятичную.
Определяем дробь
Для начала нужно определить, с какими дробями вы работаете. Всего существует 4 вида дробей:
- обыкновенная правильная;
- обыкновенная неправильная;
- смешанная;
- десятичная.
8/5 – это обыкновенная дробь, потому что она записана в отношении двух чисел с использованием горизонтальной или же наклонной черты. Также 8/5 – это неправильная дробь, ведь ее числитель больше по значению, чем знаменатель: то есть 8 больше 5.
Делим числитель на знаменатель
Для того, чтобы преобразовать обычную неправильную дробь в десятичную, нужно числитель дроби разделить на ее знаменатель. То есть 8 разделить на 5. Можно использовать калькулятор или же разделить в столбик. Получаем 1,6.
Объяснение результатов
В результате преобразования обычной дроби в десятичную вышло значение 1,6 (читаем: одна целая шесть десятых). Теперь это числовое значение мы записываем без горизонтальной или же наклонной черты, а с помощью запятой. В данной десятичной дроби имеем: 1 – целая часть, 0,6 – дробная.
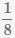 и
и 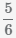
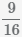 и
и 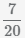
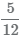
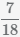 и
и