Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге «Угол вписанный в окружность. Часть 1!» и про вписанный четырёхугольник, либо соответствующий раздел в учебной литературе.
Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?
Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?
Начнём с самого простого. Чему равен данный угол?
Конечно же, 90 градусам.
Чему равен этот угол?
Понятно, что 45 градусам.
А этот?
Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).
А такой?
225 градусов (180 + 45 или 360 – 135).
Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.
Ещё раз напомню основное свойство вписанного угла.
«Вписанный угол равен половине центрального,
опирающегося на ту же дугу»
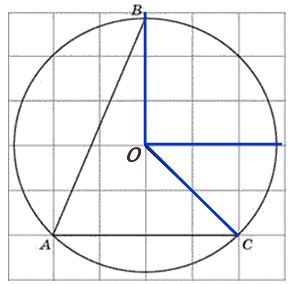
27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC. Ответ дайте в градусах.
Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.
Построим центральный угол соответствующий дуге ВС:
Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:
По клеткам видно, что угол ВОС равен 900 + 450 = 1350 (ОС проходит по диагонали клеток).
Ответ: 135
27887. Найдите величину угла ABC. Ответ дайте в градусах.
Посмотреть решение
27888. Найдите величину угла ABC. Ответ дайте в градусах.
Посмотреть решение
27889. Найдите величину угла ABC. Ответ дайте в градусах.
Посмотреть решение
27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC. Ответ дайте в градусах.
Посмотреть решение
Небольшой итог!
Нужно знать свойство вписанного угла (обязательно).
Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.
На этом всё. Успеха Вам!
С уважением, Александр Крутицких
Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
На клетчатой бумаге изображён вписанный угол
Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге « Угол вписанный в окружность. Часть 1! » и про вписанный четырёхугольник , либо соответствующий раздел в учебной литературе.
Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?
Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?
Начнём с самого простого. Чему равен данный угол?
Конечно же, 90 градусам.
Чему равен этот угол?
Понятно, что 45 градусам.
Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).
225 градусов (180 + 45 или 360 – 135).
Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.
Ещё раз напомню основное свойство вписанного угла.
«Вписанный угол равен половине центрального,
опирающегося на ту же дугу»
27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC . Ответ дайте в градусах.
Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.
Построим центральный угол соответствующий дуге ВС:
Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:
По клеткам видно, что угол ВОС равен 90 0 + 45 0 = 135 0 (ОС проходит по диагонали клеток).
27887. Найдите величину угла ABC . Ответ дайте в градусах.
27888. Найдите величину угла ABC. Ответ дайте в градусах.
27889. Найдите величину угла ABC . Ответ дайте в градусах.
27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC . Ответ дайте в градусах.
Нужно знать свойство вписанного угла (обязательно).
Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.
На этом всё. Успеха Вам!
С уважением, Александр Крутицких
Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».
Углы в окружности на клетчатой бумаге как решать
На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.
Читатели, знакомые с теоремой «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», могут решить эту задачу в одно действие: ∠ABC = 72° : 2 = 36°.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 56°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 62° = 28°.
Читатель, знающий правило «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», может решить эту задачу в одно действие:
Найдите угол ABC. Ответ дайте в градусах.
Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата отсекают на окружности равные дуги. Поэтому градусная мера дуги AC, на которую опирается угол ABC, составляет полного угла 360°, т. е. равна 270°. Угол ABC вписанный, поэтому он равен половине дуги, на которую опирается. Следовательно, угол ABC равен 135°.
Как находить угол в окружности по клеточкам
На клетчатой бумаге изображён вписанный угол
Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге « Угол вписанный в окружность. Часть 1! » и про вписанный четырёхугольник , либо соответствующий раздел в учебной литературе.
Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?
Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?
Начнём с самого простого. Чему равен данный угол?
Конечно же, 90 градусам.
Чему равен этот угол?
Понятно, что 45 градусам.
Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).
225 градусов (180 + 45 или 360 – 135).
Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.
Ещё раз напомню основное свойство вписанного угла.
«Вписанный угол равен половине центрального,
опирающегося на ту же дугу»
27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC . Ответ дайте в градусах.
Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.
Построим центральный угол соответствующий дуге ВС:
Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:
По клеткам видно, что угол ВОС равен 90 0 + 45 0 = 135 0 (ОС проходит по диагонали клеток).
27887. Найдите величину угла ABC . Ответ дайте в градусах.
27888. Найдите величину угла ABC. Ответ дайте в градусах.
27889. Найдите величину угла ABC . Ответ дайте в градусах.
27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC . Ответ дайте в градусах.
Нужно знать свойство вписанного угла (обязательно).
Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.
На этом всё. Успеха Вам!
С уважением, Александр Крутицких
Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».
Круг на клетчатой бумаге
Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.
Для решения обеих задач надо определить величину соответствующего ему центрального угла.
Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.
Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.
Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).
Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).
1) На клетчатой бумаге изображён круг площадью 60.
Найти площадь заштрихованного сектора.
Так как центральный угол, соответствующий данному сектору, равен 90º, то
2) На клетчатой бумаге изображён круг.
Какова площадь круга, если площадь заштрихованного сектора равна 17?
Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.
Следовательно, площадь сектора составляет 1/4 от площади круга: Sкруга=Sсектора:(1/4)=17·4=68.
3) Найти площадь круга, если площадь заштрихованного сектора равна 21.
Площадь заштрихованного сектора составляет 3/4 площади круга.
Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:
4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?
Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).
Так как 45° составляет от 360° 1/8 часть, то
5) На клетчатой бумаге изображен круг площадью 96.
Найдите площадь заштрихованного сектора.
Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.
Sзакрашенного сектора=Sнезакрашенного сектора-Sкруга=96-12=84.
А как определить на клетчатой бумаге центральные углы в 60° и 30°?
Можно рассуждать следующим образом.
Рассмотрим треугольник ABC.
Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.
Но AO=BO (как радиусы).
Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.
6) Найти площадь заштрихованного сектора, если площадь круга равна 30.
Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и Sсектора=Sкруга:6=30:6=5.
7) Найти площадь круга, если площадь заштрихованного сектора равна 24.
Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.
8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.
Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.
Следовательно, на площадь закрашенной части приходится 5/6 круга:
В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.
9) Центральный угол равен 30+45=75°,
площадь заштрихованного сектора составляет
1/12+1/8=5/24 площади круга, то есть
10) Центральный угол равен 180-30=150°,
площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,
11) Центральный угол равен 60-45=15°,
площадь заштрихованного сектора составляет 1/24 площади круга
12) Центральный угол равен 15+90=105°
Как находить угол в окружности по клеточкам
На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.
Читатели, знакомые с теоремой «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», могут решить эту задачу в одно действие: ∠ABC = 72° : 2 = 36°.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 56°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 62° = 28°.
Читатель, знающий правило «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», может решить эту задачу в одно действие:
Найдите угол ABC. Ответ дайте в градусах.
Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата отсекают на окружности равные дуги. Поэтому градусная мера дуги AC, на которую опирается угол ABC, составляет полного угла 360°, т. е. равна 270°. Угол ABC вписанный, поэтому он равен половине дуги, на которую опирается. Следовательно, угол ABC равен 135°.
[spoiler title=”источники:”]
http://oge.sdamgia.ru/search?search=%D0%9D%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5%20%D1%83%D0%B3%D0%BE%D0%BB%20ABC
http://b4.cooksy.ru/articles/kak-nahodit-ugol-v-okruzhnosti-po-kletochkam
[/spoiler]
Приветствую читателей и подписчиков канала Тесты_математика!
Эта задача была опубликована на моём канале полтора года назад. И я заметила, что в комментариях очень много негативных отзывов по поводу решения задачи. Причём охват статьи был немалый.
7K прочитали.
А задача по геометрии, в которой из данных значится только чертёж с элементами задачи, нет никаких чисел, обозначающих размер того или иного параметра фигур, изображённых на чертеже. В частности, здесь изображён угол, вписанный в окружность. Смотрите на элементы фигур, изображённых на чертеже.
То есть необходимо найти все данные, используя клетки листа. В чём сложность задачи? В её необычности. Есть чертёж, и есть привязка к клеточкам листа, и данных нет. В этом и сложность.
Задача.
Найти вписанный в окружность угол используя данные чертежа, то есть угол АВС вписанный в окружность.
Скрин рисунка (чертежа)
Чертёж более крупным планом.
Чертёж условия задачи.
В этой галерее рисунков дополнительные построения для решения.
Точка С находится не в узле сетки, а на линии, это точка пересечения окружности с линией на высоте 3 кл от диаметра, проходящего через точки А и О. Поэтому находим СН правильно, если нет другого способа решения.
В этом и “сложность задачи” Хотя многие считают её устной. Всё равно дополнительные построения нужны, чтобы доказать, что <АОС=30.
Решение можно просмотреть в данной статье (по желанию(
А можно сразу написать ответ, чему равен угол АВС, не просматривая статью, в которой есть решение.
Проверить ответ можно в этом тесте.
Тест.
Спасибо за решение любого из тестов и ответы в комментариях!
Подпишитесь на канал, Тесты_математика!
чтобы не пропустить новые публикации!
#задачи на логику, #головоломки, #математика, #тесты
Сегодня говорим о типе задач на окружности, которые встретятся в КИМах ОГЭ по математике. Приготовьте тетрадки и ручки (ну или кнопки для скринов), ведь мы начинаем!
Типы задач на окружности
На самом деле, список этих задач немаленький. Взгляните сам:
- Окружность №16. Центральные и вписанные углы;
- Треугольники №15. Медиана, проведенная из прямого угла;
- Окружность №18. Центральные и вписанные углы;
- Окружность №16. Вписанные многоугольники;
- Окружность №16. Описанные многоугольники;
- Окружность №16. Квадрат и окружность;
- Окружность №16. Свойства хорд, касательных, секущих.
Сегодня подробно говорим о первом пункте – центральных и вписанных углах, с которыми встречаемся в номере 16. Поехали!
Немного теории
Итак, начинать разговор про окружности нужно с объяснения базовых понятий.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны опираются на окружность.
Центральный угол – это угол, вершина которого лежит в центре окружности, а стороны опираются на окружность. Равен градусной мере дуги, на которую опирается.
Свойства вписанного угла
- Вписанный угол равен половине центрального угла, если они оба опираются на одну дугу.
Задача №1
В окружность вписан равносторонний восьмиугольник. Найдите величину угла RAV.
Решение:
Как поступаем первым делом? Рисуем центральный угол, который опирается на те же самые точки. Именно так впоследствии мы придем к нужному нам вписанному углу.
Можем ли мы как-нибудь его посчитать? Ответ положительный! Перед нами восьмиугольник, своеобразная пицца, сумма углов которой дает 360 градусов. Соответственно “цена” одного кусочка =45 градусам.
Вписанный угол по правилам будет вдвое меньше. То есть наш RAV=22,5 градусам.
Вуаля, записываем ответ!
Задача №2
Найдите угол RAV (дан только рисунок)
Решение:
На первый взгляд выглядит нерешаемо. Но вы точно сможете это сделать))
На этом рисунке нам даны клетки. А в математике, как у Чехова, если ружье висит, то обязательно должно выстрелить.
Клетки, конечно, стрелять не будут, но вот найти центральный угол нам точно помогут. Благодаря ним мы можем разделить окружность ровно на 4 части, сделав это, мы видим, что точка V находится ровно посередине между двумя точками.
Снова делим пиццу на 8 частей. 360 делим на 8 и получаем 45, а 45 снова уменьшаем вдвоем и получаем 22,5.
Вот такой постоянный наш угол RAV, равный 22,5 градусам.
Задача №3
Найдите угол RAV (дан только рисунок)
Решение:
Рисуем центральный угол с точкой О. Потом снова действуем по рабочей системе пиццы. Делим на 8 частей, обнаруживаем, что центральный угол состоит сразу из трех кусочков нашей пиццы.
Выполняем махинации с числами: 360/8 и получаем 45. А 45 уже умножаем на 3. 135 градусов – наш центральный угол.
Вписанный по теореме вдвое меньше центрального, соответственно наш RAV=135/2=67,5.
Задача №4
Итак, приступаем к нашему боссу, как в старых компьютерных играх, помните? Хотя девятиклассники часто путаются и ошибаются в этом месте, вам повезло – сегодня вы раз и навсегда запомните, какой же чит надо использовать, чтобы пройти уровень.
Найдите угол RAV (дан только рисунок)
Решение:
Как мы можем заметить, здесь нам дан тупой угол. Мы снова делим нашу пиццу на 8 частей и ищем середину. Рисуем центральный угол, опирающийся на точки R и V.
Вот тут-то и сыплются ошибки, ведь многие забывают, что центральный и вписанный углы должны опираться на одну дугу! Вы по старинке считаете 145 градусов, не замечая, что сейчас нас интересует другая, бОльшая дуга.
Итак, центральный угол состоит из пяти кусочков, 45*5=225 градусов. Наш RAV, как мы помним, вдвое меньше, делим 225 на 2 и в ответе получаем 112,5.
Готово!
Секретная информация
Почему же мы делим центральный угол на 2? Секрет в том, что мы действуем аналогично поиску углов в равнобедренном треугольнике. Послушаем нашего Данира Баева, который сказал, что доказывать это очень и очень скучно даже фанатикам математики, и просто примем это к сведению.
Надеемся, что сегодняшние задачи если и попадутся вам в КИМах, то будут решены без ошибок. Мы разобрали первый тип заданий на окружность ОГЭ по математике. Впереди еще много интересного.
Стремитесь к заветным пятеркам и готовьтесь к экзаменам с удовольствием вместе с Умскул!
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 529 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Тип 25 № 52
i
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .
В треугольнике ABC угол C прямой, BC = 8 , sin A = 0,4. Найдите AB.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен Найдите радиус вписанной окружности треугольника ABC.
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
Источники:
Банк заданий ФИПИ.
Основания трапеции равны 18 и 12, одна из боковых сторон равна а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
Основания трапеции равны 18 и 10, одна из боковых сторон равна а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
В равнобедренном треугольнике боковая сторона равна 10, основание —
а угол, лежащий напротив основания, равен 150°. Найдите площадь треугольника.
Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера центрального ∠AOC равна 96°.
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)
В треугольнике ABC угол C равен 90°,
Найдите AB.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)
В треугольнике ABC угол C равен 90°,
Найдите AB.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Источник: ГИА-2013. Математика. Экзамен. Вариант 1
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
Источник: ГИА-2013. Математика. Экзамен. Вариант 2
В треугольнике ABC угол C прямой,
Найдите AB.
Источник: ГИА-2013. Математика. Экзамен. Вариант 9
В треугольнике ABC угол C прямой,
Найдите AB.
Источник: ГИА-2013. Математика. Экзамен. Вариант 10
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
Источник: ГИА-2012. Математика. Диагностическая работа № 2(1вар)
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
Источник: ГИА-2012. Математика. Диагностическая работа №2(2вар)
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Источник: ГИА-2013. Математика. Диагностическая работа № 1. (вар. 1) 02.10.2012г.
Всего: 529 1–20 | 21–40 | 41–60 | 61–80 …