Как найти вписаный угол acb

Углы в окружности, центральный и вписанный. Свойства и способы нахождения

Планиметрия – это раздел геометрии, изучающий свойства плоских фигур. К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?

Что такое центральный угол?

Для того чтобы понять, что такое центральный угол, нужно дать определение окружности. Окружность – это совокупность всех точек, равноудаленных от данной точки (центра окружности).

Очень важно отличать ее от круга. Нужно запомнить, что окружность – это замкнутая линия, а круг – это часть плоскости, ограниченная ею. В окружность может быть вписан многоугольник или угол.

Центральный угол – это такой угол, вершина которого совпадает с центром окружности, а стороны пересекают окружность в двух точках. Дуга, которую угол ограничивает точками пересечения, называется дугой, на которую опирается данный угол.

Рассмотрим пример №1.

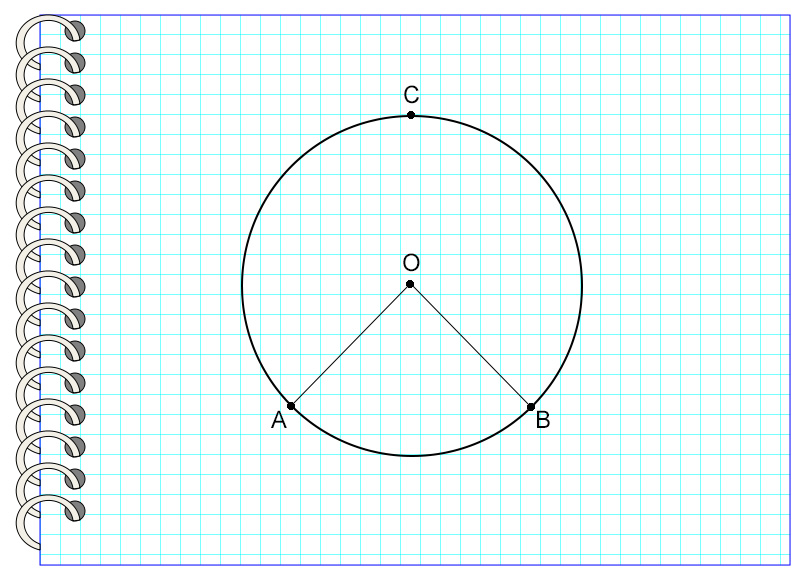
На картинке угол AOB – центральный, потому что вершина угла и центр окружности – это одна точка О. Он опирается на дугу AB, не содержащую точку С.

Чем вписанный угол отличается от центрального?

Однако кроме центральных существуют также вписанные углы. В чем же их различие? Так же как и центральный, вписанный в окружность угол опирается на определенную дугу. Но его вершина не совпадает с центром окружности, а лежит на ней.

Приведем следующий пример.

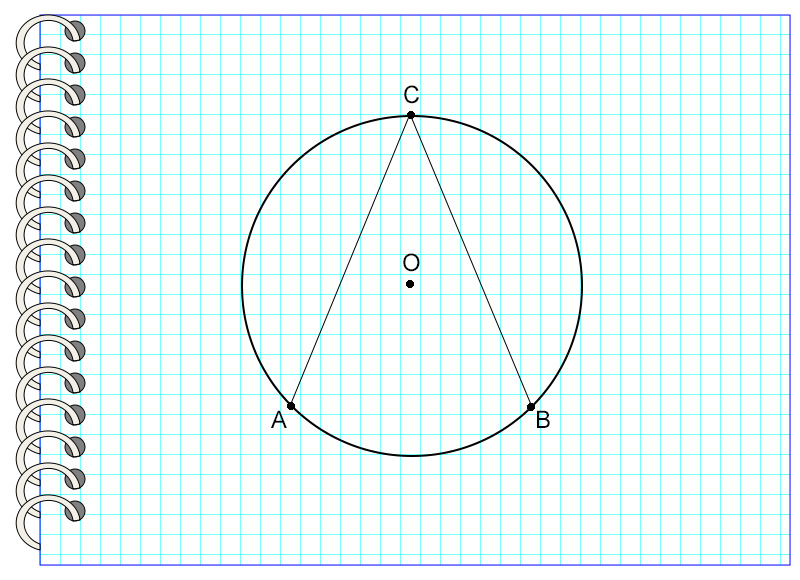
Угол ACB называется углом, вписанным в окружность с центром в точке О. Точка С принадлежит окружности, то есть лежит на ней. Угол опирается на дугу АВ.

Чему равен центральный угол

Для того чтобы успешно справляться с задачами по геометрии, недостаточно уметь различать вписанный и центральный углы. Как правило, для их решения нужно точно знать, как найти центральный угол в окружности, и уметь вычислить его значение в градусах.

Итак, центральный угол равен градусной мере дуги, на которую он опирается.

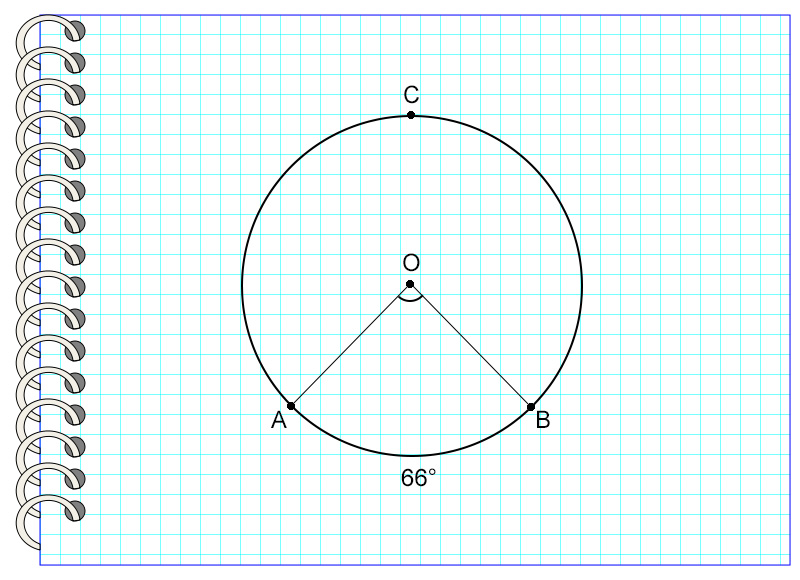
На картинке угол АОВ опирается на дугу АВ, равную 66°. Значит, угол АОВ также равен 66°.

Таким образом, центральные углы, опирающиеся на равные дуги, равны.

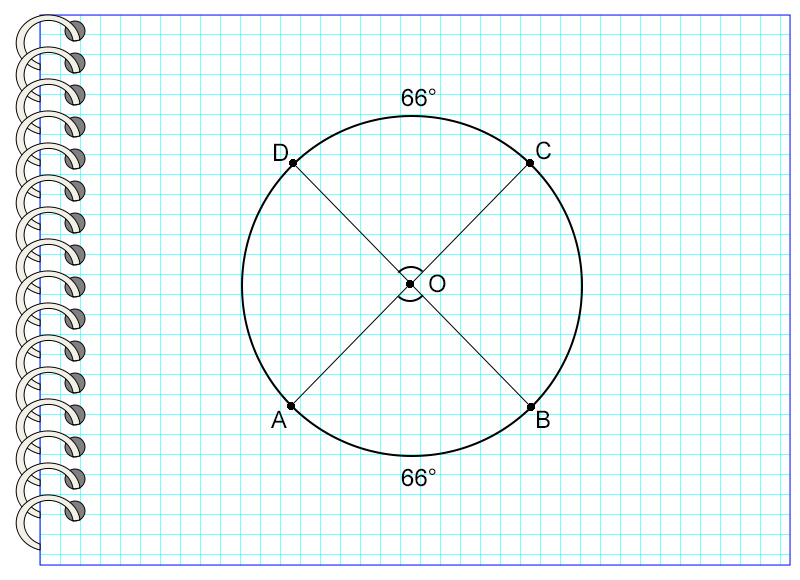
На рисунке дуга DC равна дуге AB. Значит, угол АОВ равен углу DOC.

Как найти вписанный угол

Может показаться, что угол, вписанный в окружность, равен центральному углу, который опирается на ту же дугу. Однако это грубая ошибка. На самом деле, даже просто посмотрев на чертеж и сравнив эти углы между собой, можно увидеть, что их градусные меры будут иметь разные значения. Так чему же равен вписанный в окружность угол?

Градусная мера вписанного угла равна одной второй от дуги, на которую он опирается, или половине центрального угла, если они опираются на одну дугу.

Рассмотрим пример. Угол АСВ опирается на дугу, равную 66°.

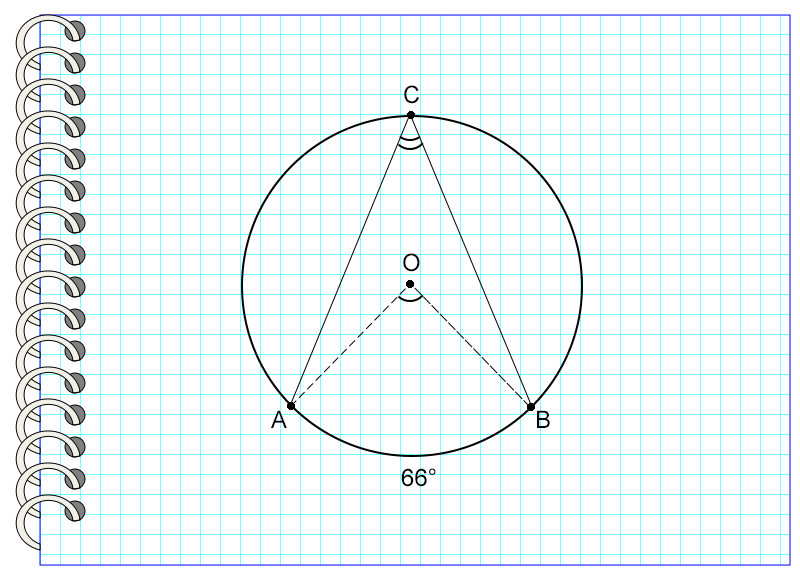
Значит, угол АСВ = 66° : 2 = 33°

Рассмотрим некоторые следствия из этой теоремы.

• Вписанные углы, если они опираются на одну и ту же дугу, хорду или равные дуги, равны.
• Если вписанные углы опираются на одну хорду, но их вершины лежат по разные стороны от нее, сумма градусных мер таких углов составляет 180°, так как в этом случае оба угла опираются на дуги, градусная мера которых в сумме составляет 360° (вся окружность), 360° : 2 = 180°
• Если вписанный угол опирается на диаметр данной окружности, его градусная мера равна 90°, так как диаметр стягивает дугу равную 180°, 180° : 2 = 90°
• Если центральный и вписанный углы в окружности опираются на одну дугу или хорду, то вписанный угол равен половине центрального.

Где могут встретиться задачи на эту тему? Их виды и способы решения

Так как окружность и ее свойства – это один из важнейших разделов геометрии, планиметрии в частности, то вписанный и центральный углы в окружности – это тема, которая широко и подробно изучается в школьном курсе. Задачи, посвященные их свойствам, встречаются в основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Как правило, для решения этих задач следует найти углы на окружности в градусах.

Углы, опирающиеся на одну дугу

Этот тип задач является, пожалуй, одним из самых легких, так как для его решения нужно знать всего два простых свойства: если оба угла являются вписанными и опираются на одну хорду, они равны, если один из них – центральный, то соответствующий вписанный угол равен его половине. Однако при их решении нужно быть крайне внимательным: иногда бывает сложно заметить это свойство, и ученики при решении таких простейших задач заходят в тупик. Рассмотрим пример.

Дана окружность с центром в точке О. Угол АОВ равен 54°. Найти градусную меру угла АСВ.

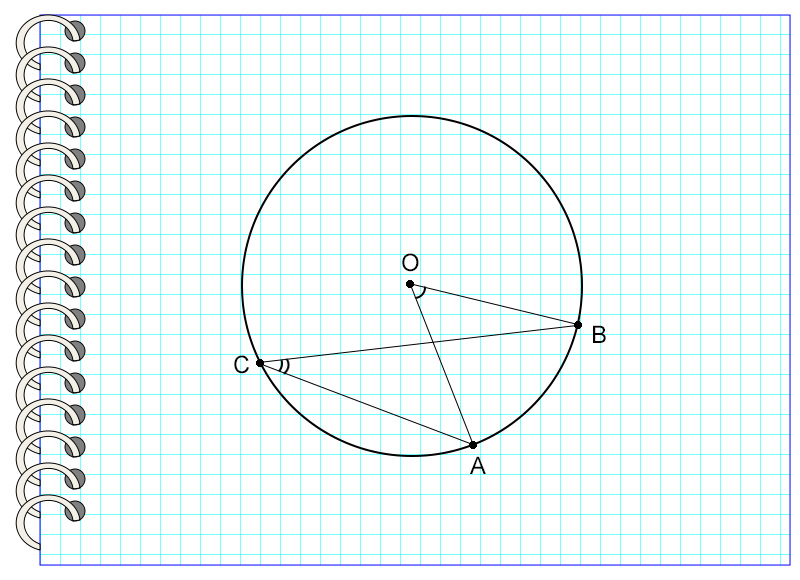
Эта задача решается в одно действие. Единственное, что нужно для того, чтобы найти ответ на нее быстро – заметить, что дуга, на которую опираются оба угла – общая. Увидев это, можно применять уже знакомое свойство. Угол АСВ равен половине угла АОВ. Значит,

1) АОВ = 54° : 2 = 27°.

Углы, опирающиеся на разные дуги одной окружности

Иногда в условиях задачи напрямую не прописана величина дуги, на которую опирается искомый угол. Для того чтобы ее вычислить, нужно проанализировать величину данных углов и сопоставить их с известными свойствами окружности.

В окружности с центром в точке О угол АОС равен 120°, а угол АОВ – 30°. Найдите угол ВАС.

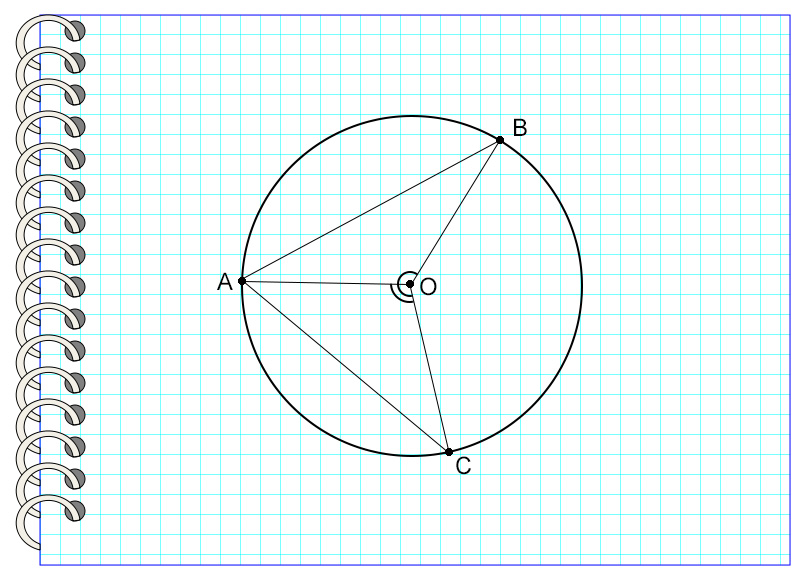
Для начала стоит сказать, что возможно решение этой задачи с помощью свойств равнобедренных треугольников, однако для этого потребуется выполнить большее количество математических действий. Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.

Итак, угол АОС опирается на дугу АС и является центральным, значит, дуга АС равна углу АОС.

Точно так же угол АОВ опирается на дугу АВ.

Зная это и градусную меру всей окружности (360°), можно с легкостью найти величину дуги ВС.

ВС = 360° – АС – АВ

ВС = 360° – 120° – 30° = 210°

Вершина угла САВ, точка А, лежит на окружности. Значит, угол САВ является вписанным и равен половине дуги СВ.

Угол САВ = 210° : 2 = 110°

Задачи, основанные на соотношении дуг

Некоторые задачи вообще не содержат данных о величинах углов, поэтому их нужно искать, исходя только из известных теорем и свойств окружности.

Найдите угол, вписанный в окружность, который опирается на хорду, равную радиусу данной окружности.

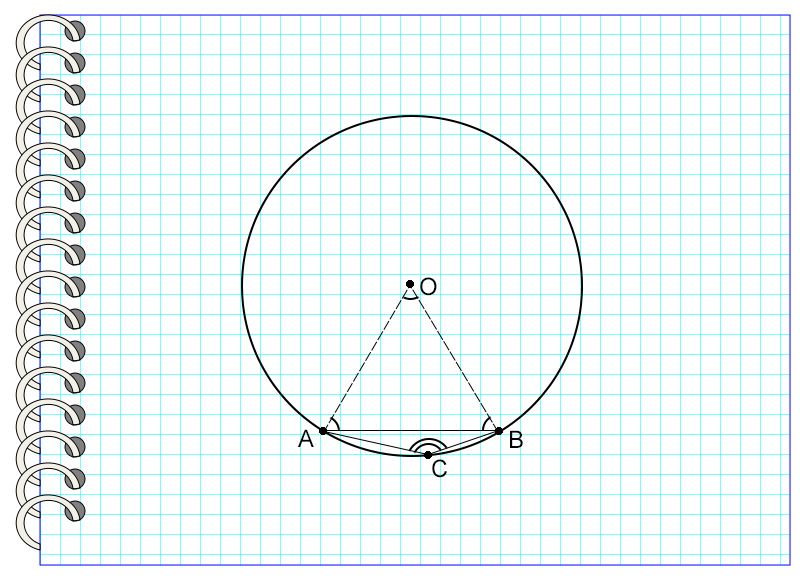
Если мысленно провести линии, соединяющие концы отрезка с центром окружности, то получится треугольник. Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.

АВ = 360° – 60° = 300°

Угол АВС = 300° : 2 = 150°

В окружности с центром в точке О дуги соотносятся как 3:7. Найдите меньший вписанный угол.

Для решения обозначим одну часть за Х, тогда одна дуга равна 3Х, а вторая соответственно 7Х. Зная, что градусная мера окружности равна 360°, составим уравнение.

По условию, нужно найти меньший угол. Очевидно, что если величина угла прямо пропорциональна дуге, на которую он опирается, то искомый (меньший) угол соответствует дуге, равной 3Х.

Значит, меньший угол равен (36° * 3) : 2 = 108° : 2 = 54°

В окружности с центром в точке О угол АОВ равен 60°, а длина меньшей дуги – 50. Вычислите длину большей дуги.

Для того чтобы вычислить длину большей дуги, нужно составить пропорцию – как меньшая дуга относится к большей. Для этого вычислим величину обеих дуг в градусах. Меньшая дуга равна углу, который на нее опирается. Ее градусная мера составит 60°. Большая дуга равна разности градусной меры окружности (она равна 360° вне зависимости от остальных данных) и меньшей дуги.

Большая дуга равна 360° – 60° = 300°.

Так как 300° : 60° = 5, то большая дуга в 5 раз больше меньшей.

Большая дуга = 50 * 5 = 250

Итак, конечно, существуют и другие подходы к решению подобных задач, но все они так или иначе основаны на свойствах центральных и вписанных углов, треугольников и окружности. Для того чтобы успешно их решать, необходимо внимательно изучать чертеж и сопоставлять его с данными задачи, а также уметь применять свои теоретические знания на практике.

Углы, связанные с окружностью

Вписанные и центральные углы

Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.

Теоремы о вписанных и центральных углах

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Фигура	Рисунок	Теорема
Вписанный угол
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
Вписанный угол		Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды
Вписанный угол		Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
Окружность, описанная около прямоугольного треугольника

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу равны.

Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды

Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Теоремы об углах, образованных хордами, касательными и секущими

Вписанный угол

Окружность, описанная около прямоугольного треугольника

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами
Угол, образованный секущими, которые пересекаются вне круга
Угол, образованный касательной и хордой, проходящей через точку касания
Угол, образованный касательной и секущей
Угол, образованный двумя касательными к окружности

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Угол, образованный пересекающимися хордами хордами

Формула:

Угол, образованный секущими секущими , которые пересекаются вне круга

Формула:

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Угол, образованный касательной и хордой хордой , проходящей через точку касания

Формула:

Угол, образованный касательной и секущей касательной и секущей

Формула:

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Угол, образованный двумя касательными касательными к окружности

Формулы:

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Доказательства теорем об углах, связанных с окружностью Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Центральные и вписанные углы О чем эта статья: Центральный угол и вписанный угол Окружность — замкнутая линия, все точки которой равноудалены от ее центра. Определение центрального угла: Центральный угол — это угол, вершина которого лежит в центре окружности. Центральный угол равен градусной мере дуги, на которую он опирается. На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF Определение вписанного угла: Вписанный угол — это угол, вершина которого лежит на окружности. Вписанный угол равен половине дуги, на которую опирается. На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC Свойства центральных и вписанных углов Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро. Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу: Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC. Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается: Вписанные углы окружности равны друг другу, если опираются на одну дугу: ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC. Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой: ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ. Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так: На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла. Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство. Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart! Хорда — отрезок, соединяющий две точки на окружности. Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой. AB * AC = AE * AD Получается, что стороны вписанного в окружность угла — это хорды. Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды. ㄥBAC = ㄥCAB, поскольку лежат на хорде BC. Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды. ㄥBAC + ㄥBDC = 180° Примеры решения задач Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно. Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ? Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80° По теореме: вписанный угол равен дуге ½. ㄥACB = ½ AB = 40° Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла. Мы уже потренировались и знаем, как найти вписанный угол. На рисунке в окружности центральный угол и дуга AC = 140° Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70° Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности? СB = ⅕ от 360° = 72° Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36° [spoiler title=”источники:”] http://www.resolventa.ru/spr/planimetry/cangle.htm http://skysmart.ru/articles/mathematic/centralnye-i-vpisannye-ugly [/spoiler]

Ключевые слова:         угол,   окружность,   хорда,    дуга,   центральный угол,    вписанный угол,    касательная,   секущая,    теорема о секущих,   теорема о касательной и секущей,   градусная мера дуги,    угол опирается на хорду,    угол опирается на дугу,   дуга стягивает хорду,    угол между хордой и касательной,    внутренный угол окружности,    внешний угол окружности.

Центральные и вписанные углы в окружности    

Центральный угол     в   окружности – угол с вершиной в ее центре и сторонами-радиусами.

Дуга окружности ,    соответствующей центральному углу – часть окружности внутри плоского угла.

Градусная мера     дуги окружности – градусная мера соответствующего центрального угла.

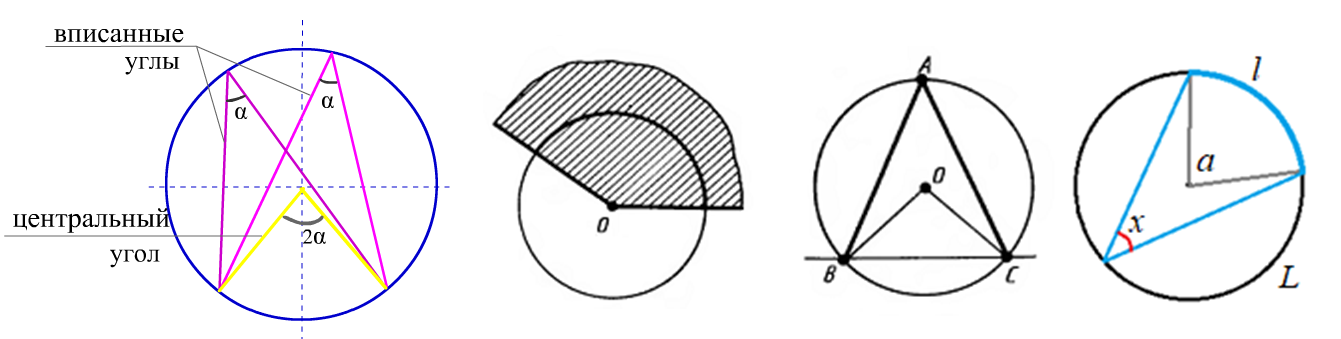
Вписанный угол – вершина которого лежит на окружности, а стороны пересекают эту окружность (хорды).

• Вписанный угол опирается на хорду , которая соединяет точки пересечения сторон угла и окружности.
• Вписанный угол опирается на дугу, заключенную между его сторонами.
• Обозначение:   $AB^o$ – градусная мера дуги    $AB$   ,     равна центральному    углу   $AOB$.

_____________________________________________________________________________________

Теорема    Вписанный угол равен   половине   центрального    угла, что опирается    на ту же дугу.

Теорема$angle BAC=frac{angle BOC}{2}=frac{BC^o}{2}$       $angle BAD=frac{angle BOD}{2}=frac{BD^o}{2}$       $angle DAC=frac{angle DOC}{2}=frac{DC^o}{2}$

_____________________________________________________________________________________

               

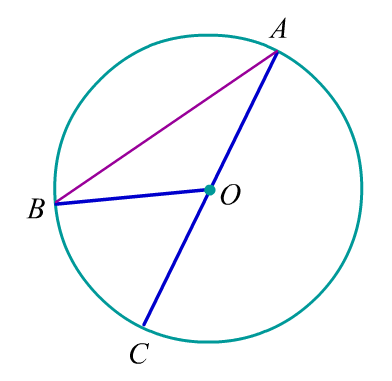
Случай 1:       Точка   $O$ принадлежит лучу   $AC$.

• Пусть   $angle A = alpha$    ,   тогда   и    $angle B = alpha$ ,   ведь      $bigtriangleup AOB$   – равнобедренный, его стороны    $OB=OA$   как радиусы.   
• $angle BOC$   является внешним для треугольника , а значит равен сумме двух других углов:       $alpha+alpha=2alpha$     
• угловое измерение дуги   $BC$   есть    $2alpha$       $Rightarrow$      вписанный угол   равен    половине дуги,    на которую он опирается.

Случай 2:       Точка   $O$ лежит   внутри   вписанного угла $angle BAC$ .   

• Проведем диаметр    $AD$, обозначим      $angle BAD = alpha$    и тогда    дуга $BD$   равна   $2alpha$   (см. случай 1).
• Обозначим $angle BAD$   за    $beta$ ,   тогда    дуга    $DC$   равна   $2beta$   ( так же из-за случая 1)          
• $Rightarrow$         вся дуга     $BC = 2alpha + 2beta = 2left(alpha+betaright)$.    Но     $angle BAC$   ,   в свою очередь, равен     $alpha + beta$            
• $Rightarrow$       вписанный угол   равен    половине дуги,   на которую он опирается.

Случай 3:       Точка   $O$   находится   вне   вписанного угла .     

• Проведем диаметр   $AD$, обозначим   угол   $angle BAD$   через    $alpha$ ,   тогда   дуга    $BD$   равна   $2alpha$   (из-за случай 1).
• $angle CAD$   обозначим через    $beta$ ,   тогда   дуга   $DC = 2beta$ (из-за случай 1).
• Дуга     $BC$    является разностью большой   дуги   $BD$    и    дуги    $DC$       :       $BC=BD-DC=2alpha-2beta=2left(alpha-betaright)$
• $Rightarrow$        Вписанный угол     $angle BAD = alpha – beta$. … вписанный угол   равен    половине дуги опирания.

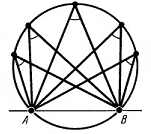
Следствия теоремы о вписанном угле:

             

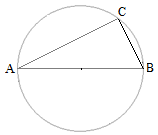
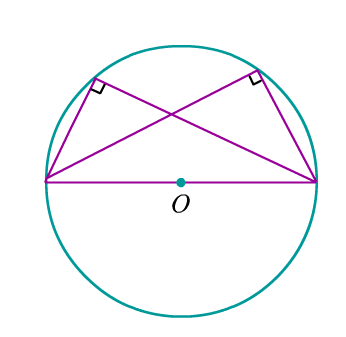
Задача 1:        Точки   $A$,   $B$,    $C$   находятся на окружности   и делят ее на три дуги, градусные величины которых относятся как 1 : 3 : 5.               Найдите больший   угол   треугольника    $ABC$   в градусах.

• Решение:      Пусть   меньшая   дуга   окружности   равна   $x$ ,    тогда     $x + 3x + 5x = 360^o$    ,     $9x = 360^o$    ,     $x = 40^o$           
• Больший   угол    $bigtriangleup ABC$     опирается   на   большую дугу   и   равен    $5cdot40^o$    ,   для окружности   он   является   вписанным           
• и   значит равен половине этой дуги   $frac{200}{2}$.                                   Ответ:     $100^o$

            

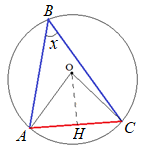
Задача 2:        В треугольнике   $ABC$     угол $B$    равен   $25^o$   .    Найти   угол   между   радиусом   описанной окружности   и   противоположной   стороной   $AC$.

• Решение:          Обозначим   $angle ABC$     за   $x$   . Он вписанный     и     опирается на дугу   $AC$ , на   которую   так же опирается   центральный   угол   $AOC$.   
• Вписанный   угол в два раза   меньше    центрального         $Rightarrow$       $angle AOC = 2x$.                 
• $bigtriangleup AOC$   –    равнобедренный, т.к.   две его   стороны   являются радиусами ,
• значит   углы   при    основании – хорде      $AC$ равны     и     $OAC=OCA=frac{180-2x}{2}=90-x=90-25=65$    .
• Кстати, угол    $HOC=ABC=x$.          Ответ:     $65^o$

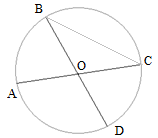
Задача 3:        Отрезки $AC$   и   $BD$ — диаметры окружности с центром   $O$ ,   образовали меж собой   угол   $COD$   равный    $58^o$.   Найти     $angle ACB$.

• Решение:          Углы    $BOA$    и       $COD$      равны    как   вертикальные ,     поэтому      $angle BOA = 58^o$ .   
• Искомый угол   $ACB$   – вписанный   и   он   опирается на   ту же дугу , что и центральный угол   $BOA$   .
• По теореме о вписанных и центральных углах     $ACB=frac{1}{2}BOA=frac{1}{2}cdot58=29$            Ответ:     $angle ACB = 29^o$

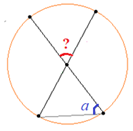
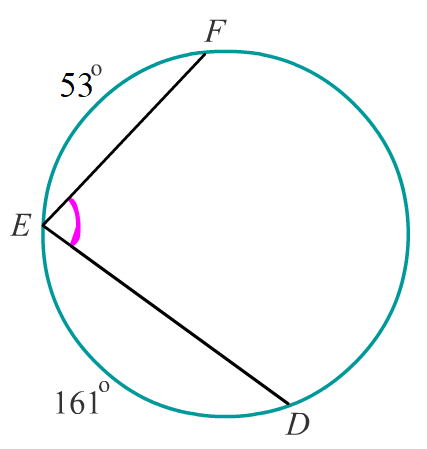
Задача 4:        Найдите     $angle DEF$,     если градусные меры дуг $DE$ и   $EF$   равны    $161^o$   и   $53^o$    соответственно.                        

• Решение:   $angle DEF$ — вписанный,   его градусная   мера   равна половине дуги, на которую он опирается.
• Дуга    $FD = 360° – (161° + 53°) = 146°$         $Rightarrow$         $angle$ $DEF=frac{1}{2}146=73$                        Ответ:     $73^o$

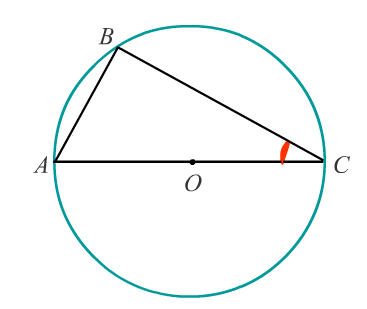
Задача 5:        Найдите градусную меру   $angle ACB$ , если известно, что   $BC$ является диаметром окружности, а градусная мера центрального $angle AOC$    равна $96^o$.

• Решение:          $angle ACB$ — вписанный, опирается на дугу    $AB$   и   равен   её половине. Найдем дугу $AB$.        
• $BC$ — диаметр окружности,   дуга   $CAB$ равна   $180^o$.    $angle AOC$ – центральный угол.     По условию   $angle AOC = 96^o$ .   
• $Rightarrow$       дуга   $AC = 96^o$ ,   а дуга    $AB = 180^o – 96^o = 84^o$ ,    тогда     $angle$ $ACB=frac{1}{2}84=42$.   Ответ:             $angle ACB = 42^o$

              

Задача 6:        Сторона   $AC$    треугольника   $ABC$   содержит   центр описанной около него окружности.   Найдите $angle C$,   если $angle A = 69^o$.

• Решение: Важное свойство: вписанный     $angle В$ , опирающийся   на   диаметр     $AC$ ,    равен   $90^o$ .
• Любой диаметр – развернутый центральный угол – опирается на   дугу   $180^o$           $Rightarrow$       $bigtriangleup ABC$    —    прямоугольный.
• По свойству прямоугольного треугольника   сумма острых углов   равна      $90^o$    $Rightarrow$     $angle C=90^o-angle A=90^o – 69^o=21^o$ .
• Ответ:     $angle C = 21^o$

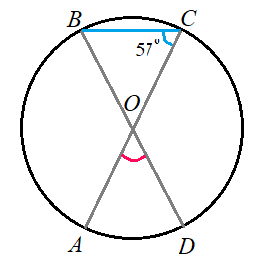
Задача 7:         $AC$   и    $BD$ — диаметры окружности с центром   $O$.      $angle ACB$    равен     $57^o$.     Найдите    $angle AOD$ .

• Решение:   $angle ACB$    является     вписанным     углом ,    значит     равен     половине    дуги,    на    которую    опирается …
• градусная мера   дуги    $AB= 2B = 2cdot57^o=114^o$ .           $O$ — центр окружности лежит на    $BD$   ,     значит $BAD = 180^o$,        
• тогда    дуга    $AD = 180^o – 114^o= 66^o$.     $angle AOD$ — центральный    и опирается    на    дугу   $AD$ ,
• значит их градусные меры совпадают.           $Rightarrow$                  Ответ:     $angle AOD = 66^o$

                 

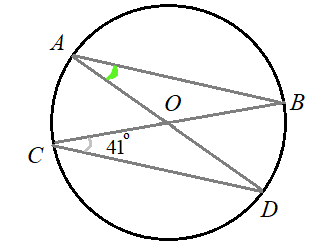
Задача 8:         В   окружности с   центром в   точке     $O$ проведены   диаметры    $AD$   и     $BC$ , угол    $OCD$   равен    $41^o$.     Найдите величину   $angle OAB$   .

• Решение:   $angle OCD$       и     $angle OAB$ — вписанные    и    опираются на одну и ту же дугу     $DB$ , тогда …
• … по свойству вписанных углов    они равны.      Таким образом,   $angle OAB$   то же    равен     $41^o$.         Ответ:     $angle OAB = 41^o$

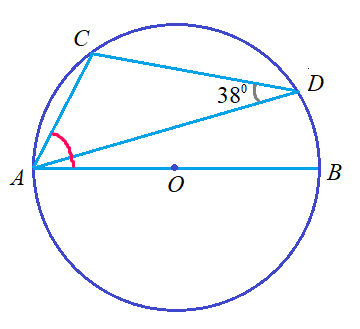
Задача 9:        Диаметр    $AB$,    угол   $CDA$   равен   38°.        Найдите    величину     угла     $CAB$.

• Решение: угол   $CDA$ –   вписанный,    значит     его   дуга     $AC^o=2cdot38^o=76^o$.         Тогда дуга     $BCD$    равна     $180 – 76 = 104^o$ ,
• но на   нее опирается   вписанный угол   $CAB$        $Rightarrow$          $CAB=frac{1}{2}104^o$            Ответ:     $CAB = 52^o$   

О главном по теме:   Центральные и вписанные углы в окружности.            1.   Центральный угол     в   окружности – угол с вершиной в ее центре и сторонами-радиусами.         2.   Дуга окружности ,    соответствующей центральному углу – часть окружности внутри плоского угла.         3.   Градусная мера     дуги окружности – градусная мера соответствующего центрального угла.   4.   Вписанный угол – вершина которого лежит на окружности, а стороны пересекают эту окружность (хорды).   ….     Вписанный угол опирается на хорду , которая соединяет точки пересечения сторон угла и окружности. …. Вписанный угол опирается на дугу, заключенную между его сторонами.     Теорема    Вписанный угол равен   половине того центрального    угла, которая опирается    на ту же дугу.

Интерактивные Упражнения:

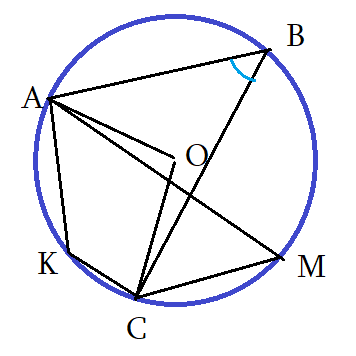
Задача 21:   Угол АВС равен 66. Найти все что можно. (Т)

Задачи из сайта https://resh.edu.ru :

Задача 22: Градусные меры дуг окружности относятся как 3 : 2 : 2 : 5. Найдите градусную меру большей из этих дуг.

Задача 23: Точки А, В, С, D отметили на окружности в порядке следования их в латинском алфавите. При этом оказалось, что дуга ВСD в 3 раза больше дуги BАD. Найдите градусную меру дуги BCD.

Задача 24: В окружности с центром О проведены две равные хорды MK и PN. Найдите градусную меру большей из дуг с концами M и K, если угол PON равен 110°

Задача 25: Вписанный угол CBA равен 80°, где AB – диаметр. Найдите угол CAB.

Задача 26: На окружности с центром в точке O взяли последовательно точки A, B, C так, что ∠AOC = 150°. Найдите градусную меру угла ABC.

Задача 27: Точки А, В и С лежат на окружности с центром О, ∠ВАС – вписанный угол. Про градусные меры дуг известно, что ∪AB : ∪BC : ∪AC = 3 : 1 : 2. Найдите АВС.

Задача 28: В окружности проведен диаметр AB и равные хорды AC и AD так, что ∠DAB = 40°. Найдите градусную меру угла CBD.

Задача 29: Три точки A,B,C делят окружность на части так, что ∪AB : ∪BC : ∪AC = 3 : 4 : 5. Найдите градусные меры из этих дуг.

Задача 30: Дана окружность с центром в точке О. На окружности взяты точки N, P, Q так, что угол РОQ в 2 раза меньше угла PON и в 3 раза меньше угла QON. Найдите градусную меру дуги PQ, которая не содержит точку N.

Задача 31: Вписанный угол ВСD равен 25°, дуга ВС имеет градусную меру 80°. Найдите градусную меру дуги CD.

Задача 32: На окружности взяли последовательно точки A, B, C, D так, что ∠ABC = 120°. Найдите градусную меру угла ADC.

Задача 33: На окружности с центром в точке О взяты точки K, М, N так, что MK – диаметр, а угол КОN равен 80°. Найдите угол КМN.

Вписанный угол, теория задачи. Друзья! В этой статье речь пойдёт о заданиях, для решения которых необходимо знать свойства вписанного угла. Это целая группа задач, они включены в ЕГЭ. Большинство из них решаются очень просто, в одно действие.

Есть задачи посложнее, но и они большой трудности для вас не представят, необходимо знать свойства вписанного угла. Постепенно мы разберём все прототипы задач, приглашаю вас на блог!

Теперь необходимая теория. Вспомним, что такое центральный и вписанный угол, хорда, дуга, на которые опираются эти углы:

Центральным углом в окружности называется плоский угол с вершиной в ее центре.

Часть окружности, расположенная внутри плоского угла, называется дугой окружности.

Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.

Угол, называется вписанным в окружность, если вершина угла лежит на окружности, а стороны угла пересекают эту окружность.

Отрезок соединяющий две точки окружности называется хордой. Самая большая хорда проходит через центр окружности и называется диаметр.

Для решения задач на вписанные в окружность углы, вам необходимо знать следующие свойства:

1. Вписанный угол равен половине центрального, опирающегося на ту же дугу.

2. Все вписанные углы, опирающиеся на одну и ту же дугу, равны. 

3. Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны.

4. Любая пара углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°.

Следствие: противолежащие углы четырёхугольника вписанного в окружность в сумме составляют 180 градусов.

5. Все вписанные углы, опирающиеся на диаметр, прямые.

Вообще, это свойство является следствием из свойства (1), это его частный случай. Посмотрите – центральный угол равен 180 градусам (и этот развёрнутый угол есть не что иное, как диаметр), значит по первому свойству вписанный угол С равен его половине, то есть 90 градусам.

Знание данного свойства помогает в решении многих задач и часто позволяет избежать лишних расчётов. Хорошо усвоив его — вы более половины задач такого типа сможете решать устно. Два следствие, которые можно сделать:

Многие прототипы стереометрических задач также решаются благодаря использованию этого свойства и данных следствий. Запомните сам факт: если диаметр окружности является стороной вписанного треугольника, то этот треугольник прямоугольный (угол лежащий против диаметра равен 90 градусов). Все остальные выводы и следствия вы сможете сделать сами, учить их не надо.

Как правило, половина  задач на вписанный угол даётся с эскизом, но без обозначений. Для понимания процесса рассуждения при решении задач (ниже в статье) введены обозначения вершин (углов). На ЕГЭ вы можете этого не делать. Рассмотрим задачи:

Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Построим центральный угол для заданного вписанного угла, обозначим вершины:

По свойству вписанного в окружность угла:

Угол АОВ равен 60⁰, так как треугольник АОВ равносторонний, а в равностороннем треугольнике все углы равны по 60⁰. Стороны треугольника равны, так как в условии сказано, что хорда равна радиусу.

Таким образом, вписанный угол АСВ равен 30⁰.

Ответ: 30 

Найдите хорду, на которую опирается угол 30⁰, вписанный в окружность радиуса 3.

Это по сути обратная задача (предыдущей). Построим центральный угол.

Он в два раза больше вписанного, то есть угол АОВ равен 60⁰. От сюда можно сделать вывод, что треугольник АОВ равносторонний. Таким образом, хорда равна радиусу, то есть трём.

Ответ: 3

Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.

Построим центральный угол:

Зная радиус и хорду мы можем найти центральный угол  АСВ. Это можно сделать по теореме косинусов. Зная центральный угол мы без труда найдём вписанный угол АСВ.

Теорема косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус  угла между ними.

Следовательно, второй центральный угол равен 360⁰ – 90⁰ = 270⁰.

Угол АСВ по свойству вписанного угла равен его половине, то есть 135 градусам.

Ответ: 135

Найдите хорду, на которую опирается угол 120 градусов, вписанный в окружность радиуса  корень из трёх.

Соединим точки А и В с центром окружности. Обозначим её как О:

Нам известен радиус и вписанный угол АСВ. Мы можем найти центральный угол АОВ (больший 180 градусов), затем найти угол АОВ в треугольнике АОВ. А далее по теореме косинусов вычислить АВ.

По свойству вписанного угла центральный угол АОВ (который больше 180 градусов) будет равен вдвое больше  вписанного, то есть 240 градусам. Значит, угол АОВ в треугольнике АОВ равен  360⁰ – 240⁰ = 120⁰.

По теореме косинусов:

Ответ:3

Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах.

По свойству вписанного угла он вдвое меньше центрального угла, опирающегося на ту же дугу, в данном случае речь идёт о дуге АВ.

Сказано, дуга АВ составляет 20 процентов от окружности. Это означает, что центральный угол АОВ составляет так же 20 процентов от 360⁰. *Окружность это угол в 360 градусов. Значит,

Таким образом, вписанный угол АСВ равен 36 градусам.

Ответ: 36

Дуга окружности AC, не содержащая точки B, составляет 200 градусов. А дуга окружности BC, не содержащая точки A, составляет 80 градусов. Найдите вписанный угол ACB. Ответ дайте в градусах.

Обозначим для наглядности дуги, угловые меры которых даны. Дуга соответствующая 200 градусам – синий цвет, дуга соответствующая 80 градусам – красный цвет, оставшаяся часть окружности – жёлтый цвет.

Таким образом, градусная мера дуги АВ (жёлтый цвет), а значит и центральный угол АОВ составляет:  360⁰ – 200⁰ – 80⁰ = 80⁰.

Вписанный угол АСВ вдвое меньше центрального угла АОВ,то есть равен 40 градусам.

Ответ: 40

Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.

Посмотреть решение

Найдите хорду, на которую опирается угол 90⁰, вписанный в окружность радиуса 1.

Посмотреть решение

Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Посмотреть решение

Радиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.

Посмотреть решение

Центральный угол на 36⁰ больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.

Посмотреть решение

Найдите вписанный угол, опирающийся на дугу АВ, которая составляет  0,2 окружности. Ответ дайте в градусах.

Посмотреть решение

Хорда делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

Посмотреть решение

Точки А, В, С, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:3:5. Найдите больший угол треугольника АВС. Ответ дайте в градусах.

Посмотреть решение

На что обратить внимание при решении подобных задач?

Необходимо знать свойство вписанного угла; понимать, когда и как необходимо использовать теорему косинусов, подробнее о ней посмотрите здесь.

На этом всё! Успехов Вам!

С уважением, Александр Крутицких

Учительница математики в школе в третьем классе:
— Дети, а скажите мне, сколько будет 6*6?
Дети дружно хором отвечают:
— Семьдесят шесть!
— Ну, что вы, такое говорите детки! Шесть на шесть будет тридцать шесть… ну может быть еще 37, 38, 39… ну максимум 40… но никак не семьдесят шесть!

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Сегодня рассмотрим с вами вопросы геометрии. Данные задачи встречаются в ОГЭ. Пусть ОГЭ отменили в этом году, но для тех, кто собирается в 9 класс, эта тема будет актуальной.

Итак, если вершина угла лежит в центре окружности, такой угол называется центральным. Если вершина угла лежит на окружности, а стороны угла являются хордами этой окружности, то угол называется вписанным.

При этом градусная мера дуги окружности и центрального угла, опирающегося на эту дугу, равны. Заметим еще, что для дуги можно построить только один центральный угол, который на нее опирается.

А вот вписанных углов, опирающихся на одну дугу, может быть множество. И их градусные меры будут равны половине градусной меры дуги, на которую они опираются.

Рассмотрим несколько задач на данную тему.

Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 59°. Ответ дайте в градусах.

Так как точки O и C лежат в одной полуплоскости относительно прямой AB, значит, углы AOB и ACB опираются на одну и ту же дугу. При этом угол AOB – центральный (вершина его в точке O), а угол ACB – вписанный. Тогда градусная мера дуги АВ равна градусной мере угла AOB. А угол ACB равен половине градусной мере дуги, то половине угла AOB. Угол АСВ равен 29,5°.

Следующая задача звучит так. Отрезки AC и BD – диаметры окружности с центром O. Угол ACB равен 19°. Найдите угол AOD. Ответ дайте в градусах.

Решать эту задачу можно и не зная ничего про вписанные и центральные углы, помня, что диаметр – это два радиуса, а углы при основании равнобедренного треугольника равны.

Угол ACB опирается на дугу AB, а угол AOD на дугу AD. При этом дуги AB и AD образуют половину окружности, так как BD – диаметр. А градусная мера половине окружности равна 360°/2=180°. Градусную меру дуги AB найти легко, достаточно просто умножить величину угла ACB на 2, так как угол ACB – вписанный, AB=38°. Тогда величина AD=180°-AB=180°-38°=142°. Угол AOD – центральный и поэтому равен 142°.

Сегодня мы рассмотрели две задачи на вписанные и центральные углы, а завтра продолжим, поэтому подписывайтесь, если хотите позаниматься на каникулах и хорошо сдать ОГЭ!

Окружность. Центральный и вписанный угол

Центральный угол — это угол, вершина которого находится в центре окружности.

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее.

Отрезок, соединяющий две точки окружности, называется хорда.

Самая большая хорда проходит через центр окружности и называется диаметр.

На рисунках — центральные и вписанные углы, а также их важнейшие свойства.

Угол, вершина которого лежит в центре окружности, называется центральным. Величина центрального угла равна угловой величине дуги, на которую он опирается. Угол тоже можно назвать центральным. Только он опирается на дугу, которая больше 180

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. Величина вписанного угла равна половине центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на диаметр, – прямой.

Величина центрального угла равна угловой величине дуги, на которую он опирается. Значит, центральный угол величиной в градусов будет опираться на дугу, равную , то есть круга. Центральный угол, равный , опирается на дугу в 60 градусов, то есть на шестую часть круга.

Докажем, что величина вписанного угла в два раза меньше центрального, опирающегося на ту же дугу.

Пусть угол AOC — центральный и опирается на дугу АС, тогда ОА и ОС — радиусы окружности.

Пусть ABC — вписанный угол, опирающийся на дугу АС,

АВ и ВС — хорды окружности.

Первый случай: Точка O лежит на BC, то есть ВС — диаметр окружности.

Треугольник AOB — равнобедренный, АО = ОВ как радиусы. Значит,

— внешний угол а внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Получили, что

Второй случай: Центр окружности точка О не лежит на ВС. Построим диаметр BК:

Если точка О лежит внутри вписанного угла АВС, как на рисунке слева, то

Если О лежит вне вписанного угла АВС, как на рисунке справа, то

Мы получили, что в каждом из этих случаев величина центрального угла в два раза больше, чем величина вписанного угла, опирающегося на ту же дугу.

Теорема доказана.

При решении задач по геометрии также применяются следующие теоремы:

1. Равные центральные углы опираются на равные хорды.

2. Равные вписанные углы опираются на равные хорды.

3. Равные хорды стягивают равные дуги.

Докажем теорему 3.

Пусть хорды AB и CD равны. Докажем, что AMB дуги CND имеют одинаковую градусную меру, то есть равны.

Доказательство:

По условию, AB = CD. Соединим концы хорд с центром окружности. Получим: AO = BO = CO = DO = r.

по трем сторонам, отсюда следует, что центральные углы равны, т.е. Значит, и дуги, на которые они опираются, также равны, т.е. дуги AMB и CND имеют одинаковую градусную меру.

Теорема доказана.

Верна и обратная теорема:

Если две дуги окружности равны, то равны и хорды, их стягивающие.

Пусть дуги AMB и CND равны. Тогда как центральные углы, опирающиеся на эти дуги. Значит, треугольники и равны по двум сторонам и углу между ними, и тогда что и требовалось доказать.

Эти две теоремы можно объединить в одну, которая формулируется так:

Хорды окружности равны тогда и только тогда, когда равны дуги, которые они стягивают.

Разберем задачи ЕГЭ и ОГЭ по теме: Окружность, центральный угол, вписанный угол.

Задача 1, ЕГЭ. Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.

Вписанный угол, опирающийся на диаметр, — прямой.

Ответ: 90.

Задача 2, ЕГЭ. Центральный угол на больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.

Решение:

Пусть центральный угол равен , а вписанный угол, опирающийся на ту же дугу, равен .

Мы знаем, что

Отсюда

Ответ: 36.

Задача 3, ЕГЭ. Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную Ответ дайте в градусах.

Решение:

Пусть хорда AB равна  Тупой вписанный угол, опирающийся на эту хорду, обозначим В треугольнике AOB стороны AO и OB равны 1, сторона AB равна  Нам уже встречались такие треугольники. Очевидно, что треугольник AOB — прямоугольный и равнобедренный, то есть угол AOB равен 90 Тогда дуга ACB равна 90 а дуга AKB равна Вписанный угол  опирается на дугу AKB и равен половине угловой величины этой дуги, то есть 135.

Ответ: 135.

Задача 4, ЕГЭ. Хорда AB делит окружность на две части, градусные величины которых относятся как 5 : 7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

Решение:

Главное в этой задаче — правильный чертеж и понимание условия. Как вы понимаете вопрос: «Под каким углом хорда видна из точки С?»

Представьте, что вы сидите в точке С и вам необходимо видеть всё, что происходит на хорде AB. Так, как будто хорда AB — это экран в кинотеатре 🙂
Очевидно, что найти нужно угол ACB.
Сумма двух дуг, на которые хорда AB делит окружность, равна то есть

Отсюда и тогда вписанный угол ACB опирается на дугу, равную Величина вписанного угла равна половине угловой величины дуги, на которую он опирается, значит, угол ACB равен

Ответ: 105.

Задача 5, ЕГЭ.

Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32

Решение:

Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

Значит,

Ответ: 64.

Задача 6, ЕГЭ. Найдите центральный угол AOB, если он на больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах.

Решение:

Пусть величина угла АОВ равна градусов. Величина вписанного угла АСВ равна половине центрального угла, опирающегося на ту же дугу, то есть градусов.

Получим уравнение: откуда

Ответ: 30.

Задача 7, ЕГЭ. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Решение.

Рассмотрим треугольник AOB. Он равносторонний, так как AO = OB = AB = R.

Поэтому угол AOB = 60. Вписанный угол ACB равен половине дуги, на которую он опирается, то есть 30

Ответ: 30.

Задача 8, ЕГЭ.

Дуга окружности AC, не содержащая точки B, составляет 200 А дуга окружности BC, не содержащая точки A, составляет 80 Найдите вписанный угол ACB. Ответ дайте в градусах.

Решение:

Вписанный угол равен половине угловой величины дуги, на которую он опирается. Дуга АВ равна Тогда

Ответ: 40.

Задачи ОГЭ по теме: Центральный и вписанный угол, градусная мера дуги.

Задача 9, ОГЭ. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен Найдите радиус окружности.

Решение.

Рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу окружности.

Углы при основании равнобедренного треугольника равны. Пусть AOB равен , тогда где Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.

Ответ: 6.

Задача 10, ОГЭ. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен Найдите величину угла OAB.

Решение.

Вписанные углы ВСD и ВАD опираются на одну и ту же дугу окружности, поэтому они равны, угол

Ответ: 30.

Задача 11, ОГЭ. Найдите градусную меру центрального MON, если известно, что NP — диаметр, а градусная мера MNP равна 18

Решение:

Треугольник MON — равнобедренный. Тогда −

Ответ: 144.

Задача 12, ОГЭ.

Найдите DEF, если градусные меры дуг DE и EF равны и соответственно.

Решение.

Дуга FD, не содержащая точку Е, равна Вписанный угол DEF, опирающийся на эту дугу, равен половине ее угловой величины,

Ответ: 71.

Задача 13, ОГЭ. В окружности с центром O AC и BD — диаметры. Угол ACB равен Найдите угол AOD. Ответ дайте в градусах.

Решение.

Угол ACB — вписанный, он равен половине центрального угла, опирающегося на ту же дугу, то есть AОВ = 52 Угол ВОD — развернутый, поэтому угол AOD равен

Ответ: 128.