Как найти вращательный момент системы - Сайт, где вы сможете решить свои вопросы

Момент силы

Размерность	L²MT⁻²
Единицы измерения
СИ	Н·м
СГС	Дина-сантиметр
Примечания
Псевдовектор

Моме́нт си́лы (момент силы относительно точки) — векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение. Определяется как векторное произведение радиус-вектора точки приложения силы и вектора силы vec{F} . Моменты сил, образующиеся в разных условиях, в технике могут иметь названия: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент, скру́чивающий момент.

Момент силы обозначается символом или, реже, (тау).

Единица измерения в СИ: Н⋅м. Величина момента силы зависит от выбора начала отсчёта радиус-векторов O.

Понятие момента силы используется, в основном, в области задач статики и задач, связанных с вращением деталей (рычагов и др.) в технической механике. Особенно важен случай вращения твёрдого тела вокруг фиксированной оси — тогда O выбирают на этой оси, а вместо самого момента рассматривают его проекцию на ось ${displaystyle M_{parallel }}$ ; такая проекция называется моментом силы относительно оси.

Наличие момента силы влечёт изменение момента импульса тела vec{L} относительно того же начала O со временем : имеет место соотношение . В статике равенство нулю суммы моментов всех приложенных к телу сил является одним из условий (наряду с равенством нулю суммы сил) реализации состояния покоя.

Определение, общие сведения[править | править код]

В физике момент силы играет роль вращающего воздействия на тело.

Видеоурок: вращающий момент

В простейшем случае, если сила vec{F} приложена к рычагу перпендикулярно ему и оси вращения, то момент силы определяется как произведение величины на расстояние от места приложения силы до оси вращения рычага, называемое «плечом силы»:

Например, сила в 3 ньютона, приложенная на расстоянии 2 м от оси, создаёт такой же момент, что и сила в 1 ньютон с плечом 6 м.

Если действуют две силы, говорят о моменте пары сил (такая формулировка восходит к трудам Архимеда). При этом равновесие достигается в ситуации ${displaystyle F_{1}x_{1}=F_{2}x_{2}}$ .

Для случаев более сложных движений и более сложных объектов определение момента как произведения требует универсализации.

Момент силы иногда называют вращающим или крутящим моментом. «Вращающий» момент понимается в технике как внешнее усилие, прикладываемое к объекту, а «крутящий» — как внутреннее, возникающее в самом объекте под действием приложенных нагрузок (этим понятием оперируют в сопромате).

Момент силы относительно точки[править | править код]

Момент силы, приложенный к гаечному ключу. Направлен от зрителя

В общем случае момент силы vec{F} , приложенной к телу, определяется как векторное произведение

{displaystyle {vec {M}}=left[{vec {r}}times {vec {F}}right]}

где — радиус-вектор точки приложения силы. Вектор перпендикулярен векторам и vec{F} .

Начало отсчета радиус-векторов O может быть любым. Обычно O выбирают в чем-либо выделенной точке: в месте закрепления подвеса, в центре масс, на оси вращения и т.д.. Если одновременно анализируется момент импульса тела vec{L} , то начало O всегда выбирается одинаковым для vec{L} и .

Если не оговорено иное, то «момент силы» — это момент силы относительно точки (O), а не некоей оси.

В случае нескольких приложенных сосредоточенных сил их моменты векторно суммируются:

${displaystyle {vec {M}}=sum _{i}left[{vec {r}}_{i}times {vec {F}}_{i}right]}$

где ${displaystyle {vec {r}}_{i}}$ — радиус-вектор точки приложения -й силы ${displaystyle {vec {F}}_{i}}$ . В случае силы, распределённой с плотностью ,

${displaystyle {vec {M}}=int limits _{V}left[{vec {r}}times {frac {d{vec {F}}}{dV}}right]dV}$

Если (Н/м³) — обобщённая функция, которая может содержать и дельтаобразные члены, то последней формулой охватываются и две предыдущие.

Момент силы относительно оси[править | править код]

Моментом силы относительно оси называется алгебраическое значение проекции момента на ось, то есть

${displaystyle M_{parallel }={vec {M}}cdot {vec {e}}_{o}}$

где ${displaystyle {vec {e}}_{o}}$ — единичный вектор вдоль оси, а начало отсчёта O выбрано на оси. Момент силы относительно оси может быть рассчитан как

${displaystyle M_{parallel }=pm left|{vec {r}}_{perp }times {vec {F}}_{perp }right|}$

где через ${displaystyle {vec {r}}_{perp }}$ и ${displaystyle {vec {F}}_{perp }}$ обозначены составляющие радиус-вектора и силы в плоскости, перпендикулярной оси.

В отличие от момента силы , величина момента силы относительно оси ${displaystyle M_{parallel }}$ не претерпевает изменения при сдвиге точки O вдоль оси.

Для краткости символ параллельности и знак могут опускаться, а ${displaystyle M_{parallel }}$ (как и ) именоваться «моментом силы».

Единицы измерения[править | править код]

Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.

Формально, размерность (Н·м) совпадает с размерностями энергии и механической работы.

Некоторые примеры[править | править код]

Формула момента рычага[править | править код]

Момент, действующий на рычаг

Момент силы, действующей на рычаг, равен

${displaystyle {vec {M}}=rFsin alpha cdot {vec {e}}_{o}}$

или, если записать момент силы относительно оси,

${displaystyle M_{parallel }=rFsin alpha }$

где alpha — угол между направлением силы и рычагом. Плечо силы равно . Максимальное значение момента достигается при перпендикулярности рычага и силы, то есть при . При сонаправленности vec{F} и рычага момент равен нулю.

Статическое равновесие[править | править код]

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма моментов всех сил вокруг любой точки.

Для двумерного случая с горизонтальными и вертикальными силами требование сводится к тому, чтобы нулевыми были сумма сил в двух измерениях: ${displaystyle Sigma F_{horizontal}=0,,Sigma F_{vertical}=0}$ и момент силы в третьем измерении: .

Движение твёрдого тела[править | править код]

Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.

Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.

${displaystyle {vec {L_{o}}}=I_{c},{vec {omega }}+[M({vec {r_{o}}}-{vec {r_{c}}}),{vec {v_{c}}}].}$

Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.

Продифференцируем это выражение по времени. И если — постоянная величина во времени, то

${displaystyle {vec {M}}=I{frac {d{vec {omega }}}{dt}}=I{vec {alpha }},}$

где — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с²). Пример: вращается однородный диск.

Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:

${displaystyle {vec {M_{c}}}=I_{c}{frac {d{vec {omega }}}{dt}}+[{vec {w}},I_{c}{vec {w}}].}$

Связь с другими величинами[править | править код]

С моментом импульса[править | править код]

Момент силы — производная момента импульса относительно точки O по времени:

${displaystyle {vec {M}}={frac {d{vec {L}}}{dt}}}$

Аналогичную формулу можно записать для моментов относительно оси:

${displaystyle M_{parallel }={frac {dL_{parallel }}{dt}}}$

Если момент силы или ${displaystyle M_{parallel }}$ равен нулю, момент импульса относительно соответствующей точки или оси сохраняется.

С мощностью[править | править код]

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу и развивает мощность (где vec{v} — скорость материальной точки). Так же и в случае момента силы: если он совершает действие через «угловое расстояние», развивается мощность

{displaystyle P={vec {M}}cdot {vec {omega }}}

В системе СИ мощность измеряется в ваттах, угловая скорость — в радианах в секунду.

С механической работой[править | править код]

Если под действием момента силы происходит поворот тела на угол dvarphi , то совершается механическая работа

{displaystyle dA=left|{vec {M}}right|dvarphi }

Для поворота, скажем, рычага вокруг фиксированной оси на угол ${displaystyle varphi _{2}-varphi _{1}}$ получим

${displaystyle A=int _{varphi _{1}}^{varphi _{2}}left|{vec {M}}right|dvarphi =left|{vec {M}}right|(varphi _{2}-varphi _{1})=left|{vec {M}}right|int _{t_{1}}^{t_{2}}omega (t)dt}$

В системе СИ работа измеряется в джоулях, угол — в радианах.

Размерность работы (и энергии) совпадает с размерностью момента силы («ньютон-метр» и джоуль — это одни и те же единицы). Момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию 2pi джоуля.

Измерение момента силы[править | править код]

Измерение момента силы осуществляется с помощью специальных приборов — торсиометров. Принцип их действия обычно основан на измерении угла закручивания упругого вала, передающего крутящий момент, либо на измерении деформации некоторого упругого рычага. Измерения деформации и угла закручивания производится различными датчиками деформации — тензометрическими, магнитоупругими, а также измерителями малых перемещений — оптическими, ёмкостными, индуктивными, ультразвуковыми, механическими.

Существуют специальные динамометрические ключи для измерения крутящего момента затягивания резьбовых соединений и регулируемые и нерегулируемые ограничители крутящего момента, так называемые «трещотки», применяемые в гаечных ключах, шуруповёртах, винтовых микрометрах и др.

Из истории понятия[править | править код]

Для того чтобы понять, откуда появилось понятие момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы на рычаг , совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол dvarphi . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между векторами и равен beta , а угол между векторами и равен alpha .

Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке , равна скалярному произведению вектора и вектора силы, то есть .

Теперь попытаемся выразить модуль вектора через радиус-вектор , а проекцию вектора силы на вектор — через угол alpha .

Так как для бесконечно малого перемещения рычага можно считать, что траектория перемещения перпендикулярна рычагу , используя соотношения для прямоугольного треугольника, можно записать следующее равенство: , где в случае малого угла справедливо и, следовательно, .

Для проекции вектора силы на вектор видно, что угол ${displaystyle beta ={frac {pi }{2}}-alpha }$ , а так как ${displaystyle cos {left({frac {pi }{2}}-alpha right)}=sin alpha }$ , получаем, что .

Теперь запишем бесконечно малую работу через новые равенства: , или .

Видно, что произведение есть не что иное, как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы , или модуль вектора момента силы .

Теперь полная работа записывается просто: ${displaystyle A=int limits _{0}^{varphi }left|{vec {r}}times {vec {F}}right|dvarphi }$ , или ${displaystyle A=int limits _{0}^{varphi }left|{vec {M}}right|dvarphi }$ .

См. также[править | править код]

Момент инерции
Момент импульса
Теорема Вариньона

Источник

Вращение является типичным видом механического движения, которое часто встречается в природе и технике. Любое вращение возникает в результате воздействия некоторой внешней силы на рассматриваемую систему. Эта сила создает так называемый вращающий момент. Что он собой представляет, от чего зависит, рассматривается в статье.

Процесс вращения

Прежде чем рассматривать концепцию вращающего момента, дадим характеристику систем, к которым может быть применена эта концепция. Система вращения предполагает наличие в ней оси, вокруг которой осуществляется круговое движение или поворот. Расстояние от этой оси до материальных точек системы называется радиусом вращения.

С точки зрения кинематики, процесс характеризуется тремя угловыми величинами:

углом поворота θ (измеряется в радианах);
угловой скоростью ω (измеряется в радианах в секунду);
ускорением угловым α (измеряется в радианах в секунду квадратную).

Эти величины связаны друг с другом следующими равенствами:

ω = dθ/dt;

α = dω/dt.

Примерами вращения в природе являются движения планет по своим орбитам и вокруг своих осей, движения смерчей. В быту и технике рассматриваемое движение характерно для моторов двигателей, гаечных ключей, строительных кранов, открывания дверей и так далее.

Определение момента силы

Теперь перейдем к непосредственной теме статьи. Согласно физическому определению, момент силы представляет собой векторное произведение вектора приложения силы относительно оси вращения на вектор самой силы. Соответствующее математическое выражение можно записать так:

M¯ = [r¯*F¯].

Здесь вектор r¯ направлен от оси вращения к точке приложения силы F¯.

В этой формуле вращающего момента M¯ сила F¯ может быть направлена как угодно относительно направления оси. Тем не менее параллельная оси компонента силы не будет создавать вращения, если ось жестко закреплена. В большинстве задач по физике приходится рассматривать силы F¯, которые лежат в плоскостях перпендикулярных оси вращения. В этих случаях абсолютное значение вращающего момента можно определить по следующей формуле:

|M¯| = |r¯|*|F¯|*sin(β).

Где β является углом между векторами r¯ и F¯.

Что такое рычаг силы?

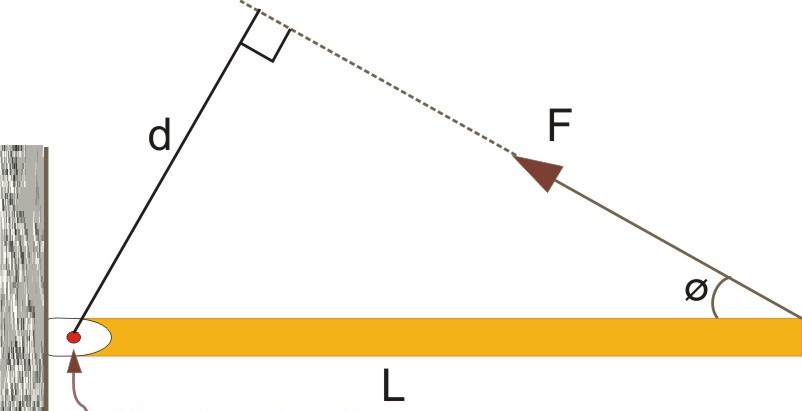
Рычаг силы играет важную роль при определении величины момента силы. Чтобы понять, о чем идет речь, рассмотрим следующий рисунок.

Здесь показан некоторый стержень длиною L, который закреплен в точке вращения одним из своих концов. На другой конец действует сила F, направленная под острым углом φ. Согласно определению момента силы, можно записать:

M = F*L*sin(180^o-φ).

Угол (180^o-φ) появился потому, что вектор L¯ направлен от закрепленного конца к свободному. Учитывая периодичность тригонометрической функции синуса, можно переписать это равенство в таком виде:

M = F*L*sin(φ).

Теперь обратим внимание на прямоугольный треугольник, построенный на сторонах L, d и F. По определению функции синуса, произведение гипотенузы L на синус угла φ дает значение катета d. Тогда приходим к равенству:

M = F*d.

Линейная величина d называется рычагом силы. Он равен расстоянию от вектора силы F¯ до оси вращения. Как видно из формулы, понятием рычага силы удобно пользоваться при вычислении момента M. Полученная формула говорит о том, что вращающий момент максимальный для некоторой силы F будет возникать только тогда, когда длина радиус-вектора r¯ (L¯ на рисунке выше) будет равна рычагу силы, то есть r¯ и F¯ будут взаимно перпендикулярны.

Направление действия величины M¯

Выше было показано, что вращающий момент – это векторная характеристика для данной системы. Куда направлен этот вектор? Ответить на этот вопрос не представляет особого труда, если вспомнить, что результатом произведения двух векторов является третий вектор, который лежит на оси, перпендикулярной плоскости расположения исходных векторов.

Остается решить, будет ли направлен момент силы вверх или вниз (на читателя или от него) относительно упомянутой плоскости. Определить это можно или по правилу буравчика, или с помощью правила правой руки. Приведем оба правила:

Правило правой руки. Если расположить правую кисть таким образом, чтобы четыре ее пальца двигались от начала вектора r¯ к его концу, а затем от начала вектора F¯ к его концу, то большой палец, оттопыренный, укажет на направление момента M¯.
Правило буравчика. Если направление вращения воображаемого буравчика совпадает с направлением вращательного движения системы, то поступательное движение буравчика укажет на направление вектора M¯. Напомним, что он вращается только по часовой стрелке.

Оба правила являются равноправными, поэтому каждый может использовать то, которое является для него более удобным.

При решении практических задач разное направление вращающего момента (вверх – вниз, влево – вправо) учитывается с помощью знаков “+” или “-“. Следует запомнить, что за положительное направление момента M¯ принято считать такое, которое приводит к вращению системы против часовой стрелки. Соответственно, если некоторая сила приводит к вращению системы по ходу стрелки часов, то создаваемый ее момент будет иметь отрицательную величину.

Физический смысл величины M¯

В физике и механике вращения величина M¯ определяет способность силы или суммы сил совершать вращение. Поскольку в математическом определении величины M¯ стоит не только сила, но и радиус-вектор ее приложения, то именно последний во многом определяет отмеченную вращательную способность. Чтобы понятнее было, о какой способности идет речь, приведем несколько примеров:

Каждый человек, хотя бы один раз в жизни пытался открыть дверь, взявшись не за ручку, а толкнув ее недалеко от петель. В последнем случае приходится прилагать значительное усилие, чтобы добиться желаемого результата.
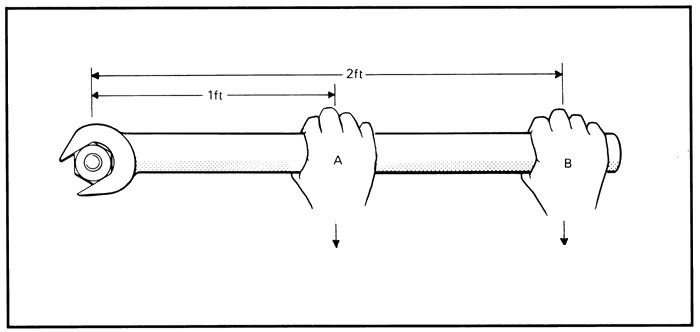
Чтобы открутить гайку с болта, используют специальные гаечные ключи. Чем длиннее ключ, тем легче открутить гайку.
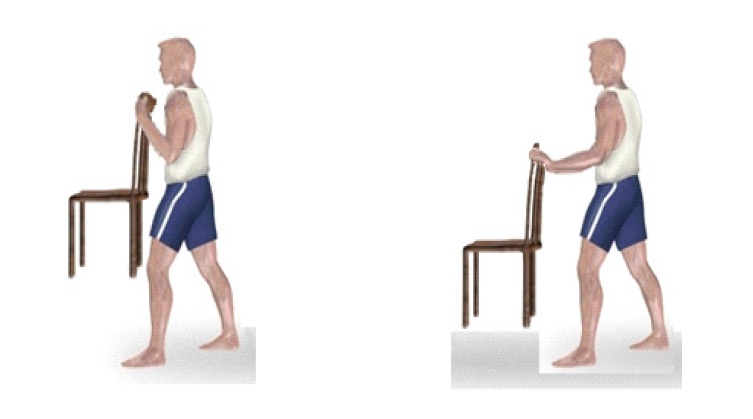
Чтобы ощутить важность рычага силы, предлагаем читателям проделать следующий эксперимент: взять стул и попытаться удержать его одной рукой на весу, в одном случае руку прислонить к телу, в другом – выполнить задачу на прямой руке. Последнее для многих окажется непосильной задачей, хотя вес стула остался тем же самым.

Единицы измерения момента силы

Несколько слов также следует сказать о том, в каких единицах в СИ измеряется вращающий момент. Согласно записанной для него формуле, он измеряется в ньютонах на метр (Н*м). Однако в этих единицах также измеряется работа и энергия в физике (1 Н*м = 1 джоуль). Джоуль для момента M¯ не применяется, поскольку работа является скалярной величиной, M¯ же – это вектор.

Тем не менее совпадение единиц момента силы с единицами энергии не является случайным. Работа по вращению системы, совершенная моментом M, рассчитывается по формуле:

A = M*θ.

Откуда получаем, что M также может быть выражен в джоулях на радиан (Дж/рад).

Динамика вращения

В начале статьи мы записали кинематические характеристики, которые используются для описания движения вращения. В динамике вращения главным уравнением, которое использует эти характеристики, является следующее:

M = I*α.

Действие момента M на систему, имеющую момент инерции I, приводит к появлению углового ускорения α.

Данную формулу применяют, для определения угловых частот вращения в технике. Например, зная вращающий момент асинхронного двигателя, который зависит от частоты тока в катушке статора и от величины изменяющегося магнитного поля, а также зная инерционные свойства вращающегося ротора, можно определить, до какой скорости вращения ω раскручивается ротор двигателя за известное время t.

Пример решения задачи

Невесомый рычаг, длина которого составляет 2 метра, посередине имеет опору. Какой вес следует положить на один конец рычага, чтобы он находился в состоянии равновесия, если с другой стороны опоры на расстоянии 0,5 метра от нее лежит груз массой 10 кг?

Очевидно, что равновесие рычага наступит, если моменты сил, создаваемые грузами, будут равны по модулю. Сила, создающая момент в данной задаче, представляет собой вес тела. Рычаги силы равны расстояниям от грузов до опоры. Запишем соответствующее равенство:

M₁ = M₂ =>

m₁*g*d₁ = m₂*g*d₂=>

P₂ = m₂*g = m₁*g*d₁/d₂.

Вес P₂ получим, если подставим из условия задачи значения m₁ = 10 кг, d₁ = 0,5 м, d₂ = 1 м. Записанное равенство дает ответ: P₂ = 49,05 ньютона.

Источник

Загрузить PDF

Самое лучшее определение вращательного момента – это тенденция силы вращать предмет вокруг оси, точки опоры или точки вращения. Вращательный момент можно рассчитать с помощью силы и плеча момента (перпендикулярное расстояние от оси до линии действия силы), или используя момент инерции и угловое ускорение.

1
Определите силы, действующие на тело и соответствующие им моменты. Если сила не перпендикулярна рассматриваемому плечу момента (т.е. она действует под углом), то вам может понадобиться найти ее составляющие с использованием тригонометрических функций, таких как синус или косинус.
- Рассматриваемая составляющая силы будет зависеть от эквивалента перпендикулярной силы.
- Представьте себе горизонтальный стержень, к которому нужно приложить силу 10 Н под углом 30° над горизонтальной плоскостью, чтобы вращать его вокруг центра.
- Поскольку вам нужно использовать силу, не перпендикулярную плечу момента, то для вращения стержня вам необходима вертикальная составляющая силы.
- Следовательно, нужно рассматривать y-составляющую, или использовать F = 10sin30° Н.
2
Воспользуйтесь уравнением момента, τ = Fr, и просто замените переменные заданными или полученными данными.
- Простой пример: Представьте себе ребенка массой 30 кг, сидящего на одном конце качели-доски. Длина одной стороны качели составляет 1,5 м.
- Поскольку ось вращения качели находится в центре, вам не нужно умножать длину.
- Вам необходимо определить силу, прилагаемую ребенком, с помощью массы и ускорения.
- Поскольку дана масса, вам нужно умножить ее на ускорение свободного падения, g, равное 9,81 м/с². Следовательно:
- Теперь у вас есть все необходимые данные для использования уравнения момента:
3
Воспользуйтесь знаками (плюс или минус), чтобы показать направление момента. Если сила вращает тело по часовой стрелке, то момент отрицательный. Если же сила вращает тело против часовой стрелки, то момент положительный.
- В случае нескольких приложенных сил, просто сложите все моменты в теле.
- Поскольку каждая сила стремится вызвать различные направления вращения, важно использовать знак поворота для того, чтобы следить за направлением действия каждой силы.
- Например, к ободу колеса, имеющего диаметр 0,050 м, были приложены две силы, F₁= 10,0 Н, направленная по часовой стрелке, и F₂ = 9,0 Н, направленная против часовой стрелки.
- Поскольку данное тело – круг, фиксированная ось является его центром. Вам нужно разделить диаметр и получить радиус. Размер радиуса будет служить плечом момента. Следовательно, радиус равен 0,025 м.
- Для ясности мы можем решить отдельные уравнения для каждого из моментов, возникающих от соответствующей силы.
- Для силы 1 действие направлено по часовой стрелке, следовательно, создаваемый ею момент отрицательный:
- Для силы 2 действие направлено против часовой стрелки, следовательно, создаваемый ею момент положительный:
- Теперь мы можем сложить все моменты, чтобы получить результирующий вращательный момент:
Реклама

1
Чтобы начать решать задачу, разберитесь в том, как действует момент инерции тела. Момент инерции тела – это сопротивление тела вращательному движению. Момент инерции зависит как от массы, так и от характера ее распределения.
- Чтобы четко понимать это, представьте себе два цилиндра одинакового диаметра, но разной массы.
- Представьте себе, что вам нужно повернуть оба цилиндра вокруг их центральной оси.
- Очевидно, что цилиндр с большей массой будет сложнее повернуть, чем другой цилиндр, поскольку он “тяжелее”.
- А теперь представьте себе два цилиндра различных диаметров, но одинаковой массы. Чтобы выглядеть цилиндрическими и иметь разную массу, но в то же время иметь разные диаметры, форма, или распределение массы обоих цилиндров должна отличаться.
- Цилиндр с большим диаметром будет выглядеть как плоская закругленная пластина, тогда как меньший цилиндр будет выглядеть как цельная трубка из ткани.
- Цилиндр с большим диаметром будет сложнее вращать, поскольку вам нужно приложить большую силу, чтобы преодолеть более длинное плечо момента.
2
Выберите уравнение, которое вы будете использовать для расчета момента инерции. Есть несколько уравнений, которые можно использовать для этого.
- Первое уравнение – самое простое: суммирование масс и плечей моментов всех частиц.
- Это уравнение используется для материальных точек, или частиц. Идеальная частица – это тело, имеющее массу, но не занимающее пространства.
- Другими словами, единственной значимой характеристикой этого тела является масса; вам не нужно знать его размер, форму или строение.
- Идея материальной частицы широко используется в физике с целью упрощения расчетов и использования идеальных и теоретических схем.
- Теперь представьте себе объект вроде полого цилиндра или сплошной равномерной сферы. Эти предметы имеют четкую и определенную форму, размер и строение.
- Следовательно, вы не можете рассматривать их как материальную точку.
- К счастью, можно использовать формулы, применимые к некоторым распространенным объектам:
3
Найдите момент инерции. Чтобы начать рассчитывать вращательный момент, нужно найти момент инерции. Воспользуйтесь следующим примером как руководством:
- Два небольших “груза” массой 5,0 кг и 7,0 кг установлены на расстоянии 4,0 м друг от друга на легком стержне (массой которого можно пренебречь). Ось вращения находится в середине стержня. Стержень раскручивается из состояния покоя до угловой скорости 30,0 рад/с за 3,00 с. Рассчитайте производимый вращательный момент.
- Поскольку ось вращения находится в середине стержня, то плечо момента обоих грузов равно половине его длины, т.е. 2,0 м.
- Поскольку форма, размер и строение “грузов” не оговаривается, мы можем предположить, что грузы являются материальными частицами.
- Момент инерции можно вычислить следующим образом:
4
Найдите угловое ускорение, α. Для расчета углового ускорения можно воспользоваться формулой α= at/r.
- Первая формула, α= at/r, может использоваться в том случае, если дано тангенциальное ускорение и радиус.
- Тангенциальное ускорение – это ускорение, направленное по касательной к направлению движения.
- Представьте себе объект, двигающийся по криволинейному пути. Тангенциальное ускорение – это попросту его линейное ускорение на любой из точек всего пути.
- В случае второй формулы, легче всего проиллюстрировать ее, связав с понятиями из кинематики: смещением, линейной скоростью и линейным ускорением.
- Смещение – это расстояние, пройденное объектом (единица СИ – метры, м); линейная скорость – это показатель изменения смещения за единицу времени (единица СИ – м/с); линейное ускорение – это показатель изменения линейной скорости за единицу времени (единица СИ – м/с²).
- Теперь давайте рассмотрим аналоги этих величин при вращательном движении: угловое смещение, θ – угол поворота определенной точки или отрезка (единица СИ – рад); угловая скорость, ω – изменение углового смещения за единицу времени (единица СИ – рад/с); и угловое ускорение, α – изменение угловой скорости за единицу времени (единица СИ – рад/с²).
- Возвращаясь к нашему примеру – нам были даны данные для углового момента и время. Поскольку вращение начиналось из состояния покоя, то начальная угловая скорость равна 0. Мы можем воспользоваться уравнением, чтобы найти:
5
Воспользуйтесь уравнением, τ = Iα, чтобы найти вращательный момент. Просто замените переменные ответами, полученными на предыдущих шагах.
- Вы можете заметить, что единица “рад” не подходит к нашим единицам измерения, поскольку считается безразмерной величиной.
- Это значит, что вы можете пренебречь ею и продолжить ваши расчеты.
- Для анализа единиц измерения мы можем выразить угловое ускорение в с^-2.
Реклама

Советы

В первом методе, если тело является кругом и ось его вращения находится в центре, то рассчитывать составляющие силы не нужно (при условии, что сила не приложена под наклоном), поскольку сила лежит на касательной к окружности, т.е. перпендикулярно плечу момента.
Если вам сложно представить, как происходит вращение, то возьмите ручку и попробуйте воссоздать задачу. Для более точного воспроизведения не забудьте скопировать положение оси вращения и направление приложенной силы.

Об этой статье

Эту страницу просматривали 23 880 раз.

Была ли эта статья полезной?

Источник

Словосочетания «момент силы» и «вращательный момент» — это синонимы. Можно употреблять любой из них.

Сила может заставлять тело двигаться:

поступательно,
или вращательно.

В этой статье будем рассматривать вращательное движение.

Рекомендую также ознакомиться со статьей о видах механического движения (откроется в новой вкладке).

Что такое линия действия силы

Линия действия – это прямая линия, на которой лежит вектор.

Провести эту линию легко. Приложить линейку к вектору и пунктиром провести прямую, продолжив ее в обе стороны от вектора.

Рис. 1. Линия (пунктир), на которой лежит вектор, называется линией действия вектора

Что такое плечо силы и как его нарисовать

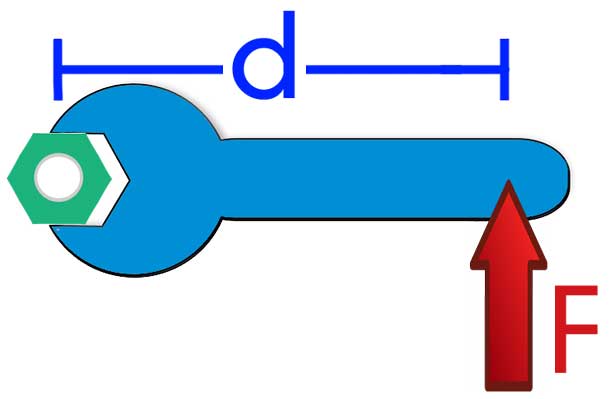
Предположим, нужно с помощью ключа закрутить гайку (см. рис. 2).

Рис. 2. Красная точка, вокруг которой вращается ключ — это центр гайки

Винт, на который накручена гайка – это ось вращения. Ключ может вращаться вокруг красной точки. Для упрощения назовем ее кратко: «точка вращения».

Примечание:

Ось вращения проходит перпендикулярно плоскости рисунка через красную точку. Используем вместо оси вращения термин «точка вращения» для простоты.

Рассмотрим следующий рисунок (см. рис. 3)

Рис. 3. Плечо силы – это перпендикуляр ( l ). Он соединяет линию действия силы с точкой вращения

На рисунке 3 черная стрелка – это вектор силы, которая вращает ключ. Пунктир – линия действия силы. Из красной точки к линии действия силы проведен перпендикуляр. Этот перпендикуляр, обозначенный ( l ), называется плечом силы.

Перпендикуляр к линии действия легко провести с помощью прямоугольного треугольника (см. рис. 4):

Рис. 4. Один катет приложим к линии действия силы, вдоль второго проведем перпендикуляр к точке вращения

Плечо силы проводят так:

взять прямоугольный треугольник;
приложить один из катетов к линии действия;
провести перпендикуляр к точке вращения, используя второй катет;

Момент силы, формула

Момент силы (вращательный момент) можно вычислить, когда известны сила и ее плечо.

Перемножим силу на плечо силы, получим момент силы.

[ large boxed { M = F cdot l } ]

( M left( H cdot text{м} right) ) – момент силы (вращательный момент);

( F left( H right) ) – сила, которая вращает тело;

( l left( text{м} right) ) – плечо этой силы;

Примечание:

Отрезок, не перпендикулярный силе, плечом силы не является. Сила и ее плечо всегда перпендикулярны!

Еще одна формула для момента силы

Вращательный момент можно рассчитать еще одним способом.

Для этого вместо плеча силы нужно использовать:

величину ( d ) и
угол ( gamma ) между силой и этим расстоянием.

Величина ( d ) – это расстояние между двумя точками:

точкой, к которой приложена сила
и точкой, вокруг которой происходит вращение.

Рис. 5. Момент силы можно рассчитать, зная: — силу; — расстояние между точками приложения силы и вращения; — угол между силой и этим расстоянием

На рисунке 5: черная стрелка – это вектор вращающей силы ( vec{ F } ); красная линия – это расстояние ( d ) между точкой приложения силы и точкой вращения.

[ large boxed { M = F cdot d cdot sin(gamma) } ]

Этой формулой во многих случаях пользоваться удобнее, чем формулой, содержащей ( l ) плечо силы.

Когда момент силы обращается в ноль

Рассмотрим внимательнее формулу для момента силы.

[ M = F cdot d cdot sin(gamma) ]

В правой части формулы находятся три множителя: ( F ) , (d) и ( sin(gamma) )

Если любой из трех множителей будет равен нулю, то правая часть уравнения обратится в ноль.

Левая часть уравнения, при этом, также, обратится в ноль. Потому, что между левой и правой частями записан знак равенства.

Кратко: Вращательный момент будет нулевым в любом из таких случаев:

( F = 0) – когда вращающая сила отсутствует;
(d = 0 ) – когда сила приложена к точке вращения;
( sin(gamma) = 0 ) – когда сила ( F ) и величина (d ) лежат на одной прямой. В таком случает, угол между величинами ( F ) и (d ) равен нулю;

Действительно: ( sin(0) = 0 ), такое будет, когда ( F || d )

Эти три случая изображены на рисунке 6.

Рис. 6. Сверху вниз представлены три случая, в которых вращательный момент обращается в ноль

На рисунке 6: черная стрелка – это вектор силы, красная линия – это расстояние между точкой приложения силы и точкой вращения.

Сверху вниз представлены три случая для нулевого вращательного момента.

В верхней части рисунка сила отсутствует;
Средняя часть рисунка соответствует случаю, когда сила (черная стрелка) приложена к точке, вокруг которой тело может вращаться;
Внизу — сила ( F ) параллельна величине (d ) — расстоянию между точкой приложения силы и точкой вращения.

Источник

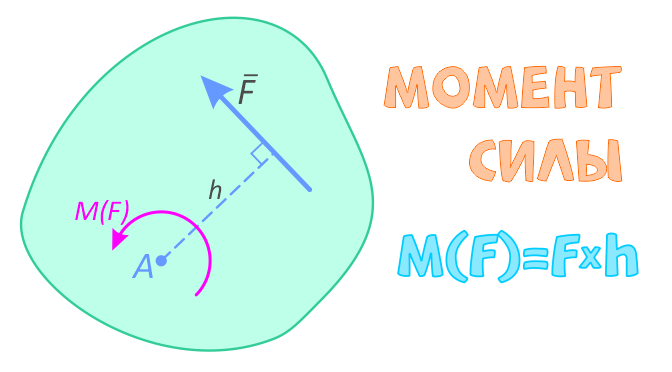
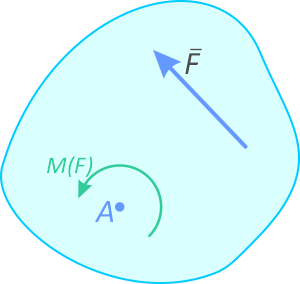
Моментом силы называют вращательное усилие создаваемое вектором силы относительно твердого тела, оси или точки.

Обозначение: M, m или M(F).

Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]

Аналогом момента силы является момент пары сил.

Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.

Определение

Момент определяется как произведение силы F на плечо h:

M(F)=F×h

Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.

Наш короткий видеоурок про момент силы с примерами:

Другие видео

Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки вращения создает момент M=7×0,35=2,45 кНм.

Пример момента силы

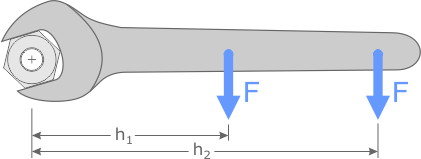
Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.

Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.

Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h2>h1).

Плечом при этом служит расстояние от центра гайки до точки приложения силы.

Плечо момента силы

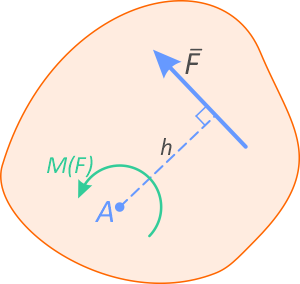
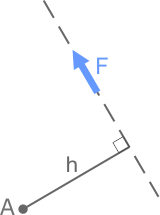
Рассмотрим порядок определения плеча h момента:

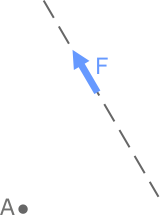
Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.

Покажем линию действия силы F (штриховая линия)

Проведем из точки A перпендикуляр h к линии действия силы

Длина отрезка h есть плечо момента силы F относительно точки A.

Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).

Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.

Примеры расчета момента силы

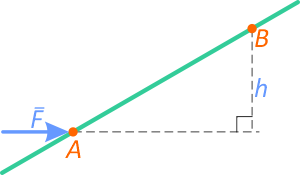
Сила расположена перпендикулярно оси стержня

Если сила F приложена перпендикулярно к оси бруса и известно расстояние между точками A и B.

То момент силы F относительно точки A:

М_A=F×AB

Сила расположена под углом к оси стержня

В случае, если сила F приложена под углом α к оси балки

Момент силы относительно точки B:

M_B=F×cosα×AB

Известно расстояние от точки до линии действия силы

Если известно расстояние от точки где определяется момент до линии действия силы (плечо h)

Момент силы относительно точки B:

M_B=F×h

См. также:

Примеры решения задач >
Момент силы относительно точки
Момент силы относительно оси

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Определение, общие сведения[править | править код]

Момент силы относительно точки[править | править код]

Момент силы относительно оси[править | править код]

Единицы измерения[править | править код]

Некоторые примеры[править | править код]

Формула момента рычага[править | править код]

Статическое равновесие[править | править код]

Движение твёрдого тела[править | править код]

Связь с другими величинами[править | править код]

С моментом импульса[править | править код]

С мощностью[править | править код]

С механической работой[править | править код]

Измерение момента силы[править | править код]

Из истории понятия[править | править код]

См. также[править | править код]

Процесс вращения

Определение момента силы

Что такое рычаг силы?

Направление действия величины M¯

Физический смысл величины M¯

Единицы измерения момента силы

Динамика вращения

Пример решения задачи

Советы

Об этой статье

Была ли эта статья полезной?

Что такое линия действия силы

Что такое плечо силы и как его нарисовать

Момент силы, формула

Еще одна формула для момента силы

Когда момент силы обращается в ноль

Определение

Пример момента силы

Плечо момента силы

Примеры расчета момента силы

Сила расположена перпендикулярно оси стержня

Сила расположена под углом к оси стержня

Известно расстояние от точки до линии действия силы

Вам также может понравиться

Как найти более престижную работу

Сваха как найти жену

Как найти радиус конуса по развертке

Добавить комментарий Отменить ответ