Расчет крутящего момента для вращения диска
-
Woodmaster
- Опытный
- Сообщения: 112
- Зарегистрирован: 10 сен 2011, 18:18
- Репутация: 11
- Контактная информация:
Расчет крутящего момента для вращения диска
Всем привет! Прошу помощи с расчетом крутящего момента.
Надо подобрать ШД для вращения диска диаметром 1 м. Вес диска примерно 8 кг. Скорость вращения 1 об/сек.
Диск расположен в вертикальной плоскости. Во вложении чертеж.
Так как центр массы диска совпадает с осью вращения, правильно ли считать момент = радиус диска * (масса диска/2).
Или как его вообще считать?
-

Сергей Саныч
- Мастер
- Сообщения: 9116
- Зарегистрирован: 30 май 2012, 14:20
- Репутация: 2856
- Откуда: Тюмень
- Контактная информация:
Re: Расчет крутящего момента для вращения диска
Сообщение
Сергей Саныч » 28 мар 2017, 09:20
Woodmaster писал(а):правильно ли считать момент = радиус диска * (масса диска/2).
Это момент инерции вашего диска. Если радиус возвести в квадрат. К требуемому моменту двигателя имеет достаточно косвенное отношение. Играет роль только при раскрутке и торможении. Больше момент ШД – можно сделать меньшее время раскрутки до нужной скорости.
Для поддержания вращения нужно учитывать такие вещи, как трение в подшипниках и аэродинамическое сопротивление – диск довольно большой, да еще с отверстиями на периферии.
Вообще, ШД в данном случае не лучший вариант, если диск надо просто вращать с постоянной скоростью. Асинхронный или коллекторный движок с редуктором подойдут лучше.
Последний раз редактировалось Сергей Саныч 28 мар 2017, 10:13, всего редактировалось 1 раз.
Чудес не бывает. Бывают фокусы.
-

Сергей Саныч
- Мастер
- Сообщения: 9116
- Зарегистрирован: 30 май 2012, 14:20
- Репутация: 2856
- Откуда: Тюмень
- Контактная информация:
Re: Расчет крутящего момента для вращения диска
Сообщение
Сергей Саныч » 28 мар 2017, 10:12
Для расчета нужно знать требуемое время раскрутки и остановки.
Если мне склероз не изменяет, то что-то вроде
M = I * 2 * Pi * R / t
где M – требуемый вращающий момент двигателя, нм
I – момент инерции диска. I = (m * R^2) / 2
R – радиус диска, метры
m – его масса, кг
t – заданное время раскрутки или останова, сек.
Это без учета разных аэродинамических фокусов.
С учетом особенностей именно ШД полезно полученный результат удвоить.
Чудес не бывает. Бывают фокусы.
-

Сергей Саныч
- Мастер
- Сообщения: 9116
- Зарегистрирован: 30 май 2012, 14:20
- Репутация: 2856
- Откуда: Тюмень
-
Контактная информация:
Re: Расчет крутящего момента для вращения диска
Сообщение
Сергей Саныч » 30 мар 2017, 03:18
Виноват, в формулу затесалась ошибка при переписывании ![]()
Правильная вроде бы
M = I * 2 * Pi * n / t
n – конечная скорость, оборотов в секунду (при раскрутке от нулевой скорости)
Woodmaster писал(а): А откуда такая формула?
Для равноускоренного прямолинейного движения, как известно
сила = масса * ускорение = масса * (приращение_скорости / время)
Для вращательного движения заменяем
– силу на вращающий момент
– массу на момент инерции https://ru.wikipedia.org/wiki/%D0%A1%D0 … 0%B8%D0%B8
– линейную скорость на угловую (радиан в секунду). (2*Pi*n)
Получается 6,28 Нм
Чудес не бывает. Бывают фокусы.
Вращение является типичным видом механического движения, которое часто встречается в природе и технике. Любое вращение возникает в результате воздействия некоторой внешней силы на рассматриваемую систему. Эта сила создает так называемый вращающий момент. Что он собой представляет, от чего зависит, рассматривается в статье.
Процесс вращения
Прежде чем рассматривать концепцию вращающего момента, дадим характеристику систем, к которым может быть применена эта концепция. Система вращения предполагает наличие в ней оси, вокруг которой осуществляется круговое движение или поворот. Расстояние от этой оси до материальных точек системы называется радиусом вращения.
С точки зрения кинематики, процесс характеризуется тремя угловыми величинами:
- углом поворота θ (измеряется в радианах);
- угловой скоростью ω (измеряется в радианах в секунду);
- ускорением угловым α (измеряется в радианах в секунду квадратную).
Эти величины связаны друг с другом следующими равенствами:
ω = dθ/dt;
α = dω/dt.
Примерами вращения в природе являются движения планет по своим орбитам и вокруг своих осей, движения смерчей. В быту и технике рассматриваемое движение характерно для моторов двигателей, гаечных ключей, строительных кранов, открывания дверей и так далее.
Определение момента силы
Теперь перейдем к непосредственной теме статьи. Согласно физическому определению, момент силы представляет собой векторное произведение вектора приложения силы относительно оси вращения на вектор самой силы. Соответствующее математическое выражение можно записать так:
M¯ = [r¯*F¯].
Здесь вектор r¯ направлен от оси вращения к точке приложения силы F¯.
В этой формуле вращающего момента M¯ сила F¯ может быть направлена как угодно относительно направления оси. Тем не менее параллельная оси компонента силы не будет создавать вращения, если ось жестко закреплена. В большинстве задач по физике приходится рассматривать силы F¯, которые лежат в плоскостях перпендикулярных оси вращения. В этих случаях абсолютное значение вращающего момента можно определить по следующей формуле:
|M¯| = |r¯|*|F¯|*sin(β).
Где β является углом между векторами r¯ и F¯.
Что такое рычаг силы?
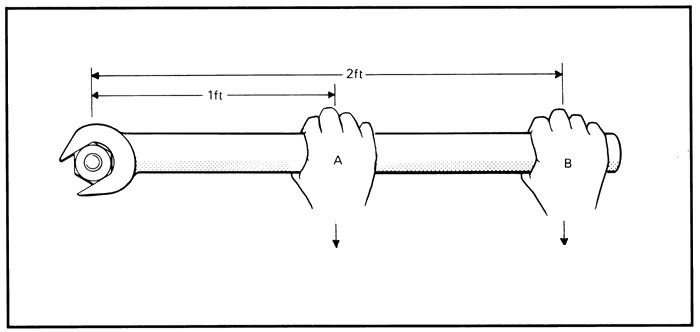
Рычаг силы играет важную роль при определении величины момента силы. Чтобы понять, о чем идет речь, рассмотрим следующий рисунок.
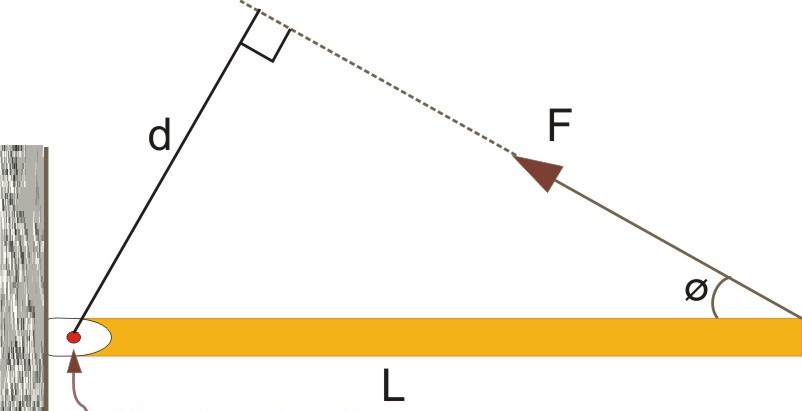
Здесь показан некоторый стержень длиною L, который закреплен в точке вращения одним из своих концов. На другой конец действует сила F, направленная под острым углом φ. Согласно определению момента силы, можно записать:
M = F*L*sin(180o-φ).
Угол (180o-φ) появился потому, что вектор L¯ направлен от закрепленного конца к свободному. Учитывая периодичность тригонометрической функции синуса, можно переписать это равенство в таком виде:
M = F*L*sin(φ).
Теперь обратим внимание на прямоугольный треугольник, построенный на сторонах L, d и F. По определению функции синуса, произведение гипотенузы L на синус угла φ дает значение катета d. Тогда приходим к равенству:
M = F*d.
Линейная величина d называется рычагом силы. Он равен расстоянию от вектора силы F¯ до оси вращения. Как видно из формулы, понятием рычага силы удобно пользоваться при вычислении момента M. Полученная формула говорит о том, что вращающий момент максимальный для некоторой силы F будет возникать только тогда, когда длина радиус-вектора r¯ (L¯ на рисунке выше) будет равна рычагу силы, то есть r¯ и F¯ будут взаимно перпендикулярны.
Направление действия величины M¯
Выше было показано, что вращающий момент – это векторная характеристика для данной системы. Куда направлен этот вектор? Ответить на этот вопрос не представляет особого труда, если вспомнить, что результатом произведения двух векторов является третий вектор, который лежит на оси, перпендикулярной плоскости расположения исходных векторов.
Остается решить, будет ли направлен момент силы вверх или вниз (на читателя или от него) относительно упомянутой плоскости. Определить это можно или по правилу буравчика, или с помощью правила правой руки. Приведем оба правила:
- Правило правой руки. Если расположить правую кисть таким образом, чтобы четыре ее пальца двигались от начала вектора r¯ к его концу, а затем от начала вектора F¯ к его концу, то большой палец, оттопыренный, укажет на направление момента M¯.
- Правило буравчика. Если направление вращения воображаемого буравчика совпадает с направлением вращательного движения системы, то поступательное движение буравчика укажет на направление вектора M¯. Напомним, что он вращается только по часовой стрелке.
Оба правила являются равноправными, поэтому каждый может использовать то, которое является для него более удобным.
При решении практических задач разное направление вращающего момента (вверх – вниз, влево – вправо) учитывается с помощью знаков “+” или “-“. Следует запомнить, что за положительное направление момента M¯ принято считать такое, которое приводит к вращению системы против часовой стрелки. Соответственно, если некоторая сила приводит к вращению системы по ходу стрелки часов, то создаваемый ее момент будет иметь отрицательную величину.
Физический смысл величины M¯
В физике и механике вращения величина M¯ определяет способность силы или суммы сил совершать вращение. Поскольку в математическом определении величины M¯ стоит не только сила, но и радиус-вектор ее приложения, то именно последний во многом определяет отмеченную вращательную способность. Чтобы понятнее было, о какой способности идет речь, приведем несколько примеров:
- Каждый человек, хотя бы один раз в жизни пытался открыть дверь, взявшись не за ручку, а толкнув ее недалеко от петель. В последнем случае приходится прилагать значительное усилие, чтобы добиться желаемого результата.
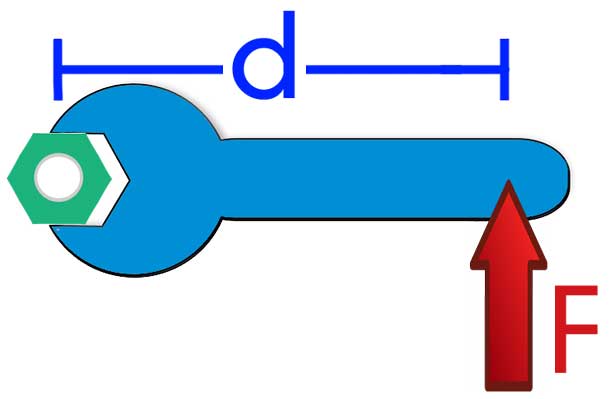
- Чтобы открутить гайку с болта, используют специальные гаечные ключи. Чем длиннее ключ, тем легче открутить гайку.
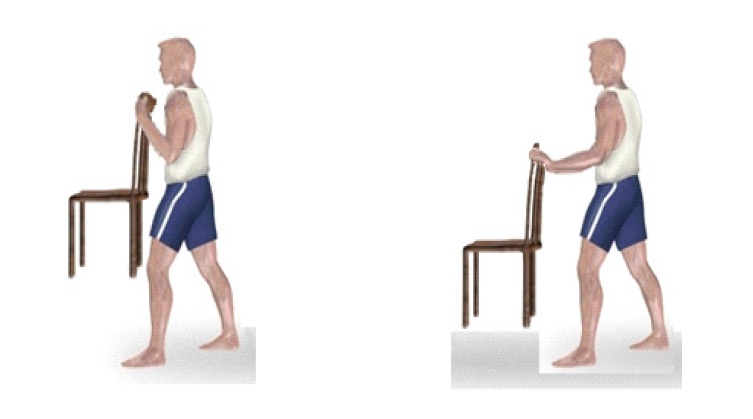
- Чтобы ощутить важность рычага силы, предлагаем читателям проделать следующий эксперимент: взять стул и попытаться удержать его одной рукой на весу, в одном случае руку прислонить к телу, в другом – выполнить задачу на прямой руке. Последнее для многих окажется непосильной задачей, хотя вес стула остался тем же самым.
Единицы измерения момента силы
Несколько слов также следует сказать о том, в каких единицах в СИ измеряется вращающий момент. Согласно записанной для него формуле, он измеряется в ньютонах на метр (Н*м). Однако в этих единицах также измеряется работа и энергия в физике (1 Н*м = 1 джоуль). Джоуль для момента M¯ не применяется, поскольку работа является скалярной величиной, M¯ же – это вектор.
Тем не менее совпадение единиц момента силы с единицами энергии не является случайным. Работа по вращению системы, совершенная моментом M, рассчитывается по формуле:
A = M*θ.
Откуда получаем, что M также может быть выражен в джоулях на радиан (Дж/рад).
Динамика вращения
В начале статьи мы записали кинематические характеристики, которые используются для описания движения вращения. В динамике вращения главным уравнением, которое использует эти характеристики, является следующее:
M = I*α.
Действие момента M на систему, имеющую момент инерции I, приводит к появлению углового ускорения α.

Данную формулу применяют, для определения угловых частот вращения в технике. Например, зная вращающий момент асинхронного двигателя, который зависит от частоты тока в катушке статора и от величины изменяющегося магнитного поля, а также зная инерционные свойства вращающегося ротора, можно определить, до какой скорости вращения ω раскручивается ротор двигателя за известное время t.
Пример решения задачи
Невесомый рычаг, длина которого составляет 2 метра, посередине имеет опору. Какой вес следует положить на один конец рычага, чтобы он находился в состоянии равновесия, если с другой стороны опоры на расстоянии 0,5 метра от нее лежит груз массой 10 кг?

Очевидно, что равновесие рычага наступит, если моменты сил, создаваемые грузами, будут равны по модулю. Сила, создающая момент в данной задаче, представляет собой вес тела. Рычаги силы равны расстояниям от грузов до опоры. Запишем соответствующее равенство:
M1 = M2 =>
m1*g*d1 = m2*g*d2 =>
P2 = m2*g = m1*g*d1/d2.
Вес P2 получим, если подставим из условия задачи значения m1 = 10 кг, d1 = 0,5 м, d2 = 1 м. Записанное равенство дает ответ: P2 = 49,05 ньютона.
Загрузить PDF
Загрузить PDF
Самое лучшее определение вращательного момента – это тенденция силы вращать предмет вокруг оси, точки опоры или точки вращения. Вращательный момент можно рассчитать с помощью силы и плеча момента (перпендикулярное расстояние от оси до линии действия силы), или используя момент инерции и угловое ускорение.
-

1
Определите силы, действующие на тело и соответствующие им моменты. Если сила не перпендикулярна рассматриваемому плечу момента (т.е. она действует под углом), то вам может понадобиться найти ее составляющие с использованием тригонометрических функций, таких как синус или косинус.
- Рассматриваемая составляющая силы будет зависеть от эквивалента перпендикулярной силы.
- Представьте себе горизонтальный стержень, к которому нужно приложить силу 10 Н под углом 30° над горизонтальной плоскостью, чтобы вращать его вокруг центра.
- Поскольку вам нужно использовать силу, не перпендикулярную плечу момента, то для вращения стержня вам необходима вертикальная составляющая силы.
- Следовательно, нужно рассматривать y-составляющую, или использовать F = 10sin30° Н.
-

2
Воспользуйтесь уравнением момента, τ = Fr, и просто замените переменные заданными или полученными данными.
- Простой пример: Представьте себе ребенка массой 30 кг, сидящего на одном конце качели-доски. Длина одной стороны качели составляет 1,5 м.
- Поскольку ось вращения качели находится в центре, вам не нужно умножать длину.
- Вам необходимо определить силу, прилагаемую ребенком, с помощью массы и ускорения.
- Поскольку дана масса, вам нужно умножить ее на ускорение свободного падения, g, равное 9,81 м/с2. Следовательно:
- Теперь у вас есть все необходимые данные для использования уравнения момента:
-

3
Воспользуйтесь знаками (плюс или минус), чтобы показать направление момента. Если сила вращает тело по часовой стрелке, то момент отрицательный. Если же сила вращает тело против часовой стрелки, то момент положительный.
- В случае нескольких приложенных сил, просто сложите все моменты в теле.
- Поскольку каждая сила стремится вызвать различные направления вращения, важно использовать знак поворота для того, чтобы следить за направлением действия каждой силы.
- Например, к ободу колеса, имеющего диаметр 0,050 м, были приложены две силы, F1= 10,0 Н, направленная по часовой стрелке, и F2 = 9,0 Н, направленная против часовой стрелки.
- Поскольку данное тело – круг, фиксированная ось является его центром. Вам нужно разделить диаметр и получить радиус. Размер радиуса будет служить плечом момента. Следовательно, радиус равен 0,025 м.
- Для ясности мы можем решить отдельные уравнения для каждого из моментов, возникающих от соответствующей силы.
- Для силы 1 действие направлено по часовой стрелке, следовательно, создаваемый ею момент отрицательный:
- Для силы 2 действие направлено против часовой стрелки, следовательно, создаваемый ею момент положительный:
- Теперь мы можем сложить все моменты, чтобы получить результирующий вращательный момент:
Реклама
-

1
Чтобы начать решать задачу, разберитесь в том, как действует момент инерции тела. Момент инерции тела – это сопротивление тела вращательному движению. Момент инерции зависит как от массы, так и от характера ее распределения.
- Чтобы четко понимать это, представьте себе два цилиндра одинакового диаметра, но разной массы.
- Представьте себе, что вам нужно повернуть оба цилиндра вокруг их центральной оси.
- Очевидно, что цилиндр с большей массой будет сложнее повернуть, чем другой цилиндр, поскольку он “тяжелее”.
- А теперь представьте себе два цилиндра различных диаметров, но одинаковой массы. Чтобы выглядеть цилиндрическими и иметь разную массу, но в то же время иметь разные диаметры, форма, или распределение массы обоих цилиндров должна отличаться.
- Цилиндр с большим диаметром будет выглядеть как плоская закругленная пластина, тогда как меньший цилиндр будет выглядеть как цельная трубка из ткани.
- Цилиндр с большим диаметром будет сложнее вращать, поскольку вам нужно приложить большую силу, чтобы преодолеть более длинное плечо момента.
-

2
Выберите уравнение, которое вы будете использовать для расчета момента инерции. Есть несколько уравнений, которые можно использовать для этого.
- Первое уравнение – самое простое: суммирование масс и плечей моментов всех частиц.
- Это уравнение используется для материальных точек, или частиц. Идеальная частица – это тело, имеющее массу, но не занимающее пространства.
- Другими словами, единственной значимой характеристикой этого тела является масса; вам не нужно знать его размер, форму или строение.
- Идея материальной частицы широко используется в физике с целью упрощения расчетов и использования идеальных и теоретических схем.
- Теперь представьте себе объект вроде полого цилиндра или сплошной равномерной сферы. Эти предметы имеют четкую и определенную форму, размер и строение.
- Следовательно, вы не можете рассматривать их как материальную точку.
- К счастью, можно использовать формулы, применимые к некоторым распространенным объектам:
-

3
Найдите момент инерции. Чтобы начать рассчитывать вращательный момент, нужно найти момент инерции. Воспользуйтесь следующим примером как руководством:
- Два небольших “груза” массой 5,0 кг и 7,0 кг установлены на расстоянии 4,0 м друг от друга на легком стержне (массой которого можно пренебречь). Ось вращения находится в середине стержня. Стержень раскручивается из состояния покоя до угловой скорости 30,0 рад/с за 3,00 с. Рассчитайте производимый вращательный момент.
- Поскольку ось вращения находится в середине стержня, то плечо момента обоих грузов равно половине его длины, т.е. 2,0 м.
- Поскольку форма, размер и строение “грузов” не оговаривается, мы можем предположить, что грузы являются материальными частицами.
- Момент инерции можно вычислить следующим образом:
-

4
Найдите угловое ускорение, α. Для расчета углового ускорения можно воспользоваться формулой α= at/r.
- Первая формула, α= at/r, может использоваться в том случае, если дано тангенциальное ускорение и радиус.
- Тангенциальное ускорение – это ускорение, направленное по касательной к направлению движения.
- Представьте себе объект, двигающийся по криволинейному пути. Тангенциальное ускорение – это попросту его линейное ускорение на любой из точек всего пути.
- В случае второй формулы, легче всего проиллюстрировать ее, связав с понятиями из кинематики: смещением, линейной скоростью и линейным ускорением.
- Смещение – это расстояние, пройденное объектом (единица СИ – метры, м); линейная скорость – это показатель изменения смещения за единицу времени (единица СИ – м/с); линейное ускорение – это показатель изменения линейной скорости за единицу времени (единица СИ – м/с2).
- Теперь давайте рассмотрим аналоги этих величин при вращательном движении: угловое смещение, θ – угол поворота определенной точки или отрезка (единица СИ – рад); угловая скорость, ω – изменение углового смещения за единицу времени (единица СИ – рад/с); и угловое ускорение, α – изменение угловой скорости за единицу времени (единица СИ – рад/с2).
- Возвращаясь к нашему примеру – нам были даны данные для углового момента и время. Поскольку вращение начиналось из состояния покоя, то начальная угловая скорость равна 0. Мы можем воспользоваться уравнением, чтобы найти:
-

5
Воспользуйтесь уравнением, τ = Iα, чтобы найти вращательный момент. Просто замените переменные ответами, полученными на предыдущих шагах.
- Вы можете заметить, что единица “рад” не подходит к нашим единицам измерения, поскольку считается безразмерной величиной.
- Это значит, что вы можете пренебречь ею и продолжить ваши расчеты.
- Для анализа единиц измерения мы можем выразить угловое ускорение в с-2.
Реклама
Советы
- В первом методе, если тело является кругом и ось его вращения находится в центре, то рассчитывать составляющие силы не нужно (при условии, что сила не приложена под наклоном), поскольку сила лежит на касательной к окружности, т.е. перпендикулярно плечу момента.
- Если вам сложно представить, как происходит вращение, то возьмите ручку и попробуйте воссоздать задачу. Для более точного воспроизведения не забудьте скопировать положение оси вращения и направление приложенной силы.
Реклама
Об этой статье
Эту страницу просматривали 23 928 раз.
Была ли эта статья полезной?
В статье рассматривается связь между крутящим моментом и моментом инерции вращающегося тела и ее решаемые задачи.
Крутящий момент и момент инерции поддерживают вращательное движение тела. Когда на тело наводится крутящий момент, оно начинает ускоряться обратно пропорционально его моменту инерции. Вот почему крутящий момент, действующий на тело, является произведением его момента инерции и углового ускорения.
Законы движения Ньютона заявить, что тело остается неподвижным или движется из одной точки в другую с определенной скоростью; если на него не действует внешняя сила. Это означает, что тело получает ускорение, зависящее от его полной массы и силы приложенной внешней силы.
Используя принцип Ньютона во вращательном движении, когда крутящий момент или момент силы создается на неподвижном или движущемся теле, оно инициирует угловое ускорение. Поэтому каждое твердое тело, совершая вращательное движение вокруг своей оси, несет угловое ускорение когда возникает крутящий момент.
В предыдущих статьях мы поняли, что инерция – это свойство тела, выражающееся в стремлении тела сопротивляться движению. Поэтому инерция обратно пропорциональна ускорению тела.. Следовательно, первый закон движения Ньютона также назвал Закон инерции.

Каждая частица внутри такого вращающегося тела имеет свою массу, и все они вращаются вокруг центральной оси вращения тела. Следовательно, величина крутящего момента, необходимая для ускорения частиц внутри тела, зависит от распределения массы всего тела. Величина тела, выражающая распределение массы, называетсямомент инерции”.

(Кредит: Shutterstock)
При вращательном движении под величиной инерции понимается момент инерции тела, определяемый интегрированием полных масс М частиц и их расстояний R от оси его вращения.
Следовательно, момент инерции тела (I) равен я = МР2.
Крутящий момент и момент инерции
Законы движения Ньютона связывают крутящий момент и момент инерции при вращательном движении.
Когда мы включаем вентилятор, мы наводим на него крутящий момент. Теперь ускорение вентилятора будет зависеть от того, насколько велик момент инерции вентилятора и насколько крутящий момент нам нужно вызвать.
Момент инерции — это вращательная масса тела, а крутящий момент — вращательная сила, действующая на него. Крутящий момент τ, который необходимо приложить к телу, пропорционален обоим угловое ускорение и момент инерции. Но момент инерции I уменьшает угловое ускорение α тела.
Утверждение дает связь между крутящим моментом и моментом инерции как,
т=1α

Читать о крутящем моменте и угловом моменте
Какой крутящий момент необходим для вращения со скоростью 15 рад/с?2 чтобы тело имело момент инерции 5 кгм2?
Данный:
я = 5 кгм2
α = 15 рад/с2
Найти: т =?
Формула:
т = я а
Решения:
Крутящий момент, необходимый для того, чтобы заставить тело вращаться со скоростью 15 рад/с.2 рассчитывается с использованием соотношение между крутящим моментом и моментом инерции,
т = я а
Подставляя все значения,
т = 5 х 15
т= 75
Крутящий момент, необходимый для поворота кузова, составляет 75 Нм.
Какой крутящий момент должен возникнуть на расстоянии 2 м от тела массой 4 кг, чтобы оно вращалось со скоростью 5 рад/с?2?
Данный:
М = 4 кг
R = 2 м
α = 5 рад/с2
Найти: т =?
Формула:
т = я а
Решения:
Крутящий момент, необходимый для тела, рассчитывается как
т = Iα
Но момент инерции диска равен I = MR.2.
т = МС2α
Подставляя все значения,
т = 4 х 22 х 5
т = 4 х 4 х 5
т = 80
Крутящий момент, необходимый для поворота кузова, составляет 80 Нм.
Формула крутящего момента и момента инерции
Формула крутящего момента и момента инерции легко определяется путем замены линейного эквивалента в формуле закона движения Ньютона его угловым эквивалентом.
Крутящий момент τ является угловым эквивалентом приложенной силы F, а момент инерции I является угловым эквивалентом массы m. Следовательно, закон движения Ньютона (F = ma) для вращательного движения принимает вид
т = Iα
Как найти крутящий момент по моменту инерции
Крутящий момент от момента инерции является производным от изменения углового момента.
Вращательное движение также подчиняется законам движения Ньютона. Поэтому, когда на тело действует крутящий момент, его угловой момент изменяется из-за ускорения. Поскольку угловой момент является произведением инерции и угловой скорости, мы можем получить необходимый крутящий момент из его момента инерции.

Компания угловая импульс тела, когда крутящий момент индуцируется равен L = rx P
Где P линейный импульс. т. е. P = mv
L = гх мв
Связь между линейной скоростью v и угловой скоростью ω есть (rxω)
L = rxm (rx ω)
Л = г-н2ω
Но мистер2 срок принадлежит момент инерции (I).
L = я ш
Мы узнали, что крутящий момент, действующий на тело, представляет собой скорость изменения углового момента..
τ = дл/дт
Подставляя формула углового момента,
τ = dIω/dt
τ = Idω/dt
Член dω/dt – это угловое ускорение α тела. т. е. α= dω/dt
Наконец, крутящий момент получается из момента инерции,
т = ла
Читать о крутящем моменте и скорости
Диск массой 0.1 кг и радиусом 1 м вращается со скоростью 2 рад/с.2. Момент инерции диска I = 1/2mr.2. Рассчитайте крутящий момент, действующий на диск.
Данный:
m = 0.1 кг
г = 1 м
α = 2 рад/с2
Найти: т=?
Формула:
т = я а
Решения:
Крутящий момент, создаваемый диском, рассчитывается как
т = я а
Для диска момент инерции I = 1/2mr.2 ……………..(Дано)
τ= 1/2мр2 α
Подставляя все значения,
т = 1/2 х 0.1 х 12 x2
т = 0.2/2
т = 0.2/2
т = 0.1
Крутящий момент на диске составляет 0.1 Нм.
Тонкий стержень массой 100 кг и длиной 6 м вращается со скоростью 20 рад/с.2. Момент инерции тонкого стержня I=1/12mr.2. Рассчитайте крутящий момент на тонком стержне.
Данный:
m = 100 кг
г = 6 м
α= 20 рад/с2
Найти: т =?
Формула:
т = я а
Решения:
Крутящий момент, действующий на тонкий стержень, рассчитывается как
т = я а
Для тонкого стержня момент инерции I = 1/12mr.2 ……………..(Дано)
τ= 1/12мр2α
Подставляя все значения,
т = 1/12 х 100 х 62 х 20
т = 72000/12
т = 6000
Крутящий момент на диске составляет 6000 Нм.
Download Article
Download Article
You likely know that if you push or pull on an object (exert force), it will move a distance. The distance it moves depends on how heavy the object is and how much force you apply. However, if the object is fixed at some point (called the “rotational point” or “axis”), and you push or pull on the object at some distance from that point, the object will instead rotate around that axis. The magnitude of that rotation is torque (τ), expressed in newton-meters (N∙m). The most basic way to calculate torque is to multiply the Newtons of force exerted by the meters of distance from the axis. There’s also a rotational version of this formula for 3-dimensional objects that uses the moment of inertia and angular acceleration. Calculating torque is a physics concept requiring an understanding of algebra, geometry, and trigonometry.[1]
-

1
Find the length of the moment arm. The distance from the axis or rotational point to the point where force is applied is called the moment arm. This distance is typically expressed in meters (m).[2]
- Since torque is a rotational force, this distance is also a radius. For this reason, you’ll sometimes see it represented with an “r” in the basic torque equation.
-

2
Work out the force being applied perpendicular to the moment arm. The force applied perpendicular to the moment arm produces the greatest torque. The simplest torque equation assumes the force is being applied perpendicular to the moment arm.[3]
- In torque problems, you’ll typically be given the magnitude force. However, if you have to work it out yourself, you’ll need to know the mass of the object and the acceleration of the object in m/s2. According to Newton’s Second Law, force is equal to mass times acceleration (
).
Advertisement
- In torque problems, you’ll typically be given the magnitude force. However, if you have to work it out yourself, you’ll need to know the mass of the object and the acceleration of the object in m/s2. According to Newton’s Second Law, force is equal to mass times acceleration (
-

3
Multiply the force times the distance to find the torque. The basic formula for torque is
, where torque is represented by the Greek letter tau (τ) and equals the force (F) times the distance (or radius, r). If you know the magnitude of the force (in Newtons) and the distance (in meters), you can solve for the torque, expressed in newton-meters (N∙m).[4]
- For example, suppose you have a force perpendicular to your object exerting 20 Newtons of force on the object 10 meters from the axis. The magnitude of the torque is 200 N∙m:
- For example, suppose you have a force perpendicular to your object exerting 20 Newtons of force on the object 10 meters from the axis. The magnitude of the torque is 200 N∙m:
-

4
Show the direction of the force with positive or negative torque. You now know the magnitude of the torque, but you don’t know if it’s positive or negative. This depends on the direction of the rotation. If the object is rotating counterclockwise, the torque is positive. If the object is rotating clockwise, the torque is negative.[5]
- For example, if the object is moving clockwise and the magnitude of the torque is 200 N∙m, you would express this as -200 N∙m of torque. No sign is necessary if the magnitude of the torque is positive.
- The value given for the magnitude of the torque remains the same. If a negative sign appears before the value, it simply means that the object in question is rotating clockwise.
-

5
Total individual torques around a given axis to find the net torque (Στ). It’s possible to have more than one force acting on an object at a different distance from the axis. If one force is pushing or pulling in the opposite direction of the other force, the object will rotate in the direction of the stronger torque. If the net torque is zero, you have a balanced system. If you’re given the net torque but not some other variable, such as the force, use basic algebraic principles to solve for the missing variable.[6]
Advertisement
-

1
Start with the distance of the radial vector. The radial vector is the line that extends from the axis or point of rotation. It could also be any object, such as a door or the minute-hand of a clock. The distance to measure for the purposes of calculating torque is the distance from the axis to the point where the force is applied to rotate the vector.[7]
- For most physics problems, this distance is measured in meters.
- In the torque equation, this distance is represented by “r” for radius or radial vector.
-

2
Work out the amount of force being applied. In most torque problems, this value will also be given to you. The amount of force is measured in Newtons and will be applied in a particular direction. However, rather than being perpendicular to the radial vector, the force is applied at an angle, giving you a radial vector.[8]
- If you’re not provided with the amount of force, you would multiply mass times acceleration to find the force, which means you would need to be given those values. You might also be given the torque and told to solve for the force.
- In the torque equation, force is represented by “F.”
-

3
Measure the angle made by the force vector and the radial vector. The angle you measure is the one to the right of the force vector. If the measurement isn’t provided for you, use a compass to measure the angle. If the force is being applied to the end of the radial vector, extend the radial vector out in a straight line to get your angle.[9]
- In the torque equation, this angle is represented by the Greek letter theta, “θ.” You’ll typically see it referred to as “angle θ” or “angle theta.”
-

4
Use your calculator to find the sine of the angle θ. In the torque equation, you multiply the distance of the radial vector and the amount of force with the sine of the angle you just measured. Put the angle measurement into your calculator, then press the “sin” button to get the sine of the angle.[10]
- If you were determining the sine of the angle by hand, you would need the measurements for the opposite side and the hypotenuse side of a right triangle. Since most torque problems don’t involve making exact measurements, however, you shouldn’t have to worry about this.
-

5
Multiply the distance, force, and sine to find the torque. The full formula for torque when you have angled force is
. The result is expressed in newton-meters (N∙m).[11]
- For example, suppose you have a radial vector 10 meters long. You’re told that 20 Newtons of force is being applied to that radial vector at a 70° angle. You would find that the torque is 188 N∙m:
- For example, suppose you have a radial vector 10 meters long. You’re told that 20 Newtons of force is being applied to that radial vector at a 70° angle. You would find that the torque is 188 N∙m:
Advertisement
-

1
Find the moment of inertia. The amount of torque required to move an object with angular acceleration depends on the distribution of the object’s mass, or its moment of inertia, expressed in kg∙m2. When the moment of inertia isn’t provided, you can also look it up online for common objects.[12]
-

2
Determine the angular acceleration. If you’re trying to find torque, the angular acceleration will typically be given to you. This is the amount, in radians/s2, that the object’s velocity is changing as it rotates.[13]
- Remember that the angular acceleration can be zero if the object is moving at a constant speed and is neither speeding up nor slowing down.
-

3
Multiply the moment of inertia by the angular acceleration to find the torque. The full formula for torque using the moment of inertia and the angular acceleration is
, where “τ” stands for torque, “I” stands for the moment of inertia, and “α” stands for the angular acceleration. If you’re trying to find torque, simply multiply the moment of inertia and the angular acceleration to get your result. As with other equations, if you’re trying to find one of the other values, you can re-order the equation using common algebraic principles.[14]
Advertisement
Add New Question
-
Question
What is the formula to find the torque from the weight?

Tiagoroth
Community Answer
Torque is measured in Newton meters and is calculated by N·m = (kg*m²)/s². Manipulating the formula to find mass, we get kg = (N·m*s²)/m².
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
The equation for torque is very similar to the equation for work (the physical force required for an object to move). However, with work, the force is parallel to the distance, whereas, with torque, the force is perpendicular to the distance vector.[15]
Thanks for submitting a tip for review!
Advertisement
-
Calculating torque requires knowledge of advanced algebraic concepts, geometry, and trigonometry. If you’re not strong in these areas, you might want to refresh your knowledge before you attempt torque calculations.
Advertisement
References
About This Article
Article SummaryX
To calculate torque, start multiplying the mass of the object exerting force by the acceleration due to gravity, which is 9.81. When the force is clockwise, its torque is negative, and when it’s moving counterclockwise, it’s positive. If more than one force is present, add up all the torques to get the net torque of the combined forces. For tips on how to calculate torque using angular acceleration, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 207,394 times.


