Как найти временные характеристики

Динамические
свойства линейных звеньев и систем
автоматического управления в целом
могут быть описаны дифференциальными
уравнениями и передаточными функциями,
а также с помощью временных
и
частотных
характеристик.
Временная характеристика представляет
собой функцию времени, описывающую
выходной сигнал звена (или системы) при
подаче на вход звена определенного
тестирующего сигнала. Частотные
характеристики описывают установившиеся
вынужденные колебания на выходе звена,
вызванные гармоническим воздействием
на входе.

Указанные
характеристики могут быть сняты
экспериментально или построены по
уравнению звена. Имеется и обратная
возможность – по экспериментально
полученным характеристикам составить
уравнение звена. Кроме того, с помощью
этих характеристик можно определить
реакцию звена на любое возмущение
произвольного вида. Переходные и
частотные характеристики однозначно
связаны с дифференциальным уравнением
звена и его передаточной функцией и
наряду с ними являются исчерпывающим
описанием динамических свойств звена.

К
числу основных временных
характеристик
звена или системы относятся переходная
функция
и
функция
веса.

Переходная
функция звена представляет собой сигнал
на выходе звена (реакцию
звена),
вызванный подачей на его вход единичного
ступенчатого воздействия.
Единичное ступенчатое воздействие
(единичная
ступенчатая функция, функция Хевисайда)
– это воздействие, которое мгновенно
возрастает
от нуля до единицы и далее остается
неизменным (рис. 2.4). Единичное ступенчатое
воздействие обозначается
и может быть описано следующим выражением:

(2.20)

Переходная
функция обычно обозначается
.
Следовательно,– это выражение дляпри=.

Наряду
с переходной функцией при описании
звеньев и систем применяется функция
веса,
общепринятое обозначение которой
.
Эта временная характеристика представляет
собой реакцию звена надельта-функцию
(единичную
импульсную функцию, иглу Дирака).
Дельта-функция, которая обозначается
,
– это математическая идеализация
предельно короткого импульсного сигнала
бесконечно большой амплитуды. Математически
дельта-функцию можно описать следующим
образом:

(2.21)

При этом согласно
определению дельта-функции

.
(2.22)

Таким
образом,
–
этопри=.

Поскольку
дельта-функция равна производной по
времени от единичного ступенчатого
воздействия, то и между переходной
функцией, и функцией веса линейных
звеньев существует аналогичная связь:

.
(2.23)

И наоборот

.

Зная
переходную и функцию веса, можно
определить реакцию звена на произвольное
входное воздействие при нулевых начальных
условиях с помощью следующих формул:

;
(2.24)

,
(2.25)

где
,– значенияиприt
= 0;

Выражения
(2.24) и (2.25) легко получаются друг из
друга, являясь вариантами интеграла
Дюамеля
или интеграла
свертки.
У реальных инерционных звеньев и систем
h(0)=0,
так как реакция на их выходе всегда
отстает от входного воздействия. Поэтому
в дальнейшем выражения (2.24) и (2.25)
приводятся без первого слагаемого.

Временные
характеристики могут быть выражены
непосредственно через передаточную
функцию звена с помощью преобразований
Лапласа.

Поскольку

,
в случае,
когда входное воздействие
(t)
представляет собой единичный импульс
,
и с учетом того, что его изображение по
Лапласу,
получим следующее выражение для
изображения функции веса звена:

w(p)
=W(p) или ,
т.е.

.
(2.26)

Таким образом,
функция веса определяется через
передаточную функцию по формуле обратного
преобразования Лапласа, т.е. является
ее оригиналом.

В
случае, когда
(t)
= 1(t),
учитывая, что L
= 1/p,
получаем следующее выражение для
изображения переходной характеристики:

Следовательно,
переходная характеристика звена равна:

При
рассмотрении частотных
характеристик
считаем, что на входе системы дейст­вует
гармонический сигнал с амплитудой
и часто­той:

.
(2.27)

По
окончании переходного процесса на
выходе линейной системы будут существовать
гармонические колебания с той же
частотой, что и у входного сигнала, но
в общем случае отличающиеся от него по
амплитуде и фазе, т.е. в установившемся
режиме выходная величина звена равна:

,
(2.28)

где
– амплитуда установившихся выходных
колебаний;– фазовый сдвиг между входными и
выходными синусоидальными колебаниями.

При
изменении частоты
изменяется, как соотношение между
амплитудами входных и выходных колебаний,
так и фазовый сдвигмежду ними. При этом зависимость от
частоты отношения амплитуд называетсяамплитудно-частотной
характеристикой
(АЧХ), т.е.

.

Зависимость
величины фазового сдвига от частоты
называетсяфазо-частотной
характеристикой (ФЧХ).

Определив
амплитудно- и фазо-частотную характеристики
системы, например, получив
их экспериментально, можно построить
еще одну частотную характеристику
– амплитудно-фазовую
(АФЧХ).

Амплитудно-фазовую
характеристику, используя
в качестве полярных координат, строят
на комплексной плоскости по следующим
правилам. Задаются значением частотыω_i,
для которого
по графику ФЧХ
определяют
величину фазового сдвига φ(ω_i)
, а по графику АЧХ – величину A(ω_i).

Из
начала координат комплексной плоскости
проводится луч под угломφ(ω_i)
к положительной
действительной полуоси. Угол откладывается
против часовой стрелки, если φ(ω_i)
> 0, т.е.
когда выходной гармонический сигнал
опережает входной, и в противоположном
направлении, если φ(ω_i)
< 0 .Из начала
координат по этому лучу откладывается
отрезок, длина которого в выбранном
масштабе равна A(ω_i)
(рис.
2.5, в).

Каждая
точка амплитудно-фазовой частотной
характеристики соответствует определенному
значению частоты. Значения для конечного
количества точек характеристики
наносятся вдоль характеристики и
указывают направление возрастания
частоты ω.

Очевидно,
что возможно и решение обратной задачи:
по годографу
амплитудно-фазовую частотную
характеристику можно построить
характеристики
и.
На рис. 2.5 приведен примерный вид этих
характеристик для инерционной системы.

Как
показано на этих рисунках, у таких
звеньев в силу их инерционности
амплитудная частотная характеристика
по мере увеличения частоты в конце
концов спадает до нуля. При этом, чем
менее инерционно звено, тем шире его
амплитудная частотная характеристика,
т.е. тем больше полоса пропускаемых
звеном частот, или просто его полоса
пропускания.

Теоретически
частотная характеристика продолжается
до бесконечности, но практически полоса
пропускания оценивается значением
частоты, при котором отношение амплитуд
окончательно становится меньше
определенного, достаточно малого
конечного значения. Это значение обычно
берут равным 0,05 (на этой частоте амплитуда
выходных колебаний падает до 5 % амплитуды
входных колебаний). Наличие максимума
у амплитудной частотной характеристики
говорит о резонансных свойствах звена.
Частота, соответствующая максимуму
амплитудной характеристики, называется
резонансной
().

Фазовая
характеристика у обычных инерционных
звеньев (рис. 2.5, б) отрицательна ((ω)<
0), т.е. выходные колебания отстают по
фазе от входных, и это отставание растет
с частотой.

Используя
символическую форму записи гармонических
сигналов x_вх(t)
и x_вых(t),
получим аналитические выражения для
рассмотренных характеристик, их
зависимость между собой и с передаточной
функцией системы.

Символическая
запись сигналов (2.27) и (2.28):

,

.

Определим
амплитудно-фазовую характеристику
системы, как отношение выходного сигнала
системы к входному, выраженное в
комплексной форме:

.
(2.29)

Из
выражения (2.29) следует, что амплитудно-частотная
и фазо-частотная характеристики является
соответственно модулем и фазой
(аргументом) амплидудно-фазовой
характеристики:

A(ω)
= |W(jω)|
и φ(ω)
= argW(jω).
(2.30)

Очевидно,
что на приведенных зависимостях между
характеристиками основывалась
рассмотренная методика построении
W(jω)
по A(ω)
и φ(ω).

Комплексное
выражение для W(jω)
может быть представлено, как в форме
(2.29), так и в виде:

W(jω)
= P(ω)
+ jQ(ω),
(2.31)

где
P(ω),
Q(ω)
– соответственно вещественная
и мнимая
частотные характеристики
системы.

Таким
образом, получаем всего пять частотных
характеристик: амплитудно-фазовую
W(jω),
амплитудно-частотную A(ω),
фазо-частотную φ(ω),
вещественную частотную P(ω)
и мнимую
частотную Q(ω).
Между этими характеристиками, кроме
зависимостей (2.30) – (2.31), имеются следующие
очевидные связи:

;
(2.32)

(2.33)

.
(2.34)

Частотные
характеристики системы не зависят от
времени. В этом их принципиальное отличие
от временных характеристик. Если
временные характеристики определяют
поведение системы в переходном процессе
при различных типовых входных воздействиях,
то частотные выражают зависимость
параметров установившихся выходных
синусоидальных колебаний от тех же
параметров входных колебаний при
различных частотах.

Частотные
характеристики широко используются в
инженерной практике при анализе и
синтезе САУ. Особым их достоинством
является то, что они могут быть получены
экспериментальным путем, что особенно
важно для систем, аналитические уравнения
которых не представляется возможным
получить из-за их сложности или
малоизученности технологического
процесса.

Несмотря на то,
что частотные характеристики, например
W(jω),отображают только установившиеся
процессы в системе, они в полной мере
определяет и ее динамические свойства.

Подставляя
производные сигналов
(t)иравные

….

….
,

в дифференциальное
уравнение (2.5), получим:

=

= .

Из полученного
выражения определяем АФХ системы:

.
(2.35)

Сравнивая выражения
(2.18) и (2.35) делаем заключение, что выражения
для АФЧХ W(jω)системы может быть получено по ее
передаточной функцииW(p),
в которой достаточно переменнуюp
заменить на jω:

W(
jω) =
.(2.36)

Если
в выражении (2.18) осуществить аналогичную
замену p
на jω,
получим:

,
(2.37)

где
и– изображения Фурье входного и выходного
сигналов.

На
основании выражения (2.37) амплитудно-фазовую
частотную характеристику
можно определить как отношение изображений
Фурье выходного и входного сигналов
системы при нулевых начальных условиях:

.

Выражению
(2.26), связывающему с помощью преобразования
Лапласа передаточную функцию системы
с ее временной характеристикой –
функцией веса
,
соответствуют следующие зависимости
для амплитудно-фазовой частотной
характеристики:

(2.38)

и

(2.39)

Первое
выражение определяет амплитудно-фазовую
частотную характеристику системы по
его весовой функции, а второе, наоборот,
– весовую функцию по
.
По частотным характеристикам САУ можно
непосредственно определить ее реакцию
не только на импульсное воздействие,
но и на входное воздействие любого вида.

Преобразуя выражение
(2.35), в котором приняты следующие
обозначения:

A(jω)=;

B(jω)=

получим:

,
(2.40)

где
индексами
и

отмечены действительные (U)
и мнимые (V)
части соответствующих комплексных
величин в числителе и знаменателе.

Преобразуя (2.40),
окончательно имеем:

,

где:

Для инженерных
расчетов особенно широко используются
частотные характеристики, построенные
в логарифмическом масштабе, в том числе
логарифмическая амплитудно-частотная
L(ω), связанная с АЧХ системы зависимостью:

L(ω)
= 20lg
A(ω).
(2.41)

Смысл
приведенного выражения заключается в
следующем. Определим усиление системой
мощности сигнала, в виде отношения
мощности на выходе Р_вых
к мощности на входе Р_вх.
Этот показатель, для удобства оцениваемый
в логарифмическом масштабе, с учетом
того, что мощность сигнала пропорциональна
квадрату его амплитуды, записывается
в виде:

.

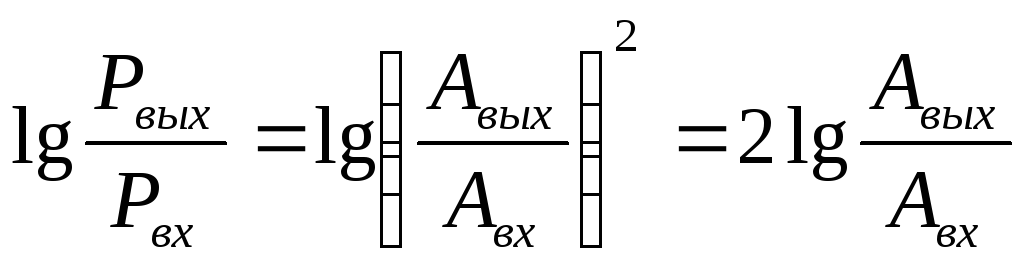
В качестве единицы
усиления или ослабления мощности сигнала
при прохождении его через какое-либо
устройство принят Бел (по имени
американского

Рис.
2.6.
Логарифмическая
амплитудно-частотная L(ω)
и фазо-частотная
характеристики в совмещенной системе
координат

изобретателя
А. Белла). Но поскольку 1 Бел является
слишком крупной единицей (ей соответствует
изменение мощности в десять раз), в
теории автоматического регулирования
за единицу измерения принят децибел 1
дБ = 0,1 Б.

С учетом этого
можно записать:

,

где величина L(ω
) выражена в децибелах.

Используемая
совместно с L(ω
) фазо-частотная
характеристика
строится в полулогарифмическом масштабе:
по оси ординат откладывается значение
фазы в градусах или радианах, а по оси
абсцисс –.
При этом единицей измерения частоты
являетсядекада.
Декадой
называется
частотный интервал, граничные значения
которого соотносятся в десять раз. В
логарифмическом масштабе частот отрезок
в одну декаду не зависит от частоты и
имеет длину, равную единице.

При
решении практических задач на оси
абсцисс указываются не значения lgω,
а, что более удобно, значения самой
частоты ω.
Очевидно, что при использовании
логарифмического масштаба точка на оси
абсцисс, соответствующая ω
= 0, находится слева в бесконечности,
т.е. логарифмические характеристики
строятся не от нулевой частоты, а от
некоторого значения, которое определяется
данными конкретной задачи. На рис. 2.6
приведен примерный вид логарифмической
амплитудно-частотной характеристики
L(ω)
и фазо-частотной
характеристик
,
построенных в совмещенной системе
координат.

В
дальнейшем для краткости будем в названии
различных частотных характеристик
опускать слово «частотная», говоря
просто о логарифмической амплитудной
характеристике L(ω)
(ЛАХ),
амплитудно-фазовой характеристике
W(jω)
(АФХ) и т.п.

5.1. Понятие временных характеристик

Для оценки динамических
свойств системы и отдельных звеньев принято исследовать их реакцию на типовые
входные воздействия, которые наиболее полно отражают особенности реальных
возмущений. Во – первых, это позволяет сравнивать отдельные элементы между собой
с точки зрения их динамических свойств. Во – вторых, зная реакцию системы на типовые
воздействия, можно судить о том, как она будет вести себя при сложных изменениях
входной величины.

Наиболее распространенными типовыми воздействиями являются:
ступенчатое, импульсное и гармоническое воздействия. Любой сигнал
u(t), имеющий сложную форму, можно разложить на сумму типовых воздействий
u_i(t) и исследовать реакцию системы
на каждую из составляющих, а затем, пользуясь принципом суперпозиции, получить
результирующее изменение выходной величины y(t) суммируя полученные таким
образом составляющие выходного сигнала y_i(t).

Особенно важное значение в ТАУ придают ступенчатому воздействию 1(t) = . Все остальные воздействия
могут быть сведены к нему. Так, например, реальный импульсный сигнал может быть
представлен двумя ступенчатыми сигналами одинаковой величины, но противоположными
по знаку, поданными один за другим через интервал времени t
(рис.42).

Зависимость изменения выходной величины системы от времени при
подаче на ее вход единичного ступенчатого воздействия при нулевых начальных условиях
называется переходной характеристикой и обозначается h(t).

Не менее важное значение в ТАУ уделяется импульсной переходной характеристике,
которая описывает реакцию системы на единичное импульсное воздействие при нулевых
начальных условиях, обозначают (t).
Единичный импульс физически представляет из себя очень узкий импульс, ширина
которого стремится к нулю, а высота – к бесконечности, ограничивающий единичную
площадь. Математически он описывается дельта – функцией d(t) = 1’(t).

Переходная
и импульсная переходная характеристики называются временными характеристиками.
Каждая из них является исчерпывающей характеристиками системы и любого ее звена
при нулевых начальных условиях. По ним можно однозначно определить выходную величину
при произвольном входном воздействии.

Зная передаточную функцию W(p) = K(p)/D(p), выражение для переходной
функции можно найти из формулы Хевисайда: , где p_k
– корни характеристического уравнения D(p) = 0. Взяв производную от переходной
функции можно получить выражение для импульсной переходной функции (t)
= h’(t).

5.2. Переходные характеристики элементарных
звеньев

Здесь мы рассмотрим только самые основные
звенья.

5.2.1. Безынерционное (пропорциональное,
усилительное) звено

Это звено, для которого
в любой момент времени выходная величина пропорциональна входной.

Его уравнение: y(t) = ku(t).

Передаточная функция: W(p) = k.

Переходная характеристика: h(t) = k1(t).

В ответ на единичное ступенчатое воздействие сигнал на выходе мгновенно достигает величины в k раз большей, чем на входе и сохраняет
это значение (рис.43). При k = 1 звено никак себя не проявляет, а при
k = – 1 – инвертирует входной сигнал.

Любое реальное звено обладает инерционностью, но с определенной
точностью некоторые реальные звенья могут рассматриваться как безынерционные,
например, жесткий механический рычаг, редуктор, потенциометр, электронный усилитель
и т.п.

5.2.2. Интегрирующее (астатическое) звено

Его
уравнение , или , или py = ku.

Передаточная
функция: W(p) = k/p.

Переходная характеристика: (рис.44).

При k = 1 звено представляет собой “чистый” интегратор
W(p) = 1/p. Интегрирующее звено неограниченно “накапливает”
входное воздействие. Примеры интегрирующих звеньев: электродвигатель, поршневой
гидравлический двигатель, емкость и т.п. Введение его в САУ превращает систему
в астатическую, то есть ликвидирует статическую ошибку.

5.2.3. Инерционное звено первого порядка
(апериодическое)

Уравнение динамики: , или Tpy + y = ku.

Передаточная
функция: W(p) = .

Переходная характеристика может быть получена с помощью формулы Хевисайда:

,

где p₁
= – 1/T – корень уравнения D(p) = Tp + 1 = 0; D’(p₁)
= T.

Переходная характеристика имеет вид экспоненты (рис.45), по
которой можно определить передаточный коэффициент k, равный установившемуся
значению h(t), и постоянную времени Т по времени t, соответствующему
точке пересечения касательной к кривой в начале координат с ее асимптотой. При
достаточно больших Т звено на начальном участке может рассматриваться
как интегрирующее, при малых Т звено приближенно можно рассматривать
как безынерционное. Примеры апериодического звена: термопара, электродвигатель,
четырехполюсник из сопротивления и емкости или сопротивления и индуктивности.

5.2.4. Инерционные
звенья второго порядка

Его уравнение: T₁²p²y
+ T₂py + y = ku.

Передаточная функция:
W(p) = .

Решение уравнения зависит
от соотношения постоянных времени T₁ и
T₂, которое определяет коэффициент затухания
r = . Можно записать W(p) = , где T = T₁.

Если r
1, то знаменатель W(p) имеет два вещественных корня p₁
и p2 и раскладывается на два сомножителя:

T₂p²
+ 2rTp + 1 = T²(p
– p₁).(p – p₂).

Такое звено можно разложить на два апериодических звена первого порядка, поэтому оно не является элементарным.

При r<1 корни полинома знаменателя W(p) комплексно
сопряженные: p_1,2 =
± j. Переходная
характеристика представляет собой выражение, характеризующее затухающий колебательный
процесс с затуханием
и частотой
(рис.46). Такое звено называется колебательным. При r = 0 колебания
носят незатухающий характер. Такое звено является частным случаем колебательного
звена и называется консервативным. Примерами колебательного звена могут
служить пружина, имеющая успокоительное устройство, электрический колебательный
контур с активным сопротивлением и т.п. Зная характеристики реального устройства
можно определить его параметры как колебательного звена. Передаточный коэффициент
k равен установившемуся значению переходной функции.

5.2.5. Дифференцирующее звено

Различают идеальное и реальное дифференцирующие звенья. Уравнение динамики
идеального звена: y(t) = , или y = kpu. Здесь выходная
величина пропорциональна скорости изменения входной величины. Передаточная функция:
W(p) = kp. При k = 1 звено осуществляет чистое дифференцирование
W(p) = p. Переходная характеристика: h(t) = k1’(t)
= d(t).

Идеальное дифференцирующее звено реализовать невозможно, так
как величина всплеска выходной величины при подаче на вход единичного ступенчатого
воздействия всегда ограничена. На практике используют реальные дифференцирующие
звенья, осуществляющие приближенное дифференцирование входного сигнала.

Его
уравнение: Tpy + y = kTpu.

Передаточная функция: W(p) = .

При малых Т
звено можно рассматривать как идеальное дифференцирующее. Переходную характеристики
можно вывести с помощью формулы Хевисайда:

,

здесь p₁
= – 1/T – корень характеристического уравнения D(p) = Tp + 1 = 0; кроме
того, D’(p₁) = T.

При подаче на вход единичного ступенчатого воздействия выходная величина оказывается ограничена
по величине и растянута во времени (рис.47). По переходной характеристике, имеющей
вид экспоненты, можно определить передаточный коэффициент k и постоянную
времени Т. Примерами таких звеньев могут являться четырехполюсник из сопротивления
и емкости или сопротивления и индуктивности, демпфер и т.п. Дифференцирующие звенья
являются главным средством, применяемым для улучшения динамических свойств САУ.

Кроме рассмотренных имеется еще ряд звеньев, на которых подробно
останавливаться не будем. К ним можно отнести идеальное форсирующее звено (W(p)
= Tp + 1, практически не реализуемо), реальное форсирующее звено (W(p)
= , при T₁
>> T₂), запаздывающее
звено (W(p) = e ^{– pT}),
воспроизводящее входное воздействие с запаздыванием по времени и другие.

Вопросы

1. Что
   называется и какие Вы знаете типовые входные воздействия? Для чего они нужны?
2. Что
   называется переходной характеристикой?
3. Что называется импульсной переходной
   характеристикой?
4. Что называется временными характеристиками?
5. Для
   чего служит формула Хевисайда?
6. Как получить кривую переходного процесса
   при сложной форме входного воздействия, если известна переходная характеристика
   звена?
7. Что называется безынерционным звеном, его уравнение динамики, передаточная
   функция, вид переходной характеристики?
8. Что называется интегрирующим звеном,
   его уравнение динамики, передаточная функция, вид переходной характеристики?
9. Что
   называется апериодическим звеном, его уравнение динамики, передаточная функция,
   вид переходной характеристики?
10. Что называется колебательным звеном, его
    уравнение динамики, передаточная функция, вид переходной характеристики?
11. Что
    называется консервативным звеном, его уравнение динамики, передаточная функция,
    вид переходной характеристики?
12. Почему не являются элементарными инерционные
    звенья второго порядка с коэффициентом затухания большим или равным единице?
13. Что
    называется идеальным дифференцирующим звеном? Почему его нельзя реализовать?
14. Что
    называется реальным дифференцирующим звеном, его уравнение динамики, передаточная
    функция, вид переходной характеристики?

Далее…

Макеты страниц