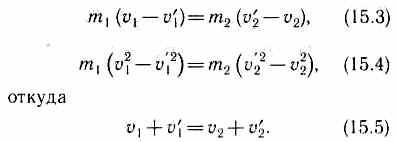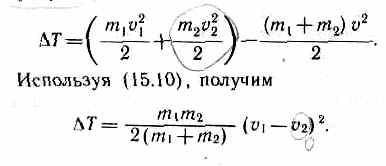Примером применения
законов сохранения импульса и энергии
при решении реальной физической
задачи является удар абсолютно упругих
и неупругих тел.
Удар
(или соударение)
—
это столкновение двух или более тел,
при котором взаимодействие длится очень
короткое время. Исходя из данного
определения, кроме явлений, которые
можно отнести к ударам в прямом смысле
этого слова
28
(столкновения
атомов или биллиардных шаров), сюда
можно отнести и такие, как удар человека
о землю при прыжке с трамвая и т. д. При
ударе в телах возникают столь
значительные внутренние силы, что
внешними силами, действующими на
них, можно пренебречь. Это позволяет
рассматривать соударяющиеся тела
как замкнутую систему и применять к ней
законы сохранения.
Тела
во время удара претерпевают деформацию.
Сущность удара заключается в том,
что кинетическая энергия относительного
движения соударяющихся тел на короткое
время преобразуется в энергию упругой
деформации. Во время удара имеет
место перераспределение энергии между
соударяющимися телами. Наблюдения
показывают, что относительная скорость
тел после удара не достигает своего
прежнего значения. Это объясняется
тем, что нет идеально упругих тел и
идеально гладких поверхностей.
Отношение нормальных составляющих
относительной скорости тел после и до
удара называется коэффициентом
восстановления :
=
v’n/vn.
Если
для сталкивающихся тел =0,
то такие тела называются абсолютно
неупругими, если
=1—абсолютно
упругими.
На
практике для всех тел 0<<1
(например, для стальных шаров 0,56,
для шаров из слоновой кости 0,89,
для свинца 0).
Однако в некоторых случаях тела можно
с большой точностью рассматривать либо
как абсолютно упругие, либо как
абсолютно неупругие.
Прямая,
проходящая через точку соприкосновения
тел и нормальная к поверхности их
соприкосновения, называется линией
удара. Удар
называется центральным,
если
тела до удара движутся вдоль прямой,
проходящей через их центры масс. Мы
будем рассматривать только центральные
абсолютно упругие и абсолютно
неупругие удары.
Абсолютно
упругий удар — столкновение
двух тел, в результате которого в обоих
взаимодействующих телах не остается
никаких деформаций и вся кинетическая
энергия, которой обладали тела до удара,
после удара снова превращается в
кинетическую энергию
.
Для абсолютно
упругого удара выполняются закон
сохранения импульса и закон сохранения
кинетической энергии.
Обозначим
скорости шаров массами m1
и
m2
до удара через v1
и
v2,
после
удара — через v’1
и
v’2
(рис.
18). При прямом центральном ударе
векторы скоростей шаров до и после удара
лежат на прямой линии, соединяющей их
центры. Проекции векторов скорости на
эту линию равны модулям скоростей. Их
направления учтем знаками: положительное
значение припишем движению вправо,
отрицательное — движению влево.
При указанных
допущениях законы сохранения имеют вид
Произведя
соответствующие преобразования в
выражениях (15.1) и (15.2), получим
Решая уравнения
(15.3) и (15.5), находим
Разберем несколько
примеров.
29
Проанализируем
выражения (15.8) и (15.9) для двух шаров
различных масс:
а) m1
=m2.
Если
второй шар до удара висел неподвижно
(v2=0)
(рис.
19), то после удара остановится первый
шар (v’1=0),
а второй будет двигаться с той же
скоростью и в том же направлении, в
котором двигался первый шар до удара
(v’2
= v1);
б)
m1>m2.
Первый
шар продолжает двигаться в том же
направлении, как и до удара, но с меньшей
скоростью (v’1<v1).
Скорость
второго шара после удара больше, чем
скорость первого после удара (v’2>v’1)
(рис.20);
в)
m1<m2.
Направление
движения первого шара при ударе изменяется
— шар отскакивает обратно. Второй шар
движется в ту же сторону, в которую
двигался первый шар до удара, но с меньшей
скоростью, т.е. v’2<v1
(рис.
21);
г)
m2>>m1
(например,
столкновение шара со стеной). Из уравнений
(15.8) и (15.9) следует, что v’1=-v1,
v’22m1v1/m20.
2) При
m1=m2
выражения
(15.6) и (15.7) будут иметь вид
v’1=v2,
v’2=v1,
т. е. шары равной
массы «обмениваются» скоростями.
Абсолютно
неупругий удар — столкновение
двух тел, в результате которого тела
объединяются, двигаясь дальше как единое
целое.
Продемонстрировать
абсолютно неупругий удар можно с
помощью шаров из пластилина (глины),
движущихся навстречу друг другу (рис.
22).
Если
массы шаров m1
и
m2,
их скорости до удара v1
и
v2,
то,
используя закон сохранения импульса,
можно записать
Если
шары движутся навстречу друг другу, то
они вместе будут продолжать двигаться
в ту сторону, в которую двигался шар,
обладающий большим импульсом. В частном
случае если массы шаров равны (m1=m2),
то
v
= (v1+v2)/2.
Выясним, как
изменяется кинетическая энергия
шаров при центральном абсолютно
неупругом ударе. Так как в процессе
соударения шаров между ними дей-
30
ствуют силы,
зависящие не от самих деформаций, а от
их скоростей, то мы имеем дело с силами,
подобными силам трения, поэтому закон
сохранения механической энергии не
должен соблюдаться. Вследствие деформации
происходит «потеря» кинетической
энергии, перешедшей в тепловую или
другие формы энергии. Эту «потерю» можно
определить по разности кинетической
энергии тел до и после удара:
Если
ударяемое тело было первоначально
неподвижно (v2=0),
то
Когда
m2>>m1
(масса
неподвижного тела очень большая), то
v<<v1
и
почти
вся кинетическая энергия тела при ударе
переходит в другие формы энергии.
Поэтому, например, для получения
значительной деформации наковальня
должна быть массивнее молотка.
Наоборот, при забивании гвоздей в стену
масса молотка должна быть гораздо
большей (m1>>m2),
тогда
vv1
и
практически вся энергия затрачивается
на возможно большее перемещение гвоздя,
а не на остаточную деформацию стены.
Абсолютно неупругий
удар — пример того, как происходит
«потеря» механической энергии под
действием диссипативных сил.
Контрольные
вопросы
• В чем различие
между понятиями энергии и работы?
• Как найти
работу переменной силы?
• Какую работу
совершает равнодействующая всех сил,
приложенных к телу, равномерно движущемуся
по окружности?
• Что такое
мощность? Вывести ее формулу.
• Дайте определения
и выведите формулы для известных вам
видов механической энергии. • Какова
связь между силой и потенциальной
энергией?
• Почему изменение
потенциальной энергии обусловлено
только работой консервативных сил?
• В чем заключается
закон сохранения механической энергии?
Для каких систем он выполняется?
• Необходимо
ли условие замкнутости системы для
выполнения закона сохранения механической
энергии?
• В чем физическая
сущность закона сохранения и превращения
энергии? Почему он является фундаментальным
законом природы?
• Каким свойством
времени обусловливается справедливость
закона сохранения механической энергии?
• Что такое
потенциальная яма? потенциальный барьер?
• Какие заключения
о характере движения тел можно сделать
из анализа потенциальных кривых?
• Как
охарактеризовать положения устойчивого
и неустойчивого равновесия? В чем их
различие?
• Чем отличается
абсолютно упругий удар от абсолютно
неупругого?
• Как определить
скорости тел после центрального абсолютно
упругого удара? Следствием каких законов
являются эти выражения?
31
Задачи
3.1. Определить:
1) работу поднятия груза по наклонной
плоскости; 2) среднюю и 3) максимальную
мощности подъемного устройства, если
масса груза 10 кг, длина наклонной
плоскости 2 м, угол ее наклона к горизонту
45°, коэффициент трения 0,1 и время подъема
2 с. [1) 170 Дж; 2) 85 Вт; 3) 173 Вт |
3.2. С башни высотой
35 м горизонтально брошен камень массой
0,3 кг. Пренебрегая сопротивлением
воздуха, определить: 1) скорость, с которой
брошен камень, если через 1 с после начала
движения его кинетическая энергия 60
Дж; 2) потенциальную энергию камня через
1 с после начала движения. [1) 17,4 м/с; 2)
88,6 Дж ]
3.3. Пренебрегая
трением, определить наименьшую высоту,
с которой должна скатываться тележка
с человеком по желобу, переходящему в
петлю радиусом 10 м, чтобы она сделала
полную петлю и не выпала из желоба. [25
м]
3.4.
Пуля массой m=
10 г, летевшая горизонтально со скоростью
v
= 500 м/с, попадает в баллистический
маятник длиной l=
1 м и массой М = 5 кг и застревает в нем.
Определить угол отклонения маятника.
[ 18°30′ ]
3.5.
Зависимость потенциальной энергии
частицы в центральном силовом поле от
расстояния r
до
центра
поля задается выражением П(r)
=A/r2
-B/r,
где А
и
В —
положительные постоянные.
Определить
значение r0,
соответствующее
равновесному положению частицы. Является
ли это положение положением устойчивого
равновесия? [r0
= 2А/В]
3.6.
При центральном абсолютно упругом ударе
движущееся тело массой m1
ударяется
в покоящееся тело массой m2,
в результате чего скорость первого тела
уменьшается в n=
1,5 раза. Определить: 1) отношение m1/m2;
2)
кинетическую энергию T’2,
с
которой начнет двигаться второе
тело, если первоначальная кинетическая
энергия первого тела T1
=
1000 Дж. [ 1) 5; 2) 555 Дж ]
3.7.
Тело массой m1=4
кг движется со скоростью v1=3
м/с
и ударяется о неподвижное тело такой
же массы. Считая удар центральным и
неупругим, определить количество
теплоты, выделившееся при ударе. [9 Дж ]
* У. Гамильтон
(1805—1865) — ирландский математик и
физик.
Соседние файлы в папке Трофимова
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Закон сохранения механической энергии и закон сохранения импульса при упругом ударе способствует нахождению решения механических задач с неизвестными действующими силами, то есть задания с ударным взаимодействием тел.
Применение такого вида задач используется в технике и физике элементарных частиц.
Удар или столкновение – это кратковременное взаимодействие тел с последующим изменением их скорости.
При столкновении действуют неизвестные кратковременные ударные силы. Закон Ньютона не разрешит ударное взаимодействие, а позволит только исключить сам процесс столкновения и получить связь между скоростями тел до и после столкновений без промежуточных значений.
Механика применяет такое определения абсолютно упругих и абсолютно неупругих ударов.
Абсолютно неупругий удар. Скорость
Абсолютно неупругий удар – это ударное взаимодействие с соединением (слипанием) движущихся тел.
Сохранение механической энергии отсутствует, так как переходит во внутреннюю, то есть нагревание.
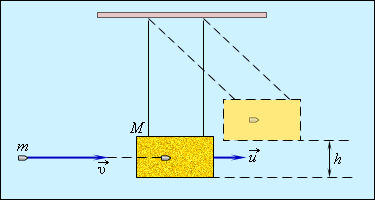
Попадание пули в баллистический маятник – характерный пример действия энергии абсолютно неупругого удара, где
М – подвешенный ящик с песком, показанный на рисунке 1.21.1, m – горизонтально летящая пуля с v→ скоростью движения, застревающая в ящике. Определение скорости пули возможно по отклонению маятника.
Если скорость ящика с пулей обозначить как u→, тогда, используя формулу сохранения импульса, получаем:
mv=(M+m)u; u=mM+mv.
Когда пуля застревает в песке, то механическая энергия теряется:
∆E=mv22-(M+m)u22=MM+m·mv22.
M (M + m) обозначает долю кинетической энергии выпущенной пули и прошедшей во внутреннюю энергию системы. Тогда
∆EE0=MM+m=11+mM.
Использование формулы подходит для задач с наличием баллистического маятника и другого неупругого соударения разномасных тел.
Когда m << М ∆EE0→12, тогда происходит переход кинетической энергии во внутреннюю. Когда m = M ∆EE0→0, только половина кинетической переходит во внутреннюю. Если имеется неупругое соударение движущегося тела большей массой с неподвижным, имеющим (m>>М), отношение принимает вид ∆EE0→0.
Расчет движения маятника производится по закону сохранения механической энергии. Получаем
(M+m)u22=(M+m)gh; u2=2gh.
В данном случае h является максимальной высотой подъема маятника. Отсюда следует, что
v=M+mm2gh.
При известной высоте h возможно определение скорости пули v.
Рисунок 1.21.1. Баллистический маятник.
Абсолютно упругий удар
Абсолютный упругий удар – это столкновение с сохранением механической энергии системы тел.
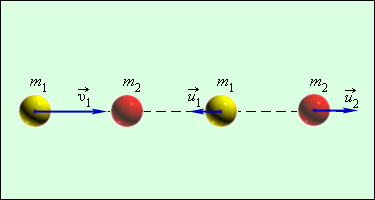
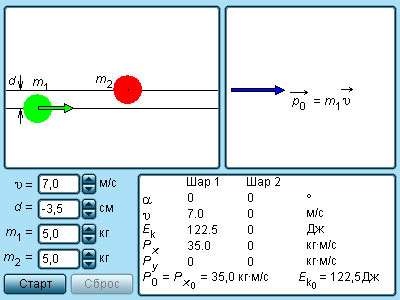
Большинство случаев столкновения атомов подчинено законам абсолютного упругого центрального удара. Закон сохранения импульса и механической энергии сохраняются при таком ударе. Для примера используется столкновение при помощи центрального удара бильярдных шаров. Один из них находится в состоянии покоя, как изображено подробно на рисунке 1.21.2.
Центральный удар – это соударение, когда скорости шаров направлены по линии центра.
Рисунок 1.21.2. Абсолютно упругий центральный удар шаров.
Встречаются случаи, когда массы m1 и m2 не равны. Тогда, используя закон сохранения механической энергии, получаем
m1v122=m1v122+m2v222.
За v1 принимается скорость при абсолютном упругом ударе первого шара перед столкновением, а v2=0 скорость второго шара, u1 и u2 – скорости после столкновения.
Запись закона сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, принимает вид:
m1v1=m1u1+m2u2.
Полученная система из двух уравнений позволяет найти неизвестные скорости u1 и u2 шаров после столкновения.
u1=m1-m2v1m1+m2; u2=2m1v1m1+m2.
Если массы равны, то есть, тогда происходит остановка первого шара (u1=0), а второй продолжает движение u2=v1. происходит обмен скоростями и импульсами.
При наличии нулевой скорости второго шара (v2≠0), задача могла бы свестись к предыдущей с переходим в новую систему отсчета с равномерным и прямолинейным движением и скоростью v2 относительно «неподвижной» системы. В такой системе второй шар покоится до удара, а первый имеет скорость v1’=v1–v2. После определения скорости шаров v1 и v2 производится переход к «неподвижной» системе.
С помощью закона сохранения механической энергии и импульса, можно определить скорости шаров после столкновений только с известными скоростями до соударения.
Рисунок 1.21.3. Модель упругие и неупругие соударения.
При столкновении атомов или молекул применяется понятие центрального или лобового удара, который редко применим на практике. Нецентральный упругий удар не направлен по одной прямой.
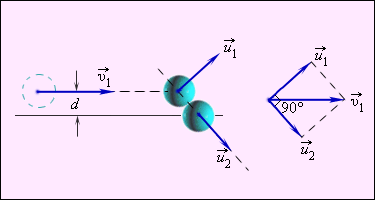
Частный случай нецентрального упругого удара – соударение бильярдных шаров с одинаковой массой при обездвиженном одним из них, а другим направленным не по линии центра. Данная ситуация приведена на рисунке 1.21.4.
Рисунок 1.21.4. Нецентральное упругое соударение шаров с одинаковой массой, где d является прицельным расстоянием.
Нецентральное ударение характеризуется тем, что разлетатание шаров происходит под углом относительно друг друга. Чтобы определить скорости v1 и v2 после соударения, необходимо знать нахождение положения линии центров в момент удара или предельное расстояние d, изображенное на рисунке 1.21.4.
Предельное расстояние
Предельным расстоянием называют расстояние между двумя линиями, которые проведены через центры шаров параллельно относительно вектора скорости v1→ летящего шара.
При одинаковых массах шаров векторы v1→ и v2→ имеют перпендикулярное направление друг к другу. Это возможно показать с помощью применения законов сохранения импульса и энергии. Если m1=m2=m, тогда определение примет вид
v1→=u1→+u2→; v12=u12+u22.
Первое равенство значит, что векторы v1→, u1→, u2→ образуют треугольник, называемый диаграммой импульсов, второе – для его разрешения применяют теорему Пифагора. Угол, располагаемый между u1→ и u2→, равняется 90 градусов.
Рисунок 1.21.5. Модель соударения упругих шаров
Длительность удара
Задача 1. Оценить время упругого удара твердых тел, рассматривая столкновение стержня, налетающего торцом на неподвижную недеформируемую стенку (рис.).
Чаще всего в задачах считают, что упругий удар твердых тел происходит мгновенно, но совершенно очевидно, что это предположение является идеализацией. Столкновение реальных тел всегда занимает конечный промежуток времени $tau$. В самом деле, если бы изменение импульса тела при столкновении происходило мгновенно,
$F = frac{mDelta v}{t_{rightarrow infty}}$,
то сила взаимодействия тел при ударе была бы бесконечно большой, чего, естественно, не бывает.
От чего же может зависеть длительность столкновения?
Допустим, что мы рассматриваем отражение упругого тела от недеформируемой стенки. При столкновении кинетическая энергия тела в течение первой половины столкновения превращается в потенциальную энергию упругой деформации тела. В течение второй половины происходит обратное превращение энергии деформации в кинетическую энергию отскакивающего тела. Такая идея была заложена в задаче тестирования 2005 г. Решите эту задачу, для осмысления этого момента.
Задача 2. Две абсолютно упругие шайбы массами m1 = m2 = 240 г каждая скользят поступательно по гладкой горизонтальной поверхности навстречу друг другу со скоростями, модули которых v1 = 21 м/с и v2 = 9,0 м/с . Максимальное значение потенциальной энергии E упругой деформации шайб при их центральном столкновении равно … Дж.
Поэтому очевидно, что упругие свойства тела играют определенную роль при столкновении. Итак, можно ожидать, что длительность удара зависит от модуля Юнга материала тела Е, его плотности $rho$ и его геометрических размеров. Возможно, что длительность удара $tau$ зависит и от скорости v, с которой тело налетает на преграду. Нетрудно убедиться, что оценить время столкновения с помощью одних только соображений размерности не удастся. Действительно, если даже взять в качестве налетающего тела шар, размеры которого характеризуются только одним параметром — радиусом R, то из величин Е, $rho$, R и v можно составить бесчисленное множество выражений, имеющих размерность времени:
$tau = sqrt{frac{rho}{E}} cdot f(frac{rho v^2}{E})$, (1)
где $f$ — произвольная функция безразмерной величины $frac{rho v^2}{E}. Поэтому для нахождения $tau$ необходимо динамическое рассмотрение.
Проще всего такое рассмотрение провести для тела, имеющего форму длинного стержня. Пусть стержень, движущийся со скоростью $v$, налетает торцом на неподвижную стенку. При соприкосновении торцевого сечения стержня со стенкой скорости лежащих в этом сечении частиц стержня мгновенно обращаются в нуль. В следующий момент времени останавливаются частицы, расположенные в соседнем сечении, и т. д.
Участок стержня, частицы которого к данному моменту уже остановились, находится в деформированном состоянии. Другими словами, в этот момент времени деформированной оказывается та часть стержня, до которой дошла волна упругой деформации, распространяющаяся по стержню от места контакта с преградой. Эта волна деформации распространяется по стержню со скоростью звука $u$. Если считать, что стержень пришел в соприкосновение со стенкой в момент времени t = 0, то в момент времени t длина сжатой части стержня равна $ut$. Эта часть стержня на рис. а заштрихована.
В незаштрихованной части стержня скорости всех его частиц попрежнему равны $u$, а в сжатой (заштрихованной) части стержня все частицы покоятся. Первый этап процесса столкновения стержня со стенкой закончится в тот момент, когда весь стержень окажется деформированным, а скорости всех его частиц обратятся в нуль (рис. б).
В этот момент кинетическая энергия налетающего стержня целиком превращается в потенциальную энергию упругой деформации. Сразу после этого начинается второй этап столкновения, при котором стержень возвращается в недеформированное состояние. Этот процесс начинается у свободного конца стержня и, распространяясь по стержню со скоростью звука, постепенно приближается к преграде. На рис. в
стержень показан в тот момент, когда незаштрихованная часть уже не деформирована и все ее частицы имеют скорость $v$, направленную влево. Заштрихованный участок по-прежнему деформирован, и скорости всех его частиц равны нулю. Конец второго этапа столкновения наступит в тот момент, когда весь стержень окажется недеформированным, а все частицы стержня приобретут скорость $v$, направленную противоположно скорости стержня до удара. В этот момент правый конец стержня отделяется от преграды: недеформированный стержень отскакивает от стенки и движется в противоположную сторону с прежней по модулю скоростью (рис. г).
Энергия упругой деформации стержня при этом целиком переходит обратно в кинетическую энергию. Из изложенного ясно, что длительность столкновения τ равна времени прохождения фронта волны упругой деформации по стержню туда и обратно:
$tau = frac{2l}{u}$, (2)
где l — длина стержня. Определить скорость звука в стержне $u$ можно следующим образом.
Рассмотрим стержень в момент времени t (рис. а), когда волна деформации распространяется влево. Длина деформированной части стержня в этот момент равна $ut$. По отношению к недеформированному состоянию эта часть укоротилась на величину $vt$, равную расстоянию, пройденному к этому моменту еще недеформированной частью стержня. Поэтому относительная деформация этой части стержня равна $frac{v}{u}$.
На основании закона Гука
$frac{v}{u} = frac{1}{E} cdot frac{F}{S}$, (3)
где S — площадь поперечного сечения стержня, F — сила, действующая на стержень со стороны стенки, Е — модуль Юнга.
Поскольку относительная деформация $v/u$ одинакова во все моменты времени, пока стержень находится в контакте с преградой, то, как видно из формулы (3), сила F постоянна. Для нахождения этой силы применим закон сохранения импульса к остановившейся части стержня. До контакта с преградой рассматриваемая часть стержня имела импульс $rho Sut cdot v$, а в момент времени t ее импульс равен нулю. Поэтому
$rho Sut cdot v = Ft$. (4)
Подставляя отсюда силу F в формулу (3), получаем
$u = sqrt{frac{E}{rho}}$. (5)
Теперь выражение для времени $tau$.
Деформация столкновения стержня со стенкой (2) принимает вид
$tau = 2l cdot sqrt{frac{rho}{E}}$. (6)
Время столкновения $tau$ можно найти и иначе, воспользовавшись для этого законом сохранения энергии. Перед столкновением стержень недеформирован и вся его энергия — это кинетическая энергия поступательного движения $frac{1}{2}mv^2$. Спустя время $tau$/2 с начала столкновения скорости всех его частиц, как мы видели, обращаются в нуль, а весь стержень сказывается деформированным (рис. б). Длина стержня уменьшилась на величину $Delta l$ по сравнению с его недеформированным состоянием (рис. д).
В этот момент вся энергия стержня — это энергия его упругой деформации. Эту энергию можно записать в виде
$W = frac{1}{2}kDelta l^2$
где k — коэффициент пропорциональности между силой и деформацией: $F = kDelta l$.
Этот коэффициент с помощью закона Гука выражается через модуль Юнга E и размеры стержня:
$sigma = frac{F}{S} = frac{Delta l}{l}E, F = SEfrac{Delta l}{l}$ и $F = kDelta l$,
отсюда
$k = frac{ES}{l}$. (7)
Максимальная деформация $Delta l$ равна тому расстоянию, на которое перемещаются частицы левого конца стержня за время $tau$/2 (рис. д). Так как эти частицы двигались со скоростью $v$, то
$Delta l = frac{vtau}{2}$. (8)
Приравниваем кинетическую энергию стержня до удара и потенциальную энергию деформации. Учитывая, что масса стержня $m = rho Sl$, и используя соотношения (7) и (8), получаем
$frac{rho Slv^2}{2} = frac{ES}{2l} cdot (frac{vtau}{2})^2$,
откуда для $tau$ снова получаем формулу (6). Это время столкновения обычно очень мало.
Например, для стального стержня (E = 2 x 1011 Па, $rho$ = 7,8 x 103 кг/м3) длиной 28 см вычисление по формуле (6) дает $tau$ = 10-4 с. Силу F, действующую на стенку во время удара, можно найти, подставляя скорость звука в стержне (5) в формулу (4):
$F = Svsqrt{rho E}$. (9)
Видно, что сила, действующая на стенку, пропорциональна скорости стержня перед ударом. Но для применимости приведенного решения необходимо, чтобы механическое напряжение стержня F/S не превосходило предела упругости материала, из которого изготовлен стержень. Например, для стали предел упругости (F/S)max = 4 x 108 Па. Поэтому максимальная скорость v стального стержня, при которой его соударение с преградой все еще можно считать упругим, оказывается согласно формуле (9) равной 10 м/с. Это соответствует скорости свободного падения тела с высоты всего лишь 5 м. Укажем для сравнения, что скорость звука в стали $u$ = 5000 м/с, т. е. $v << u$. Время столкновения стержня с неподвижной преградой (в отличие от силы) оказалось не зависящим от скорости стержня.
Этот результат, однако, не является универсальным, а связан со специфической формой рассматриваемого тела. Например, для упругого шара время столкновения со стенкой зависит от его скорости. Динамическое рассмотрение этого случая оказывается более сложным. Связано это с тем, что и площадь соприкосновения деформированного шара со стенкой, и действующая на шар сила в процессе столкновения не остаются постоянными.
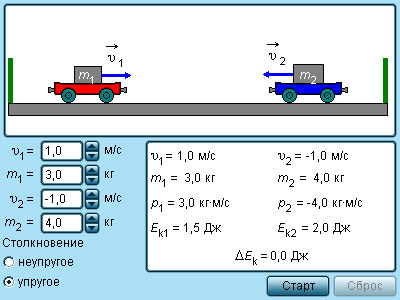
Упругое соударение
Соударение — это столкновение двух тел.
При соприкосновении тела обмениваются энергией и импульсом.
После соударения они двигаются со скоростями, которые отличаются по направлению и величине от их скоростей до столкновения.
При лобовом центральном соударении центры масс обоих тел двигаются вдоль одной линии.
Силы взаимодействия, возникающие при соударении, параллельны направлению движения.
Если применить к такой системе двух тел закон сохранения импульса, то полный импульс системы будет равен алгебраической сумме импульсов обоих тел.
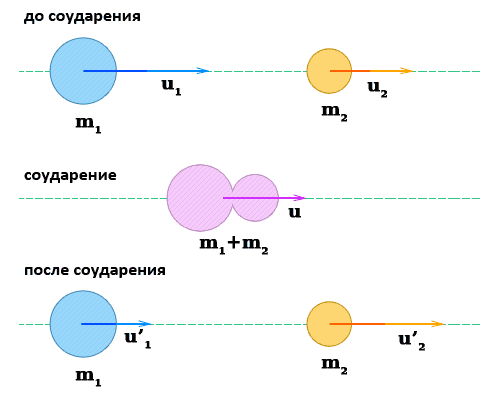
Упругое соударение
При упругом соударении на протяжении кратковременного соприкосновения тела двигаются с общей скоростью,
затем они разлетаются и продолжают двигаться с разными скоростями.
Если
| m1 | масса первого тела, | кг |
|---|---|---|
| m2 | масса второго тела, | кг |
| u1 | скорость первого тела до соударения, | метр/секунда |
| u2 | масса второго тела до соударения, | метр/секунда |
| u`1 | скорость первого тела после соударения, | метр/секунда |
| u`2 | масса второго тела после соударения, | метр/секунда |
то из закона сохранения импульса следует
[ m_1 u_1 + m_2 u_2 = m_1 u`_1 + m_2 u`_2 ]
или
[ m_1 (u_1 – u`_1) = m_2 (u`_2 – u_2) ]
Из закона сохранения энергии получаем
[ frac{m_1 u_1 ^2}{2} + frac{m_2 u_2 ^2}{2} = frac{m_1 u`_1 ^2}{2} + frac{m_2 u`_2 ^2}{2} ]
или
[ m_1 (u_1 ^2 – u`_1 ^2) = m_2 (u`_2 ^2 – u_2 ^2) ]
подставив формулу разность квадратов получим
[ m_1 (u_1 – u`_1)(u_1 + u`_1) = m_2 (u`_2 – u_2)(u`_2 + u_2) ]
воспользовавшись законом сохранения импульса, находим
[ u_1 + u`_1 = u`_2 + u_2 ]
Сумма скоростей до и после соударения одинакова при любом соударении тел.
Из формулы (6) следует
[ u`_2 = u`_1 + u_1 – u_2 ]
[ u`_1 = u`_2 + u_2 – u_1 ]
Подставив эти выражения в видоизмененный закон сохранения импульса, получим
[ m_1 (u_1 – u`_1) = m_2 (u`_1 + u_1 – u_2 – u`_2) ]
[ m_1 (u_1 – u_2 – u`_2 + u_1) = m_2 (u`_2 – u_2) ]
откуда, разрешив относительно u`1 и u`2 найдем
[ u`_1 = frac{ (m_1 – m_2) u_1 + 2 m_2 u_2 }{ m_1 + m_2 } ]
[ u`_2 = frac{ (m_2 – m_1) u_2 + 2 m_1 u_1 }{ m_1 + m_2 } ]
Упругое соударение, вычислить скорости тел после упругого соударения
Упругое соударение |
стр. 477 |
|---|
Заключение – дополнение к тексту
Мы применили закон сохранения импульса (одного из основных законов природы) к абсолютно неупругому и абсолютно упругому удару шаров.
При абсолютно неупругом ударе шары (тела) не сохраняют свою форму, то есть испытывают пластическую деформацию. К такому удару
можно отнести удар свинцовых шаров. При неупругом ударе не выполняется закон сохранения механической энергии, но выполняется закон сохранения полной энергии. При неупругом ударе механическая энергия полностью или частично переходит во внутреннюю энергию тел (тела нагреваются). В случае нецентрального (косого) удара тел их общий импульс и общая скорость после абсолютно неупругого удара находятся путём векторного сложения импульсов отдельных тел.
При абсолютно упругом ударе (сюда можно грубо приближённо отнести удар стальных шаров) выполняется и закон сохранения импульса, и закон сохранения механической энергии. При упругом ударе механическая энергия шаров частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела принимают первоначальную форму, отталкивая друг друга. Потенциальная энергия упругой деформации снова переходит в кинетическую энергию шаров. Шары приобретают скорости
направления и модули которых определяются законами сохранения полного импульса и полной энергии системы. Последний 3) частный случай говорит о том, что если лёгкий шарик испытает абсолютно упругий удар о неподвижную стенку, то он отскочит от неё без потери скорости. Пусть теперь шарик падает на неподвижную стенку под углом.
Тогда нормальная составляющая скорости шарика изменит своё направление на обратное, а по модулю останется прежней. Тангенциальная же составляющая скорости не изменится, поэтому угол падения будет равен углу отражения.
На рисунке вектора скорости падения и скорости отражения шарика перенесены в точку падения. Вектор изменения скорости направлен вверх перпендикулярно поверхности стенки. Такие же направления имеют импульсы шарика до удара и после удара о стенку, а вектор приращения импульса шарика
направлен по нормали от стенки.
В молекулярной физике происходит то же самое, когда молекулы газа ударяются о стенку сосуда. Проявляется это давлением газа на стенку сосуда.
Подумаем, что можно найти, если в условии задачи сказано, что шарик летит под прямым углом к движущейся навстречу стенке и между ними происходит упругий удар:
Сразу можно сказать, что скорость шарика относительно движущейся стенки равна
(см. занятие 12 на относительность движения). От стенки шарик отскочит со скоростью
относительно стенки, а относительно земли его скорость после удара
Далее можно найти импульс шара относительно земли до и после удара. Сможем найти изменение его импульса, его кинетическую энергию до и после удара.
Изменение кинетической энергии даст работу, совершённую силой упругости за время удара. Работу же можно выразить через произведение силы удара на перемещение стенки за время удара и найти силу удара.
Таким образом, через данные в условии задачи сможем охарактеризовать упругий удар между шаром и движущейся стенкой.
Абсолютно неупругий удар и абсолютно упругий удар – это предельные случаи кратковременного взаимодействия шаров (тел). При взаимодействии реальных тел имеют место и упругие, и неупругие деформации. Формула, связывающая скорости шаров до удара и после удара имеет вид:
коэффициент восстановления относительной скорости при ударе. В случае абсолютно неупругого удара он равен нулю; в случае абсолютно упругого удара он равен единице.
При ударе реальных тел этот коэффициент принимает промежуточные значения между нулём и единицей. Для стали этот коэффициент равен 0,56.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Занятие 23. Импульс системы тел. Центр масс системы
Следующая запись:Задачи 1 – 4 к занятиям 22 – 24
Первая запись на канале: Занятие 1. Физика. Механика. Кинематика